Grafische Lösung einer quadratischen Gleichung Festigung der Fähigkeit, Graphen verschiedener Funktionen zu erstellen; Die Fähigkeit zur grafischen Lösung quadratischer Gleichungen bilden. Brdsk 2009 Städtische Bildungseinrichtung - Ökonomisches Lyzeum Allgemeiner Unterricht zum Thema "Quadratische Funktion", Algebra-Lehrerin der 8. Klasse Fedoseeva T.M.

Zeichnen einer quadratischen Funktion Bestimmen Sie die Richtung der Zweige: a>0 Zweige nach oben; a 0 verzweigt sich nach oben; a"> 0 verzweigt nach oben; a"> 0 verzweigt nach oben; a" title="(!LANG:Plotten einer quadratischen Funktion Verzweigungsrichtung bestimmen: a>0 verzweigt nach oben; a"> title="Zeichnen einer quadratischen Funktion Bestimmen Sie die Richtung der Zweige: a>0 Zweige nach oben; a"> !}

0 Äste sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Finden Sie den Punkt "title="(!LANG: Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 mit dem Algorithmus erstellen: 1) a=1>0 die Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden" class="link_thumb"> 3 !} Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 unter Verwendung des Algorithmus erstellen: 1) a=1>0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Wir finden die Schnittpunkte mit der OX-Achse: x 1 \u003d -1; x 2 \u003d 3 1 Möglichkeit, die Gleichung x 2 -2x-3 \u003d 0 y x zu lösen. Lösen Sie die Gleichung x 2 +2x-3 \u003d 0 0 Äste sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Wir finden den Punkt "\u003e 0 die Zweige sind nach oben gerichtet; 2) die Spitze y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3) , (3; 0) und symmetrisch um die Achse x = 1 Wir bauen eine Parabel.Finden Sie die Schnittpunkte mit der OX-Achse: x 1 \u003d -1; x 2 \u003d 3 1 Weg zur Lösung der Gleichung x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Lösen Sie die Gleichung x 2 + 2x-3 \u003d 0 "\u003e 0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Finden Sie den Punkt "title="(!LANG: Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 mit dem Algorithmus erstellen: 1) a=1>0 die Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden"> title="Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 unter Verwendung des Algorithmus erstellen: 1) a=1>0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden"> !}

Der zweite Weg: a). Teilen wir die Gleichung x 2 -2x-3=0 in Teile x 2 = 2x+3 auf. Schreiben wir zwei Funktionen y= x 2 ; y \u003d 2x + 3 Wir erstellen Graphen dieser Funktionen in einem Koordinatensystem. Die Abszissen der Schnittpunkte sind die Wurzeln der Gleichung. 0 1 x y Lösen Sie die Gleichung x 2 +2x-3=0

Der dritte Weg: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Wir erstellen Graphen dieser Funktionen in einem Koordinatensystem. Die Abszissen der Schnittpunkte sind die Wurzeln der Gleichung. 0 1 x y Lösen Sie die Gleichung x 2 +2x-3=0

Grafische Lösung von Gleichungen

Blütezeit, 2009

Einführung

Die Notwendigkeit, quadratische Gleichungen in der Antike zu lösen, wurde durch die Notwendigkeit verursacht, Probleme im Zusammenhang mit der Suche nach Landgebieten und Erdarbeiten militärischer Natur sowie der Entwicklung der Astronomie und Mathematik selbst zu lösen. Die Babylonier wussten etwa 2000 v. Chr., wie man quadratische Gleichungen löst. Die in den babylonischen Texten angegebene Regel zur Lösung dieser Gleichungen stimmt im Wesentlichen mit den modernen überein, aber es ist nicht bekannt, wie die Babylonier zu dieser Regel kamen.

Formeln zur Lösung quadratischer Gleichungen in Europa wurden erstmals im Buch des Abakus dargelegt, das 1202 vom italienischen Mathematiker Leonardo Fibonacci geschrieben wurde. Sein Buch trug zur Verbreitung des algebraischen Wissens nicht nur in Italien, sondern auch in Deutschland, Frankreich und anderen europäischen Ländern bei.

Aber die allgemeine Regel zum Lösen quadratischer Gleichungen mit allen möglichen Kombinationen der Koeffizienten b und c wurde in Europa erst 1544 von M. Stiefel formuliert.

1591 Francois Viet Formeln zum Lösen quadratischer Gleichungen eingeführt.

Einige Arten von quadratischen Gleichungen konnten im alten Babylon gelöst werden.

Diophantos von Alexandria und Euklid , Al-Chwarizmi und Omar Khayyam gelöste Gleichungen auf geometrische und grafische Weise.

In der 7. Klasse haben wir Funktionen studiert y \u003d C, y= kx , y = kx + m , y = x 2 ,y = - x 2 , in der 8. Klasse - y = √ x , y = |x |, y= Axt 2 + bx + c , y = k / x. Im Algebra-Lehrbuch der 9. Klasse sah ich Funktionen, die mir noch nicht bekannt waren: y= x 3 , y= x 4 ,y= x 2 n , y= x - 2 n , y= 3 √x , ( x – a ) 2 + (ja - b ) 2 = r 2 und andere. Es gibt Regeln zum Erstellen von Graphen dieser Funktionen. Ich habe mich gefragt, ob es andere Funktionen gibt, die diesen Regeln gehorchen.

Meine Aufgabe ist es, Funktionsgraphen zu untersuchen und Gleichungen grafisch zu lösen.

1. Was sind die Funktionen

Der Graph einer Funktion ist die Menge aller Punkte der Koordinatenebene, deren Abszissen gleich den Werten der Argumente sind und deren Ordinaten gleich den entsprechenden Werten der Funktion sind.

Die lineare Funktion ist durch die Gleichung gegeben y= kx + b, wo k und b- einige Zahlen. Der Graph dieser Funktion ist eine Gerade.

Umgekehrte proportionale Funktion y= k / x, wobei k¹ 0 ist. Der Graph dieser Funktion wird Hyperbel genannt.

Funktion ( x – a ) 2 + (y – b ) 2 = r 2 , wo a , b und r- einige Zahlen. Der Graph dieser Funktion ist ein Kreis mit Radius r, dessen Mittelpunkt der Punkt A ist ( a , b).

quadratische Funktion j = Axt 2 + bx + c wo a, b , Mit- einige Zahlen und a¹ 0. Der Graph dieser Funktion ist eine Parabel.

Die gleichung ja 2 ( a – x ) = x 2 ( a + x ) . Der Graph dieser Gleichung ist eine Kurve, die als Strophoid bezeichnet wird.

Die gleichung ( x 2 + j 2 ) 2 = a ( x 2 – j 2 ) . Der Graph dieser Gleichung heißt Bernoulli-Lemniskate.

Die gleichung. Der Graph dieser Gleichung wird als Astroid bezeichnet.

Kurve (x 2 y 2 - 2 a x) 2 \u003d 4 ein 2 (x 2 + y 2). Diese Kurve wird als Niere bezeichnet.

Funktionen: y= x 3 - kubische Parabel, y= x 4 , y = 1/ x 2 .

2. Das Konzept einer Gleichung, ihre grafische Lösung

Die gleichung ist ein Ausdruck, der eine Variable enthält.

löse die Gleichung- das bedeutet, alle seine Wurzeln zu finden oder zu beweisen, dass sie nicht existieren.

Wurzel der Gleichung ist eine Zahl, die, wenn sie in die Gleichung eingesetzt wird, die korrekte numerische Gleichheit erzeugt.

Gleichungen grafisch lösen ermöglicht es Ihnen, den genauen oder ungefähren Wert der Wurzeln zu finden, ermöglicht es Ihnen, die Anzahl der Wurzeln der Gleichung zu finden.

Beim Zeichnen von Graphen und beim Lösen von Gleichungen werden die Eigenschaften einer Funktion verwendet, daher wird die Methode oft als Funktionsgrafik bezeichnet.

Um die Gleichung zu lösen, „teilen“ wir sie in zwei Teile, führen zwei Funktionen ein, erstellen ihre Graphen und finden die Koordinaten der Schnittpunkte der Graphen. Die Abszissen dieser Punkte sind die Wurzeln der Gleichung.

3. Algorithmus zum Erstellen eines Graphen einer Funktion

Den Graphen der Funktion kennen y= f ( x ) , können Sie Funktionen zeichnen y= f ( x + m ) ,y= f ( x )+ l und y= f ( x + m )+ l. Alle diese Graphen werden aus dem Graphen der Funktion erhalten y= f ( x ) unter Verwendung der parallelen Übersetzungstransformation: on │ m │ Skalierungseinheiten nach rechts oder links entlang der x-Achse und weiter │ l │ Einheiten entlang der Achse nach oben oder unten skalieren j .

4. Graphische Lösung der quadratischen Gleichung

Am Beispiel einer quadratischen Funktion betrachten wir eine grafische Lösung einer quadratischen Gleichung. Der Graph einer quadratischen Funktion ist eine Parabel.

Was wussten die alten Griechen über die Parabel?

Die moderne mathematische Symbolik entstand im 16. Jahrhundert.

Die antiken griechischen Mathematiker hatten weder die Koordinatenmethode noch den Begriff einer Funktion. Die Eigenschaften der Parabel wurden jedoch von ihnen eingehend untersucht. Der Erfindungsreichtum der antiken Mathematiker ist einfach erstaunlich, denn sie konnten nur Zeichnungen und verbale Beschreibungen von Abhängigkeiten verwenden.

Am vollständigsten erforscht die Parabel, Hyperbel und Ellipse Apollonius von Perge, der im 3. Jahrhundert v. Chr. lebte. Er gab diesen Kurven auch Namen und gab an, welche Bedingungen die auf einer bestimmten Kurve liegenden Punkte erfüllen (schließlich gab es keine Formeln!).

Es gibt einen Algorithmus zum Konstruieren einer Parabel:

Wir finden die Koordinaten des Scheitelpunkts der Parabel A (x 0; y 0): x 0 =- b /2 a ;

Y 0 \u003d Axt ungefähr 2 + in 0 + c;

Wir finden die Symmetrieachse der Parabel (Gerade x \u003d x 0);

Erstellen einer Wertetabelle für Gebäudekontrollpunkte;

Wir konstruieren die erhaltenen Punkte und konstruieren dazu bezüglich der Symmetrieachse symmetrische Punkte.

1. Lassen Sie uns eine Parabel nach dem Algorithmus bauen j = x 2 – 2 x – 3 . Abszissen der Schnittpunkte mit der Achse x und sind die Wurzeln der quadratischen Gleichung x 2 – 2 x – 3 = 0.

Es gibt fünf Möglichkeiten, diese Gleichung grafisch zu lösen.

2. Zerlegen wir die Gleichung in zwei Funktionen: j = x 2 und j = 2 x + 3

3. Teilen wir die Gleichung in zwei Funktionen auf: j = x 2 –3 und j =2 x. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Parabel mit der Geraden.

4. Transformiere die Gleichung x 2 – 2 x – 3 = 0 indem Sie das volle Quadrat auf der Funktion auswählen: j = ( x –1) 2 und j =4. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Parabel mit der Geraden.

5. Wir dividieren Term für Term beide Teile der Gleichung x 2 – 2 x – 3 = 0 auf der x, wir bekommen x – 2 – 3/ x = 0 Lassen Sie uns diese Gleichung in zwei Funktionen aufteilen: j = x – 2, j = 3/ x . Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Geraden und der Hyperbel.

5. Graphische Lösung von Gradgleichungen n

Beispiel 1 löse die Gleichung x 5 = 3 – 2 x .

j = x 5 , j = 3 – 2 x .

Antworten: x = 1.

Beispiel 2 löse die Gleichung 3 √ x = 10 – x .

Die Wurzeln dieser Gleichung ist die Abszisse des Schnittpunkts der Graphen zweier Funktionen: j = 3 √ x , j = 10 – x .

Antworten: x=8.

Fazit

Betrachten der Funktionsgraphen: y= Axt 2 + bx + c , y = k / x , y = √ x , y = |x |, y= x 3 , y= x 4 ,y= 3 √x , Mir ist aufgefallen, dass alle diese Graphen nach der Regel der Parallelverschiebung relativ zu den Achsen aufgebaut sind x und j .

Am Beispiel der Lösung einer quadratischen Gleichung können wir schlussfolgern, dass die grafische Methode auch auf Gleichungen vom Grad n anwendbar ist.

Grafische Methoden zum Lösen von Gleichungen sind schön und verständlich, aber sie geben keine 100%ige Garantie für das Lösen einer Gleichung. Die Abszissen der Schnittpunkte der Graphen können ungefähr sein.

In der 9. Klasse und in den Oberstufenklassen werde ich noch andere Funktionen kennenlernen. Ich bin daran interessiert zu wissen, ob diese Funktionen beim Zeichnen ihrer Diagramme den Regeln der parallelen Übersetzung gehorchen.

Im nächsten Jahr möchte ich mich auch mit Fragen der grafischen Lösung von Gleichungssystemen und Ungleichungen befassen.

Literatur

1. Algebra. 7. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

2. Algebra. 8. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

3. Algebra. Klasse 9 Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

4. Glaser G.I. Geschichte der Mathematik in der Schule. Klassen VII-VIII. – M.: Aufklärung, 1982.

5. Zeitschrift Mathematik №5 2009; Nr. 8 2007; Nr. 23 2008.

6. Graphische Lösung von Gleichungen Internetseiten: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Grafische Lösung von Gleichungen

Blütezeit, 2009

Einführung

Die Notwendigkeit, quadratische Gleichungen in der Antike zu lösen, wurde durch die Notwendigkeit verursacht, Probleme im Zusammenhang mit der Suche nach Landgebieten und Erdarbeiten militärischer Natur sowie der Entwicklung der Astronomie und Mathematik selbst zu lösen. Die Babylonier wussten etwa 2000 v. Chr., wie man quadratische Gleichungen löst. Die in den babylonischen Texten angegebene Regel zur Lösung dieser Gleichungen stimmt im Wesentlichen mit den modernen überein, aber es ist nicht bekannt, wie die Babylonier zu dieser Regel kamen.

Formeln zur Lösung quadratischer Gleichungen in Europa wurden erstmals im Buch des Abakus dargelegt, das 1202 vom italienischen Mathematiker Leonardo Fibonacci geschrieben wurde. Sein Buch trug zur Verbreitung des algebraischen Wissens nicht nur in Italien, sondern auch in Deutschland, Frankreich und anderen europäischen Ländern bei.

Aber die allgemeine Regel zum Lösen quadratischer Gleichungen mit allen möglichen Kombinationen der Koeffizienten b und c wurde in Europa erst 1544 von M. Stiefel formuliert.

1591 Francois Viet Formeln zum Lösen quadratischer Gleichungen eingeführt.

Einige Arten von quadratischen Gleichungen konnten im alten Babylon gelöst werden.

Diophantos von Alexandria und Euklid, Al-Chwarizmi und Omar Khayyam gelöste Gleichungen auf geometrische und grafische Weise.

In der 7. Klasse haben wir Funktionen studiert y \u003d C, y=kx, y =kx+ m, y =x 2,y = -x 2, in der 8. Klasse - y = √x, y =|x|, y=Axt2 + bx+ c, y =k/ x. Im Algebra-Lehrbuch der 9. Klasse sah ich Funktionen, die mir noch nicht bekannt waren: y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– a) 2 + (ja -b) 2 = r 2 und andere. Es gibt Regeln zum Erstellen von Graphen dieser Funktionen. Ich habe mich gefragt, ob es andere Funktionen gibt, die diesen Regeln gehorchen.

Meine Aufgabe ist es, Funktionsgraphen zu untersuchen und Gleichungen grafisch zu lösen.

1. Was sind die Funktionen

Der Graph einer Funktion ist die Menge aller Punkte der Koordinatenebene, deren Abszissen gleich den Werten der Argumente sind und deren Ordinaten gleich den entsprechenden Werten der Funktion sind.

Die lineare Funktion ist durch die Gleichung gegeben y=kx+ b, wo k und b- einige Zahlen. Der Graph dieser Funktion ist eine Gerade.

Umgekehrte proportionale Funktion y=k/ x, wobei k ¹ 0. Der Graph dieser Funktion wird Hyperbel genannt.

Funktion (x– a) 2 + (j -b) 2 = r2 , wo a, b und r- einige Zahlen. Der Graph dieser Funktion ist ein Kreis mit Radius r, dessen Mittelpunkt der Punkt A ist ( a, b).

quadratische Funktion j= Axt2 + bx+ c wo a,b, Mit- einige Zahlen und a¹ 0. Der Graph dieser Funktion ist eine Parabel.

Die gleichung bei2 (a– x) = x2 (a+ x) . Der Graph dieser Gleichung ist eine Kurve, die als Strophoid bezeichnet wird.

/>Gleichung (x2 + j2 ) 2 = a(x2 – j2 ) . Der Graph dieser Gleichung heißt Bernoulli-Lemniskate.

Die gleichung. Der Graph dieser Gleichung wird als Astroid bezeichnet.

Kurve (x2 j2 – 2 x)2 =4 ein2 (x2 +y2 ) . Diese Kurve wird als Niere bezeichnet.

Funktionen: y=x 3 - kubische Parabel, y=x 4, y = 1/x 2.

2. Das Konzept einer Gleichung, ihre grafische Lösung

Die gleichung ist ein Ausdruck, der eine Variable enthält.

löse die Gleichung- das bedeutet, alle seine Wurzeln zu finden oder zu beweisen, dass sie nicht existieren.

Wurzel der Gleichung ist eine Zahl, die, wenn sie in die Gleichung eingesetzt wird, die korrekte numerische Gleichheit erzeugt.

Gleichungen grafisch lösen ermöglicht es Ihnen, den genauen oder ungefähren Wert der Wurzeln zu finden, ermöglicht es Ihnen, die Anzahl der Wurzeln der Gleichung zu finden.

Beim Zeichnen von Graphen und beim Lösen von Gleichungen werden die Eigenschaften einer Funktion verwendet, daher wird die Methode oft als Funktionsgrafik bezeichnet.

Um die Gleichung zu lösen, „teilen“ wir sie in zwei Teile, führen zwei Funktionen ein, erstellen ihre Graphen und finden die Koordinaten der Schnittpunkte der Graphen. Die Abszissen dieser Punkte sind die Wurzeln der Gleichung.

3. Algorithmus zum Erstellen eines Graphen einer Funktion

Den Graphen der Funktion kennen y=f(x) , können Sie Funktionen zeichnen y=f(x+ m) ,y=f(x)+ l und y=f(x+ m)+ l. Alle diese Graphen werden aus dem Graphen der Funktion erhalten y=f(x) unter Verwendung der parallelen Übersetzungstransformation: on │ m│ Skalierungseinheiten nach rechts oder links entlang der x-Achse und weiter │ l│ Einheiten entlang der Achse nach oben oder unten skalieren j.

4. Graphische Lösung der quadratischen Gleichung

Am Beispiel einer quadratischen Funktion betrachten wir eine grafische Lösung einer quadratischen Gleichung. Der Graph einer quadratischen Funktion ist eine Parabel.

Was wussten die alten Griechen über die Parabel?

Die moderne mathematische Symbolik entstand im 16. Jahrhundert.

Die antiken griechischen Mathematiker hatten weder die Koordinatenmethode noch den Begriff einer Funktion. Die Eigenschaften der Parabel wurden jedoch von ihnen eingehend untersucht. Der Erfindungsreichtum der antiken Mathematiker ist einfach erstaunlich, denn sie konnten nur Zeichnungen und verbale Beschreibungen von Abhängigkeiten verwenden.

Am vollständigsten erforscht die Parabel, Hyperbel und Ellipse Apollonius von Perge, der im 3. Jahrhundert v. Chr. lebte. Er gab diesen Kurven auch Namen und gab an, welche Bedingungen die auf einer bestimmten Kurve liegenden Punkte erfüllen (schließlich gab es keine Formeln!).

Es gibt einen Algorithmus zum Konstruieren einer Parabel:

Finden Sie die Koordinaten des Scheitelpunkts der Parabel A (x0; y0): X=- b/2 a;

y0=aho2+in0+s;

Finden Sie die Symmetrieachse der Parabel (Gerade x=x0);

SEITENUMBRUCH--

Erstellen einer Wertetabelle für Gebäudekontrollpunkte;

Wir konstruieren die erhaltenen Punkte und konstruieren dazu bezüglich der Symmetrieachse symmetrische Punkte.

1. Lassen Sie uns eine Parabel nach dem Algorithmus bauen j= x2 – 2 x– 3 . Abszissen der Schnittpunkte mit der Achse x und sind die Wurzeln der quadratischen Gleichung x2 – 2 x– 3 = 0.

Es gibt fünf Möglichkeiten, diese Gleichung grafisch zu lösen.

2. Zerlegen wir die Gleichung in zwei Funktionen: j= x2 und j= 2 x+ 3

3. Teilen wir die Gleichung in zwei Funktionen auf: j= x2 –3 und j=2 x. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Parabel mit der Geraden.

4. Transformiere die Gleichung x2 – 2 x– 3 = 0 indem Sie das volle Quadrat auf der Funktion auswählen: j= (x–1) 2 und j=4. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Parabel mit der Geraden.

5. Wir dividieren Term für Term beide Teile der Gleichung x2 – 2 x– 3 = 0 auf der x, wir bekommen x– 2 – 3/ x= 0 Lassen Sie uns diese Gleichung in zwei Funktionen aufteilen: j= x– 2, j= 3/ x. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Geraden und der Hyperbel.

5. Graphische Lösung von Gradgleichungenn

Beispiel 1 löse die Gleichung x5 = 3 – 2 x.

j= x5 , j= 3 – 2 x.

Antworten: x = 1.

Beispiel 2 löse die Gleichung 3 √ x= 10 – x.

Die Wurzeln dieser Gleichung ist die Abszisse des Schnittpunkts der Graphen zweier Funktionen: j= 3 √ x, j= 10 – x.

Antworten: x=8.

Fazit

Betrachten der Funktionsgraphen: y=Axt2 + bx+ c, y =k/ x, y = √x, y =|x|, y=x 3, y=x 4,y= 3√x, Mir ist aufgefallen, dass alle diese Graphen nach der Regel der Parallelverschiebung relativ zu den Achsen aufgebaut sind x und j.

Am Beispiel der Lösung einer quadratischen Gleichung können wir schlussfolgern, dass die grafische Methode auch auf Gleichungen vom Grad n anwendbar ist.

Grafische Methoden zum Lösen von Gleichungen sind schön und verständlich, aber sie geben keine 100%ige Garantie für das Lösen einer Gleichung. Die Abszissen der Schnittpunkte der Graphen können ungefähr sein.

In der 9. Klasse und in den Oberstufenklassen werde ich noch andere Funktionen kennenlernen. Ich bin daran interessiert zu wissen, ob diese Funktionen beim Zeichnen ihrer Diagramme den Regeln der parallelen Übersetzung gehorchen.

Im nächsten Jahr möchte ich mich auch mit Fragen der grafischen Lösung von Gleichungssystemen und Ungleichungen befassen.

Literatur

1. Algebra. 7. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

2. Algebra. 8. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

3. Algebra. Klasse 9 Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

4. Glaser G.I. Geschichte der Mathematik in der Schule. Klassen VII-VIII. – M.: Aufklärung, 1982.

5. Zeitschrift Mathematik №5 2009; Nr. 8 2007; Nr. 23 2008.

6. Graphische Lösung von Gleichungen Internetseiten: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

In dieser Videolektion wird das Thema „Funktion y \u003d x 2. Grafische Lösung von Gleichungen. In dieser Lektion können sich die Schüler mit einer neuen Methode zum Lösen von Gleichungen vertraut machen - grafisch, die auf dem Wissen über die Eigenschaften von Funktionsgraphen basiert. Der Lehrer zeigt Ihnen, wie Sie die Funktion y=x 2 grafisch lösen.

Thema:Funktion

Lektion:Funktion. Grafische Lösung von Gleichungen

Die grafische Lösung von Gleichungen basiert auf der Kenntnis von Funktionsgraphen und deren Eigenschaften. Wir listen die Funktionen auf, deren Graphen wir kennen:

1) ist der Graph eine gerade Linie parallel zur x-Achse, die durch einen Punkt auf der y-Achse verläuft. Betrachten Sie ein Beispiel: y=1:

Für verschiedene Werte erhalten wir eine Schar von Geraden parallel zur x-Achse.

2) Direkte Proportionalitätsfunktion Der Graph dieser Funktion ist eine Gerade, die durch den Ursprung geht. Betrachten Sie ein Beispiel:

Wir haben diese Diagramme bereits in früheren Lektionen erstellt. Denken Sie daran, dass Sie zum Erstellen jeder Linie einen Punkt auswählen müssen, der sie erfüllt, und den Ursprung als zweiten Punkt nehmen müssen.

Erinnern Sie sich an die Rolle des Koeffizienten k: Mit zunehmender Funktion wird der Winkel zwischen der Geraden und der positiven Richtung der x-Achse spitz; bei abnehmender Funktion ist der Winkel zwischen der Geraden und der positiven Richtung der x-Achse stumpf. Außerdem besteht zwischen zwei Parametern k gleichen Vorzeichens folgender Zusammenhang: Bei positivem k steigt die Funktion umso schneller an, je größer er ist, und bei negativen nimmt die Funktion für große Werte von k modulo schneller ab.

3) Lineare Funktion. Wenn - erhalten wir den Schnittpunkt mit der y-Achse und alle Linien dieser Art gehen durch den Punkt (0; m). Außerdem wird mit zunehmender Funktion der Winkel zwischen der Linie und der positiven Richtung der x-Achse spitz; bei abnehmender Funktion ist der Winkel zwischen der Geraden und der positiven Richtung der x-Achse stumpf. Und natürlich beeinflusst der Wert von k die Änderungsrate des Funktionswerts.

vier). Der Graph dieser Funktion ist eine Parabel.

Betrachten Sie Beispiele.

Beispiel 1 - Lösen Sie die Gleichung grafisch:

Wir kennen keine Funktionen dieser Art, also müssen wir die gegebene Gleichung umformen, um mit bekannten Funktionen zu arbeiten:

Wir haben bekannte Funktionen in beiden Teilen der Gleichung:

Lassen Sie uns Graphen von Funktionen erstellen:

Graphen haben zwei Schnittpunkte: (-1; 1); (2; 4)

Lassen Sie uns überprüfen, ob die Lösung richtig gefunden wurde, ersetzen Sie die Koordinaten in der Gleichung:

Der erste Punkt wird richtig gefunden.

, , , , , ,

Auch der zweite Punkt wird korrekt gefunden.

Die Lösungen der Gleichung sind also und

Wir gehen ähnlich wie im vorherigen Beispiel vor: Wir transformieren die gegebene Gleichung in die uns bekannten Funktionen, zeichnen ihre Graphen auf, finden die Schnittströme und geben von hier aus die Lösungen an.

Wir erhalten zwei Funktionen:

Lassen Sie uns Diagramme erstellen:

Diese Graphen haben keine Schnittpunkte, was bedeutet, dass die gegebene Gleichung keine Lösungen hat

Fazit: In dieser Lektion haben wir die uns bekannten Funktionen und ihre Graphen überprüft, uns an ihre Eigenschaften erinnert und einen grafischen Weg zum Lösen von Gleichungen in Betracht gezogen.

1. Dorofeev G. V., Suvorova S. B., Bunimovich E. A. ua Algebra 7. 6. Auflage. M.: Aufklärung. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. ua Algebra 7 .M .: Bildung. 2006

Aufgabe 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al., Algebra 7, Nr. 494, S. 110;

Aufgabe 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. ua Algebra 7, Nr. 495, Punkt 110;

Aufgabe 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al., Algebra 7, Nr. 496, S. 110;

DAGESTAN INSTITUT FÜR BERUFLICHE ENTWICKLUNG

PÄDAGOGISCHES PERSONAL

ABTEILUNG FÜR KÖRPER- UND MATHEMATISCHE ERZIEHUNG UND IKT

Projekt

zum Thema:

« Konstruktion und p Reformen

Funktionsgraphen

in der Schulmathematik »

Rabadanova P.A.

Mathematiklehrer

MBOU "Kochubey-Sekundarschule"

Bezirk Tarumovsky

2015

1. Einleitung………………………………………………………………….….3

2. Kapitel ich. Literaturrecherche zum Thema des Projekts ………………………….….5

3. Kapitel II. Empirischer Teil:

3.1. Grundlegende Methoden zum Konvertieren von Funktionsgraphen……….….7

3.2. Einen geraden Plottenundungerade Funktionen …………….. 10

3.3. Zeichnen einer Umkehrfunktion ………………………... 11

3.4. Verformung (Kompression und Spannung) von Graphen………………….12

3.5. Kombination von Übertragung, Reflexion und Verformung………………......13

4. Aufgaben zur selbstständigen Lösung………………………..…...14

5. Schlussfolgerung ……………………………………………………………………15

6. Schlussfolgerungen…………………………………………………………..………17

EINLEITUNG

Die Transformation von Funktionsgraphen ist eines der grundlegenden mathematischen Konzepte, die in direktem Zusammenhang mit praktischen Aktivitäten stehen. Die Graphen spiegeln die Variabilität und Dynamik der realen Welt, die gegenseitigen Beziehungen realer Objekte und Phänomene wider.

Die Funktionslinie ist das grundlegende Thema der Grundprüfung und der Einheitlichen Staatsprüfung.Auch viele mathematische Konzepte werden durch graphische Methoden berücksichtigt. Zum Beispiel zuquadratischdie Funktion wird in engem Zusammenhang mit quadratischen Gleichungen und Ungleichungen eingeführt und untersucht.Daraus folgt dasSchülern beizubringen, wie man Graphen einer Funktion erstellt und transformiert, ist eine der Hauptaufgaben des Mathematikunterrichts in der Schule.

Das Studium der Funktion ermöglicht es, ungefähr zu findenDefinitionsbereich und Umfang der Funktion, GeltungsbereichSinkende oder steigende Raten, Asymptoten, IntervalleZeichenkonstanz usw. Um jedoch einen Graphen zu erstellenkov können viele Funktionen seinverwenden Sie eine Reihe von Methodenmach es einfacherGebäude. Studierende sollten daher die Kompetenz besitzen, Graphen nach methodischen Schemata zu erstellen.

Das obige definiertRelevanz Forschungsthemen.

Studienobjekt ist die Untersuchung der Transformation funktionaler Liniengraphen in der Schulmathematik.

Gegenstand der Studie - der Prozess der Konstruktion und Transformation von Funktionsgraphen in einer weiterführenden Schule.

Zweck der Studie: Bildung - besteht darin, ein methodologisches Schema zum Konstruieren und Konvertieren von Graphen einer Funktion zu identifizieren;Entwicklung - Entwicklung von abstraktem, algorithmischem, logischem Denken, räumlichem Vorstellungsvermögen;lehrreich - Bildung der grafischen Kultur von Schulkindern, Bildung geistiger Fähigkeiten.

Die Tore führten zu folgender EntscheidungAufgaben:

1. Analysieren Sie die pädagogischen und methodologischen Aspekte des untersuchten Problems.

2. Identifizieren Sie methodische SchemataTransformation von Funktionsgraphen im Schulfach Mathematik.

3. Wählen Sie die effektivsten Methoden und Mittel ausKonstruktion und Transformation von Funktionsgraphen in einer weiterführenden SchuleBeitrag zu: sinnvoller Assimilation von Lehrmaterial; Steigerung der kognitiven Aktivität von Schülern; Entwicklung ihrer kreativen Fähigkeiten.

HYPOTHESE Forschung: die Bildung von grafischen Fähigkeiten im Prozess des Studiums der Funktionen und der Ausbildung der grafischen Kultur der Studenten effektiv, wenn die Studierenden ein methodisches Schema zur Konstruktion und Transformation von Funktionsgraphen im Schulmathematikunterricht haben.

KAPITEL ich . ÜBERPRÜFUNG DER LITERATUR ZUM THEMA DES PROJEKTS.

In Vorbereitung auf das Projekt haben wir folgende Literatur studiert:

Sivashinsky, I. Kh. Sätze und Probleme in der Algebra, Elementarfunktionen - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funktionen und Graphen (Grundtechniken) - M., 1985. - 120 s

V. Z. Zaitsev, V. V. Ryschkow, M.I. Scanavi. Elementare Mathematik - M., 2010 (Neuauflage). - 590 S.

Kuzmin, M. K. Konstruktion eines Funktionsgraphen - J. Mathematik in der Schule. - 2003. - Nr. 5. - S. 61-62.

Shilov G.E. Wie erstellt man Diagramme? -M., 1982.

Isaak Tanatar. Geometrische Transformationen von Funktionsgraphen - MTsNMO, 2012

BEIEs wird darauf hingewiesen, dass die Fähigkeit, das Verhalten einer Funktion auf einer bestimmten Menge unter Verwendung eines Graphen zu „lesen“, nicht nur im Verlauf der Mathematik, sondern auch bei jeder praktischen menschlichen Tätigkeit verwendet wird, bei der er sich mit bestimmten grafischen Darstellungen von beschäftigen muss Abhängigkeiten. Daher sollten die Schüler in der Lage sein, einige ihrer Eigenschaften aus dem Graphen einer Funktion zu bestimmen.

Das theoretische Material für die Transformation von Graphen ist streng angegeben in. Die Technik wird von Illustrationen mit Zeichnungen, Beispielen unterschiedlicher Komplexität und deren Lösungen begleitet, die es ermöglichen, das Wissen zu vertiefen und komplexe Funktionen darzustellen.

Stellt einen elektronischen Lehrgang dar, dessen Umfang und Inhalt den Anforderungen an einen Mathematikunterricht an Gymnasien entspricht. Das theoretische Material wird durch grafische Animationsillustrationen unterstützt, die eine visuelle Darstellung des zu untersuchenden Themas geben. Der Kurs umfasst drei Module: ein theoretisches Materialstudienmodul, ein Selbstprüfungsmodul und ein Wissenskontrollmodul.

Für den empirischen Teil des Projekts wurden aus , , methodischen Charting-Schemata Beispiele für selbstständiges Arbeiten herangezogen.

Schlussfolgerungen zu Kapitel 1

Das Studium der pädagogischen und methodischen Literatur ermöglichte:

1. Identifizieren Sie das methodische SchemaStudium, Konstruktion und Transformation von Funktionsgraphen im Schulmathematikkurs.

2. Wählen Sie die effektivsten Methoden und Mittel ausKonstruktion und Transformation von Funktionsgraphen in der Schulmathematik,beitragen:

sinnvolle Aneignung von Unterrichtsmaterial;

Steigerung der kognitiven Aktivität von Schülern;

Entwicklung ihrer kreativen Fähigkeiten.

3. Zeigen Sie das Die Funktionslinie hat einen erheblichen Einfluss auf das Studium verschiedener Konzepte in der Mathematik.

Kapitel 2. Empirischer Teil

In diesem Kapitel werden wir die wichtigsten Methoden zum Transformieren von Funktionsgraphen betrachten und methodologische Schemata zum Konstruieren verschiedener Kombinationen von Graphen für verschiedene Funktionen geben.

2.1. GRUNDLEGENDE TECHNIKEN ZUR KONVERTIERUNG VON FUNKTIONSGRAPHEN

Translation entlang der y-Achse

f ( x ) f ( x )+ b .

ZumZeichnen einer Funktionj = f( x) + bverfolgensie:

1. Erstellen Sie einen Funktionsgraphenj= f( x)

2. Achse bewegenAbszisse auf| b| Einheiten aufb>0 oder bei| b| Essenniederwerfen beib < 0. Erhalten im neuen SystemDinat-Graph ist der Graph einer Funktionj = f( x) + b.

2. Übertragen eine lange Achsen Abszisse

f ( x ) f ( x + a ) .

j = f( x+ a) verfolgensie:

3. Zeichnen einer Funktion des Formulars j = f (- x )

f (x ) f (- x ).

Um eine Funktion zu plottenj = f( - x) folgt:

Zeichnen Sie eine Funktionj = f( x)

spiegeln es zurückrelativ zur y-Achse

der resultierende Graph istFunktionsgraphj = f( - X).

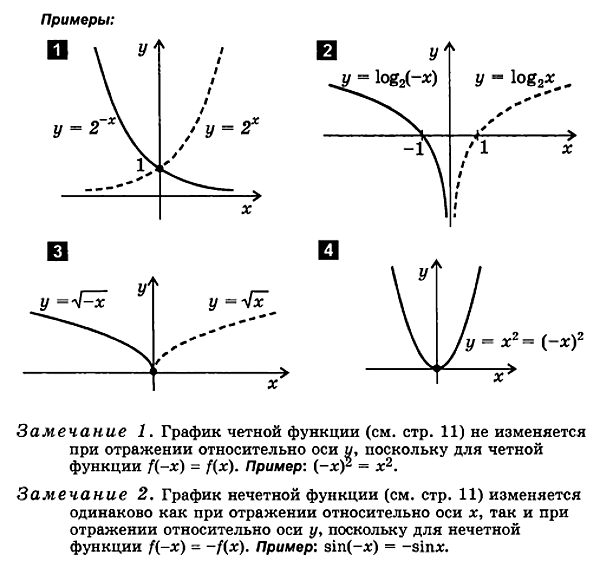
4. Zeichnen einer Funktion des Formulars y= - f ( x )

f ( x ) - f ( x )

- f( x) folgt:

Zeichnen Sie eine Funktionj= f( x)

an der x-Achse spiegeln

2.2. Einen geraden Plotten und seltsame Eigenschaften

Beim PlottenFür gerade und ungerade Funktionen ist es praktisch, die folgenden Eigenschaften zu verwenden:

1. Graph einer geraden Funktion simmetricen relativ zur y-Achse.

2. Der Graph einer ungeraden Funktion ist symmetrisch zum Ursprung.

Um Graphen einer geraden und ungeraden Funktion zu erstellen, reicht es aus, nur den rechten Zweig des Graphen für positive Werte des Arguments zu zeichnen. Der linke Zweig wird symmetrisch um den Ursprung für eine ungerade Funktion und um die y-Achse für eine gerade Funktion abgeschlossen.

Um eine gerade Funktion zu zeichnen j = f ( x ) nach Duett:

Konstruieren Sie einen Zweig des Graphen dieser Funktion nur inBereich positiver Werte des Arguments x≥0.

ÖVerfolgen Sie diesen Zweig um die y-Achse

Um eine ungerade Funktion zu zeichnen j = f ( x ) folgt:

Erstellen Sie einen Graphenzweig dieser Funktion nur inBereich positiver Werte des Arguments (х≥0).

ÖVerfolgen Sie diesen Zweig in Bezug auf den Ursprungin den Bereich negativer x-Werte.

2.3. Plotten der Umkehrfunktion

Wie bereits erwähnt, die direkten und umgekehrten Funktionenzeigen die gleiche Beziehung zwischen Variablenx und y, mit dem einzigen Unterschied, dass diese invers funktionierenVariablen haben ihre Rollen geändert, was einem Wechsel entsprichtNotation der Koordinatenachsen. Daher die Grafikdie Umkehrfunktion ist symmetrisch zum Graphen der direkten Funktionüber die WinkelhalbierendeichundIIIKoordinatenwinkel,d.h. relativ geradey = x. So bekommen wirnächste Regel.

Um die Funktion y = zu zeichnen (x) invers zur Funktionj = f( x), gebaut werden sollzeitlicher Ablaufj = f( x) und an der Geraden y = x spiegeln.

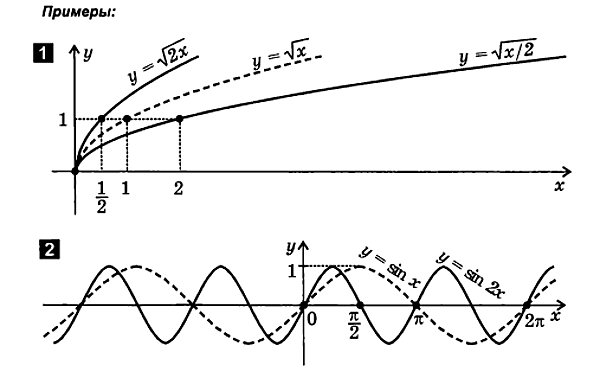
2.4. Verformung (Kompression und Spannung) von Graphen

1. Komprimierung (Expansion) des Diagramms entlang der y-Achse

f ( x ) EIN ∙ f ( x ).

Um eine Funktion zu plottenj= EIN∙ f( x) folgt:

8. Kompression (Expansion) des Graphen entlang der x-Achse

f( x)

Um die Funktion y zu plotten= f( x) folgt:

2.5. Kombination aus Translation, Reflexion und Deformation

Sehr oft beim Zeichnen von Funktionsgraphen fürdie Kombination ändern.

Konsequente Anwendung einer Reihe solcher Haltungstechnikenermöglicht es, die Konstruktion eines Diagramms mit erheblich zu vereinfachenLauffunktion und reduzieren sie am Ende oft aufKonstruktion einer der einfachsten elementaren Funktionengen. Überlegen Sie, wie es im Hinblick auf das Vorhergehende folgtFunktionsgraphen erstellen.

Beachten wir, dass es an der Zeit istEs empfiehlt sich, den Vereinfachungsdock im nächsten Nachfolger durchzuführenness.

Mit Parität oderFunktion Seltsamkeit.

Achsen übertragen.

Reflexion und Verformung.

Der Aufbau des Graphen erfolgt in umgekehrter Reihenfolge.

Beispiel. Zeichnen Sie eine Funktion

Der Bau erfolgt in folgenden Schritten:

1. Zeichnen Sie den natürlichen Logarithmus:

2. drückenzur AchseOY2 Mal:;
3. symmetrisch anzeigenum die AchseOY: ;
4. Bewegen Sie sich entlang der AchseOCHSEauf der(!!!) Nach rechts::

5. Anzeige symmetrisch um die AchseOCHSE: ;
6. bewegenentlang der AchseOY3 Einheiten höher::

BEISPIELE ZUR KONSTRUKTION UND UMWANDLUNG VON FUNKTIONSGRAPHEN

Beispiel 1 Zeichnen Sie eine Funktion.

Zeichnen Sie zuerst ein Sinusdiagramm, dessen Periode gleich ist:

Funktionsgrapherhalten durch Komprimieren des Graphenzweimal zur y-Achse. Protokoll .

Zeichnen Sie eine Funktionbei = 2 cosX.

Zeichnen Sie eine Funktionj = Sündex .

FAZIT

Während der Arbeit an der Projektarbeit wurde verschiedene pädagogische und methodische Literatur zu diesem Thema analysiert. Die Ergebnisse der Studie ermöglichten es, die charakteristischsten positiven Aspekte der Studie zu identifizieren, Konstruktion und Transformation von Funktionsgraphen im Schulmathematikunterricht

Das Hauptziel des Projekts ist es, die Fähigkeiten und Fertigkeiten der Schüler beim Lesen und Zeichnen von Zeichnungen zu entwickeln und rationale Methoden für unabhängige Aktivitäten zu entwickeln.

Die Notwendigkeit, die Grafikausbildung insgesamt zu verbessern, wird nicht nur durch moderne Produktionsanforderungen bestimmt, sondern auch durch die Rolle der Grafik bei der Entwicklung des technischen Denkens und der kognitiven Fähigkeiten der Schüler. Die Fähigkeit einer Person, grafische Informationen zu verarbeiten, ist einer der Indikatoren für ihre geistige Entwicklung. Daher sollte die Graphikausbildung ein fester Bestandteil der allgemeinbildenden Ausbildung werden.

Schlussfolgerungen

Daher konzentriert sich das entwickelte Projekt "Konstruktion und Transformation von Funktionsgraphen", das einem der zentralen Konzepte der Mathematik - der funktionalen Abhängigkeit - gewidmet ist, auf die Systematisierung und Erweiterung des studentischen Wissens. Das Studium spezifischer Methoden zur Transformation von Funktionsgraphen erfolgt analytisch und grafisch nach strengen methodischen Schemata. Das gesammelte Material kann im Unterricht und für das Selbststudium der Schüler verwendet werden. Für die Durchführung des Unterrichts können verschiedene Formen und Methoden der Organisation und des Trainings verwendet werden.