- the determinant of the matrix A is calculated;
- through algebraic additions, the inverse matrix A -1 is found;
- a solution template is created in Excel;
Instruction. To obtain a solution by the inverse matrix method, it is necessary to specify the dimension of the matrix. Next, in the new dialog box, fill in the matrix A and the result vector B .
See also Solution of matrix equations.Solution algorithm
- The determinant of the matrix A is calculated. If the determinant is zero, then the end of the solution. The system has an infinite number of solutions.
- When the determinant is different from zero, the inverse matrix A -1 is found through algebraic additions.
- The decision vector X =(x 1 , x 2 , ..., x n ) is obtained by multiplying the inverse matrix by the result vector B .
Algebraic additions.
| A 1.1 = (-1) 1+1 |
| ∆ 1,1 = (1 (-2)-0 2) = -2 |
| A 1,2 = (-1) 1+2 |
| ∆ 1,2 = -(3 (-2)-1 2) = 8 |
| A 1.3 = (-1) 1+3 |
| ∆ 1,3 = (3 0-1 1) = -1 |
| A 2.1 = (-1) 2+1 |
| ∆ 2,1 = -(-2 (-2)-0 1) = -4 |
| A 2.2 = (-1) 2+2 |
| ∆ 2,2 = (2 (-2)-1 1) = -5 |
| A 2.3 = (-1) 2+3 |
| ∆ 2,3 = -(2 0-1 (-2)) = -2 |
| A 3.1 = (-1) 3+1 |
| ∆ 3,1 = (-2 2-1 1) = -5 |
| 3 |
| -2 |
| -1 |
X T = (1,0,1)
x 1 = -21 / -21 = 1
x 2 = 0 / -21 = 0
x 3 = -21 / -21 = 1
Examination:
2 1+3 0+1 1 = 3
-2 1+1 0+0 1 = -2
1 1+2 0+-2 1 = -1
Topic 2. SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS.
Basic concepts.
Definition 1. system m linear equations with n unknown is a system of the form:
where and are numbers.
Definition 2. The solution of the system (I) is such a set of unknowns, in which each equation of this system turns into an identity.
Definition 3. System (I) is called joint if it has at least one solution and incompatible if it has no solutions. The joint system is called certain if it has a unique solution, and uncertain otherwise.
Definition 4. Type equation
called zero, and an equation of the form
called incompatible. Obviously, a system of equations containing an inconsistent equation is inconsistent.
Definition 5. The two systems of linear equations are called equivalent if every solution of one system is a solution of another and, conversely, every solution of the second system is a solution of the first.
Matrix notation for a system of linear equations.
Consider system (I) (see §1).
Denote:
Coefficient matrix for unknowns
Matrix - column of free members
Matrix - column of unknowns
.
Definition 1. The matrix is called the main matrix of the system(I), and the matrix is the augmented matrix of system (I).
By the definition of matrix equality, system (I) corresponds to the matrix equality:
.
The right side of this equality by the definition of the product of matrices ( see definition 3 § 5 chapter 1) can be factorized:
, i.e.
Equality (2) called matrix notation of the system (I).
Solving a system of linear equations by Cramer's method.
Let in system (I) (see §1) m=n, i.e. the number of equations is equal to the number of unknowns, and the main matrix of the system is nondegenerate, i.e. . Then system (I) from §1 has a unique solution
where ∆ = det A called the main system determinant(I), ∆ i is obtained from the determinant Δ by replacing i-th column to the column of free members of the system (I).
Example. Solve the system by Cramer's method:
.
By formulas (3)
.
We calculate the determinants of the system:
,
,
.
To get the determinant, we have replaced the first column in the determinant with a column of free members; replacing the 2nd column in the determinant with a column of free members, we obtain ; similarly, replacing the 3rd column in the determinant with a column of free members, we obtain . System solution:
Solving systems of linear equations using an inverse matrix.
Let in system (I) (see §1) m=n and the main matrix of the system is nondegenerate. We write system (I) in matrix form ( see §2):
because matrix A is nondegenerate, then it has an inverse matrix ( see Theorem 1 §6 of Chapter 1). Multiply both sides of the equation (2) to the matrix, then
By definition of the inverse matrix . From equality (3) we have
Solve the system using the inverse matrix
.
Denote
In the example (§ 3) we calculated the determinant , therefore, the matrix A has an inverse matrix. Then in force (4) , i.e.
. (5)
Find the matrix ( see §6 chapter 1)
, 
, 
,
, 
, 
,
,
.
Gauss method.
Let the system of linear equations be given:
. (I)
It is required to find all solutions of system (I) or to make sure that the system is inconsistent.
Definition 1.Let us call the elementary transformation of the system(I) any of the three actions:
1) deletion of the zero equation;
2) adding to both parts of the equation the corresponding parts of the other equation, multiplied by the number l;
3) swapping terms in the equations of the system so that unknowns with the same numbers in all equations occupy the same places, i.e. if, for example, in the 1st equation we changed the 2nd and 3rd terms, then the same must be done in all equations of the system.
The Gauss method consists in the fact that the system (I) with the help of elementary transformations is reduced to an equivalent system, the solution of which is found directly or its unsolvability is established.
As described in §2, system (I) is uniquely determined by its extended matrix, and any elementary transformation of system (I) corresponds to an elementary transformation of the extended matrix:
.
Transformation 1) corresponds to deleting the zero row in the matrix , transformation 2) is equivalent to adding to the corresponding row of the matrix its other row multiplied by the number l, transformation 3) is equivalent to rearranging the columns in the matrix .
It is easy to see that, on the contrary, each elementary transformation of the matrix corresponds to an elementary transformation of the system (I). In view of what has been said, instead of operations with the system (I), we will work with the augmented matrix of this system.
In the matrix, the 1st column consists of coefficients at x 1, 2nd column - from the coefficients at x 2 etc. In the case of rearrangement of columns, it should be taken into account that this condition is violated. For example, if we swap the 1st and 2nd columns, then now in the 1st column there will be coefficients at x 2, and in the 2nd column - coefficients at x 1.
We will solve system (I) by the Gauss method.
1. Cross out all zero rows in the matrix, if there are any (i.e., cross out all zero equations in system (I).
2. Check if there is a row among the rows of the matrix in which all elements except the last one are equal to zero (let's call such a row inconsistent). Obviously, such a line corresponds to an inconsistent equation in system (I), therefore, system (I) has no solutions, and this is where the process ends.
3. Let the matrix not contain inconsistent rows (system (I) does not contain inconsistent equations). If a a 11 =0, then we find in the 1st row some element (except the last one) that is different from zero and rearrange the columns so that there is no zero in the 1st row in the 1st place. We now assume that (i.e., we swap the corresponding terms in the equations of system (I)).
4. Multiply the 1st row by and add the result to the 2nd row, then multiply the 1st row by and add the result to the 3rd row, etc. Obviously, this process is equivalent to eliminating the unknown x 1 from all equations of system (I), except for the 1st. In the new matrix, we get zeros in the 1st column under the element a 11:
.
5. Cross out all zero rows in the matrix, if any, check if there is an inconsistent row (if there is, then the system is inconsistent and the solution ends there). Let's check if a 22 / =0, if yes, then we find an element in the 2nd row that is different from zero and rearrange the columns so that . Next, we multiply the elements of the 2nd row by 
and add with the corresponding elements of the 3rd row, then - the elements of the 2nd row on and add with the corresponding elements of the 4th row, etc., until we get zeros under a 22 /
.
The performed actions are equivalent to the elimination of the unknown x 2 from all equations of system (I), except for the 1st and 2nd. Since the number of rows is finite, therefore, after a finite number of steps, we will get that either the system is inconsistent, or we will come to a step matrix ( see definition 2 §7 chapter 1) :
,
Let us write down the system of equations corresponding to the matrix . This system is equivalent to the system (I)
.
From the last equation we express ; we substitute into the previous equation, find, etc., until we get .
Remark 1. Thus, when solving system (I) by the Gauss method, we arrive at one of the following cases.
1. System (I) is inconsistent.
2. System (I) has a unique solution if the number of rows in the matrix is equal to the number of unknowns ().
3. System (I) has an infinite number of solutions if the number of rows in the matrix is less than the number of unknowns ().
Hence the following theorem holds.
Theorem. The system of linear equations is either inconsistent, or has a unique solution, or there is an infinite set of solutions.
Examples. Solve the system of equations by the Gauss method or prove its inconsistency:
b) 
;
a) Let us rewrite the given system in the form:
.
We swapped the 1st and 2nd equations of the original system to simplify the calculations (instead of fractions, we will operate only with integers using such a permutation).
We compose an expanded matrix:
.
There are no null lines; no incompatible lines, ; we exclude the 1st unknown from all equations of the system, except for the 1st one. To do this, we multiply the elements of the 1st row of the matrix by "-2" and add them to the corresponding elements of the 2nd row, which is equivalent to multiplying the 1st equation by "-2" and adding it to the 2nd equation. Then we multiply the elements of the 1st row by "-3" and add them to the corresponding elements of the third row, i.e. multiply the 2nd equation of the given system by "-3" and add it to the 3rd equation. Get
.
The matrix corresponds to a system of equations). - (see Definition 3 § 7 of Chapter 1).
System of m linear equations with n unknowns called a system of the form
where aij and b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n- unknown. In the notation of the coefficients aij first index i denotes the number of the equation, and the second j is the number of the unknown at which this coefficient stands.
The coefficients for the unknowns will be written in the form of a matrix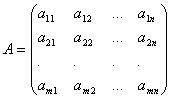 
, which we will call system matrix.
The numbers on the right sides of the equations b 1 ,…,b m called free members.
Aggregate n numbers c 1 ,…,c n called decision of this system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.
Our task will be to find solutions to the system. In this case, three situations may arise:
A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called incompatible.
Consider ways to find solutions to the system.
MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS
Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:
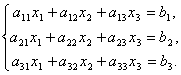
Consider the matrix of the system 
and matrix columns of unknown and free members 
Let's find the product
those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then, using the definition of matrix equality, this system can be written as
or shorter A∙X=B.
Here matrices A and B are known, and the matrix X unknown. She needs to be found, because. its elements are the solution of this system. This equation is called matrix equation.
Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, the inverse of the matrix A: . Because the A -1 A = E and E∙X=X, then we obtain the solution of the matrix equation in the form X = A -1 B .
Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations is the same as the number of unknowns. However, the matrix notation of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A is not square and therefore it is impossible to find a solution to the system in the form X = A -1 B.
Examples. Solve systems of equations.
CRAMER'S RULE
Consider a system of 3 linear equations with three unknowns:
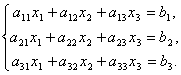
Third-order determinant corresponding to the matrix of the system, i.e. composed of coefficients at unknowns,
called system determinant.
We compose three more determinants as follows: we replace successively 1, 2 and 3 columns in the determinant D with a column of free members
Then we can prove the following result.
Theorem (Cramer's rule). If the determinant of the system is Δ ≠ 0, then the system under consideration has one and only one solution, and
Proof. So, consider a system of 3 equations with three unknowns. Multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation - on A21 and 3rd - on A 31:
Let's add these equations:
Consider each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in terms of the elements of the 1st column
Similarly, it can be shown that and .
Finally, it is easy to see that 
Thus, we get the equality: .
Consequently, .
The equalities and are derived similarly, whence the assertion of the theorem follows.
Thus, we note that if the determinant of the system is Δ ≠ 0, then the system has a unique solution and vice versa. If the determinant of the system is equal to zero, then the system either has an infinite set of solutions or has no solutions, i.e. incompatible.
Examples. Solve a system of equations
GAUSS METHOD
The previously considered methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gaussian method is more universal and is suitable for systems with any number of equations. It consists in the successive elimination of unknowns from the equations of the system.
Consider again a system of three equations with three unknowns:
.
We leave the first equation unchanged, and from the 2nd and 3rd we exclude the terms containing x 1. To do this, we divide the second equation by a 21 and multiply by - a 11 and then add with the 1st equation. Similarly, we divide the third equation into a 31 and multiply by - a 11 and then add it to the first one. As a result, the original system will take the form:
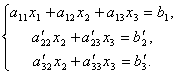
Now, from the last equation, we eliminate the term containing x2. To do this, divide the third equation by , multiply by and add it to the second. Then we will have a system of equations:
Hence from the last equation it is easy to find x 3, then from the 2nd equation x2 and finally from the 1st - x 1.
When using the Gaussian method, the equations can be interchanged if necessary.
Often, instead of writing a new system of equations, they limit themselves to writing out the extended matrix of the system:
and then bring it to a triangular or diagonal form using elementary transformations.
To elementary transformations matrices include the following transformations:
- permutation of rows or columns;
- multiplying a string by a non-zero number;
- adding to one line other lines.
Examples: Solve systems of equations using the Gauss method.
Thus, the system has an infinite number of solutions.
Consider system of linear algebraic equations(SLOW) regarding n unknown x 1 , x 2 , ..., x n :
This system in a "folded" form can be written as follows:
S n i=1 a ij x j = b i , i=1,2, ..., n.
In accordance with the rule of matrix multiplication, the considered system of linear equations can be written in matrix form ax=b, where
,
,.
Matrix A, whose columns are the coefficients for the corresponding unknowns, and the rows are the coefficients for the unknowns in the corresponding equation is called system matrix. column matrix b, whose elements are the right parts of the equations of the system, is called the matrix of the right part or simply right side of the system. column matrix x , whose elements are unknown unknowns, is called system solution.
The system of linear algebraic equations written as ax=b, is matrix equation.
If the matrix of the system non-degenerate, then it has an inverse matrix, and then the solution to the system ax=b is given by the formula:
x=A -1 b.
Example Solve the system 
matrix method.
Solution find the inverse matrix for the coefficient matrix of the system
Calculate the determinant by expanding over the first row:
Because the Δ ≠ 0 , then A -1 exists.
The inverse matrix is found correctly.
Let's find a solution to the system 
Consequently, x 1 = 1, x 2 = 2, x 3 = 3 .
Examination: 
7. The Kronecker-Capelli theorem on the compatibility of a system of linear algebraic equations.
System of linear equations looks like:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.1)
a m1 x 1 + a m1 x 2 +... + a mn x n = b m .
Here a i j and b i (i = ; j = ) are given, and x j are unknown real numbers. Using the concept of a product of matrices, we can rewrite system (5.1) in the form:
where A = (a i j) is the matrix consisting of the coefficients of the unknowns of the system (5.1), which is called system matrix, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T - column vectors composed respectively of unknown x j and free terms b i .
Ordered collection n real numbers (c 1 , c 2 ,..., c n) is called system solution(5.1) if as a result of substitution of these numbers instead of the corresponding variables x 1 , x 2 ,..., x n each equation of the system turns into an arithmetic identity; in other words, if there exists a vector C= (c 1 , c 2 ,..., c n) T such that AC B.
System (5.1) is called joint, or solvable if it has at least one solution. The system is called incompatible, or insoluble if it has no solutions.
,
formed by assigning a column of free terms to the matrix A on the right, is called extended matrix system.
The question of the compatibility of system (5.1) is solved by the following theorem.
Kronecker-Capelli theorem . The system of linear equations is consistent if and only if the ranks of the matrices A and A coincide, i.e. r(A) = r(A) = r.
For the set M of solutions to system (5.1), there are three possibilities:
1) M = (in this case the system is inconsistent);
2) M consists of one element, i.e. the system has a unique solution (in this case the system is called certain);
3) M consists of more than one element (then the system is called uncertain). In the third case, system (5.1) has an infinite number of solutions.
The system has a unique solution only if r(A) = n. In this case, the number of equations is not less than the number of unknowns (mn); if m>n, then m-n equations are consequences of the rest. If 0 To solve an arbitrary system of linear equations, one must be able to solve systems in which the number of equations is equal to the number of unknowns, the so-called Cramer type systems: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 , a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.3) ...
... ... ...
... ... a n1 x 1 + a n1 x 2 +... + a nn x n = b n . Systems (5.3) are solved in one of the following ways: 1) by the Gauss method, or by the method of eliminating unknowns; 2) according to Cramer's formulas; 3) by the matrix method. Example 2.12. Investigate the system of equations and solve it if it is compatible: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x1 + x2 + 4x3 - 2x4 = 1, x 1 - 3x 2 - 6x 3 + 5x 4 = 0. Solution. We write out the extended matrix of the system:
Let us calculate the rank of the main matrix of the system. It is obvious that, for example, the second-order minor in the upper left corner = 7 0; the third-order minors containing it are equal to zero: Therefore, the rank of the main matrix of the system is 2, i.e. r(A) = 2. To calculate the rank of the extended matrix A, consider the bordering minor hence, the rank of the extended matrix is r(A) = 3. Since r(A) r(A), the system is inconsistent. (sometimes this method is also called the matrix method or the inverse matrix method) requires prior familiarization with such a concept as the matrix form of writing SLAE. The inverse matrix method is intended for solving those systems of linear algebraic equations for which the system matrix determinant is nonzero. Naturally, this implies that the matrix of the system is square (the concept of determinant exists only for square matrices). The essence of the inverse matrix method can be expressed in three points: Any SLAE can be written in matrix form as $A\cdot X=B$, where $A$ is the matrix of the system, $B$ is the matrix of free terms, $X$ is the matrix of unknowns. Let the matrix $A^(-1)$ exist. Multiply both sides of the equality $A\cdot X=B$ by the matrix $A^(-1)$ on the left: $$A^(-1)\cdot A\cdot X=A^(-1)\cdot B.$$ Since $A^(-1)\cdot A=E$ ($E$ is the identity matrix), then the equality written above becomes: $$E\cdot X=A^(-1)\cdot B.$$ Since $E\cdot X=X$, then: $$X=A^(-1)\cdot B.$$ Example #1 Solve the SLAE $ \left \( \begin(aligned) & -5x_1+7x_2=29;\\ & 9x_1+8x_2=-11. \end(aligned) \right.$ using the inverse matrix. $$ A=\left(\begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right);\; B=\left(\begin(array) (c) 29\\ -11 \end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \end(array)\right). $$ Let's find the inverse matrix to the matrix of the system, i.e. calculate $A^(-1)$. In example #2 $$ A^(-1)=-\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right) . $$ Now let's substitute all three matrices ($X$, $A^(-1)$, $B$) into the equation $X=A^(-1)\cdot B$. Then we perform matrix multiplication $$ \left(\begin(array) (c) x_1\\ x_2 \end(array)\right)= -\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right)\cdot \left(\begin(array) (c) 29\\ -11 \end(array)\right)=\\ =-\frac (1)(103)\cdot \left(\begin(array) (c) 8\cdot 29+(-7)\cdot (-11)\\ -9\cdot 29+(-5)\cdot (- 11) \end(array)\right)= -\frac(1)(103)\cdot \left(\begin(array) (c) 309\\ -206 \end(array)\right)=\left( \begin(array) (c) -3\\ 2\end(array)\right). $$ So we got $\left(\begin(array) (c) x_1\\ x_2 \end(array)\right)=\left(\begin(array) (c) -3\\ 2\end(array )\right)$. From this equality we have: $x_1=-3$, $x_2=2$. Answer: $x_1=-3$, $x_2=2$. Example #2 Solve SLAE $ \left\(\begin(aligned) & x_1+7x_2+3x_3=-1;\\ & -4x_1+9x_2+4x_3=0;\\ & 3x_2+2x_3=6. \end(aligned)\right .$ by the inverse matrix method. Let us write down the matrix of the system $A$, the matrix of free terms $B$ and the matrix of unknowns $X$. $$ A=\left(\begin(array) (ccc) 1 & 7 & 3\\ -4 & 9 & 4 \\0 & 3 & 2\end(array)\right);\; B=\left(\begin(array) (c) -1\\0\\6\end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right). $$ Now it's time to find the inverse matrix of the system matrix, i.e. find $A^(-1)$. In example #3 on the page dedicated to finding inverse matrices, the inverse matrix has already been found. Let's use the finished result and write $A^(-1)$: $$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array)\right). $$ Now we substitute all three matrices ($X$, $A^(-1)$, $B$) into the equality $X=A^(-1)\cdot B$, after which we perform matrix multiplication on the right side of this equality. $$ \left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)= \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)\cdot \left(\begin(array) (c) -1\\0\ \6\end(array)\right)=\\ =\frac(1)(26)\cdot \left(\begin(array) (c) 6\cdot(-1)+(-5)\cdot 0 +1\cdot 6 \\ 8\cdot (-1)+2\cdot 0+(-16)\cdot 6 \\ -12\cdot (-1)+(-3)\cdot 0+37\cdot 6 \end(array)\right)=\frac(1)(26)\cdot \left(\begin(array) (c) 0\\-104\\234\end(array)\right)=\left( \begin(array) (c) 0\\-4\\9\end(array)\right) $$ So we got $\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)=\left(\begin(array) (c) 0\\-4\ \9\end(array)\right)$. From this equality we have: $x_1=0$, $x_2=-4$, $x_3=9$.
.
