When preparing for the exam in mathematics, students have to systematize their knowledge of algebra and geometry. I would like to combine all known information, for example, how to calculate the area of a pyramid. Moreover, starting from the base and side faces to the entire surface area. If the situation is clear with the side faces, since they are triangles, then the base is always different.
What to do when finding the area of the base of the pyramid?
It can be absolutely any figure: from an arbitrary triangle to an n-gon. And this base, in addition to the difference in the number of angles, can be a regular figure or an incorrect one. In the USE tasks of interest to schoolchildren, there are only tasks with the correct figures at the base. Therefore, we will only talk about them.
right triangle
That is equilateral. One in which all sides are equal and denoted by the letter "a". In this case, the area of \u200b\u200bthe base of the pyramid is calculated by the formula:
S = (a 2 * √3) / 4.
Square
The formula for calculating its area is the simplest, here "a" is the side again:
Arbitrary regular n-gon
The side of a polygon has the same designation. For the number of corners, the Latin letter n is used.
S = (n * a 2) / (4 * tg (180º/n)).

How to proceed when calculating the lateral and total surface area?
Since the base is a regular figure, all the faces of the pyramid are equal. Moreover, each of them is an isosceles triangle, since the side edges are equal. Then, in order to calculate the lateral area of \u200b\u200bthe pyramid, you need a formula consisting of the sum of identical monomials. The number of terms is determined by the number of sides of the base.
The area of an isosceles triangle is calculated by the formula in which half the product of the base is multiplied by the height. This height in the pyramid is called apothem. Its designation is "A". The general formula for lateral surface area is:
S \u003d ½ P * A, where P is the perimeter of the base of the pyramid.
There are situations when the sides of the base are not known, but the side edges (c) and the flat angle at its vertex (α) are given. Then it is supposed to use such a formula to calculate the lateral area of \u200b\u200bthe pyramid:
S = n/2 * in 2 sin α .

Task #1
Condition. Find the total area of the pyramid if its base lies with a side of 4 cm, and the apothem has a value of √3 cm.
Solution. You need to start by calculating the perimeter of the base. Since this is a regular triangle, then P \u003d 3 * 4 \u003d 12 cm. Since the apothem is known, you can immediately calculate the area of \u200b\u200bthe entire lateral surface: ½ * 12 * √3 = 6√3 cm 2.
For a triangle at the base, the following area value will be obtained: (4 2 * √3) / 4 \u003d 4√3 cm 2.
To determine the entire area, you will need to add the two resulting values: 6√3 + 4√3 = 10√3 cm 2.
Answer. 10√3 cm2.
Task #2
Condition. There is a regular quadrangular pyramid. The length of the side of the base is 7 mm, the side edge is 16 mm. You need to know its surface area.
Solution. Since the polyhedron is quadrangular and regular, then its base is a square. Having learned the areas of the base and side faces, it will be possible to calculate the area of \u200b\u200bthe pyramid. The formula for the square is given above. And at the side faces, all sides of the triangle are known. Therefore, you can use Heron's formula to calculate their areas.
The first calculations are simple and lead to this number: 49 mm 2. For the second value, you will need to calculate the semi-perimeter: (7 + 16 * 2): 2 = 19.5 mm. Now you can calculate the area of an isosceles triangle: √ (19.5 * (19.5-7) * (19.5-16) 2) = √2985.9375 = 54.644 mm 2. There are only four such triangles, so when calculating the final number, you will need to multiply it by 4.
It turns out: 49 + 4 * 54.644 \u003d 267.576 mm 2.
Answer. The desired value is 267.576 mm 2.
Task #3
Condition. For a regular quadrangular pyramid, you need to calculate the area. In it, the side of the square is 6 cm and the height is 4 cm.
Solution. The easiest way is to use the formula with the product of the perimeter and the apothem. The first value is easy to find. The second is a little more difficult.
We'll have to remember the Pythagorean theorem and consider It is formed by the height of the pyramid and the apothem, which is the hypotenuse. The second leg is equal to half the side of the square, since the height of the polyhedron falls into its middle.
The desired apothem (the hypotenuse of a right triangle) is √(3 2 + 4 2) = 5 (cm).
Now you can calculate the desired value: ½ * (4 * 6) * 5 + 6 2 \u003d 96 (cm 2).
Answer. 96 cm2.

Task #4
Condition. The correct side of its base is 22 mm, the side ribs are 61 mm. What is the area of the lateral surface of this polyhedron?
Solution. The reasoning in it is the same as described in problem No. 2. Only there was given a pyramid with a square at the base, and now it is a hexagon.
First of all, the area of \u200b\u200bthe base is calculated using the above formula: (6 * 22 2) / (4 * tg (180º / 6)) \u003d 726 / (tg30º) \u003d 726√3 cm 2.
Now you need to find out the semi-perimeter of an isosceles triangle, which is a lateral face. (22 + 61 * 2): 2 = 72 cm. It remains to calculate the area of \u200b\u200beach such triangle using the Heron formula, and then multiply it by six and add it to the one that turned out for the base.
Calculations using the Heron formula: √ (72 * (72-22) * (72-61) 2) \u003d √ 435600 \u003d 660 cm 2. Calculations that will give the lateral surface area: 660 * 6 \u003d 3960 cm 2. It remains to add them up to find out the entire surface: 5217.47≈5217 cm 2.
Answer. Base - 726√3 cm 2, side surface - 3960 cm 2, entire area - 5217 cm 2.
The surface area of the pyramid. In this article, we will consider with you problems with regular pyramids. Let me remind you that a regular pyramid is a pyramid whose base is a regular polygon, the top of the pyramid is projected into the center of this polygon.
The side face of such a pyramid is an isosceles triangle.The height of this triangle, drawn from the top of a regular pyramid, is called an apothem, SF is an apothem:
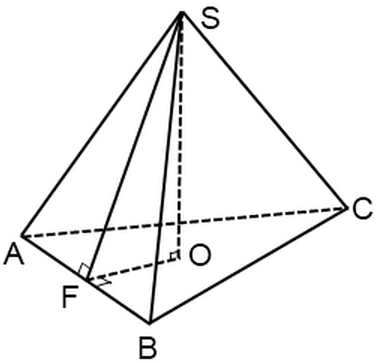
In the type of problems presented below, it is required to find the surface area of the entire pyramid or the area of its lateral surface. The blog has already considered several problems with regular pyramids, where the question was raised about finding elements (height, base edge, side edge), .
In the tasks of the exam, as a rule, regular triangular, quadrangular and hexagonal pyramids are considered. I have not seen problems with regular pentagonal and heptagonal pyramids.
The formula for the area of the entire surface is simple - you need to find the sum of the area of \u200b\u200bthe base of the pyramid and the area of its lateral surface:
![]()
Consider the tasks:
The sides of the base of a regular quadrangular pyramid are 72, the side edges are 164. Find the surface area of this pyramid.

The surface area of the pyramid is equal to the sum of the areas of the lateral surface and the base:
*The lateral surface consists of four triangles of equal area. The base of the pyramid is a square.
The area of the side of the pyramid can be calculated using:

Thus, the surface area of the pyramid is:
Answer: 28224
The sides of the base of a regular hexagonal pyramid are 22, the side edges are 61. Find the area of the lateral surface of this pyramid.

The base of a regular hexagonal pyramid is a regular hexagon.
The lateral surface area of this pyramid consists of six areas of equal triangles with sides 61.61 and 22:
Find the area of a triangle using Heron's formula:

So the lateral surface area is:
![]()
Answer: 3240
*In the problems presented above, the area of the side face could be found using a different triangle formula, but for this you need to calculate the apothem.
27155. Find the surface area of a regular quadrangular pyramid whose base sides are 6 and whose height is 4.

In order to find the surface area of a pyramid, we need to know the area of the base and the area of the side surface:
The area of the base is 36, since it is a square with a side of 6.
The side surface consists of four faces, which are equal triangles. In order to find the area of such a triangle, you need to know its base and height (apothem):
* The area of a triangle is equal to half the product of the base and the height drawn to this base.
The base is known, it is equal to six. Let's find the height. Consider a right triangle (highlighted in yellow):

One leg is equal to 4, since this is the height of the pyramid, the other is equal to 3, since it is equal to half the edge of the base. We can find the hypotenuse using the Pythagorean theorem:
![]()
So the area of the lateral surface of the pyramid is:

Thus, the surface area of the entire pyramid is:
Answer: 96
27069. The sides of the base of a regular quadrangular pyramid are 10, the side edges are 13. Find the surface area of this pyramid.
27070. The sides of the base of a regular hexagonal pyramid are 10, the side edges are 13. Find the area of the side surface of this pyramid.
There are also formulas for the lateral surface area of a regular pyramid. In a regular pyramid, the base is an orthogonal projection of the lateral surface, therefore:
P- perimeter of the base, l- apothem of the pyramid
*This formula is based on the formula for the area of a triangle.
If you want to learn more about how these formulas are derived, do not miss it, follow the publication of articles.That's all. Good luck to you!
Sincerely, Alexander Krutitskikh.
P.S: I would be grateful if you tell about the site in social networks.
The area of the lateral surface of an arbitrary pyramid is equal to the sum of the areas of its lateral faces. It makes sense to give a special formula for expressing this area in the case of a regular pyramid. So, let a regular pyramid be given, at the base of which lies a regular n-gon with a side equal to a. Let h be the height of the side face, also called apothema pyramids. The area of one side face is 1/2ah, and the entire side surface of the pyramid has an area equal to n/2ha. Since na is the perimeter of the base of the pyramid, we can write the found formula as follows:
Lateral surface area of a regular pyramid is equal to the product of its apothem by half the perimeter of the base.
Concerning total surface area, then simply add the area of \u200b\u200bthe base to the side.
Inscribed and circumscribed sphere and ball. It should be noted that the center of the sphere inscribed in the pyramid lies at the intersection of the bisector planes of the internal dihedral angles of the pyramid. The center of the sphere described near the pyramid lies at the intersection of planes passing through the midpoints of the edges of the pyramid and perpendicular to them.

Truncated pyramid. If the pyramid is cut by a plane parallel to its base, then the part enclosed between the cutting plane and the base is called truncated pyramid. The figure shows a pyramid, discarding its part lying above the cutting plane, we get a truncated pyramid. It is clear that the small pyramid to be discarded is homothetic to the large pyramid with the center of the homothety at the apex. The similarity coefficient is equal to the ratio of heights: k=h 2 /h 1 , or side ribs, or other corresponding linear dimensions of both pyramids. We know that the areas of similar figures are related as squares of linear dimensions; so the areas of the bases of both pyramids (i.e. spare the bases of the truncated pyramid) are related as
Here S 1 is the area of the lower base, and S 2 is the area of the upper base of the truncated pyramid. The side surfaces of the pyramids are in the same ratio. There is a similar rule for volumes.
Volumes of similar bodies are related as cubes of their linear dimensions; for example, the volumes of the pyramids are related as the products of their heights by the area of the bases, from which our rule immediately follows. It has a completely general character and directly follows from the fact that the volume always has the dimension of the third power of length. Using this rule, we derive a formula expressing the volume of a truncated pyramid in terms of the height and areas of the bases.
Let a truncated pyramid with height h and base areas S 1 and S 2 be given. If we imagine that it is extended to the full pyramid, then the similarity coefficient of the full pyramid and the small pyramid can be easily found as the root of the S 2 /S 1 ratio. The height of the truncated pyramid is expressed as h = h 1 - h 2 = h 1 (1 - k). Now we have for the volume of the truncated pyramid (V 1 and V 2 denote the volumes of the full and small pyramids)
truncated pyramid volume formula

We derive the formula for the area S of the lateral surface of a regular truncated pyramid through the perimeters P 1 and P 2 of the bases and the length of the apothem a. We argue in exactly the same way as when deriving the formula for volume. We supplement the pyramid with the upper part, we have P 2 \u003d kP 1, S 2 \u003d k 2 S 1, where k is the similarity coefficient, P 1 and P 2 are the perimeters of the bases, and S 1 and S 2 are the horses of the side surfaces of the entire resulting pyramid and its top, respectively. For the lateral surface we find (a 1 and a 2 - apothems of the pyramids, a \u003d a 1 - a 2 \u003d a 1 (1-k))
formula for the lateral surface area of a regular truncated pyramid

Typical geometric problems in the plane and in three-dimensional space are the problems of determining the surface areas of different figures. In this article, we present the formula for the area of the lateral surface of a regular quadrangular pyramid.
What is a pyramid?
Let us give a strict geometric definition of a pyramid. Suppose there is some polygon with n sides and n corners. We choose an arbitrary point in space that will not be in the plane of the specified n-gon, and connect it to each vertex of the polygon. We will get a figure that has some volume, which is called an n-gonal pyramid. For example, let's show in the figure below what a pentagonal pyramid looks like.
Two important elements of any pyramid are its base (n-gon) and top. These elements are connected to each other by n triangles, which in general are not equal to each other. The perpendicular dropped from the top to the base is called the height of the figure. If it intersects the base in the geometric center (coincides with the center of mass of the polygon), then such a pyramid is called a straight line. If, in addition to this condition, the base is a regular polygon, then the entire pyramid is called regular. The figure below shows what regular pyramids look like with triangular, quadrangular, pentagonal, and hexagonal bases.

The surface of the pyramid
Before turning to the question of the area of the lateral surface of a regular quadrangular pyramid, one should dwell in more detail on the concept of the surface itself.
As mentioned above and shown in the figures, any pyramid is formed by a set of faces or sides. One side is the base and n sides are triangles. The surface of the whole figure is the sum of the areas of each of its sides.
It is convenient to study the surface using the example of a figure unfolding. A scan for a regular quadrangular pyramid is shown in the figures below.

We see that its surface area is equal to the sum of four areas of identical isosceles triangles and the area of a square.
The total area of all the triangles that form the sides of the figure is called the area of the lateral surface. Next, we show how to calculate it for a regular quadrangular pyramid.
Lateral surface area of a rectangular regular pyramid
To calculate the lateral surface area of the specified figure, we again turn to the above sweep. Suppose we know the side of the square base. Let's denote it by symbol a. It can be seen that each of the four identical triangles has a base of length a. To calculate their total area, you need to know this value for one triangle. From the course of geometry it is known that the area of \u200b\u200bthe triangle S t is equal to the product of the base and the height, which should be divided in half. That is:
Where h b is the height of the isosceles triangle drawn to the base a. For a pyramid, this height is the apothem. Now it remains to multiply the resulting expression by 4 to get the area S b of the lateral surface for the pyramid in question:
S b = 4*S t = 2*h b *a.
This formula contains two parameters: the apothem and the side of the base. If the latter is known in most conditions of the problems, then the former has to be calculated knowing other quantities. Here are the formulas for calculating apotema h b for two cases:
- when the length of the side rib is known;
- when the height of the pyramid is known.
If we denote the length of the lateral edge (the side of an isosceles triangle) with the symbol L, then the apotema h b is determined by the formula:
h b \u003d √ (L 2 - a 2 / 4).
This expression is the result of applying the Pythagorean theorem for the lateral surface triangle.
If the height h of the pyramid is known, then the apotema h b can be calculated as follows:
h b = √(h 2 + a 2 /4).
It is also not difficult to obtain this expression if we consider a right triangle inside the pyramid formed by the legs h and a / 2 and the hypotenuse h b.
We will show how to apply these formulas by solving two interesting problems.
Problem with Known Surface Area
It is known that the area of the lateral surface of a quadrangular is 108 cm 2 . It is necessary to calculate the value of the length of its apothem h bif the height of the pyramid is 7 cm.
We write the formula for the area S b of the lateral surface through the height. We have:
S b = 2*√(h 2 + a 2 /4) *a.
Here we have simply substituted the corresponding apotema formula into the expression for S b . Let's square both sides of the equation:
S b 2 \u003d 4 * a 2 * h 2 + a 4.
To find the value of a, we make a change of variables:
t 2 + 4*h 2 *t - S b 2 = 0.
We now substitute the known values and solve the quadratic equation:
t 2 + 196*t - 11664 = 0.
We have written only the positive root of this equation. Then the sides of the base of the pyramid will be equal to:
a = √t = √47.8355 ≈ 6.916 cm.
To get the length of apotema, just use the formula:
h b \u003d √ (h 2 + a 2 / 4) \u003d √ (7 2 + 6.916 2 / 4) ≈ 7.808 cm.
Lateral surface of the pyramid of Cheops
Let's determine the value of the lateral surface area for the largest Egyptian pyramid. It is known that at its base lies a square with a side length of 230.363 meters. The height of the structure was originally 146.5 meters. Substitute these numbers into the corresponding formula for S b , we get:
S b \u003d 2 * √ (h 2 + a 2 / 4) * a \u003d 2 * √ (146.5 2 + 230.363 2 / 4) * 230.363 ≈ 85860 m 2.
The found value is slightly larger than the area of 17 football fields.
In this lesson:
- Task 1. Find the total surface area of the pyramid
- Task 2. Find the area of the lateral surface of a regular triangular pyramid
.
Note . If you need to solve a problem in geometry, which is not here - write about it in the forum. In tasks, instead of the "square root" symbol, the sqrt () function is used, in which sqrt is the square root symbol, and the radical expression is indicated in brackets. For simple radical expressions, the sign "√" can be used.
Task 1. Find the total surface area of a regular pyramid
The height of the base of a regular triangular pyramid is 3 cm, and the angle between the side face and the base of the pyramid is 45 degrees.Find the total surface area of the pyramid
Solution.
At the base of a regular triangular pyramid lies an equilateral triangle.
Therefore, to solve the problem, we use the properties of a regular triangle: 
We know the height of the triangle, from where we can find its area.
h = √3/2a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3
From where the area of the base will be equal to:
S = √3/4 a 2
S = √3/4 (6 / √3) 2
S = 3√3
In order to find the area of the side face, we calculate the height KM. The OKM angle, according to the problem statement, is 45 degrees.
In this way:
OK / MK = cos 45
Let's use the table of values of trigonometric functions and substitute the known values.
OK / MK = √2/2
We take into account that OK is equal to the radius of the inscribed circle. Then
OK = √3/6 a
OK = √3/6 * 6/√3 = 1
Then
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2
The area of the side face is then equal to half the product of the height and the base of the triangle.
Sside = 1/2 (6 / √3) (2/√2) = 6/√6
Thus, the total surface area of the pyramid will be equal to
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6
Answer: 3√3 + 18/√6
Task 2. Find the lateral surface area of a regular pyramid
In a regular triangular pyramid, the height is 10 cm, and the side of the base is 16 cm . Find the lateral surface area .Solution.
Since the base of a regular triangular pyramid is an equilateral triangle, then AO is the radius of the circumscribed circle around the base.
(It follows from)
The radius of a circle circumscribed around an equilateral triangle is found from its properties 
Whence the length of the edges of a regular triangular pyramid will be equal to:
AM 2 = MO 2 + AO 2
the height of the pyramid is known by the condition (10 cm), AO = 16√3/3
AM 2 = 100 + 256/3
AM = √(556/3)
Each side of the pyramid is an isosceles triangle. The area of an isosceles triangle is found from the first formula below 
S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) - 8))
S = 8 sqrt((556/3) - 64)
S = 8 sqrt(364/3)
S = 16 sqrt(91/3)
Since all three faces of a regular pyramid are equal, the lateral surface area will be equal to
3S = 48√(91/3)
Answer: 48 √(91/3)
Task 3. Find the total surface area of a regular pyramid
The side of a regular triangular pyramid is 3 cm and the angle between the side face and the base of the pyramid is 45 degrees. Find the total surface area of the pyramid.
Solution.
Since the pyramid is regular, it has an equilateral triangle at its base. So the area of the base is 
So = 9 * √3/4
In order to find the area of the side face, we calculate the height KM. The OKM angle, according to the problem statement, is 45 degrees.
In this way:
OK / MK = cos 45
Let's use

