Cтраница 1

Колебательный процесс в низковольтной цепи прекращается уже в течение первого периода высокочастотных колебаний, так как во второй половине периода этих колебаний направление тока становится противоположным по отношению к току в силовой цепи. Для увеличения яркости искры в генераторе предусмотрена возможность дальнейшего увеличения емкости.  

Колебательные процессы охватывают обширный круг явлений, для которых характерно повторение их характеристик через определенные промежутки времени.  

Колебательный процесс возникает в системе, когда наряду с силой, выводящей ее из состояния равновесия, есть и восстанавливающая (возвращающая) сила. Что будет, если восстанавливающая сила действует на систему с некоторым постоянным запаздыванием. Причем, если такая неустойчивость, связанная с эффектами запаздывания, вредна для корабельных стабилизирующих механизмов, то она полезна при разработке электронных генераторов.  

Колебательные процессы, обусловливающие величину динамических нагрузок на штанги, по существу определяют форму динамо-грамм, записываемых у полированного штока.  

Колебательный процесс в контуре происходит при ненулевых начальных условиях. Начальный ток в индуктивности х определяется из следующих соображений. Выключатель В разрывает цепь при прохождении тока tB - i0 - ic через нуль.  

Колебательные процессы могут возникать также в электрических машинах и других электрических установках, имеющих значительные индуктивности и вращающиеся массы, при включениях, отключениях и резких изменениях режима работы. При некоторых условиях появляются не затухающие, а раскачивающиеся колебания. Такие колебания могут привести к серьезным нарушениям работы электрических установок и даже вызвать аварии. Поэтому при разработке систем управления электрическими машинами и другими установками необходимо в ряде случаев применять специальные меры для быстрейшего затухания колебательных процессов (вводить в их цепи сопротивления и пр.  

Колебательные процессы и колебательные границы устойчивости всевозможных нелинейных систем часто можно определять методом гармонической линеаризации, понятие о которой было дано выше. Существуют и другие методы. Наиболее эффективными здесь оказываются численно-графические методы построения переходных процессов, а также, особенно, методы электрического моделирования на математических машинах непрерывного и дискретного действия.  

Колебательные процессы и колебательные границы устойчивости всевозможных нелинейных систем часто можно определять методом гармонической линеаризации, понятие о которой было дано выше.  

Колебательные процессы широко распространены в природе и технике. Качание маятника часов, волны на воде, переменный электрический ток, свет, звук являются примерами колебаний различных физических величин. При движении маятника колеблется координата его центра тяжести. В случае переменного тока колеблются напряжение и ток в цепи. Эти два процесса качественно совершенно различны по своей физической природе. Однако количественные закономерности этих процессов имеют между собой очень много общего.  

Колебательные процессы в штангах вызываются не только работой поверхностного оборудования, но и движением плунжера. Здесь более желательны синхронные колебания, так как в данном случае они не приводят к перегрузкам.  

Колебательные процессы широко распространены в природе и технике. Качание маятника часов, волны на воде, переменный электрический ток, свет, звук являются примерами колебаний различных физических величин. При движении маятника колеблется координата его центра тяжести. В случае переменного тока колеблются напряжение и ток в цепи. Эти два процесса качественно совершенно различны по своей физической природе. Однако количественные закономерности этих процессов имеют между собой очень много общего.  

Свободные колебания в контуре.

Рассмотренные в предыдущих разделах цепи переменного тока наводят на мысль, что пара элементов − конденсатор и катушка индуктивности образуют своеобразную колебательную систему. Сейчас мы покажем, что это действительно так, в цепи состоящей только из этих элементов (рис. 669) возможны даже свободные колебания, то есть без внешнего источника ЭДС.

рис. 669
 Поэтому цепь (или часть другой цепи), состоящая из конденсатора и катушки индуктивности называется колебательным контуром .
 Пусть конденсатор зарядили до заряда qo и затем подключили к нему катушку индуктивности. Такую процедуру легко осуществить с помощью цепи, схема которой показана на рис. 670: сначала ключ замыкают в положении 1 , при этом конденсатор заряжается до напряжения, равного ЭДС источника, после чего ключ перебрасывают в положения 2 , после чего начинается разрядка конденсатора через катушку.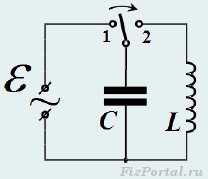

рис. 670
 Для определения зависимости заряда конденсатора от времени q(t) применим закон Ома, согласно которому напряжение на конденсаторе U C = q/C равно ЭДС самоиндукции, возникающей в катушке

здесь, «штрих» означает производную по времени.
 Таким образом, оказывается справедливым уравнение

 В этом уравнении содержится две неизвестных функции − зависимости от времени заряда q(t) и силы тока I(t) , поэтому его решить нельзя. Однако сила тока является производной от заряда конденсатора q / (t) = I(t) , поэтому производная от силы тока является второй производной от заряда

 С учетом этого соотношения, перепишем уравнение (1) в виде

 Поразительно, но это уравнение полностью совпадает с хорошо изученным нами уравнением гармонических колебаний (вторая производная от неизвестной функции пропорциональна самой этой функции с отрицательным коэффициентом пропорциональности x // = −ω o 2 x )! Следовательно, решением этого уравнения будет гармоническая функция

с круговой частотой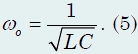

 Эта формула определяет собственную частоту колебательного контура . Соответственно период колебаний заряда конденсатора (и силы тока в контуре) равен

 Полученное выражение для периода колебаний называется формулой Дж. Томпсона .
 Как обычно, для определения произвольных параметров A , φ в общем решении (4) необходимо задать начальные условия − заряд и силу тока в начальный момент времени. В частности, для рассмотренного примера цепи рис. 670, начальные условия имеют вид: при t = 0 , q = q o , I = 0 , поэтому зависимость заряда конденсатора от времени будет описываться функцией

а сила тока изменяется со временем по закону

 Приведенное рассмотрение колебательного контура является приближенным − любой реальный контур обладает активным сопротивлением (соединительных проводов и обмотки катушки).

рис. 671
 Поэтому в уравнении (1) следует учесть падение напряжения на этом активном сопротивлении, поэтому это уравнение приобретет вид

который с учетом связи между зарядом и силой тока, преобразуется к форме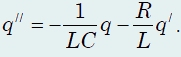

 Это уравнение нам также знакомо – это уравнение затухающих колебаний

причем коэффициент затухания, как и следовало ожидать, пропорционален активному сопротивлению цепи β = R/L .
 Процессы, происходящие в колебательном контуре, могут быть также описаны и с помощью закона сохранения энергии. Если пренебречь активным сопротивлением контура, то сумма энергий электрического поля конденсатора и магнитного поля катушки остается постоянной, что выражается уравнением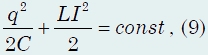

которое также является уравнением гармонических колебаний с частотой, определяемой формулой (5). По свое форме это уравнение также совпадает уравнениями, следующими из закона сохранения энергии при механических колебаниях. Так как, уравнения, описывающие колебания электрического заряда конденсатора, аналогичны уравнениям, описывающим механические колебания, то можно провести аналогию между процессами, протекающими в колебательном контуре, и процессами в любой механической системе. На рис. 672 такая аналогия проведена для колебаний математического маятника. В этом случае аналогами являются «заряд конденсатора q(t) − угол отклонения маятника φ(t) » и «сила тока I(t) = q / (t) − скорость движения маятника V(t) ».



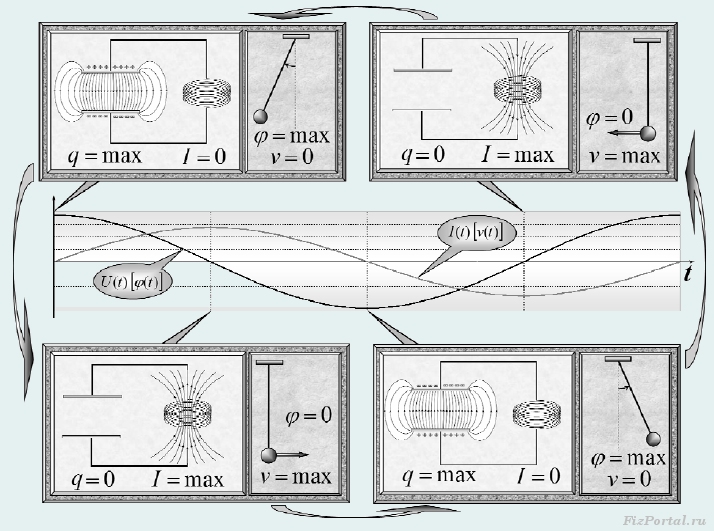
рис. 672
 Пользуясь этой аналогией, качественно опишем процесс колебаний заряда и электрического тока в контуре. В начальный момент времени конденсатор заряжен, сила электрического тока равна нулю, вся энергия заключена в энергии электрического поля конденсатора (что аналогично максимальному отклонения маятника от положения равновесия). Затем конденсатор начинает разряжаться, сила тока возрастает, при этом в катушке возникает ЭДС самоиндукции, которая препятствует возрастанию тока; энергия конденсатора уменьшается, переходя в энергию магнитного поля катушки (аналогия – маятник движется к нижней точки с возрастанием скорости движения). Когда заряд на конденсаторе становится равным нулю, сила тока достигает максимального значения, при этом вся энергия превращается в энергию магнитного поля (маятник достиг нижней точки, скорость его максимальна). Затем магнитное поле начинает убывать, при этом ЭДС самоиндукции поддерживает ток в прежнем направлении, при этом конденсатор начинает заряжаться, причем знаки зарядов на обкладках конденсатора противоположны начальному распределению (аналог − маятник движется к противоположному начальному максимальному отклонению). Затем ток в цепи прекращается, при этом заряд конденсатора становится опять максимальным, но противоположным по знаку (маятник достиг максимального отклонения), после чего процесс повторятся в противоположном направлении.

ЛЕКЦИЯ №8

Механика

Колебания

Колебательное движение. Кинематические и динамические характеристики колебательного движения. Математический, физический и пружинный маятник.

Мы живем в мире, где колебательные процессы являются неотъемлемой частью нашего мира и встречаются повсеместно.

Колебательным процессом или колебанием называется процесс, отличающийся той или иной степенью повторяемости.

Если колеблющаяся величина повторяет свои значения через равные промежутки времени, то такие колебания называются периодическими, а эти промежутки времени называются периодом колебания.

В зависимости от физической природы явления различают колебания: механические, электромеханические, электромагнитные и т.д.

Колебания широко распространены природе и технике. Колебательные процессы лежат в основе некоторых отраслей механики. В рамках этого курса лекций мы будем говорить только о механических колебаниях.

В зависимости от характера воздействия на колебательную систему различают колебания: 1. Свободные или собственные, 2. Вынужденные колебания, 3. Автоколебания, 4. Параметрические колебания.

Свободными колебаниями называются колебания происходящие без внешнего воздействия и вызванные первоначальным «толчком».

Вынужденные колебания происходят под действием периодической внешней силы

Автоколебания так же совершаются под действием внешней силы, но момент воздействия силы на систему определяется самой колебательной системой.

При параметрических колебаниях за счет внешних воздействий происходит периодическое изменение параметров системы, которое и вызывает этот тип колебаний .

Простейшими по форме являются гармонические колебания

Гармоническими колебаниями называются колебания, происходящие по закону sin или cos . Примером гармонических колебаний является колебание математического маятника

Максимальное отклонение колеблющейся величины в процессе колебаний называетсяамплитудой колебаний (А). Время, за которое совершается одно полное колебание, называется периодом колебаний (Т). Обратная величина периоду колебаний называется частотой колебаний (). Часто колебаний умноженная на 2 называется циклической частотой (). Таким образом гармонические колебания описываются выражением

Здесь ( t +  0 ) фаза колебания, а  0 – начальная фаза

Простейшими механическими колебательными системами являются так называемые: математический, пружинный и физический маятники. Рассмотрим эти маятники более подробно

8.1. Математический маятник

Математическим маятником называется колебательная система состоящая из массивного точечного тела подвешенного в поле сил тяжести на нерастяжимой невесомой нити.

В нижней точке маятник обладает минимумом потенциальной энергии. Отклоним маятник на угол  . Центр тяжести массивного точечного тела поднимется на высоту  h и при этом потенциальная энергия маятника возрастет на величину mg  h . Кроме того в отклоненном положении на груз действует сила тяжести и сила натяжения нити. Линии действия этих сил не совпадают, и на груз действует результирующая сила стремящаяся вернуть его в положение равновесия. Если груз не удерживать, то под действием этой силы он начнет перемещаться в исходное равновесное положение, его кинетическая энергия вследствие возрастания скорости будет увеличиваться, при этом потенциальная энергия будет уменьшаться. При достижении точки равновесия на тело уже не будет действовать результирующая сила (сила тяжести в этой точке компенсируется силой натяжения нити). Потенциальная энергия тела в этой точке будет минимальна, а кинетическая энергия напротив, будет иметь свое максимальное значение. Тело, двигаясь по инерции, пройдет положение равновесия и начнет от него удаляться, что приведет к возникновению результирующей силы (от силы натяжения и силы тяжести), которая будет направлена против движения тела, тормозя его. При этом начинается уменьшение кинетической энергии груза и возрастания его потенциальной энергии. Этот процесс будет продолжаться до полного исчерпания запасов кинетической энергии и перехода ее в потенциальную. При этом отклонение груза от положения равновесия достигнет максимальной величины и процесс повторится. Если в системе нет трения, колебания груза будут происходить бесконечно долгое время.

Таким образом, колебательные механические системы характеризуются тем, что при отклонении их из положения равновесия в системе возникает возвращающая сила стремящаяся вернуть систему в положение равновесия. При этом возникают колебания сопровождающиеся периодическим переходом потенциальной энергии системы в ее кинетическую энергию и обратно.

Рассчитаем колебательный процесс. Момент сил М действующий на маятник очевидно равен - mglsin  Знак минус отражает тот факт, что момент сил стремится вернуть груз в положение равновесия. С другой стороны по основному закону вращательного движения М= Id 2  / dt 2 . Таким образом, получим равенство

Б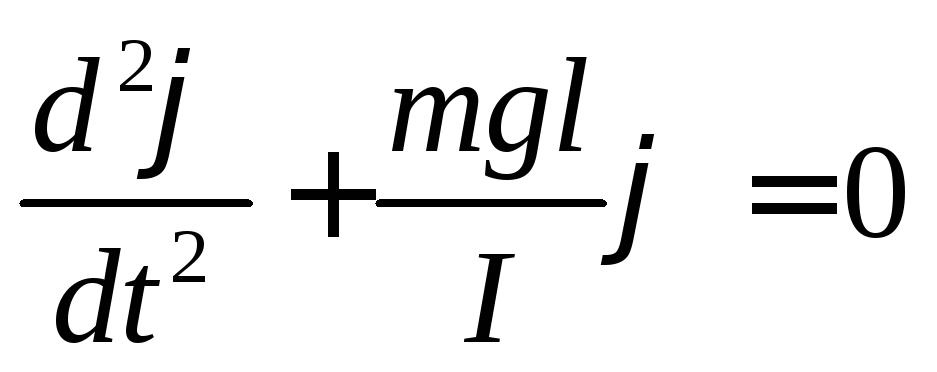

удем рассматривать только малые углы отклонения маятника из положения равновесия. Тогдаsin  ≈  . И наше равенство примет вид:

Д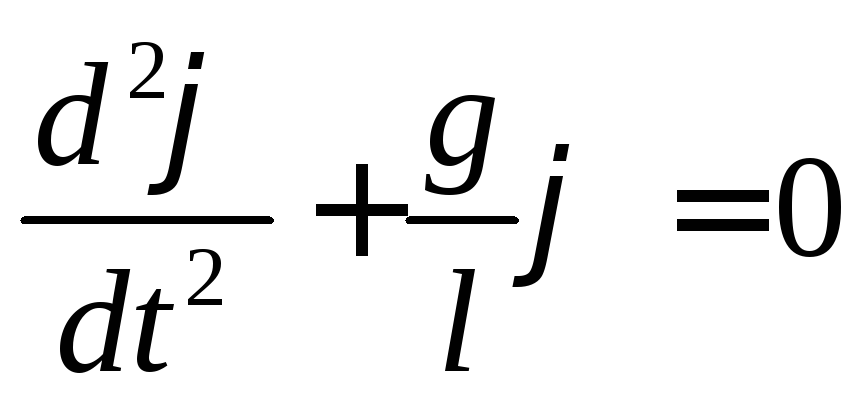

ля математического маятника справедливоI = ml 2 . Подставляя это равенство в полученное выражение, получаем уравнение описывающее процесс колебания математического маятника:

Это дифференциальное уравнение описывает колебательный процесс. Решением этого уравнения являются гармонические функции sin ( t +  0 ) или cos ( t +  0 ) Действительно подставим любую из этих функций в уравнение и получим:  2 = g / l . Таким образом, если это условие выполнено, то функции sin ( t +  0 ) или cos ( t +  0 ) превращают дифференциальное уравнение колебаний в тождество.

О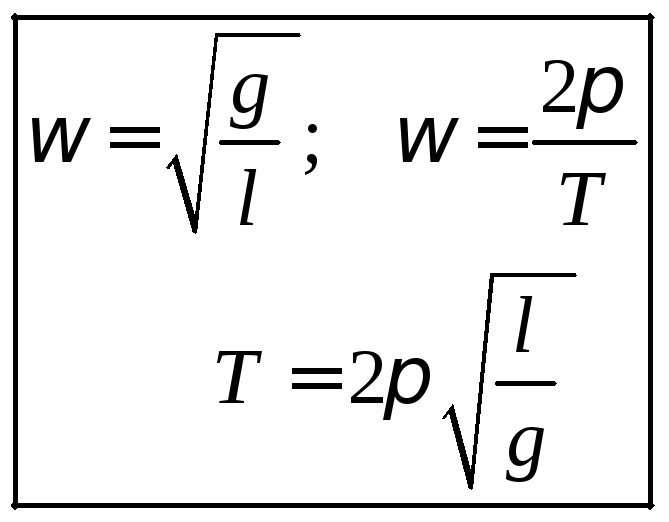

тсюда циклическая частота и период колебаний гармонического маятника выражается как:

Амплитуда колебаний находится из начальных условий задачи.

Как видим, частота и период колебаний математического маятника не зависит от массы груза и зависят только от ускорения свободного падения и длины нити подвеса, что позволяет использовать маятник как простой, но очень точный прибор для определения ускорения свободного падения.

Другим видом маятника является любое физическое тело, подвешенное за какую либо точку тела и имеющее возможность совершать колебательное движение.

8.2. Физический маятник

Возьмем произвольное тело, пронзим его в какой либо точке несовпадающей с его центром масс осью вокруг которой тело может свободно поворачиваться. Подвесим тело на этой оси, и отклоним его из положения равновесия на некоторый угол .

Т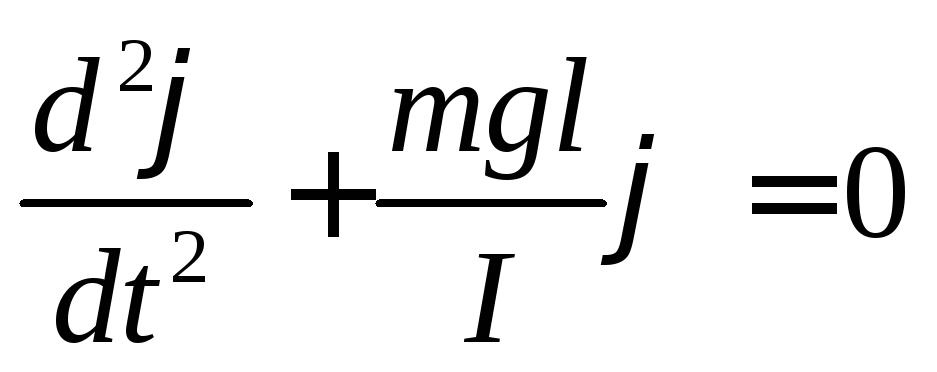

огда на тело с моментом инерцииI относительно оси О будет действовать возвращающий в положение равновесия момент М = - mglsin  и колебания физического маятника как и математического будут описываться дифференциальным уравнением:

Так как для разных физических маятников момент инерции будет выражаться по разному, то его не будем расписывать как в случае с математическим маятником. Это уравнение так же имеет вид уравнения колебаний, решением которого являются функции описывающие гармонических колебаний. При этом циклическая частота ( ) , период колебаний (Т) определяются как:

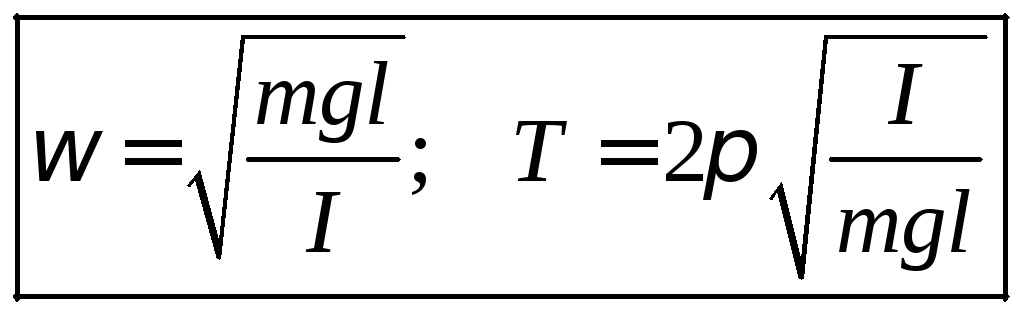
Мы видим, что в случае физического маятника период колебаний зависит от геометрии тела маятника, а не от его массы, как и в случае математического маятника. Действительно в выражение для момента инерции входит масса маятника в первой степени. Момент инерции в выражении для периода колебаний стоит в числителе, в то время как масса маятника входит в знаменатель и тоже в первой степени. Таким образом, масса в числителе сокращается с массой в знаменателе.

Физический маятник обладает еще одной характеристикой это приведенная длина.

Приведенной длиной физического маятника называется длина математического маятника период, которого совпадает с периодом физического маятника.

Это определение позволяет легко определить выражение для приведенной длины.

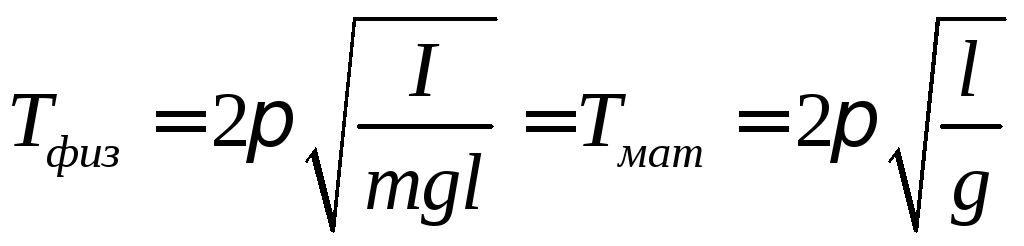
Сравнивая эти выражения получим

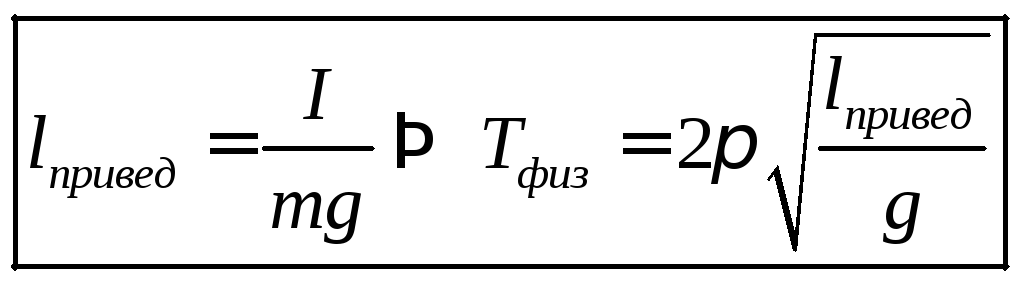
Если на линии проведенной от точки подвеса через центр масс физического маятника отложить (начиная от точки подвеса) приведенную длину физического маятника, то в конце этого отрезка будет точка, которая обладает замечательным свойством. Если физический маятник подвесить за эту точку, то его период колебаний будет тот же, что и в случае подвешивания маятника в прежней точке подвеса. Эти точки называются центрами качания физического маятника.

Рассмотрим еще одну простейшую колебательную систему совершающую гармонические колебания

8.3. Пружинный маятник

П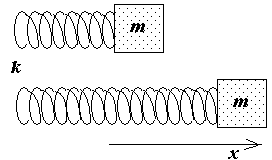редставим, что к концу пружины с коэффициентом жесткостиk прикреплен груз массой m .

Если мы переместим груз вдоль оси х растянув пружину то на груз будет действовать возвращающая в положение равновесия сила F возвр = - kx . Если груз отпустить, то эта сила вызовет ускорение d 2 x / dt 2 . Согласно второму закону Ньютона мы получим:

md 2 x / dt 2 = - kx из этого уравнения получаем уравнение колебания груза на пружине в окончательном виде: d 2 x / dt 2 + (k / m ) x = 0

Э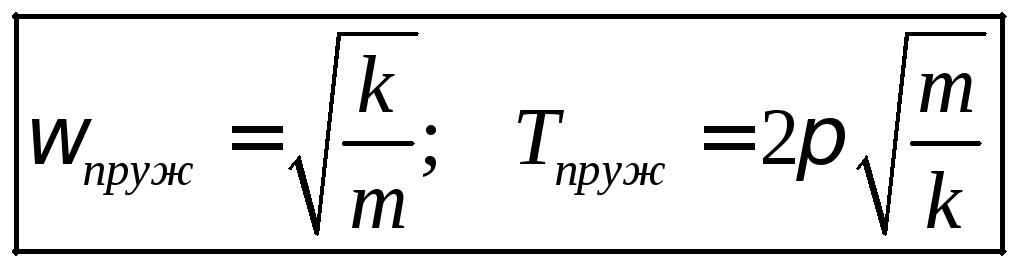

то уравнение колебаний имеет такой же вид как и уравнения колебаний в уже рассматриваемых случаях, а это значит, что решением этого уравнения будут такие же гармонические функции. Частота и период колебаний будут соответственно равны

Причем сила тяжести ни коем образом не влияет на колебания пружинного маятника. Так как в этом случае она является постоянно действующим фактором, действующим все время в одну сторону и не имеющая ничего общего с возвращающей силой.

Таким образом как мы видим колебательный процесс в механической колебательной системе характеризуется прежде всего наличие в системе возвращающей силы действующей на систему, а сами колебания характеризуются: амплитудой колебания их периодом, частотой и фазой колебаний.