Виды чисел. Натуральные, целые, рациональные и действительные.Число - абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.

Для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел. Основные виды чисел включают в себя: натуральные числа, целые числа, рациональные числа, действительные числа.

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N ={1,2,3,....}

Целые числа – это числа из множества {0, 1, -1, 2, -2, ....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z . Можно сказать, что Z ={...,-3,-2,-1,0,1,2,3,....}.

Рациональные числа – это числа, представимые в виде дроби , где m - целое число, а n - натуральное число. При этом число m называется числителем , а число n - знаменателем дроби . Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся. Для обозначения рациональных чисел используется латинская буква Q . Q = {... ;-3;-2,5;-2;-1;0; ;1;2;3;3,5....}. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести: , , . В реальной жизни рациональные числа используются для счёта частей некоторых целых, но делимых объектов, например, тортов или других продуктов, разрезаемых на несколько частей, или для грубой оценки пространственных отношений протяжённых объектов.

Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это , , .

Любое действительное число можно отобразить на числовой прямой:

Для перечисленных выше множеств чисел справедливо следующее высказывание:

То есть множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. А множество рациональных чисел входит во множество действительных чисел. Это высказывание можно проиллюстрировать с помощью кругов Эйлера.

Цель: Знать, что такое натуральное, целое, рациональное число, периодическая дробь; уметь записывать бесконечную десятичную дробь в виде обыкновенной, уметь выполнять действия с десятичными и обыкновенными дробями.

1. Закрепить изученный материал, меняя виды работы, по данной теме “Целые и рациональные числа”.
2. Развивать навыки и умения, в выполнении действий с десятичными и обыкновенными дробями, развивать логическое мышление, правильную и грамотную математическую речь, развитие самостоятельности и уверенности в своих знаниях и умениях при выполнении разных видов работ.
3. Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся.

I. Организационный момент.
II. Новая тема:
“Целые и рациональные числа”.
1.Теоретическая часть.
2. Практическая часть.
3. Работа по учебнику и у доски.
4. Самостоятельная работа по вариантам.
III. Итог.
1. По вопросам.
IV. Домашнее задание.

Ход урока

I. Организационный момент.

Эмоциональный настрой и готовность преподавателя и обучающихся на урок. Сообщение цели и задач.

II. Новая тема: “Целые и рациональные числа”:

Теоретическая часть.

1. Первоначально под числом понимали лишь натуральные числа. Которых достаточно для счёта отдельных предметов.

Множество N = {1; 2; 3...} натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что сумма и произведение натуральных чисел являются числами натуральными.

2. Однако разность двух натуральных чисел уже не всегда является натуральным числом.

(Приведите примеры: 5 – 5 = 0; 5 – 7 = – 2, числа 0 и – 2 не являются натуральными).

Так, результат вычитания двух одинаковых натуральных чисел приводит к понятию нуля и введению множества целых неотрицательных чисел

Z 0 = {0; 1; 2;...}.

3. Чтобы сделать выполнимой операцию вычитания, вводят отрицательные целые числа, то есть числа, противоположные натуральным. Таким образом получают множество целых чисел Z = {...; -3; -2; -1; 0; 1; 2;...}.

Чтобы сделать выполнимой операцию деления на любое число, не равное нулю, необходимо к множеству всех целых чисел присоединить множество всех положительных и отрицательных дробей. В результате получается множество рациональных чисел Q = .

При выполнении четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.

4. Каждое рациональное число можно представить в виде периодической десятичной дроби.

Вспомним, что такое периодическая дробь . Это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. Например, 0,3333…= 0,(3);

1,057373…=1,05(73).

Читаются эти дроби так: “0 целых и 3 в периоде”, “1 целая, 5 сотых и 73 в периоде”.

Запишем рациональные числа в виде бесконечной периодической десятичной дроби:

натуральное число 25 = 25,00…= 25,(0);

целое число -7 = -7,00…= -7,(0);

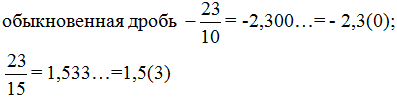
(пользуемся алгоритмом деления уголком).

5. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби , где m – целое число, n – натуральное число.

Рассмотрим пример:

1) Пусть x= 0,2(18) умножая на 10, получаем 10x = 2,1818…(Нужно умножить дробь на 10 n , где n – количество десятичных знаков, содержащихся в записи этой дроби до периода: x10 n).

2) Умножая обе части последнего равенства на 100, находим

1000x = 218,1818…(Умножая на 10 k , где k – количество цифр в периоде x10 n 10 k = x10 n+k).

3) Вычитая из равенства (2) равенство (1), получаем 990x = 216, x = .

Практическая часть.

1. Записать в виде десятичной дроби:

1) – на доске;

3) – за доской один учащийся записывает решение, остальные решают на местах, потом проверяют друг друга;

4) – под диктовку, все выполняют задание, а один проговаривает вслух.

2. Выполнить действия и записать результат в виде десятичной дроби:

1) – на доске;

3) – под диктовку, все выполняют задание, а один проговаривает вслух;

5) – самостоятельно с последующей проверкой.

3. Записать в виде обыкновенной дроби бесконечную десятичную дробь:

6) -2,3(82) – преподаватель показывает на доске решение, опираясь на алгоритм.

Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа: 1; 2; 3; 4;...

Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица - это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:

Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:

с - это всегда натуральное число.

Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе - нет.

Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b

где с - натуральное число, то это значит, что a делится на b нацело. В этом примере a - делимое, b - делитель, c - частное.

Делитель натурального числа - это натуральное число, на которое первое число делится нацело.

Каждое натуральное число делится на единицу и на себя.

Простые натуральные числа делятся только на единицу и на себя. Здесь, имеется ввиду, делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.

Единицу не считают простым числом.

Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел: 4; 6; 8; 9; 10

Единицу не считают составным числом.

Множество натуральных чисел составляют единица, простые числа и составные числа.

Множество натуральных чисел обозначается латинской буквой N.

Свойства сложения и умножения натуральных чисел:

переместительное свойство сложения

сочетательное свойство сложения

(a + b) + c = a + (b + c);

переместительное свойство умножения

сочетательное свойство умножения

(ab) c = a (bc);

распределительное свойство умножения

a (b + c) = ab + ac;

Целые числа

Целые числа - это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным - это целые отрицательные числа, например: -1; -2; -3; -4;...

Множество целых чисел обозначается латинской буквой Z.

Рациональные числа

Рациональные числа - это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Примеры: -1,(0); 3,(6); 0,(0);...

Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера: 22/6 = 3,(6);

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Ещё пример: рациональное число -9 может быть представлено в виде простой дроби как -18/2 или как -72/8.

Множество рациональных чисел обозначается латинской буквой Q.

Иррациональные числа

Иррациональные числа - это бесконечные непериодические десятичные дроби.

Примеры: число пи = 3,141592... число е = 2,718281...

Действительные числа

Действительные числа – это все рациональные и все иррациональные числа.

Множество действительных чисел обозначается латинской буквой R.