परिभाषा 9.3.वेक्टर एक्स बुलाया खुद का वेक्टरमैट्रिक्स लेकिनअगर ऐसी कोई संख्या है λ, कि समानता रखती है: लेकिन एक्स= λ एक्स, अर्थात्, आवेदन करने का परिणाम एक्स मैट्रिक्स द्वारा दिया गया रैखिक परिवर्तन लेकिन, संख्या से इस सदिश का गुणन है λ . नंबर ही λ बुलाया अपना नंबरमैट्रिक्स लेकिन.
सूत्रों में प्रतिस्थापन (9.3) x` j = x j ,हम eigenvector के निर्देशांक निर्धारित करने के लिए समीकरणों की एक प्रणाली प्राप्त करते हैं:
. (9.5)
इस रैखिक सजातीय प्रणाली का एक गैर-तुच्छ समाधान तभी होगा जब इसका मुख्य निर्धारक 0 (क्रैमर का नियम) हो। इस शर्त को फॉर्म में लिखकर:
हमें eigenvalues निर्धारित करने के लिए एक समीकरण मिलता है λ बुलाया विशेषता समीकरण. संक्षेप में, इसे निम्नानुसार दर्शाया जा सकता है:
| ए-λई | = 0, (9.6)
चूँकि इसका बायाँ भाग आव्यूह का निर्धारक है ए-λई. के संबंध में बहुपद | ए-λई| बुलाया विशेषता बहुपदमैट्रिसेस ए.
विशेषता बहुपद के गुण:
1) एक रैखिक परिवर्तन की विशेषता बहुपद आधार की पसंद पर निर्भर नहीं करता है। प्रमाण। 
(देखें (9.4)), लेकिन 
इस तरह, । इस प्रकार, आधार की पसंद पर निर्भर नहीं करता है। इसलिए, और | ए-λई| नए आधार पर संक्रमण पर नहीं बदलता है।
2) यदि मैट्रिक्स लेकिनरैखिक परिवर्तन है सममित(वे। एक ij = एक जी), तो अभिलक्षणिक समीकरण (9.6) के सभी मूल वास्तविक संख्याएँ हैं।
eigenvalues और eigenvectors के गुण:
1) यदि हम eigenvectors में से एक आधार चुनते हैं एक्स 1, एक्स 2, एक्स 3 eigenvalues के अनुरूप 1 , 2 , 3मैट्रिक्स लेकिन, तो इस आधार पर रैखिक परिवर्तन ए में एक विकर्ण मैट्रिक्स है:
(9.7) इस गुण का प्रमाण eigenvectors की परिभाषा से मिलता है।
2) यदि परिवर्तन eigenvalues लेकिनभिन्न हैं, तो उनके संगत eigenvectors रैखिक रूप से स्वतंत्र हैं।
3) यदि आव्यूह का अभिलक्षणिक बहुपद लेकिनतीन अलग-अलग जड़ें हैं, तो किसी आधार पर मैट्रिक्स लेकिनएक विकर्ण आकार है।
आइए मैट्रिक्स के eigenvalues और eigenvectors खोजें आइए विशेषता समीकरण बनाएं: 
(1- λ
)(5 - λ
)(1 - λ
) + 6 - 9(5 - λ
) - (1 - λ
) - (1 - λ
) = 0, λ
- 7 λ
+ 36 = 0, λ
1 = -2, λ
2 = 3, λ
3 = 6.
प्रत्येक पाए गए मान के अनुरूप eigenvectors के निर्देशांक खोजें λ. (9.5) से यह इस प्रकार है कि यदि एक्स (1) ={एक्स 1 , एक्स 2 , एक्स 3) के अनुरूप आइजनवेक्टर है λ 1 = -2, तब
एक सहयोगी लेकिन अनिश्चित प्रणाली है। इसका हल इस प्रकार लिखा जा सकता है एक्स (1)
={ए,0,-ए), जहां a कोई संख्या है। विशेष रूप से, यदि आपको इसकी आवश्यकता है | एक्स (1)
|=1, एक्स (1)
=
सिस्टम में प्रतिस्थापन (9.5) λ 2 = 3, हमें दूसरे eigenvector के निर्देशांक निर्धारित करने के लिए एक प्रणाली मिलती है - एक्स (2) ={y1,y2,y3}:
, कहाँ पे एक्स (2)
={बी,-बी,बी) या, प्रदान किया गया | एक्स (2)
|=1, एक्स (2)
= 
के लिए λ 3 = 6 eigenvector खोजें एक्स (3) ={जेड1, जेड2, जेड3}:
, एक्स (3)
={सी,2सी, सी) या सामान्यीकृत संस्करण में
एक्स (3) = 
यह देखा जा सकता है एक्स (1) एक्स (2)
= अब-अब= 0, एक्स (1) एक्स (3)
= एसी-एसी= 0, एक्स (2) एक्स (3)
= बीसी- 2बीसी + बीसी= 0. इस प्रकार, इस मैट्रिक्स के eigenvectors जोड़ीदार ओर्थोगोनल हैं।
व्याख्यान 10
द्विघात रूप और सममित मैट्रिक्स के साथ उनका संबंध। एक सममित मैट्रिक्स के eigenvectors और eigenvalues के गुण। द्विघात रूप को विहित रूप में घटाना।
परिभाषा 10.1।द्विघात रूपवास्तविक चर एक्स 1, एक्स 2,…, एक्स एनइन चरों के संबंध में दूसरी डिग्री का एक बहुपद है जिसमें एक मुक्त शब्द और पहली डिग्री की शर्तें शामिल नहीं हैं।
द्विघात रूपों के उदाहरण:
(एन = 2),
(एन = 3). (10.1)
पिछले व्याख्यान में दी गई सममित मैट्रिक्स की परिभाषा को याद करें:
परिभाषा 10.2.वर्ग मैट्रिक्स को कहा जाता है सममित, यदि , अर्थात्, यदि मैट्रिक्स तत्व मुख्य विकर्ण के संबंध में सममित हैं, तो समान हैं।
सममित मैट्रिक्स के eigenvalues और eigenvectors के गुण:
1) एक सममित मैट्रिक्स के सभी eigenvalues वास्तविक हैं।
सबूत (के लिए एन = 2).
चलो मैट्रिक्स लेकिनकी तरह लगता है: 
. आइए विशेषता समीकरण बनाते हैं:
(10.2) विभेदक का पता लगाएं:
इसलिए, समीकरण के केवल वास्तविक मूल हैं।
2) सममित मैट्रिक्स के आइजेनवेक्टर ओर्थोगोनल होते हैं।
सबूत (के लिए एन= 2).
eigenvectors के निर्देशांक और समीकरणों को संतुष्ट करना चाहिए।
विकर्ण-प्रकार के मैट्रिसेस सबसे सरल रूप से व्यवस्थित होते हैं। सवाल यह उठता है कि क्या ऐसा आधार खोजना संभव है जिसमें रैखिक संचालिका के मैट्रिक्स का विकर्ण रूप हो। ऐसा आधार मौजूद है।
मान लीजिए कि एक रैखिक स्थान R n और इसमें कार्यरत एक रैखिक संकारक A दिया गया है; इस मामले में, ऑपरेटर A, R n को अपने आप में लेता है, अर्थात A:R n → R n।
परिभाषा।
एक गैर-शून्य वेक्टर को ऑपरेटर ए का एक आइजनवेक्टर कहा जाता है यदि ऑपरेटर ए इसके लिए एक वेक्टर कॉललाइनर में अनुवाद करता है, अर्थात। संख्या को eigenvector के अनुरूप ऑपरेटर A का eigenvalue या eigenvalue कहा जाता है।
हम eigenvalues और eigenvectors के कुछ गुणों पर ध्यान देते हैं।
1. eigenvectors का कोई रैखिक संयोजन 
एक ही eigenvalue के अनुरूप ऑपरेटर A का eigenvector समान eigenvalue वाला एक eigenvector है।
2. आइजनवेक्टर संचालिका A, जोड़ीवार भिन्न eigenvalues 1 , 2 , …, m के साथ रैखिक रूप से स्वतंत्र हैं।
3. यदि eigenvalues 1 =λ 2 = m = , तो eigenvalue m से अधिक रैखिक रूप से स्वतंत्र eigenvectors से मेल नहीं खाता है।
इसलिए, यदि n रैखिक रूप से स्वतंत्र eigenvectors हैं 
विभिन्न eigenvalues 1, λ 2, …, n के अनुरूप, तो वे रैखिक रूप से स्वतंत्र हैं, इसलिए, उन्हें अंतरिक्ष R n के आधार के रूप में लिया जा सकता है। आइए हम रैखिक ऑपरेटर ए के मैट्रिक्स के रूप को उसके आइजेनवेक्टर के आधार पर खोजें, जिसके लिए हम ऑपरेटर ए के साथ वैक्टर के आधार पर कार्य करते हैं: 
तब 
.
इस प्रकार, रैखिक ऑपरेटर ए के मैट्रिक्स में इसके eigenvectors के आधार पर एक विकर्ण रूप होता है, और ऑपरेटर ए के eigenvalues विकर्ण पर होते हैं।
क्या कोई अन्य आधार है जिसमें मैट्रिक्स का विकर्ण रूप है? इस प्रश्न का उत्तर निम्नलिखित प्रमेय द्वारा दिया गया है।
प्रमेय। आधार में एक रैखिक ऑपरेटर ए के मैट्रिक्स (i = 1..n) में एक विकर्ण रूप होता है यदि और केवल अगर आधार के सभी वैक्टर ऑपरेटर ए के आइजेनवेक्टर हैं।
eigenvalues और eigenvectors खोजने के लिए नियम
चलो वेक्टर
, जहाँ x 1 , x 2 ,…, x n - आधार के सापेक्ष सदिश के निर्देशांक 
और रेखीय संकारक A का eigenvector है जो eigenvalue के संगत है, अर्थात । इस संबंध को मैट्रिक्स रूप में लिखा जा सकता है 
. (*)
समीकरण (*) को खोजने के लिए एक समीकरण के रूप में माना जा सकता है, और, अर्थात, हम गैर-तुच्छ समाधानों में रुचि रखते हैं, क्योंकि आइजेनवेक्टर शून्य नहीं हो सकता। यह ज्ञात है कि रैखिक समीकरणों की एक सजातीय प्रणाली के गैर-तुच्छ समाधान मौजूद हैं यदि और केवल अगर det(A - E) = 0. इस प्रकार, λ के लिए ऑपरेटर A का एक आइजनवैल्यू होना आवश्यक और पर्याप्त है कि det(A - E) ) = 0.
यदि समीकरण (*) को निर्देशांक रूप में विस्तार से लिखा जाए, तो हमें रैखिक समांगी समीकरणों का एक निकाय प्राप्त होता है:
(1)
कहाँ पे 
रैखिक ऑपरेटर का मैट्रिक्स है।
सिस्टम (1) का एक गैर-शून्य समाधान है यदि इसका निर्धारक डी शून्य के बराबर है
हमें eigenvalues खोजने के लिए एक समीकरण मिला है।
इस समीकरण को अभिलक्षणिक समीकरण कहा जाता है, और इसके बाईं ओर को मैट्रिक्स (ऑपरेटर) A का विशेषता बहुपद कहा जाता है। यदि विशेषता बहुपद की कोई वास्तविक जड़ें नहीं हैं, तो मैट्रिक्स A में कोई आइजनवेक्टर नहीं है और इसे विकर्ण रूप में कम नहीं किया जा सकता है।
मान लीजिए λ 1, λ 2, …, n अभिलक्षणिक समीकरण के वास्तविक मूल हैं, और उनमें गुणज भी हो सकते हैं। इन मूल्यों को बदले में सिस्टम (1) में प्रतिस्थापित करते हुए, हम eigenvectors पाते हैं।
उदाहरण 12.
रैखिक ऑपरेटर ए कानून के अनुसार आर 3 में कार्य करता है, जहां x 1, x 2, .., x n आधार में वेक्टर के निर्देशांक हैं 
, 
, 
. इस ऑपरेटर के eigenvalues और eigenvectors खोजें।
फेसला।
हम इस ऑपरेटर के मैट्रिक्स का निर्माण करते हैं: 
.
हम eigenvectors के निर्देशांक निर्धारित करने के लिए एक प्रणाली बनाते हैं: 
हम विशेषता समीकरण बनाते हैं और इसे हल करते हैं: 
.
1,2 = -1, 3 = 3।
सिस्टम में = -1 को प्रतिस्थापित करते हुए, हमारे पास है: 
या 
जैसा 
, तो दो आश्रित चर और एक मुक्त चर हैं।
मान लीजिए x 1 एक मुक्त अज्ञात है, तब 
हम इस प्रणाली को किसी भी तरह से हल करते हैं और इस प्रणाली का सामान्य समाधान ढूंढते हैं: समाधान की मौलिक प्रणाली में एक समाधान होता है, क्योंकि n - r = 3 - 2 = 1।
eigenvalue = -1 के अनुरूप eigenvectors के सेट का रूप है: , जहां x 1 शून्य के अलावा कोई भी संख्या है। आइए इस सेट से एक वेक्टर चुनें, उदाहरण के लिए, x 1 = 1 सेट करके: 
.
इसी तरह तर्क करते हुए, हम eigenvalue = 3 के अनुरूप eigenvector पाते हैं: 
.
अंतरिक्ष R 3 में आधार में तीन रैखिक रूप से स्वतंत्र वैक्टर होते हैं, लेकिन हमने केवल दो रैखिक रूप से स्वतंत्र आइजेनवेक्टर प्राप्त किए हैं, जिनसे R 3 में आधार नहीं बनाया जा सकता है। नतीजतन, एक रैखिक ऑपरेटर के मैट्रिक्स ए को एक विकर्ण रूप में कम नहीं किया जा सकता है।
उदाहरण 13
एक मैट्रिक्स दिया गया 
.
1. सिद्ध कीजिए कि सदिश 
मैट्रिक्स A का एक eigenvector है। इस eigenvector के अनुरूप eigenvalue खोजें।
2. एक आधार खोजें जिसमें मैट्रिक्स A का विकर्ण रूप हो।
फेसला।
1. यदि , तो एक eigenvector है 
.
सदिश (1, 8, -1) एक eigenvector है। आइजनवैल्यू = -1।
मैट्रिक्स के आधार में एक विकर्ण रूप है जिसमें eigenvectors शामिल हैं। उनमें से एक प्रसिद्ध है। चलिए बाकी ढूंढते हैं।
हम सिस्टम से eigenvectors की तलाश कर रहे हैं: 
विशेषता समीकरण: 
;
(3 + )[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
1 = -3, 2 = 1, 3 = -1।
eigenvalue = -3 के अनुरूप eigenvector खोजें: 
इस प्रणाली के मैट्रिक्स की रैंक दो के बराबर है और अज्ञात की संख्या के बराबर है, इसलिए इस प्रणाली का केवल एक शून्य समाधान x 1 = x 3 = 0 है। x 2 यहां शून्य के अलावा कुछ भी हो सकता है, उदाहरण के लिए, x 2 = 1. इस प्रकार, सदिश (0,1,0) = -3 के संगत एक eigenvector है। चलो देखते है: 
.
यदि = 1, तो हमें निकाय प्राप्त होता है 
मैट्रिक्स की रैंक दो है। अंतिम समीकरण को पार करें।
मान लीजिए x 3 मुक्त अज्ञात है। फिर x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
x 3 = 1 मानते हुए, हमारे पास (-3,-9,1) - एक eigenvector है जो eigenvalue = 1 के अनुरूप है। जाँच करें: 
.
चूंकि eigenvalues वास्तविक और भिन्न हैं, उनके अनुरूप वैक्टर रैखिक रूप से स्वतंत्र हैं, इसलिए उन्हें R 3 में आधार के रूप में लिया जा सकता है। इस प्रकार, आधार में 
, 
, 
मैट्रिक्स ए का रूप है: 
.
एक रैखिक संकारक A:R n → R n के प्रत्येक मैट्रिक्स को एक विकर्ण रूप में कम नहीं किया जा सकता है, क्योंकि कुछ रैखिक ऑपरेटरों के लिए n रैखिक रूप से स्वतंत्र eigenvectors से कम हो सकते हैं। हालाँकि, यदि मैट्रिक्स सममित है, तो बिल्कुल m रैखिक रूप से स्वतंत्र वैक्टर गुणन m के विशेषता समीकरण की जड़ के अनुरूप हैं।
परिभाषा।
एक सममित मैट्रिक्स एक वर्ग मैट्रिक्स है जिसमें मुख्य विकर्ण के संबंध में सममित तत्व समान होते हैं, अर्थात जिसमें .
टिप्पणियों।
1. एक सममित मैट्रिक्स के सभी eigenvalues वास्तविक हैं।
2. एक सममित मैट्रिक्स के eigenvectors जोड़ीवार अलग-अलग eigenvalues के अनुरूप ऑर्थोगोनल हैं।
अध्ययन किए गए उपकरण के कई अनुप्रयोगों में से एक के रूप में, हम दूसरे क्रम के वक्र के रूप को निर्धारित करने की समस्या पर विचार करते हैं।
आव्यूह A के साथ, यदि ऐसी कोई संख्या l है कि AX = lX है।
इस मामले में, संख्या l कहा जाता है eigenvalueवेक्टर एक्स के अनुरूप ऑपरेटर (मैट्रिक्स ए)।
दूसरे शब्दों में, एक eigenvector एक वेक्टर है, जो एक रैखिक ऑपरेटर की कार्रवाई के तहत, एक कोलिनियर वेक्टर में बदल जाता है, अर्थात। बस कुछ संख्या से गुणा करें। इसके विपरीत, अनुचित वैक्टर को बदलना अधिक कठिन होता है।
हम eigenvector की परिभाषा को समीकरणों की एक प्रणाली के रूप में लिखते हैं:
आइए सभी शर्तों को बाईं ओर ले जाएं:
अंतिम प्रणाली को मैट्रिक्स रूप में निम्नानुसार लिखा जा सकता है:
(ए - एलई)एक्स \u003d ओ
परिणामी प्रणाली में हमेशा एक शून्य समाधान X = O होता है। ऐसे सिस्टम जिनमें सभी मुक्त पद शून्य के बराबर होते हैं, कहलाते हैं सजातीय. यदि ऐसी प्रणाली का मैट्रिक्स वर्गाकार है, और इसका निर्धारक शून्य के बराबर नहीं है, तो क्रैमर के सूत्रों के अनुसार, हमें हमेशा एक अनूठा समाधान मिलेगा - शून्य। यह साबित किया जा सकता है कि सिस्टम में गैर-शून्य समाधान हैं यदि और केवल अगर इस मैट्रिक्स का निर्धारक शून्य के बराबर है, अर्थात।
|ए - एलई| = 
= 0
अज्ञात l के साथ इस समीकरण को कहा जाता है विशेषता समीकरण (विशेषता बहुपद) मैट्रिक्स ए (रैखिक ऑपरेटर)।
यह सिद्ध किया जा सकता है कि एक रैखिक संकारक का अभिलक्षणिक बहुपद आधार के चुनाव पर निर्भर नहीं करता है।
उदाहरण के लिए, आइए मैट्रिक्स A = द्वारा दिए गए रैखिक ऑपरेटर के eigenvalues और eigenvectors खोजें।
ऐसा करने के लिए, हम विशेषता समीकरण की रचना करते हैं |А - lЕ| = 
\u003d (1 - एल) 2 - 36 \u003d 1 - 2l + एल 2 - 36 \u003d एल 2 - 2l - 35 \u003d 0; डी \u003d 4 + 140 \u003d 144; eigenvalues l 1 = (2 - 12)/2 = -5; एल 2 \u003d (2 + 12) / 2 \u003d 7.
eigenvectors खोजने के लिए, हम समीकरणों की दो प्रणालियों को हल करते हैं
(ए + 5ई) एक्स = ओ
(ए - 7ई) एक्स = ओ
उनमें से पहले के लिए, विस्तारित मैट्रिक्स रूप लेगा
,
जहां से x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, अर्थात्। एक्स (1) \u003d (- (2/3) एस; एस)।
उनमें से दूसरे के लिए, विस्तारित मैट्रिक्स रूप लेगा
,
जहां से x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; एक्स 1 \u003d (2/3) एस 1, यानी। एक्स (2) \u003d ((2/3) एस 1; एस 1)।
इस प्रकार, इस रैखिक संचालिका के eigenvectors फॉर्म के सभी वैक्टर हैं (-(2/3)c; c) eigenvalue (-5) के साथ और फॉर्म के सभी वैक्टर ((2/3)c 1 ; c 1) के साथ ईजेनवैल्यू 7.
यह साबित किया जा सकता है कि ऑपरेटर ए का मैट्रिक्स इसके eigenvectors के आधार पर विकर्ण है और इसका रूप है:
,
जहां मैं इस मैट्रिक्स के आइजनवैल्यू हैं।
इसका विलोम भी सत्य है: यदि मैट्रिक्स A किसी आधार पर विकर्ण है, तो इस आधार के सभी सदिश इस मैट्रिक्स के eigenvectors होंगे।
यह भी साबित किया जा सकता है कि यदि एक रैखिक ऑपरेटर के पास n जोड़ीदार विशिष्ट eigenvalues है, तो संबंधित eigenvectors रैखिक रूप से स्वतंत्र हैं, और इसी आधार पर इस ऑपरेटर के मैट्रिक्स का एक विकर्ण रूप है।
आइए इसे पिछले उदाहरण से समझाते हैं। आइए हम मनमाना गैर-शून्य मान c और c 1 लें, लेकिन ऐसे कि वैक्टर X (1) और X (2) रैखिक रूप से स्वतंत्र हों, अर्थात। आधार बनेगा। उदाहरण के लिए, चलो c \u003d c 1 \u003d 3, फिर X (1) \u003d (-2; 3), X (2) \u003d (2; 3)।
आइए हम इन वैक्टरों की रैखिक स्वतंत्रता को सत्यापित करें:
12 0. इस नए आधार में मैट्रिक्स A, A * = का रूप लेगा।
इसे सत्यापित करने के लिए, हम सूत्र A * = C -1 AC का उपयोग करते हैं। आइए पहले सी -1 खोजें।
सी -1 = 
;
द्विघात रूप
द्विघात रूप n चरों से f (x 1, x 2, x n) को योग कहा जाता है, जिसका प्रत्येक पद या तो किसी एक चर का वर्ग होता है, या दो भिन्न चरों का गुणनफल होता है, जिसे एक निश्चित गुणांक के साथ लिया जाता है: f (x 1 , एक्स 2, एक्स एन) = 
(एक ij = एक जी)।
इन गुणांकों से बना मैट्रिक्स A कहलाता है आव्यूहद्विघात रूप। यह हमेशा के लिए है सममितमैट्रिक्स (यानी, मुख्य विकर्ण के बारे में एक मैट्रिक्स सममित, एक ij = a ji)।
मैट्रिक्स नोटेशन में, द्विघात रूप का रूप f(X) = X T AX होता है, जहां
वास्तव में
उदाहरण के लिए, आइए द्विघात रूप को मैट्रिक्स रूप में लिखें।
ऐसा करने के लिए, हम द्विघात रूप का एक मैट्रिक्स पाते हैं। इसके विकर्ण तत्व चर के वर्गों पर गुणांक के बराबर होते हैं, और शेष तत्व द्विघात रूप के संबंधित गुणांक के आधे के बराबर होते हैं। इसलिए
मान लें कि चर X का आव्यूह-स्तंभ आव्यूह-स्तंभ Y के एक गैर-अपक्षयी रैखिक रूपांतरण द्वारा प्राप्त किया जाता है, अर्थात्। X = CY, जहाँ C क्रम n का एक अपक्षयी मैट्रिक्स है। तब द्विघात रूप f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y।
इस प्रकार, एक गैर-पतित रैखिक परिवर्तन सी के तहत, द्विघात रूप का मैट्रिक्स रूप लेता है: ए * = सी टी एसी।
उदाहरण के लिए, आइए द्विघात रूप f(y 1, y 2) को द्विघात रूप f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 से रैखिक रूपांतरण द्वारा प्राप्त किया गया है।
द्विघात रूप कहलाता है कैनन का(यह है विहित दृश्य) यदि इसके सभी गुणांक a ij = 0 i j के लिए, अर्थात।
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =।
इसका मैट्रिक्स विकर्ण है।
प्रमेय(सबूत यहां नहीं दिया गया है)। गैर-पतित रैखिक परिवर्तन का उपयोग करके किसी भी द्विघात रूप को एक विहित रूप में कम किया जा सकता है।
उदाहरण के लिए, आइए हम द्विघात रूप को विहित रूप में कम करें
एफ (एक्स 1, एक्स 2, एक्स 3) \u003d 2x 1 2 + 4x 1 एक्स 2 - 3x 2 2 - एक्स 2 एक्स 3।
ऐसा करने के लिए, पहले चर x 1 के लिए पूर्ण वर्ग का चयन करें:
f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3।
अब हम चर x 2 के लिए पूर्ण वर्ग का चयन करते हैं:
f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.
फिर गैर-पतित रैखिक परिवर्तन y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 और y 3 \u003d x 3 इस द्विघात रूप को विहित रूप में लाता है f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 ।
ध्यान दें कि द्विघात रूप के विहित रूप को अस्पष्ट रूप से परिभाषित किया गया है (एक ही द्विघात रूप को विभिन्न तरीकों से विहित रूप में घटाया जा सकता है)। हालांकि, विभिन्न तरीकों से प्राप्त विहित रूपों में कई सामान्य गुण होते हैं। विशेष रूप से, द्विघात रूप के धनात्मक (ऋणात्मक) गुणांक वाले पदों की संख्या इस बात पर निर्भर नहीं करती है कि प्रपत्र को इस रूप में कैसे घटाया जाता है (उदाहरण के लिए, माना गया उदाहरण में हमेशा दो ऋणात्मक और एक धनात्मक गुणांक होगा)। इस संपत्ति को द्विघात रूपों की जड़ता का नियम कहा जाता है।
आइए हम एक ही द्विघात रूप को विहित रूप में एक अलग तरीके से कम करके इसे सत्यापित करें। आइए चर x 2 के साथ परिवर्तन शुरू करें:
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, जहां y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) एक्स 3 और वाई 3 = एक्स 1। यहाँ, y 1 पर एक ऋणात्मक गुणांक -3 और y 2 और y 3 पर दो धनात्मक गुणांक 3 और 2 (और दूसरी विधि का उपयोग करके, हमें y 2 पर एक ऋणात्मक गुणांक (-5) और दो धनात्मक गुणांक प्राप्त हुए: 2 y 1 पर और y 3 के लिए 1/20)।
यह भी ध्यान दिया जाना चाहिए कि द्विघात रूप के एक मैट्रिक्स की रैंक, जिसे कहा जाता है द्विघात रूप की रैंक, विहित रूप के गैर-शून्य गुणांक की संख्या के बराबर है और रैखिक परिवर्तनों के तहत नहीं बदलता है।
द्विघात रूप f(X) कहलाता है सकारात्मक (नकारात्मक) निश्चित, यदि चर के सभी मानों के लिए जो एक साथ शून्य के बराबर नहीं हैं, तो यह धनात्मक है, अर्थात्। f(X) > 0 (ऋणात्मक, अर्थात्।
एफ (एक्स)< 0).
उदाहरण के लिए, द्विघात रूप f 1 (X) \u003d x 1 2 + x 2 2 धनात्मक निश्चित है, क्योंकि वर्गों का योग है, और द्विघात रूप f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 ऋणात्मक निश्चित है, क्योंकि प्रतिनिधित्व करता है इसे f 2 (X) \u003d - (x 1 - x 2) 2 के रूप में दर्शाया जा सकता है।
अधिकांश व्यावहारिक स्थितियों में, द्विघात रूप की संकेत-निश्चितता को स्थापित करना कुछ अधिक कठिन होता है, इसलिए इसके लिए निम्नलिखित प्रमेयों में से एक का उपयोग किया जाता है (हम उन्हें बिना प्रमाण के बनाते हैं)।
प्रमेय. एक द्विघात रूप धनात्मक (ऋणात्मक) निश्चित होता है यदि और केवल यदि इसके मैट्रिक्स के सभी प्रतिजन मान धनात्मक (ऋणात्मक) हों।
प्रमेय(सिलवेस्टर की कसौटी)। एक द्विघात रूप सकारात्मक निश्चित है यदि और केवल यदि इस रूप के मैट्रिक्स के सभी प्रमुख नाबालिग सकारात्मक हैं।
मेजर (कोने) माइनर n-वें क्रम के मैट्रिक्स A के k-वें क्रम को मैट्रिक्स का निर्धारक कहा जाता है, जो मैट्रिक्स A () की पहली k पंक्तियों और स्तंभों से बना होता है।
ध्यान दें कि ऋणात्मक-निश्चित द्विघात रूपों के लिए, मुख्य अवयस्कों के चिह्न वैकल्पिक होते हैं, और प्रथम-क्रम अवयस्क ऋणात्मक होने चाहिए।
उदाहरण के लिए, हम चिह्न-निश्चितता के लिए द्विघात रूप f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 की जांच करते हैं।
= (2 - एल)*
*(3 - एल) - 4 \u003d (6 - 2 एल - 3 एल + एल 2) - 4 \u003d एल 2 - 5 एल + 2 \u003d 0; डी = 25 - 8 = 17; 
. इसलिए, द्विघात रूप सकारात्मक निश्चित है।
विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग A D 1 = a 11 = 2> 0. दूसरे क्रम का मुख्य नाबालिग D 2 = = 6 - 4 = 2> 0. इसलिए, सिल्वेस्टर मानदंड के अनुसार, द्विघात रूप सकारात्मक निश्चित है।
हम संकेत-निश्चितता के लिए एक और द्विघात रूप की जांच करते हैं, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2।
विधि 1. आइए द्विघात रूप = के एक मैट्रिक्स की रचना करें। विशेषता समीकरण का रूप होगा 
= (-2 - एल)*
*(-3 - एल) - 4 = (6 + 2 एल + 3 एल + एल 2) - 4 = एल 2 + 5 एल + 2 = 0; डी = 25 - 8 = 17; 
. इसलिए, द्विघात रूप ऋणात्मक निश्चित है।
विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग ए डी 1 = ए 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. इसलिए, सिल्वेस्टर मानदंड के अनुसार, द्विघात रूप ऋणात्मक निश्चित है (प्रमुख अवयस्कों के चिन्ह वैकल्पिक रूप से, ऋण से प्रारंभ करते हुए)।
और एक अन्य उदाहरण के रूप में, हम साइन-निश्चितता के लिए द्विघात रूप f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 की जांच करते हैं।
विधि 1. आइए द्विघात रूप = के एक मैट्रिक्स की रचना करें। विशेषता समीकरण का रूप होगा 
= (2 - एल)*
*(-3 - एल) - 4 = (-6 - 2 एल + 3 एल + एल 2) - 4 = एल 2 + एल - 10 = 0; डी = 1 + 40 = 41; 
.
इनमें से एक संख्या ऋणात्मक है और दूसरी धनात्मक है। eigenvalues के संकेत अलग हैं। इसलिए, एक द्विघात रूप या तो ऋणात्मक या धनात्मक निश्चित नहीं हो सकता है, अर्थात। यह द्विघात रूप निश्चित चिह्न नहीं है (यह किसी भी चिन्ह का मान ले सकता है)।
विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग A D 1 = a 11 = 2> 0. दूसरे क्रम का मुख्य नाबालिग D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).
सजातीय रैखिक समीकरणों की प्रणाली
सजातीय रैखिक समीकरणों की एक प्रणाली फॉर्म की एक प्रणाली है
स्पष्ट है कि इस मामले में 
, क्योंकि इन निर्धारकों में से किसी एक स्तंभ के सभी अवयव शून्य के बराबर हैं।
चूंकि अज्ञात सूत्रों द्वारा पाए जाते हैं 
, तो उस स्थिति में जब 0, सिस्टम का एक अद्वितीय शून्य समाधान होता है एक्स = आप = जेड= 0. हालांकि, कई समस्याओं में यह सवाल दिलचस्पी का है कि क्या एक सजातीय प्रणाली में शून्य के अलावा अन्य समाधान हैं।
प्रमेय।रैखिक सजातीय समीकरणों की एक प्रणाली के लिए एक गैर-शून्य समाधान होने के लिए, यह आवश्यक और पर्याप्त है कि 0।
इसलिए, यदि सारणिक 0 है, तो निकाय का एक अद्वितीय हल है। यदि 0 है, तो रैखिक समांगी समीकरणों के निकाय के अनंत हल हैं।
उदाहरण।
Eigenvectors और मैट्रिक्स Eigenvalues
मान लीजिए एक वर्ग आव्यूह दिया गया है 
, एक्सकुछ मैट्रिक्स-कॉलम है जिसकी ऊंचाई मैट्रिक्स के क्रम से मेल खाती है ए. .
कई समस्याओं में, के लिए समीकरण पर विचार करना पड़ता है एक्स
जहाँ कुछ संख्या है। यह स्पष्ट है कि किसी भी के लिए इस समीकरण का एक शून्य हल होता है।
वह संख्या जिसके लिए इस समीकरण के शून्येतर हल हैं, कहलाती है eigenvalueमैट्रिक्स ए, ए एक्सऐसे को कहा जाता है खुद का वेक्टरमैट्रिक्स ए.
आइए मैट्रिक्स के आइजेनवेक्टर को खोजें ए. जहां तक कि इ∙एक्स = एक्स, तो मैट्रिक्स समीकरण को फिर से लिखा जा सकता है 
या 
. विस्तारित रूप में, इस समीकरण को रैखिक समीकरणों की एक प्रणाली के रूप में फिर से लिखा जा सकता है। सच में 
.
और इसीलिए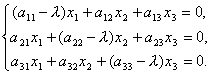 
तो, हमें निर्देशांक निर्धारित करने के लिए सजातीय रैखिक समीकरणों की एक प्रणाली मिली है एक्स 1, x2, एक्स 3वेक्टर एक्स. सिस्टम के गैर-शून्य समाधान होने के लिए, यह आवश्यक और पर्याप्त है कि सिस्टम का निर्धारक शून्य के बराबर हो, अर्थात।
यह के संबंध में तीसरी डिग्री का समीकरण है। यह कहा जाता है विशेषता समीकरणमैट्रिक्स एऔर eigenvalues को निर्धारित करने का कार्य करता है।
प्रत्येक eigenvalue λ एक eigenvector से मेल खाता है एक्स, जिनके निर्देशांक के संगत मान पर सिस्टम से निर्धारित किए जाते हैं।
उदाहरण।
वेक्टर बीजगणित। वेक्टर अवधारणा
भौतिकी की विभिन्न शाखाओं का अध्ययन करते समय, ऐसी मात्राएँ होती हैं जो पूरी तरह से उनके संख्यात्मक मूल्यों को निर्धारित करके निर्धारित की जाती हैं, उदाहरण के लिए, लंबाई, क्षेत्र, द्रव्यमान, तापमान, आदि। ऐसे मान अदिश कहलाते हैं। हालांकि, उनके अलावा, मात्राएं भी हैं, जिनके निर्धारण के लिए, संख्यात्मक मान के अलावा, अंतरिक्ष में उनकी दिशा जानना भी आवश्यक है, उदाहरण के लिए, शरीर पर कार्य करने वाला बल, गति और त्वरण जब शरीर अंतरिक्ष में गति करता है, तो अंतरिक्ष में दिए गए बिंदु पर चुंबकीय क्षेत्र की ताकत और आदि। ऐसी मात्राओं को सदिश राशियाँ कहते हैं।
आइए एक कठोर परिभाषा पेश करें।
दिशात्मक खंडआइए एक खंड कहते हैं, जिसके सिरों के सापेक्ष यह ज्ञात होता है कि उनमें से कौन पहला है और कौन सा दूसरा है।
वेक्टरएक निर्देशित खंड कहा जाता है, जिसकी एक निश्चित लंबाई होती है, अर्थात। यह एक निश्चित लंबाई का एक खंड है, जिसमें इसे सीमित करने वाले बिंदुओं में से एक को शुरुआत के रूप में लिया जाता है, और दूसरा - अंत के रूप में। यदि एक एवेक्टर की शुरुआत है, बीइसका अंत है, तो वेक्टर को प्रतीक द्वारा दर्शाया जाता है, इसके अलावा, वेक्टर को अक्सर एक अक्षर द्वारा दर्शाया जाता है। आकृति में, वेक्टर एक खंड द्वारा इंगित किया गया है, और इसकी दिशा एक तीर द्वारा इंगित की गई है।
मापांकया लंबावेक्टर को निर्देशित खंड की लंबाई कहा जाता है जो इसे परिभाषित करता है। द्वारा निरूपित || या ||.
तथाकथित शून्य सदिश, जिसका आरंभ और अंत मेल खाता है, को सदिश भी कहा जाएगा। यह अंकित है। शून्य सदिश की कोई निश्चित दिशा नहीं होती है और इसका मापांक शून्य के बराबर होता है ||=0.
सदिश और कहलाते हैं समरेखयदि वे एक ही रेखा पर या समानांतर रेखाओं पर स्थित हों। इस मामले में, यदि वैक्टर और समान रूप से निर्देशित हैं, तो हम इसके विपरीत लिखेंगे।
एक ही तल के समांतर सीधी रेखाओं पर स्थित सदिश कहलाते हैं समतलीय.
दो सदिश और कहलाते हैं बराबरयदि वे संरेख हैं, तो उनकी दिशा समान है, और लंबाई में बराबर हैं। इस मामले में, लिखें।
यह सदिशों की समानता की परिभाषा का अनुसरण करता है कि एक सदिश को अंतरिक्ष में किसी भी बिंदु पर अपनी उत्पत्ति रखकर अपने आप के समानांतर स्थानांतरित किया जा सकता है।
उदाहरण के लिए.
वैक्टर पर रैखिक संचालन
- एक वेक्टर को एक संख्या से गुणा करना।
एक संख्या द्वारा एक सदिश का गुणनफल एक नया सदिश है जैसे:
एक सदिश और एक संख्या का गुणनफल किसके द्वारा निरूपित किया जाता है।
उदाहरण के लिए,एक वेक्टर है जो वेक्टर के समान दिशा में इंगित करता है और वेक्टर की लंबाई आधा है।
दर्ज किए गए ऑपरेशन में निम्नलिखित हैं गुण:
- वैक्टर का जोड़।
आज्ञा देना और दो मनमाना सदिश हो। एक मनमाना बिंदु लें हेऔर एक वेक्टर का निर्माण करें। उसके बाद, बिंदु से एवेक्टर को अलग रखें। पहले वेक्टर की शुरुआत को दूसरे के अंत से जोड़ने वाले वेक्टर को कहा जाता है जोड़इन वैक्टरों में से और निरूपित किया जाता है
.
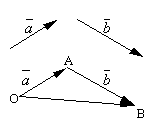
सदिश योग की सूत्रबद्ध परिभाषा कहलाती है समांतर चतुर्भुज नियम, क्योंकि सदिशों का समान योग निम्नानुसार प्राप्त किया जा सकता है। बिंदु से अलग सेट करें हेवैक्टर और। इन सदिशों पर एक समांतर चतुर्भुज की रचना कीजिए ओएबीसी. सदिशों के बाद से सदिश, जो शीर्ष से खींचे गए समांतर चतुर्भुज का विकर्ण है हे, स्पष्ट रूप से वैक्टर का योग होगा।
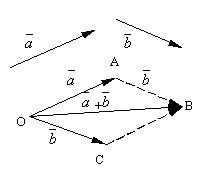
निम्नलिखित की जांच करना आसान है वेक्टर जोड़ गुण.
- वैक्टर का अंतर।
किसी दिए गए सदिश के समरेखीय सदिश, लंबाई के बराबर और विपरीत दिशा में निर्देशित, कहलाता है विलोमएक वेक्टर के लिए वेक्टर और द्वारा निरूपित किया जाता है। विपरीत सदिश को = -1: संख्या से सदिश गुणन का परिणाम माना जा सकता है।
