लघुगणक की परिभाषा

संख्या b से आधार a तक का लघुगणक वह घातांक है जिससे आपको b प्राप्त करने के लिए a को ऊपर उठाने की आवश्यकता होती है।

संख्या ईगणित में, यह उस सीमा को निरूपित करने के लिए प्रथागत है जिस तक व्यंजक का झुकाव होता है

संख्या ईहै अपरिमेय संख्या- एक के साथ अतुलनीय संख्या, इसे पूर्ण रूप से या भिन्न के रूप में बिल्कुल व्यक्त नहीं किया जा सकता है तर्कसंगतसंख्या।

पत्र इ- एक लैटिन शब्द का पहला अक्षर एक्सोनरे- फ्लॉन्ट करना, इसलिए गणित में नाम घातीय- घातांक प्रकार्य।

संख्या इगणित में व्यापक रूप से उपयोग किया जाता है, और सभी विज्ञानों में, एक तरह से या किसी अन्य गणितीय गणनाओं का उपयोग उनकी आवश्यकताओं के लिए किया जाता है।

लघुगणक। लघुगणक के गुण

परिभाषा: एक धनात्मक संख्या b का आधार लघुगणक वह घातांक c है जिससे संख्या b प्राप्त करने के लिए संख्या a को ऊपर उठाया जाना चाहिए।

मूल लघुगणकीय पहचान:

7) नए आधार पर संक्रमण का सूत्र:

lna = लॉग ई ए, ई 2.718…

"लघुगणक" विषय पर कार्य और परीक्षण। लघुगणक के गुण »

• लघुगणक - गणित में परीक्षा दोहराने के लिए महत्वपूर्ण विषय

इस विषय पर कार्यों को सफलतापूर्वक पूरा करने के लिए, आपको लघुगणक की परिभाषा, लघुगणक के गुण, मूल लघुगणकीय पहचान, दशमलव की परिभाषा और प्राकृतिक लघुगणक का ज्ञान होना चाहिए। इस विषय पर मुख्य प्रकार के कार्य लॉगरिदमिक अभिव्यक्तियों की गणना और रूपांतरण के लिए कार्य हैं। आइए निम्नलिखित उदाहरणों पर उनके समाधान पर विचार करें।

समाधान:लघुगणक के गुणों का उपयोग करते हुए, हम प्राप्त करते हैं

समाधान:डिग्री के गुणों का उपयोग करके, हम प्राप्त करते हैं

1) (2 2) लघुगणक 2 5 =(2 लघुगणक 25) 2 =5 2 =25

लघुगणक, सूत्र और प्रमाण के गुण।

लघुगणक में कई विशिष्ट गुण होते हैं। इस लेख में, हम मुख्य का विश्लेषण करेंगे लघुगणक के गुण. यहां हम उनके सूत्र देते हैं, लघुगणक के गुणों को सूत्रों के रूप में लिखते हैं, उनके अनुप्रयोग के उदाहरण दिखाते हैं, और लघुगणक के गुणों का प्रमाण भी देते हैं।

पृष्ठ नेविगेशन।

लघुगणक, सूत्रों के मूल गुण

याद रखने और उपयोग करने में आसानी के लिए, हम प्रस्तुत करते हैं लघुगणक के मूल गुणसूत्रों की सूची के रूप में। अगले भाग में हम उनके सूत्र, प्रमाण, उपयोग के उदाहरण और आवश्यक स्पष्टीकरण देंगे।

यूनिट लॉग प्रॉपर्टी: किसी भी a>0 , a≠1 के लिए 1=0 लॉग करें।

आधार के बराबर किसी संख्या का लघुगणक: a>0 , a≠1 के लिए a a=1 लॉग करें।

आधार अंश लघुगणक गुण: log a a p =p , जहाँ a>0 , a≠1 और p कोई वास्तविक संख्या है।

दो धनात्मक संख्याओं के गुणनफल का लघुगणक: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
और n धनात्मक संख्याओं के गुणनफल के लघुगणक का गुण: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 >0, …, xn >0 ।

निजी लघुगणक संपत्ति: , जहां a>0 , a≠1 , x>0 , y>0 ।

किसी संख्या की घात का लघुगणक: log a b p =p log a |b| , जहां a>0 , a≠1 , b और p ऐसी संख्याएं हैं कि b p की डिग्री समझ में आती है और b p >0 ।

परिणाम: , जहां a>0 , a≠1 , n एक से बड़ी प्राकृत संख्या है, b>0 ।

परिणाम 1: , a>0 , a≠1 , b>0 , b≠1 ।

परिणाम 2: , a>0 , a≠1 , b>0 , p और q वास्तविक संख्याएं हैं, q≠0 , विशेष रूप से, b=a के लिए हमारे पास है .

संपत्तियों के विवरण और प्रमाण

हम लघुगणक के रिकॉर्ड किए गए गुणों के निर्माण और प्रमाण को पास करते हैं। लघुगणक के सभी गुण लघुगणक की परिभाषा और उससे आने वाली मूल लघुगणकीय पहचान के साथ-साथ डिग्री के गुणों के आधार पर सिद्ध होते हैं।

चलो साथ - साथ शुरू करते हैं एकता के लघुगणक के गुण. इसका सूत्रीकरण इस प्रकार है: एकता का लघुगणक शून्य के बराबर होता है, अर्थात, लॉग ए 1=0किसी के लिए a>0 , a≠1 । प्रमाण सीधा है: चूंकि a 0 =1 किसी भी a के लिए जो उपरोक्त शर्तों a>0 और a≠1 को संतुष्ट करता है, तो सिद्ध समानता लॉग a 1=0 तुरंत लघुगणक की परिभाषा से अनुसरण करता है।

आइए मानी गई संपत्ति के आवेदन के उदाहरण दें: लॉग 3 1=0 , lg1=0 तथा ।

आइए अगली संपत्ति पर चलते हैं: आधार के बराबर किसी संख्या का लघुगणक एक के बराबर होता है, वह है, लॉग ए = 1 a>0 , a≠1 के लिए। वास्तव में, चूंकि a 1 =a किसी भी a के लिए है, तो लघुगणक की परिभाषा के अनुसार a a=1 लॉग करें।

लघुगणक के इस गुण का उपयोग करने के उदाहरण हैं log 5 5=1 , log 5.6 5.6 और lne=1 ।

लघुगणक के आधार के बराबर किसी संख्या की घात का लघुगणक घातांक के बराबर होता है. लघुगणक की यह संपत्ति फॉर्म के सूत्र से मेल खाती है लॉग एपी = पी, जहां a>0 , a≠1 और p कोई वास्तविक संख्या है। यह गुण लघुगणक की परिभाषा से सीधे अनुसरण करता है। ध्यान दें कि यह आपको लॉगरिदम के मूल्य को तुरंत निर्दिष्ट करने की अनुमति देता है, यदि आधार की डिग्री के रूप में लॉगरिदम के संकेत के तहत संख्या का प्रतिनिधित्व करना संभव है, तो हम लेख में लॉगरिदम की गणना में इसके बारे में अधिक बात करेंगे।

उदाहरण के लिए, लघुगणक 2 2 7 =7 , लघुगणक 10 -4 = -4 और .

दो धनात्मक संख्याओं के गुणनफल का लघुगणक x और y इन संख्याओं के लघुगणक के गुणनफल के बराबर हैं: log a (x y)=log a x+log a y, a>0 , a≠1 । आइए हम उत्पाद के लघुगणक के गुण को सिद्ध करें। डिग्री के गुणों के कारण a log a x + log a y =a log a x a log a y , और चूंकि मुख्य लघुगणकीय पहचान द्वारा a log a x =x और log a y =y , तो a log a x a log a y =x y । इस प्रकार, a log a x+log a y =x y , जहां से आवश्यक समानता लघुगणक की परिभाषा के अनुसार होती है।

आइए उत्पाद के लघुगणक की संपत्ति का उपयोग करने के उदाहरण दिखाएं: लॉग 5 (2 3)=लॉग 5 2+लॉग 5 3 और .

गुणनफल लघुगणक गुण को धनात्मक संख्याओं x 1, x 2, ..., x n की एक परिमित संख्या n के गुणनफल के रूप में सामान्यीकृत किया जा सकता है लॉग a (x 1 x 2 ... x n)= लॉग a x 1 +लॉग a x 2 +...+लॉग a x n. इस समानता को गणितीय आगमन विधि द्वारा आसानी से सिद्ध किया जा सकता है।

उदाहरण के लिए, किसी उत्पाद के प्राकृतिक लघुगणक को संख्या 4, ई, और के तीन प्राकृतिक लघुगणकों के योग से बदला जा सकता है।

दो धनात्मक संख्याओं के भागफल का लघुगणक x और y इन संख्याओं के लघुगणक के बीच के अंतर के बराबर हैं। भागफल लघुगणक की संपत्ति फॉर्म के सूत्र से मेल खाती है , जहाँ a>0 , a≠1 , x और y कुछ धनात्मक संख्याएँ हैं। इस सूत्र की वैधता उत्पाद के लघुगणक के सूत्र की तरह सिद्ध होती है: चूँकि , फिर लघुगणक की परिभाषा के अनुसार .

लघुगणक की इस संपत्ति का उपयोग करने का एक उदाहरण यहां दिया गया है: .

चलिए आगे बढ़ते हैं डिग्री के लघुगणक की संपत्ति. एक डिग्री का लघुगणक घातांक के गुणनफल और इस डिग्री के आधार के मापांक के लघुगणक के बराबर होता है। हम डिग्री के लघुगणक के इस गुण को सूत्र के रूप में लिखते हैं: लॉग ए बी पी = पी लॉग ए |बी|, जहां a>0 , a≠1 , b और p ऐसी संख्याएं हैं कि b p की डिग्री समझ में आती है और b p >0 ।

हम पहले इस गुण को धनात्मक b के लिए सिद्ध करते हैं। मूल लघुगणकीय पहचान हमें संख्या b को a log a b के रूप में निरूपित करने की अनुमति देती है, फिर b p =(a log a b) p, और परिणामी व्यंजक, power गुण के कारण, a p log a b के बराबर होता है। इसलिए हम समानता b p =a p log a b पर पहुंचते हैं, जिससे, लघुगणक की परिभाषा से, हम यह निष्कर्ष निकालते हैं कि log a b p =p log a b ।

यह इस गुण को ऋणात्मक b के लिए सिद्ध करना शेष है। यहाँ हम ध्यान दें कि ऋणात्मक b के लिए व्यंजक log a b p केवल सम घातांक p के लिए अर्थ रखता है (क्योंकि घात b p का मान शून्य से अधिक होना चाहिए, अन्यथा लघुगणक का कोई अर्थ नहीं होगा), और इस स्थिति में b p =|b| पी । तब b p=|b| p =(a log a |b|) p =a p log a |b| , कहाँ से लॉग a b p =p log a |b| .

उदाहरण के लिए, और ln(-3) 4 =4 ln|-3|=4 ln3 ।

यह पिछली संपत्ति से इस प्रकार है जड़ से लघुगणक की संपत्ति: nth डिग्री के मूल का लघुगणक भिन्न 1/n के गुणनफल और मूल व्यंजक के लघुगणक के बराबर होता है, अर्थात, जहां a>0, a≠1, n एक से बड़ी प्राकृतिक संख्या है, बी> 0।

सबूत एक समानता पर आधारित है (एक भिन्नात्मक घातांक के साथ घातांक की परिभाषा देखें), जो किसी भी सकारात्मक b के लिए मान्य है, और डिग्री के लघुगणक की संपत्ति: .

इस संपत्ति का उपयोग करने का एक उदाहरण यहां दिया गया है: .

चलिए अब साबित करते हैं लघुगणक के नए आधार में रूपांतरण सूत्रमेहरबान . ऐसा करने के लिए, यह समानता लॉग c b=log a b log c a की वैधता को साबित करने के लिए पर्याप्त है। मूल लघुगणकीय पहचान हमें संख्या b को लॉग a b के रूप में निरूपित करने की अनुमति देती है, फिर log c b=log c a log a b के रूप में। यह डिग्री के लघुगणक की संपत्ति का उपयोग करने के लिए बनी हुई है: log c a log a b = log a b log c a । इस प्रकार, समानता लॉग c b=log a b log c a सिद्ध होता है, जिसका अर्थ है कि लघुगणक के नए आधार में संक्रमण का सूत्र भी सिद्ध होता है .

आइए लघुगणक के इस गुण को लागू करने के कुछ उदाहरण दिखाते हैं: और .

एक नए आधार पर जाने का सूत्र आपको "सुविधाजनक" आधार वाले लघुगणक के साथ काम करने की अनुमति देता है। उदाहरण के लिए, इसका उपयोग प्राकृतिक या दशमलव लघुगणक पर स्विच करने के लिए किया जा सकता है ताकि आप लघुगणक की तालिका से लघुगणक के मान की गणना कर सकें। लघुगणक के एक नए आधार में संक्रमण का सूत्र कुछ मामलों में किसी दिए गए लघुगणक के मूल्य को खोजने की अनुमति देता है, जब अन्य आधारों के साथ कुछ लघुगणक के मान ज्ञात होते हैं।

प्रपत्र के c=b के लिए लघुगणक के नए आधार पर संक्रमण सूत्र का एक विशेष मामला अक्सर उपयोग किया जाता है। इससे पता चलता है कि log a b और log b a परस्पर प्रतिलोम संख्याएँ हैं। उदाहरण के लिए, .

सूत्र का भी अक्सर उपयोग किया जाता है, जो लघुगणक मान ज्ञात करते समय सुविधाजनक होता है। अपने शब्दों की पुष्टि करने के लिए, हम दिखाएंगे कि फॉर्म के लॉगरिदम के मूल्य की गणना कैसे की जाती है। हमारे पास है . सूत्र को सिद्ध करने के लिए, लघुगणक के नए आधार के लिए संक्रमण सूत्र का उपयोग करना पर्याप्त है: .

यह लघुगणक के तुलनात्मक गुणों को साबित करने के लिए बनी हुई है।

आइए विपरीत विधि का उपयोग करें। मान लीजिए कि a 1 >1 , a 2 >1 और a 1 2 और 0 1 log a 1 b≤log a 2 b सत्य है। लघुगणक के गुणों से, इन असमानताओं को फिर से लिखा जा सकता है तथा क्रमशः, और उनसे यह निम्नानुसार है कि लॉग बी ए 1 लॉग बी ए 2 और लॉग बी ए 1 लॉग बी ए 2, क्रमशः। फिर, समान आधार वाले घातों के गुणों से, समानताएं b log b a 1 ≥b log b a 2 और b log b a 1 ≥b log b a 2 को संतुष्ट किया जाना चाहिए, अर्थात a 1 a 2 । इस प्रकार, हम शर्त a 1 2 के अंतर्विरोध पर पहुंच गए हैं। यह सबूत पूरा करता है।

लघुगणक के मूल गुण

• पाठ के लिए सामग्री
• सभी सूत्र डाउनलोड करें

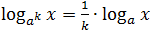
लॉगरिदम, किसी भी संख्या की तरह, हर संभव तरीके से जोड़ा, घटाया और परिवर्तित किया जा सकता है। लेकिन चूंकि लॉगरिदम बिल्कुल सामान्य संख्या नहीं हैं, इसलिए यहां नियम हैं, जिन्हें कहा जाता है बुनियादी गुण.

इन नियमों को अवश्य जानना चाहिए - इनके बिना कोई भी गंभीर लघुगणकीय समस्या हल नहीं हो सकती है। इसके अलावा, उनमें से बहुत कम हैं - एक दिन में सब कुछ सीखा जा सकता है। तो चलो शुरू करते है।

लघुगणक का जोड़ और घटाव

समान आधार वाले दो लघुगणक पर विचार करें: a x लॉग करें और a y लॉग करें। फिर उन्हें जोड़ा और घटाया जा सकता है, और:

तो, लघुगणक का योग उत्पाद के लघुगणक के बराबर है, और अंतर भागफल का लघुगणक है। कृपया ध्यान दें: यहाँ मुख्य बिंदु है - एक ही आधार. यदि आधार भिन्न हैं, तो ये नियम काम नहीं करते हैं!

ये सूत्र लघुगणकीय व्यंजक की गणना करने में मदद करेंगे, भले ही इसके अलग-अलग हिस्सों पर विचार न किया गया हो (पाठ "एक लघुगणक क्या है" देखें)। उदाहरणों पर एक नज़र डालें - और देखें:

एक कार्य। व्यंजक का मान ज्ञात कीजिए: लघुगणक 6 4 + लघुगणक 6 9।

चूंकि लघुगणक के आधार समान हैं, इसलिए हम योग सूत्र का उपयोग करते हैं:
लॉग 6 4 + लॉग 6 9 = लॉग 6 (4 9) = लॉग 6 36 = 2।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: लघुगणक 2 48 - लघुगणक 2 3।

आधार समान हैं, हम अंतर सूत्र का उपयोग करते हैं:
लॉग 2 48 - लॉग 2 3 = लॉग 2 (48: 3) = लॉग 2 16 = 4।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: लघुगणक 3 135 - लघुगणक 3 5.

फिर से, आधार समान हैं, इसलिए हमारे पास है:
लघुगणक 3 135 - लघुगणक 3 5 = लघुगणक 3 (135: 5) = लघुगणक 3 27 = 3.

जैसा कि आप देख सकते हैं, मूल भाव "खराब" लघुगणक से बने होते हैं, जिन्हें अलग से नहीं माना जाता है। लेकिन परिवर्तनों के बाद काफी सामान्य संख्याएँ निकलती हैं। कई परीक्षण इस तथ्य पर आधारित हैं। हां, वह नियंत्रण - पूरी गंभीरता से समान भाव (कभी-कभी - वस्तुतः कोई बदलाव नहीं) परीक्षा में पेश किए जाते हैं।

घातांक को लघुगणक से हटाना

अब कार्य को थोड़ा जटिल करते हैं। क्या होगा यदि लघुगणक के आधार या तर्क में कोई डिग्री हो? तब इस डिग्री के घातांक को निम्न नियमों के अनुसार लघुगणक के चिह्न से निकाला जा सकता है:

• लॉग a x n = n लॉग a x ;
• 
• 

यह देखना आसान है कि अंतिम नियम उनके पहले दो का अनुसरण करता है। लेकिन इसे वैसे भी याद रखना बेहतर है - कुछ मामलों में यह गणना की मात्रा को काफी कम कर देगा।

बेशक, ये सभी नियम समझ में आते हैं यदि ओडीजेड लॉगरिदम मनाया जाता है: ए> 0, ए ≠ 1, एक्स> 0. और एक और बात: न केवल बाएं से दाएं, बल्कि इसके विपरीत भी सभी सूत्रों को लागू करना सीखें, यानी। आप लघुगणक के चिह्न से पहले संख्याओं को लघुगणक में ही दर्ज कर सकते हैं। यह वही है जो सबसे अधिक बार आवश्यक होता है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log 7 49 6 ।

आइए पहले सूत्र के अनुसार तर्क में डिग्री से छुटकारा पाएं:
लघुगणक 7 49 6 = 6 लघुगणक 7 49 = 6 2 = 12

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

[आंकड़ा अनुशीर्षक]

ध्यान दें कि हर एक लघुगणक है जिसका आधार और तर्क सटीक शक्तियाँ हैं: 16 = 2 4; 49 = 72। हमारे पास है:

[आंकड़ा अनुशीर्षक]

मुझे लगता है कि अंतिम उदाहरण को स्पष्टीकरण की आवश्यकता है। लघुगणक कहाँ चले गए हैं? अंतिम क्षण तक, हम केवल हर के साथ काम करते हैं। उन्होंने वहां खड़े लघुगणक के आधार और तर्क को डिग्री के रूप में प्रस्तुत किया और संकेतक निकाले - उन्हें "तीन मंजिला" अंश मिला।

अब आइए मुख्य अंश को देखें। अंश और हर की संख्या समान है: लॉग 2 7. चूंकि लॉग 2 7 0, हम भिन्न को कम कर सकते हैं - 2/4 हर में रहेगा। अंकगणित के नियमों के अनुसार, चार को अंश में स्थानांतरित किया जा सकता है, जो किया गया था। परिणाम उत्तर है: 2.

एक नई नींव में संक्रमण

लॉगरिदम जोड़ने और घटाने के नियमों के बारे में बोलते हुए, मैंने विशेष रूप से जोर दिया कि वे केवल एक ही आधार के साथ काम करते हैं। क्या होगा यदि आधार अलग हैं? क्या होगा यदि वे एक ही संख्या की सटीक शक्तियां नहीं हैं?

एक नए आधार पर संक्रमण के लिए सूत्र बचाव के लिए आते हैं। हम उन्हें एक प्रमेय के रूप में तैयार करते हैं:

मान लीजिए कि लघुगणक लघुगणक a x दिया गया है। फिर किसी भी संख्या c जैसे कि c > 0 और c ≠ 1 के लिए, समानता सत्य है:

[आंकड़ा अनुशीर्षक]

विशेष रूप से, यदि हम c = x डालते हैं, तो हमें प्राप्त होता है:

[आंकड़ा अनुशीर्षक]

यह दूसरे सूत्र से इस प्रकार है कि आधार और लघुगणक के तर्क को आपस में बदलना संभव है, लेकिन इस मामले में पूरी अभिव्यक्ति "उलट" है, अर्थात। लघुगणक हर में है।

ये सूत्र सामान्य संख्यात्मक अभिव्यक्तियों में बहुत कम पाए जाते हैं। यह मूल्यांकन करना संभव है कि लॉगरिदमिक समीकरणों और असमानताओं को हल करते समय ही वे कितने सुविधाजनक होते हैं।

हालाँकि, ऐसे कार्य हैं जिन्हें एक नई नींव में जाने के अलावा हल नहीं किया जा सकता है। आइए इनमें से कुछ पर विचार करें:

एक कार्य। व्यंजक का मान ज्ञात कीजिए: लघुगणक 5 16 लघुगणक 2 25.

ध्यान दें कि दोनों लघुगणक के तर्क सटीक घातांक हैं। आइए संकेतक निकालें: लॉग 5 16 = लॉग 5 2 4 = 4लॉग 5 2; लघुगणक 2 25 = लघुगणक 2 5 2 = 2 लघुगणक 2 5;

अब दूसरा लघुगणक पलटें:

[आंकड़ा अनुशीर्षक]

चूंकि उत्पाद कारकों के क्रमपरिवर्तन से नहीं बदलता है, हमने शांति से चार और दो को गुणा किया, और फिर लघुगणक का पता लगाया।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log 9 100 lg 3.

पहले लघुगणक का आधार और तर्क सटीक शक्तियाँ हैं। आइए इसे लिख लें और संकेतकों से छुटकारा पाएं:

[आंकड़ा अनुशीर्षक]

आइए अब एक नए आधार पर जाकर दशमलव लघुगणक से छुटकारा पाएं:

[आंकड़ा अनुशीर्षक]

मूल लघुगणकीय पहचान

अक्सर हल करने की प्रक्रिया में किसी दिए गए आधार के लिए एक संख्या को लघुगणक के रूप में प्रस्तुत करना आवश्यक होता है। इस मामले में, सूत्र हमारी मदद करेंगे:

1. n = लॉग a n

2. पहले मामले में, संख्या n तर्क में घातांक बन जाती है। संख्या n बिल्कुल कुछ भी हो सकती है, क्योंकि यह केवल लघुगणक का मान है।

   दूसरा सूत्र वास्तव में एक व्याख्यात्मक परिभाषा है। इसे मूल लघुगणकीय पहचान कहते हैं।

   वास्तव में, क्या होगा यदि संख्या b को इतनी घात तक बढ़ा दिया जाए कि इस घात की संख्या b संख्या a दे दे? यह सही है: यह वही संख्या a है। इस पैराग्राफ को फिर से ध्यान से पढ़ें - बहुत से लोग इसे "लटका" देते हैं।

   नए आधार रूपांतरण फ़ार्मुलों की तरह, मूल लघुगणकीय पहचान कभी-कभी एकमात्र संभव समाधान होता है।

   [आंकड़ा अनुशीर्षक]

   ध्यान दें कि लॉग 25 64 = लॉग 5 8 - बस आधार का वर्ग और लॉगरिदम का तर्क लें। समान आधार से घातों को गुणा करने के नियमों को देखते हुए, हम प्राप्त करते हैं:

   [आंकड़ा अनुशीर्षक]

   अगर किसी को पता नहीं है, तो यह एकीकृत राज्य परीक्षा से एक वास्तविक कार्य था

   लघुगणक इकाई और लघुगणक शून्य

   अंत में, मैं दो पहचान दूंगा जिन्हें गुणों को कॉल करना मुश्किल है - बल्कि, ये लॉगरिदम की परिभाषा से परिणाम हैं। वे लगातार समस्याओं में पाए जाते हैं और आश्चर्यजनक रूप से, "उन्नत" छात्रों के लिए भी समस्याएं पैदा करते हैं।

   1. log a = 1 लघुगणक इकाई है। एक बार और सभी के लिए याद रखें: किसी भी आधार के लिए लघुगणक उस आधार से ही एक के बराबर होता है।
   2. log a 1 = 0 लघुगणकीय शून्य है। आधार a कुछ भी हो सकता है, लेकिन यदि तर्क एक है - लघुगणक शून्य है! क्योंकि 0 = 1 परिभाषा का प्रत्यक्ष परिणाम है।

   वह सब गुण है। उन्हें अभ्यास में लाने का अभ्यास करना सुनिश्चित करें! पाठ की शुरुआत में चीट शीट डाउनलोड करें, उसका प्रिंट आउट लें - और समस्याओं का समाधान करें।

   लघुगणक। लघुगणक के गुण (जोड़ और घटाव)।

   लघुगणक के गुणइसकी परिभाषा से अनुसरण करें। और इसलिए संख्या का लघुगणक बीवजह से एकघातांक के रूप में परिभाषित किया गया है जिसके लिए एक संख्या को उठाया जाना चाहिए एकनंबर पाने के लिए बी(लघुगणक केवल सकारात्मक संख्याओं के लिए मौजूद है)।

   इस सूत्रीकरण से यह निष्कर्ष निकलता है कि गणना एक्स = एक बी लॉग इन करें, समीकरण को हल करने के बराबर है कुल्हाड़ी = ख।उदाहरण के लिए, लॉग 2 8 = 3इसलिये 8 = 2 3 . लघुगणक का निरूपण यह उचित ठहराना संभव बनाता है कि यदि बी = एक सी, तो संख्या का लघुगणक बीवजह से एकबराबरी साथ. यह भी स्पष्ट है कि लघुगणक का विषय किसी संख्या की घात के विषय से निकटता से संबंधित है।

   लघुगणक के साथ, किसी भी संख्या के साथ, आप प्रदर्शन कर सकते हैं जोड़, घटाव संचालनऔर हर संभव तरीके से रूपांतरित करें। लेकिन इस तथ्य को ध्यान में रखते हुए कि लॉगरिदम बिल्कुल सामान्य संख्या नहीं हैं, उनके अपने विशेष नियम यहां लागू होते हैं, जिन्हें कहा जाता है बुनियादी गुण.

   लघुगणक का जोड़ और घटाव।

   समान आधार वाले दो लघुगणक लें: लॉग एक्सतथा आप लॉग इन करें. फिर इसे हटा दें जोड़ और घटाव संचालन करना संभव है:

   जैसा कि हम देखते हैं, लघुगणक का योगउत्पाद के लघुगणक के बराबर है, और अंतर लघुगणक- भागफल का लघुगणक। और यह सच है अगर संख्या एक, एक्सतथा परसकारात्मक और एक 1.

   यह ध्यान रखना महत्वपूर्ण है कि इन सूत्रों में मुख्य पहलू समान आधार हैं। यदि आधार एक दूसरे से भिन्न हैं, तो ये नियम लागू नहीं होते हैं!

   समान आधार वाले लघुगणक को जोड़ने और घटाने के नियमों को न केवल बाएं से दाएं पढ़ा जाता है, बल्कि इसके विपरीत भी पढ़ा जाता है। नतीजतन, हमारे पास उत्पाद के लघुगणक और भागफल के लघुगणक के लिए प्रमेय हैं।

   उत्पाद का लघुगणकदो धनात्मक संख्याएँ उनके लघुगणक के योग के बराबर होती हैं ; इस प्रमेय की व्याख्या करने पर, हमें निम्नलिखित प्राप्त होते हैं, यदि संख्याएँ एक, एक्सतथा परसकारात्मक और एक 1, फिर:

   भागफल का लघुगणकदो धनात्मक संख्याओं का योग लाभांश और भाजक के लघुगणक के बीच के अंतर के बराबर होता है। दूसरे शब्दों में, यदि संख्या एक, एक्सतथा परसकारात्मक और एक 1, फिर:

   हम उपरोक्त प्रमेयों को हल करने के लिए लागू करते हैं उदाहरण:

   अगर संख्या एक्सतथा परनकारात्मक हैं, तो उत्पाद लघुगणक सूत्रअर्थहीन हो जाता है। इसलिए, यह लिखना मना है:

   चूंकि व्यंजक लॉग 2 (-8) और लॉग 2 (-4) बिल्कुल भी परिभाषित नहीं हैं (लघुगणक कार्य पर= लॉग 2 एक्सकेवल तर्क के सकारात्मक मूल्यों के लिए परिभाषित एक्स).

   उत्पाद प्रमेयन केवल दो के लिए, बल्कि असीमित संख्या में कारकों के लिए भी लागू होता है। इसका मतलब है कि हर प्राकृतिक के लिए कऔर कोई सकारात्मक संख्या एक्स 1 , एक्स 2 , . . . ,एक्स एनएक पहचान है:

   से भागफल लघुगणक प्रमेयलघुगणक का एक और गुण प्राप्त किया जा सकता है। यह सर्वविदित है कि लॉग एक 1= 0, इसलिए,

   तो एक समानता है:

   दो परस्पर पारस्परिक संख्याओं के लघुगणकएक ही आधार पर केवल चिन्ह में एक दूसरे से भिन्न होंगे। इसलिए:

   लघुगणक। लघुगणक के गुण

   लघुगणक। लघुगणक के गुण

   समानता पर विचार करें। आइए मूल्यों को जानते हैं और हम इसका मूल्य खोजना चाहते हैं।

   यही है, हम एक ऐसे घातांक की तलाश कर रहे हैं, जिसे प्राप्त करने के लिए आपको मुर्गा बनाना होगा।

   होने देना चर कोई भी वास्तविक मान ले सकता है, फिर चरों पर निम्नलिखित प्रतिबंध लगाए जाते हैं: o” title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″/ >

   यदि हम और के मूल्यों को जानते हैं, और हमें अज्ञात को खोजने के कार्य का सामना करना पड़ता है, तो इस उद्देश्य के लिए एक गणितीय ऑपरेशन पेश किया जाता है, जिसे कहा जाता है लोगारित्म.

   हम जो मूल्य लेते हैं उसे खोजने के लिए किसी संख्या का लघुगणकपर नींव :

   किसी संख्या का आधार से लघुगणक वह घातांक है जिसे प्राप्त करने के लिए आपको ऊपर उठाना होगा।

   वह है बुनियादी लघुगणकीय पहचान:

   ओ" शीर्षक = "ए> ओ" />, 1 शीर्षक = "ए 1" />, 0 शीर्षक = "बी> 0″ />

   अनिवार्य रूप से एक गणितीय संकेतन है लघुगणक परिभाषाएँ.

   गणितीय ऑपरेशन लॉगरिदम घातांक का विलोम है, इसलिए लघुगणक के गुणडिग्री के गुणों से निकटता से संबंधित हैं।

   हम मुख्य सूचीबद्ध करते हैं लघुगणक के गुण:

   (ओ" शीर्षक = "ए> ओ" />, 1 शीर्षक = "ए 1" />, 0 शीर्षक = "बी> 0″ />, 0,

   d>0″/>, 1″ शीर्षक="d1″/>

   4.

   5.

   गुणों का निम्नलिखित समूह आपको लघुगणक के संकेत के तहत अभिव्यक्ति के घातांक का प्रतिनिधित्व करने की अनुमति देता है, या लघुगणक के आधार पर लघुगणक के संकेत से पहले गुणांक के रूप में खड़ा होता है:

   6.

   7.

   8.

   9.

   सूत्रों का अगला समूह आपको दिए गए आधार वाले लघुगणक से मनमाने आधार वाले लघुगणक में जाने की अनुमति देता है, और इसे कहा जाता है एक नए आधार के लिए संक्रमण सूत्र:

   10.

   12. (संपत्ति 11 से परिणाम)

   

   निम्नलिखित तीन गुण अच्छी तरह से ज्ञात नहीं हैं, लेकिन उनका उपयोग अक्सर लॉगरिदमिक समीकरणों को हल करते समय, या लॉगरिदम वाले अभिव्यक्तियों को सरल करते समय किया जाता है:

   13.

   14.

   15.

   विशेष स्थितियां:

   — दशमलव लघुगणक

   — प्राकृतिक

   लघुगणक युक्त अभिव्यक्तियों को सरल बनाते समय, एक सामान्य दृष्टिकोण लागू किया जाता है:

   1. हम दशमलव भिन्नों को साधारण अंशों के रूप में निरूपित करते हैं।

   2. हम मिश्रित संख्याओं को अनुचित भिन्नों के रूप में निरूपित करते हैं।

   3. लघुगणक के आधार पर और लघुगणक के चिह्न के नीचे की संख्याएँ अभाज्य गुणनखंडों में विघटित हो जाती हैं।

   4. हम सभी लघुगणक को एक ही आधार पर लाने का प्रयास करते हैं।

   5. लघुगणक के गुणों को लागू करें।

   आइए लघुगणक वाले व्यंजकों को सरल बनाने के उदाहरण देखें।

   उदाहरण 1

   गणना करें:

   आइए सभी घातांक को सरल करें: हमारा कार्य उन्हें लघुगणक में लाना है, जिसका आधार घातांक के आधार के समान संख्या है।

   ==(संपत्ति से 7)=(संपत्ति 6 ​​द्वारा) =

   मूल व्यंजक में हमें जो संकेतक प्राप्त हुए हैं, उन्हें प्रतिस्थापित कीजिए। हम पाते हैं:

   उत्तर: 5.25

   उदाहरण 2 गणना करें:

   

   हम सभी लघुगणक को आधार 6 पर लाते हैं (इस मामले में, अंश के हर से लघुगणक अंश में "माइग्रेट" करेंगे):

   आइए लॉगरिदम के चिन्ह के तहत संख्याओं को प्रमुख कारकों में विघटित करें:

   गुण 4 और 6 लागू करें:

   हम प्रतिस्थापन का परिचय देते हैं

   हम पाते हैं:

   उत्तर 1

   लोगारित्म . बुनियादी लघुगणकीय पहचान।

   लघुगणक के गुण। दशमलव लघुगणक। प्राकृतिक।

   लोगारित्म आधार में धनात्मक संख्या N (बी > 0, बी 1) घातांक x कहलाता है, जिससे आपको N प्राप्त करने के लिए b को ऊपर उठाना होगा .

   यह प्रविष्टि निम्नलिखित के बराबर है: बी एक्स = एन .

   उदाहरण: लॉग 3 81 = 4 क्योंकि 3 4 = 81;

   लॉग 1/3 27 = – 3 क्योंकि (1/3) - 3 = 3 3 = 27।

   लघुगणक की उपरोक्त परिभाषा को एक पहचान के रूप में लिखा जा सकता है:

   

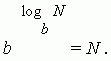
   लघुगणक के मूल गुण।

   2) लॉग 1 = 0 क्योंकि बी 0 = 1 .

   3) उत्पाद का लघुगणक कारकों के लघुगणक के योग के बराबर है:

   4) भागफल का लघुगणक लाभांश और भाजक के लघुगणक के बीच के अंतर के बराबर है:

   5) डिग्री का लघुगणक घातांक के गुणनफल और उसके आधार के लघुगणक के बराबर होता है:

   इस संपत्ति का परिणाम निम्नलिखित है: लॉग रूट जड़ की शक्ति से विभाजित मूल संख्या के लघुगणक के बराबर होती है:

   

   6) यदि लघुगणक का आधार एक घात है, तो मान घातांक के व्युत्क्रम को तुकबंदी लॉग साइन से निकाला जा सकता है:

   

   अंतिम दो गुणों को एक में जोड़ा जा सकता है:

   

   7) संक्रमण मापांक का सूत्र (अर्थात लघुगणक के एक आधार से दूसरे आधार में संक्रमण):

   

   किसी विशेष मामले में, जब एन = एअपने पास:

   

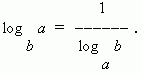
   दशमलव लघुगणक बुलाया आधार लघुगणक 10. इसे lg से दर्शाया जाता है, अर्थात्। लॉग 10 एन= लॉग एन. संख्या 10, 100, 1000, के लघुगणक। p क्रमशः 1, 2, 3, ..., अर्थात् हैं। बहुत सारे सकारात्मक हैं

   इकाइयाँ, एक के बाद एक लघुगणक संख्या में कितने शून्य होते हैं। संख्या 0.1, 0.01, 0.001, के लघुगणक। p क्रमशः -1, -2, -3, ..., अर्थात् हैं। के रूप में कई ऋणात्मक हैं क्योंकि लघुगणक संख्या में एक से पहले शून्य हैं (शून्य पूर्णांक सहित)। शेष संख्याओं के लघुगणक में एक भिन्नात्मक भाग होता है जिसे कहा जाता है अपूर्णांश. लघुगणक का पूर्णांक भाग कहलाता है विशेषता. व्यावहारिक अनुप्रयोगों के लिए, दशमलव लघुगणक सबसे सुविधाजनक हैं।

   प्राकृतिक बुलाया आधार लघुगणक इ. इसे ln से निरूपित किया जाता है, अर्थात्। लकड़ी का लट्ठा इ एन= एलएन एन. संख्या इअपरिमेय है, इसका अनुमानित मान 2.718281828 है। यह वह सीमा है जिसकी ओर संख्या (1 + 1 / एन) एनअसीमित वृद्धि के साथ एन(सेमी। पहली अद्भुत सीमासंख्या अनुक्रम सीमा पृष्ठ पर)।
   यह अजीब लग सकता है, कार्यों के विश्लेषण से संबंधित विभिन्न कार्यों को करते समय प्राकृतिक लघुगणक बहुत सुविधाजनक साबित हुए। आधार लघुगणक की गणना इकिसी भी अन्य आधार की तुलना में बहुत तेज।

• रूस में बच्चे को गोद लेने के लिए आज आपको क्या चाहिए? रूस में गोद लेने, एक जिम्मेदार व्यक्तिगत निर्णय के अलावा, उम्मीदवारों के राज्य सत्यापन के लिए कई प्रक्रियाएं शामिल हैं। प्रारंभिक चरण में कठोर चयन से अधिक […]
• पूरे रूस में टैक्स रजिस्टर से टीआईएन या ओजीआरएन द्वारा नि:शुल्क जानकारी - ऑनलाइन यूनिफाइड पोर्टल ऑफ टैक्स सर्विसेज पर, कानूनी संस्थाओं, व्यक्तिगत उद्यमियों के राज्य पंजीकरण की जानकारी, […]
• दस्तावेजों के बिना ड्राइविंग के लिए सजा (ड्राइविंग लाइसेंस, बीमा, एसटीएस) कभी-कभी, भूलने की बीमारी के कारण, ड्राइवर बिना लाइसेंस के पहिया के पीछे हो जाते हैं और बिना दस्तावेजों के ड्राइविंग के लिए जुर्माना प्राप्त करते हैं। याद कीजिए कि एक मोटर चालक बिना किसी असफलता के उसके साथ गाड़ी चला रहा था […]
• पुरुषों के लिए फूल। आप एक आदमी को किस तरह के फूल दे सकते हैं? एक आदमी को कौन से फूल दिए जा सकते हैं? इतने सारे "नर" फूल नहीं हैं, लेकिन ऐसे भी हैं जो पुरुषों को दिए जाते हैं। आपके सामने फूलों की एक छोटी सूची: गुलदाउदी। गुलाब कार्नेशन्स। […]
• मेमो एक दस्तावेज़ का एक विशेष रूप है जो किसी उद्यम के आंतरिक वातावरण में उपयोग किया जाता है और वर्तमान उत्पादन समस्याओं को जल्दी से हल करने का कार्य करता है। आमतौर पर इस दस्तावेज़ को कुछ बनाने के उद्देश्य से तैयार किया जाता है […]
• Sberbank में पेंशन का वित्त पोषित हिस्सा कब और कैसे प्राप्त करें? Sberbank राज्य पेंशन कोष का एक भागीदार बैंक है। इसके आधार पर, जिन नागरिकों ने एक वित्त पोषित पेंशन जारी की है, वे वित्त पोषित […]
• 2018 में उल्यानोवस्क और उल्यानोवस्क क्षेत्र में बाल भत्ते इसके अलावा, संघीय कानून द्वारा अनुमोदित कार्यक्रम सभी क्षेत्रों में चल रहे हैं। आइए देखें कि कौन और किन लाभों पर भरोसा कर सकता है। क्षेत्रीय अधिकारियों के रूप में […]
• अदालत में किसी व्यक्ति के हितों का प्रतिनिधित्व करने के लिए पावर ऑफ अटॉर्नी कैसे तैयार करें, इस पर विस्तृत गाइड एक सिविल या मध्यस्थता मुकदमे में, एक प्रशासनिक या आपराधिक मामले में, वादी और प्रतिवादी दोनों के हितों का प्रतिनिधित्व एक वकील द्वारा किया जा सकता है: […]

बुनियादी गुण.

1. लॉगैक्स + लोगे = लॉग (एक्स वाई);
2. लघुगणक - लघुगणक = लघुगणक (x: y)।

एक ही आधार

लॉग 6 4 + लॉग 6 9.

अब कार्य को थोड़ा जटिल करते हैं।

लघुगणक हल करने के उदाहरण

क्या होगा यदि लघुगणक के आधार या तर्क में कोई डिग्री हो? तब इस डिग्री के घातांक को निम्न नियमों के अनुसार लघुगणक के चिह्न से निकाला जा सकता है:

बेशक, ये सभी नियम समझ में आते हैं यदि ODZ लघुगणक मनाया जाता है: a > 0, a 1, x >

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

एक नई नींव में संक्रमण

बता दें कि लघुगणक लघुगणक दिया जाता है। फिर किसी भी संख्या c जैसे कि c > 0 और c ≠ 1 के लिए, समानता सत्य है:

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

यह सभी देखें:

लघुगणक के मूल गुण

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

घातांक 2.718281828…. प्रतिपादक को याद करने के लिए, आप नियम का अध्ययन कर सकते हैं: प्रतिपादक 2.7 है और लियो टॉल्स्टॉय के जन्म के वर्ष का दोगुना है।

लघुगणक के मूल गुण

इस नियम को जानकर आप घातांक का सही मूल्य और लियो टॉल्स्टॉय की जन्म तिथि दोनों को जान जाएंगे।

लघुगणक के उदाहरण

व्यंजकों का लघुगणक लें

उदाहरण 1
एक)। x=10ac^2 (ए>0, सी>0)।

गुण 3,5 से हम गणना करते हैं

2.

3.

4. कहाँ पे .

उदाहरण 2 x ज्ञात कीजिए यदि

उदाहरण 3. मान लीजिए कि लघुगणक का मान दिया गया है

लॉग (x) की गणना करें यदि

लघुगणक के मूल गुण

लॉगरिदम, किसी भी संख्या की तरह, हर संभव तरीके से जोड़ा, घटाया और परिवर्तित किया जा सकता है। लेकिन चूंकि लॉगरिदम बिल्कुल सामान्य संख्या नहीं हैं, इसलिए यहां नियम हैं, जिन्हें कहा जाता है बुनियादी गुण.

इन नियमों को अवश्य जानना चाहिए - इनके बिना कोई भी गंभीर लघुगणकीय समस्या हल नहीं हो सकती है। इसके अलावा, उनमें से बहुत कम हैं - एक दिन में सब कुछ सीखा जा सकता है। तो चलो शुरू करते है।

लघुगणक का जोड़ और घटाव

समान आधार वाले दो लघुगणक पर विचार करें: लघुगणक और लघुगणक। फिर उन्हें जोड़ा और घटाया जा सकता है, और:

1. लॉगैक्स + लोगे = लॉग (एक्स वाई);
2. लघुगणक - लघुगणक = लघुगणक (x: y)।

तो, लघुगणक का योग उत्पाद के लघुगणक के बराबर है, और अंतर भागफल का लघुगणक है। कृपया ध्यान दें: यहाँ मुख्य बिंदु है - एक ही आधार. यदि आधार भिन्न हैं, तो ये नियम काम नहीं करते हैं!

ये सूत्र लघुगणकीय व्यंजक की गणना करने में मदद करेंगे, भले ही इसके अलग-अलग हिस्सों पर विचार न किया गया हो (पाठ "एक लघुगणक क्या है" देखें)। उदाहरणों पर एक नज़र डालें और देखें:

चूंकि लघुगणक के आधार समान हैं, इसलिए हम योग सूत्र का उपयोग करते हैं:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log2 48 - log2 3.

आधार समान हैं, हम अंतर सूत्र का उपयोग करते हैं:
log2 48 - log2 3 = log2 (48: 3) = log2 16 = 4।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log3 135 - log3 5.

फिर से, आधार समान हैं, इसलिए हमारे पास है:
log3 135 - log3 5 = log3 (135: 5) = log3 27 = 3।

जैसा कि आप देख सकते हैं, मूल भाव "खराब" लघुगणक से बने होते हैं, जिन्हें अलग से नहीं माना जाता है। लेकिन परिवर्तनों के बाद काफी सामान्य संख्याएँ निकलती हैं। कई परीक्षण इस तथ्य पर आधारित हैं। हां, नियंत्रण - पूरी गंभीरता से समान भाव (कभी-कभी - वस्तुतः कोई बदलाव नहीं) परीक्षा में पेश किए जाते हैं।

घातांक को लघुगणक से हटाना

यह देखना आसान है कि अंतिम नियम उनके पहले दो का अनुसरण करता है। लेकिन इसे वैसे भी याद रखना बेहतर है - कुछ मामलों में यह गणना की मात्रा को काफी कम कर देगा।

बेशक, ये सभी नियम समझ में आते हैं यदि ओडीजेड लॉगरिदम मनाया जाता है: ए> 0, ए ≠ 1, एक्स> 0. और एक और बात: न केवल बाएं से दाएं, बल्कि इसके विपरीत भी सभी सूत्रों को लागू करना सीखें, यानी। आप लघुगणक के चिह्न से पहले संख्याओं को लघुगणक में ही दर्ज कर सकते हैं। यह वही है जो सबसे अधिक बार आवश्यक होता है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log7 496।

आइए पहले सूत्र के अनुसार तर्क में डिग्री से छुटकारा पाएं:
log7 496 = 6 log7 49 = 6 2 = 12

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

ध्यान दें कि हर एक लघुगणक है जिसका आधार और तर्क सटीक शक्तियाँ हैं: 16 = 24; 49 = 72. हमारे पास है:

मुझे लगता है कि अंतिम उदाहरण को स्पष्टीकरण की आवश्यकता है। लघुगणक कहाँ चले गए हैं? अंतिम क्षण तक, हम केवल हर के साथ काम करते हैं।

लघुगणक के सूत्र। लघुगणक समाधान के उदाहरण हैं।

उन्होंने वहां खड़े लघुगणक के आधार और तर्क को डिग्री के रूप में प्रस्तुत किया और संकेतक निकाले - उन्हें "तीन मंजिला" अंश मिला।

अब आइए मुख्य अंश को देखें। अंश और हर की संख्या समान है: log2 7. चूंकि log2 7 0, हम भिन्न को कम कर सकते हैं - 2/4 हर में रहेगा। अंकगणित के नियमों के अनुसार, चार को अंश में स्थानांतरित किया जा सकता है, जो किया गया था। परिणाम उत्तर है: 2.

एक नई नींव में संक्रमण

लॉगरिदम जोड़ने और घटाने के नियमों के बारे में बोलते हुए, मैंने विशेष रूप से जोर दिया कि वे केवल एक ही आधार के साथ काम करते हैं। क्या होगा यदि आधार अलग हैं? क्या होगा यदि वे एक ही संख्या की सटीक शक्तियां नहीं हैं?

एक नए आधार पर संक्रमण के लिए सूत्र बचाव के लिए आते हैं। हम उन्हें एक प्रमेय के रूप में तैयार करते हैं:

बता दें कि लघुगणक लघुगणक दिया जाता है। फिर किसी भी संख्या c जैसे कि c > 0 और c ≠ 1 के लिए, समानता सत्य है:

विशेष रूप से, यदि हम c = x रखते हैं, तो हमें प्राप्त होता है:

यह दूसरे सूत्र से इस प्रकार है कि आधार और लघुगणक के तर्क को आपस में बदलना संभव है, लेकिन इस मामले में पूरी अभिव्यक्ति "उलट" है, अर्थात। लघुगणक हर में है।

ये सूत्र सामान्य संख्यात्मक अभिव्यक्तियों में बहुत कम पाए जाते हैं। यह मूल्यांकन करना संभव है कि लॉगरिदमिक समीकरणों और असमानताओं को हल करते समय ही वे कितने सुविधाजनक होते हैं।

हालाँकि, ऐसे कार्य हैं जिन्हें एक नई नींव में जाने के अलावा हल नहीं किया जा सकता है। आइए इनमें से कुछ पर विचार करें:

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log5 16 log2 25.

ध्यान दें कि दोनों लघुगणक के तर्क सटीक घातांक हैं। आइए संकेतक निकालें: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

अब दूसरा लघुगणक पलटें:

चूंकि उत्पाद कारकों के क्रमपरिवर्तन से नहीं बदलता है, हमने शांति से चार और दो को गुणा किया, और फिर लघुगणक का पता लगाया।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log9 100 lg 3.

पहले लघुगणक का आधार और तर्क सटीक शक्तियाँ हैं। आइए इसे लिख लें और संकेतकों से छुटकारा पाएं:

आइए अब एक नए आधार पर जाकर दशमलव लघुगणक से छुटकारा पाएं:

मूल लघुगणकीय पहचान

अक्सर हल करने की प्रक्रिया में किसी दिए गए आधार के लिए एक संख्या को लघुगणक के रूप में प्रस्तुत करना आवश्यक होता है। इस मामले में, सूत्र हमारी मदद करेंगे:

पहले मामले में, संख्या n तर्क में घातांक बन जाती है। संख्या n बिल्कुल कुछ भी हो सकती है, क्योंकि यह केवल लघुगणक का मान है।

दूसरा सूत्र वास्तव में एक व्याख्यात्मक परिभाषा है। इसे इस तरह कहा जाता है:

वास्तव में, क्या होगा यदि संख्या b को इस हद तक बढ़ा दिया जाए कि इस अंश की संख्या b संख्या a दे दे? यह सही है: यह वही संख्या है a. इस पैराग्राफ को फिर से ध्यान से पढ़ें - बहुत से लोग इसे "लटका" देते हैं।

नए आधार रूपांतरण फ़ार्मुलों की तरह, मूल लघुगणकीय पहचान कभी-कभी एकमात्र संभव समाधान होता है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

ध्यान दें कि log25 64 = log5 8 - बस आधार से वर्ग निकाल लिया और लघुगणक का तर्क। समान आधार से घातों को गुणा करने के नियमों को देखते हुए, हम प्राप्त करते हैं:

अगर किसी को पता नहीं है, तो यह एकीकृत राज्य परीक्षा से एक वास्तविक कार्य था

लघुगणक इकाई और लघुगणक शून्य

अंत में, मैं दो पहचान दूंगा जिन्हें गुणों को कॉल करना मुश्किल है - बल्कि, ये लॉगरिदम की परिभाषा से परिणाम हैं। वे लगातार समस्याओं में पाए जाते हैं और आश्चर्यजनक रूप से, "उन्नत" छात्रों के लिए भी समस्याएं पैदा करते हैं।

1. लोगा = 1 है। एक बार और सभी के लिए याद रखें: किसी भी आधार के लिए लघुगणक उस आधार से ही एक के बराबर होता है।
2. लॉगा 1 = 0 है। आधार a कुछ भी हो सकता है, लेकिन यदि तर्क एक है, तो लघुगणक शून्य है! क्योंकि a0 = 1 परिभाषा का प्रत्यक्ष परिणाम है।

वह सब गुण है। उन्हें अभ्यास में लाने का अभ्यास करना सुनिश्चित करें! पाठ की शुरुआत में चीट शीट डाउनलोड करें, उसका प्रिंट आउट लें और समस्याओं का समाधान करें।

यह सभी देखें:

संख्या b का आधार a का लघुगणक व्यंजक को दर्शाता है। लघुगणक की गणना करने का अर्थ है ऐसी घात x () ज्ञात करना जिस पर समानता सत्य हो

लघुगणक के मूल गुण

उपरोक्त गुणों को जानने की आवश्यकता है, क्योंकि उनके आधार पर लगभग सभी समस्याओं और उदाहरणों को लघुगणक के आधार पर हल किया जाता है। शेष विदेशी गुण इन सूत्रों के साथ गणितीय जोड़तोड़ द्वारा प्राप्त किए जा सकते हैं

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

योग और लघुगणक (3.4) के अंतर के सूत्रों की गणना करते समय अक्सर सामना किया जाता है। बाकी कुछ जटिल हैं, लेकिन कई कार्यों में वे जटिल अभिव्यक्तियों को सरल बनाने और उनके मूल्यों की गणना के लिए अनिवार्य हैं।

लघुगणक के सामान्य मामले

कुछ सामान्य लघुगणक वे हैं जिनमें आधार सम भी दस, घातांक या ड्यूस है।
आधार दस लघुगणक को आमतौर पर आधार दस लघुगणक कहा जाता है और इसे केवल lg(x) के रूप में दर्शाया जाता है।

रिकॉर्ड से यह देखा जा सकता है कि मूल बातें रिकॉर्ड में नहीं लिखी गई हैं। उदाहरण के लिए

प्राकृतिक लघुगणक वह लघुगणक है जिसका आधार घातांक (निरूपित ln(x)) है।

घातांक 2.718281828…. प्रतिपादक को याद करने के लिए, आप नियम का अध्ययन कर सकते हैं: प्रतिपादक 2.7 है और लियो टॉल्स्टॉय के जन्म के वर्ष का दोगुना है। इस नियम को जानकर आप घातांक का सही मूल्य और लियो टॉल्स्टॉय की जन्म तिथि दोनों को जान जाएंगे।

और दूसरा महत्वपूर्ण आधार दो लघुगणक है

फ़ंक्शन के लघुगणक का व्युत्पन्न चर द्वारा विभाजित एक के बराबर है

अभिन्न या प्रतिपक्षी लघुगणक निर्भरता द्वारा निर्धारित किया जाता है

उपरोक्त सामग्री आपके लिए लघुगणक और लघुगणक से संबंधित समस्याओं की एक विस्तृत श्रेणी को हल करने के लिए पर्याप्त है। सामग्री को आत्मसात करने के लिए, मैं स्कूली पाठ्यक्रम और विश्वविद्यालयों से केवल कुछ सामान्य उदाहरण दूंगा।

लघुगणक के उदाहरण

व्यंजकों का लघुगणक लें

उदाहरण 1
एक)। x=10ac^2 (ए>0, सी>0)।

गुण 3,5 से हम गणना करते हैं

2.
लघुगणक के अंतर गुण से, हमारे पास है

3.
गुण 3.5 का उपयोग करके हम पाते हैं

4. कहाँ पे .

नियमों की एक श्रृंखला का उपयोग करके प्रतीत होने वाली जटिल अभिव्यक्ति को फॉर्म में सरल बनाया गया है

लघुगणक मान ढूँढना

उदाहरण 2 x ज्ञात कीजिए यदि

समाधान। गणना के लिए, हम गुण 5 और 13 को अंतिम पद तक लागू करते हैं

रिकॉर्ड में स्थानापन्न करें और शोक करें

चूँकि आधार समान हैं, हम व्यंजकों को समान करते हैं

लघुगणक। प्रथम स्तर।

मान लीजिए लघुगणक का मान दिया गया है

लॉग (x) की गणना करें यदि

हल: पदों के योग से लघुगणक लिखने के लिए चर का लघुगणक लें

यह लघुगणक और उनके गुणों से परिचित होने की शुरुआत है। गणना का अभ्यास करें, अपने व्यावहारिक कौशल को समृद्ध करें - लॉगरिदमिक समीकरणों को हल करने के लिए आपको जल्द ही अर्जित ज्ञान की आवश्यकता होगी। ऐसे समीकरणों को हल करने के लिए बुनियादी तरीकों का अध्ययन करने के बाद, हम आपके ज्ञान को एक और समान रूप से महत्वपूर्ण विषय - लघुगणकीय असमानताओं के लिए विस्तारित करेंगे ...

लघुगणक के मूल गुण

लॉगरिदम, किसी भी संख्या की तरह, हर संभव तरीके से जोड़ा, घटाया और परिवर्तित किया जा सकता है। लेकिन चूंकि लॉगरिदम बिल्कुल सामान्य संख्या नहीं हैं, इसलिए यहां नियम हैं, जिन्हें कहा जाता है बुनियादी गुण.

इन नियमों को अवश्य जानना चाहिए - इनके बिना कोई भी गंभीर लघुगणकीय समस्या हल नहीं हो सकती है। इसके अलावा, उनमें से बहुत कम हैं - एक दिन में सब कुछ सीखा जा सकता है। तो चलो शुरू करते है।

लघुगणक का जोड़ और घटाव

समान आधार वाले दो लघुगणक पर विचार करें: लघुगणक और लघुगणक। फिर उन्हें जोड़ा और घटाया जा सकता है, और:

1. लॉगैक्स + लोगे = लॉग (एक्स वाई);
2. लघुगणक - लघुगणक = लघुगणक (x: y)।

तो, लघुगणक का योग उत्पाद के लघुगणक के बराबर है, और अंतर भागफल का लघुगणक है। कृपया ध्यान दें: यहाँ मुख्य बिंदु है - एक ही आधार. यदि आधार भिन्न हैं, तो ये नियम काम नहीं करते हैं!

ये सूत्र लघुगणकीय व्यंजक की गणना करने में मदद करेंगे, भले ही इसके अलग-अलग हिस्सों पर विचार न किया गया हो (पाठ "एक लघुगणक क्या है" देखें)। उदाहरणों पर एक नज़र डालें और देखें:

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log6 4 + log6 9.

चूंकि लघुगणक के आधार समान हैं, इसलिए हम योग सूत्र का उपयोग करते हैं:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log2 48 - log2 3.

आधार समान हैं, हम अंतर सूत्र का उपयोग करते हैं:
log2 48 - log2 3 = log2 (48: 3) = log2 16 = 4।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log3 135 - log3 5.

फिर से, आधार समान हैं, इसलिए हमारे पास है:
log3 135 - log3 5 = log3 (135: 5) = log3 27 = 3।

जैसा कि आप देख सकते हैं, मूल भाव "खराब" लघुगणक से बने होते हैं, जिन्हें अलग से नहीं माना जाता है। लेकिन परिवर्तनों के बाद काफी सामान्य संख्याएँ निकलती हैं। कई परीक्षण इस तथ्य पर आधारित हैं। हां, नियंत्रण - पूरी गंभीरता से समान भाव (कभी-कभी - वस्तुतः कोई बदलाव नहीं) परीक्षा में पेश किए जाते हैं।

घातांक को लघुगणक से हटाना

अब कार्य को थोड़ा जटिल करते हैं। क्या होगा यदि लघुगणक के आधार या तर्क में कोई डिग्री हो? तब इस डिग्री के घातांक को निम्न नियमों के अनुसार लघुगणक के चिह्न से निकाला जा सकता है:

यह देखना आसान है कि अंतिम नियम उनके पहले दो का अनुसरण करता है। लेकिन इसे वैसे भी याद रखना बेहतर है - कुछ मामलों में यह गणना की मात्रा को काफी कम कर देगा।

बेशक, ये सभी नियम समझ में आते हैं यदि ओडीजेड लॉगरिदम मनाया जाता है: ए> 0, ए ≠ 1, एक्स> 0. और एक और बात: न केवल बाएं से दाएं, बल्कि इसके विपरीत भी सभी सूत्रों को लागू करना सीखें, यानी। आप लघुगणक के चिह्न से पहले संख्याओं को लघुगणक में ही दर्ज कर सकते हैं।

लघुगणक कैसे हल करें

यह वही है जो सबसे अधिक बार आवश्यक होता है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log7 496।

आइए पहले सूत्र के अनुसार तर्क में डिग्री से छुटकारा पाएं:
log7 496 = 6 log7 49 = 6 2 = 12

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

ध्यान दें कि हर एक लघुगणक है जिसका आधार और तर्क सटीक शक्तियाँ हैं: 16 = 24; 49 = 72. हमारे पास है:

मुझे लगता है कि अंतिम उदाहरण को स्पष्टीकरण की आवश्यकता है। लघुगणक कहाँ चले गए हैं? अंतिम क्षण तक, हम केवल हर के साथ काम करते हैं। उन्होंने वहां खड़े लघुगणक के आधार और तर्क को डिग्री के रूप में प्रस्तुत किया और संकेतक निकाले - उन्हें "तीन मंजिला" अंश मिला।

अब आइए मुख्य अंश को देखें। अंश और हर की संख्या समान है: log2 7. चूंकि log2 7 0, हम भिन्न को कम कर सकते हैं - 2/4 हर में रहेगा। अंकगणित के नियमों के अनुसार, चार को अंश में स्थानांतरित किया जा सकता है, जो किया गया था। परिणाम उत्तर है: 2.

एक नई नींव में संक्रमण

लॉगरिदम जोड़ने और घटाने के नियमों के बारे में बोलते हुए, मैंने विशेष रूप से जोर दिया कि वे केवल एक ही आधार के साथ काम करते हैं। क्या होगा यदि आधार अलग हैं? क्या होगा यदि वे एक ही संख्या की सटीक शक्तियां नहीं हैं?

एक नए आधार पर संक्रमण के लिए सूत्र बचाव के लिए आते हैं। हम उन्हें एक प्रमेय के रूप में तैयार करते हैं:

बता दें कि लघुगणक लघुगणक दिया जाता है। फिर किसी भी संख्या c जैसे कि c > 0 और c ≠ 1 के लिए, समानता सत्य है:

विशेष रूप से, यदि हम c = x रखते हैं, तो हमें प्राप्त होता है:

यह दूसरे सूत्र से इस प्रकार है कि आधार और लघुगणक के तर्क को आपस में बदलना संभव है, लेकिन इस मामले में पूरी अभिव्यक्ति "उलट" है, अर्थात। लघुगणक हर में है।

ये सूत्र सामान्य संख्यात्मक अभिव्यक्तियों में बहुत कम पाए जाते हैं। यह मूल्यांकन करना संभव है कि लॉगरिदमिक समीकरणों और असमानताओं को हल करते समय ही वे कितने सुविधाजनक होते हैं।

हालाँकि, ऐसे कार्य हैं जिन्हें एक नई नींव में जाने के अलावा हल नहीं किया जा सकता है। आइए इनमें से कुछ पर विचार करें:

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log5 16 log2 25.

ध्यान दें कि दोनों लघुगणक के तर्क सटीक घातांक हैं। आइए संकेतक निकालें: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

अब दूसरा लघुगणक पलटें:

चूंकि उत्पाद कारकों के क्रमपरिवर्तन से नहीं बदलता है, हमने शांति से चार और दो को गुणा किया, और फिर लघुगणक का पता लगाया।

एक कार्य। व्यंजक का मान ज्ञात कीजिए: log9 100 lg 3.

पहले लघुगणक का आधार और तर्क सटीक शक्तियाँ हैं। आइए इसे लिख लें और संकेतकों से छुटकारा पाएं:

आइए अब एक नए आधार पर जाकर दशमलव लघुगणक से छुटकारा पाएं:

मूल लघुगणकीय पहचान

अक्सर हल करने की प्रक्रिया में किसी दिए गए आधार के लिए एक संख्या को लघुगणक के रूप में प्रस्तुत करना आवश्यक होता है। इस मामले में, सूत्र हमारी मदद करेंगे:

पहले मामले में, संख्या n तर्क में घातांक बन जाती है। संख्या n बिल्कुल कुछ भी हो सकती है, क्योंकि यह केवल लघुगणक का मान है।

दूसरा सूत्र वास्तव में एक व्याख्यात्मक परिभाषा है। इसे इस तरह कहा जाता है:

वास्तव में, क्या होगा यदि संख्या b को इस हद तक बढ़ा दिया जाए कि इस अंश की संख्या b संख्या a दे दे? यह सही है: यह वही संख्या है a. इस पैराग्राफ को फिर से ध्यान से पढ़ें - बहुत से लोग इसे "लटका" देते हैं।

नए आधार रूपांतरण फ़ार्मुलों की तरह, मूल लघुगणकीय पहचान कभी-कभी एकमात्र संभव समाधान होता है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

ध्यान दें कि log25 64 = log5 8 - बस आधार से वर्ग निकाल लिया और लघुगणक का तर्क। समान आधार से घातों को गुणा करने के नियमों को देखते हुए, हम प्राप्त करते हैं:

अगर किसी को पता नहीं है, तो यह एकीकृत राज्य परीक्षा से एक वास्तविक कार्य था

लघुगणक इकाई और लघुगणक शून्य

अंत में, मैं दो पहचान दूंगा जिन्हें गुणों को कॉल करना मुश्किल है - बल्कि, ये लॉगरिदम की परिभाषा से परिणाम हैं। वे लगातार समस्याओं में पाए जाते हैं और आश्चर्यजनक रूप से, "उन्नत" छात्रों के लिए भी समस्याएं पैदा करते हैं।

1. लोगा = 1 है। एक बार और सभी के लिए याद रखें: किसी भी आधार के लिए लघुगणक उस आधार से ही एक के बराबर होता है।
2. लॉगा 1 = 0 है। आधार a कुछ भी हो सकता है, लेकिन यदि तर्क एक है, तो लघुगणक शून्य है! क्योंकि a0 = 1 परिभाषा का प्रत्यक्ष परिणाम है।

वह सब गुण है। उन्हें अभ्यास में लाने का अभ्यास करना सुनिश्चित करें! पाठ की शुरुआत में चीट शीट डाउनलोड करें, उसका प्रिंट आउट लें और समस्याओं का समाधान करें।

आदिम स्तर के बीजगणित के तत्वों में से एक लघुगणक है। यह नाम ग्रीक भाषा से "नंबर" या "डिग्री" शब्द से आया है और इसका मतलब है कि अंतिम संख्या खोजने के लिए आधार पर संख्या को बढ़ाने के लिए आवश्यक डिग्री है।

लघुगणक के प्रकार

• लॉग ए बी संख्या बी का आधार ए (ए> 0, ए ≠ 1, बी> 0) का लॉगरिदम है;
• एलजी बी - दशमलव लघुगणक (लघुगणक आधार 10, ए = 10);
• एलएन बी - प्राकृतिक लॉगरिदम (लघुगणक आधार ई, ए = ई)।

लघुगणक कैसे हल करें?

संख्या b से आधार a का लघुगणक एक घातांक है, जिसके लिए आधार a को संख्या b तक बढ़ाना आवश्यक है। परिणाम इस तरह उच्चारित किया जाता है: "बी का लॉगरिदम टू बेस ए"। लॉगरिदमिक समस्याओं का समाधान यह है कि आपको निर्दिष्ट संख्याओं द्वारा दी गई डिग्री को संख्याओं द्वारा निर्धारित करने की आवश्यकता है। लघुगणक को निर्धारित करने या हल करने के साथ-साथ संकेतन को बदलने के लिए कुछ बुनियादी नियम हैं। उनका उपयोग करके, लॉगरिदमिक समीकरण हल किए जाते हैं, व्युत्पन्न पाए जाते हैं, इंटीग्रल हल किए जाते हैं, और कई अन्य ऑपरेशन किए जाते हैं। मूल रूप से, लघुगणक का समाधान ही इसका सरलीकृत अंकन है। नीचे मुख्य सूत्र और गुण हैं:

किसी के लिए; ए > 0; a 1 और किसी भी x के लिए; वाई> 0।

• a log a b = b मूल लघुगणकीय पहचान है
• लॉग ए 1 = 0
• लॉग ए = 1
• log a (x y ) = log a x + log a y
• लॉग a x/ y = लॉग a x – लॉग a y
• लॉग ए 1/x = -लॉग ए x
• लॉग a x p = p लॉग a x
• लॉग a k x = 1/k लॉग a x , k 0 . के लिए
• लॉग a x = लॉग a c x c
• लॉग ए एक्स \u003d लॉग बी एक्स / लॉग बी ए - एक नए आधार पर संक्रमण के लिए सूत्र
• लॉग एक्स = 1/लॉग एक्स ए

लघुगणक कैसे हल करें - हल करने के लिए चरण दर चरण निर्देश

• सबसे पहले, आवश्यक समीकरण लिखिए।

कृपया ध्यान दें: यदि आधार लघुगणक 10 है, तो रिकॉर्ड छोटा हो जाता है, एक दशमलव लघुगणक प्राप्त होता है। यदि कोई प्राकृतिक संख्या ई है, तो हम एक प्राकृतिक लघुगणक को कम करते हुए लिखते हैं। इसका अर्थ है कि सभी लघुगणक का परिणाम वह शक्ति है जिससे संख्या b प्राप्त करने के लिए आधार संख्या को ऊपर उठाया जाता है।

सीधे तौर पर, समाधान इस डिग्री की गणना में निहित है। किसी व्यंजक को लघुगणक के साथ हल करने से पहले, इसे नियम के अनुसार सरल बनाना चाहिए, अर्थात सूत्रों का उपयोग करना। आप लेख में थोड़ा पीछे जाकर मुख्य पहचान पा सकते हैं।

दो अलग-अलग संख्याओं के साथ लेकिन एक ही आधार के साथ लॉगरिदम जोड़ते और घटाते समय, क्रमशः बी और सी के उत्पाद या विभाजन के साथ एकल लॉगरिदम के साथ प्रतिस्थापित करें। इस मामले में, आप संक्रमण सूत्र को दूसरे आधार पर लागू कर सकते हैं (ऊपर देखें)।

यदि आप लघुगणक को सरल बनाने के लिए व्यंजकों का उपयोग कर रहे हैं, तो कुछ सीमाएँ हैं जिनके बारे में पता होना चाहिए। और वह है: लघुगणक का आधार केवल एक धनात्मक संख्या है, लेकिन एक के बराबर नहीं है। संख्या b, जैसे a, शून्य से बड़ी होनी चाहिए।

ऐसे मामले हैं जब अभिव्यक्ति को सरल बनाने के बाद, आप संख्यात्मक रूप में लघुगणक की गणना करने में सक्षम नहीं होंगे। ऐसा होता है कि इस तरह की अभिव्यक्ति का कोई मतलब नहीं है, क्योंकि कई डिग्री अपरिमेय संख्याएं हैं। इस शर्त के तहत, संख्या की शक्ति को लघुगणक के रूप में छोड़ दें।

एक धनात्मक संख्या b का आधार a (a>0, a 1 के बराबर नहीं है) का लघुगणक एक संख्या c है जैसे a c = b: log a b = c ⇔ a c = b (a > 0, a 1, b > 0)       

ध्यान दें कि एक गैर-धनात्मक संख्या का लघुगणक परिभाषित नहीं है। साथ ही, लघुगणक का आधार एक धनात्मक संख्या होनी चाहिए, न कि 1 के बराबर। उदाहरण के लिए, यदि हम -2 का वर्ग करते हैं, तो हमें संख्या 4 प्राप्त होती है, लेकिन इसका मतलब यह नहीं है कि 4 का आधार -2 लघुगणक 2 है।

मूल लघुगणकीय पहचान

एक लॉग ए बी = बी (ए> 0, ए ≠ 1) (2)

यह महत्वपूर्ण है कि इस सूत्र के दाएं और बाएं भागों की परिभाषा के डोमेन अलग-अलग हों। बाईं ओर केवल b>0, a>0 और a 1 के लिए परिभाषित किया गया है। किसी भी b के लिए दाईं ओर परिभाषित किया गया है, और यह बिल्कुल भी निर्भर नहीं करता है। इस प्रकार, समीकरणों और असमानताओं को हल करने में मूल लघुगणकीय "पहचान" के अनुप्रयोग से डीपीवी में परिवर्तन हो सकता है।

लघुगणक की परिभाषा के दो स्पष्ट परिणाम

लॉग ए ए = 1 (ए> 0, ए ≠ 1) (3)
लॉग ए 1 = 0 (ए> 0, ए ≠ 1) (4)

दरअसल, संख्या को पहली शक्ति तक बढ़ाने पर, हमें वही संख्या मिलती है, और जब इसे शून्य शक्ति तक बढ़ाया जाता है, तो हमें एक मिलता है।

उत्पाद का लघुगणक और भागफल का लघुगणक

लॉग ए (बी सी) = लॉग ए बी + लॉग ए सी (ए> 0, ए 1, बी> 0, सी> 0) (5)

लॉग ए बी सी = लॉग ए बी - लॉग ए सी (ए> 0, ए 1, बी> 0, सी> 0) (6)

मैं स्कूली बच्चों को लॉगरिदमिक समीकरणों और असमानताओं को हल करते समय इन सूत्रों के विचारहीन उपयोग के खिलाफ चेतावनी देना चाहता हूं। जब उनका उपयोग "बाएं से दाएं" किया जाता है, तो ODZ संकुचित हो जाता है, और जब लघुगणक के योग या अंतर से उत्पाद या भागफल के लघुगणक की ओर बढ़ते हैं, तो ODZ फैलता है।

वास्तव में, व्यंजक लॉग a (f (x) g (x)) को दो स्थितियों में परिभाषित किया गया है: जब दोनों फलन पूर्णतः धनात्मक हों या जब f(x) और g(x) दोनों शून्य से कम हों।

इस व्यंजक को योग लॉग a f (x) + log a g (x) में बदलने पर, हम स्वयं को केवल उस स्थिति तक सीमित रखने के लिए बाध्य होते हैं जब f(x)>0 और g(x)>0। स्वीकार्य मूल्यों की सीमा का एक संकुचन है, और यह स्पष्ट रूप से अस्वीकार्य है, क्योंकि इससे समाधान का नुकसान हो सकता है। इसी तरह की समस्या सूत्र (6) के लिए मौजूद है।

डिग्री को लघुगणक के चिन्ह से निकाला जा सकता है

लॉग ए बी पी = पी लॉग ए बी (ए> 0, ए 1, बी> 0) (7)

और फिर से मैं सटीकता के लिए कॉल करना चाहूंगा। निम्नलिखित उदाहरण पर विचार करें:

लॉग ए (एफ (एक्स) 2 = 2 लॉग ए एफ (एक्स)

समानता के बाईं ओर शून्य को छोड़कर f(x) के सभी मानों के लिए स्पष्ट रूप से परिभाषित किया गया है। दायां पक्ष केवल f(x)>0 के लिए है! लघुगणक से शक्ति निकालते हुए, हम ODZ को फिर से संकीर्ण करते हैं। रिवर्स प्रक्रिया स्वीकार्य मूल्यों की सीमा के विस्तार की ओर ले जाती है। ये सभी टिप्पणियां न केवल 2 की शक्ति पर लागू होती हैं, बल्कि किसी भी शक्ति पर भी लागू होती हैं।

नए आधार पर जाने का फॉर्मूला

लॉग ए बी = लॉग सी बी लॉग सी ए (ए> 0, ए 1, बी> 0, सी> 0, सी ≠ 1) (8)

वह दुर्लभ मामला जब रूपांतरण के दौरान ODZ नहीं बदलता है। यदि आपने आधार c को बुद्धिमानी से चुना है (सकारात्मक और 1 के बराबर नहीं), तो नए आधार पर जाने का सूत्र पूरी तरह से सुरक्षित है।

यदि हम संख्या b को नए आधार c के रूप में चुनते हैं, तो हमें सूत्र (8) का एक महत्वपूर्ण विशेष मामला प्राप्त होता है:

लॉग ए बी = 1 लॉग बी ए (ए> 0, ए 1, बी> 0, बी ≠ 1) (9)

लघुगणक के साथ कुछ सरल उदाहरण

उदाहरण 1 गणना करें: lg2 + lg50।
समाधान। lg2 + lg50 = lg100 = 2. हमने लघुगणक (5) के योग और दशमलव लघुगणक की परिभाषा के लिए सूत्र का उपयोग किया।

उदाहरण 2 परिकलित करें: lg125/lg5.
समाधान। lg125/lg5 = log 5 125 = 3. हमने नए आधार संक्रमण सूत्र (8) का उपयोग किया।

लघुगणक से संबंधित सूत्रों की तालिका

एक लॉग ए बी = बी (ए> 0, ए ≠ 1)

लॉग ए ए = 1 (ए> 0, ए ≠ 1)

लॉग ए 1 = 0 (ए> 0, ए ≠ 1)

लॉग ए (बी सी) = लॉग ए बी + लॉग ए सी (ए> 0, ए 1, बी> 0, सी> 0)

लॉग ए बी सी = लॉग ए बी - लॉग ए सी (ए> 0, ए 1, बी> 0, सी> 0)

लॉग ए बी पी = पी लॉग ए बी (ए> 0, ए 1, बी> 0)

लॉग ए बी = लॉग सी बी लॉग सी ए (ए> 0, ए 1, बी> 0, सी> 0, सी ≠ 1)

लॉग ए बी = 1 लॉग बी ए (ए> 0, ए 1, बी> 0, बी ≠ 1)