परिभाषा

त्रिकोणमितीय असमानताएँ वे असमानताएँ हैं जिनमें त्रिकोणमितीय फलन के चिह्न के नीचे एक चर होता है।

त्रिकोणमितीय असमानताओं को हल करना

त्रिकोणमितीय असमानताओं का समाधान अक्सर फॉर्म की सबसे सरल त्रिकोणमितीय असमानताओं को हल करने के लिए नीचे आता है: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg) ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)

सरलतम त्रिकोणमितीय असमानताओं को ग्राफिक रूप से या एक इकाई त्रिकोणमितीय सर्कल का उपयोग करके हल किया जाता है।

परिभाषा के अनुसार, कोण की ज्या \(\ \alpha \) इकाई वृत्त के बिंदु \(\ P_(\alpha)(x, y) \) की कोटि है (चित्र 1), और कोज्या है इस बिंदु की अनुपस्थिति। इस तथ्य का उपयोग यूनिट सर्कल का उपयोग करके कोसाइन और साइन के साथ सबसे सरल त्रिकोणमितीय असमानताओं को हल करने में किया जाता है।

त्रिकोणमितीय असमानताओं को हल करने के उदाहरण

व्यायाम

असमानता को हल करें \(\ \sin x \leq \frac(\sqrt(3))(2) \)

समाधान

चूँकि \(\ \left|\frac(\sqrt(3))(2)\right| , इस असमानता का एक समाधान है और इसे दो तरीकों से हल किया जा सकता है

पहला तरीका। आइए इस असमानता को ग्राफिक रूप से हल करें। ऐसा करने के लिए, हम उसी समन्वय प्रणाली में साइन \(\ y=\sin x \) (चित्र 2) और सीधी रेखा \(\ y=\frac(\sqrt(3))) का एक ग्राफ बनाते हैं। 2)\)

आइए उन अंतरालों का चयन करें जहां साइनसॉइड सीधी रेखा के ग्राफ के नीचे स्थित है \(\ y=\frac(\sqrt(3))(2) \) । इन ग्राफ़ के प्रतिच्छेदन बिंदुओं के भुज \(\ x_(1) \) और \(\ x_(2) \) खोजें: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

हमें अंतराल मिला \(\ \बाएं[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) लेकिन समारोह के बाद से \(\ y=\sin x \) आवधिक है और इसकी अवधि \(\ 2 \pi \) है, तो उत्तर अंतरालों का संघ है: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)

दूसरा तरीका। एक इकाई वृत्त और एक रेखा बनाएँ \(\ y=\frac(\sqrt(3))(2) \) , उनके प्रतिच्छेदन बिंदुओं को निरूपित करें \(\ P_(x_(1)) \) और \(\ P_(x_ (2 )) \) (चित्र 3)। मूल असमानता का समाधान कोटि बिंदुओं का समुच्चय होगा जो \(\ \frac(\sqrt(3))(2) \) से कम हैं। आइए वामावर्त, \(\ x_(1) चित्र 3 में जाकर \(\ \boldsymbol(I)_(1) \) और \(\ \boldsymbol(I)_(2) \) का मान ज्ञात करें।

\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

साइन फ़ंक्शन की आवधिकता को ध्यान में रखते हुए, हम अंत में अंतराल प्राप्त करते हैं \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ पाई\दाएं] \), \(\k\in Z\)

उत्तर\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\ k \ जेड में \)

व्यायाम

असमानता को हल करें \(\ \sin x>2 \)

फेसला

साइन एक सीमित कार्य है: \(\ |\sin x| \leq 1 \) , और इस असमानता का दाहिना भाग एक से बड़ा है, इसलिए कोई समाधान नहीं है।

उत्तर: कोई उपाय नहीं हैं।

व्यायाम

असमानता को हल करें \(\ \cos x>\frac(1)(2) \)

फेसला

इस असमानता को दो तरीकों से हल किया जा सकता है: ग्राफिक रूप से और एक यूनिट सर्कल का उपयोग करके। आइए प्रत्येक विधियों पर विचार करें।

पहला तरीका। आइए एक समन्वय प्रणाली में उन कार्यों को चित्रित करें जो असमानता के बाएँ और दाएँ भागों का वर्णन करते हैं, अर्थात् \(\ y=\cos x \) और \(\ y=\frac(1)(2) \) । आइए हम उन अंतरालों का चयन करें जहां कोज्या फलन का ग्राफ \(\ y=\cos x \) सीधी रेखा के ग्राफ के ऊपर स्थित है \(\ y=\frac(1)(2) \) (चित्र 4 )

बिंदुओं के भुज खोजें \(\ \boldsymbol(x)_(1) \) और \(\ x_(2) \) - फ़ंक्शन के ग्राफ़ के प्रतिच्छेदन बिंदु \(\ y=\cos x \ ) और \(\ y=\frac (1)(2) \) , जो एक अंतराल के अंत हैं जिस पर संकेतित असमानता है। \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

यह देखते हुए कि कोसाइन एक आवधिक कार्य है, एक अवधि \(\ 2 \pi \) के साथ, उत्तर अंतराल से \(\ x \) का मान होगा \(\ \left(-\frac(\pi)( 3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)

दूसरा तरीका। आइए एक इकाई वृत्त और एक सीधी रेखा \(\ x=\frac(1)(2) \) का निर्माण करें (चूंकि x-अक्ष इकाई वृत्त पर कोसाइनों से मेल खाती है)। मान लीजिए \(\ P_(x_(1)) \) और \(\ P_(x_(2)) \) (चित्र 5) रेखा और इकाई वृत्त के प्रतिच्छेदन बिंदु हैं। मूल समीकरण का समाधान भुज बिंदुओं का समुच्चय होगा जो \(\ \frac(1)(2) \) से कम है। वामावर्त यात्रा करते हुए \(\ x_(1) \) और \(\ 2 \) का मान ज्ञात कीजिए ताकि \(\ x_(1) कोसाइन की आवधिकता को ध्यान में रखते हुए, हम अंत में अंतराल प्राप्त करें \( \ \बाएं(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)

उत्तर: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ के \ जेड में \)

व्यायाम

असमानता को हल करें \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)

फेसला

आइए एक समन्वय प्रणाली में \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) के कार्यों के ग्राफ को प्लॉट करें

आइए उन अंतरालों का चयन करें जहां फ़ंक्शन का ग्राफ \(\ y=\operatorname(ctg) x \) सीधी रेखा के ग्राफ से अधिक नहीं है \(\ y=-\frac(\sqrt(3))(3 ) \) (चित्र 6)।

बिंदु का भुज ज्ञात कीजिए \(\ x_(0) \) , जो एक अंतराल का अंत है जिस पर असमानता \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\) sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)

इस अंतराल का दूसरा सिरा बिंदु \(\ \pi \) है, और फ़ंक्शन \(\ y=\operatorname(ctg) x \) इस बिंदु पर अपरिभाषित है। इस प्रकार, इस असमानता का एक समाधान अंतराल \(\ \frac(2 \pi)(3) \leq x है

उत्तर: \(\ x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\right) \), \(\ k \in Z \)

जटिल तर्क के साथ त्रिकोणमितीय असमानताएं

एक जटिल तर्क के साथ त्रिकोणमितीय असमानताओं को प्रतिस्थापन का उपयोग करके सरलतम त्रिकोणमितीय असमानताओं में घटाया जा सकता है। इसे हल करने के बाद, रिवर्स प्रतिस्थापन किया जाता है और मूल अज्ञात व्यक्त किया जाता है।

व्यायाम

असमानता को हल करें \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

फेसला

इस असमानता के दाईं ओर कोसाइन व्यक्त करें: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

हम प्रतिस्थापन करते हैं \(\ t=2 x+100^(\circ) \) , जिसके बाद यह असमानता सबसे सरल असमानता में बदल जाती है \(\ \cos t \leq-\frac(1)(2) \ )

आइए इसे यूनिट सर्कल का उपयोग करके हल करें। आइए एक इकाई वृत्त और एक रेखा बनाएं \(\ x=-\frac(1)(2) \) । आइए हम \(\ P_(1) \) और \(\ P_(2) \) को रेखा और इकाई वृत्त के प्रतिच्छेदन बिंदुओं के रूप में निरूपित करें (चित्र 7)।

मूल असमानता का समाधान भुज बिन्दुओं का समुच्चय होगा, जो अधिकतम \(\ -\frac(1)(2) \) हैं। बिंदु \(\ P_(1) \) कोण से मेल खाता है \(\ 120^(\circ) \) , और बिंदु \(\ P_(2) \) । इस प्रकार, कोज्या अवधि को देखते हुए, हमें \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ मिलता है। ) , \(\ n \in Z \)

हम रिवर्स प्रतिस्थापन करते हैं \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)

हम व्यक्त करते हैं \(\ \mathbf(x) \), ऐसा करने के लिए, पहले घटाएं \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ एन \ जेड में \); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in जेड\)

और फिर, 2 से विभाजित करें \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)

उत्तर\(\ x \in\बाएं(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \), \ (\ x \in\बाएं(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \)

दोहरी त्रिकोणमितीय असमानताएं

व्यायाम

डबल त्रिकोणमितीय असमानता को हल करें \(\ \frac(1)(2)

फेसला

आइए हम प्रतिस्थापन का परिचय दें \(\ t=\frac(x)(2) \) , तो मूल असमानता \(\ \frac(1)(2) का रूप ले लेगी।

आइए इसे यूनिट सर्कल का उपयोग करके हल करें। चूँकि कोटि अक्ष इकाई वृत्त पर ज्या से मेल खाती है, इसलिए हम उस पर निर्देशांकों के समुच्चय का चयन करते हैं जो \(\ x=\frac(1)(2) \) से अधिक और \(\ से कम या बराबर हो) \frac(\sqrt(2))(2 ) \) । चित्र 8 में, ये बिंदु चाप \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) और \(\ P_(t_(3)) \) पर स्थित होंगे। , \( \ P_(t_(4)) \) । आइए मान पाते हैं \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , वामावर्त यात्रा करते हुए, और \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3 \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)

इस प्रकार, हम दो अंतराल प्राप्त करते हैं, जो, साइन फ़ंक्शन की आवधिकता को ध्यान में रखते हुए, निम्नानुसार लिखा जा सकता है \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), इसके लिए हम दोनों असमानताओं के सभी पक्षों को 2 से गुणा करते हैं, हमें प्राप्त होता है \(\ \frac (\pi)(3)+4 \pi k \leq x

उत्तर\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\right] \ cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\right) \), \(\ k \in Z \)

असमानताएँ a › b के रूप के संबंध हैं, जहाँ a और b कम से कम एक चर वाले व्यंजक हैं। असमानताएँ सख्त हो सकती हैं - , › और गैर-सख्त - , ।

त्रिकोणमितीय असमानताएं फॉर्म की अभिव्यक्ति हैं: एफ (एक्स) › ए, एफ (एक्स) ‹ ए, एफ (एक्स) ≤ ए, एफ (एक्स) ≥ ए, जिसमें एफ (एक्स) को एक या अधिक त्रिकोणमितीय कार्यों द्वारा दर्शाया जाता है .

सबसे सरल त्रिकोणमितीय असमानता का एक उदाहरण है: sin x 1/2। ऐसी समस्याओं को ग्राफिक रूप से हल करने की प्रथा है, इसके लिए दो तरीके विकसित किए गए हैं।

विधि 1 - फ़ंक्शन प्लॉट करके असमानताओं को हल करना

एक अंतराल खोजने के लिए जो असमानता पाप x ‹ 1/2 की शर्तों को पूरा करता है, आपको निम्नलिखित कार्य करने होंगे:

1. निर्देशांक अक्ष पर, एक साइनसॉइड y = sin x की रचना करें।
2. उसी अक्ष पर, असमानता के संख्यात्मक तर्क का एक ग्राफ बनाएं, यानी ओए कोटि के बिंदु ½ से गुजरने वाली एक सीधी रेखा।
3. दो रेखांकन के प्रतिच्छेदन बिंदुओं को चिह्नित करें।
4. उस खंड को छायांकित करें जो उदाहरण का समाधान है।

जब एक व्यंजक में मजबूत संकेत होते हैं, तो प्रतिच्छेदन बिंदु समाधान नहीं होते हैं। चूँकि साइनसॉइड का सबसे छोटा धनात्मक आवर्त 2π है, इसलिए हम उत्तर इस प्रकार लिखते हैं:

यदि व्यंजक के चिह्न सख्त नहीं हैं, तो समाधान अंतराल को वर्गाकार कोष्ठकों में संलग्न किया जाना चाहिए - . समस्या का उत्तर एक अन्य असमानता के रूप में भी लिखा जा सकता है:

विधि 2 - इकाई वृत्त का उपयोग करके त्रिकोणमितीय असमानताओं को हल करना

त्रिकोणमितीय वृत्त की सहायता से इसी प्रकार की समस्याओं को आसानी से हल किया जाता है। खोज एल्गोरिथ्म बहुत सरल है:

1. सबसे पहले, एक यूनिट सर्कल बनाएं।
2. फिर आपको वृत्त के चाप पर असमानता के दाईं ओर के तर्क के चाप फ़ंक्शन के मान को नोट करने की आवश्यकता है।
3. x-अक्ष (OX) के समांतर चाप फलन के मान से गुजरने वाली एक सीधी रेखा खींचना आवश्यक है।
4. उसके बाद, यह केवल एक सर्कल के चाप का चयन करने के लिए रहता है, जो त्रिकोणमितीय असमानता के समाधान का सेट है।
5. उत्तर को आवश्यक रूप में लिखें।

आइए एक उदाहरण के रूप में असमानता sin x › 1/2 का उपयोग करके समाधान चरणों का विश्लेषण करें। अंक α और β सर्कल पर चिह्नित होते हैं - मान

α और β के ऊपर स्थित चाप के बिंदु दी गई असमानता को हल करने के लिए अंतराल हैं।

यदि आपको कॉस के लिए एक उदाहरण को हल करने की आवश्यकता है, तो उत्तर का चाप सममित रूप से ओएक्स अक्ष पर स्थित होगा, न कि ओए। आप पाठ में नीचे दिए गए आरेखों में sin और cos के समाधान अंतराल के बीच के अंतर पर विचार कर सकते हैं।

स्पर्शरेखा और कोटैंजेंट असमानताओं के लिए ग्राफिकल समाधान साइन और कोसाइन दोनों से भिन्न होंगे। यह कार्यों के गुणों के कारण है।

चाप स्पर्शरेखा और चाप स्पर्शरेखा त्रिकोणमितीय वृत्त की स्पर्श रेखाएँ हैं, और दोनों फलनों के लिए न्यूनतम धनात्मक अवधि है। दूसरी विधि का जल्दी और सही ढंग से उपयोग करने के लिए, आपको यह याद रखना होगा कि किस अक्ष पर sin, cos, tg और ctg के मान प्लॉट किए गए हैं।

स्पर्शरेखा स्पर्शरेखा ओए अक्ष के समानांतर चलती है। यदि हम इकाई वृत्त पर arctg a का मान आलेखित करते हैं, तो दूसरा आवश्यक बिंदु विकर्ण तिमाही में स्थित होगा। कोने

वे फ़ंक्शन के लिए ब्रेकप्वाइंट हैं, क्योंकि ग्राफ़ उनके पास जाता है लेकिन उन तक कभी नहीं पहुंचता है।

कोटैंजेंट के मामले में, टेंगेंट ओएक्स अक्ष के समानांतर चलता है, और फ़ंक्शन और 2π बिंदुओं पर बाधित होता है।

जटिल त्रिकोणमितीय असमानताएं

यदि असमानता फ़ंक्शन के तर्क को न केवल एक चर द्वारा दर्शाया जाता है, बल्कि एक अज्ञात युक्त संपूर्ण अभिव्यक्ति द्वारा दर्शाया जाता है, तो हम एक जटिल असमानता के बारे में बात कर रहे हैं। इसके समाधान का क्रम और क्रम ऊपर वर्णित विधियों से कुछ भिन्न है। मान लीजिए कि हमें निम्नलिखित असमानता का समाधान खोजने की आवश्यकता है:

चित्रमय समाधान x के मनमाने ढंग से चुने गए मानों के लिए एक साधारण साइनसॉइड y = sin x के निर्माण के लिए प्रदान करता है। आइए चार्ट के संदर्भ बिंदुओं के लिए निर्देशांक वाली तालिका की गणना करें:

परिणाम एक अच्छा वक्र होना चाहिए।

समाधान खोजने में आसानी के लिए, हम जटिल फ़ंक्शन तर्क को प्रतिस्थापित करते हैं

दो रेखांकन का प्रतिच्छेदन आपको वांछित मूल्यों के क्षेत्र को निर्धारित करने की अनुमति देता है जिसके लिए असमानता की स्थिति संतुष्ट है।

पाया गया खंड चर t का समाधान है:

हालांकि, कार्य का लक्ष्य अज्ञात x के सभी संभावित रूपों को खोजना है:

दोहरी असमानता को हल करना काफी सरल है, आपको π / 3 को समीकरण के चरम भागों में ले जाने और आवश्यक गणना करने की आवश्यकता है:

कार्य का उत्तरसख्त असमानता के लिए एक अंतराल की तरह दिखेगा:

इस तरह के कार्यों के लिए त्रिकोणमितीय कार्यों को संभालने में छात्रों के अनुभव और कौशल की आवश्यकता होगी। तैयारी की प्रक्रिया में जितने अधिक प्रशिक्षण कार्य हल होंगे, छात्र को परीक्षा परीक्षा के प्रश्न का उत्तर उतना ही आसान और तेज मिलेगा।

सरलतम त्रिकोणमितीय समीकरणों का हल

सबसे पहले, आइए सबसे सरल त्रिकोणमितीय समीकरणों को हल करने के सूत्रों को याद करें।

1. $sinx=a$

1. $cosx=a$

1. $tgx=a$

1. $ctgx=a$

सरलतम त्रिकोणमितीय असमानताओं का समाधान।

सबसे सरल त्रिकोणमितीय असमानताओं को हल करने के लिए, हमें पहले संबंधित समीकरण को हल करना होगा, और फिर त्रिकोणमितीय सर्कल का उपयोग करके असमानता का समाधान खोजना होगा। उदाहरण के द्वारा सरलतम त्रिकोणमितीय असमानताओं के समाधान पर विचार करें।

उदाहरण 1

$sinx\ge \frac(1)(2)$

त्रिकोणमितीय असमानता का समाधान खोजें $sinx=\frac(1)(2)$

\ \

चित्र 1. असमानता का समाधान $sinx\ge \frac(1)(2)$।

चूंकि असमानता में "इससे बड़ा या बराबर" चिह्न होता है, इसलिए समाधान वृत्त के ऊपरी चाप (समीकरण के समाधान के संबंध में) पर स्थित होता है।

उत्तर: $\बाएं[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$।

उदाहरण 2

त्रिकोणमितीय असमानता का समाधान खोजें $cosx=\frac(\sqrt(3))(2)$

\ \

त्रिकोणमितीय वृत्त पर हल नोट करें

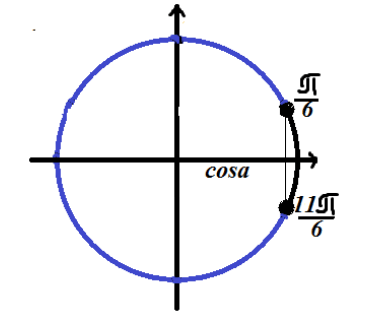
चूंकि असमानता में "से कम" का चिह्न होता है, समाधान बाईं ओर स्थित वृत्त के चाप पर स्थित होता है (समीकरण के समाधान के संबंध में)।

उत्तर: $\बाएं(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$।

उदाहरण 3

$tgx\le \frac(\sqrt(3))(3)$

त्रिकोणमितीय असमानता का समाधान खोजें $tgx=\frac(\sqrt(3))(3)$

\ \

यहां हमें परिभाषा के क्षेत्र की भी आवश्यकता है। जैसा कि हमें याद है, स्पर्शरेखा फलन $x\ne \frac(\pi )(2)+\pi n,n\in Z$

त्रिकोणमितीय वृत्त पर हल नोट करें

चित्र 3. असमानता का समाधान $tgx\le \frac(\sqrt(3))(3)$।

चूंकि असमानता में "इससे कम या इसके बराबर" चिह्न होता है, इसलिए समाधान चित्र 3 में नीले रंग से चिह्नित वृत्त के चापों पर स्थित होता है।

उत्तर: $\ \बाएं(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\ cup \left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$

उदाहरण 4

त्रिकोणमितीय असमानता का समाधान खोजें $ctgx=\sqrt(3)$

\ \

यहां हमें परिभाषा के क्षेत्र की भी आवश्यकता है। जैसा कि हमें याद है, स्पर्शरेखा फलन $x\ne \pi n,n\in Z$

त्रिकोणमितीय वृत्त पर हल नोट करें

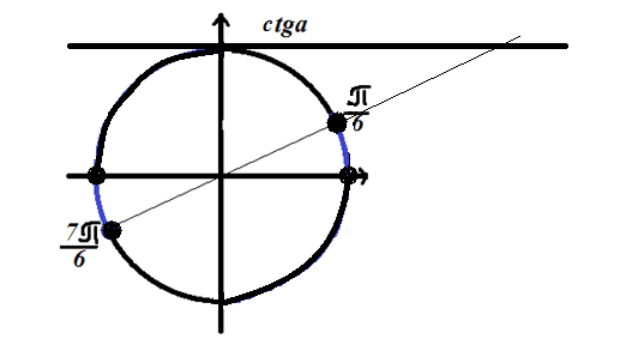
चित्र 4. असमानता का समाधान $ctgx\le \sqrt(3)$।

चूंकि असमानता में "से बड़ा" चिह्न होता है, इसलिए समाधान चित्र 4 में नीले रंग में चिह्नित वृत्त के चापों पर स्थित होता है।

उत्तर: $\ \ left(2\pi n,\frac(\pi )(6)+2\pi n\right)\ cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\right)$

त्रिकोणमितीय असमानताओं को हल करने के तरीके

प्रासंगिकता। ऐतिहासिक रूप से त्रिकोणमितीय समीकरणों और असमानताओं को स्कूली पाठ्यक्रम में विशेष स्थान दिया गया है। हम कह सकते हैं कि त्रिकोणमिति स्कूल पाठ्यक्रम और सामान्य रूप से सभी गणितीय विज्ञान के सबसे महत्वपूर्ण वर्गों में से एक है।

त्रिकोणमितीय समीकरण और असमानताएं एक हाई स्कूल गणित पाठ्यक्रम में केंद्रीय स्थानों में से एक पर कब्जा कर लेती हैं, दोनों शैक्षिक सामग्री की सामग्री और शैक्षिक और संज्ञानात्मक गतिविधि के तरीकों के संदर्भ में जो उनके अध्ययन के दौरान बनाई जा सकती हैं और एक बड़े को हल करने के लिए लागू की जानी चाहिए। सैद्धांतिक और व्यावहारिक प्रकृति की समस्याओं की संख्या। ।

त्रिकोणमितीय समीकरणों और असमानताओं का समाधान त्रिकोणमिति में सभी शैक्षिक सामग्री से संबंधित छात्रों के ज्ञान को व्यवस्थित करने के लिए पूर्वापेक्षाएँ बनाता है (उदाहरण के लिए, त्रिकोणमितीय कार्यों के गुण, त्रिकोणमितीय अभिव्यक्तियों को बदलने के तरीके, आदि) और इसके साथ प्रभावी संबंध स्थापित करना संभव बनाता है। बीजगणित में अध्ययन की गई सामग्री (समीकरण, समीकरणों की तुल्यता, असमानताएं, बीजगणितीय अभिव्यक्तियों के समान परिवर्तन, आदि)।

दूसरे शब्दों में, त्रिकोणमितीय समीकरणों और असमानताओं को हल करने के तरीकों पर विचार में इन कौशलों को एक नई सामग्री में स्थानांतरित करना शामिल है।

सिद्धांत का महत्व और इसके कई अनुप्रयोग चुने हुए विषय की प्रासंगिकता का प्रमाण हैं। यह, बदले में, आपको पाठ्यक्रम कार्य के लक्ष्यों, उद्देश्यों और अनुसंधान के विषय को निर्धारित करने की अनुमति देता है।

इस अध्ययन का उद्देश्य: उपलब्ध प्रकार की त्रिकोणमितीय असमानताओं का सामान्यीकरण, उनके समाधान के लिए बुनियादी और विशेष तरीके, स्कूली बच्चों द्वारा त्रिकोणमितीय असमानताओं को हल करने के लिए कार्यों का एक सेट चुनें।

अनुसंधान के उद्देश्य:

1. शोध विषय पर उपलब्ध साहित्य के विश्लेषण के आधार पर सामग्री को व्यवस्थित करें।

2. "त्रिकोणमितीय असमानताएं" विषय को समेकित करने के लिए आवश्यक कार्यों का एक सेट दें।

अध्ययन की वस्तु स्कूल गणित पाठ्यक्रम में त्रिकोणमितीय असमानताएँ हैं।

अध्ययन का विषय: त्रिकोणमितीय असमानताओं के प्रकार और उनके समाधान के तरीके।

सैद्धांतिक महत्व सामग्री को व्यवस्थित करना है।

व्यवहारिक महत्व: समस्याओं को हल करने में सैद्धांतिक ज्ञान का अनुप्रयोग; त्रिकोणमितीय असमानताओं को हल करने के लिए मुख्य अक्सर सामना की जाने वाली विधियों का विश्लेषण।

तलाश पद्दतियाँ : वैज्ञानिक साहित्य का विश्लेषण, अर्जित ज्ञान का संश्लेषण और सामान्यीकरण, समस्या समाधान का विश्लेषण, असमानताओं को हल करने के लिए इष्टतम तरीकों की खोज।

§एक। त्रिकोणमितीय असमानताओं के प्रकार और उनके समाधान के लिए बुनियादी तरीके

1.1. सबसे सरल त्रिकोणमितीय असमानताएँ

किसी चिन्ह या > से जुड़े दो त्रिकोणमितीय व्यंजक त्रिकोणमितीय असमानताएँ कहलाते हैं।

त्रिकोणमितीय असमानता को हल करने का अर्थ है असमानता में शामिल अज्ञात के मूल्यों का एक सेट खोजना, जिसके तहत असमानता संतुष्ट है।

त्रिकोणमितीय असमानताओं का मुख्य भाग उन्हें सरलतम को हल करने के लिए कम करके हल किया जाता है:

यह गुणनखंडन की एक विधि हो सकती है, चर का परिवर्तन (
,
आदि), जहां सामान्य असमानता को पहले हल किया जाता है, और फिर फॉर्म की असमानता
आदि, या अन्य तरीकों से।

सबसे सरल असमानताओं को दो तरीकों से हल किया जाता है: यूनिट सर्कल का उपयोग करके या ग्राफिक रूप से।

रहने दोच (एक्स  बुनियादी त्रिकोणमितीय कार्यों में से एक है। असमानता को दूर करने के लिए
यह एक आवर्त में इसका समाधान खोजने के लिए पर्याप्त है, अर्थात्। किसी भी खंड पर जिसकी लंबाई फलन की अवधि के बराबर हैएफ  एक्स  . तब मूल असमानता का समाधान मिल जाएगाएक्स , साथ ही वे मान जो फ़ंक्शन के किसी भी पूर्णांक संख्या द्वारा पाए गए मानों से भिन्न होते हैं। इस मामले में, ग्राफिकल विधि का उपयोग करना सुविधाजनक है।

आइए हम असमानताओं को हल करने के लिए एक एल्गोरिथ्म का उदाहरण दें
(
) और
.

असमानता को हल करने के लिए एल्गोरिदम
(
).

1. किसी संख्या की ज्या की परिभाषा तैयार कीजिएएक्स यूनिट सर्कल पर।

3. y-अक्ष पर, निर्देशांक के साथ एक बिंदु चिह्नित करेंए .

4. इस बिंदु से होकर OX अक्ष के समांतर एक रेखा खींचिए और इसके प्रतिच्छेदन बिंदुओं को वृत्त से चिह्नित कीजिए।

5. एक वृत्त का एक चाप चुनें, जिसकी कोटि से कम होए .

6. बायपास की दिशा (वामावर्त) निर्दिष्ट करें और फ़ंक्शन की अवधि को अंतराल के अंत में जोड़कर उत्तर लिखें2πn ,
.

असमानता को हल करने के लिए एल्गोरिदम
.

1. किसी संख्या की स्पर्श रेखा की परिभाषा बनाइएएक्स यूनिट सर्कल पर।

2. एक इकाई वृत्त खींचिए।

3. स्पर्श रेखाओं की एक रेखा खींचिए और उस पर एक कोटि से एक बिंदु अंकित कीजिएए .

4. इस बिंदु को मूल बिंदु से जोड़ें और परिणामी खंड के प्रतिच्छेदन बिंदु को इकाई वृत्त से चिह्नित करें।

5. एक वृत्त के एक चाप का चयन करें, जिसके सभी बिंदुओं की स्पर्श रेखा पर एक कोटि होती है जो से कम होती हैए .

6. ट्रैवर्सल की दिशा को इंगित करें और एक अवधि जोड़कर, फ़ंक्शन के दायरे को ध्यान में रखते हुए उत्तर लिखेंपीएन ,
(रिकॉर्ड के बाईं ओर की संख्या हमेशा दाईं ओर की संख्या से कम होती है)।

सामान्य रूप में असमानताओं को हल करने के लिए सरलतम समीकरणों और सूत्रों के समाधान की चित्रमय व्याख्या परिशिष्ट (परिशिष्ट 1 और 2) में दी गई है।

उदाहरण 1 असमानता को हल करें
.

इकाई वृत्त पर एक रेखा खींचे
, जो वृत्त को बिंदु A और B पर काटती है।

सभी मानआप अंतराल पर एनएम अधिक , चाप AMB के सभी बिंदु इस असमानता को संतुष्ट करते हैं। घूर्णन के सभी कोणों पर, बड़ा , लेकिन छोटा ,
से अधिक मूल्यों पर ले जाएगा (लेकिन एक से अधिक नहीं)।

चित्र .1

इस प्रकार, असमानता का समाधान अंतराल में सभी मान होंगे
, अर्थात।
. इस असमानता के सभी समाधान प्राप्त करने के लिए, इस अंतराल के सिरों को जोड़ने के लिए पर्याप्त है
, कहाँ पे
, अर्थात।
,
. ध्यान दें कि मान
और
समीकरण की जड़ें हैं
,

वे।
;
.

जवाब:
,
.

1.2. ग्राफिक विधि

व्यवहार में, त्रिकोणमितीय असमानताओं को हल करने के लिए एक चित्रमय विधि अक्सर उपयोगी होती है। असमानता के उदाहरण पर विधि के सार पर विचार करें
:

1. यदि तर्क जटिल है (से भिन्नएक्स ), फिर हम इसे . से बदल देते हैंटी .

2. हम एक समन्वय विमान में निर्माण करते हैंटू ओय फ़ंक्शन ग्राफ़
और
.

3. हम पाते हैं किग्राफ़ के प्रतिच्छेदन के दो आसन्न बिंदु, जिसके बीचsinusoidस्थितउच्चतर सीधा
. इन बिंदुओं के भुज ज्ञात कीजिए।

4. तर्क के लिए दोहरी असमानता लिखेंटी , कोसाइन अवधि को देखते हुए (टी पाए गए एब्सिसास के बीच होगा)।

5. एक उल्टा प्रतिस्थापन करें (मूल तर्क पर लौटें) और मान व्यक्त करेंएक्स दोहरी असमानता से, हम उत्तर को एक संख्यात्मक अंतराल के रूप में लिखते हैं।

उदाहरण 2 असमानता को हल करें: .

एक ग्राफिकल विधि द्वारा असमानताओं को हल करते समय, यथासंभव सटीक रूप से कार्यों के ग्राफ बनाना आवश्यक है। आइए असमानता को रूप में बदलें:

आइए हम एक समन्वय प्रणाली में कार्यों के रेखांकन का निर्माण करें
और
(रेखा चित्र नम्बर 2)।

रेखा चित्र नम्बर 2

फ़ंक्शन ग्राफ़ एक बिंदु पर प्रतिच्छेद करते हैंलेकिन निर्देशांक के साथ
;
. बीच में
ग्राफ अंक
चार्ट बिंदुओं के नीचे
. और जब
फ़ंक्शन मान समान हैं। इसलिए
पर
.

जवाब:
.

1.3. बीजगणितीय विधि

अक्सर, एक अच्छी तरह से चुने गए प्रतिस्थापन द्वारा मूल त्रिकोणमितीय असमानता को बीजीय (तर्कसंगत या तर्कहीन) असमानता में घटाया जा सकता है। इस पद्धति में असमानता को बदलना, एक प्रतिस्थापन की शुरुआत करना, या एक चर को बदलना शामिल है।

आइए विशिष्ट उदाहरणों पर इस पद्धति के अनुप्रयोग पर विचार करें।

उदाहरण 3 सरलतम रूप में कमी
.

(चित्र 3)

अंजीर.3

,
.

जवाब:
,

उदाहरण 4 असमानता को हल करें:

ओडीजेड:
,
.

सूत्रों का उपयोग करना:
,

हम फॉर्म में असमानता लिखते हैं:
.

या, मान कर
सरल परिवर्तनों के बाद हमें मिलता है

,

,

.

अंतराल विधि द्वारा अंतिम असमानता को हल करने पर, हम प्राप्त करते हैं:

चित्र 4

, क्रमश
. फिर अंजीर से। 4 अनुसरण करता है
, कहाँ पे
.

चित्र 5

जवाब:
,
.

1.4. रिक्ति विधि

अंतराल विधि द्वारा त्रिकोणमितीय असमानताओं को हल करने की सामान्य योजना:

त्रिकोणमितीय सूत्रों का उपयोग करके, गुणनखंड करें।

फ़ंक्शन के ब्रेकपॉइंट और शून्य खोजें, उन्हें सर्कल पर रखें।

कोई भी बिंदु लेंसेवा (लेकिन पहले नहीं मिला) और उत्पाद के संकेत का पता लगाएं। यदि गुणनफल धनात्मक है, तो एकांक वृत्त के बाहर किरण के संगत कोण पर एक बिंदु लगाएं। अन्यथा, बिंदु को सर्कल के अंदर रखें।

यदि कोई बिंदु सम संख्या में आता है, तो हम इसे सम गुणन का बिंदु कहते हैं; यदि विषम संख्या में बार, तो हम इसे विषम गुणन का बिंदु कहते हैं। चाप इस प्रकार बनाएं: एक बिंदु से शुरू करेंसेवा , यदि अगला बिंदु विषम गुणन का है, तो चाप वृत्त को इस बिंदु पर काटता है, लेकिन यदि बिंदु सम गुणन का है, तो यह प्रतिच्छेद नहीं करता है।

एक सर्कल के पीछे चाप सकारात्मक अंतराल हैं; सर्कल के अंदर नकारात्मक अंतराल हैं।

उदाहरण 5 असमानता को हल करें

,
.

पहली श्रृंखला के अंक:
.

दूसरी श्रृंखला के अंक:
.

प्रत्येक बिंदु एक विषम संख्या में आता है, अर्थात विषम गुणन के सभी बिंदु।

पर उत्पाद के चिन्ह का पता लगाएं
: . हम यूनिट सर्कल पर सभी बिंदुओं को चिह्नित करते हैं (चित्र 6):

चावल। 6

जवाब:
,
;
,
;
,
.

उदाहरण 6 . असमानता को हल करें.

फेसला:

आइए व्यंजक के शून्य ज्ञात करें .

पानाऐएम :

,
;

,
;

,
;

,
;

इकाई वृत्त पर, श्रृंखला मानएक्स 1 डॉट्स द्वारा दर्शाया गया
. श्रृंखलाएक्स 2 अंक देता है
. एक श्रृंखलाएक्स 3 हमें दो अंक मिलते हैं
. अंत में, एक श्रृंखलाएक्स 4 अंक का प्रतिनिधित्व करेंगे
. हम इन सभी बिंदुओं को इकाई वृत्त पर रखते हैं, जो इसकी प्रत्येक बहुलता के आगे कोष्ठकों में इंगित करता है।

अब नंबर आने दो बराबर होगा। हम संकेत द्वारा एक अनुमान लगाते हैं:

तो बिंदुए कोण बनाने वाले बीम पर चुना जाना चाहिए बीम के साथओह, यूनिट सर्कल के बाहर। (ध्यान दें कि सहायक बीमहे ए इसे चित्र में दिखाने की आवश्यकता नहीं है। दूरसंचार विभागए लगभग चयनित।)

अब बिंदु सेए हम सभी चिह्नित बिंदुओं पर क्रमिक रूप से एक लहराती निरंतर रेखा खींचते हैं। और बिंदुओं पर
हमारी रेखा एक क्षेत्र से दूसरे क्षेत्र में जाती है: यदि वह इकाई वृत्त के बाहर होती है, तो वह उसमें से गुजरती है। बिंदु के करीब , रेखा आंतरिक क्षेत्र में लौट आती है, क्योंकि इस बिंदु की बहुलता सम है। इसी प्रकार बिंदु पर (सम बहुलता के साथ) रेखा को बाहरी क्षेत्र में घुमाना पड़ता है। इसलिए, हमने अंजीर में दर्शाए गए एक निश्चित चित्र को खींचा। 7. यह यूनिट सर्कल पर वांछित क्षेत्रों को उजागर करने में मदद करता है। उन्हें "+" के साथ चिह्नित किया गया है।

चित्र 7

आख़री जवाब:

टिप्पणी। यदि लहराती रेखा, इकाई वृत्त पर अंकित सभी बिंदुओं को पार करने के बाद, बिंदु पर वापस नहीं आ सकती हैए , एक "अवैध" जगह में सर्कल को पार किए बिना, इसका मतलब है कि समाधान में एक त्रुटि हुई थी, अर्थात्, विषम संख्या में जड़ों को छोड़ दिया गया था।

जवाब: .

2. त्रिकोणमितीय असमानताओं को हल करने के लिए कार्यों का एक सेट

त्रिकोणमितीय असमानताओं को हल करने के लिए स्कूली बच्चों की क्षमता विकसित करने की प्रक्रिया में, 3 चरणों को भी प्रतिष्ठित किया जा सकता है।

1. प्रारंभिक,

2. सरलतम त्रिकोणमितीय असमानताओं को हल करने के लिए कौशल का निर्माण;

3. अन्य प्रकार की त्रिकोणमितीय असमानताओं का परिचय।

प्रारंभिक चरण का उद्देश्य यह है कि स्कूली बच्चों में असमानताओं को हल करने के लिए एक त्रिकोणमितीय सर्कल या ग्राफ का उपयोग करने की क्षमता का निर्माण करना आवश्यक है, अर्थात्:

फॉर्म की साधारण असमानताओं को हल करने की क्षमता
,
,
,
, साइन और कोसाइन कार्यों के गुणों का उपयोग करना;

संख्यात्मक वृत्त के चापों के लिए या फलनों के रेखांकन के चापों के लिए दोहरी असमानताएँ बनाने की क्षमता;

त्रिकोणमितीय अभिव्यक्तियों के विभिन्न परिवर्तनों को करने की क्षमता।

त्रिकोणमितीय कार्यों के गुणों के बारे में स्कूली बच्चों के ज्ञान को व्यवस्थित करने की प्रक्रिया में इस चरण को लागू करने की अनुशंसा की जाती है। मुख्य साधन छात्रों को दिए जाने वाले कार्य हो सकते हैं और या तो शिक्षक के मार्गदर्शन में या स्वतंत्र रूप से किए जा सकते हैं, साथ ही त्रिकोणमितीय समीकरणों को हल करने में प्राप्त कौशल भी हो सकते हैं।

ऐसे कार्यों के उदाहरण यहां दिए गए हैं:

1 . इकाई वृत्त पर एक बिंदु अंकित करें , अगर

.

2. निर्देशांक तल के किस चौथाई में बिंदु है , अगर बराबर:

3. त्रिकोणमितीय वृत्त पर अंक अंकित करें , अगर:

4. व्यंजक को त्रिकोणमितीय फलनों में लाएँमैंक्वार्टर

ए)
, बी)
, में)

5. चाप MR को देखते हुए।एम - मध्यमैंचौथी तिमाही,आर - मध्यद्वितीयचौथी तिमाही। एक चर के मान को प्रतिबंधित करेंटी के लिए: (एक दोहरी असमानता लिखें) ए) चाप एमपी; बी) आरएम आर्क्स।

6. ग्राफ़ के चयनित अनुभागों के लिए दोहरी असमानता लिखें:

चावल। एक

7. असमानताओं को हल करें
,
,
,
.

8. अभिव्यक्ति परिवर्तित करें .

त्रिकोणमितीय असमानताओं को हल करने के लिए सीखने के दूसरे चरण में, हम छात्रों की गतिविधियों के आयोजन के लिए कार्यप्रणाली से संबंधित निम्नलिखित सिफारिशें पेश कर सकते हैं। साथ ही, त्रिकोणमितीय वृत्त या ग्राफ के साथ काम करने के लिए छात्रों के कौशल पर ध्यान देना आवश्यक है, जो सरलतम त्रिकोणमितीय समीकरणों के समाधान के दौरान बनते हैं।

सबसे पहले, उदाहरण के लिए, फॉर्म की असमानता को संदर्भित करके सरलतम त्रिकोणमितीय असमानताओं को हल करने के लिए एक सामान्य विधि प्राप्त करने की समीचीनता को प्रेरित करना संभव है।
. प्रारंभिक चरण में प्राप्त ज्ञान और कौशल का उपयोग करते हुए, छात्र प्रस्तावित असमानता को फॉर्म में लाएंगे
, लेकिन परिणामी असमानता के समाधान का एक सेट खोजना मुश्किल हो सकता है, क्योंकि केवल साइन फ़ंक्शन के गुणों का उपयोग करके इसे हल करना असंभव है। उपयुक्त दृष्टांत का हवाला देकर इस कठिनाई से बचा जा सकता है (रेखीय रूप से समीकरण का समाधान या एक इकाई वृत्त का उपयोग करके)।

दूसरे, शिक्षक को छात्रों का ध्यान कार्य को पूरा करने के विभिन्न तरीकों की ओर आकर्षित करना चाहिए, असमानता को ग्राफिक रूप से और त्रिकोणमितीय वृत्त का उपयोग करके हल करने का एक उपयुक्त उदाहरण देना चाहिए।

असमानता को हल करने के लिए ऐसे विकल्पों पर विचार करें
.

1. इकाई वृत्त का उपयोग करके असमानता को हल करना।

त्रिकोणमितीय असमानताओं को हल करने के पहले पाठ में, हम छात्रों को एक विस्तृत समाधान एल्गोरिदम प्रदान करेंगे, जो चरण-दर-चरण प्रस्तुति में असमानता को हल करने के लिए आवश्यक सभी बुनियादी कौशल को दर्शाता है।

स्टेप 1।एक इकाई वृत्त बनाएं, y-अक्ष पर एक बिंदु चिह्नित करें और इससे होकर x-अक्ष के समांतर एक सीधी रेखा खींचिए। यह रेखा इकाई वृत्त को दो बिंदुओं पर काटेगी। इनमें से प्रत्येक बिंदु उन संख्याओं को दर्शाता है जिनकी ज्या के बराबर है .

चरण 2इस सीधी रेखा ने वृत्त को दो चापों में विभाजित किया। आइए एक को बाहर करें जिस पर संख्या प्रदर्शित की जाती है जिसमें से अधिक साइन होता है . स्वाभाविक रूप से, यह चाप खींची गई सीधी रेखा के ऊपर स्थित होता है।

चावल। 2

चरण 3आइए चिह्नित चाप के सिरों में से एक को चुनें। आइए उन संख्याओं में से एक को लिखें जो इकाई वृत्त के इस बिंदु द्वारा दर्शायी जाती हैं .

चरण 4चयनित चाप के दूसरे छोर के अनुरूप एक संख्या चुनने के लिए, हम इस चाप के साथ नामित छोर से दूसरे छोर तक "पास" करते हैं। उसी समय, हम याद करते हैं कि वामावर्त चलते समय, हम जो संख्याएँ पास करेंगे, वे बढ़ जाएँगी (विपरीत दिशा में जाने पर संख्याएँ घट जाएँगी)। आइए अंकित चाप के दूसरे छोर तक इकाई वृत्त पर दर्शाई गई संख्या को लिख लें .

इस प्रकार, हम देखते हैं कि असमानता
उन संख्याओं को संतुष्ट करें जिनके लिए असमानता
. हमने साइन फ़ंक्शन की समान अवधि में स्थित संख्याओं के लिए असमानता को हल किया। इसलिए, असमानता के सभी समाधानों को इस प्रकार लिखा जा सकता है:

छात्रों को इस आंकड़े पर ध्यान से विचार करने और यह पता लगाने के लिए कहा जाना चाहिए कि असमानता के सभी समाधान क्यों हैं
फॉर्म में लिखा जा सकता है
,
.

चावल। 3

छात्रों का ध्यान इस तथ्य की ओर आकर्षित करना आवश्यक है कि कोज्या फलन के लिए असमानताओं को हल करते समय, हम y-अक्ष के समानांतर एक सीधी रेखा खींचते हैं।

असमानता को हल करने के लिए ग्राफिकल तरीका।

बिल्डिंग चार्ट
और
, मान लीजिये
.

चावल। 4

फिर हम समीकरण लिखते हैं
और उसका समाधान
,
,
, सूत्रों का उपयोग करके पाया गया
,
,
.

(देनाएन मान 0, 1, 2, हम रचित समीकरण की तीन जड़ें पाते हैं)। मूल्यों
ग्राफ़ के प्रतिच्छेदन बिंदुओं के लगातार तीन भुज हैं
और
. जाहिर है, हमेशा इंटरवल पर
असमानता
, और अंतराल पर
- असमानता
. हम पहले मामले में रुचि रखते हैं, और फिर इस अंतराल के अंत में एक संख्या जोड़ते हैं जो कि साइन अवधि का एक गुणक है, हम असमानता का समाधान प्राप्त करते हैं
जैसा:
,
.

चावल। 5

संक्षेप। असमानता को दूर करने के लिए
, आपको संबंधित समीकरण लिखने और उसे हल करने की आवश्यकता है। परिणामी सूत्र से मूल ज्ञात कीजिए और , और इस रूप में असमानता का उत्तर लिखें: ,
.

तीसरा, संबंधित त्रिकोणमितीय असमानता की जड़ों के सेट के बारे में तथ्य को ग्राफिक रूप से हल करते समय बहुत स्पष्ट रूप से पुष्टि की जाती है।

चावल। 6

विद्यार्थियों को यह प्रदर्शित करना आवश्यक है कि कुण्डली, जो असमानता का समाधान है, त्रिकोणमितीय फलन की अवधि के बराबर, समान अंतराल में दोहराती है। आप साइन फ़ंक्शन के ग्राफ़ के लिए भी इसी तरह के उदाहरण पर विचार कर सकते हैं।

चौथा, त्रिकोणमितीय असमानताओं को हल करने में इन विधियों की भूमिका पर स्कूली बच्चों का ध्यान आकर्षित करने के लिए, छात्रों के बीच त्रिकोणमितीय कार्यों के योग (अंतर) को उत्पाद में बदलने के तरीकों को अद्यतन करने पर काम करना उचित है।

इस तरह के काम को छात्रों द्वारा शिक्षक द्वारा प्रस्तावित कार्यों की स्वतंत्र पूर्ति के माध्यम से आयोजित किया जा सकता है, जिनमें से हम निम्नलिखित पर प्रकाश डालते हैं:

पांचवां, छात्रों को ग्राफ या त्रिकोणमितीय सर्कल का उपयोग करके प्रत्येक साधारण त्रिकोणमितीय असमानता के समाधान को स्पष्ट करना होगा। इसकी समीचीनता पर ध्यान देना सुनिश्चित करें, विशेष रूप से एक सर्कल के उपयोग के लिए, क्योंकि त्रिकोणमितीय असमानताओं को हल करते समय, संबंधित चित्रण किसी दिए गए असमानता के समाधान के सेट को ठीक करने के लिए एक बहुत ही सुविधाजनक साधन के रूप में कार्य करता है।

त्रिकोणमितीय असमानताओं को हल करने के तरीकों के साथ छात्रों का परिचित, जो सबसे सरल नहीं हैं, निम्नलिखित योजना के अनुसार किया जाना चाहिए: एक विशिष्ट त्रिकोणमितीय असमानता का जिक्र करते हुए संबंधित त्रिकोणमितीय समीकरण संयुक्त खोज (शिक्षक-छात्र) के समाधान के लिए स्वतंत्र हस्तांतरण एक ही प्रकार की अन्य असमानताओं के लिए मिली तकनीक का।

त्रिकोणमिति के छात्रों के ज्ञान को व्यवस्थित करने के लिए, हम विशेष रूप से ऐसी असमानताओं का चयन करने की सलाह देते हैं, जिनके समाधान के लिए विभिन्न परिवर्तनों की आवश्यकता होती है जिन्हें इसे हल करने की प्रक्रिया में लागू किया जा सकता है, जिससे छात्रों का ध्यान उनकी विशेषताओं पर केंद्रित होता है।

ऐसी उत्पादक असमानताओं के रूप में, हम निम्नलिखित का प्रस्ताव कर सकते हैं, उदाहरण के लिए:

अंत में, हम त्रिकोणमितीय असमानताओं को हल करने के लिए समस्याओं के एक समूह का उदाहरण देते हैं।

1. असमानताओं को हल करें:

2. असमानताओं को हल करें: 3. असमानताओं के सभी समाधान खोजें: 4. असमानताओं के सभी समाधान खोजें:

ए)
, शर्त को संतुष्ट करना
;

बी)
, शर्त को संतुष्ट करना
.

5. असमानताओं के सभी समाधान खोजें:

ए) ;

बी) ;

में)
;

जी)
;

इ)
.

6. असमानताओं को हल करें:

ए) ;

बी) ;

में) ;

जी)
;

इ) ;

इ) ;

जी)
.

7. असमानताओं को हल करें:

ए)
;

बी) ;

में) ;

जी) ।

8. असमानताओं को हल करें:

ए) ;

बी) ;

में) ;

जी)
;

इ)
;

इ) ;

जी)
;

एच) ।

गणित के गहन अध्ययन के साथ कक्षाओं में छात्रों को उन्नत स्तर पर गणित का अध्ययन करने वाले छात्रों को कार्य 6 और 7 की पेशकश करना उचित है।

3. त्रिकोणमितीय असमानताओं को हल करने के लिए विशेष तरीके

त्रिकोणमितीय समीकरणों को हल करने की विशेष विधियाँ - अर्थात वे विधियाँ जिनका उपयोग केवल त्रिकोणमितीय समीकरणों को हल करने के लिए किया जा सकता है। ये विधियाँ त्रिकोणमितीय फलनों के गुणों के उपयोग के साथ-साथ विभिन्न त्रिकोणमितीय सूत्रों और सर्वसमिकाओं के उपयोग पर आधारित हैं।

3.1. सेक्टर विधि

त्रिकोणमितीय असमानताओं को हल करने के लिए सेक्टर विधि पर विचार करें। फॉर्म की असमानताओं का समाधान

, कहाँ पेपी ( एक्स ) औरक्यू ( एक्स ) - परिमेय त्रिकोणमितीय फलन (साइन, कोसाइन, स्पर्शरेखा और कोटंगेंट उन्हें तर्कसंगत रूप से दर्ज करते हैं), इसी तरह तर्कसंगत असमानताओं के समाधान के लिए। वास्तविक अक्ष पर अंतराल की विधि द्वारा तर्कसंगत असमानताओं को हल करना सुविधाजनक है। तर्कसंगत त्रिकोणमितीय असमानताओं को हल करने में इसका एनालॉग त्रिकोणमितीय सर्कल में क्षेत्रों की विधि है, के लिएsinx औरcosx (
) या के लिए एक त्रिकोणमितीय अर्धवृत्तटीजीएक्स औरसीटीजीएक्स (
).

अंतराल विधि में, रूप के अंश और हर के प्रत्येक रैखिक गुणनखंड
संख्या अक्ष पर बिंदु , और इस बिंदु से गुजरते समय
संकेत बदलता है। सेक्टर विधि में, फॉर्म के प्रत्येक गुणक
, कहाँ पे
- कार्यों में से एकsinx याcosx और
, एक त्रिकोणमितीय वृत्त में दो कोण होते हैं और
, जो वृत्त को दो सेक्टरों में विभाजित करते हैं। गुजरते समय और समारोह
संकेत बदलता है।

निम्नलिखित को याद रखना चाहिए:

a) फॉर्म के गुणक
और
, कहाँ पे
, सभी मानों के लिए चिह्न बनाए रखें . अंश और हर के ऐसे गुणक त्याग दिए जाते हैं, बदलते हैं (यदि .)
) ऐसी प्रत्येक अस्वीकृति पर, असमानता का चिन्ह उलट जाता है।

b) फॉर्म के गुणक
और
भी त्याग दिए जाते हैं। इसके अलावा, यदि ये हर के कारक हैं, तो फॉर्म की असमानताओं को असमानताओं की समतुल्य प्रणाली में जोड़ दिया जाता है
और
. यदि ये अंश के गुणनखंड हैं, तो बाधाओं की समतुल्य प्रणाली में वे असमानताओं के अनुरूप होते हैं
और
सख्त प्रारंभिक असमानता और समानता के मामले में
और
एक गैर-सख्त प्रारंभिक असमानता के मामले में। गुणक गिराते समय
या
असमानता का चिन्ह उलट जाता है।

उदाहरण 1 असमानताओं को हल करें: ए)
, बी)
. हमारे पास एक फ़ंक्शन है, बी)। हमारे पास मौजूद असमानता को हल करें

3.2. संकेंद्रित वृत्त विधि

यह विधि परिमेय असमानताओं की प्रणालियों को हल करने में समानांतर संख्यात्मक अक्षों की विधि के अनुरूप है।

असमानताओं की एक प्रणाली के उदाहरण पर विचार करें।

उदाहरण 5 सरल त्रिकोणमितीय असमानताओं की एक प्रणाली को हल करें

सबसे पहले, हम प्रत्येक असमानता को अलग-अलग हल करते हैं (चित्र 5)। आकृति के ऊपरी दाएं कोने में, हम संकेत देंगे कि किस तर्क के लिए त्रिकोणमितीय वृत्त माना जाता है।

चित्र 5

अगला, हम तर्क के लिए संकेंद्रित वृत्तों की एक प्रणाली बनाते हैंएक्स . हम पहली असमानता के समाधान के अनुसार एक वृत्त खींचते हैं और इसे छायांकित करते हैं, फिर हम एक बड़े त्रिज्या का एक वृत्त खींचते हैं और दूसरे के समाधान के अनुसार इसे छायांकित करते हैं, फिर हम तीसरी असमानता और आधार वृत्त के लिए एक वृत्त बनाते हैं। . हम प्रणाली के केंद्र से चापों के सिरों तक किरणें खींचते हैं ताकि वे सभी वृत्तों को प्रतिच्छेद करें। हम बेस सर्कल (चित्रा 6) पर एक समाधान बनाते हैं।

चित्र 6

जवाब:
,
.

निष्कर्ष

पाठ्यक्रम के सभी उद्देश्यों को पूरा किया गया। सैद्धांतिक सामग्री को व्यवस्थित किया जाता है: त्रिकोणमितीय असमानताओं के मुख्य प्रकार और उनके समाधान के लिए मुख्य तरीके (चित्रमय, बीजगणितीय, अंतराल की विधि, सेक्टर और संकेंद्रित वृत्तों की विधि) दिए गए हैं। प्रत्येक विधि के लिए, असमानता को हल करने का एक उदाहरण दिया गया था। सैद्धांतिक भाग के बाद व्यावहारिक भाग था। इसमें त्रिकोणमितीय असमानताओं को हल करने के लिए कार्यों का एक सेट शामिल है।

इस शोध कार्य का उपयोग छात्र स्वतंत्र कार्य के लिए कर सकते हैं। छात्र इस विषय को आत्मसात करने के स्तर की जांच कर सकते हैं, विभिन्न जटिलता के कार्यों को करने का अभ्यास कर सकते हैं।

इस मुद्दे पर प्रासंगिक साहित्य के माध्यम से काम करने के बाद, जाहिर है, हम यह निष्कर्ष निकाल सकते हैं कि बीजगणित के स्कूल पाठ्यक्रम में त्रिकोणमितीय असमानताओं को हल करने की क्षमता और कौशल और विश्लेषण की शुरुआत बहुत महत्वपूर्ण है, जिसके विकास के लिए काफी प्रयास की आवश्यकता है। गणित के शिक्षक।

इसलिए, यह कार्य गणित के शिक्षकों के लिए उपयोगी होगा, क्योंकि यह "त्रिकोणमितीय असमानताओं" विषय पर छात्रों के प्रशिक्षण को प्रभावी ढंग से व्यवस्थित करना संभव बनाता है।

अध्ययन को अंतिम योग्यता कार्य तक विस्तारित करके जारी रखा जा सकता है.

प्रयुक्त साहित्य की सूची

बोगोमोलोव, एन.वी. गणित में समस्याओं का संग्रह [पाठ] / एन.वी. बोगोमोलोव। - एम।: बस्टर्ड, 2009। - 206 पी।

वायगोडस्की, एम। वाई। प्राथमिक गणित की हैंडबुक [पाठ] / एम.वाई.ए. वायगोडस्की। - एम .: बस्टर्ड, 2006. - 509 पी।

ज़ुर्बेंको, एल.एन. उदाहरणों और कार्यों में गणित [पाठ] / एल.एन. ज़ुर्बेंको। - एम।: इंफ्रा-एम, 2009। - 373 पी।

इवानोव, ओ.ए. स्कूली बच्चों, छात्रों और शिक्षकों के लिए प्राथमिक गणित [पाठ] / ओ.ए. इवानोव। - एम .: एमटीएसएनएमओ, 2009. - 384 पी।

कार्प, ए.पी. 11 वीं कक्षा में अंतिम पुनरावृत्ति और प्रमाणन के संगठन के लिए बीजगणित और विश्लेषण की शुरुआत [पाठ] / ए.पी. कार्प। - एम .: ज्ञानोदय, 2005। - 79 पी।

कुलानिन, ई.डी. गणित में 3000 प्रतिस्पर्धी समस्याएं [पाठ] / ई.डी. कुलानिन। - एम .: आइरिस-प्रेस, 2007. - 624 पी।

लीबसन, के.एल. गणित में व्यावहारिक कार्यों का संग्रह [पाठ] / के.एल. लीबसन। - एम .: बस्टर्ड, 2010. - 182 पी।

कोहनी, वी.वी. मापदंडों और उनके समाधान के साथ समस्याएं। त्रिकोणमिति: समीकरण, असमानता, सिस्टम। ग्रेड 10 [पाठ] / वी.वी. कोहनी। - एम।: अर्कटी, 2008। - 64 पी।

मनोवा, ए.एन. गणित। परीक्षा की तैयारी के लिए एक्सप्रेस ट्यूटर: खाता। भत्ता [पाठ] / ए.एन. मनोवा। - रोस्तोव-ऑन-डॉन: फीनिक्स, 2012. - 541 पी।

मोर्दकोविच, ए.जी. बीजगणित और गणितीय विश्लेषण की शुरुआत। 10-11 ग्रेड। शैक्षिक संस्थानों के छात्रों के लिए पाठ्यपुस्तक [पाठ] / ए.जी. मोर्दकोविच। - एम।: आइरिस-प्रेस, 2009। - 201 पी।

नोविकोव, ए.आई. त्रिकोणमितीय फलन, समीकरण और असमानताएँ [पाठ] / ए.आई. नोविकोव। - एम .: फ़िज़मैटलिट, 2010. - 260 पी।

ओगनेस्यान, वी.ए. माध्यमिक विद्यालय में गणित पढ़ाने के तरीके: सामान्य कार्यप्रणाली। प्रोक। भौतिकी के छात्रों के लिए भत्ता। - चटाई। नकली पेड इन-कॉमरेड। [पाठ] / वी.ए. ओगनेस्यान। - एम .: ज्ञानोदय, 2006। - 368 पी।

ओलेचनिक, एस.एन. समीकरण और असमानताएँ। गैर-मानक समाधान विधियां [पाठ] / एस.एन. ओलेखनिक। - एम।: पब्लिशिंग हाउस फैक्टरियल, 1997. - 219 पी।

सेवरीयुकोव, पी.एफ. त्रिकोणमितीय, घातीय और लघुगणकीय समीकरण और असमानताएं [पाठ] / पी.एफ. सेवरीयुकोव. - एम।: राष्ट्रीय शिक्षा, 2008। - 352 पी।

सर्गेव, आई.एन. उपयोग: गणित में उत्तर और समाधान के साथ 1000 कार्य। समूह सी के सभी कार्य [पाठ] / आई.एन. सर्गेव। - एम .: परीक्षा, 2012। - 301 पी।

सोबोलेव, ए.बी. प्राथमिक गणित [पाठ] / ए.बी. सोबोलेव। - येकातेरिनबर्ग: GOU VPO USTU-UPI, 2005. - 81 पी।

फेन्को, एल.एम. असमानताओं को हल करने और कार्यों का अध्ययन करने में अंतराल की विधि [पाठ] / एल.एम. फेन्को। - एम .: बस्टर्ड, 2005। - 124 पी।

फ्राइडमैन, एल.एम. गणित पढ़ाने की पद्धति की सैद्धांतिक नींव [पाठ] / एल.एम. फ्राइडमैन। - एम।: बुक हाउस "लिब्रोकॉम", 2009। - 248 पी।

परिशिष्ट 1

सरलतम असमानताओं के समाधान की चित्रमय व्याख्या

चावल। एक

चावल। 2

अंजीर.3

चित्र 4

चित्र 5

चित्र 6

चित्र 7

चित्र 8

परिशिष्ट 2

सरलतम असमानताओं का समाधान

व्यावहारिक पाठ में, हम "त्रिकोणमिति" विषय से मुख्य प्रकार के कार्यों को दोहराएंगे, हम अतिरिक्त रूप से बढ़ी हुई जटिलता की समस्याओं का विश्लेषण करेंगे और विभिन्न त्रिकोणमितीय असमानताओं और उनकी प्रणालियों को हल करने के उदाहरणों पर विचार करेंगे।

यह पाठ आपको B5, B7, C1 और C3 प्रकार के कार्यों में से एक के लिए तैयार करने में मदद करेगा।

आइए मुख्य प्रकार के कार्यों को दोहराकर शुरू करें जिनकी हमने त्रिकोणमिति विषय में समीक्षा की थी और कई गैर-मानक कार्यों को हल करते हैं।

कार्य 1. कोणों को रेडियन और डिग्री में बदलें: a); बी) ।

a) डिग्री को रेडियन में बदलने के लिए सूत्र का उपयोग करें

इसमें दिए गए मान को प्रतिस्थापित करें।

बी) रेडियन को डिग्री में बदलने के लिए सूत्र लागू करें

आइए प्रतिस्थापन करते हैं .

जवाब। ए) ; बी) ।

कार्य #2. गणना करें: ए); बी) ।

a) चूंकि कोण तालिका से बहुत दूर है, हम इसे ज्या के आवर्त को घटाकर घटाते हैं। क्योंकि कोण रेडियन में दिया गया है, तो अवधि को माना जाएगा।

बी) इस मामले में, स्थिति समान है। चूँकि कोण को अंशों में निर्दिष्ट किया जाता है, तो हम स्पर्शरेखा के आवर्त को मानेंगे।

परिणामी कोण, हालांकि अवधि से कम है, अधिक है, जिसका अर्थ है कि यह अब मुख्य को नहीं, बल्कि तालिका के विस्तारित भाग को संदर्भित करता है। ट्राइगोफ़ंक्शन मानों की एक विस्तारित तालिका को याद करके हमारी स्मृति को एक बार फिर से प्रशिक्षित नहीं करने के लिए, हम स्पर्शरेखा अवधि को फिर से घटाते हैं:

हमने स्पर्शरेखा फलन की विषमता का लाभ उठाया।

जवाब। ए) 1; बी) ।

कार्य #3. गणना , अगर ।

हम भिन्न के अंश और हर को से विभाजित करके संपूर्ण व्यंजक को स्पर्शरेखा में लाते हैं। साथ ही, हम इससे डर नहीं सकते, क्योंकि इस मामले में, स्पर्शरेखा का मान मौजूद नहीं होगा।

टास्क #4. अभिव्यक्ति को सरल बनाएं।

निर्दिष्ट अभिव्यक्तियों को कास्ट सूत्रों का उपयोग करके परिवर्तित किया जाता है। यह सिर्फ इतना है कि वे असामान्य रूप से डिग्री का उपयोग करके लिखे गए हैं। पहली अभिव्यक्ति आम तौर पर एक संख्या है। बारी-बारी से सभी ट्राइगोफंक्शन को सरल बनाएं:

क्योंकि , तो फ़ंक्शन एक कॉफ़ंक्शन में बदल जाता है, अर्थात। कोटंगेंट के लिए, और कोण दूसरी तिमाही में पड़ता है, जिसमें मूल स्पर्शरेखा का चिह्न ऋणात्मक होता है।

पिछली अभिव्यक्ति के समान कारणों से, फ़ंक्शन एक कॉफ़ंक्शन में बदल जाता है, अर्थात। कोटैंजेंट के लिए, और कोण पहली तिमाही में पड़ता है, जिसमें प्रारंभिक स्पर्शरेखा का सकारात्मक चिन्ह होता है।

सब कुछ एक सरलीकृत अभिव्यक्ति में बदलना:

कार्य #5. अभिव्यक्ति को सरल बनाएं।

आइए दोहरे कोण की स्पर्शरेखा को संबंधित सूत्र के अनुसार लिखें और व्यंजक को सरल बनाएं:

अंतिम पहचान कोसाइन के लिए सार्वभौमिक प्रतिस्थापन सूत्रों में से एक है।

टास्क #6. गणना करें।

मुख्य बात यह है कि मानक त्रुटि न करें और ऐसा उत्तर न दें कि अभिव्यक्ति बराबर है। चाप स्पर्शरेखा के मुख्य गुण का उपयोग करना असंभव है जबकि इसके पास दो के रूप में एक कारक है। इससे छुटकारा पाने के लिए हम द्विकोण की स्पर्शरेखा के सूत्र के अनुसार व्यंजक लिखते हैं, जबकि हम इसे एक साधारण तर्क मानते हैं।

अब चाप स्पर्शरेखा की मुख्य संपत्ति को लागू करना पहले से ही संभव है, याद रखें कि इसके संख्यात्मक परिणाम पर कोई प्रतिबंध नहीं है।

टास्क #7. प्रश्न हल करें।

एक भिन्नात्मक समीकरण को हल करते समय जो शून्य के बराबर होता है, यह हमेशा इंगित किया जाता है कि अंश शून्य है और हर नहीं है, क्योंकि आप शून्य से विभाजित नहीं कर सकते।

पहला समीकरण सरलतम समीकरण का एक विशेष मामला है, जिसे त्रिकोणमितीय वृत्त का उपयोग करके हल किया जाता है। इस उपाय के बारे में आप स्वयं सोचें। दूसरी असमानता को स्पर्शरेखा की जड़ों के लिए सामान्य सूत्र का उपयोग करके सबसे सरल समीकरण के रूप में हल किया जाता है, लेकिन केवल चिह्न के बराबर नहीं होता है।

जैसा कि हम देख सकते हैं, जड़ों का एक परिवार दूसरे को बिल्कुल वही जड़ों का परिवार छोड़ देता है जो समीकरण को संतुष्ट नहीं करते हैं। वे। कोई जड़ें नहीं हैं।

जवाब। कोई जड़ें नहीं हैं।

कार्य #8. प्रश्न हल करें।

तुरंत ध्यान दें कि आप सामान्य कारक निकाल सकते हैं और इसे कर सकते हैं:

समीकरण को मानक रूपों में से एक में घटा दिया गया है, जब कई कारकों का उत्पाद शून्य के बराबर होता है। हम पहले से ही जानते हैं कि इस मामले में या तो उनमें से एक शून्य के बराबर है, या दूसरा, या तीसरा। हम इसे समीकरणों के एक सेट के रूप में लिखते हैं:

पहले दो समीकरण सरलतम के विशेष मामले हैं, हम पहले ही कई बार समान समीकरणों से मिल चुके हैं, इसलिए हम तुरंत उनके समाधान का संकेत देंगे। हम दोहरे कोण ज्या सूत्र का उपयोग करके तीसरे समीकरण को एक फलन में घटाते हैं।

आइए अंतिम समीकरण को अलग से हल करें:

इस समीकरण का कोई मूल नहीं है, क्योंकि साइन का मूल्य आगे नहीं जा सकता .

इस प्रकार, जड़ों के केवल पहले दो परिवार ही समाधान हैं, उन्हें एक में जोड़ा जा सकता है, जो त्रिकोणमितीय सर्कल पर दिखाना आसान है:

यह सभी हिस्सों का परिवार है, यानी।

आइए त्रिकोणमितीय असमानताओं को हल करने के लिए आगे बढ़ें। सबसे पहले, आइए सामान्य समाधान सूत्रों का उपयोग किए बिना एक उदाहरण को हल करने के दृष्टिकोण का विश्लेषण करें, लेकिन एक त्रिकोणमितीय सर्कल की मदद से।

टास्क #9. असमानता को हल करें।

के बराबर ज्या के मान के संगत त्रिकोणमितीय वृत्त पर एक सहायक रेखा खींचिए और असमानता को संतुष्ट करने वाले कोणों के अंतराल को दिखाइए।

यह समझना बहुत महत्वपूर्ण है कि परिणामी कोण अंतराल को कैसे निर्दिष्ट किया जाए, अर्थात। इसकी शुरुआत क्या है और इसका अंत क्या है। अंतराल की शुरुआत उस बिंदु के अनुरूप कोण होगी जिसे हम अंतराल की शुरुआत में प्रवेश करेंगे यदि हम वामावर्त चलते हैं। हमारे मामले में, यह वह बिंदु है जो बाईं ओर है, क्योंकि वामावर्त चलते हुए और सही बिंदु से गुजरते हुए, इसके विपरीत, हम आवश्यक कोण अंतराल से बाहर निकलते हैं। इसलिए सही बिंदु अंतराल के अंत के अनुरूप होगा।

अब हमें असमानता के समाधान के हमारे अंतराल के शुरुआत और अंत कोणों के मूल्यों को समझने की जरूरत है। एक विशिष्ट गलती तुरंत इंगित करना है कि दायां बिंदु कोण से मेल खाता है, बाएं और उत्तर दें। यह सच नहीं है! कृपया ध्यान दें कि हमने सर्कल के ऊपरी हिस्से के अनुरूप अंतराल को इंगित किया है, हालांकि हम निचले हिस्से में रुचि रखते हैं, दूसरे शब्दों में, हमने उन समाधानों के अंतराल की शुरुआत और अंत को मिश्रित किया है जिनकी हमें आवश्यकता है।

अंतराल के लिए दाएं बिंदु के कोने से शुरू होने और बाएं बिंदु के कोने पर समाप्त होने के लिए, पहला निर्दिष्ट कोण दूसरे से कम होना चाहिए। ऐसा करने के लिए, हमें समकोण के कोण को ऋणात्मक संदर्भ दिशा में मापना होगा, अर्थात। दक्षिणावर्त और यह के बराबर होगा। फिर, इससे सकारात्मक दक्षिणावर्त दिशा में शुरू करते हुए, हम बाएं बिंदु के बाद दाएं बिंदु पर पहुंचेंगे और इसके लिए कोण मान प्राप्त करेंगे। अब कोणों के अंतराल की शुरुआत के अंत से कम है, और हम अवधि को ध्यान में रखे बिना समाधान के अंतराल को लिख सकते हैं:

यह देखते हुए कि इस तरह के अंतराल किसी भी पूर्णांक संख्या के घूर्णन के बाद अनंत बार दोहराए जाएंगे, हम सामान्य समाधान प्राप्त करते हैं, साइन अवधि को ध्यान में रखते हुए:

हम गोल कोष्ठक लगाते हैं क्योंकि असमानता सख्त है, और हम सर्कल के उन बिंदुओं को पंचर करते हैं जो अंतराल के सिरों के अनुरूप होते हैं।

अपने उत्तर की तुलना उस सामान्य समाधान के सूत्र से करें जो हमने व्याख्यान में दिया था।

जवाब। .

यह विधि यह समझने के लिए अच्छी है कि सरलतम त्रिकोणीय असमानताओं के सामान्य समाधान के सूत्र कहाँ से आते हैं। इसके अलावा, यह उन लोगों के लिए उपयोगी है जो इन सभी बोझिल फ़ार्मुलों को सीखने के लिए बहुत आलसी हैं। हालाँकि, विधि स्वयं भी आसान नहीं है, चुनें कि समाधान के लिए कौन सा दृष्टिकोण आपके लिए सबसे सुविधाजनक है।

त्रिकोणमितीय असमानताओं को हल करने के लिए, आप फ़ंक्शन ग्राफ़ का भी उपयोग कर सकते हैं, जिस पर सहायक लाइन बनाई गई है, उसी तरह यूनिट सर्कल का उपयोग करके दिखाया गया तरीका। यदि आप रुचि रखते हैं, तो समाधान के लिए इस दृष्टिकोण को स्वयं समझने का प्रयास करें। निम्नलिखित में, हम सरलतम त्रिकोणमितीय असमानताओं को हल करने के लिए सामान्य सूत्रों का उपयोग करेंगे।

कार्य #10. असमानता को हल करें।

हम सामान्य समाधान सूत्र का उपयोग करते हैं, इस बात को ध्यान में रखते हुए कि असमानता सख्त नहीं है:

हम अपने मामले में प्राप्त करते हैं:

जवाब।

टास्क #11. असमानता को हल करें।

हम इसी सख्त असमानता के लिए सामान्य समाधान सूत्र का उपयोग करते हैं:

जवाब। .

टास्क #12. असमानताओं को हल करें: ए); बी) ।

इन असमानताओं में, किसी को सामान्य समाधान या त्रिकोणमितीय सर्कल के लिए सूत्रों का उपयोग करने में जल्दबाजी नहीं करनी चाहिए, यह केवल साइन और कोसाइन के मूल्यों की सीमा को याद रखने के लिए पर्याप्त है।

क) क्योंकि , तो असमानता व्यर्थ है। इसलिए, कोई समाधान नहीं हैं।

बी) क्योंकि इसी तरह, किसी भी तर्क की ज्या हमेशा शर्त में निर्दिष्ट असमानता को संतुष्ट करती है। इसलिए, असमानता तर्क के सभी वास्तविक मूल्यों से संतुष्ट है।

जवाब। ए) कोई समाधान नहीं हैं; बी) ।

टास्क 13. असमानता को हल करें .