Esta é uma seção bastante interessante da matemática que absolutamente todos os estudantes e estudantes de pós-graduação enfrentam. No entanto, nem todo mundo gosta de matan. Alguns não conseguem entender até mesmo coisas básicas como o estudo de função aparentemente padrão. Este artigo visa corrigir esse descuido. Quer saber mais sobre análise de funções? Gostaria de saber o que são pontos extremos e como encontrá-los? Então esse artigo é para você.
Investigação do gráfico de uma função
Para começar, vale a pena entender por que é necessário analisar o gráfico. Existem funções simples que são fáceis de desenhar. Um exemplo notável de tal função é a parábola. Não é difícil desenhar o gráfico dela. Tudo o que é necessário é, usando uma transformação simples, encontrar os números nos quais a função assume o valor 0. E, em princípio, isso é tudo o que você precisa saber para desenhar um gráfico de parábola.
Mas e se a função que precisamos representar graficamente for muito mais complicada? Como as propriedades das funções complexas não são óbvias, é necessário realizar uma análise completa. Só então a função pode ser representada graficamente. Como fazer isso? Você pode encontrar a resposta para essa pergunta neste artigo.
Plano de análise de função
A primeira coisa a fazer é realizar um estudo superficial da função, durante o qual encontraremos o domínio de definição. Então, vamos começar em ordem. O domínio de definição é o conjunto daqueles valores pelos quais a função é definida. Simplificando, esses são os números que podem ser usados na função em vez de x. Para determinar o escopo, você só precisa olhar para o registro. Por exemplo, é óbvio que a função y (x) \u003d x 3 + x 2 - x + 43 tem um domínio de definição - o conjunto dos números reais. Bem, com uma função como (x 2 - 2x) / x, tudo fica um pouco diferente. Como o número no denominador não deve ser igual a 0, o domínio dessa função será todos os números reais, exceto o zero.
Em seguida, você precisa encontrar os chamados zeros da função. Esses são os valores do argumento para os quais toda a função assume o valor zero. Para fazer isso, é necessário igualar a função a zero, considerá-la detalhadamente e realizar algumas transformações. Tomemos a já familiar função y(x) = (x 2 - 2x)/x. Do curso escolar, sabemos que uma fração é 0 quando o numerador é zero. Portanto, descartamos o denominador e começamos a trabalhar com o numerador, igualando-o a zero. Obtemos x 2 - 2x \u003d 0 e tiramos x dos colchetes. Portanto, x (x - 2) \u003d 0. Como resultado, descobrimos que nossa função é igual a zero quando x é igual a 0 ou 2.
Durante o estudo do gráfico de uma função, muitos se deparam com um problema na forma de pontos extremos. E é estranho. Afinal, os extremos são um tópico bastante simples. Não acredito? Veja por si mesmo lendo esta parte do artigo, na qual falaremos sobre os pontos mínimos e máximos.

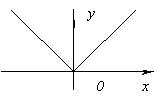
Para começar, vale a pena entender o que é um extremo. Um extremo é o valor limite que uma função atinge em um gráfico. A partir disso, verifica-se que existem dois valores extremos - um máximo e um mínimo. Para maior clareza, você pode olhar para a imagem acima. Na área investigada, o ponto -1 é o máximo da função y (x) \u003d x 5 - 5x, e o ponto 1, respectivamente, é o mínimo.
Além disso, não confunda conceitos entre si. Os pontos extremos de uma função são aqueles argumentos nos quais a função dada adquire valores extremos. Por sua vez, o extremo é o valor dos mínimos e máximos da função. Por exemplo, considere a figura acima novamente. -1 e 1 são os pontos extremos da função, e 4 e -4 são os próprios extremos.
Encontrar pontos extremos

Mas como você encontra os pontos extremos de uma função? Tudo é bem simples. A primeira coisa a fazer é encontrar a derivada da equação. Digamos que recebemos a tarefa: "Encontre os pontos extremos da função y (x), x é o argumento. Para maior clareza, vamos pegar a função y (x) \u003d x 3 + 2x 2 + x + 54. Vamos derivar e obtenha a seguinte equação: 3x 2 + 4x + 1. Como resultado, obtivemos uma equação quadrática padrão. Tudo o que precisa ser feito é igualá-la a zero e encontrar as raízes. Como o discriminante é maior que zero (D \u003d 16 - 12 \u003d 4), esta equação é determinada por duas raízes. Nós as encontramos e obtemos dois valores: 1/3 e -1. Esses serão os pontos extremos da função. No entanto, como você ainda pode determinar quem é quem? Qual ponto é o máximo e qual é o mínimo? Para fazer isso, você precisa pegar um ponto vizinho e descobrir seu valor. Por exemplo, vamos pegar o número -2, que está à esquerda ao longo da coordenada linha de -1. Substituímos esse valor em nossa equação y (-2) = 12 - 8 + 1 = 5. Como resultado, obtivemos um número positivo. Isso significa que no intervalo de 1/3 a -1 o função aumenta, o que, por sua vez, significa que nos intervalos de min de infinito a 1/3 e de -1 a mais infinito, a função diminui. Assim, podemos concluir que o número 1/3 é o ponto de mínimo da função no intervalo investigado, e -1 é o ponto de máximo.

Vale ressaltar também que o exame requer não apenas encontrar pontos extremos, mas também realizar algum tipo de operação com eles (somar, multiplicar, etc.). É por isso que vale a pena prestar atenção especial às condições do problema. Afinal, devido à desatenção, você pode perder pontos.
A partir deste artigo, o leitor aprenderá sobre o que é um extremo de valor funcional, bem como sobre as características de seu uso na prática. O estudo de tal conceito é extremamente importante para a compreensão dos fundamentos da matemática superior. Este tema é fundamental para um estudo mais aprofundado do curso.
Em contato com
O que é um extremo?
No curso escolar, são dadas muitas definições do conceito de "extremo". Este artigo pretende dar a compreensão mais profunda e clara do termo para aqueles que desconhecem o assunto. Assim, entende-se o termo em que medida o intervalo funcional adquire um valor mínimo ou máximo em um determinado conjunto.
O extremo é o valor mínimo da função e o máximo ao mesmo tempo. Existe um ponto mínimo e um ponto máximo, ou seja, os valores extremos do argumento no gráfico. As principais ciências em que esse conceito é usado:
- Estatisticas;
- controle da máquina;
- econometria.
Os pontos extremos desempenham um papel importante na determinação da sequência de uma determinada função. O melhor sistema de coordenadas no gráfico mostra a mudança na posição extrema dependendo da mudança na funcionalidade.
Extrema da função derivada
Existe também algo como um "derivado". É necessário determinar o ponto extremo. É importante não confundir os pontos mínimo ou máximo com os valores maiores e menores. São conceitos diferentes, embora possam parecer semelhantes.
O valor da função é o principal fator para determinar como encontrar o ponto máximo. A derivada não é formada a partir dos valores, mas exclusivamente de sua posição extrema em uma ordem ou outra.
A própria derivada é determinada com base nos dados dos pontos extremos, e não no maior ou menor valor. Nas escolas russas, a linha entre esses dois conceitos não é claramente traçada, o que afeta a compreensão desse tópico em geral.
Vamos agora considerar uma coisa como um "extremo sustenido". Até o momento, existe um valor mínimo agudo e um valor máximo agudo. A definição é dada de acordo com a classificação russa de pontos críticos de uma função. O conceito de um ponto extremo é a base para encontrar pontos críticos em um gráfico.

Para definir tal conceito, utiliza-se o teorema de Fermat. É o mais importante no estudo de pontos extremos e dá uma ideia clara de sua existência de uma forma ou de outra. Para garantir o extremo, é importante criar certas condições para diminuir ou aumentar no gráfico.
Para responder com precisão à pergunta "como encontrar o ponto máximo", você deve seguir estas disposições:
- Encontrar a área exata de definição no gráfico.
- Procure a derivada de uma função e um ponto extremo.
- Resolva as desigualdades padrão para o domínio do argumento.
- Ser capaz de provar em quais funções um ponto de um gráfico é definido e contínuo.

Atenção! A busca por um ponto crítico de uma função só é possível se houver uma derivada de pelo menos segunda ordem, o que é garantido por uma alta proporção da presença de um ponto extremo.
Condição necessária para o extremo da função
Para que exista um extremo, é importante que existam pontos mínimos e pontos máximos. Se esta regra for observada apenas parcialmente, a condição para a existência de um extremo é violada.

Cada função em qualquer posição deve ser diferenciada para identificar seus novos significados. É importante entender que o caso em que um ponto desaparece não é o princípio principal de encontrar um ponto diferenciável.
Um extremo afiado, assim como um mínimo de função, é um aspecto extremamente importante na resolução de um problema matemático usando valores extremos. Para entender melhor esse componente, é importante consultar os valores tabulares para atribuição do funcional.
| Uma exploração completa do significado | Plotando um valor |
| 1. Determinação de pontos de aumento e diminuição de valores. 2. Encontrar pontos de ruptura, extremos e interseções com eixos coordenados. 3. O processo de determinar mudanças na posição no gráfico. 4. Determinação do índice e direção de convexidade e convexidade, levando em consideração a presença de assíntotas. 5. Criação de um quadro resumo do estudo em termos de determinação das suas coordenadas. 6. Encontrar intervalos de aumento e diminuição de pontos extremos e agudos. 7. Determinação da convexidade e concavidade da curva. 8. Construir um gráfico com base no estudo permite encontrar um mínimo ou máximo. |
O elemento principal, quando é necessário trabalhar com extremos, é a construção exata de seu gráfico. Os professores das escolas muitas vezes não prestam a máxima atenção a um aspecto tão importante, que é uma violação grosseira do processo educacional. O gráfico é construído apenas com base nos resultados do estudo de dados funcionais, na definição de extremos agudos, bem como em pontos no gráfico. Extremos agudos da derivada de uma função são exibidos em um gráfico de valores exatos usando o procedimento padrão para determinar assíntotas. |
Considere o gráfico de uma função contínua y=f(x) mostrado na figura.
Valor da função no ponto x 1 será maior que os valores da função em todos os pontos vizinhos tanto à esquerda quanto à direita de x 1 . Neste caso, diz-se que a função tem no ponto x 1 máx. No ponto x A função 3 obviamente também tem um máximo. Se considerarmos o ponto x 2 , então o valor da função nele é menor que todos os valores vizinhos. Neste caso, diz-se que a função tem no ponto x 2 mínimo. Da mesma forma para o ponto x 4 .
Função y=f(x) no ponto x 0 tem máximo, se o valor da função neste ponto for maior que seus valores em todos os pontos de algum intervalo contendo o ponto x 0, ou seja se existe tal vizinhança do ponto x 0 , que é para todos x≠x 0 , pertencentes a este bairro, temos a desigualdade f(x)<f(x 0 ) .
Função y=f(x) Tem mínimo no ponto x 0 , se existe tal vizinhança do ponto x 0 , o que é para todos x≠x 0 pertencente a esta vizinhança, temos a desigualdade f(x)>f(x0.
Os pontos em que a função atinge seu máximo e mínimo são chamados de pontos extremos, e os valores da função nesses pontos são os extremos da função.
Prestemos atenção ao fato de que uma função definida em um segmento pode atingir seu máximo e seu mínimo somente em pontos contidos dentro do segmento considerado.
Observe que se uma função tem um máximo em um ponto, isso não significa que nesse ponto a função tem o valor máximo em todo o domínio. Na figura discutida acima, a função no ponto x 1 tem um máximo, embora haja pontos em que os valores da função são maiores do que no ponto x 1 . Em particular, f(x 1) < f(x 4) ou seja o mínimo da função é maior que o máximo. Da definição do máximo, segue-se apenas que este é o maior valor da função em pontos suficientemente próximos do ponto máximo.
Teorema 1. (Uma condição necessária para a existência de um extremo.) Se a função diferenciável y=f(x) tem no ponto x= x 0 extremo, então sua derivada neste ponto desaparece.
Prova. Seja, por definição, no ponto x 0 a função tem um máximo. Então, para incrementos suficientemente pequenos Δ x temos f(x 0 + Δ x)
Passando essas desigualdades ao limite como Δ x→ 0 e levando em consideração que a derivada f "(x 0) existe e, portanto, o limite à esquerda não depende de como Δ x→ 0, temos: para Δ x → 0 – 0 f"(x 0) ≥ 0 e em Δ x → 0 + 0 f"(x 0) ≤ 0. Desde f"(x 0) define um número, então essas duas desigualdades são compatíveis somente se f"(x 0) = 0.
O teorema provado afirma que os pontos máximo e mínimo só podem estar entre aqueles valores do argumento para os quais a derivada se anula.
Consideramos o caso em que uma função tem uma derivada em todos os pontos de um determinado segmento. O que acontece quando a derivada não existe? Considere exemplos.
Exemplos.
- y=|x|.
A função não tem uma derivada em um ponto x=0 (neste ponto, o gráfico da função não tem uma tangente definida), mas neste ponto a função tem um mínimo, pois y(0)=0, e para todos x≠ 0y > 0.
- Deixar x< x
0. Então c< x
0 e f "(c)> 0.
É por isso f "(c)(x-x 0)<
0 e, portanto,
f(x) - f(x 0 )< 0, ou seja f(x)< f(x 0 ).
- Deixar x > x 0. Então c>x 0 e f"(c)< 0. Significa f "(c)(x-x 0)< 0. É por isso f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Encontrar o escopo de uma função f(x).
- Encontrar a primeira derivada de uma função f"(x).
- Determine pontos críticos, para isso:
- encontre as raízes reais da equação f"(x)=0;
- encontrar todos os valores x em que a derivada f"(x) não existe.
- Determine o sinal da derivada à esquerda e à direita do ponto crítico. Como o sinal da derivada permanece constante entre dois pontos críticos, basta determinar o sinal da derivada em qualquer ponto à esquerda e em um ponto à direita do ponto crítico.
- Calcule o valor da função nos pontos extremos.
- Encontre todos os pontos críticos de uma função no intervalo ( a, b) e calcule os valores da função nesses pontos.
- Calcule os valores da função nas extremidades do segmento para x=a, x=b.
- De todos os valores obtidos, escolha o maior e o menor.
A função não tem derivada em x=0, pois vai ao infinito quando x=0. Mas neste ponto, a função tem um máximo.

A função não tem derivada em x=0 porque ![]() no x→0. Neste ponto, a função não tem máximo nem mínimo. Sério, f(x)=0 e em x<0f(x)<0, а при x>0f(x)>0.
no x→0. Neste ponto, a função não tem máximo nem mínimo. Sério, f(x)=0 e em x<0f(x)<0, а при x>0f(x)>0.

Assim, a partir dos exemplos dados e do teorema formulado fica claro que a função pode ter um extremo apenas em dois casos: 1) nos pontos onde a derivada existe e é igual a zero; 2) no ponto em que a derivada não existe.
No entanto, se em algum momento x 0 sabemos que f"(x 0 ) =0, então não se pode concluir disso que no ponto x 0 a função tem um extremo.
Por exemplo. ![]() .
.

Mas aponte x=0 não é um ponto extremo, pois à esquerda deste ponto os valores da função estão localizados abaixo do eixo Boi, e acima à direita.
Os valores de um argumento do domínio de uma função, para os quais a derivada da função desaparece ou não existe, são chamados Pontos críticos.
De todos os itens acima, segue-se que os pontos extremos da função estão entre os pontos críticos e, no entanto, nem todo ponto crítico é um ponto extremo. Portanto, para encontrar o extremo da função, você precisa encontrar todos os pontos críticos da função e, em seguida, examinar cada um desses pontos separadamente para máximo e mínimo. Para isso, serve o seguinte teorema.
Teorema 2. (Uma condição suficiente para a existência de um extremo.) Seja a função contínua em algum intervalo contendo o ponto crítico x 0 , e é diferenciável em todos os pontos deste intervalo (exceto, talvez, o próprio ponto x 0). Se, ao passar da esquerda para a direita por este ponto, a derivada muda de sinal de mais para menos, então no ponto x = x 0 a função tem um máximo. Se, ao passar por x 0 da esquerda para a direita, a derivada muda de sinal de menos para mais, então a função tem um mínimo neste ponto.
Assim, se
Prova. Suponhamos primeiro que ao passar por x 0, a derivada muda o sinal de mais para menos, ou seja para todos x perto do ponto x 0 f"(x)> 0 para x< x 0 , f"(x)< 0 para x > x 0. Vamos aplicar o teorema de Lagrange à diferença f(x) - f(x 0 ) = f "(c)(x-x 0), onde c encontra-se entre x e x 0 .
Assim, para todos os valores x perto o suficiente para x 0 f(x)< f(x 0 ) . E isso significa que no ponto x 0 a função tem um máximo.
A segunda parte do teorema do mínimo é provada de forma semelhante.

Vamos ilustrar o significado deste teorema na figura. Deixar f"(x 1 ) =0 e para qualquer x, perto o suficiente para x 1 , as desigualdades
f"(x)< 0 em x< x 1 , f"(x)> 0 em x > x 1 .
Em seguida, à esquerda do ponto x 1 a função é crescente e decrescente à direita, portanto, quando x = x 1 função vai de crescente para decrescente, ou seja, tem um máximo.
Da mesma forma, pode-se considerar os pontos x 2 e x 3 .

Esquematicamente, todos os itens acima podem ser representados na imagem:
A regra para estudar a função y=f(x) para um extremo
Exemplos. Explore funções para mínimo e máximo.
OS MAIORES E MÍNIMOS VALORES DE FUNÇÃO NA INTERCEPÇÃO
o melhor o valor de uma função em um segmento é o maior de todos os seus valores neste segmento, e ao menosé o menor de todos os seus valores.
Considere a função y=f(x) contínua no intervalo [ a, b]. Como se sabe, tal função atinge seus valores máximo e mínimo, seja na fronteira do segmento, seja dentro dele. Se o valor máximo ou mínimo da função é atingido no ponto interno do segmento, então esse valor é o máximo ou mínimo da função, ou seja, é atingido em pontos críticos.
Assim, obtemos o seguinte a regra para encontrar os maiores e menores valores de uma função no segmento [ a, b] :
>> Extremos
Função extrema
Definição de extremo
Função y = f(x) é chamado aumentando (minguante) em algum intervalo se para x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).
Se uma função diferenciável y \u003d f (x) em um segmento aumenta (diminui), então sua derivada neste segmento f " (x)> 0
(f"(x)< 0).
Ponto x cerca de chamado ponto máximo local (mínimo) da função f (x ) se houver uma vizinhança do ponto x o, para todos os pontos dos quais a desigualdade f (x)≤ f (x o) (f (x)≥ f(xo)).
Os pontos de máximo e mínimo são chamados pontos extremos, e os valores da função nesses pontos são seus extremos.
pontos extremos
Condições necessárias para um extremo . Se ponto x cerca de é um ponto extremo da função f (x), então ou f " (x o ) = 0, ou f(x o ) não existe. Tais pontos são chamados crítico, onde a própria função é definida no ponto crítico. Os extremos de uma função devem ser procurados entre seus pontos críticos.
A primeira condição suficiente. Deixar x cerca de - ponto crítico. Se f" (x) ao passar pelo ponto x cerca de muda o sinal de mais para menos, então no ponto x o a função tem um máximo, caso contrário, tem um mínimo. Se a derivada não muda de sinal ao passar por um ponto crítico, então no ponto x cerca de não há extremo.
A segunda condição suficiente.
Seja a função f(x)
f" (x) nas proximidades do ponto x
cerca de
e a segunda derivada no ponto exato x o. Se f"(x o) = 0, >0 ( <0), то точка x oé um ponto de mínimo (máximo) local da função f(x). Se =0, então deve-se usar a primeira condição suficiente ou envolver outras mais altas.
Em um segmento, a função y \u003d f (x) pode atingir o menor ou o maior valor em pontos críticos ou nas extremidades do segmento.
Exemplo 3.22.
Solução. Porque f " (
Tarefas para encontrar o extremo de uma função
Exemplo 3.23. uma
Solução. x e y y
0
≤ x≤
> 0, enquanto x >a /4S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funções quadrado.
unidades).
Exemplo 3.24. p ≈
Solução. pp
S"
R = 2, H = 16/4 = 4.
Exemplo 3.22.Encontre os extremos da função f (x) = 2x 3 - 15x 2 + 36x - 14.
Solução. Porque f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), então os pontos críticos da função x 1 \u003d 2 e x 2 \u003d 3. Os pontos extremos só podem estar nesses pontos. Como ao passar pelo ponto x 1 \u003d 2, a derivada muda de sinal de mais para menos, então neste ponto a função tem um máximo. Ao passar pelo ponto x 2 \u003d 3, a derivada muda de sinal de menos para mais, portanto, no ponto x 2 \u003d 3, a função tem um mínimo. Calculando os valores da função em pontos
x 1 = 2 e x 2 = 3, encontramos os extremos da função: máximo f (2) = 14 e mínimo f (3) = 13.
Exemplo 3.23.É necessário construir uma área retangular perto do muro de pedra para que seja cercado com tela de arame em três lados e contíguo ao muro no quarto lado. Para isso existe uma metros lineares da rede. Em qual proporção o site terá a maior área?
Solução.Denote os lados do site por meio de x e y. A área do local é igual a S = xy. Deixar yé o comprimento do lado adjacente à parede. Então, por condição, a igualdade 2x + y = a deve valer. Portanto y = a - 2x e S = x (a - 2x), onde
0
≤ x≤ a /2 (o comprimento e a largura do pad não podem ser negativos). S "= a - 4x, a - 4x = 0 para x = a/4, de onde
y \u003d a - 2 × a / 4 \u003d a / 2. Porque o x = a /4 é o único ponto crítico, vamos verificar se o sinal da derivada muda ao passar por este ponto. Para x a /4 S "> 0, enquanto x >a /4S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funções S(a/4) = a/4(a - a/2) = a 2/8 (quadrado.
unidades).
Como S é contínuo e seus valores nas extremidades de S(0) e S(a/2) são iguais a zero, então o valor encontrado será o maior valor da função. Assim, a razão de aspecto mais favorável do site nas condições dadas do problema é y = 2x.
Exemplo 3.24.É necessário fazer um tanque cilíndrico fechado com capacidade de V=16 p ≈ 50m3. Quais devem ser as dimensões do tanque (raio R e altura H) para que se utilize a menor quantidade de material para sua fabricação?
Solução.A área total da superfície do cilindro é S = 2 p R(R+H). Sabemos que o volume do cilindro V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Então S(R) = 2 p (R2+16/R). Encontramos a derivada desta função:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0 para R 3 = 8, portanto,
R = 2, H = 16/4 = 4.
Funções, não é necessário saber sobre a presença da primeira e segunda derivadas e entender seu significado físico. Primeiro você precisa entender o seguinte:
- os extremos da função maximizam ou, inversamente, minimizam o valor da função em uma vizinhança arbitrariamente pequena;
- no ponto extremo não deve haver descontinuidade da função.
E agora a mesma coisa, apenas em termos simples. Olhe para a ponta de uma caneta esferográfica. Se a caneta for colocada verticalmente, com a escrita para cima, o meio da bola será o ponto extremo - o ponto mais alto. Neste caso, falamos sobre o máximo. Agora, se você virar a caneta com a ponta da escrita para baixo, no meio da bola já haverá um mínimo da função. Com a ajuda da figura dada aqui, você pode imaginar as manipulações listadas para um lápis de papelaria. Assim, os extremos de uma função são sempre pontos críticos: seus máximos ou mínimos. A seção adjacente do gráfico pode ser arbitrariamente nítida ou suave, mas deve existir em ambos os lados, somente neste caso o ponto é um extremo. Se o gráfico estiver presente apenas em um lado, esse ponto não será um extremo, mesmo que as condições extremas sejam atendidas em um de seus lados. Agora vamos estudar os extremos da função do ponto de vista científico. Para que um ponto seja considerado extremo, é necessário e suficiente que:
- a primeira derivada era igual a zero ou não existia no ponto;
- a primeira derivada muda de sinal neste ponto.

A condição é interpretada de maneira um pouco diferente do ponto de vista das derivadas de ordem superior: para uma função diferenciável em um ponto, é suficiente que haja uma derivada de ordem ímpar que não seja igual a zero, enquanto todas as derivadas de ordem inferior devem existir e ser igual a zero. Esta é a interpretação mais simples dos teoremas dos livros didáticos, mas para as pessoas mais comuns, vale a pena explicar este ponto com um exemplo. A base é uma parábola comum. Faça imediatamente uma reserva, no ponto zero tem um mínimo. Só um pouco de matemática:
- primeira derivada (X 2) | = 2X, para ponto zero 2X = 0;
- segunda derivada (2X) | = 2, para ponto zero 2 = 2.

Desta forma simples, são ilustradas as condições que determinam os extremos da função tanto para derivadas de primeira ordem quanto para derivadas de ordem superior. Podemos acrescentar a isso que a segunda derivada é apenas a mesma derivada de ordem ímpar, diferente de zero, que foi discutida um pouco mais acima. Quando se trata de extremos de uma função de duas variáveis, as condições devem ser atendidas para ambos os argumentos. Quando a generalização ocorre, então as derivadas parciais entram em jogo. Ou seja, é necessário para a presença de um extremo em um ponto que ambas as derivadas de primeira ordem sejam iguais a zero, ou pelo menos uma delas não exista. Para a suficiência da presença de um extremo, investiga-se uma expressão, que é a diferença entre o produto das derivadas de segunda ordem e o quadrado da derivada mista de segunda ordem da função. Se esta expressão for maior que zero, então há um extremo, e se houver uma igualdade a zero, então a questão permanece em aberto, e pesquisas adicionais são necessárias.
