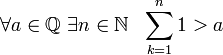Sa kasaysayan, ang una mga integer$N$, bilang resulta ng muling pagkalkula ng mga umutot. Ang set ng mga numerong ito ay walang hanggan at bumubuo ng natural na serye $N=\(1, 2, 3, ..., n, ...\)$. Sa set na ito, ang mga operasyon ng pagdaragdag at pagpaparami ay magagawa. Upang maisagawa ang operasyon ng pagbabawas, kailangan ng mga bagong numero, na humantong sa paglitaw ng isang hanay ng mga integer: $Z$. $Z=N_+\cup N_- \cup \(0\)$. Kaya, sa hanay ng mga integer, ang mga pagpapatakbo ng karagdagan, pagpaparami, pagbabawas ay palaging ginagawa.
Mga rational na numero
Ang pangangailangang magsagawa ng paghahati ay humantong sa hanay ng mga rational na numero na $Q$. $Q=\(\frac(m)(n), m\in Z, n\in N\)$.
Kahulugan. Dalawang rational na numero ang magkapareho: $\frac(m_1)(n_1)=\frac(m_2)(n_2)$ - kung $m_1\cdot n_2=n_1\cdot m_2$. Nangangahulugan ito na ang bawat makatwirang numero maaaring natatanging kinakatawan bilang isang hindi mababawasang bahagi na $\frac(m)(n)$. $gcd(m, n)=1$.
Mga katangian ng hanay ng mga rational na numero
1. Bilang resulta mga operasyon sa aritmetika higit sa mga rational na numero (pagdaragdag, pagpaparami, pagbabawas, paghahati, maliban sa paghahati ng zero), isang rational na numero ang nakuha.
2. Ang hanay ng mga rational na numero ay inayos, iyon ay, para sa anumang pares ng mga rational na numero na $a$ at $b$ o $a
3. Ang hanay ng mga rational na numero ay siksik, ibig sabihin, para sa alinmang pares ng mga rational na numero na $a$ at $b$ mayroong isang rational na numero na $c$ na ang $a Ang anumang positibong rational na numero ay maaaring palaging kinakatawan bilang isang decimal fraction: alinman sa may hangganan o walang katapusan na periodic. Halimbawa: $\frac(3)(5)=0.6$, $\frac(1)(3)=0.333...=0,(3)$. $\frac(m)(n)=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$. $b_1b_2b_3...b_n...$ - ay tinatawag na panahon ng decimal fraction, kung saan hindi lahat ng $b_i=0$. Tandaan na ang isang finite fraction ay maaaring isulat bilang isang infinite periodic fraction na may zero sa period. $\frac(m)(n)=a_0,a_1a_1...a_k000000...$, $a_k\ne0$. Gayunpaman, ang isa pang representasyon ng mga rational na numero bilang isang decimal fraction ay mas karaniwan: $\frac(m)(n)=a_0,a_1a_1...(a_k-1)999...$. Ang mga negatibong rational na numero na $-\frac(m)(n)$ ay isinulat bilang decimal expansion ng isang rational na numero ng anyong $\frac(m)(n)$ na kinuha gamit ang kabaligtaran na sign. Ang bilang na $0$ ay kinakatawan bilang $0,000...$. Kaya, ang anumang rational na numero ay palaging kinakatawan bilang isang walang katapusang decimal periodic fraction na hindi naglalaman ng $0$ sa period, maliban sa numerong $0$ mismo. Ang pananaw na ito ay nag-iisa. Ang hanay ng mga rational na numero ay sarado sa ilalim ng apat na aritmetika na operasyon. Gayunpaman, sa hanay ng mga rational na numero, ang solusyon ng pinakasimpleng equation ng anyong $x^2-n=0$ ay hindi palaging nagaganap. Samakatuwid, may pangangailangan na magpakilala ng mga bagong numero. Ipakita natin na sa mga rational na numero ay walang numero na ang parisukat ay katumbas ng tatlo. Ang patunay ay isinasagawa sa pamamagitan ng paraan ng kontradiksyon. Ipagpalagay na mayroong isang rational number na $\frac(m)(n)$ na ang parisukat nito ay tatlo: $\left(\frac(m)(n)\right)^2=3\;\;\;( 1 )$. $\frac(m^2)(n^2)=3$, $m^2=3n^2.\;\;\;(2)$ Ang kanang bahagi ng pagkakapantay-pantay (2) ay nahahati ng 3. Kaya, ang $m^2$ ay nahahati din ng 3, kaya ang $m$ ay nahahati ng 3, na nangangahulugang $m=3k$. Ipalit sa equation (2), makuha natin ang: $3k^2=n^2.\;\;\;(3)$ Ang kaliwang bahagi ng $(3)$ ay nahahati sa $3$, kaya ang kanang bahagi ay nahahati din ng $3$. Kaya ang $n^2$ ay nahahati ng $3$, kaya ang $n$ ay nahahati din ng $3$, kung saan ang $n=3p$. Bilang resulta, nakukuha namin ang: $\frac(m)(n)=\frac(3k)(3p)$, ibig sabihin, ang fraction na $\frac(m)(n)$ ay naging reducible, na sumasalungat sa palagay . Nangangahulugan ito na sa mga nakapangangatwiran na mga numero ay walang ganoong numero, ang parisukat na kung saan ay katumbas ng tatlo. Ngunit mayroong isang numero na ang parisukat ay tatlo. Maaari itong katawanin bilang isang walang katapusang non-periodic fraction. At nakakuha kami ng bagong uri ng mga numero. Tawagin natin silang hindi makatwiran. Kahulugan. Ang di-makatwirang numero ay anumang walang katapusang non-periodic fraction. Ang set ng lahat ng infinite non-periodic fraction ay tinatawag na set ng mga irrational na numero at tinutukoy ng $I$. Ang pagsasama-sama ng hanay ng mga rational na numero na $Q$ at mga irrational na numero na $I$ ay nagbibigay ng hanay ng mga tunay na numero $R$: $Q\cup I=R$. Kaya, ang anumang tunay na numero ay maaaring katawanin bilang isang walang katapusang decimal fraction: periodic sa kaso ng rational number at non-periodic sa kaso ng irrational number. Para sa mga tunay na numero $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ ang paghahambing ay ang mga sumusunod: 1) Hayaang maging positibo ang $a$ at $b$: $a>0$, $b>0$, pagkatapos: $a=b$ kung para sa alinmang $k$ $a_k=b_k$; $a>b$ kung $\umiiral s$ $\forall k 2) Hayaan ang $a>0$, $b<0$, или иначе: $b<0 3) Hayaang parehong negatibo ang $a$ at $b$: $a<0$, $b<0$, тогда: $a=b$ kung para sa $-a=-b$; Mayroong iba't ibang mga numero - ang operasyon ng pagkuha ng isang square root ay madalas na humahantong sa kanila (at hindi lamang ito, hindi pa natin alam ito). Kaya, kailangan nating kilalanin ang mga bagong numero nang mas detalyado. Ngunit una, subukan nating i-systematize ang ating kaalaman sa "luma", ibig sabihin, makatuwiran, mga numero. 1. Ilang simbolo ng wikang matematika
Ito ay mga buong numero, karaniwang fraction, decimal fraction. Para sa lahat ng mga numerong ito, maaari mong gamitin ang parehong notasyon, na tatalakayin natin ngayon. 5 = 5.00000... = 5,(0). Ang parehong ay totoo para sa numerong 8.377: 8.377 = 8.377000... = 8.377(0). Upang gawing maayos ang lahat, sinasabi nila ito: 8.377 ay isang finite decimal fraction, at 8.377000 ... ay isang infinite decimal fraction. Sa pangkalahatan, ang anumang rational na numero ay maaaring isulat bilang isang walang katapusang decimal periodic fraction. Magkomento.
Ang konklusyon na ito ay maginhawa para sa teorya, ngunit hindi masyadong maginhawa para sa pagsasanay. Pagkatapos ng lahat, kung ang panghuling bahagi ng decimal na 8.377 ay ibinigay, kung gayon bakit kailangan itong isulat sa anyo na 8.377 (0)? Samakatuwid, karaniwan nilang sinasabi ito: anumang rational na numero ay maaaring isulat bilang isang finite decimal fraction o bilang isang infinite decimal periodic fraction. Ang hanay ng mga rational na numero ay ipinahiwatig at maaaring isulat tulad ng sumusunod: Lumalabas na ang iba't ibang mga entry ay maaaring kumatawan sa parehong fraction, halimbawa, at , (lahat ng mga fraction na maaaring makuha mula sa bawat isa sa pamamagitan ng multiply o paghahati sa parehong natural na numero ay kumakatawan sa parehong rational na numero). Dahil sa pamamagitan ng paghahati ng numerator at denominator ng isang fraction sa kanilang pinakamalaking karaniwang divisor, makukuha ng isa ang tanging hindi mababawas na representasyon ng isang rational na numero, masasabi ng isa ang kanilang set bilang isang set hindi mababawasan mga fraction na may coprime integer numerator at natural denominator: Narito ang pinakamalaking karaniwang divisor ng mga numero at . Ang hanay ng mga rational na numero ay isang natural na paglalahat ng hanay ng mga integer. Madaling makita na kung ang isang rational na numero ay may denominator , kung gayon ito ay isang integer. Ang hanay ng mga rational na numero ay nasa lahat ng dako sa axis ng numero: sa pagitan ng alinmang dalawang magkaibang rational na numero ay mayroong kahit isang rational na numero (at samakatuwid ay isang walang katapusang hanay ng mga rational na numero). Gayunpaman, lumalabas na ang hanay ng mga rational na numero ay may mabibilang na cardinality (iyon ay, ang lahat ng mga elemento nito ay maaaring palitan ng numero). Pansinin, sa pamamagitan ng paraan, na kahit na ang mga sinaunang Greeks ay kumbinsido sa pagkakaroon ng mga numero na hindi maaaring kinakatawan bilang isang fraction (halimbawa, pinatunayan nila na walang rational na numero na ang parisukat ay 2) Ari-arian Mga pangunahing katangian Ang hanay ng mga rational na numero ay nakakatugon sa labing-anim na pangunahing katangian na madaling makuha mula sa mga katangian ng mga integer. Mga karagdagang katangian Ang lahat ng iba pang mga katangian na likas sa mga makatwirang numero ay hindi tinutukoy bilang mga pangunahing, dahil, sa pangkalahatan, hindi na sila direktang nakabatay sa mga katangian ng mga integer, ngunit maaaring patunayan sa batayan ng mga ibinigay na pangunahing katangian o direkta sa pamamagitan ng kahulugan ng ilang bagay sa matematika. Mayroong maraming mga karagdagang pag-aari. Makatuwiran dito na banggitin lamang ang ilan sa mga ito. 25..Itakda ang J ng mga hindi makatwirang numero Mga halimbawa ng mga hindi makatwirang numero: Ang hanay ng mga hindi makatwirang numero ay tinutukoy ng malaking letrang Ingles [ai] - "I". Sa hanay ng mga numero, ang mga hindi makatwirang numero ay sumasakop sa isang espesyal na lugar. Hindi sila kasama sa mga rational na numero. Hindi nakapangangatwiran numero(hindi katulad ng mga makatwiran) ay hindi maaaring katawanin bilang isang fraction a / b , kung saan ang a ∈ Z (a ay kabilang sa mga integer), b∈N (b ay kabilang sa mga natural na numero). 26. Ang set R ng mga tunay na numero totoong numero Mula sa Wikipedia, ang malayang ensiklopedya Tumalon sa: nabigasyon, paghahanap totoo, o totoong numero- isang mathematical abstraction na nagmula sa pangangailangang sukatin ang geometriko at pisikal na dami ng nakapaligid na mundo, pati na rin ang pagsasagawa ng mga operasyon tulad ng pagkuha ng ugat, pagkalkula ng logarithms, paglutas ng mga algebraic equation. Linya ng numero Kung ang mga natural na numero ay lumitaw sa proseso ng pagbibilang, mga rational na numero - mula sa pangangailangan na gumana sa mga bahagi ng isang kabuuan, kung gayon ang mga tunay na numero ay inilaan para sa pagsukat ng tuluy-tuloy na dami. Kaya, ang pagpapalawak ng stock ng mga numero na isinasaalang-alang ay humantong sa hanay ng mga tunay na numero, na, bilang karagdagan sa mga rational na numero, kasama rin ang iba pang mga elemento na tinatawag na hindi nakapangangatwiran numero. Ang konsepto ng isang tunay na numero ay maaaring makita gamit ang linya ng numero. Kung pipili ka ng direksyon sa isang tuwid na linya, isang panimulang punto at isang yunit ng haba para sa pagsukat ng mga segment, kung gayon ang bawat tunay na numero ay maaaring iugnay sa isang tiyak na punto sa tuwid na linya na ito, at kabaliktaran, ang bawat punto ay kumakatawan sa ilan, at higit pa rito , isa lang, totoong numero. Dahil sa sulat na ito, ang terminong linya ng numero ay karaniwang ginagamit bilang kasingkahulugan para sa hanay ng mga tunay na numero. Ang konsepto ng isang tunay na numero ay malayo na ang narating. Kahit na sa sinaunang Greece, sa paaralan ng Pythagoras, na naglalagay ng mga buong numero at ang kanilang mga relasyon bilang batayan para sa lahat, ang pagkakaroon ng hindi masusukat na dami(incommensurability ng gilid at dayagonal ng isang parisukat), iyon ay, sa modernong terminolohiya, mga numero na hindi makatwiran. Kasunod nito, si Eudoxus ng Cnidus ay gumawa ng isang pagtatangka na bumuo ng isang pangkalahatang teorya ng bilang na kasama ang hindi matutumbasan na dami. Pagkatapos nito, sa loob ng higit sa dalawang libong taon, walang naramdaman ang pangangailangan para sa isang tiyak na kahulugan ng konsepto ng isang tunay na numero, sa kabila ng unti-unting pagpapalawak ng konseptong ito. Sa ikalawang kalahati lamang ng ika-19 na siglo, nang ang pag-unlad ng pagsusuri sa matematika ay nangangailangan ng muling pagsasaayos ng mga pundasyon nito sa isang bago, mas mataas na antas ng higpit, isang mahigpit na teorya ng tunay na mga numero ang nilikha sa mga gawa ni K. Weierstrass, R. Dedekind , G. Cantor, E. Heine, S. Mere . Mula sa punto ng view ng modernong matematika, ang hanay ng mga tunay na numero ay isang tuluy-tuloy na ordered field. Ang kahulugan na ito, o isang katumbas na sistema ng mga axiom, ay eksaktong tumutukoy sa konsepto ng isang tunay na numero sa diwa na mayroon lamang isa, hanggang sa isomorphism, tuluy-tuloy na nakaayos na larangan. Ang hanay ng mga tunay na numero ay may karaniwang notasyon - R("bold R"), o (eng. naka-bold ang pisara"R") mula sa lat. makatotohanan- may bisa. 27. Mga sistema ng numero Notasyon- isang simbolikong paraan ng pagsulat ng mga numero, na kumakatawan sa mga numero gamit ang mga nakasulat na character. Notasyon: Ang mga sistema ng numero ay nahahati sa posisyonal, hindi nakaposisyon at magkakahalo.Hindi nakapangangatwiran numero
Mga totoong numero
Paghahambing ng mga tunay na numero
Isaalang-alang, halimbawa, ang integer 5, ang karaniwang fraction, at ang decimal na 8.377. Ang integer 5 ay maaaring isulat bilang isang walang katapusang decimal: 5.0000... Ang decimal 8.377 ay maaari ding isulat bilang isang walang katapusan decimal fraction: 8.377000... Para sa numero, gamitin natin ang "angle division" na paraan:
Tulad ng nakikita mo, simula sa pangalawang digit pagkatapos ng decimal point, ang parehong pangkat ng mga numero ay paulit-ulit: 18, 18, 18, .... Kaya = 0.3181818... . Sa madaling salita, ito ay nakasulat na ganito: 0.3 (18). Ang umuulit na pangkat ng mga digit pagkatapos ng decimal point ay tinatawag na period, at ang decimal fraction mismo ay tinatawag na infinite decimal periodic fraction.
infinite decimal periodic fraction. Upang gawin ito, isulat ang numero 0 sa tuldok:
Kaya, ang numero 5, at ang numero, at ang numero 8.377 ay isinulat bilang isang walang katapusang decimal periodic fraction.![]()