1. Aufgabe.
Bei welchen Werten des Parameters a Die gleichung ( a - 1)x 2 + 2x + a- 1 = 0 hat genau eine Wurzel?

1. Entscheidung.
Bei a= 1 Gleichung hat die Form 2 x= 0 und hat offensichtlich eine einzelne Wurzel x= 0. Wenn a Nr. 1, dann ist diese Gleichung quadratisch und hat eine einzelne Wurzel für diejenigen Werte des Parameters, für die die Diskriminante des quadratischen Trinoms gleich Null ist. Indem wir die Diskriminante mit Null gleichsetzen, erhalten wir eine Gleichung für den Parameter a 4a 2 - 8a= 0, woher a= 0 bzw a = 2.

1. Antwort: Die Gleichung hat eine einzelne Wurzel bei a O(0; 1; 2).

2. Aufgabe.
Finden Sie alle Parameterwerte a, für die die Gleichung zwei verschiedene Wurzeln hat x 2 +4Axt+8a+3 = 0.
2. Entscheidung.
Die gleichung x 2 +4Axt+8a+3 = 0 hat genau dann zwei unterschiedliche Wurzeln D = 16a 2 -4(8a+3) > 0. Wir erhalten (nach Reduktion um den gemeinsamen Faktor 4) 4 a 2 -8a-3 > 0, woher

2. Antwort:

a O (-Ґ ; 1 -

C 7 2

) UND (1 +

C 7 2

; Ґ ).

3. Aufgabe.
Es ist bekannt, dass
f 2 (x) = 6x-x 2 -6.
a) Stellen Sie die Funktion graphisch dar f 1 (x) bei a = 1.
b) Zu welchem ​​Wert a Funktionsgraphen f 1 (x) und f 2 (x) haben einen einzigen gemeinsamen Punkt?

3. Lösung.
3.a. Verwandeln wir uns f 1 (x) auf die folgende Weise
Der Graph dieser Funktion a= 1 ist in der Abbildung rechts dargestellt.
3.b. Wir bemerken sofort, dass die Funktionsgraphen j = kx+b und j = Axt 2 +bx+c (a Nr. 0) schneiden sich genau dann in einem einzigen Punkt, wenn die quadratische Gleichung kx+b = Axt 2 +bx+c hat eine einzige Wurzel. Ansicht verwenden f 1 von 3.a, setzen wir die Diskriminante der Gleichung gleich a = 6x-x 2 -6 zu null. Aus Gleichung 36-24-4 a= 0 erhalten wir a= 3. Machen Sie dasselbe mit Gleichung 2 x-a = 6x-x 2 -6 finden a= 2. Es ist leicht zu überprüfen, ob diese Parameterwerte die Bedingungen des Problems erfüllen. Antworten: a= 2 bzw a = 3.

4. Aufgabe.
Finden Sie alle Werte a, unter der die Menge der Lösungen der Ungleichung x 2 -2Axt-3a i 0 enthält das Segment .

4. Lösung.
Die erste Koordinate des Scheitelpunkts der Parabel f(x) = x 2 -2Axt-3a ist gleich x 0 = a. Aus den Eigenschaften einer quadratischen Funktion die Bedingung f(x) i 0 auf dem Intervall entspricht der Gesamtheit von drei Systemen
genau zwei Lösungen hat?

5. Entscheidung.
Lassen Sie uns diese Gleichung in der Form umschreiben x 2 + (2a-2)x - 3a+7 = 0. Dies ist eine quadratische Gleichung, sie hat genau zwei Lösungen, wenn ihre Diskriminante strikt größer als Null ist. Wenn wir die Diskriminante berechnen, erhalten wir, dass die Bedingung dafür, genau zwei Wurzeln zu haben, die Erfüllung der Ungleichung ist a 2 +a-6 > 0. Lösen der Ungleichung, finden wir a < -3 или a> 2. Offensichtlich hat die erste der Ungleichungen keine Lösungen in natürlichen Zahlen, und die kleinste natürliche Lösung der zweiten ist die Zahl 3.

5. Antwort: 3.

6. Aufgabe (10 Zellen)
Finden Sie alle Werte a, für die der Graph der Funktion oder nach offensichtlichen Transformationen a-2 = | 2-a| . Die letzte Gleichung ist äquivalent zur Ungleichung a ich 2.

6. Antwort: a O , und hängt nicht vom Vorzeichen der Diskriminante ab. Machen wir schematische Zeichnungen (für D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

Für jeden der drei Fälle a), b), c) der kleinste Wert der Funktion f(t) = t2-8at+7a2

auf dem Segment wird jeweils an den Punkten bei x = 1, x = 2a, x = 1/4 erreicht. Dann ist die zu beantwortende Frage die Lösung der Gesamtheit der drei Systeme:

1≤4a 1/4<4а<1 4а<1/4

f(1)<0 или f(4а)<0 или f(1/4)<0

a≥1/4 1/16<а<1/4 а≤1/16

1 - 8a + 7a2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

Antworten: 1/28<а<1.

Testaufgaben

eines). Für welche Werte des Parameters a schneiden sich die Graphen der Funktionen y = 2x – a und y = (a + 1)x2 + 1 nur in einem Punkt?

2). Finden Sie alle Werte des Parameters a, für die die Graphen der Funktionen y = (a + 5)x2 - 1 und

y \u003d (3a + 15) x - 4 haben keine gemeinsamen Punkte?

3). Für welche Werte des Parameters a hat die Gleichung (a +4)x2 +6x –1 = 0 eine eindeutige Lösung?

vier). Für welche Werte des Parameters a hat die Gleichung (2a + 8) x2 - (a + 4) x + 3 = 0 eine eindeutige Lösung?

5). Für welche Werte des Parameters a hat die Gleichung mehr als eine Lösung?

a) (a + 6)x2 - 8x + a \u003d 0

b) a (2a + 4) x2 - (a + 2) x - 5a - 10 = 0.

6). Finden Sie alle Werte des Parameters k, für die die Kurve y = x2 + kx + 4 die x-Achse berührt.

7). Was ist der kleinste ganzzahlige Wert des Parameters k für das quadratische Trinom?

(k–2)x2+8x + k+4 für alle reellen Werte von x positiv ist?

acht). Die Zahlen x, y und sind so, dass x + y = a -1, x2 + y2 = 5a2 - 3a + 0,5. Bei welchen Werten des Parameters a nimmt das Produkt xy den maximalen Wert an?

9). Die Zahlen x, y und sind so, dass x + y = a +1, xy = a2 - 3a + 4. Für welche Werte des Parameters

und die Summe x2 + y2 nimmt den Maximalwert an?

zehn). Finden Sie den größten und 1 kleinsten Wert der Funktion y \u003d 2x2 - 2ax + auf dem Segment

elf). Finden Sie den größten Wert des quadratischen Trinoms 1 - (a - 2) x - x2 auf dem Segment

12). Bei welchen Werten des Parameters a ist der kleinste Wert der Funktion y = x2 + (a + 4) x + 2a + 3 auf dem Segment gleich -4?

13). Bei welchen Werten des Parameters a ist der kleinste Wert der Funktion y \u003d x2 - (a + 2) x + a2 auf dem Segment [-1; 1] gleich 4?

vierzehn). Bei welchen Werten des Parameters a ist der Maximalwert der Funktion

f (x) \u003d - (1 / a) x + (7 / a) 3-x - 3a2 auf dem Segment [-1; 0] ist negativ?

Antworten auf die Testaufgabe

1) a=-2, a=-1, a=0.

2) –19/3<а≤-5.

3) a=-4, a=-13.

5) a) -8<а<-6 и -6<а<2

b) a=-2; -1/40 0.

10) Wenn a<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

wenn -2≤a<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

wenn 0 ≤ a<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

wenn a≥2, dann der kleinste Wert der Funktion bei x=1 und gleich 3–2a, der größte Wert der Funktion bei x=-1 und gleich 3+2a;

11) Wenn a≤0, dann -6a2-a+2, wenn 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

13) a=-2 oder a=(1+√21)/2

14) |a|>(7√3)/12.

Lage der Wurzeln eines quadratischen Trinoms

Betrachten Sie eine Reihe typischer Probleme im Zusammenhang mit der Position der Wurzeln des quadratischen Trinoms ax2 + bx + c. Wir führen die gesamte Argumentation unter der Annahme von a > 0 durch. Wenn ein<0,то рассуждения проводятся аналогично.

Aufgabe Nummer 1.

Unter welchen Bedingungen sind beide Wurzeln der quadratischen Gleichung ax2 + bx + c = 0 (nicht notwendigerweise verschieden) größer als eine gegebene Zahl k?

Lösung.

Wir konstruieren schematische Graphen der Funktion eines quadratischen Trinoms y= ax2+bx+c, wobei x1 und x2 die Bedingungen erfüllen: x1>k, x2>k. Sei f(x)=ax2+bx+c. Der Graph y= f(x) schneidet entweder die OX-Achse (D>0) oder berührt sie (D=0). Dann muss die Bedingung erfüllt werden: х>к, y(к)>0. Wenn ein< 0 условие: х1>k, x2>k sind durch das Ungleichungssystem bestimmt:

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

Abb.4

Aufgabe 11. Finden Sie alle Werte des Parameters a, für die alle Wurzeln der Gleichung gelten

x2–6ax+2–2a+9a2 = 0 mehr als 3.

Lösung.

Wenn die geforderte Bedingung erfüllt ist, sind folgende Positionen der Parabel möglich, die der Graph der Funktion f(x)= x2–6ax+2–2a+9a2 ist

Abb.5

Lösen wir das Ungleichungssystem:

https://pandia.ru/text/78/525/images/image026_8.jpg" align="left" width="324" height="239 src=">

Es genügt die Bedingung zu erfüllen: y(k)<0, если а >0.Wenn a<0, y(к) > 0.

Reis. 6

Aufgabe 12. Finden Sie alle Werte des Parameters a, für die 1 zwischen den Wurzeln der Gleichung x2–2ax+3–4a+2a2=0 liegt.

Lösung.

Da der führende Koeffizient positiv ist, genügt es, die Bedingung f(1) zu erfüllen<0, где f(х)=х2–2ах+3–4а+2а2

4–6a+2a2<0, 1<а<2.

Antworten: 1<а<2

Aufgabe Nummer 3. Unter welchen Bedingungen liegt genau eine Wurzel der quadratischen Gleichung ax2 + bx + c = 0, die verschiedene Wurzeln hat, auf dem Intervall (k, e)?

Konstruieren wir schematisch Graphen y = ax2 + bx + c gemäß der Bedingung dieses Problems für a > 0.

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

Lösen Sie die Ungleichung: f(1) f(2)<0.

(a2+8a+7)(a2+14a+16)<0

7-√33< а<-7; -7+√33<а<-1.

Antworten: -7-√33< а<-7; -7+√33<а<-1.

Aufgabe 14. Finden Sie alle Werte des Parameters a, für die die Gleichung 2cos(2x)+2asin(x)+a-1=0 eine eindeutige Lösung auf dem Intervall (-π/2;0) hat.

Lösung.

2cos(2x)+2a sinx+a-1=0

2(1–2 sin2х)+ 2a sinx+a–1=0

4 sin2х–2а sinx –a–1=0

Sei sinx=t Da -π/2<х<0, то -1< t <0

Finden Sie die Werte des Parameters a, für die die Gleichung 4t2– 2at–a–1=0 eine eindeutige Lösung im Intervall (-1; 0) hat.

Die Gleichung 4t2– 2at–a–1=0 hat eine eindeutige Lösung auf dem Intervall (-1; 0), wenn:

eines). D \u003d 0 D / 4 \u003d (a + 2) 2 D \u003d 0 für a \u003d -2.

2). Betrachten Sie die Funktion f(t)= 4t2– 2at–a–1

Wir konstruieren einen schematischen Graphen der Funktion y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) f(1) ≤ 0 a ≤ –3; a≥-1

Antworten: a ≤ –3; a ≥ –1; a=-2.

Aufgabe Nummer 4. Unter welchen Bedingungen liegen beide Nullstellen (nicht notwendigerweise verschieden) der quadratischen Gleichung ax2 + bx + c auf der Strecke [k; e]. Betrachten Sie unter der Bedingung a>0. Es gebe eine Funktion f(x)= ax2+bx+c

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110"> D≥0

k ≤ ho ≤ e

Aufgabe 15. Finden Sie die Werte des Parameters a, für die alle Wurzeln der Gleichung gelten

х2- 2(а–3)х–а +3=0 liegen im Intervall (-3; 0).

Lösung.

Vorausgesetzt, dass mindestens eine Wurzel vorhanden ist, kann der Graph der Funktion f (x) \u003d x2- 2 (a-3) x-a + 3 schematisch auf zwei Arten lokalisiert werden

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110"> D≥0 4(à – 3)(à – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5à – 6>0

f(0) >0 - +3>0

Gleichung sin x - 1 + a = sin x - 2 . Sünde x − 2 Sünde x − 3 Lösung. Setzen wir t = sin x, reduzieren wir die Gleichung auf die Form at2 − 5at + 6a − 1 = 0. Wenn a = 0, dann gibt es keine Lösungen. Für a = 0 und unter der Bedingung a ∈ (−∞; −4] ∪ (0; +∞) √ 2 + 4a erhalten wir die Wurzeln der Gleichung t1,2 = 5a ± 2aa . Da der Scheitelpunkt der Parabel f (t) = at2 − 5at + 6a − 1 an der Stelle tв = 2 , 5 liegt, ist die Bedingung |t|1 für die kleinste der Wurzeln erfüllt, wenn die Funktion an den Enden der Strecke [− unterschiedliche Vorzeichen hat 1;1]: f (−1) f (1) 0 oder (2a−1)(12a−1) 0. Die Lösung der letzten 1 Ungleichung ist das Intervall a ∈ 12 ;1 .2 √ a2 Antwort: Wenn a ∈ 12 ;2: x = (−1)n arcsin 5a− 2a +4a +πn, n∈Z, 1 1 es gibt keine Lösungen für andere a. Aufgabe 6.7 Für welche Werte des Parameters a die Funktion f (x) = 8ax − a sin 6x − 7x − sin 5x wächst auf der ganzen reellen Achse und hat keine kritischen Punkte Lösung: Die Funktion f (x) ist differenzierbar für jeden Wert von a und f (x) = 8a − 6a cos 6x − 7 − 5 cos 5x Das Problem kann wie folgt umformuliert werden: für die a die Ungleichung 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. Betrachten wir nun, dass 6a cos 6x + 5 cos 5x 6|a| +5< 8a − 7, приходим к выводу, что при a >6 Die Ungleichung gilt für jedes x. Antwort: a > 6. Probleme zur unabhängigen Lösung Problem 6.8. (SGAU) Löse abhängig von den Werten des Parameters a die Gleichung cos4 x − (a + 2) cos2 x √ a − 3 = 0. − Antwort: Wenn a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, falls a ∈ [−3; −2] : keine Lösungen. Aufgabe 6.9. (SGAU) Löse abhängig von den Werten des Parameters a die Gleichung sin4 x + cos4 x + sin 2x + a = 0. 61 √ Antwort: Wenn a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; 1: keine Lösungen. falls a ∈ − 2 2 k ∈ Z, Aufgabe 6.10. (SGAU) Für welche Werte des Parameters a gilt die Gleichung (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10 =0 Lösungen? Antwort: a< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 gilt für alle Werte von x? Antwort: a ∈ (−∞; −23) ∪ (−10; −9). Aufgabe 6.20. Löse abhängig von den Werten des Parameters a die Ungleichung cos x 2 − a2 . Antwort: |a| √ : x ∈ R, 1 1<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>3: keine Lösungen. k∈Z Problem 6.21. Für welche Werte des Parameters a hat die Gleichung tg x (a + 1) tg2 x − 2 cos x + a = 0 keine Lösungen? Antwort: a -3; a 1. 63 Studienführer PROBLEM MIT PARAMETERN Zusammengestellt von: Efimov Evgeny Alexandrovich Kolomiets Lyudmila Vadimovna Computersatz und Layout E.A. Efimov Samara State Aerospace University, benannt nach Akademiker S.P. Königin. 443086, Samara, Autobahn Moskau, 34. - RIO Samara State Aerospace University, benannt nach Akademiker S.P. Königin. 443086, Samara, Autobahn Moskau, 34.

Ministerium für Bildung und Wissenschaft der Region Samara

Staatliche autonome Bildungseinrichtung für die berufliche Zusatzausbildung (Qualifikationsentwicklung) von Fachkräften

SAMARA REGIONAL INSTITUT FÜR BERUFLICHE ENTWICKLUNG

UND UMSCHULUNG VON PERSONAL IM BILDUNGSWESEN

Abschlussarbeit

Auf Weiterbildungskursen

Laut WB IOCH

"Methodische Merkmale des Unterrichts zur Lösung von Problemen mit einem Parameter im Kontext des Übergangs zu neuen Bildungsstandards"

(15.06 - 19.06.2015)

Entwerfen eines mehrstufigen Aufgabensystems mit einem Themenparameter:

"Derivat"

Aufgeführt:

Valieva F. G.,

Mathematiklehrer

GBOU Sekundarschule ihnen. M.K. Owsjannikowa

Mit. Isakla

Samara

2015

ERLÄUTERUNGEN

Vollständiger Name (vollständiger Name)

Valieva Fanuzya Galimzyanovna

Arbeitsplatz

GBOU Sekundarschule ihnen. M.K. Ovsyannikova Dorf Isakly,

Bezirk Isaklinsky, Region Samara

Berufsbezeichnung

Mathematiklehrer

Thema

Mathe

Klasse

Ziele:

1. Umsetzung der Anforderungen des Landesbildungsstandards GmbH beim Studium des Themas: „Ableitung“

   Verallgemeinerung und Systematisierung von Kenntnissen und Tätigkeitsmethoden zum Thema "Derivative"; Bildung von Fähigkeiten zur Lösung von Problemen mit Parametern.

   Entwicklung von Forschung und kognitiver Aktivität.

Das Konzept der spirituellen und moralischen Entwicklung und Erziehung der Persönlichkeit eines Bürgers Russlandsist die methodische Grundlage für die Entwicklung und Umsetzung des Landesbildungsstandards für die Allgemeinbildung.

Landesbildungsstandard für die allgemeine Grundbildung im Schulfach Mathematik.

Die Norm basiert aufSystemaktivitätsansatz.

Die Norm legt Anforderungen an die Ergebnisse des Masterings durch Studenten des Hauptbildungsprogramms der allgemeinen Grundbildung fest:

persönlich;

Metasubjekt ;

Thema .

Aufgaben:

- lehrreich: den Text der Aufgabe analysieren und verstehen, ein kognitives Ziel selbstständig identifizieren und formulieren, die Bedingung umformulieren, eine logische Argumentationskette aufbauen, die erhaltene Antwort kritisch bewerten, eine Sprachaussage bewusst und willkürlich konstruieren, den effektivsten Lösungsweg wählen Probleme, ein Problem formulieren und formulieren, Hypothesen aufstellen und begründen, semantisches Lesen;

- Entwicklung: Ziele setzen, ihre Aktivitäten in Abhängigkeit von bestimmten Bedingungen planen; Reflexion der Methoden und Bedingungen des Handelns, Kontrolle und Bewertung des Ablaufs und der Ergebnisse der Aktivitäten, Selbstkontrolle,durch Problemlösung, um die kreative und geistige Aktivität der Schüler zu entwickeln, intellektuelle Qualitäten: die Fähigkeit, das Problem zu "sehen", bewertende Handlungen, Unabhängigkeit, Flexibilität des Denkens;

- lehrreich: Sinnesbildung, die Fähigkeit zuzuhören und in einen Dialog einzutreten, sich an einer gemeinsamen Diskussion von Problemen zu beteiligen, Verantwortung und Genauigkeit zu kultivieren.

Aufgaben mit Parametern - dies sind nicht standardmäßige Aufgaben, d.h.ungewöhnlich sowohl in Formulierung und Inhalt als auch in den Lösungsmethoden. Die Rolle eines solchenAufgaben, ihre Bedeutung und Nutzen für die Entwicklung von logischem Denken, Intuition,kreative Fähigkeiten der Studenten, die Bildung ihrer hohen mathematischenKulturen sind sehr groß. Es ist bekannt, dass Erzieher ernsthaft konfrontiert sindmethodische Probleme in der Lehre, um solche Probleme zu lösen, trotz der Anwesenheit,eine ziemlich große Anzahl von Tutorials und Zeitschriftenartikeln. Der Grund dafür liegt auf der Hand: Die Hauptstrategie des mathematischen Unterrichts in der Schule ist die Entwicklung von Fähigkeiten und Fertigkeiten zur Lösung einer bestimmten Reihe von Standardproblemen, von denen die meisten mit der Technik algebraischer Transformationen zusammenhängen. Gleichungen (Ungleichungen) mit Parametern beziehen sich auf eine andere Art von Aufgaben - Aufgaben, für deren Lösung zunächst die Fähigkeit zu - manchmal recht verzweigten - logischen Konstruktionen und Recherchen erforderlich ist.

Das Lösen von Problemen mit Parametern erfordert Recherche, auch wenn dieses Wort in der Problemstellung nicht vorkommt. Die mechanische Anwendung von Formeln reicht nicht aus, es ist notwendig, die Muster zu verstehen, die Fähigkeit, einen bestimmten Fall basierend auf den bekannten allgemeinen Eigenschaften des Objekts zu analysieren, die Konsistenz und Konsistenz in der Lösung, die Fähigkeit, die betrachteten Einzelfälle zu kombinieren zu einem einzigen Ergebnis. Dies liegt an den Schwierigkeiten, die die Schüler haben, solche Probleme zu lösen.

Gegenwärtig ist die Idee, das Lernen zum Lösen von Problemen mit dem Lernen zu deren Gestaltung zu kombinieren, weit verbreitet. Indem wir eine Aufgabe erstellen, verstehen wir den Prozess der Erstellung einer neuen Aufgabe. Die Konstruktion des Problems basiert auf der Fähigkeit, ein quadratisches Trinom zu bilden. In diesem Fall werden verschiedene Techniken verwendet: Analogie, Variation der Koeffizienten eines quadratischen Trinoms, Variation einer neuen Variablen, Variation der Anforderungen von Aufgaben. Komplexere Funktionen können als Koeffizienten und als neue Variable fungieren. Daher können Sie ein solches quadratisches Trinom verwenden, das bei der Organisation der Wiederholung komplexerer Funktionen hilft: exponentiell, logarithmisch, trigonometrisch. Einerseits müssen Sie die Eigenschaften des quadratischen Trinoms kennen, andererseits werden die Eigenschaften der Funktion wiederholt, wodurch eine Kombination des Problems erreicht wird.

Die Auswahl eines Problems mit Parametern zur Vermittlung ihrer Lösung und Gestaltung lässt sich durch folgende Umstände erklären:

beim Lösen von Problemen mit Parametern kommt es zu Wiederholungen und als Ergebnis zu einer tieferen, solideren Assimilation von Programmproblemen;

das Lösen von Problemen mit Parametern erweitert den mathematischen Horizont, gibt neue Ansätze zur Problemlösung;

es gibt eine Entwicklung des mathematischen, logischen Denkens, der Fähigkeit zu analysieren, zu vergleichen, zu verallgemeinern;

Fähigkeiten für die Forschungsarbeit werden erworben;

Unterstützung bei der Prüfungsvorbereitung;

Es bilden sich Persönlichkeitsmerkmale wie Fleiß, Zielstrebigkeit, Ausdauer, Willenskraft, Genauigkeit.

Gebildete UUD im Rahmen des Landesbildungsstandards beim Lösen von Aufgaben mit Parametern:

Phasen der Problemlösung

UUD gebildet

Zustandsanalyse(Einführung von Buchstaben)

• Ziele setzen;

  Hervorheben von Materialinformationen;

  Formulierung des Problems und Vorhersage von Lösungen;

  Abstraktion;

  Analogie;

  Klassifikation (Typologie);

  symbolische Aktionen.

Schematische Erfassung des Problemzustands in Form einer Tabelle, eines Diagramms, einer Grafikmit eingegebenen Buchstaben

• Planung;

  Systematisierung;

  symbolische Handlungen;

  Modellieren.

Erstellen eines Modells(Suche nach einem Analogon, Anziehung eines bekannten Gesetzes aus Mathematik oder Physik)

• Erstellung einer Methode zur Lösung von Zalachi;

  Zustandsanpassung;

  Modellierung in grafischer Form.

Lösen von Gleichungen, Systemen usw.(Suche nach dem Unbekannten)

• Analyse und Identifizierung von wesentlichen Informationen;

  Ableitung von Konsequenzen;

  Aufbau einer Argumentationskette;

  Entwicklung und Prüfung von Hypothesen;

  Modelltransformation.

Modellinterpretation(Verifikation und Bewertung von Lösungen, Wurzeln)

• Analyse;

  Ableitung von Konsequenzen;

  Spezifikation;

  symbolische Aktion (Interpretation).

Lernen(Verallgemeinerung des Problems oder eine Methode zu seiner Lösung für modifizierte Bedingungen, andere Lösungsansätze)

• Analyse;

  Synthese;

  Suche nach Analoga;

  Aufbau einer Argumentationskette;

  die Fähigkeit, Inhalte prägnant zu vermitteln;

  Fertigkeitsdiagramme, Symbole, Modelle;

  Schaffung von Wegen zur Lösung von Problemen suchender, kreativer Natur.

Betrachtung

• Bedeutungsbildung;

  Planung;

  Kontrolle;

  Korrektur;

  Klasse;

  freiwillige Selbstregulierung;

  Bereitschaft zur Selbstentfaltung, zur Selbstbildung;

  die Fähigkeit, die Ziele ihrer Ausbildung unabhängig zu bestimmen;

  sich selbst neue Aufgaben stellen und formulieren;

  die Motive und Interessen ihrer pädagogischen Aktivitäten zu entwickeln.

Mehrstufiges Aufgabensystem

Die Grundlage der auf einem mehrstufigen Aufgabensystem basierenden Lehrmethodik ist die schrittweise Entwicklung der Blöcke ihrer Matrix. Das Hauptmerkmal dieser Technik ist, dass auf jeder Ebene, d.h. Beim Bewältigen der entsprechenden Spalte der Matrix trifft der Schüler jedes Mal auf alle drei Arten von Lernsituationen, die beim Lösen von Problemen auftreten.

Ein mehrstufiges Aufgabensystem für jedes Thema des Kurses wird anhand seiner Matrixdarstellung gebildet, indem eine Rangliste von Grundelementen der Bildungsinhalte und den ihnen entsprechenden Grundaufgaben einerseits und Lernniveaus hervorgehoben wird die wiederum die Fähigkeit widerspiegeln, bekannte, veränderte und unbekannte Aufgaben zu lösen .

Eine solche Matrix des Themenaufgabensystems enthält 3 Zeilen, die drei Arten von Lernsituationen entsprechen, die beim Lösen von Problemen auftreten, undN Spalten, die die Anzahl der grundlegenden Aufgaben des Themas widerspiegeln. Eine solche tabellarische (Matrix-)Darstellung des Aufgabensystems des Themas hilft dabei, auf jeder Ebene seiner mathematischen und tätigkeitsbezogenen (UUD-Bildung) Komponenten eine vollwertige Befüllung durchzuführen und damit umzusetzenKriterien für die Vollständigkeit von Fach und Aktivität (d. h. kognitive UUD) das gebildete System der Bildungsaufgaben. Wenn dabei die Grundaufgaben im System die Rolle einer Art Integratoren der fachlich-inhaltlichen Komponente spielen, dann sollten bei der Gestaltung und Umsetzung des Lernprozesses universelle Lernaktivitäten (allgemeine Methoden u Handlungstechniken) in ausgewählten Situationen.

Die pädagogische Aktivität zur Lösung von Problemen, die in der ersten Zeile der Matrix enthalten sind, ist reproduktiver Natur (wie allgemeine pädagogische Maßnahmen wie Klassifizierung, Zusammenfassung unter einem Konzept, Ableitung von Konsequenzen, Handlungen, Aufbau einer logischen Argumentationskette, Beweis usw. ) werden verwendet. Die damit verbundenen Aufgaben sind unterschiedlich.explizite Verbindungen zwischen den Daten und den erforderlichen (bekannten und unbekannten) Elementen. Der Schüler identifiziert (erkennt vertraute Aufgaben in einer Reihe ähnlicher), reproduziert die erlernten Methoden oder Handlungsalgorithmen, wendet das erworbene Wissen in praktischer Hinsicht auf eine bekannte Klasse von Aufgaben an und erhält neue Informationen basierend auf der Anwendung des erlernten Aktivitätsmusters .

Beim Lösen von Aufgaben der zweiten Linie wird reproduktive Lernaktivität mit rekonstruktiver Aktivität kombiniert, bei der Aktivitätsmuster nicht einfach aus dem Gedächtnis reproduziert, sondern unter etwas modifizierten Bedingungen rekonstruiert werden (hier solche allgemeinbildenden Handlungen wie die Auswahl und Formulierung einer kognitives Ziel, die Suche und Auswahl der notwendigen Informationen, symbolische symbolische Handlungen, einschließlich mathematischer Modellierung, Wissensstrukturierung).

Schließlich ist die pädagogische Tätigkeit bei der Lösung von Problemen der dritten Linie forschungsschöpferischer Natur. Der Student muss in der Lage sein, sich in neuen Situationen zurechtzufinden und grundlegend neue Handlungsprogramme zu entwickeln (eine Hypothese aufstellen, überprüfen: begründen oder widerlegen, eine neue aufstellen usw., Forschungsaktivitäten durchführen). Die Lösung der Probleme des entsprechenden Blocks erfordert vom Studierenden einen umfangreichen Fundus an erprobten und schnell einsetzbaren Algorithmen; die Fähigkeit, Informationen schnell von einer zeichensymbolischen in eine grafische und umgekehrt von einer grafischen in eine zeichensymbolische Form umzukodieren; systemische Vision des Kurses. Dabei geht es nicht nur um den Einsatz alter Algorithmen unter neuen Bedingungen und eine Erhöhung der technischen Komplexität, sondern zeichnet sich durch die Nichtoffensichtlichkeit der Anwendung und Kombination der untersuchten Algorithmen aus. Die Aufgaben dieser Stufe haben eine komplizierte logische Struktur und zeichnen sich durch Präsenz auslatente Verbindungen zwischen den Daten und den gesuchten Elementen. Solche Aufgaben werden in der Regel als die schwierigsten bei Aufnahmeprüfungen an Hochschulen mit hohen Anforderungen an die mathematische Vorbereitung der Bewerber und in den Aufgaben 17, 18, 20, 21 des KIM USE angeboten.

Mehrstufiges Aufgabensystem zum Thema „Derivat“

№ Art.-Nr

Aufgabennname

Aufgabentyp

Ableitungsrechnung per Definition.

33

MOH

Neuseeland

Finden von Ableitungen von Summen, Produkten, privaten Funktionen

33

MOH

Neuseeland

Untersuchung der Monotonie einer Funktion

33

Funktion steigt entlang der ganzen Zahlengeraden?

MOH

Bei welchen Werten des Parameters Funktion fallend für alle Werte ?

Neuseeland

Finden Sie die Menge aller Zahlen a, für die jeweils die Funktionf(x) = Sünde 2 x – 8(a + 1) Sünde + (4 a 2 + 8 a – 14) xnimmt auf der gesamten reellen Linie zu und hat keine kritischen Punkte.

Extrempunkte finden

33

hat einen Fixpunkt?

MOH

Bestimmen Sie, bei welchem ​​Wert der Parameter Funktion maximal ist 9

Neuseeland

Für welche Werte des Parameters a die Funktionf(x) = (a 2 – 3 a + 2) (cos 2 – Sünde 2 + (a – 1) x + Sünde1 hat keine kritischen Punkte?

Finden der größten und kleinsten Werte einer stetigen Funktion auf einem Intervall und differenzierbar auf einem Intervall

33

Finden Sie heraus, für welche Werte der Parametera kleinster Funktionswertj = x 2 -12 x + a auf dem Segment ist Null.

MOH

Bei welchem ​​Wert des Parameters kleinster Funktionswert gleich

Neuseeland

Bei welchen Werten des Parameters Funktion nimmt für alle Werte kleiner als 5 an

Komplette Erkundung und Plotten

33

3+3x2

MOH

Bei welchem ​​Wert des Parameters a ist das Minimum der Funktion f(x) = ax 2 - 6ax + a 2 - 9 ist gleich 1?

Neuseeland

Die Gleichung der Tangente an den Graphen einer Funktion an einem bestimmten Punkt

33

Bei welchen Werten des Parameters gerade tangiert den Funktionsgraphen ?

MOH

Bei welchen Werten des Parameters Tangente an den Funktionsgraphen schneidet vom ersten Viertel ein gleichschenkliges Dreieck mit Fläche ab

Neuseeland

Bei welchen Werten des Parameters Tangente an den Graphen der Funktion an den Schnittpunkten mit der Achse gezeichnet, bilden einen Winkel

Anwendung der Ableitung zur Lösung von Problemen in Geometrie, Physik und Wirtschaft

33

Was sollten die Seiten eines Rechtecks ​​​​mit einem Umfang sein?Pseine Fläche zu maximieren?

MOH

Das Fenster hat die Form eines Rechtecks, das oben von einem Halbkreis begrenzt wird (Abbildung 3). Der Umfang des Fensters ist P. Bestimmen Sie den Radius des Halbkreises R, bei dem die Fläche des Fensters am größten ist.

Neuseeland

Ein Bild der Höhe a wird so an die Wand gehängt, dass seine Unterkante h Einheiten über der Augenhöhe des Betrachters liegt. In welchem ​​Abstand x zur Wand sollte sich der Betrachter befinden, damit der Blickwinkel auf das Gemälde am größten ist (Abbildung 7a)?

Lösungen

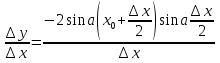
Lösung :

1. Die Funktion f(x) nimmt für alle Werte von x ab, wenn die Ableitung

f′(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

für alle x.

2. Daher finden wir, dass a< 0.

3 . Antwort: a (–∞; 0).

1. Finden Sie die Menge aller Zahlen a, für die jeweils die Funktion f (x) \u003d sin 2x - 8 (a + 1) sinx + (4a 2 + 8a - 14) x auf der gesamten reellen Linie zunimmt und nicht kritische Punkte haben.

1. Für jedes feste a ist diese Funktion an jedem Punkt der reellen Geraden differenzierbar.

2. Da die Funktion f(x) wächst, muss an jedem Punkt x die Ungleichung f′(x) ≥ 0 gelten.

3. Da außerdem f(x) keine kritischen Punkte hat, muss für jedes x die Ungleichung f′(x) ≠ 0 gelten.

4. Wenn also die Funktion die Bedingung des Problems erfüllt, dann muss für alle x die Ungleichung f (x) > 0 erfüllt sein.

5. Gilt dagegen die Ungleichung f′(x) > 0 für alle x, so hat die Funktion offensichtlich keine kritischen Stellen und wächst.

6. Finden Sie die Ableitung dieser Funktion:

f′( x) = 2 cos 2 x – 8( a + 1) cos + 4 a 2 + 8 a – 14.

Nun kann das Problem wie folgt umformuliert werden: Finden Sie alle Werte des Parameters a, für die jeweils, für jedes x, die Ungleichung

cos 2x – 4(a + 1) cos x + 2a 2 + 4a – 7 > 0.(1)

7. Angenommen, cos 2x = 2 cos 2 x – 1, und setzen wir cos x = t, wobei –1 ≤ t ≤ 1, schreiben wir die Ungleichung (1) wie folgt um:

2t 2 – 1 – 4(a + 1)t + 2a 2 + 4a – 7 > 0,

oder

t 2 – 2(a + 1)t + a 2 + 2a – 4 > 0. (2)

8. Indem wir die Funktion auf der linken Seite der Ungleichung (2) mit ϕ(t) bezeichnen, geben wir eine neue Formulierung des ursprünglichen Problems: Finden Sie alle Werte von a, für die jeweils der kleinste Wert der Funktion ϕ( t) auf dem Intervall [–1; 1] ist positiv.

9. Die Ableitung ϕ′(t) = 2t – 2(a + 1) verschwindet bei t 0 = ein + 1.

10. Der kleinste Wert der Funktion ϕ(t) auf dem Intervall [–1; 1] ist:

ϕ (–1) = ein 2 + 4a – 1,wenna + 1 ≤ –1;

ϕ (a + 1) = -5,wenn –1 < a + 1 < 1;

ϕ(1) = a 2 – 5, wenn a + 1 ≥ 1.

11. Da der kleinste Wert der Funktion ϕ(t) auf der Strecke [–1; 1] positiv sein muss, dann gehören die Werte des Parameters a, die die Bedingung des Problems erfüllen, zu zwei Intervallen: a ≤ –2 und a ≥ 0.

12. Wenn a ≤ –2, dann erfüllen die gewünschten Werte des Parameters a die Ungleichung a 2 + 4a – 1 > 0.

13. Wenn a ≥ 0, dann erfüllen die gewünschten Werte des Parameters a die Ungleichung a 2 – 5 > 0.

14. Folglich ist die Menge der gewünschten Werte a die Vereinigung von Lösungen zweier Ungleichungssysteme:

(3)

a ≥ 0

a 2 -5 > 0 (4)

15. Die Lösungsmenge von System (3) ist das Intervall –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

16. Antwort: a (–∞; –2 –√5) (√5; +∞).

1. Da diese Funktion auf der ganzen reellen Geraden differenzierbar ist, sind die kritischen Punkte der Funktion f(x) diejenigen Punkte, an denen die Ableitung f′(x) = 0 ist.

2. In diesem Fall gilt f (x) =(a – 1)(a – 2) (–sünde+ (a – 1).

3. Wenn a = 1 ist, dann ist offensichtlich f (x) = 0 für jedes x R, d.h.

für eine gegebene Funktion jeder Punkt x R ist kritisch.

4. Nehmen Sie an, dass a 1. Dann nimmt die Gleichung f (x) = 0 die Form an

(a - 2) Sünde = 2. (1)

Daraus folgt, dass wenn |a – 2|< 2, т. е. если a (0; 1) (1; 4),

dann hat Gleichung (1) keine Wurzeln und daher hat die Funktion f(x) für die angegebenen Werte von a keine kritischen Punkte.

5 . Antworten: a (0; 1) (1; 4).

Der kleinste Wert des Zählers und der größte Wert des Nenners werden bei unterschiedlichen Werten von x erreicht. Um den kleinsten Wert einer Funktion zu finden, ist es daher praktisch, die Ableitung zu verwenden. Schreiben wir die Ungleichung in die Form um

Wot=3- cos 2 x, t

Finden Sie den kleinsten Wert der Funktionf( t) = , auf dem Segment. Da die Ableitungf "( t) = negativ beitdannfnimmt ab und nimmt den kleinsten Wert ant=3, f Name = f(3) = .

Antworten:a

Was ist das kleinste natürliche k, für das die Gleichung x 3+3x2 – 45x + k = 0 genau eine Wurzel hat?

1. Konstruieren Sie eine Skizze des Graphen der Funktion y 1 = x 3 + 3x 2 – 45x und bestimme den kleinsten natürlichen Wert von k, für den dieser Graph die Gerade y schneidet 2 = –k an genau einer Stelle.

2. a) D(j 1 ) = R;

Buh 1 / = 3x 2 + 6x - 45; 1 / in den Intervallen (–∞; –5), (–5; 3) und (3; +∞) ist in Abb. 1. In Abb. 2 ist eine schematische Darstellung des Graphen der Funktion y 1 .

3. Offensichtlich hat diese Gleichung eine eindeutige Lösung, wenn –k > 175 oder –k< –81, т. е. k < –175 или k >81. Der kleinste natürliche Wert von k ist 82.

4. Antwort: k = 82.

Bei welchem ​​Wert des Parameters a ist das Minimum der Funktion f(x) = ax2 – 6ax + a2 – 9 gleich 1?

1. f′(x) = –6x 2 + 6x + 12.

2. y′ = 0 für x 1 = 2.

6. Antwort: a = 2.

Bei welchem ​​Wert des Parameters a ist das Minimum der Funktion f(x) = –2x 3 + 3x 2 + 12x + 4a ist 1?

Für welche Werte des Parameters a tangiert die Linie y=ax-2 den Graphen der Funktion y=1+ln⁡ x?

Bei welchen Werten des Parameters a schneidet die Tangente an den Graphen der Funktion y=a-x^2 ein gleichschenkliges Dreieck mit einer Fläche von 9/32 vom ersten Viertel ab

als , muss die Tangente die Funktion in schneidenViertel bedeutet. Ein gleichschenkliges Dreieck ist ein rechtwinkliges Dreieck, also sind die anderen Winkel gleich, aberwoher die Tangente die Form annimmt der Berührungspunkt der Tangente mit dem Graphen entlang der x-Achse ist gleich . nach der Formel Tangente an den Graphen da sollte die Fläche ein Dreieck sein , dann als Quartal.Wo

Bei welchen Werten des Parameters a bilden die Tangenten an den Graphen der Funktion y=4x^2-|a|x, gezeichnet an den Schnittpunkten mit der x-Achse, einen Winkel von 60° zwischen sich

Wie groß müssen die Seiten eines Rechtecks ​​mit dem Umfang P sein, damit seine Fläche maximal wird?

Das Fenster hat die Form eines Rechtecks, das oben von einem Halbkreis begrenzt wird (Abbildung 3). Der Umfang des Fensters ist P. Bestimmen Sie den Radius des Halbkreises R, bei dem die Fläche des Fensters am größten ist.

Ein Bild der Höhe a wird so an die Wand gehängt, dass seine Unterkante h Einheiten über der Augenhöhe des Betrachters liegt. In welchem ​​Abstand x zur Wand sollte sich der Betrachter befinden, damit der Blickwinkel auf das Gemälde am größten ist (Abbildung 7a)?

Literatur

Azarov A.I., Barvenov S.A., Fedosenko V.S.Methoden zur Lösung von Problemen mit Parametern. Mathematik für Gymnasiasten. Minsk: "Aversev", 2003.

VS. Vysotsky, Aufgaben mit Parametern zur Vorbereitung auf die Prüfung

Gorshtein P.I., Polonsky V.B., Yakir M.S. Aufgaben mit Parametern. - K.: RIA "Text"; MP "OKO", 1992. -290 p.

Kachalova G. A. Zur Notwendigkeit, die inhaltlich-methodische Linie "Probleme mit Parametern" in das Bildungsmodul "Grundlagen der Mathematik" aufzunehmen //Angelegenheitł yMię dzynarodowej Naukowi- PraktycznejkonferencjiPostę pó wwnauce. Nowepoglą dy, problematisch, innowacje. 29.07.2012. - 31.07.2012. część 2. - Łodź, 2012. - S. 67–70.

Kozko A. I., Panferov V. S., Sergeev I. N., Chirsky V. G. USE 2011. Mathematik. Aufgabe C5. Aufgaben mit Parameter / Ed. A. L. Semenova und I. V. Yashchenko. - M.: MTsNMO, 2011.-144 p.

Rodionov E. M. Probleme mit Parametern lösen. M.: MP "Rus-90", 1995