Es wird auch Aufgaben für eine eigenständige Lösung geben, zu denen Sie die Antworten sehen können.

Vektorkonzept

Bevor Sie alles über Vektoren und Operationen mit ihnen lernen, schalten Sie ein, um ein einfaches Problem zu lösen. Es gibt einen Vektor Ihres Unternehmens und einen Vektor Ihrer Innovationsfähigkeiten. Der Vektor des Unternehmertums führt Sie zu Ziel 1 und der Vektor der innovativen Fähigkeiten zu Ziel 2. Die Spielregeln sind so, dass Sie sich nicht gleichzeitig in die Richtungen dieser beiden Vektoren bewegen und zwei Ziele gleichzeitig erreichen können. Vektoren interagieren, oder, mathematisch gesprochen, wird eine Operation an Vektoren durchgeführt. Das Ergebnis dieser Operation ist der „Ergebnis“-Vektor, der Sie zu Ziel 3 führt.

Sagen Sie mir jetzt: Das Ergebnis welcher Operation auf den Vektoren "Unternehmen" und "Innovative Fähigkeiten" ist der Vektor "Ergebnis"? Wenn Sie es nicht sofort sagen können, lassen Sie sich nicht entmutigen. Während Sie diese Lektion studieren, werden Sie in der Lage sein, diese Frage zu beantworten.

Wie wir oben gesehen haben, kommt der Vektor zwangsläufig irgendwann EIN in einer geraden Linie bis zu einem gewissen Punkt B. Folglich hat jeder Vektor nicht nur einen Zahlenwert – Länge, sondern auch eine physikalische und geometrische – Richtung. Daraus leitet sich die erste, einfachste Definition eines Vektors ab. Ein Vektor ist also eine gerichtete Strecke, die von einem Punkt ausgeht EIN auf den Punkt B. Es ist so gekennzeichnet:

Und anders anfangen Vektoroperationen , müssen wir uns mit einer weiteren Definition eines Vektors vertraut machen.

Ein Vektor ist eine Art Darstellung eines Punktes, der von einem Ausgangspunkt aus erreicht werden soll. Beispielsweise wird ein dreidimensionaler Vektor normalerweise geschrieben als (x, y, z) . Ganz einfach, diese Zahlen bedeuten, wie weit Sie in drei verschiedene Richtungen gehen müssen, um auf den Punkt zu kommen.

Gegeben sei ein Vektor. Dabei x = 3 (rechte Hand zeigt nach rechts) j = 1 (linke Hand zeigt nach vorne) z = 5 (Unter dem Punkt führt eine Leiter nach oben). Ausgehend von diesen Daten finden Sie den Punkt, indem Sie 3 Meter in die von der rechten Hand angegebene Richtung gehen, dann 1 Meter in die von der linken Hand angegebene Richtung, und dann erwartet Sie eine Leiter, und wenn Sie 5 Meter klettern, werden Sie schließlich finden selbst am Endpunkt.

Alle anderen Begriffe sind Verfeinerungen der oben gegebenen Erklärung, die für verschiedene Operationen an Vektoren notwendig sind, dh zum Lösen praktischer Probleme. Gehen wir diese strengeren Definitionen durch und verweilen bei typischen Vektorproblemen.

Physikalische Beispiele Vektorgrößen können die Verschiebung eines sich im Raum bewegenden materiellen Punktes, die Geschwindigkeit und Beschleunigung dieses Punktes sowie die auf ihn wirkende Kraft sein.

geometrischer Vektor im zweidimensionalen und dreidimensionalen Raum in der Form dargestellt gerichtetes Segment. Dies ist ein Abschnitt, der einen Anfang und ein Ende hat.

Wenn ein EIN ist der Anfang des Vektors, und B ist sein Ende, dann wird der Vektor durch das Symbol oder einen einzelnen Kleinbuchstaben gekennzeichnet. In der Abbildung ist das Ende des Vektors durch einen Pfeil gekennzeichnet (Abb. 1)

Länge(oder Modul) eines geometrischen Vektors ist die Länge des Segments, das ihn erzeugt

Die beiden Vektoren werden aufgerufen gleich , wenn sie (wenn die Richtungen übereinstimmen) durch Paralleltranslation kombiniert werden können, d.h. wenn sie parallel sind, zeigen sie in die gleiche Richtung und sind gleich lang.

In der Physik wird es oft betrachtet gepinnte Vektoren, gegeben durch Angriffspunkt, Länge und Richtung. Wenn der Angriffspunkt des Vektors keine Rolle spielt, kann er unter Beibehaltung der Länge und Richtung auf einen beliebigen Punkt im Raum übertragen werden. In diesem Fall wird der Vektor aufgerufen frei. Wir vereinbaren, nur zu prüfen freie Vektoren.

Lineare Operationen auf geometrischen Vektoren

Multipliziere einen Vektor mit einer Zahl

Vektorprodukt pro Zahl Ein Vektor wird als Vektor bezeichnet, der aus einem Vektor durch Strecken (bei ) oder Schrumpfen (bei ) mal erhalten wird, und die Richtung des Vektors bleibt erhalten, wenn , und umgekehrt, wenn . (Abb. 2)

Aus der Definition folgt, dass die Vektoren und = immer auf einer oder parallelen Geraden liegen. Solche Vektoren werden genannt kollinear. (Man kann auch sagen, dass diese Vektoren parallel sind, aber in der Vektoralgebra ist es üblich, „kollinear“ zu sagen.) Das Umgekehrte gilt auch: Wenn die Vektoren und kollinear sind, dann sind sie durch die Beziehung miteinander verbunden

Daher drückt Gleichheit (1) die Bedingung der Kollinearität zweier Vektoren aus.

Vektoraddition und -subtraktion

Wenn Sie Vektoren hinzufügen, müssen Sie das wissen Summe Vektoren und wird als Vektor bezeichnet, dessen Anfang mit dem Anfang des Vektors und dessen Ende mit dem Ende des Vektors zusammenfällt, vorausgesetzt, dass der Anfang des Vektors an das Ende des Vektors angehängt ist. (Abb. 3)

Diese Definition kann auf beliebig viele Vektoren verteilt werden. Lassen Sie Platz gegeben n freie Vektoren. Beim Addieren mehrerer Vektoren wird ihre Summe als Schlussvektor genommen, dessen Anfang mit dem Anfang des ersten Vektors und dessen Ende mit dem Ende des letzten Vektors zusammenfällt. Das heißt, wenn der Anfang des Vektors an das Ende des Vektors angehängt wird und der Anfang des Vektors an das Ende des Vektors usw. und schließlich bis zum Ende des Vektors - dem Anfang des Vektors, dann ist die Summe dieser Vektoren der schließende Vektor , dessen Anfang mit dem Anfang des ersten Vektors zusammenfällt und dessen Ende mit dem Ende des letzten Vektors zusammenfällt . (Abb. 4)

Die Terme heißen die Komponenten des Vektors, und die formulierte Regel ist es Polygonregel. Dieses Polygon darf nicht flach sein.

Wenn ein Vektor mit der Zahl -1 multipliziert wird, erhält man den entgegengesetzten Vektor. Die Vektoren und haben die gleiche Länge und entgegengesetzte Richtungen. Ihre Summe ergibt Nullvektor, deren Länge Null ist. Die Richtung des Nullvektors ist nicht definiert.

In der Vektoralgebra muss die Operation der Subtraktion nicht gesondert betrachtet werden: Einen Vektor von einem Vektor subtrahieren bedeutet, den entgegengesetzten Vektor zu dem Vektor zu addieren, d.h.

Beispiel 1 Den Ausdruck vereinfachen:

.

,

h., Vektoren lassen sich wie Polynome addieren und mit Zahlen multiplizieren (insbesondere auch Probleme zum Vereinfachen von Ausdrücken). Normalerweise entsteht die Notwendigkeit, linear ähnliche Ausdrücke mit Vektoren zu vereinfachen, bevor die Produkte von Vektoren berechnet werden.

Beispiel 2 Die Vektoren und dienen als Diagonalen des Parallelogramms ABCD (Abb. 4a). Drücken Sie in Form von und die Vektoren , , und aus, die die Seiten dieses Parallelogramms sind.

Lösung. Der Schnittpunkt der Diagonalen eines Parallelogramms halbiert jede Diagonale. Die Längen der in der Aufgabenstellung benötigten Vektoren ergeben sich entweder als halbe Summen der Vektoren, die mit den gesuchten ein Dreieck bilden, oder als halbe Differenzen (je nach Richtung des als Diagonale dienenden Vektors), oder, wie im letzteren Fall, die Hälfte der Summe mit einem Minuszeichen. Das Ergebnis sind die in der Bedingung des Problems erforderlichen Vektoren:

Es gibt allen Grund zu der Annahme, dass Sie die Frage zu den Vektoren „Unternehmen“ und „Innovationsfähigkeiten“ zu Beginn dieser Lektion jetzt richtig beantwortet haben. Richtige Antwort: Diese Vektoren werden einer Additionsoperation unterzogen.

Lösen Sie selbst Probleme mit Vektoren und schauen Sie sich dann die Lösungen an

Wie findet man die Länge der Summe von Vektoren?

Dieses Problem nimmt bei Operationen mit Vektoren einen besonderen Platz ein, da es um die Verwendung trigonometrischer Eigenschaften geht. Angenommen, Sie haben eine Aufgabe wie die folgende:

Angesichts der Länge von Vektoren und die Länge der Summe dieser Vektoren. Finden Sie die Länge der Differenz dieser Vektoren.

Lösungen für dieses und andere ähnliche Probleme und Erklärungen zu deren Lösung - in der Lektion " Vektoraddition: die Länge der Summe von Vektoren und der Kosinussatz ".

Und Sie können die Lösung solcher Probleme auf überprüfen Online-Rechner "Unbekannte Seite eines Dreiecks (Vektoraddition und Kosinussatz)" .

Wo sind die Produkte von Vektoren?

Die Produkte eines Vektors mit einem Vektor sind keine linearen Operationen und werden separat betrachtet. Und wir haben Lektionen „Punktprodukt von Vektoren“ und „Vektor- und gemischte Produkte von Vektoren“.

Projektion eines Vektors auf eine Achse

Die Projektion eines Vektors auf eine Achse ist gleich dem Produkt aus der Länge des projizierten Vektors und dem Kosinus des Winkels zwischen dem Vektor und der Achse:

Bekanntlich ist die Projektion ein Punkt EIN auf der Linie (Ebene) ist die Basis der von diesem Punkt auf die Linie (Ebene) fallenden Senkrechten.

Lassen Sie - einen beliebigen Vektor (Abb. 5) und und - Projektionen seines Anfangs (Punkte EIN) und Ende (Punkte B) pro Achse l. (Um die Projektion eines Punktes zu erstellen EIN) gerade durch den Punkt ziehen EIN Ebene senkrecht zur Linie. Der Schnittpunkt einer Linie und einer Ebene bestimmt die erforderliche Projektion.

Komponente des Vektors auf der l-Achse nannte einen solchen Vektor, der auf dieser Achse liegt, dessen Anfang mit der Projektion des Anfangs und dessen Ende zusammenfällt - mit der Projektion des Endes des Vektors .

Die Projektion des Vektors auf die Achse l eine Nummer angerufen

,

gleich der Länge des Komponentenvektors auf dieser Achse, mit Pluszeichen genommen, wenn die Richtung der Komponente mit der Richtung der Achse übereinstimmt l, und mit einem Minuszeichen, wenn diese Richtungen entgegengesetzt sind.

Die Haupteigenschaften von Vektorprojektionen auf der Achse:

1. Die Projektionen gleicher Vektoren auf dieselbe Achse sind einander gleich.

2. Wenn ein Vektor mit einer Zahl multipliziert wird, wird seine Projektion mit derselben Zahl multipliziert.

3. Die Projektion der Summe der Vektoren auf eine beliebige Achse ist gleich der Summe der Projektionen der Terme der Vektoren auf dieselbe Achse.

4. Die Projektion eines Vektors auf eine Achse ist gleich dem Produkt aus der Länge des projizierten Vektors und dem Kosinus des Winkels zwischen dem Vektor und der Achse:

.

Lösung. Lassen Sie uns die Vektoren auf die Achse projizieren l wie in der theoretischen Referenz oben definiert. Aus Abb. 5a ist ersichtlich, dass die Projektion der Summe der Vektoren gleich der Summe der Projektionen der Vektoren ist. Wir berechnen diese Projektionen:

Wir finden die endgültige Projektion der Summe der Vektoren:

Zusammenhang eines Vektors mit einem rechtwinkligen kartesischen Koordinatensystem im Raum

Bekanntschaft mit rechtwinkliges kartesisches Koordinatensystem im Raum fand in der entsprechenden Lektion statt, am besten in einem neuen Fenster öffnen.

In einem geordneten System von Koordinatenachsen 0xyz Achse Ochse genannt x-Achse, Achse 0j – y-Achse, und Achse 0z – Achse anwenden.

mit beliebigem Punkt M Raumbindungsvektor

genannt Radius-Vektor Punkte M und projizieren Sie es auf jede der Koordinatenachsen. Lassen Sie uns die Werte der entsprechenden Projektionen bezeichnen:

Zahlen x, y, z genannt Koordinaten des Punktes M, beziehungsweise Abszisse, Ordinate und Applikationen, und werden als geordneter Zahlenpunkt geschrieben: M(x;y;z)(Abb. 6).

Ein Vektor der Einheitslänge, dessen Richtung mit der Richtung der Achse zusammenfällt, wird genannt Einheitsvektor(oder ortom) Achsen. Bezeichne mit

Dementsprechend sind die Einheitsvektoren der Koordinatenachsen Ochse, Ey, Unze

Satz. Jeder Vektor kann in die Einheitsvektoren der Koordinatenachsen zerlegt werden:

(2)

Gleichung (2) wird als Erweiterung des Vektors entlang der Koordinatenachsen bezeichnet. Die Koeffizienten dieser Entwicklung sind die Projektionen des Vektors auf die Koordinatenachsen. Somit sind die Ausdehnungskoeffizienten (2) des Vektors entlang der Koordinatenachsen die Koordinaten des Vektors.

Nach der Wahl eines bestimmten Koordinatensystems im Raum bestimmen sich der Vektor und das Tripel seiner Koordinaten eindeutig, sodass der Vektor in der Form geschrieben werden kann

Die Vektordarstellungen in der Form (2) und (3) sind identisch.

Der Zustand kollinearer Vektoren in Koordinaten

Wie wir bereits bemerkt haben, heißen Vektoren kollinear, wenn sie durch die Relation in Beziehung stehen

Vektoren lassen . Diese Vektoren sind kollinear, wenn die Koordinaten der Vektoren durch die Beziehung in Beziehung stehen

,

das heißt, die Koordinaten der Vektoren sind proportional.

Beispiel 6 Gegebene Vektoren . Sind diese Vektoren kollinear?

Lösung. Lassen Sie uns das Verhältnis der Koordinaten dieser Vektoren herausfinden:

.

Die Koordinaten der Vektoren sind proportional, daher sind die Vektoren kollinear oder, was dasselbe ist, parallel.

Vektorlängen- und Richtungskosinus

Aufgrund der gegenseitigen Rechtwinkligkeit der Koordinatenachsen ist die Länge des Vektors

ist gleich der Länge der Diagonalen eines rechteckigen Parallelepipeds, das auf den Vektoren aufgebaut ist

und wird durch die Gleichheit ausgedrückt

(4)

Ein Vektor wird vollständig definiert, indem zwei Punkte (Anfang und Ende) angegeben werden, sodass die Koordinaten des Vektors durch die Koordinaten dieser Punkte ausgedrückt werden können.

Der Anfang des Vektors im gegebenen Koordinatensystem sei der Punkt

und das ende ist an der stelle

Von der Gleichberechtigung

Folgt dem

oder in Koordinatenform

Folglich, die Koordinaten des Vektors sind gleich den Differenzen der gleichnamigen Koordinaten von Ende und Anfang des Vektors . Formel (4) nimmt in diesem Fall die Form an

Die Richtung des Vektors wird bestimmt Richtung Kosinus . Dies sind die Kosinuswerte der Winkel, die der Vektor mit den Achsen bildet Ochse, Ey und Unze. Lassen Sie uns diese Winkel entsprechend bezeichnen α , β und γ . Dann können die Kosinusse dieser Winkel durch die Formeln gefunden werden

Die Richtungskosinusse eines Vektors sind auch die Koordinaten des Vektors des Vektors und damit des Vektors des Vektors

.

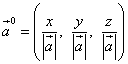
Wenn man bedenkt, dass die Länge des Vektors vektor gleich einer Einheit ist, d. h.

,

erhalten wir die folgende Gleichheit für die Richtungskosinusse:

Beispiel 7 Finde die Länge eines Vektors x = (3; 0; 4).

Lösung. Die Länge des Vektors ist

Beispiel 8 Gegebene Punkte:

Finden Sie heraus, ob das auf diesen Punkten aufgebaute Dreieck gleichschenklig ist.

Lösung. Unter Verwendung der Vektorlängenformel (6) finden wir die Längen der Seiten und finden heraus, ob zwei von ihnen gleich sind:

Es wurden zwei gleiche Seiten gefunden, so dass es nicht nötig ist, nach der Länge der dritten Seite zu suchen, und das gegebene Dreieck ist gleichschenklig.

Beispiel 9 Finden Sie die Länge eines Vektors und seine Richtungskosinusse, wenn .

Lösung. Die Vektorkoordinaten sind gegeben:

.

Die Länge des Vektors ist gleich der Quadratwurzel der Summe der Quadrate der Koordinaten des Vektors:

.

Richtungskosinus finden:

Lösen Sie das Problem mit Vektoren selbst und sehen Sie sich dann die Lösung an

Operationen auf Vektoren in Koordinatenform

Gegeben seien zwei Vektoren und gegeben durch ihre Projektionen:

Lassen Sie uns Aktionen auf diesen Vektoren angeben.

Seite 1 von 2

Frage 1. Was ist ein Vektor? Wie sind Vektoren definiert?
Antworten. Wir nennen ein gerichtetes Segment einen Vektor (Abb. 211). Die Richtung eines Vektors wird durch Angabe seines Anfangs und Endes bestimmt. In der Zeichnung ist die Richtung des Vektors mit einem Pfeil gekennzeichnet. Um Vektoren zu bezeichnen, verwenden wir lateinische Kleinbuchstaben a, b, c, ... . Sie können einen Vektor auch bestimmen, indem Sie seinen Anfang und sein Ende angeben. In diesem Fall wird der Anfang des Vektors an die erste Stelle gesetzt. Anstelle des Wortes "Vektor" wird manchmal ein Pfeil oder ein Strich über der Buchstabenbezeichnung des Vektors platziert. Der Vektor in Abbildung 211 kann wie folgt bezeichnet werden:

\(\overline(a)\), \(\overrightarrow(a)\) oder \(\overline(AB)\), \(\overrightarrow(AB)\).

Frage 2. Welche Vektoren heißen gleichgerichtet (entgegengesetzt gerichtet)?
Antworten. Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) heißen gleich gerichtet, wenn die Halbgeraden AB und CD gleich gerichtet sind.
Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) heißen entgegengesetzt gerichtet, wenn die Halbgeraden AB und CD entgegengesetzt gerichtet sind.
In Abbildung 212 haben die Vektoren \(\overline(a)\) und \(\overline(b)\) dieselbe Richtung, während die Vektoren \(\overline(a)\) und \(\overline(c) \) haben entgegengesetzte Richtungen.

Frage 3. Was ist der Betrag eines Vektors?
Antworten. Der absolute Wert (oder Modul) eines Vektors ist die Länge des Segments, das den Vektor darstellt. Der Betrag des Vektors \(\overline(a)\) wird mit |\(\overline(a)\)| bezeichnet.

Frage 4. Was ist ein Nullvektor?
Antworten. Der Anfang eines Vektors kann mit seinem Ende zusammenfallen. Ein solcher Vektor wird als Nullvektor bezeichnet. Der Nullvektor wird durch Null mit Bindestrich (\(\overline(0)\)) bezeichnet. Niemand spricht über die Richtung des Nullvektors. Der Absolutwert des Nullvektors wird als gleich Null betrachtet.

Frage 5. Welche Vektoren heißen gleich?
Antworten. Zwei Vektoren heißen gleich, wenn sie durch Paralleltranslation kombiniert werden. Dies bedeutet, dass es eine parallele Übersetzung gibt, die den Anfang und das Ende eines Vektors jeweils in den Anfang und das Ende eines anderen Vektors übersetzt.

Frage 6. Beweisen Sie, dass gleiche Vektoren die gleiche Richtung haben und betragsmäßig gleich sind. Und umgekehrt: Gleich gerichtete und betragsmäßig gleiche Vektoren sind gleich.
Antworten. Bei der Parallelverschiebung behält der Vektor seine Richtung sowie seinen Absolutwert. Das bedeutet, dass gleiche Vektoren die gleiche Richtung haben und betragsmäßig gleich sind.
Seien \(\overline(AB)\) und \(\overline(CD)\) gleichgerichtete, betragsgleiche Vektoren (Abb. 213). Eine parallele Verschiebung, die Punkt C nach Punkt A führt, kombiniert die Halblinie CD mit der Halblinie AB, da sie gleich gerichtet sind. Und da die Segmente AB und CD gleich sind, fällt der Punkt D mit dem Punkt B zusammen, d.h. parallele Übersetzung übersetzt den Vektor \(\overline(CD)\) in den Vektor \(\overline(AB)\). Die Vektoren \(\overline(AB)\) und \(\overline(CD)\) sind also wie gefordert gleich.

Frage 7. Beweisen Sie, dass man von jedem Punkt aus einen Vektor zeichnen kann, der gleich dem gegebenen Vektor ist, und nur einen.
Antworten. Sei CD eine Gerade und der Vektor \(\overline(CD)\) ein Teil der Geraden CD. Sei AB die Gerade, in die die Gerade CD bei der parallelen Translation geht, \(\overline(AB)\) der Vektor, in den der Vektor \(\overline(CD)\) bei der parallelen Translation geht, also die Vektoren \(\ overline(AB)\) und \(\overline(CD)\) sind gleich, und die Linien AB und CD sind parallel (siehe Abb. 213). Wie wir wissen, ist es möglich, durch einen Punkt, der nicht auf einer gegebenen Linie liegt, in der Ebene höchstens eine Linie parallel zu der gegebenen zu zeichnen (das Axiom der parallelen Linien). Daher kann man durch den Punkt A eine Linie parallel zur Linie CD ziehen. Da der Vektor \(\overline(AB)\) Teil der Geraden AB ist, kann ein Vektor \(\overline(AB)\) durch den Punkt A gezogen werden, gleich dem Vektor \(\overline(CD)\ ).

Frage 8. Was sind Vektorkoordinaten? Wie groß ist der Betrag des Vektors mit den Koordinaten a 1 , a 2 ?
Antworten. Der Vektor \(\overline(a)\) soll am Punkt A 1 (x 1 ; y 1) beginnen und am Punkt A 2 (x 2 ; y 2) enden. Die Koordinaten des Vektors \(\overline(a)\) sind die Zahlen a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . Wir setzen die Vektorkoordinaten neben die Buchstabenbezeichnung des Vektors, in diesem Fall \(\overline(a)\) (a 1 ; a 2) oder einfach nur \((\overline(a 1 ; a 2 ))\ ). Die Nullvektorkoordinaten sind gleich Null.
Aus der Formel, die den Abstand zwischen zwei Punkten in Bezug auf ihre Koordinaten ausdrückt, folgt, dass der Absolutwert des Vektors mit den Koordinaten a 1 , a 2 \(\sqrt(a^2 1 + a^2 2 )\) ist.

Frage 9. Beweisen Sie, dass gleiche Vektoren jeweils gleiche Koordinaten haben und Vektoren mit jeweils gleichen Koordinaten gleich sind.
Antworten. Seien A 1 (x 1 ; y 1) und A 2 (x 2 ; y 2) Anfang und Ende des Vektors \(\overline(a)\). Da der ihm gleiche Vektor \(\overline(a")\) aus dem Vektor \(\overline(a)\) durch Parallelverschiebung erhalten wird, sind sein Anfang und sein Ende jeweils A" 1 (x 1 + c ; y 1 + d ), A" 2 (x 2 + c; y 2 ​​​​+ d). Dies zeigt, dass beide Vektoren \(\overline(a)\) und \(\overline(a")\) haben dieselben Koordinaten: x 2 - x 1 , y 2 - y 1 .
Beweisen wir nun die umgekehrte Behauptung. Die entsprechenden Koordinaten der Vektoren \(\overline(A 1 A 2 )\) und \(\overline(A" 1 A" 2 )\) seien gleich. Wir beweisen, dass die Vektoren gleich sind.
Seien x" 1 und y" 1 die Koordinaten des Punktes A" 1 und x" 2, y" 2 die Koordinaten des Punktes A" 2. Nach der Bedingung des Satzes x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. Also x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Parallelübersetzung durch Formeln gegeben

x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,

überträgt Punkt A 1 zu Punkt A" 1 und Punkt A 2 zu Punkt A" 2 , d. h. die Vektoren \(\overline(A 1 A 2 )\) und \(\overline(A" 1 A" 2 )\) sind wie gefordert gleich.

Frage 10. Definiere die Summe von Vektoren.
Antworten. Die Summe der Vektoren \(\overline(a)\) und \(\overline(b)\) mit den Koordinaten a 1 , a 2 und b 1 , b 2 ist der Vektor \(\overline(c)\) mit Koordinaten a 1 + b 1 , a 2 + b a 2 , d.h.

\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).

Erstellungsdatum: 2009-04-11 15:25:51
Zuletzt bearbeitet: 08.02.2012 09:19:45

Lange wollte ich diesen Artikel nicht schreiben - ich habe darüber nachgedacht, wie ich das Material präsentieren soll. Sie müssen auch Bilder zeichnen. Aber anscheinend haben sich die Sterne heute erfolgreich gebildet und es wird einen Artikel über Vektoren geben. Allerdings ist dies nur ein Entwurf. In Zukunft werde ich diesen Artikel in mehrere separate Artikel aufteilen - es gibt genug Material. Außerdem wird sich der Artikel nach und nach verbessern: Ich werde Änderungen daran vornehmen - weil. in einer Sitzung wird es nicht möglich sein, alle Aspekte aufzudecken.

Vektoren wurden im 19. Jahrhundert in die Mathematik eingeführt, um Größen zu beschreiben, die mit Skalarwerten schwer zu beschreiben waren.

Vektoren werden häufig bei der Entwicklung von Computerspielen verwendet. Sie werden nicht nur traditionell verwendet, um Größen wie Kraft oder Geschwindigkeit zu beschreiben, sondern auch in Bereichen, die scheinbar nichts mit Vektoren zu tun haben: Farbspeicherung, Schattenerzeugung.

Skalare und Vektoren

Lassen Sie mich zunächst daran erinnern, was ein Skalar ist und wie er sich von einem Vektor unterscheidet.

Skalare Werte speichern einen Wert: Masse, Volumen. Das heißt, es ist eine Entität, die nur durch eine Zahl gekennzeichnet ist (z. B. die Menge von etwas).

Ein Vektor wird im Gegensatz zu einem Skalar mit zwei Werten beschrieben: Größe und Richtung.

Ein wichtiger Unterschied zwischen Vektoren und Koordinaten: Vektoren sind nicht an einen bestimmten Ort gebunden! Noch einmal, das Wichtigste bei einem Vektor sind Länge und Richtung.

Ein Vektor wird durch einen fetten Buchstaben des lateinischen Alphabets gekennzeichnet. Zum Beispiel: a, b, v.

In der ersten Abbildung sehen Sie, wie der Vektor in der Ebene bezeichnet wird.

Vektoren im Raum

Im Raum können Vektoren durch Koordinaten ausgedrückt werden. Aber zuerst müssen wir ein Konzept einführen:

Punktradiusvektor

Nehmen wir einen Punkt M(2,1) im Raum. Der Radiusvektor eines Punktes ist ein Vektor, der am Ursprung beginnt und am Punkt endet.

Was wir hier haben, ist nichts weiter als ein Vektor Om. Vektor-Startkoordinaten (0,0), Endkoordinaten (2,1). Bezeichnen wir diesen Vektor als a.

In diesem Fall kann der Vektor wie folgt geschrieben werden a = <2, 1>. Dies ist die Koordinatenform des Vektors a.

Die Koordinaten eines Vektors heißen seine Komponenten relativ zu den Achsen. Beispielsweise ist 2 eine Vektorkomponente a um die x-achse.

Lassen Sie uns noch einmal darauf eingehen, was die Koordinaten eines Punktes sind. Die Koordinate eines Punktes (z. B. x) ist die Projektion des Punktes auf die Achse, d.h. die Basis einer Senkrechten fällt von einem Punkt auf eine Achse. In unserem Beispiel 2.

Aber zurück zum ersten Bild. Hier haben wir zwei Punkte A und B. Die Koordinaten der Punkte seien (1,1) und (3,3). Vektor v in diesem Fall kann es definiert werden als v = <3-1, 3-1>. Ein Vektor, der an zwei Punkten im dreidimensionalen Raum liegt, sieht so aus:

v =

Ich glaube nicht, dass es hier Probleme gibt.

Multipliziere einen Vektor mit einem Skalar

Ein Vektor kann mit Skalarwerten multipliziert werden:

k v = =

Dabei wird der Skalarwert mit jeder Komponente des Vektors multipliziert.

Wenn k > 1, wird der Vektor größer, wenn k kleiner als eins, aber größer als null ist, wird der Vektor kürzer. Wenn k kleiner als Null ist, ändert der Vektor die Richtung.

Einheitsvektoren

Einheitsvektoren sind Vektoren, deren Länge gleich eins ist. Beachten Sie, dass der Vektor mit Koordinaten<1,1,1>wird nicht gleich eins sein! Das Finden der Länge eines Vektors wird unten beschrieben.

Es gibt sogenannte Orte - das sind Einheitsvektoren, die in Richtung mit den Koordinatenachsen zusammenfallen. ich- Einheitsvektor der x-Achse, j- Einheitsvektor der y-Achse, k- Einheitsvektor der z-Achse.

Dabei ich = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Jetzt wissen wir, was die Multiplikation eines Vektors mit einem Skalar ist und was Einheitsvektoren sind. Jetzt können wir schreiben v in Vektorform.

v= vx ich+vy j+vz k, wobei v x , v y , v z die entsprechenden Komponenten des Vektors sind

Vektoraddition

Um die vorherige Formel vollständig zu verstehen, müssen Sie verstehen, wie die Vektoraddition funktioniert.

Hier ist alles einfach. Nehmen Sie zwei Vektoren v1 = und v2 =

v1 + v2 =

Wir addieren einfach die entsprechenden Komponenten der beiden Vektoren.

Die Differenz wird auf die gleiche Weise berechnet.

Es geht um die mathematische Form. Der Vollständigkeit halber lohnt es sich, darüber nachzudenken, wie das Addieren und Subtrahieren von Vektoren grafisch aussehen würde.

Zwei Vektoren addieren a+b. Wir müssen den Anfang des Vektors abgleichen b und das Ende des Vektors a. Dann zwischen dem Anfang des Vektors a und das Ende des Vektors b Zeichnen Sie einen neuen Vektor. Zur Verdeutlichung siehe die zweite Abbildung (Buchstabe "a").

Um Vektoren zu subtrahieren, müssen Sie die Anfänge zweier Vektoren kombinieren und einen neuen Vektor vom Ende des zweiten Vektors bis zum Ende des ersten zeichnen. Das zweite Bild (Buchstabe "b") zeigt, wie es aussieht.

Vektorlänge und -richtung

Schauen wir uns zuerst die Länge an.

Die Länge ist der numerische Wert des Vektors, unabhängig von der Richtung.

Die Länge wird durch die Formel bestimmt (für einen dreidimensionalen Vektor):

die Quadratwurzel der Summe der Quadrate der Vektorkomponenten.

Bekannte Formel, nicht wahr? Im Allgemeinen ist dies die Formel für die Länge eines Segments

Die Richtung des Vektors wird durch die Richtungskosinusse der zwischen dem Vektor und den Koordinatenachsen gebildeten Winkel bestimmt. Um die Richtungskosinusse zu finden, werden die entsprechenden Komponenten und Längen verwendet (das Bild folgt später).

Darstellung von Vektoren in Programmen

Vektoren können in Programmen auf vielfältige Weise dargestellt werden. Sowohl mit Hilfe gewöhnlicher Variablen, was ineffizient ist, als auch mit Hilfe von Arrays, Klassen und Strukturen.

Float-Vektor3 = (1,2,3); // Array zum Speichern von Vektoren struct vector3 // Struktur zum Speichern von Vektoren (float x,y,z; );

Die größten Möglichkeiten zur Speicherung von Vektoren bieten Klassen. In Klassen können wir nicht nur den Vektor selbst (Variablen), sondern auch Vektoroperationen (Funktionen) beschreiben.

Skalarprodukt von Vektoren

Es gibt zwei Arten der Vektormultiplikation: Vektor und Skalar.

Eine Besonderheit des Skalarprodukts ist, dass das Ergebnis immer ein Skalarwert ist, d.h. Nummer.

Hier lohnt es sich, auf diesen Moment zu achten. Wenn das Ergebnis dieser Operation Null ist, sind die beiden Vektoren senkrecht - der Winkel zwischen ihnen beträgt 90 Grad. Wenn das Ergebnis größer als Null ist, ist der Winkel kleiner als 90 Grad. Wenn das Ergebnis kleiner als Null ist, ist der Winkel größer als 90 Grad.

Diese Operation wird durch die folgende Formel dargestellt:

a · b= a x * b x + a y * b y + a z * b z

Das Skalarprodukt ist die Summe der Produkte der entsprechenden Komponenten zweier Vektoren. Diese. Wir nehmen x "s von zwei Vektoren, multiplizieren sie, addieren sie dann zum Produkt von y" s und so weiter.

Kreuzprodukt von Vektoren

Das Ergebnis des Kreuzprodukts zweier Vektoren ist ein Vektor, der senkrecht zu diesen Vektoren steht.

a x b =

Wir werden diese Formel noch nicht im Detail besprechen. Außerdem ist es ziemlich schwer, sich daran zu erinnern. Wir werden auf diesen Punkt zurückkommen, nachdem wir uns mit den Determinanten vertraut gemacht haben.

Nun, für die allgemeine Entwicklung ist es nützlich zu wissen, dass die Länge des resultierenden Vektors gleich der Fläche des auf Vektoren aufgebauten Parallelogramms ist a und b.

Vektornormalisierung

Ein normalisierter Vektor ist ein Vektor, dessen Länge eins ist.

Die Formel zum Finden eines normalisierten Vektors lautet wie folgt - alle Komponenten des Vektors müssen durch seine Länge geteilt werden:

v n= v/|v| =

Nachwort

Wie Sie wahrscheinlich gesehen haben, sind Vektoren nicht schwer zu verstehen. Wir haben eine Reihe von Operationen auf Vektoren betrachtet.

In den folgenden Artikeln des Abschnitts "Mathematik" werden wir Matrizen, Determinanten und lineare Gleichungssysteme diskutieren. Es ist alles Theorie.

Danach betrachten wir Matrixtransformationen. Dann werden Sie verstehen, wie wichtig Mathematik bei der Erstellung von Computerspielen ist. Dieses Thema wird nur zu einer Übung für alle vorherigen Themen.

VEKTOREN. AKTIONENOBENVEKTOREN. SKALAR,

VEKTOR, MISCHPRODUKT VON VEKTOREN.

1. VEKTOREN, AKTIONEN AUF VEKTOREN.

Grundlegende Definitionen.

Bestimmung 1. Nennt man eine Größe, die durch ihren Zahlenwert im gewählten Einheitensystem vollständig charakterisiert ist Skalar oder Skalar .

(Körpergewicht, Volumen, Zeit usw.)

Bestimmung 2. Eine durch Zahlenwert und Richtung gekennzeichnete Größe wird aufgerufen Vektor oder Vektor .

(Weg, Kraft, Geschwindigkeit usw.)

Bezeichnungen: , oder , .

Ein geometrischer Vektor ist ein gerichtetes Segment.

Für Vektor - Punkt ABER- Startpunkt BEI ist das Ende des Vektors.

Bestimmung 3.Modul Vektor ist die Länge des Segments AB.

Bestimmung 4. Ein Vektor, dessen Modul Null ist, wird aufgerufen Null , ist angegeben.

Bestimmung 5. Vektoren, die auf parallelen Linien oder auf derselben Linie liegen, werden aufgerufen kollinear . Wenn zwei kollineare Vektoren die gleiche Richtung haben, werden sie aufgerufen gleichgerichtet .

Bestimmung 6. Es werden zwei Vektoren betrachtet gleich , wenn sie Co-Regie und im Modul gleich sind.

Aktionen auf Vektoren.

1) Addition von Vektoren.

Def. 6.Summe zwei Vektoren und ist die Diagonale des Parallelogramms, das auf diesen Vektoren aufgebaut ist und von einem gemeinsamen Punkt ihrer Anwendung ausgeht (Parallelogrammregel).

Abb.1.

Def. 7. Die Summe dreier Vektoren , , ist die Diagonale des auf diesen Vektoren aufgebauten Parallelepipeds (Parallelepiped-Regel).

Def. acht. Wenn ein ABER, BEI, AUS beliebige Punkte sind, dann + = (Dreiecksregel).

Abb.2

Zusätzliche Eigenschaften.

1 um . + = + (Verdrängungsgesetz).

2 um . + ( + ) = ( + ) + = ( + ) + (Assoziativgesetz).

3 um . + (– ) + .

2) Subtraktion von Vektoren.

Def. 9. Unter Unterschied Vektoren und Vektor verstehen = - so dass + = .

In einem Parallelogramm ist dies eine andere Diagonale SD (siehe Abb. 1).

3) Multiplikation eines Vektors mit einer Zahl.

Def. zehn. Arbeit Vektor zu Skalar k Vektor genannt

= k = k ,

lang ka , und Richtung, die:

1. fällt mit der Richtung des Vektors if zusammen k > 0;

2. entgegen der Richtung des Vektors if k < 0;

3. willkürlich, wenn k = 0.

Eigenschaften der Multiplikation eines Vektors mit einer Zahl.

1 um . (k + l ) = k + l .

k ( + ) = k + k .

2 Ö . k (l ) = (Kl ) .

3 Ö . 1  = , (–1)  = – , 0  = .

Vektoreigenschaften.

Def. elf. Zwei Vektoren und werden aufgerufen kollinear wenn sie sich befinden parallele Linien oder bei eine gerade Linie.

Der Nullvektor ist kollinear zu jedem Vektor.

Satz 1. Zwei Vektoren ungleich Null und kollinear,  wenn sie proportional sind, d.h.

= k , k - Skalar.

Def. 12. Drei Vektoren , , werden aufgerufen koplanar wenn sie parallel zu einer Ebene sind oder in ihr liegen.

Satz 2. Drei Vektoren ungleich Null , , koplanar,  wenn einer von ihnen eine Linearkombination der anderen beiden ist, d.h.

= k + l , k , l - Skalare.

Projektion eines Vektors auf eine Achse.

Satz 3. Projektion eines Vektors auf eine Achse (gerichtete Linie) l ist gleich dem Produkt aus der Länge des Vektors und dem Kosinus des Winkels zwischen der Richtung des Vektors und der Richtung der Achse, d.h. = a  c os  ,  = ( , l).

2. VEKTORKOORDINATEN

Def. 13. Vektorprojektionen auf Koordinatenachsen Oh, OU, Unze genannt Vektorkoordinaten. Bezeichnung:  a x , a j , a z .

Vektorlänge:

Beispiel: Berechne die Länge des Vektors.

Lösung:

Abstand zwischen Punkten und berechnet nach der Formel: .

Beispiel: Finde den Abstand zwischen den Punkten M (2,3,-1) und K (4,5,2).

Aktionen auf Vektoren in Koordinatenform.

Gegebene Vektoren = a x , a j , a z und = b x , b j , b z .

1. (  )= a x  b x , a j  b j , a z  b z .

2.  =   a x ,  a j ,  a z, wo  - Skalar.

Skalarprodukt von Vektoren.

Definition: Unter dem Skalarprodukt zweier Vektoren und

wird als eine Zahl verstanden, die gleich dem Produkt der Längen dieser Vektoren und dem Kosinus des Winkels zwischen ihnen ist, d.h. = , - Winkel zwischen Vektoren und .

Eigenschaften des Punktprodukts:

1.  =

2. ( + ) =

3.

4.

5. , wo sind Skalare.

6. zwei Vektoren sind senkrecht (orthogonal), wenn .

7. wenn und nur wenn .

Das Skalarprodukt in Koordinatenform hat die Form: , wo und .

Beispiel: Finden Sie das Skalarprodukt von Vektoren und

Lösung:

Vektor, der Vektoren hält.

Definition: Das Vektorprodukt zweier Vektoren und wird als Vektor verstanden, für den gilt:

Das Modul ist gleich der Fläche des auf diesen Vektoren aufgebauten Parallelogramms, d.h. , wobei der Winkel zwischen den Vektoren und ist

Dieser Vektor steht senkrecht auf den multiplizierten Vektoren, d.h.

Wenn die Vektoren nicht kollinear sind, dann bilden sie ein rechtes Tripel von Vektoren.

Produktübergreifende Eigenschaften:

1. Beim Ändern der Reihenfolge der Faktoren ändert das Vektorprodukt sein Vorzeichen ins Gegenteil, wobei der Modul erhalten bleibt, d.h.

2 .Vektorquadrat ist gleich Nullvektor, d.h.

3 .Der Skalarfaktor kann aus dem Vorzeichen des Vektorprodukts genommen werden, d.h.

4 .Für drei beliebige Vektoren die Gleichheit

5 .Notwendige und hinreichende Bedingung für die Kollinearität zweier Vektoren und :

Vektorprodukt in Koordinatenform.

Wenn die Koordinaten der Vektoren und , dann wird ihr Vektorprodukt durch die Formel gefunden:

.

Dann folgt aus der Definition des Kreuzprodukts, dass die Fläche des Parallelogramms auf den Vektoren aufgebaut ist und nach der Formel berechnet wird:

Beispiel: Berechnen Sie die Fläche eines Dreiecks mit den Eckpunkten (1;-1;2), (5;-6;2), (1;3;-1).

Lösung: .

Dann wird die Fläche des Dreiecks ABC wie folgt berechnet:

,

Mischprodukt von Vektoren.

Definition: Ein gemischtes (Vektor-Skalar-)Produkt von Vektoren ist eine Zahl, die durch die Formel bestimmt wird: .

Mischprodukteigenschaften:

1. Das Mischprodukt ändert sich bei einer zyklischen Permutation seiner Faktoren nicht, d.h. .

2. Werden zwei benachbarte Faktoren vertauscht, ändert das Mischprodukt sein Vorzeichen ins Gegenteil, d.h. .

3 .Notwendige und hinreichende Bedingung dafür, dass drei Vektoren koplanar sind : =0.

4 .Das gemischte Produkt dreier Vektoren ist gleich dem Volumen des auf diesen Vektoren aufgebauten Parallelepipeds, mit Pluszeichen genommen, wenn diese Vektoren ein rechtes Tripel bilden, und mit Minuszeichen, wenn sie ein linkes Tripel bilden, d.h. .

Wenn bekannt Koordinaten Vektoren , dann wird das Mischprodukt durch die Formel gefunden:

Beispiel: Berechnen Sie das gemischte Produkt von Vektoren.

Lösung:

3. Grundlage des Vektorsystems.

Definition. Unter einem System von Vektoren versteht man mehrere Vektoren, die zum selben Raum gehören R.

Kommentar. Wenn das System aus einer endlichen Anzahl von Vektoren besteht, werden sie mit demselben Buchstaben mit unterschiedlichen Indizes bezeichnet.

Beispiel.

Definition. Jeder Vektor der Form = heißt Linearkombination von Vektoren. Die Zahlen sind die Koeffizienten der Linearkombination.

Beispiel. .

Definition. Wenn der Vektor eine Linearkombination von Vektoren ist , dann sagen wir, dass der Vektor durch die Vektoren linear ausgedrückt wird .

Definition. Das System der Vektoren heißt linear unabhängig, wenn keiner der Vektoren des Systems eine Linearkombination der übrigen Vektoren sein kann. Andernfalls heißt das System linear abhängig.

Beispiel. Vektorsystem linear abhängig, da der Vektor .

Basisdefinition. Ein System von Vektoren bildet eine Basis, wenn:

1) es ist linear unabhängig,

2) jeder Raumvektor durch ihn wird linear ausgedrückt.

Beispiel 1 Raumbasis: .

2. Im System der Vektoren Vektoren sind die Basis: , weil linear in Form von Vektoren ausgedrückt.

Kommentar. Um die Basis eines gegebenen Vektorsystems zu finden, müssen Sie:

1) schreibe die Koordinaten der Vektoren in die Matrix,

2) Bringen Sie die Matrix mit elementaren Transformationen in eine Dreiecksform,

3) Nicht-Null-Zeilen der Matrix bilden die Grundlage des Systems,

4) die Anzahl der Vektoren in der Basis ist gleich dem Rang der Matrix.

DEFINITION

Vektor(von lat. " Vektor"-" Lager") - ein gerichtetes Segment einer geraden Linie im Raum oder in einer Ebene.

Grafisch wird ein Vektor als gerichtetes Geradenstück bestimmter Länge dargestellt. Der Vektor, dessen Anfang am Punkt und dessen Ende am Punkt ist, wird als (Fig. 1) bezeichnet. Ein Vektor kann auch durch einen einzelnen kleinen Buchstaben gekennzeichnet werden, z. B. .

Ist ein Koordinatensystem im Raum gegeben, so kann der Vektor durch eine Menge seiner Koordinaten eindeutig angegeben werden. Das heißt, unter einem Vektor wird ein Objekt verstanden, das einen Wert (Länge), eine Richtung und einen Angriffspunkt (den Anfang des Vektors) hat.

Die Anfänge der Vektorrechnung erschienen 1831 in Werken des deutschen Mathematikers, Mechanikers, Physikers, Astronomen und Landvermessers Johann Carl Friedrich Gauß (1777-1855). Arbeiten über Operationen mit Vektoren wurden von dem irischen Mathematiker, Mechaniker und theoretischen Physiker Sir William Rowan Hamilton (1805-1865) als Teil seines Quaternionenkalküls veröffentlicht. Der Wissenschaftler schlug den Begriff "Vektor" vor und beschrieb einige Operationen an Vektoren. Die Vektorrechnung wurde dank der Arbeiten des britischen Physikers, Mathematikers und Mechanikers James Clerk Maxwell (1831-1879) zum Elektromagnetismus weiterentwickelt. In den 1880er Jahren erschien das Buch „Elements of Vector Analysis“ des amerikanischen Physikers, Physikochemikers, Mathematikers und Mechanikers Josiah Willard Gibbs (1839–1903). Die moderne Vektoranalyse wurde 1903 von dem englischen Autodidakten Wissenschaftler, Ingenieur, Mathematiker und Physiker Oliver Heaviside (1850-1925) beschrieben.

DEFINITION

Länge oder Vektormodul ist die Länge des gerichteten Segments, das den Vektor definiert. Bezeichnet als .

Grundtypen von Vektoren

Nullvektor heißt ein Vektor, dessen Anfangs- und Endpunkt gleich sind. Die Länge des Nullvektors ist Null.

Vektoren, die parallel zu derselben Geraden sind oder auf derselben Geraden liegen, heißen Vektoren kollinear(Abb. 2).

gleichgerichtet wenn ihre Richtungen gleich sind.

In Abbildung 2 sind dies die Vektoren und . Die Co-Richtung von Vektoren wird wie folgt bezeichnet: .

Zwei kollineare Vektoren werden aufgerufen gegenläufige Richtungen wenn ihre Richtungen entgegengesetzt sind.

In Abbildung 3 sind dies die Vektoren und . Bezeichnung: .