Bernoulli test scheme. Bernoulli formula
Let's do a few tests. Moreover, the probability of occurrence of the event $A$ in each trial does not depend on the outcomes of other trials. Such trials are called independent with respect to event A. In different independent trials, event A can either have different probabilities, or one and the same. We will consider only those independent trials in which the event $A$ has the same probability.
By a complex event we mean a combination of simple events. Let n trials be performed. In each trial, the event $A$ may or may not occur. We assume that in each trial the probability of occurrence of the event $A$ is the same and equals $p$. Then the probability $\overline A $ (or not occurrence of A ) is equal to $P(( \overline A ))=q=1-p$.
Let it be required to calculate the probability that in n-test event $A$ will occur k- times and $n-k$ times - will not come. This probability will be denoted by $P_n (k)$. Moreover, the sequence of occurrence of the event $A$ is not important. For example: $(( AAA\overline A , AA\overline A A, A\overline A AA, \overline A AAA ))$
$P_5 (3)-$ in five trials event $A$ appeared 3 times and 2 did not appear. This probability can be found using the Bernoulli formula.
Derivation of the Bernoulli formula
By the theorem of multiplication of probabilities of independent events, the probability that the event $A$ occurs $k$ times and $n-k$ times does not occur is equal to $p^k\cdot q^ ( n-k ) $. And there can be as many such complex events as $C_n^k $ can be. Since complex events are incompatible, then according to the theorem on the sum of probabilities of incompatible events, we need to add the probabilities of all complex events, and there are exactly $C_n^k $ of them. Then the probability of occurrence of the event $A$ is exactly k once a n tests, there is $P_n (( A,\,k ))=P_n (k)=C_n^k \cdot p^k\cdot q^ ( n-k ) $ Bernoulli's formula.
Example. A die is tossed 4 times. Find the probability that one will appear half the time.
Solution. $A=$ (appearance of one)
$ P(A)=p=\frac ( 1 ) ( 6 ) \, \,P(( \overline A ))=q=1-\frac ( 1 ) ( 6 ) =\frac ( 5 ) ( 6 ) $ $ P_4 (2)=C_4^2 \cdot p^2\cdot q^ ( 4-2 ) =\frac ( 4! ) ( 2!\cdot 2! ) \cdot 6^2\cdot (( \frac ( 5 ) ( 6 ) ))^2=$0.115
It is easy to see that for large values n it is rather difficult to calculate the probability because of the huge numbers. It turns out that this probability can be calculated not only using the Bernoulli formula.
If several trials are performed, and the probability of the event A in each trial does not depend on the outcomes of other trials, then such trials are called independent with respect to the event A .
In different independent trials, event A may have either different probabilities or the same probability. We will further consider only such independent trials in which the event A has the same probability.
Below we use the concept complex events, understanding by it combination of several separate events, which are called simple .
Let it be produced n independent trials, in each of which event A may or may not occur. Let us agree to assume that the probability of the event A in each trial is the same, namely, it is equal to R . Therefore, the probability of non-occurrence of event A in each trial is also constant and equal to q = 1 - p .
Let us set ourselves the task of calculating the probability that n tests, event A will occur exactly k times and, therefore, will not be realized n-k once. It is important to emphasize that it is not required that the event A repeats exactly k times in a certain sequence.
For example, if we are talking about the occurrence of an event BUT three times in four trials, the following complex events are possible: AAA, AAA, AAA, AAA. Recording AAA means that in the first, second and third trials the event BUT came, but in the fourth test it did not appear, i.e. the opposite happened BUT; other entries have the same meaning.
Denote the desired probability R p (k) . For example, the symbol R 5 (3) means the probability that in five trials the event will occur exactly 3 times and, therefore, will not occur 2 times.
The problem can be solved using the so-called Bernoulli formula.
Derivation of the Bernoulli formula. The probability of one compound event consisting in the fact that in P test event BUT will come k once and will not come n - k times, according to the theorem of multiplication of probabilities of independent events is equal to p k q n - k . There can be as many such complex events as there are combinations of P elements by k elements, i.e. C n k .
Since these complex events incompatible, then according to the theorem of addition of probabilities of incompatible events the desired probability is equal to the sum of the probabilities of all possible complex events. Since the probabilities of all these complex events are the same, the desired probability (of the occurrence k event times BUT in P tests) is equal to the probability of one complex event, multiplied by their number:

The resulting formula is called Bernoulli formula .
Example 1. The probability that the electricity consumption during one day will not exceed the established norm is equal to p = 0.75 . Find the probability that in the next 6 days the electricity consumption for 4 days will not exceed the norm.
Solution. The probability of normal consumption of electricity during each of the 6 days is constant and equal to p = 0.75 . Therefore, the probability of overexpenditure of electricity every day is also constant and equal to q \u003d 1 - p \u003d 1 - 0.75 \u003d 0.25.
The desired probability according to the Bernoulli formula is equal to:
Brief theory
Probability theory deals with experiments that can be repeated (at least in theory) an unlimited number of times. Let some experiment be repeated once, and the results of each repetition do not depend on the outcomes of previous repetitions. Such series of repetitions are called independent trials. A special case of such tests are independent Bernoulli trials, which are characterized by two conditions:
1) the result of each test is one of two possible outcomes, called respectively "success" or "failure".
2) the probability of "success" in each subsequent test does not depend on the results of previous tests and remains constant.
Bernoulli's theorem
If a series of independent Bernoulli trials is made, in each of which "success" occurs with probability , then the probability that "success" in the trials occurs exactly once is expressed by the formula:
where is the probability of failure.
- the number of combinations of elements by (see the basic formulas of combinatorics)
This formula is called Bernoulli formula.
The Bernoulli formula allows you to get rid of a large number of calculations - addition and multiplication of probabilities - with a sufficiently large number of tests.
The Bernoulli test scheme is also called the binomial scheme, and the corresponding probabilities are called binomial, which is associated with the use of binomial coefficients.
The distribution according to the Bernoulli scheme allows, in particular, to find the most probable number of occurrence of an event .
If the number of trials n great, then enjoy:
Problem solution example
The task
The germination of seeds of a certain plant is 70%. What is the probability that out of 10 seeds sown: 8 will sprout, at least 8; at least 8?
The solution of the problem
Let's use the Bernoulli formula:
In our case
Let the event - out of 10 seeds sprout 8:
Let the event - rise at least 8 (that means 8, 9 or 10)
Let the event rise at least 8 (that means 8.9 or 10)
Answer
Medium the cost of solving the control work is 700 - 1200 rubles (but not less than 300 rubles for the entire order). The price is strongly influenced by the urgency of the decision (from days to several hours). The cost of online help in the exam / test - from 1000 rubles. for the ticket solution.
The application can be left directly in the chat, having previously thrown off the condition of the tasks and informing you of the deadlines for solving it. The response time is several minutes.
In this lesson, we will find the probability of an event occurring in independent trials when the trials are repeated. . Trials are called independent if the probability of one or another outcome of each trial does not depend on what outcomes other trials had. . Independent tests can be carried out both under the same conditions and under different conditions. In the first case, the probability of an event occurring in all trials is the same; in the second case, it varies from trial to trial.
Examples of Independent Retests :
- one of the device nodes or two or three nodes will fail, and the failure of each node does not depend on the other node, and the probability of failure of one node is constant in all tests;
- a part produced under certain constant technological conditions, or three, four, five parts, will turn out to be non-standard, and one part may turn out to be non-standard regardless of any other part, and the probability that the part will turn out to be non-standard is constant in all tests;
- out of several shots on the target, one, three or four shots hit the target regardless of the outcome of other shots and the probability of hitting the target is constant in all trials;
- when a coin is inserted, the machine will operate correctly one, two, or another number of times, regardless of what other coin insertions have had, and the probability that the machine will operate correctly is constant in all trials.
These events can be described by one scheme. Each event occurs in each trial with the same probability, which does not change if the results of previous trials become known. Such tests are called independent, and the scheme is called Bernoulli scheme . It is assumed that such tests can be repeated as many times as desired.
If the probability p event A is constant in each trial, then the probability that in n independent test event A will come m times, located on Bernoulli formula :
![]() (where q= 1 – p- the probability that the event will not occur)
(where q= 1 – p- the probability that the event will not occur)
![]()
Let's set the task - to find the probability that an event of this type in n independent trials will come m once.
Bernoulli formula: examples of problem solving
Example 1 Find the probability that among five randomly selected parts two are standard, if the probability that each part is standard is 0.9.
Solution. Event Probability BUT, consisting in the fact that a part taken at random is standard, is p=0.9 , and the probability that it is non-standard is q=1–p=0.1 . The event indicated in the condition of the problem (we denote it by AT) occurs if, for example, the first two parts are standard, and the next three are non-standard. But the event AT also occurs if the first and third parts are standard and the rest are non-standard, or if the second and fifth parts are standard and the rest are non-standard. There are other possibilities for the event to occur. AT. Any of them is characterized by the fact that out of five parts taken, two, occupying any places out of five, will turn out to be standard. Therefore, the total number of different possibilities for the occurrence of an event AT is equal to the number of possibilities for placing two standard parts in five places, i.e. is equal to the number of combinations of five elements by two, and .
The probability of each possibility, according to the probability multiplication theorem, is equal to the product of five factors, of which two, corresponding to the appearance of standard parts, are equal to 0.9, and the remaining three, corresponding to the appearance of non-standard parts, are equal to 0.1, i.e. this probability is . Since these ten possibilities are incompatible events, by the addition theorem, the probability of an event AT, which we denote
Example 2 The probability that the machine will require the attention of a worker within an hour is 0.6. Assuming that the failures on the machines are independent, find the probability that during an hour the attention of the worker will be required by any one of the four machines serviced by him.
Solution. Using Bernoulli's formula at n=4 , m=1 , p=0.6 and q=1–p=0.4 , we get
Example 3 For the normal operation of the car depot, there must be at least eight cars on the line, and there are ten of them. The probability of non-exit of each car to the line is equal to 0.1. Find the probability of normal operation of the depot in the next day.
Solution. Autobase will work fine (event F) if either or eight will enter the line (the event BUT), or nine (event AT), or all ten cars event (event C). According to the probability addition theorem,
We find each term according to the Bernoulli formula. Here n=10 , m=8; 10 and p\u003d 1-0.1 \u003d 0.9, since p should mean the probability of a car entering the line; then q=0.1 . As a result, we get
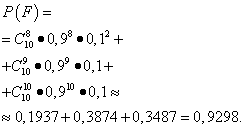
Example 4 Let the probability that a customer needs a size 41 men's shoe be 0.25. Find the probability that out of six buyers at least two need shoes of size 41.
Let n trials be carried out with respect to the event A. Let's introduce the following events: Аk -- event А was realized during the k-th test, $ k=1,2,\dots , n$. Then $\bar(A)_(k) $ is the opposite event (event A did not occur during the k-th test, $k=1,2,\dots , n$).
What are peer and independent trials
Definition
Tests are called of the same type with respect to event A if the probabilities of the events $A1, A2, \dots , An$ are the same: $P(A1)=P(A2)= \dots =P(An)$ (i.e., the probability of occurrence event A in one trial is constant in all trials).
Obviously, in this case, the probabilities of opposite events also coincide: $P(\bar(A)_(1))=P(\bar(A)_(2))=...=P(\bar(A) _(n))$.
Definition
Trials are called independent with respect to event A if the events $A1, A2, \dots , An$ are independent.
In this case
In this case, equality is preserved when any event Ak is replaced by $\bar(A)_(k) $.
Let a series of n similar independent trials be conducted with respect to event A. We carry the notation: p - the probability of the event A in one test; q is the probability of the opposite event. Thus P(Ak)=p, $P(\bar(A)_(k))=q$ for any k and p+q=1.
The probability that in a series of n trials event A will occur exactly k times (0 ≤ k ≤ n) is calculated by the formula:
$P_(n) (k)=C_(n)^(k) p^(k) q^(n-k) $ (1)
Equality (1) is called the Bernoulli formula.
The probability that in a series of n independent trials of the same type event A will occur at least k1 times and at most k2 times is calculated by the formula:
$P_(n) (k_(1) \le k\le k_(2))=\sum \limits _(k=k_(1) )^(k_(2) )C_(n)^(k) p ^(k) q^(n-k) $ (2)
Application of the Bernoulli formula for large values of n leads to cumbersome calculations, so in these cases it is better to use other formulas - asymptotic ones.
Generalization of the Bernoulli scheme
Consider a generalization of the Bernoulli scheme. If in a series of n independent trials, each of which has m pairwise incompatible and possible results Ak with corresponding probabilities Рk= рk(Аk). Then the polynomial distribution formula is valid:
Example 1
The probability of getting the flu during an epidemic is 0.4. Find the probability that out of 6 employees of the company will fall ill
- exactly 4 employees;
- no more than 4 employees.
Solution. 1) Obviously, to solve this problem, the Bernoulli formula is applicable, where n=6; k=4; p=0.4; q=1-p=0.6. Applying formula (1), we get: $P_(6) (4)=C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \approx 0.138$.
To solve this problem, formula (2) is applicable, where k1=0 and k2=4. We have:
\[\begin(array)(l) (P_(6) (0\le k\le 4)=\sum \limits _(k=0)^(4)C_(6)^(k) p^( k) q^(6-k) =C_(6)^(0) \cdot 0.4^(0) \cdot 0.6^(6) +C_(6)^(1) \cdot 0.4 ^(1) \cdot 0.6^(5) +C_(6)^(2) \cdot 0.4^(2) \cdot 0.6^(4) +) \\ (+C_(6) ^(3) \cdot 0.4^(3) \cdot 0.6^(3) +C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \ approx 0.959.) \end(array)\]
It should be noted that this task is easier to solve using the opposite event - more than 4 employees fell ill. Then, taking into account formula (7) on the probabilities of opposite events, we obtain:
Answer: $\ $0.959.
Example 2
An urn contains 20 white and 10 black balls. 4 balls are taken out, and each ball taken out is returned to the urn before the next one is drawn and the balls in the urn are mixed. Find the probability that out of the four balls drawn there will be 2 white balls in Figure 1.
Picture 1.
Solution. Let the event A be that -- a white ball is drawn. Then the probabilities $D (A)=\frac(2)(3) ,\, \, D (\overline(A))=1-\frac(2)(3) =\frac(1)(3) $ .
According to the Bernoulli formula, the required probability is $D_(4) (2)=N_(4)^(2) \left(\frac(2)(3) \right)^(2) \left(\frac(1)( 3) \right)^(2) =\frac(8)(27) $.
Answer: $\frac(8)(27) $.
Example 3
Determine the probability that a family with 5 children will have no more than 3 girls. The probabilities of having a boy and a girl are assumed to be the same.
Solution. Probability of having a girl $\partial =\frac(1)(2) ,\, q=\frac(1)(2) $-probability of having a boy. There are no more than three girls in a family, which means that either one, or two, or three girls were born, or all boys in the family.
Find the probabilities that there are no girls in the family, one, two or three girls were born: $D_(5) (0)=q^(5) =\frac(1)(32) $,
\ \ \
Therefore, the required probability is $D =D_(5) (0)+D_(5) (1)+D_(5) (2)+D_(5) (3)=\frac(13)(16) $.
Answer: $\frac(13)(16)$.
Example 4
The first shooter with one shot can hit the top ten with a probability of 0.6, the nine with a probability of 0.3, and the eight with a probability of 0.1. What is the probability that, with 10 shots, he will hit ten six times, nine three times, and eight eight times?
