Formulation of the problem

The task involves familiarizing the user with the basic concepts of numerical methods, such as the determinant and inverse matrix, and various ways to calculate them. In this theoretical report, in a simple and accessible language, the basic concepts and definitions are first introduced, on the basis of which further research is carried out. The user may not have special knowledge in the field of numerical methods and linear algebra, but can easily use the results of this work. For clarity, a program for calculating the matrix determinant by several methods, written in the C ++ programming language, is given. The program is used as a laboratory stand for creating illustrations for the report. And also a study of methods for solving systems of linear algebraic equations is being carried out. The uselessness of calculating the inverse matrix is ​​proved, therefore, the paper provides more optimal ways to solve equations without calculating it. It is explained why there are so many different methods for calculating determinants and inverse matrices and their shortcomings are analyzed. Errors in the calculation of the determinant are also considered and the achieved accuracy is estimated. In addition to Russian terms, their English equivalents are also used in the work to understand under what names to search for numerical procedures in libraries and what their parameters mean.

Basic definitions and simple properties

Determinant

Let us introduce the definition of the determinant of a square matrix of any order. This definition will recurrent, that is, to establish what the determinant of the order matrix is, you need to already know what the determinant of the order matrix is. Note also that the determinant exists only for square matrices.

The determinant of a square matrix will be denoted by or det .

Definition 1. determinant square matrix second order number is called .

determinant square matrix of order , is called the number

where is the determinant of the order matrix obtained from the matrix by deleting the first row and the column with the number .

For clarity, we write down how you can calculate the determinant of a matrix of the fourth order:

Comment. The actual calculation of determinants for matrices above the third order based on the definition is used in exceptional cases. As a rule, the calculation is carried out according to other algorithms, which will be discussed later and which require less computational work.

Comment. In Definition 1, it would be more accurate to say that the determinant is a function defined on the set of square order matrices and taking values ​​in the set of numbers.

Comment. In the literature, instead of the term "determinant", the term "determinant" is also used, which has the same meaning. From the word "determinant" the designation det appeared.

Let us consider some properties of determinants, which we formulate in the form of assertions.

Statement 1. When transposing a matrix, the determinant does not change, that is, .

Statement 2. The determinant of the product of square matrices is equal to the product of the determinants of the factors, that is, .

Statement 3. If two rows in a matrix are swapped, then its determinant will change sign.

Statement 4. If a matrix has two identical rows, then its determinant is zero.

In the future, we will need to add strings and multiply a string by a number. We will perform these operations on rows (columns) in the same way as operations on row matrices (column matrices), that is, element by element. The result will be a row (column), which, as a rule, does not match the rows of the original matrix. In the presence of operations of adding rows (columns) and multiplying them by a number, we can also talk about linear combinations of rows (columns), that is, sums with numerical coefficients.

Statement 5. If a row of a matrix is ​​multiplied by a number, then its determinant will be multiplied by that number.

Statement 6. If the matrix contains a zero row, then its determinant is zero.

Statement 7. If one of the rows of the matrix is ​​equal to the other multiplied by a number (the rows are proportional), then the determinant of the matrix is ​​zero.

Statement 8. Let the i-th row in the matrix look like . Then , where the matrix is ​​obtained from the matrix by replacing the i-th row with the row , and the matrix is ​​obtained by replacing the i-th row with the row .

Statement 9. If one of the rows of the matrix is ​​added to another, multiplied by a number, then the determinant of the matrix will not change.

Statement 10. If one of the rows of a matrix is ​​a linear combination of its other rows, then the determinant of the matrix is ​​zero.

Definition 2. Algebraic addition to a matrix element is called a number equal to , where is the determinant of the matrix obtained from the matrix by deleting the i-th row and the j-th column. The algebraic complement to a matrix element is denoted by .

Example. Let be . Then

Comment. Using algebraic additions, the definition of 1 determinant can be written as follows:

Statement 11. Decomposition of the determinant in an arbitrary string.

The matrix determinant satisfies the formula

Example. Calculate .

Decision. Let's use the expansion in the third line, it's more profitable, because in the third line two numbers out of three are zeros. Get

Statement 12. For a square matrix of order at , we have the relation .

Statement 13. All properties of the determinant formulated for rows (statements 1 - 11) are also valid for columns, in particular, the expansion of the determinant in the j-th column is valid and equality at .

Statement 14. The determinant of a triangular matrix is ​​equal to the product of the elements of its main diagonal.

Consequence. The determinant of the identity matrix is ​​equal to one, .

Conclusion. The properties listed above make it possible to find determinants of matrices of sufficiently high orders with a relatively small amount of calculations. The calculation algorithm is the following.

Algorithm for creating zeros in a column. Let it be required to calculate the order determinant . If , then swap the first line and any other line in which the first element is not zero. As a result, the determinant , will be equal to the determinant of the new matrix with the opposite sign. If the first element of each row is equal to zero, then the matrix has a zero column and, by Statements 1, 13, its determinant is equal to zero.

So, we consider that already in the original matrix . Leave the first line unchanged. Let's add to the second line the first line, multiplied by the number . Then the first element of the second row will be equal to .

The remaining elements of the new second row will be denoted by , . The determinant of the new matrix according to Statement 9 is equal to . Multiply the first line by the number and add it to the third. The first element of the new third row will be equal to

The remaining elements of the new third row will be denoted by , . The determinant of the new matrix according to Statement 9 is equal to .

We will continue the process of obtaining zeros instead of the first elements of strings. Finally, we multiply the first line by a number and add it to the last line. The result is a matrix, denoted by , which has the form

and . To calculate the determinant of the matrix, we use the expansion in the first column

Since then

The determinant of the order matrix is ​​on the right side. We apply the same algorithm to it, and the calculation of the determinant of the matrix will be reduced to the calculation of the determinant of the order matrix. The process is repeated until we reach the second-order determinant, which is calculated by definition.

If the matrix does not have any specific properties, then it is not possible to significantly reduce the amount of calculations compared to the proposed algorithm. Another good side of this algorithm is that it is easy to write a program for a computer to calculate the determinants of matrices of large orders. In standard programs for calculating determinants, this algorithm is used with minor changes associated with minimizing the effect of rounding errors and input data errors in computer calculations.

Example. Compute Matrix Determinant .

Decision. The first line is left unchanged. To the second line we add the first, multiplied by the number:

The determinant does not change. To the third line we add the first, multiplied by the number:

The determinant does not change. To the fourth line we add the first, multiplied by the number:

The determinant does not change. As a result, we get

Using the same algorithm, we calculate the determinant of a matrix of order 3, which is on the right. We leave the first line unchanged, to the second line we add the first, multiplied by the number :

To the third line we add the first, multiplied by the number :

As a result, we get

Answer. .

Comment. Although fractions were used in the calculations, the result was an integer. Indeed, using the properties of determinants and the fact that the original numbers are integers, operations with fractions could be avoided. But in engineering practice, numbers are extremely rarely integers. Therefore, as a rule, the elements of the determinant will be decimal fractions and it is not advisable to use any tricks to simplify calculations.

inverse matrix

Definition 3. The matrix is ​​called inverse matrix for a square matrix if .

It follows from the definition that the inverse matrix will be a square matrix of the same order as the matrix (otherwise one of the products or would not be defined).

The inverse matrix for a matrix is ​​denoted by . Thus, if exists, then .

From the definition of an inverse matrix, it follows that the matrix is ​​the inverse of the matrix, that is, . Matrices and can be said to be inverse to each other or mutually inverse.

If the determinant of a matrix is ​​zero, then its inverse does not exist.

Since for finding the inverse matrix it is important whether the determinant of the matrix is ​​equal to zero or not, we introduce the following definitions.

Definition 4. Let's call the square matrix degenerate or special matrix, if non-degenerate or nonsingular matrix, if .

Statement. If an inverse matrix exists, then it is unique.

Statement. If a square matrix is ​​nondegenerate, then its inverse exists and (1) where are algebraic additions to elements .

Theorem. An inverse matrix for a square matrix exists if and only if the matrix is ​​nonsingular, the inverse matrix is ​​unique, and formula (1) is valid.

Comment. Particular attention should be paid to the places occupied by algebraic complements in the inverse matrix formula: the first index shows the number column, and the second is the number lines, in which the calculated algebraic complement should be written.

Example. .

Decision. Finding the determinant

Since , then the matrix is ​​nondegenerate, and the inverse for it exists. Finding algebraic additions:

We compose the inverse matrix by placing the found algebraic additions so that the first index corresponds to the column, and the second to the row: (2)

The resulting matrix (2) is the answer to the problem.

Comment. In the previous example, it would be more accurate to write the answer like this:
(3)

However, the notation (2) is more compact and it is more convenient to carry out further calculations, if any, with it. Therefore, writing the answer in the form (2) is preferable if the elements of the matrices are integers. And vice versa, if the elements of the matrix are decimal fractions, then it is better to write the inverse matrix without a factor in front.

Comment. When finding the inverse matrix, you have to perform quite a lot of calculations and an unusual rule for arranging algebraic additions in the final matrix. Therefore, there is a high chance of error. To avoid errors, you should do a check: calculate the product of the original matrix by the final one in one order or another. If the result is an identity matrix, then the inverse matrix is ​​found correctly. Otherwise, you need to look for an error.

Example. Find the inverse of a matrix .

Decision. - exist.

Answer: .

Conclusion. Finding the inverse matrix by formula (1) requires too many calculations. For matrices of the fourth order and higher, this is unacceptable. The real algorithm for finding the inverse matrix will be given later.

Calculating the determinant and inverse matrix using the Gauss method

The Gauss method can be used to find the determinant and inverse matrix.

Namely, the matrix determinant is equal to det .

The inverse matrix is ​​found by solving systems of linear equations using the Gaussian elimination method:

Where is the j-th column of the identity matrix , is the required vector.

The resulting solution vectors - form, obviously, the columns of the matrix, since .

Formulas for the determinant

1. If the matrix is ​​nonsingular, then and (the product of the leading elements).

Since for finding the inverse matrix it is important whether the determinant of the matrix is ​​equal to zero or not, we introduce the following definitions.

Definition 14.9 Let's call the square matrix degenerate or special matrix, if non-degenerate or nonsingular matrix, if .

Offer 14.21 If an inverse matrix exists, then it is unique.

Proof. Let two matrices and be the inverse of the matrix . Then

Hence, .

Cramer's rule.

Let the matrix equation AX=B

Where ; is the determinant obtained from the determinant D replacement i-th column by the column of free members of the matrix B:

Proof The theorem is divided into three parts:

1. The solution of system (1) exists and is unique.

2. Equalities (2) are a consequence of the matrix equation (1).

3. Equalities (2) entail matrix equation (1).

Since , there also exists a unique inverse matrix .
Multiplying both parts of the matrix equation (1) on the left by , we obtain the solution of this equation:

uniqueness inverse matrix proves the first part of the theorem.

Let's move on to the proof one-to-one correspondence between formulas (1) and (2).

Using formula (4), we obtain an expression for i-th element. For this you need to multiply i-th row of the matrix

per column B.

Given that i-th row of the associated matrix is ​​composed of algebraic additions , we get the following result:

The derivation of Cramer's formulas is complete. Let us now show that the expressions

Let's change the order of summation on the right side of the resulting expression:

where is the delta Kronecker symbol.

Given that the delta symbol removes the summation over one of the indices, we get the required result:

Complex numbers: The idea is to define new objects with the help of known ones. Real numbers are located on a straight line. When passing to the plane, we obtain complex numbers. Definition: A complex number is a pair of real numbers z = (a,b). The number a = Re z is called the real part, and b = Im z the imaginary part of the complex number z .

Operations on complex numbers: The complex numbers z1 z2 are Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Addition: Z=z1+z2. ⇔Rez=Rez1+Rez2 & Imz1+ Imz2. The number (0,0) is denoted by 0. This is the neutral element. It is verified that the addition of complex numbers has properties similar to those of the addition of real numbers. (1. Z1+ z2 = z2 + z1 – commutativity; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – associativity; 3. Z1 + 0 = z1 - existence of zero (neutral element); 4. z + (−z) = 0 - the existence of the opposite element). Multiplication: z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. A complex number z lies on the real axis if Imz = 0 . The results of operations on such numbers coincide with the results of operations on ordinary real numbers. Multiplication of complex numbers has the properties of closure, commutativity and associativity. The number (1,0) is denoted by 1. It is a neutral element by multiplication. If a∈ R, z ∈C , then Re(az) = aRe z, Im(az) = a Imz . Definition The number (0,1) is denoted by i and is called the imaginary unit. In this notation, we obtain the representation of a complex number in algebraic form: z = a + ib, a,b∈ R. i=-1.(a,b)=(a,0)+(0,b) ;(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-b1b2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z!=0; a 2 + b 2 > 0 (a + ib) (a-ib / a 2 + b 2) = 1. The number is called conjugate to z if Re =Re z ; Im =- Im z.

= + ; = ; z =(a+ib)(a-ib)=a 2 +b 2 The modulus of a number z is a real number| z |= . Fair formula| z| 2 = z It follows from the definition that z ≠ 0⇔| z|≠ 0. z -1 = /|z| 2 (1)

Trigonometric form of a complex number: a=rcos(t); b=r sin(t). Z=a+ib=r(cos(t)+isin(t))(2) t-argument of a complex number. Z1=z2 =>|z1|=|z2|

arg(z1)-arg(z2)=2pk.

Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)( one)

Arg(z1z2)=arg(z1)+arg(z2) (2)

Z!=0 z -1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))

R(cos(t)-isin(t))

Definition: The root of the degree n from unity is the solution of the equation z n =1 Proposal. There are n distinct nth roots of unity. They are written as z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 . Theorem. In the set of complex numbers, the equation always has n solutions. Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-integers. K belongs to Z. k=2=E 2 =E n-1 E n ; E n =1; E n+p =E p . Thus, it is proved that the solutions of the equation are the vertices of a regular n-gon, and one of the vertices coincides with 1.

nth root of z 0. Z k \u003d Z 0; Z0 =0=>Z=0; Z 0 !=0;Z=r(cos(t)-isin(t)); Z 0 \u003d r 0 (cos (t0) + isin (t0)); r0!=0; Z n \u003d r n (cos (nt) + isin (nt))

r n \u003d r 0, nt-t 0 \u003d 2pk; r=; t=(2пk+t0)/n; z= (cos((2pk+t0)/n)+isin((2pk+t0)/n)= (cos t0/n+isin t0/n)(cos(2pk/n)+isin(2pk/n) )=Z 1 E k ;z=z 1 E k ;Z 1 n =z 0, k=0, n=1

Matrices. Definition: An m × n matrix is ​​a rectangular table containing m rows and n columns, whose elements are real or complex numbers. Matrix elements have double indices.

If m = n, then it is a square matrix of order m, and elements with the same index form the main diagonal of the matrix.

Matrix Operations: Definition: Two matrices A,B are called

equal if their sizes are the same and A = B,1≤ i ≤ m,1≤ j ≤ n

Addition. Matrices of the same size are considered. Definition:C = A + B ⇔ C = A + B, ∀i, j Offer. Matrix addition is commutative, associative, there is a neutral element and for each matrix there is an opposite element.

The neutral element is the zero matrix, all elements of which are equal to 0. It is denoted by Θ.

Multiplication. An m × n matrix A is denoted by Amn . Definition: C mk =A mn B nk ó

C= Note that, in general, multiplication is not commutative. Closedness is valid for a square matrix of a fixed size. Let three matrices Amn , Bnk , Ckr be given. Then (AB)C = A(BC). If a product of 3 matrices exists, then it is associative.

The Kronecker symbol δij . It is 1 if the indices match, and 0 otherwise. Definition. The identity matrix I n is a square matrix of order n for which the equalities n I n [ i | j] = δij Offer. Equalities I m A mn =A mn I n =A mn

The addition and multiplication of matrices is connected by the laws of distributivity. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +

Matrix transposition. A transposed matrix is ​​a matrix obtained from the original one by replacing rows with columns.

(A+B) T = A T + B T

(AB) T \u003d B T A T; (AB) T \u003d (AB) \u003d \u003d (B T A T)

Multiplying a matrix by a number. The product of the number a and the matrix A mn is called the new matrix B=aA

1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;

A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)

linear space(L) over the field F is called the set of vectors L=(α,β..)

1.α+β=β+α(commutativity) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(associativity) 3.α+θ=α, α∙1=α(existence of neutral) 4.α+(-α)=θ (existence of opposite)

a(α+β)=aα+aβ, (a+b)α=aα+bα. Documentation (|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a and b>0, |a+b|=a+b,|a|=a,|b|=b.) aα+(-a)α=θ, (a+0)α=aα

An example of a linear space is a set of fixed-size matrices with operations of addition and multiplication by a number.

The system of linear vectors is called linearly dependent, if 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ If the system is not linearly dependent, then it is linearly independent. Consider 1. n=1 α 1 depend. a 1 ≠0, a 1 α 1 =θ, a 1 -1 (a 1 α 1)= a 1 -1∙ θ=θ, (a 1 -1 a 1)α 1 =1∙α 1 =α 1 ; 2. n=2 α 1 ,α 2 depend. a 1 ≠0, a 1 α 1 + a 2 α 2 =θ, α 1 = -a 1 -1 a 2 α 2 = b 2 α 2; 3.n≥2 α 1 ..α n depend. a 1 ≠0, α 1 =Σ k =2 n b k α k , 1α 1 - Σ k =2 n b k α k =θ, (1,b 2 ..b n)≠0

Offer: A system of vectors containing more than 1 vector is linearly dependent, then some vector of the system is a linear combination of the others.

If a system of vectors contains a linearly dependent subsystem, then the entire system is linearly dependent. Documentation: (α 1 ..α n depend. System: α 1 ..α n ;α n +1 ..α m , a 1 α 1 +..+a n α n +0α n +1 +.. +0α m =θ, a 1 ..a n ,0..0≠0.) If the system contains a null vector, then it is linearly dependent. Linear space theorem: (Let 2 systems of vectors α 1 ..α m , β 1 ..β n be given. The system of vectors α is expressed in terms of β if each vector α is a linear combination β α i = Σ k =1 n a ik β k , (α ) ( (β), (β) ( (γ)→ (α) ( (γ)) Theorem: Given 2 systems of vectors, α is independent and, (α) ( (β)→m≤n Let us prove that α 1 ..α m +1 β 1 ..β m (α) ( (β)→(α) depends (Let's prove by induction. m=1: α 1 =a 11 β 1 , α 2 =a 21 β 1. a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 =θ. α 1 = a 11 β 1 +.. a 1 n -1 β n -1 .. α n = a n 1 β 1 + .. a nn -1 β n - 1 If all coefficients =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ the whole system is linearly dependent a 1 n -1 ≠0 α 2 ′= α 2 –с 2 α 1 =b 21 β 1 +..+b 2 n -2 β n -2 , c 2 =a 2 n -1 / a 1 n -1 , α 3 ′= α 3 –с 3 α 1 .. α n ′= α n –с n α 1. By pre-induction, there exists a non-zero set of numbers d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 ( α 2 –с 2 α 1)+d 3 (α 3 –с 3 α 1)+.. d n (α n –с n α 1)=θ , (α) ( (β), m>n →(α )depend if (α) independent →m≤n)

MLNP-max.line.independent.subsystem. Let a system of vectors α 1 ..α n of some subsystem be given. α i 1 ..α in is called MLIS if 1. α 1 ..α n is independent2. α i 1 ..α ir , α ij depends. Each vector of the system is a linear combination of MLLM vectors. ( α i 1 ..α ir , α ij dependent a i 1 α i 1 +.. a ir α ir +a ij α ij =θ

a i 1 ..a ir , a ij ≠0 if a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 contradiction a ij ≠0 α ij = a ij - 1 (-a i 1 α i 1 -.. a ir α ir) (α 1 ..α n) ( (α i 1 ..α ir)

Consequence: Any 2 MLIS from one system of vectors contain the same number of vectors (α i 1 ..α ir) ( (α j 1 ..α jk) , (α j 1 ..α jk) ( (α i 1 ..α ir ) k≤r, r≤k →r=k The number of MLLM vectors is called rank original system. In the case of a linear space (a system of vectors consists of all vectors in the space), the MLLM mb is either finite or infinite. We consider the final case. The number of vectors (rank) is the dimension of the linear space. MLNP base. The space of directed segments. Two non-collinear vectors make up base in the space of vectors on the plane. α 3 = α 1 ′+ α 2 ′=a 1 α 1 + a 2 α 2 . 3 vectors linearly dependent α 3 =a 1 α 1 + a 2 α 2 . Complanarity - 3 vectors are parallel to the same plane α 4 = α 4 ′+ α 5 ′ , α 4 ′=a 1 α 1 + a 2 α 2 , α 5 ′= a 3 α 3 , α 4 = a 1 α 1 + a 2 α 2 + a 3 α 3 . Space of strings of length n. α= Offer: The space of strings of length n has dimension n. ( ξ 1 =<1…0>ξ2 =<0,1…0>.. n =<0…1>,a 1 ξ 1 + a 2 ξ 2 +.. a n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (linear independence) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →the space of strings of length n has dimension and n.

Matrix rank.

Two systems of vectors α and β are called equivalent if each vector

α( β(expressed) and β( α.

Offer. The ranks of equivalent systems coincide.

α i 1 , α i 2 ,…, α ir – MLLM α , β i 1 , β i 2 ,…, β ik – MLLM β , α i 1 , α i 2 ,…, α ir< β < β i 1 , β i 2 ,…, β ik → r<=k

Swapping α and β places → r>=k >>> Hence, r=k.

Definition. Let the matrix A=

α i =

Matrix rank A is called the rank of the system of vectors α1, α2,…, αm, composed of this matrix >>rank(A)-rank

From the definition, it is obvious that when the columns are rearranged, the rank does not change. Let us show that when the columns are rearranged, the rank does not change either.

A'=

α'i=

Linear dependent:

b 1 α 1 + b 2 α 2 +…+ b m α m =θ, b 1 a 11 +b 2 a 21 +…+b m a m 1=0, b 1 α' 1 + b 2 α' 2 +…+ b m α' m , b 1 a 11 +b 2 a 21 +…+b m a m 1=0

It is equal to the sum of the products of the elements of some row or column and their algebraic complements, i.e. , where i 0 is fixed.
The expression (*) is called the decomposition of the determinant D in terms of the elements of the row with the number i 0 .

Service assignment. This service is designed to find the determinant of the matrix online with the execution of the entire solution in Word format. Additionally, a solution template is created in Excel.

Instruction. Select the dimension of the matrix, click Next.

Matrix dimension 2 3 4 5 6 7 8 9 10

There are two ways to calculate the determinant: a-priory and decomposition by row or column. If you want to find the determinant by creating zeros in one of the rows or columns, then you can use this calculator.

Algorithm for finding the determinant

1. For matrices of order n=2, the determinant is calculated by the formula: Δ=a 11 *a 22 -a 12 *a 21
2. For matrices of order n=3, the determinant is calculated through algebraic additions or Sarrus method.
3. A matrix with a dimension greater than three is decomposed into algebraic additions, for which their determinants (minors) are calculated. For example, 4th order matrix determinant is found through expansion in rows or columns (see example).

To calculate the determinant containing functions in the matrix, standard methods are used. For example, calculate the determinant of a 3rd order matrix:

Let's use the first line expansion.
Δ = sin(x)× + 1× = 2sin(x)cos(x)-2cos(x) = sin(2x)-2cos(x)

Methods for calculating determinants

Finding the determinant through algebraic additions is a common method. Its simplified version is the calculation of the determinant by the Sarrus rule. However, with a large matrix dimension, the following methods are used:

1. calculation of the determinant by order reduction
2. calculation of the determinant by the Gaussian method (by reducing the matrix to a triangular form).

In Excel, to calculate the determinant, the function = MOPRED (range of cells) is used.

Applied use of determinants

The determinants are calculated, as a rule, for a specific system, given in the form of a square matrix. Consider some types of tasks on finding matrix determinant. Sometimes it is required to find an unknown parameter a for which the determinant would be equal to zero. To do this, it is necessary to draw up an equation for the determinant (for example, according to triangle rule) and, equating it to 0 , calculate the parameter a .
decomposition by columns (by the first column):
Minor for (1,1): Delete the first row and the first column from the matrix.
Let's find the determinant for this minor. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6.

Let's determine the minor for (2,1): to do this, we delete the second row and the first column from the matrix.

Let's find the determinant for this minor. ∆ 2,1 = (0 (-2)-2 (-2)) = 4 . Minor for (3,1): Delete the 3rd row and 1st column from the matrix.
Let's find the determinant for this minor. ∆ 3,1 = (0 1-2 (-2)) = 4
The main determinant is: ∆ = (1 (-6)-3 4+1 4) = -14

Let's find the determinant using expansion by rows (by the first row):
Minor for (1,1): Delete the first row and the first column from the matrix.

Let's find the determinant for this minor. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6. Minor for (1,2): Delete the 1st row and 2nd column from the matrix. Let us calculate the determinant for this minor. ∆ 1,2 \u003d (3 (-2) -1 1) \u003d -7. And to find the minor for (1,3) we delete the first row and the third column from the matrix. Let's find the determinant for this minor. ∆ 1.3 = (3 2-1 2) = 4
We find the main determinant: ∆ \u003d (1 (-6) -0 (-7) + (-2 4)) \u003d -14

System of m linear equations with n unknowns called a system of the form

where aij and b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n- unknown. In the notation of the coefficients aij first index i denotes the number of the equation, and the second j is the number of the unknown at which this coefficient stands.

The coefficients for the unknowns will be written in the form of a matrix , which we will call system matrix.

The numbers on the right sides of the equations b 1 ,…,b m called free members.

Aggregate n numbers c 1 ,…,c n called decision of this system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.

Our task will be to find solutions to the system. In this case, three situations may arise:

A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called incompatible.

Consider ways to find solutions to the system.

MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS

Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:

Consider the matrix of the system 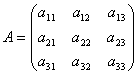and matrix columns of unknown and free members

Let's find the product

those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then, using the definition of matrix equality, this system can be written as

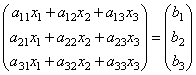or shorter A∙X=B.

Here matrices A and B are known, and the matrix X unknown. She needs to be found, because. its elements are the solution of this system. This equation is called matrix equation.

Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, the inverse of the matrix A: . Insofar as A -1 A = E and E∙X=X, then we obtain the solution of the matrix equation in the form X = A -1 B .

Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations is the same as the number of unknowns. However, the matrix notation of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A is not square and therefore it is impossible to find a solution to the system in the form X = A -1 B.

Examples. Solve systems of equations.

CRAMER'S RULE

Consider a system of 3 linear equations with three unknowns:

Third-order determinant corresponding to the matrix of the system, i.e. composed of coefficients at unknowns,

called system determinant.

We compose three more determinants as follows: we replace successively 1, 2 and 3 columns in the determinant D with a column of free terms

Then we can prove the following result.

Theorem (Cramer's rule). If the determinant of the system is Δ ≠ 0, then the system under consideration has one and only one solution, and

Proof. So, consider a system of 3 equations with three unknowns. Multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation - on A21 and 3rd - on A 31:

Let's add these equations:

Consider each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in terms of the elements of the 1st column

Similarly, it can be shown that and .

Finally, it is easy to see that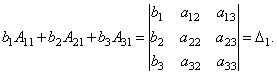

Thus, we get the equality: .

Hence, .

The equalities and are derived similarly, whence the assertion of the theorem follows.

Thus, we note that if the determinant of the system is Δ ≠ 0, then the system has a unique solution and vice versa. If the determinant of the system is equal to zero, then the system either has an infinite set of solutions or has no solutions, i.e. incompatible.

Examples. Solve a system of equations

GAUSS METHOD

The previously considered methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gaussian method is more universal and is suitable for systems with any number of equations. It consists in the successive elimination of unknowns from the equations of the system.

Consider again a system of three equations with three unknowns:

.

We leave the first equation unchanged, and from the 2nd and 3rd we exclude the terms containing x 1. To do this, we divide the second equation by a 21 and multiply by - a 11 and then add with the 1st equation. Similarly, we divide the third equation into a 31 and multiply by - a 11 and then add it to the first one. As a result, the original system will take the form:

Now, from the last equation, we eliminate the term containing x2. To do this, divide the third equation by , multiply by and add it to the second. Then we will have a system of equations:

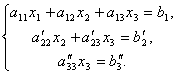
Hence from the last equation it is easy to find x 3, then from the 2nd equation x2 and finally from the 1st - x 1.

When using the Gaussian method, the equations can be interchanged if necessary.

Often, instead of writing a new system of equations, they limit themselves to writing out the extended matrix of the system:

and then bring it to a triangular or diagonal form using elementary transformations.

To elementary transformations matrices include the following transformations:

1. permutation of rows or columns;
2. multiplying a string by a non-zero number;
3. adding to one line other lines.

Examples: Solve systems of equations using the Gauss method.

Thus, the system has an infinite number of solutions.

2.If │A│=0, then the matrix A is degenerate and the inverse matrix A -1 does not exist.

If the determinant of the matrix A is not equal to zero, then the inverse matrix exists.

3. Find A T transposed to A.

4. Find the algebraic complements of the elements of the transposed matrix and compose the adjoint matrix from them. 5. We calculate the inverse matrix according to the formula: 6. Check the correctness of the calculation of the inverse matrix, based on its definition A -1 ∙A = A ∙A -1 = E.

· №28

· In an m x n matrix, by deleting any rows and columns, one can select square submatrices of the kth order, where k≤min(m; n). The determinants of such submatrices are called k-th order minors of the matrix A.

· The rank of a matrix A is the highest order of non-zero minors of this matrix.

· The rank of a matrix A is denoted by rang A or r(A).

· From the definition follows:

· 1) the rank of a matrix of size m x n does not exceed the smallest of its sizes, i.e. r(A) ≤ min (m; n).

· 2) r(A)=0 if and only if all elements of the matrix are equal to zero, i.e. A=0.

· 3) For a square matrix of the nth order, r(A) = n if and only if the matrix A is nonsingular.

· In the general case, determining the rank of a matrix by enumeration of all minors is quite laborious. To facilitate this task, elementary transformations are used that preserve the rank of the matrix:

· 1) Rejection of the zero row (column).

· 2) Multiplication of all elements of a row (column) of a matrix by a non-zero number.

· 3) Changing the order of rows (columns) of the matrix.

· 4) Adding to each element of one row (column) the corresponding elements of another row (column), multiplied by any number.

· 5) Matrix transposition.

· Theorem. The rank of a matrix will not change under elementary transformations of the matrix.

№31

— Let the number of equations in system (1) be equal to the number of variables, i.e. m=n. Then the matrix of the system is square, and its determinant Δ=│А│ is called the determinant of the system.

— Suppose that │А│ is not equal to zero, then there is an inverse matrix A -1 .

— Multiplying both parts of the matrix equality on the left by the inverse matrix A -1 we get:

— A -1 (AX) \u003d A -1 B.

The solution of the system of equations by the inverse matrix method will be the column matrix:

X \u003d A -1 B.

(A -1 A)X \u003d EX \u003d X

— Cramer's theorem. Let Δ be the determinant of the matrix of system A, and Δ j be the determinant of the matrix obtained from the matrix by replacing the jth column with a column of free terms. Then if Δ is not equal to zero, then the system has a unique solution defined by the Cramer formulas:

where j=1..n.

№33

—
The Gauss method - the method of successive elimination of variables - consists in the fact that, with the help of elementary transformations, the system of equations is reduced to an equivalent system of a stepped or triangular type.

— Consider the matrix:

— this matrix is ​​called the extended matrix of system (1), because in addition to the matrix of system A, it additionally includes a column of free members.

№26

— An N-dimensional vector is an ordered set of n real numbers written as X=(x 1,x 2,...x n) , where x i is the i-th component of the vector X.

— Two n-dimensional vectors are equal if and only if their respective components are equal, i.e. X=Y if x i =y i , i=1…n.

The set of vectors with real components, in which the operations of adding vectors and multiplying a vector by a number that satisfy the above properties, are defined, is called a vector space.

— A vector space R is called n-dimensional if there are n linearly independent vectors in it, and any n + 1 vectors are already dependent. The number n is called the dimension of the vector space R and is denoted dim(R).

№29

Linear operators

— Definition. If a law (rule) is given, according to which each vector x of the space is associated with a single vector y of the space

then they say: that the operator (transformation, mapping) A(x) is given, acting from to and

write y=A(x).

— An operator is called linear if for any vector x and y of the space

and any number λ, the following relations hold:

№37

— Let А be a set consisting of a finite number of elements a 1 , a 2 , a 3 …a n . Groups can be formed from various elements of the set A. If each group includes the same number of elements m (m out of n), then they are said to form compounds of n elements with m each. There are three types of connections: placements, combinations and permutations.

— connections, each of which includes all n elements of the set A and which, therefore, differ from each other only in the order of the elements are called permutations of n elements. The number of such permutations is denoted by the symbol Р n .

№35

The classical definition of probability is based on the concept of the equiprobability of events.

Equivalence of events means that there is no reason to prefer any one of them over others.

Let's consider a test, as a result of which event A can occur. Each outcome, in which event A occurs, is called a favorable event A.

The probability of an event A (denoted by P(A)) is the ratio of the number of outcomes favorable to the event A (denoted by k) to the number of all test outcomes - N i.e. P(A)=k/N.

— The following properties follow from the classical definition of probability:

— The probability of any event lies between zero and one.

— The probability of a certain event is equal to one.

— The probability of an impossible event is zero

№39, 40

— Addition theorem. If A and B are inconsistent, then P(A + B) = P(A) + P(B)