All the equations of the plane that are discussed in the following paragraphs can be obtained from the general equation of the plane, and also reduced to the general equation of the plane. Thus, when one speaks of the equation of a plane, one means the general equation of a plane, unless otherwise stated.

Equation of a plane in segments.

View plane equation , where a , b and c are non-zero real numbers, is called plane equation in segments.

This name is not accidental. The absolute values ​​of the numbers a, b and c are equal to the lengths of the segments that the plane cuts off on the coordinate axes Ox, Oy and Oz, respectively, counting from the origin. The sign of the numbers a, b and c shows in which direction (positive or negative) the segments on the coordinate axes should be laid.

For example, let's construct a plane in the rectangular coordinate system Oxyz, defined by the equation of the plane in the segments . To do this, mark a point that is 5 units away from the origin in the negative direction of the abscissa axis, 4 units in the negative direction of the y-axis, and 4 units in the positive direction of the applicate axis. It remains to connect these points with straight lines. The plane of the resulting triangle is the plane corresponding to the equation of the plane in segments of the form .

For more information, refer to the article plane equation in segments, it shows the reduction of the plane equation in segments to the general equation of the plane, and you will also find detailed solutions to typical examples and problems.

Normal equation of the plane.

The general view plane equation is called normal equation of the plane, if is equal to one, that is, , and .

You can often see that the normal equation of the plane is written as . Here, are the direction cosines of the normal vector of a given plane of unit length, that is, and p is a non-negative number equal to the distance from the origin to the plane.

The normal equation of a plane in the rectangular coordinate system Oxyz defines a plane that is at a distance p from the origin in the positive direction of the normal vector of this plane . If p=0 , then the plane passes through the origin.

Let us give an example of a normal plane equation.

Let the plane be given in a rectangular coordinate system Oxyz by the general equation of the plane of the form . This general equation of the plane is the normal equation of the plane. Indeed, and the normal vector of this plane has length equal to one, because .

The plane equation in its normal form allows you to find the distance from a point to a plane.

We recommend that you deal with this type of plane equation in more detail, see detailed solutions to typical examples and problems, and also learn how to bring the general plane equation to normal form. You can do this by referring to the article.

Bibliography.

• Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometry. Textbook for 10-11 grades of high school.
• Bugrov Ya.S., Nikolsky S.M. Higher Mathematics. Volume One: Elements of Linear Algebra and Analytic Geometry.
• Ilyin V.A., Poznyak E.G. Analytic geometry.

The canonical equations of a straight line in space are equations that define a straight line passing through a given point collinearly to a direction vector.

Let a point and a direction vector be given. An arbitrary point lies on a line l only if the vectors and are collinear, i.e., they satisfy the condition:

.

The above equations are the canonical equations of the line.

Numbers m , n and p are projections of the direction vector onto the coordinate axes. Since the vector is non-zero, then all numbers m , n and p cannot be zero at the same time. But one or two of them may be zero. In analytical geometry, for example, the following notation is allowed:

,

which means that the projections of the vector on the axes Oy and Oz are equal to zero. Therefore, both the vector and the straight line given by the canonical equations are perpendicular to the axes Oy and Oz, i.e. planes yOz .

Example 1 Compose equations of a straight line in space perpendicular to a plane and passing through the point of intersection of this plane with the axis Oz .

Decision. Find the point of intersection of the given plane with the axis Oz. Since any point on the axis Oz, has coordinates , then, assuming in the given equation of the plane x=y= 0 , we get 4 z- 8 = 0 or z= 2 . Therefore, the point of intersection of the given plane with the axis Oz has coordinates (0; 0; 2) . Since the desired line is perpendicular to the plane, it is parallel to its normal vector. Therefore, the normal vector can serve as the directing vector of the straight line given plane.

Now we write the desired equations of the straight line passing through the point A= (0; 0; 2) in the direction of the vector :

Equations of a straight line passing through two given points

A straight line can be defined by two points lying on it and In this case, the directing vector of the straight line can be the vector . Then the canonical equations of the line take the form

.

The above equations define a straight line passing through two given points.

Example 2 Write the equation of a straight line in space passing through the points and .

Decision. We write the desired equations of the straight line in the form given above in the theoretical reference:

.

Since , then the desired line is perpendicular to the axis Oy .

Straight as a line of intersection of planes

A straight line in space can be defined as a line of intersection of two non-parallel planes and, i.e., as a set of points that satisfy a system of two linear equations

The equations of the system are also called the general equations of a straight line in space.

Example 3 Compose canonical equations of a straight line in the space given by general equations

Decision. To write the canonical equations of a straight line or, which is the same, the equation of a straight line passing through two given points, you need to find the coordinates of any two points on the straight line. They can be the points of intersection of a straight line with any two coordinate planes, for example yOz and xOz .

Point of intersection of a line with a plane yOz has an abscissa x= 0 . Therefore, assuming in this system of equations x= 0 , we get a system with two variables:

Her decision y = 2 , z= 6 together with x= 0 defines a point A(0; 2; 6) of the desired line. Assuming then in the given system of equations y= 0 , we get the system

Her decision x = -2 , z= 0 together with y= 0 defines a point B(-2; 0; 0) intersection of a line with a plane xOz .

Now we write the equations of a straight line passing through the points A(0; 2; 6) and B (-2; 0; 0) :

,

or after dividing the denominators by -2:

,

In this lesson, we will look at how to use the determinant to compose plane equation. If you do not know what a determinant is, go to the first part of the lesson - " Matrices and determinants». Otherwise, you risk not understanding anything in today's material.

Equation of a plane by three points

Why do we need the equation of the plane at all? It's simple: knowing it, we can easily calculate angles, distances and other crap in problem C2. In general, this equation is indispensable. Therefore, we formulate the problem:

Task. There are three points in space that do not lie on the same straight line. Their coordinates:

M = (x 1 , y 1 , z 1);
N \u003d (x 2, y 2, z 2);
K \u003d (x 3, y 3, z 3);

It is required to write the equation of the plane passing through these three points. And the equation should look like:

Ax + By + Cz + D = 0

where the numbers A , B , C and D are the coefficients that, in fact, you want to find.

Well, how to get the equation of the plane, if only the coordinates of the points are known? The easiest way is to substitute the coordinates into the equation Ax + By + Cz + D = 0. You get a system of three equations that is easily solved.

Many students find this solution extremely tedious and unreliable. Last year's exam in mathematics showed that the probability of making a computational error is really high.

Therefore, the most advanced teachers began to look for simpler and more elegant solutions. And they did find it! True, the technique obtained is more likely to be related to higher mathematics. Personally, I had to rummage through the entire Federal list of textbooks to make sure that we have the right to use this technique without any justification and evidence.

Equation of the plane through the determinant

Enough ranting, let's get down to business. To begin with, a theorem on how the matrix determinant and the equation of the plane are related.

Theorem. Let the coordinates of three points through which the plane must be drawn be given: M = (x 1 , y 1 , z 1); N \u003d (x 2, y 2, z 2); K \u003d (x 3, y 3, z 3). Then the equation of this plane can be written in terms of the determinant:

For example, let's try to find a pair of planes that actually occur in C2 problems. Take a look at how fast everything counts:

A 1 = (0, 0, 1);
B = (1, 0, 0);
C 1 = (1, 1, 1);

We compose the determinant and equate it to zero:

Opening the determinant:

a = 1 1 (z − 1) + 0 0 x + (−1) 1 y = z − 1 − y;
b = (−1) 1 x + 0 1 (z − 1) + 1 0 y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

As you can see, when calculating the number d, I tweaked the equation a little so that the variables x, y, and z were in the correct sequence. That's all! The equation of the plane is ready!

Task. Write an equation for a plane passing through the points:

A = (0, 0, 0);
B 1 = (1, 0, 1);
D 1 = (0, 1, 1);

Immediately substitute the coordinates of the points in the determinant:

Expanding the determinant again:

a = 1 1 z + 0 1 x + 1 0 y = z;
b = 1 1 x + 0 0 z + 1 1 y = x + y;
d \u003d a - b \u003d z - (x + y) \u003d z - x - y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

So, the plane equation is obtained again! Again, at the last step, I had to change the signs in it in order to get a more “beautiful” formula. It is not necessary to do this in this solution, but it is still recommended - in order to simplify the further solution of the problem.

As you can see, it is now much easier to write the equation of the plane. We substitute the points into the matrix, calculate the determinant - and that's it, the equation is ready.

This could be the end of the lesson. However, many students constantly forget what is inside the determinant. For example, which line contains x 2 or x 3 , and which line just x . To finally deal with this, let's trace where each number comes from.

Where does the formula with the determinant come from?

So, let's figure out where such a harsh equation with a determinant comes from. This will help you remember it and apply it successfully.

All planes that occur in Problem C2 are defined by three points. These points are always marked on the drawing, or even indicated directly in the problem text. In any case, to compile the equation, we need to write out their coordinates:

M = (x 1 , y 1 , z 1);
N \u003d (x 2, y 2, z 2);
K \u003d (x 3, y 3, z 3).

Consider one more point on our plane with arbitrary coordinates:

T = (x, y, z)

We take any point from the first three (for example, point M ) and draw vectors from it to each of the three remaining points. We get three vectors:

MN = (x 2 - x 1, y 2 - y 1, z 2 - z 1);
MK = (x 3 - x 1, y 3 - y 1, z 3 - z 1);
MT = (x - x 1 , y - y 1 , z - z 1).

Now let's make a square matrix from these vectors and equate its determinant to zero. The coordinates of the vectors will become the rows of the matrix - and we will get the same determinant that is indicated in the theorem:

This formula means that the volume of the box built on the vectors MN , MK and MT is equal to zero. Therefore, all three vectors lie in the same plane. In particular, an arbitrary point T = (x, y, z) is exactly what we were looking for.

Replacing points and rows of the determinant

Determinants have some wonderful properties that make it even easier to solution of problem C2. For example, it does not matter to us from which point to draw vectors. Therefore, the following determinants give the same plane equation as the one above:

You can also swap the lines of the determinant. The equation will remain unchanged. For example, many people like to write a line with the coordinates of the point T = (x; y; z) at the very top. Please, if it's convenient for you:

It confuses some that one of the lines contains variables x , y and z , which do not disappear when substituting points. But they shouldn't disappear! By substituting the numbers into the determinant, you should get the following construction:

Then the determinant is expanded according to the scheme given at the beginning of the lesson, and the standard equation of the plane is obtained:

Ax + By + Cz + D = 0

Take a look at an example. He is the last one in today's lesson. I will deliberately swap the lines to make sure that the answer will be the same equation of the plane.

Task. Write an equation for a plane passing through the points:

B 1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).

So, we consider 4 points:

B 1 = (1, 0, 1);
C = (1, 1, 0);
D 1 = (0, 1, 1);
T = (x, y, z).

First, let's make a standard determinant and equate it to zero:

Opening the determinant:

a = 0 1 (z − 1) + 1 0 (x − 1) + (−1) (−1) y = 0 + 0 + y;
b = (−1) 1 (x − 1) + 1 (−1) (z − 1) + 0 0 y = 1 − x + 1 − z = 2 − x − z;
d \u003d a - b \u003d y - (2 - x - z) \u003d y - 2 + x + z \u003d x + y + z - 2;
d = 0 ⇒ x + y + z − 2 = 0;

That's it, we got the answer: x + y + z − 2 = 0 .

Now let's rearrange a couple of lines in the determinant and see what happens. For example, let's write a line with variables x, y, z not at the bottom, but at the top:

Let's expand the resulting determinant again:

a = (x − 1) 1 (−1) + (z − 1) (−1) 1 + y 0 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) 1 0 + y (−1) (−1) + (x − 1) 1 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

We got exactly the same plane equation: x + y + z − 2 = 0. So, it really does not depend on the order of the rows. It remains to write down the answer.

So, we have seen that the equation of the plane does not depend on the sequence of lines. It is possible to carry out similar calculations and prove that the equation of the plane does not depend on the point whose coordinates we subtract from the other points.

In the problem considered above, we used the point B 1 = (1, 0, 1), but it was quite possible to take C = (1, 1, 0) or D 1 = (0, 1, 1). In general, any point with known coordinates lying on the desired plane.

Any equation of the first degree with respect to coordinates x, y, z

Ax + By + Cz +D = 0 (3.1)

defines a plane, and vice versa: any plane can be represented by equation (3.1), which is called plane equation.

Vector n(A, B, C) orthogonal to the plane is called normal vector planes. In equation (3.1), the coefficients A, B, C are not equal to 0 at the same time.

Special cases of equation (3.1):

1. D = 0, Ax+By+Cz = 0 - the plane passes through the origin.

2. C = 0, Ax+By+D = 0 - the plane is parallel to the Oz axis.

3. C = D = 0, Ax + By = 0 - the plane passes through the Oz axis.

4. B = C = 0, Ax + D = 0 - the plane is parallel to the Oyz plane.

Coordinate plane equations: x = 0, y = 0, z = 0.

A straight line in space can be given:

1) as a line of intersection of two planes, i.e. system of equations:

A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)

2) its two points M 1 (x 1, y 1, z 1) and M 2 (x 2, y 2, z 2), then the straight line passing through them is given by the equations:

= ; (3.3)

3) the point M 1 (x 1 , y 1 , z 1) belonging to it, and the vector a(m, n, p), s collinear. Then the straight line is determined by the equations:

. (3.4)

Equations (3.4) are called canonical equations of the line.

Vector a called guide vector straight.

We obtain parametric ones by equating each of the relations (3.4) with the parameter t:

x \u003d x 1 + mt, y \u003d y 1 + nt, z \u003d z 1 + pt. (3.5)

Solving system (3.2) as a system of linear equations in unknowns x and y, we arrive at the equations of the straight line in projections or to reduced straight line equations:

x = mz + a, y = nz + b. (3.6)

From equations (3.6) one can pass to the canonical equations, finding z from each equation and equating the resulting values:

.

One can pass from general equations (3.2) to canonical equations in another way, if one finds some point of this line and its guide n= [n 1 , n 2], where n 1 (A 1 , B 1 , C 1) and n 2 (A 2 , B 2 , C 2) - normal vectors of the given planes. If one of the denominators m,n or R in equations (3.4) turns out to be equal to zero, then the numerator of the corresponding fraction must be set equal to zero, i.e. system

is tantamount to a system ; such a line is perpendicular to the x-axis.

System is equivalent to the system x = x 1 , y = y 1 ; the straight line is parallel to the Oz axis.

Example 1.15. Write the equation of the plane, knowing that the point A (1, -1,3) serves as the base of the perpendicular drawn from the origin to this plane.

Decision. By the condition of the problem, the vector OA(1,-1,3) is a normal vector of the plane, then its equation can be written as
x-y+3z+D=0. Substituting the coordinates of the point A(1,-1,3) belonging to the plane, we find D: 1-(-1)+3×3+D = 0 , D = -11. So x-y+3z-11=0.

Example 1.16. Write an equation for a plane passing through the Oz axis and forming an angle of 60 degrees with the 2x+y-z-7=0 plane.

Decision. The plane passing through the Oz axis is given by the equation Ax+By=0, where A and B do not vanish at the same time. Let B not
is 0, A/Bx+y=0. According to the formula for the cosine of the angle between two planes

.

Solving the quadratic equation 3m 2 + 8m - 3 = 0, we find its roots
m 1 = 1/3, m 2 = -3, from which we get two planes 1/3x+y = 0 and -3x+y = 0.

Example 1.17. Write the canonical equations of the straight line:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.

Decision. The canonical equations of a straight line have the form:

where m, n, p- coordinates of the directing vector of the straight line, x1, y1, z1- coordinates of any point belonging to the line. The straight line is defined as the line of intersection of two planes. To find a point belonging to a straight line, one of the coordinates is fixed (the easiest way is to put, for example, x=0) and the resulting system is solved as a system of linear equations with two unknowns. So, let x=0, then y + z = 0, 3y - 2z+ 5 = 0, whence y=-1, z=1. We found the coordinates of the point M (x 1, y 1, z 1) belonging to this line: M (0,-1,1). The directing vector of a straight line is easy to find, knowing the normal vectors of the original planes n 1 (5,1,1) and n 2(2,3,-2). Then

The canonical equations of the line are: x/(-5) = (y + 1)/12 =
= (z - 1)/13.

Example 1.18. In the beam defined by the planes 2x-y+5z-3=0 and x+y+2z+1=0, find two perpendicular planes, one of which passes through the point M(1,0,1).

Decision. The equation of the beam defined by these planes is u(2x-y+5z-3) + v(x+y+2z+1)=0, where u and v do not vanish at the same time. We rewrite the beam equation as follows:

(2u + v)x + (- u + v)y + (5u + 2v)z - 3u + v = 0.

In order to select a plane passing through the point M from the beam, we substitute the coordinates of the point M into the beam equation. We get:

(2u+v)×1 + (-u + v) ×0 + (5u + 2v)×1 -3u + v =0, or v = - u.

Then we find the equation of the plane containing M by substituting v = - u into the beam equation:

u(2x-y +5z - 3) - u(x + y +2z +1) = 0.

Because u ¹0 (otherwise v=0, and this contradicts the definition of a beam), then we have the equation of the plane x-2y+3z-4=0. The second plane belonging to the beam must be perpendicular to it. We write the condition for the orthogonality of planes:

(2u + v) ×1 + (v - u) ×(-2) + (5u +2v)×3 = 0, or v = - 19/5u.

Hence, the equation of the second plane has the form:

u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 or 9x +24y + 13z + 34 = 0.

ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under angle between two planes we mean one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . So . Because and , then

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

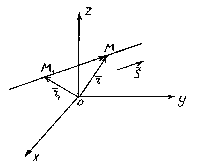
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y and z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

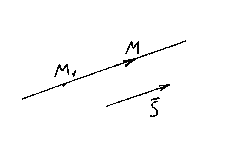
Let be M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, and is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

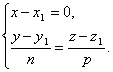
However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox and Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

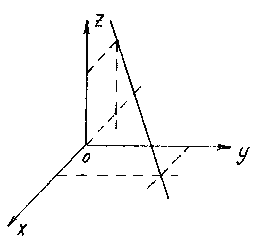
To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors and . Therefore, for the direction vector of the straight line l you can take the cross product of normal vectors:

.

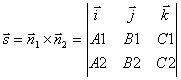Example. Give the general equations of the straight line to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

. Hence, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get