Dispersion (scattering) of a discrete random variable D(X) is the mathematical expectation of the squared deviation of a random variable from its mathematical expectation
1 property. The dispersion of the constant C is zero; D(C) = 0.
Proof. By definition of variance, D(C) = M( 2 ).
From the first property of the expectation D(C) = M[(C – C) 2 ] = M(0) = 0.
2 property. The constant factor can be taken out of the dispersion sign by squaring it:
D(CX) = C 2 D(X)
Proof. By definition of variance, D(CX) = M( 2 )
From the second expectation property D(CX)=M( 2 )= C 2 M( 2 )=C 2 D(X)
3 property. The variance of the sum of two independent random variables is equal to the sum of the variances of these variables:
D = D[X] + D.
Proof. According to the formula for calculating the variance, we have
D(X + Y) = M[(X + Y) 2 ] − 2
Opening the brackets and using the properties of the mathematical expectation of the sum of several quantities and the product of two independent random variables, we obtain
D(X + Y) = M − 2 = M(X2) + 2M(X)M(Y) + M(Y2) − M2(X) − 2M(X)M(Y) − M2(Y) = ( M(X2) − 2)+(M(Y2) − 2) = D(X) + D(Y). So D(X + Y) = D(X) + D(Y)
4 property. The variance of the difference of two independent random variables is equal to the sum of their variances:
D(X − Y) = D(X) + D(Y)
Proof. By virtue of the third property, D(X − Y) = D(X) + D(–Y). By the second property
D(X − Y) = D(X) + (–1) 2 D(Y) or D(X − Y) = D(X) + D(Y)
Numerical characteristics of systems of random variables. Correlation coefficient, properties of the correlation coefficient.
correlation moment. The characteristic of the dependence between random variables is the mathematical expectation of the product of deviations and from their centers of distributions (as the mathematical expectation of a random variable is sometimes called), which is called the correlation moment or covariance:
To calculate the correlation moment of discrete values, the following formula is used:
and for continuous quantities - the formula:
Correlation coefficient rxy of random variables X and Y is the ratio of the correlation moment to the product of standard deviations of the values:
- correlation coefficient;
Correlation coefficient properties:
1. If X and Y are independent random variables, then r = 0;
2. -1≤ r ≤1 . Moreover, if |r| =1, then between X and Y is a functional, namely a linear relationship;
3. r characterizes the relative value of the deviation of M(XY) from M(X)M(Y), and since deviation takes place only for dependent quantities, then r characterizes the tightness of the dependence.
Linear regression function.
Consider a two-dimensional random variable (X, Y), where X and Y are dependent random variables. We represent one of the quantities as a function of the other. We restrict ourselves to an approximate representation (exact approximation, generally speaking, is impossible) of Y as a linear function of X:
where α and β are parameters to be determined.
Theorem. Linear mean square regression Y on X has the form
where m x =M(X), m y =M(Y), σ x =√D(X), σ y =√D(Y), r=µ xy /(σ x σ y)- correlation coefficient of X and Y values.
The coefficient β=rσ y /σ x is called regression coefficient Y to X, and a straight line
called straight mean square regression
Y to X.
Markov's inequality.
Statement of Markov's inequality
If there are no negative values of the random variable X, then the probability that it will take on some value that exceeds the positive number A is no more than a fraction, i.e.
and the probability that it will take on some value not exceeding a positive number A is not less than , i.e.
Chebyshev's inequality.
Chebyshev's inequality. The probability that the deviation of a random variable X from its mathematical expectation in absolute value is less than a positive number ε, not less than 1 −D[X]ε 2
P(|X – M(X)|< ε) ≥ 1 –D(X)ε 2
Proof. Since the events consisting in the realization of inequalities
P(|X−M(X)|< ε) и P(|X – M(X)| ≥ε) противоположны, то сумма их вероятностей равна единице, т. е.
P(|X – M(X)|< ε) + P(|X – M(X)| ≥ ε) = 1.
Hence the probability we are interested in
P(|X – M(X)|< ε) = 1 − P(|X – M(X)| > ε).
Thus, the problem is reduced to calculating the probability P(|X –M(X)| ≥ ε).
Let's write an expression for the variance of the random variable X
D(X) = 2p1 + 2p2 + . . . + 2pn
All terms of this sum are non-negative. We discard those terms for which |x i – M(X)|< ε (для оставшихся слагаемых |x j – M(X)| ≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
D(X) ≥ 2 p k+1 + 2 p k+2 + . . . + 2pn
Both parts of the inequality |x j –M(X)| ≥ ε (j = k+1, k+2, . . ., n) are positive, therefore, squaring them, we obtain the equivalent inequality |x j – M(X)| 2 ≥ε 2 . Replacing each of the factors in the remaining sum
|xj – M(X)| 2 by the number ε 2 (in this case, the inequality can only increase), we obtain
D(X) ≥ ε 2 (p k+1 + p k+2 + . . . + p n)
By the addition theorem, the sum of probabilities is p k+1 +p k+2 +. . .+p n is the probability that X will take one, no matter which, of the values x k+1 +x k+2 +. . .+x n , and for any of them the deviation satisfies the inequality |x j – M(X)| ≥ ε. It follows that the sum p k+1 + p k+2 + . . . + p n expresses the probability
P(|X – M(X)| ≥ ε).
This allows us to rewrite the inequality for D(X) as
D(X) ≥ ε 2 P(|X – M(X)| ≥ ε)
P(|X – M(X)|≥ ε) ≤D(X)/ε 2
Finally we get
P(|X – M(X)|< ε) ≥D(X)/ε 2
Chebyshev's theorem.
Chebyshev's theorem. If a - pairwise independent random variables, and their variances are uniformly limited (do not exceed a constant number With ), then no matter how small the positive numberε , the probability of inequality
will be arbitrarily close to unity if the number of random variables is large enough.
In other words, under the conditions of the theorem
Proof. Let us introduce into consideration a new random variable - the arithmetic mean of random variables
Let us find the mathematical expectation X. Using the properties of the mathematical expectation (a constant factor can be taken out of the sign of the mathematical expectation, the mathematical expectation of the sum is equal to the sum of the mathematical expectations of the terms), we obtain
| (1) |
Applying the Chebyshev inequality to X, we have
or, taking into account relation (1)
Using the properties of the variance (the constant factor can be taken out of the variance sign by squaring it; the variance of the sum of independent random variables is equal to the sum of the variances of the terms), we obtain
By the condition, the dispersions of all random variables are limited by a constant number C, i.e. there are inequalities:
 (2)
|
Substituting the right side of (2) into inequality (1) (why the latter can only be strengthened), we have
Hence, passing to the limit as n→∞, we obtain
Finally, given that the probability cannot exceed one, we can finally write
The theorem has been proven.
Bernoulli's theorem.
Bernoulli's theorem. If in each of n independent trials the probability p of the occurrence of event A is constant, then the probability is arbitrarily close to unity that the deviation of the relative frequency from the probability p in absolute value will be arbitrarily small if the number of trials is large enough.
In other words, if ε is an arbitrarily small positive number, then under the conditions of the theorem we have the equality
Proof. Denote by x1 discrete random variable - the number of occurrences of the event in the first test, through x2- in the second, ..., X n- in n th test. It is clear that each of the quantities can take only two values: 1 (event A has occurred) with the probability p and 0 (the event did not occur) with probability .
Topic 8.12. Dispersion of a random variable.
O. The variance of a random variable is the mathematical expectation of the squared deviation of a random variable from its mathematical expectation.
Dispersion characterizes the degree of dispersion of the values of a random variable relative to its mathematical expectation. If all values of a random variable are closely concentrated around its mathematical expectation and large deviations from the mathematical expectation are unlikely, then such a random variable has a small dispersion. If the values of a random variable are scattered and there is a high probability of large deviations from the mathematical expectation, then such a random variable has a large dispersion.
Using the definition of variance, for a discrete random variable, the formula for calculating the variance can be represented as follows:
You can derive another formula for calculating the variance:
Thus, the variance of a random variable is equal to the difference between the mathematical expectation of the square of the random variable and the square of its mathematical expectation.
Dispersion properties.
We leave this property without proof.
Binomial distribution law.
Let numbers be given n belongs N and p(0 <p< one). Then each integer from the interval can be assigned a probability calculated using the Bernoulli formula. Let's get the law of distribution of a random variable (let's call it B(betta))
We will say that the random variable is distributed according to the Bernoulli law. Such a random variable is the frequency of occurrence of event A in n repeated independent trials, if in each trial event A occurs with a probability p.
Consider a separate i- e test. The space of elementary outcomes for it has the form
The law of distribution of a random variable was considered in the previous topic
For i= 1,2, ... , n we get the system from n independent random variables having the same distribution laws. 
Example.
Of the 20 product samples selected for control, 4 turned out to be non-standard. Let us estimate the probability that a randomly selected copy of the product does not meet the standard by the ratio R *= 4/20 = 0,2.
As X random value, R * is also a random variable. Values R * may vary from one experiment to another (in the case under consideration, the experiment is a random selection and control of 20 products). What is the mathematical expectation R *? Insofar as X is a random variable representing the number of successes in n Bernoulli test, M( x) = np. For the mathematical expectation of a random variable R* by definition we get: M(p*) = M(x/n), but n here is a constant, so by the expectation property
M(p*) = 1/n*M(x)=1/n np=p
Thus, “average” is the true value R, which is to be expected. This is the evaluation property R* quantities R has the name: R* is an unbiased evaluation for R. No systematic deviation from the value of the estimated parameter R confirms the feasibility of using the value R* as an estimate. We leave the question of the accuracy of the estimate open for now.
Mathematical expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of dispersion. In many problems of practice, a complete, exhaustive description of a random variable - the law of distribution - either cannot be obtained at all, or is not needed at all. In these cases, they are limited to an approximate description of a random variable using numerical characteristics.
The mathematical expectation is often referred to simply as the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, dispersion of a random variable around its mathematical expectation.
Mathematical expectation of a discrete random variable
Let's approach the concept of mathematical expectation, first proceeding from the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a mass corresponding to it from p1 , p 2 , ..., p n. It is required to choose one point on the x-axis, which characterizes the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, in which the abscissa of each point xi enters with a "weight" equal to the corresponding probability. The mean value of the random variable thus obtained X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:
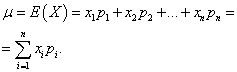
Example 1 A win-win lottery was organized. There are 1000 winnings, 400 of which are 10 rubles each. 300 - 20 rubles each 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for a person who buys one ticket?
Decision. We will find the average win if the total amount of winnings, which is equal to 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, is divided by 1000 (the total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average gain can also be represented in the following form:
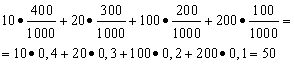
On the other hand, under these conditions, the amount of winnings is a random variable that can take on the values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average payoff is equal to the sum of the products of the size of the payoffs and the probability of receiving them.
Example 2 The publisher decided to publish a new book. He is going to sell the book for 280 rubles, of which 200 will be given to him, 50 to the bookstore, and 30 to the author. The table gives information about the cost of publishing a book and the likelihood of selling a certain number of copies of the book.
Find the publisher's expected profit.
Decision. The random variable "profit" is equal to the difference between the income from the sale and the cost of the costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publishing is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher's profit:
.
Example 3 Chance to hit with one shot p= 0.2. Determine the consumption of shells that provide the mathematical expectation of the number of hits equal to 5.
Decision. From the same expectation formula that we have used so far, we express x- consumption of shells:
.
Example 4 Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of hitting with each shot p = 0,4 .
Hint: find the probability of the values of a random variable by Bernoulli formula .
Expectation Properties
Consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the expectation sign:
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of the product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of the random variable X decrease (increase) by the same number With, then its mathematical expectation will decrease (increase) by the same number:
When you can not be limited only to mathematical expectation
In most cases, only the mathematical expectation cannot adequately characterize a random variable.
Let random variables X and Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
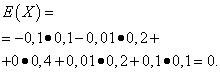
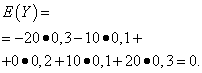
However, their distribution is different. Random value X can only take values that are little different from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the proportion of high- and low-paid workers. In other words, by mathematical expectation one cannot judge what deviations from it, at least on average, are possible. To do this, you need to find the variance of a random variable.
Dispersion of a discrete random variable
dispersion discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
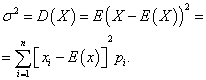
The standard deviation of a random variable X is the arithmetic value of the square root of its variance:
.
Example 5 Calculate variances and standard deviations of random variables X and Y, whose distribution laws are given in the tables above.
Decision. Mathematical expectations of random variables X and Y, as found above, are equal to zero. According to the dispersion formula for E(X)=E(y)=0 we get:
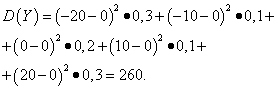
Then the standard deviations of random variables X and Y constitute
.
Thus, with the same mathematical expectations, the variance of the random variable X very small and random Y- significant. This is a consequence of the difference in their distribution.
Example 6 The investor has 4 alternative investment projects. The table summarizes the data on the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find for each alternative the mathematical expectation, variance and standard deviation.
Decision. Let us show how these quantities are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectation. This means that in the long run everyone has the same income. The standard deviation can be interpreted as a measure of risk - the larger it is, the greater the risk of the investment. An investor who doesn't want much risk will choose project 1 because it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion Properties
Let us present the properties of the dispersion.
Property 1. The dispersion of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
,
where 
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7 It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Decision. Denote by p the probability with which a random variable takes on a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let's derive the equation for mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
The law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of the variance:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then see the solution
Example 8 Discrete random variable X takes only two values. It takes the larger value of 3 with a probability of 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9 An urn contains 6 white and 4 black balls. 3 balls are taken from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Decision. Random value X can take the values 0, 1, 2, 3. The corresponding probabilities can be calculated from rule of multiplication of probabilities. The law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Mathematical expectation and dispersion of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). In contrast to a discrete random variable, for which the function argument xi changes abruptly, for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its mean value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If a density function of a continuous random variable is given, then it enters directly into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
In the previous one, we gave a number of formulas that allow us to find the numerical characteristics of functions when the laws of distribution of arguments are known. However, in many cases, to find the numerical characteristics of functions, it is not even necessary to know the laws of distribution of arguments, but it is enough to know only some of their numerical characteristics; in this case, we do without any laws of distribution at all. Determining the numerical characteristics of functions by given numerical characteristics of the arguments is widely used in probability theory and makes it possible to significantly simplify the solution of a number of problems. For the most part, such simplified methods relate to linear functions; however, some elementary non-linear functions also allow this approach.
In the present, we present a number of theorems on the numerical characteristics of functions, which in their totality represent a very simple apparatus for calculating these characteristics, applicable in a wide range of conditions.
1. Mathematical expectation of a non-random variable
The stated property is rather obvious; it can be proved by considering a non-random variable as a particular type of a random one, with one possible value with a probability of one; then according to the general formula for the mathematical expectation:
.
2. Dispersion of a non-random variable
If is a non-random value, then
3. Removal of a non-random variable beyond the sign of mathematical expectation
, (10.2.1)
i.e., a non-random value can be taken out of the expectation sign.
Proof.
a) For discontinuous quantities
b) For continuous quantities
.
4. Removal of a non-random value for the sign of the variance and standard deviation
If is a non-random variable, and is random, then
, (10.2.2)
i.e., a non-random value can be taken out of the dispersion sign by squaring it.
Proof. By definition of variance
Consequence
,
i.e., a non-random value can be taken out of the sign of the standard deviation by its absolute value. We obtain the proof by extracting the square root from the formula (10.2.2) and taking into account that the r.s.c. is an essentially positive value.
5. Mathematical expectation of the sum of random variables
Let us prove that for any two random variables and
i.e. the mathematical expectation of the sum of two random variables is equal to the sum of their mathematical expectations.
This property is known as the expectation addition theorem.
Proof.
a) Let be a system of discontinuous random variables. Let us apply to the sum of random variables the general formula (10.1.6) for the mathematical expectation of a function of two arguments:
.
Ho is nothing more than the total probability that the value will take on the value :
;
hence,
.
In a similar way, we will prove that
,
and the theorem is proven.
b) Let be a system of continuous random variables. According to the formula (10.1.7)
. (10.2.4)
We transform the first of the integrals (10.2.4):
;
likewise
,
and the theorem is proven.
It should be specially noted that the theorem of addition of mathematical expectations is valid for any random variables - both dependent and independent.
The expectation addition theorem can be generalized to an arbitrary number of terms:
, (10.2.5)
i.e. the mathematical expectation of the sum of several random variables is equal to the sum of their mathematical expectations.
To prove it, it suffices to apply the method of complete induction.
6. Mathematical expectation of a linear function
Consider a linear function of several random arguments:
where are non-random coefficients. Let's prove that
, (10.2.6)
i.e., the mean of a linear function is equal to the same linear function of the mean of the arguments.
Proof. Using the addition theorem m.o. and the rule of taking a non-random variable out of the sign of m. o., we get:
.
7. Dispepthis sum of random variables
The variance of the sum of two random variables is equal to the sum of their variances plus twice the correlation moment:
Proof. Denote
According to the addition theorem of mathematical expectations
Let's pass from random variables to the corresponding centered variables . Subtracting term by term from equality (10.2.8) equality (10.2.9), we have:
By definition of variance
Q.E.D.
Formula (10.2.7) for the variance of the sum can be generalized to any number of terms:
,
(10.2.10)
where is the correlation moment of the values , the sign under the sum means that the summation applies to all possible pairwise combinations of random variables 
.
The proof is similar to the previous one and follows from the formula for the square of a polynomial.
Formula (10.2.10) can be written in another form:
, (10.2.11)
where the double sum extends to all elements of the correlation matrix of the system of quantities , containing both correlation moments and variances.
If all random variables , included in the system, are uncorrelated (i.e., at ), formula (10.2.10) takes the form:
, (10.2.12)
i.e., the variance of the sum of uncorrelated random variables is equal to the sum of the variances of the terms.
This proposition is known as the variance addition theorem.
8. Dispersion of a linear function
Consider a linear function of several random variables.
where are non-random variables.
Let us prove that the dispersion of this linear function is expressed by the formula
, (10.2.13)
where is the correlation moment of the quantities , .
Proof. Let's introduce the notation:
. (10.2.14)
Applying formula (10.2.10) for the variance of the sum to the right side of expression (10.2.14) and taking into account that , we obtain:
where is the correlation moment of the quantities:
.
Let's calculate this moment. We have:
;
likewise
Substituting this expression into (10.2.15), we arrive at formula (10.2.13).
In the particular case when all quantities uncorrelated, formula (10.2.13) takes the form:
, (10.2.16)
i.e., the variance of a linear function of uncorrelated random variables is equal to the sum of the products of the squares of the coefficients and the variances of the corresponding arguments.
9. Mathematical expectation of the product of random variables
The mathematical expectation of the product of two random variables is equal to the product of their mathematical expectations plus the correlation moment:
Proof. We will proceed from the definition of the correlation moment:
We transform this expression using the properties of the mathematical expectation:
which is obviously equivalent to formula (10.2.17).
If random variables are uncorrelated, then formula (10.2.17) takes the form:
i.e., the mean of the product of two uncorrelated random variables is equal to the product of their mean.
This statement is known as the expectation multiplication theorem.
Formula (10.2.17) is nothing but an expression of the second mixed central moment of the system in terms of the second mixed initial moment and mathematical expectations:
. (10.2.19)
This expression is often used in practice when calculating the correlation moment in the same way that for one random variable the variance is often calculated through the second initial moment and the mathematical expectation.
The expectation multiplication theorem can also be generalized to an arbitrary number of factors, only in this case for its application it is not enough that the quantities are uncorrelated, but it is required that some higher mixed moments also vanish, the number of which depends on the number of terms in the product. These conditions are certainly satisfied if the random variables included in the product are independent. In this case
, (10.2.20)
i.e. the mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations.
This proposition can be easily proved by complete induction.
10. Dispersion of the product of independent random variables
Let us prove that for independent quantities
Proof. Let's denote . By definition of variance
Since the quantities are independent, and
For independent, the quantities are also independent; hence,
,
But there is nothing else than the second initial moment of the quantity , and, therefore, is expressed in terms of the variance:
;
likewise
.
Substituting these expressions into formula (10.2.22) and bringing like terms, we arrive at formula (10.2.21).
In the case when centered random variables are multiplied (values with mathematical expectations equal to zero), formula (10.2.21) takes the form:
, (10.2.23)
i.e., the variance of the product of independent centered random variables is equal to the product of their variances.
11. Higher moments of the sum of random variables
In some cases it is necessary to calculate the higher moments of the sum of independent random variables. Let us prove some related relations.
1) If the quantities are independent, then
Proof.
whence by the expectation multiplication theorem
But the first central moment for any quantity is zero; two middle terms vanish, and formula (10.2.24) is proved.
Relation (10.2.24) can be easily generalized by induction to an arbitrary number of independent terms:
. (10.2.25)
2) The fourth central moment of the sum of two independent random variables is expressed by the formula
where are the dispersions of and .
The proof is exactly the same as the previous one.
Using the method of complete induction, it is easy to prove the generalization of formula (10.2.26) to an arbitrary number of independent terms.
Dispersion of a random variable and its properties.
Many random variables have the same mathematical expectation but different possible values. Therefore, one mathematical expectation is not enough to characterize a random variable.
Let the income X and Y(in dollars) of two firms are given by distributions:
Sometimes it is convenient to use another formula, which can be obtained by using the properties of the mathematical expectation,
The dispersion exists if the series (respectively, the integral) converges.
Non-negative number 
called standard deviation random variable X. It has the dimension of a random variable X and defines some standard rms dispersion interval, symmetric with respect to the mathematical expectation. The value is sometimes called the standard deviation.
The random variable is called centered, if . The random variable is called normalized(standard) if .
Let's continue the example. Calculate the variance of the income of two firms:
Comparing the variance, we see that the income of the second firm varies more than the first.
Dispersion Properties.
1. The dispersion of a constant value is equal to zero, i.e. , if constant. This is obvious, since the constant value has a mathematical expectation equal to the constant value, i.e. .
2. Constant multiplier C can be taken out of the dispersion sign by first squaring it.
Really,
3. The variance of the algebraic sum of two independent random variables is equal to the sum of their variances, i.e.
The expression is called covariance of X and Y(see Topic 4, §2). For independent random variables, the covariance is zero, i.e.
Using this equality, you can add to the list of properties of the mathematical expectation. If random variables X and Y are independent, then the mathematical expectation of the product is equal to the product of the mathematical expectations, namely:
If the random variable is transformed linearly, i.e. , then
.
Example 1. Let it be produced n independent tests, probability of occurrence of an event BUT in each of which is constant and equal to p. What is the variance of the number of occurrences of the event BUT in these trials?
Decision. Let be the number of occurrence of the event BUT in the first trial, is the number of occurrence of the event BUT in the second test, and so on. Then the total number of occurrence of the event BUT in n trials equals
Using property 3 of the dispersion, we get
Here we have used the fact that 
, i= (see examples 1 and 2, item 3.3.1.).
Example 2. Let X - the amount of the deposit (in dollars) in the bank - given by the probability distribution
| X | ||||||
| i = | 0,01 | 0,03 | 0,10 | 0,30 | 0,5 | 0,06 |
Find the average contribution amount and variance.
Decision. The average deposit amount is equal to the mathematical expectation
To calculate the variance, we use the formula
D (X) \u003d 8196 - 7849.96 \u003d 348.04.
Standard deviation
Moments.
In order to take into account the influence on the mathematical expectation of those possible values of the random variable X, which are large but have a low probability, it is advisable to consider the mathematical expectations of a positive integer power of a random variable.
