Graphical solution of equations
Heyday, 2009
Introduction
The need to solve quadratic equations in ancient times was caused by the need to solve problems related to finding the areas of land and earthworks of a military nature, as well as the development of astronomy and mathematics itself. The Babylonians knew how to solve quadratic equations for about 2000 BC. The rule for solving these equations, stated in the Babylonian texts, coincides essentially with modern ones, but it is not known how the Babylonians came to this rule.
Formulas for solving quadratic equations in Europe were first set forth in the Book of the Abacus, written in 1202 by the Italian mathematician Leonardo Fibonacci. His book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries.
But the general rule for solving quadratic equations, with all possible combinations of coefficients b and c, was formulated in Europe only in 1544 by M. Stiefel.
In 1591 François Viet introduced formulas for solving quadratic equations.
Some kinds of quadratic equations could be solved in ancient Babylon.
Diophantus of Alexandria and Euclid, Al-Khwarizmi and Omar Khayyam solved equations in geometric and graphical ways.
In 7th grade we studied functions y \u003d C, y=kx, y =kx+ m, y =x 2,y = -x 2, in the 8th grade - y = √x, y =|x|, y=ax2 + bx+ c, y =k/ x. In the 9th grade algebra textbook, I saw functions that were not yet known to me: y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– a) 2 + (y -b) 2 = r 2 and others. There are rules for constructing graphs of these functions. I was wondering if there are other functions that obey these rules.
My job is to study graphs of functions and solve equations graphically.
1. What are the functions
The graph of a function is the set of all points of the coordinate plane, the abscissas of which are equal to the values of the arguments, and the ordinates are equal to the corresponding values of the function.
The linear function is given by the equation y=kx+ b, where k and b- some numbers. The graph of this function is a straight line.
Inverse Proportional Function y=k/ x, where k ¹ 0. The graph of this function is called a hyperbola.
Function (x– a) 2 + (y -b) 2 = r2 , where a, b and r- some numbers. The graph of this function is a circle of radius r centered at point A ( a, b).
quadratic function y= ax2 + bx+ c where a,b, with- some numbers and a¹ 0. The graph of this function is a parabola.
The equation at2 (a– x) = x2 (a+ x) . The graph of this equation will be a curve called a strophoid.
/>Equation (x2 + y2 ) 2 = a(x2 – y2 ) . The graph of this equation is called the Bernoulli lemniscate.
The equation. The graph of this equation is called an astroid.
Curve (x2 y2 – 2 a x)2 =4 a2 (x2 +y2 ) . This curve is called a cardioid.
Functions: y=x 3 - cubic parabola, y=x 4, y = 1/x 2.
2. The concept of an equation, its graphical solution
The equation is an expression containing a variable.
solve the equation- this means finding all its roots, or proving that they do not exist.
Root of the equation is a number that, when substituted into the equation, produces the correct numerical equality.
Solving Equations Graphically allows you to find the exact or approximate value of the roots, allows you to find the number of roots of the equation.
When plotting graphs and solving equations, the properties of a function are used, so the method is often called functional-graphic.
To solve the equation, we “divide” it into two parts, introduce two functions, build their graphs, find the coordinates of the intersection points of the graphs. The abscissas of these points are the roots of the equation.
3. Algorithm for constructing a graph of a function
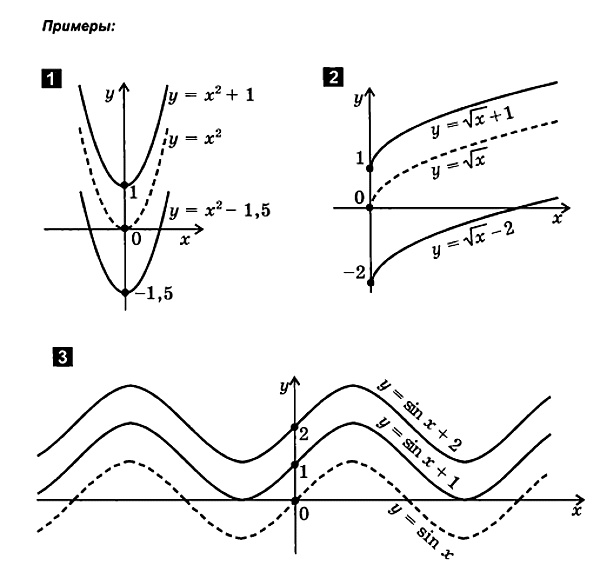
Knowing the graph of the function y=f(x) , you can plot functions y=f(x+ m) ,y=f(x)+ l and y=f(x+ m)+ l. All these graphs are obtained from the graph of the function y=f(x) using the parallel translation transformation: on │ m│ scale units to the right or left along the x-axis and on │ l│ scale units up or down along the axis y.
4. Graphical solution of the quadratic equation
Using the example of a quadratic function, we will consider a graphical solution of a quadratic equation. The graph of a quadratic function is a parabola.
What did the ancient Greeks know about the parabola?
Modern mathematical symbolism originated in the 16th century.
The ancient Greek mathematicians had neither the coordinate method nor the concept of a function. However, the properties of the parabola were studied by them in detail. The inventiveness of ancient mathematicians is simply amazing, because they could only use drawings and verbal descriptions of dependencies.
Most fully explored the parabola, hyperbola and ellipse Apollonius of Perga, who lived in the 3rd century BC. He also gave names to these curves and indicated what conditions the points lying on a particular curve satisfy (after all, there were no formulas!).
There is an algorithm for constructing a parabola:
Find the coordinates of the vertex of the parabola A (x0; y0): X=- b/2 a;
y0=aho2+in0+s;
Find the axis of symmetry of the parabola (straight line x=x0);
PAGE_BREAK--
Compiling a table of values for building control points;
We construct the obtained points and construct points symmetrical to them with respect to the axis of symmetry.
1. Let's build a parabola according to the algorithm y= x2 – 2 x– 3 . Abscissas of points of intersection with the axis x and are the roots of the quadratic equation x2 – 2 x– 3 = 0.
There are five ways to graphically solve this equation.
2. Let's break the equation into two functions: y= x2 and y= 2 x+ 3
3. Let's break the equation into two functions: y= x2 –3 and y=2 x. The roots of the equation are the abscissas of the points of intersection of the parabola with the line.
4. Transform the equation x2 – 2 x– 3 = 0 by selecting the full square on the function: y= (x–1) 2 and y=4. The roots of the equation are the abscissas of the points of intersection of the parabola with the line.
5. We divide term by term both parts of the equation x2 – 2 x– 3 = 0 on the x, we get x– 2 – 3/ x= 0 Let's split this equation into two functions: y= x– 2, y= 3/ x. The roots of the equation are the abscissas of the points of intersection of the line and the hyperbola.
5. Graphical solution of degree equationsn
Example 1 solve the equation x5 = 3 – 2 x.
y= x5 , y= 3 – 2 x.
Answer: x = 1.
Example 2 solve the equation 3 √ x= 10 – x.
The roots of this equation is the abscissa of the intersection point of the graphs of two functions: y= 3 √ x, y= 10 – x.
Answer: x=8.
Conclusion
Considering the function graphs: y=ax2 + bx+ c, y =k/ x, y = √x, y =|x|, y=x 3, y=x 4,y= 3√x, I noticed that all these graphs are built according to the rule of parallel translation relative to the axes x and y.
Using the example of solving a quadratic equation, we can conclude that the graphical method is also applicable to equations of degree n.
Graphical methods for solving equations are beautiful and understandable, but they do not give a 100% guarantee of solving any equation. The abscissas of the intersection points of the graphs can be approximate.
In the 9th grade and in the senior classes, I will still get acquainted with other functions. I'm interested to know if those functions obey the rules of parallel translation when plotting their graphs.
Next year I also want to consider the issues of graphical solution of systems of equations and inequalities.
Literature
1. Algebra. 7th grade. Part 1. Textbook for educational institutions / A.G. Mordkovich. Moscow: Mnemosyne, 2007.
2. Algebra. 8th grade. Part 1. Textbook for educational institutions / A.G. Mordkovich. Moscow: Mnemosyne, 2007.
3. Algebra. Grade 9 Part 1. Textbook for educational institutions / A.G. Mordkovich. Moscow: Mnemosyne, 2007.
4. Glazer G.I. History of mathematics at school. VII-VIII classes. – M.: Enlightenment, 1982.
5. Journal Mathematics №5 2009; No. 8 2007; No. 23 2008.
6. Graphic solution of equations Internet sites: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.
Research work of students on the topic:
"Application of a linear function in solving problems"
"Application of a Linear Function Graph to Problem Solving"
MKOU "Bogucharskaya secondary school No. 1"
Research work in mathematics.
Topic: "Application of a graph of a linear function to solve problems"
7 "B" class
Head: Fomenko Olga Mikhailovna
city of Boguchar
1. Introduction…………………………………………………………………… 2
2.Main part………………………………………………………………3-11
2.1 Technique for solving text problems using linear function graphs
2.2Solving text problems for movement using graphs
3. Conclusion…………………………………………………………………… 11
4. Literature…………………………………………………………………….12
INTRODUCTION
"Algebra.7 class" considers tasks in which, according to a given schedule, it is necessary to answer a number of questions.
For example:
№332 The summer resident went from home by car to the village. He drove first on the highway, and then on a country road, slowing down as he did so. The schedule of the movement of the summer resident is shown in the figure. Answer the questions:
a) how long did the summer resident drive along the highway and how many kilometers did he drive; what was the speed of the car on this section of the road;
b) how long did the summer resident drive along the country road and how many kilometers did he drive; what was the speed of the car in this section;
c) how long did the summer resident travel all the way from home to the village?
In the course of searching for material on this topic in the literature and the Internet, I discovered for myself that many physical, and even social and economic phenomena and processes are in a linear relationship in the world, but I settled on the movement, as the most familiar to us and popular among all. In the project, I described word problems and how to solve them using linear function graphs.
Hypothesis: with the help of graphs, you can not only get a visual representation of the properties of a function, get acquainted with the properties of a linear function and its particular form, direct proportionality, but also solve word problems.
The aim of my research was the study of the use of graphs of a linear function in solving text problems for movement. In order to achieve these goals, the following tasks:
To study the methodology for solving text problems for movement using linear function graphs;
Learn how to solve motion problems using this method;
Make comparative conclusions about the advantages and disadvantages of solving problems using linear function graphs.
Object of study: linear function graph.
Research method:
Theoretical (study and analysis), system search, practical.
Main part.
In my research, I decided to try to give a graphical interpretation of the tasks for movement presented in our textbook, then, according to the schedule, answer the question of the task. For such a solution, I took tasks with rectilinear uniform motion on one section of the path. It turned out that many problems are solved in this way more simply than in the usual way using an equation. The only drawback of this technique is that in order to accurately obtain an answer to the question of the problem, one must be able to correctly select the scale of units of measurement on the coordinate axes. A large role in the correct choice of this scale is played by the experience of solving. Therefore, in order to master the art of solving problems using graphs, I had to consider them in large numbers.
set the coordinate system sOt with the abscissa axis Ot and the ordinate axis Os . To do this, according to the condition of the problem, it is necessary to choose the origin: the beginning of the movement of the object or from several objects, the one that started moving earlier or traveled a greater distance is selected. On the abscissa axis, mark the time intervals in its units of measurement, and on the ordinate axis, mark the distance in the selected scale of its units of measurement.
Points on the coordinate plane must be marked according to the scale of the task, and the lines must be drawn accurately. The accuracy of the solution of the problem depends on this. Therefore, it is very important to choose the scale of divisions on the coordinate axes successfully: it must be chosen in such a way that the coordinates of the points are determined more accurately and, if possible, located at the nodal points, i.e. at the intersections of the divisions of the coordinate axes. Sometimes it is useful to take as a unit segment on the abscissa axis the number of cells that is a multiple of the conditions of the problem with respect to time, and on the ordinate axis - the number of cells that is a multiple of the conditions of the problem with respect to distance. For example, 12 minutes in time requires choosing the number of cells in multiples of 5, because 12 minutes is one fifth of an hour.
Solving text problems for movement using graphs
Answer: 9 km.

Solution using equation:
x/12h. - time from A to B
x/18h. - back time
Answer: 9 km
Task 2. (No. 156 in Yu.N. Makarychev's textbook "Algebra 7".)
Two cars are driving down the highway at the same speed. If the first one increases the speed by 10 km / h, and the second one reduces it by 10 km / h, then the first one will cover as much in 2 hours as the second one in 3 hours. How fast are the cars going?
Solution using equation:
Let x km/h be the speed of the cars;
(x+10) and (x-10) respectively speed after increase and decrease;
2(x+10)=3(x-10)
Answer: 50km/h
Solving with Linear Function Graph:

1. Let's set the coordinate plane sOt with the abscissa axis Оt, on which we mark the time intervals of movement, and the ordinate axis Os, on which we mark the distance traveled by vehicles
2. Let's put divisions on a scale along the abscissa axis - one hour in 5 cells (in 1 cell - 12 minutes); we apply divisions along the y-axis, but do not specify the scale.
3. Let's build a line of movement of the first car I: the beginning of movement at a point c
4. Let's build the line of movement of the second machine II: the beginning of the movement at the point with the coordinate (0; 0). Next, we mark an arbitrary point (3;s 1) on the plane, because the car with the new speed was on the road for 3 hours.
4. Let's determine the speed of cars v before its change. Let us denote the difference of the ordinates of the points lying on the lines with the abscissa 1 by the sign ∆s . According to the condition, this segment corresponds to a length of (10 + 10) km, because in one of them the speed decreased, and in the other the speed increased by 10 km/h. This means that the line of movement of cars before changing the speed should be equidistant from lines I and II and located on the coordinate plane between them .. According to the schedule, Δs \u003d 2cl. corresponds to 20 km, v = 5 cells, so we solve the proportion v = 50 km / h.
Answer: 50km/h.
Task 3
Solving with Linear Function Graph:
reference point is jetty M

mark the point N (0; 162).
Answer: 2 hours 20 minutes.
Solution using equation:
162 -45(x+0.75)-36x=0
162-45x - 33.75 -36x = 0
81x=128.25
2) ![]()
Answer: 2 hours 20 minutes.
Task 4.
A cyclist left point A. At the same time, after him, a motorcyclist 16 km/h left point B, which is 20 km away from A. The cyclist was traveling at a speed of 12 km/h. At what distance from point A will the motorcyclist overtake the cyclist?
Solving with Linear Function Graph:
1. Let's set the coordinate plane sOt with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which we will mark the distance traveled by the motorcyclist and cyclist
2. Let's draw divisions on a scale: along the y-axis - in 2 cells 8 km; along the abscissa - in 2 cells - 1h.
3. Let's build a line of movement of a motorcyclist II: we mark the beginning of his movement at the origin of coordinates B (0; 0). The motorcyclist was driving at a speed of 16 km/h, which means that straight line II must pass through the point with coordinates (1; 16).

4. Let's build a line of motion for a cyclist I: its beginning will be at point A (0; 20), because point B is located at a distance of 20 km from point A, and he left at the same time as the motorcyclist. The cyclist was traveling at a speed of 12 km/h, which means that the line I must pass through the point with coordinates (1; 32).
5. Find P (5; 80) - the point of intersection of lines I and II, reflecting the movement of a motorcyclist and a cyclist: its ordinate will show the distance from point B, at which the motorcyclist will catch up with the cyclist.
P(5; 80) |=s = 80, |=80 - 20 = 60(km) - the distance from point A at which the motorcyclist will catch up with the cyclist..
Answer: 60 km.
Solution using equation:
Let x km be the distance from point A to the meeting point
x /12 cyclist time
(x +20)/16 motorcyclist time
x /12=(x +20)/16
16x=12x+240
4x=240
x=60
Answer: 60 km
Task 5.
The distance between cities was covered by a motorcyclist in 2 hours, and by a cyclist in 5 hours. The speed of a cyclist is 18 km/h less than the speed of a motorcyclist. Find the speeds of the cyclist and motorcyclist and the distance between cities.
Solving with Linear Function Graph:

1. Set the coordinate plane sOt with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which we mark the distance.
2. Let's put a division along the abscissa axis in 2 cells for 1 hour. Let's leave the distance without divisions along the ordinate axis.
3. Let's draw the line of movement I of the cyclist in 5 hours and the line of movement of the motorcyclist II in 2 hours. The end of both lines must have the same ordinate.
4. Let's draw a segment with abscissa 1 between lines I and II. The length of this segment reflects a distance equal to 18 km. From the drawing we get that 3 cells are equal to 18 km, which means that there are 6 km in 1 cell.
5. Then, according to the schedule, we determine the speed of the cyclist is 12 km / h, the speed of the motorcyclist is 30 km / h, the distance between cities is 60 km.
Solution using equation:
Let x km/h be the speed of the cyclist, then (x +18) km/h the speed of the motorcyclist
2(x+18)=5x
2x +36=5x
x=12
2) 12+18=30(km/h) rider speed
3) (km) distance between cities
Answer: 12 km/h; 30 km/h; 60 km
Answer: 60 km.
Task 6.
A boat travels a distance of 30 km in 3 hours and 20 minutes along the river, and 28 km against the current in 4 hours. How far will the boat cover the lake in 1.5 hours?
Solving with Linear Function Graph:
1. Set the coordinate plane sOt with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which we mark the distance traveled by the boat
2. Let's draw divisions on a scale: along the y-axis - in two cells 4 km; along the abscissa axis - in 6 cells - 1 hour (in 1 cell - 10 minutes), because according to the condition of the problem, time is given in minutes.
3. Let's build a line of movement of the boat along the river I: the beginning of the line will be at the point with the coordinate (0; 0). The boat sails 30 km in 3 hours and 20 minutes, which means that the line must pass through the point with coordinate (; 30), because 3h 20min. = h.

4. Let's build a line of movement of the boat against the current of the river II: we take the beginning of the movement at a point with a coordinate (0; 0). The boat sails 28 km in 4 hours, which means that the line of motion must pass through the point with the coordinate (4; 28).
5. Let's build the line of movement of the boat on the lake: we will take the beginning of the movement at the point with the coordinate (0; 0). The line of own movement of the boat will have to be located equidistantly between the lines of movement of the boat along the river. This means that we must divide the segment, consisting of all points with abscissa 1 between the lines of movement along the river, in half and mark its middle. From (0; 0) through this marked point we will draw a ray, which will be the line of movement along the lake.
6. According to the condition of the problem, it is necessary to find the distance traveled by the boat on the lake in 1.5 hours, which means that we must determine on this line the ordinate of the point with the abscissa t \u003d 1.5, | \u003d s \u003d 12, | \u003d 12 km 1,5 hour.
Answer: 12 km.
Solution using a system of equations:
Let x km/h be the speed of the lake and y km/h the speed of the river
Answer: 12 km.
Task 7.
The boat travels along the river for 34 km in the same time as 26 km against the current. The own speed of the boat is 15 km/h. Find the speed of the river.
Solving with Linear Function Graph:
1. Set the coordinate plane sOt with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which we mark the distance traveled by the boat.
2. Let's draw divisions on a scale: along the y-axis - in 1 cell 1 km; on the abscissa axis, we leave time without divisions.
3. Let's build a line I of the boat's movement along the river from 0 km to a point of 34 km: the beginning of the line will be at the point with the coordinate (0; 0). The second coordinate will be (x; 34).
4. Let's build a line II of the boat's movement against the river current from 0 km to a point of 26 km: the beginning of the line will be at the point with the coordinate (0; 0). The second coordinate will be (x; 26).
5. Draw a ray III from the origin (0; 0) through the middle of an arbitrary segment consisting of all points with the same abscissa between the two lines of motion I and II. This beam will reflect the boat's own movement, as the boat's own speed is the arithmetic average of 2 speeds upstream and downstream of the river. On the resulting beam, we find a point with an ordinate of 15, because own speed of the boat is 15 km/h. The abscissa of the found point will correspond to a division of 1 hour.
6. To find the speed of the river, it is enough to find the length of the segment with abscissa 1 from line III to line II. The speed of the river is 2 km / h.
Answer: 2km/h
Solution using equation:
River speed x km/h
34 / (15 + x) \u003d 26 / (15-x) Solving the proportion, we get:
Answer: 2km/h
Conclusion.
Advantages:
Tasks can be briefly written down;
Disadvantages:
LITERATURE.
1. Makarychev Yu. N., Mindyuk N. G., Neshkov K. I., Suvorova S. B., Algebra: A textbook for the 7th grade of educational institutions, “Prosveshchenie”, M., 2000.
2.Bulynin V., The use of graphic methods in solving text problems, educational and methodical newspaper "Mathematics", No. 14, 2005.
3. Zvavich L.I. Didactic materials on algebra for grade 7.
View document content
"the words"
At the algebra lessons in the 7th grade, I got acquainted with the topic “Linear function. Mutual arrangement of graphs of linear functions. I learned how to build graphs of a linear function, learned its properties, learned how to determine the relative position of graphs using given formulas. I noticed that in the textbook by Yu.N. Makarychev
"Algebra.7 class" considers tasks in which, according to a given schedule, it is necessary to answer a number of questions. An example of such a task is presented on the slide.
According to the given schedule, it can be determined that
And I had a question, is it possible to solve problems for movement not by actions or using equations, but to use the graphics of a linear function for this?
Hypothesis, goals and objectives are presented on the slide
In my research, I decided to try to give a graphical interpretation of the tasks for movement presented in our textbook, then, according to the schedule, answer the question of the task. For such a solution, I took tasks with rectilinear uniform motion on one section of the path.
It turned out that many problems are solved in this way. The only drawback of this technique is that in order to accurately obtain an answer to the question of the problem, one must be able to correctly select the scale of units of measurement on the coordinate axes. A large role in the correct choice of this scale is played by the experience of solving. Therefore, in order to master the art of solving problems using graphs, I had to consider them in large numbers.
A technique for solving text problems using linear function graphs.
In order to solve a text problem using linear function graphs, you need to:
set the coordinate system To do this, according to the condition of the problem, it is necessary to choose the origin: the beginning of the movement of the object or from several objects, the one that started moving earlier or traveled a greater distance is selected. On the abscissa axis, mark the time intervals in its units of measurement, and on the ordinate axis, mark the distance in the selected scale of its units of measurement.
Draw the lines of motion of each of the objects specified in the problem statement through the coordinates of at least two points of the straight lines. Usually the speed of an object gives information about the passage of a distance in one unit of time from the beginning of its movement. If the object starts moving later, then the start point of its movement is shifted by a given number of units to the right of the origin along the x-axis. If the object starts moving from a place remote from the reference point by a certain distance, then the point of the beginning of its movement is displaced upwards along the y-axis.
The meeting point of several objects on the coordinate plane is indicated by the intersection point of the lines depicting their movement, which means that the coordinates of this point provide information about the time of the meeting and the distance of the meeting place from the origin.
The difference in the speeds of movement of two objects is determined by the length of the segment, consisting of all points with abscissa 1, located between the lines of movement of these objects.
Points on the coordinate plane must be marked according to the scale of the task, and the lines must be drawn accurately. The accuracy of the solution of the problem depends on this.
Problem 1. (No. 673 in Yu.N. Makarychev's textbook "Algebra 7".)
A cyclist traveled the path AB at a speed of 12 km/h. Returning, he developed a speed of 18 km / h and spent 15 minutes less on the way back than on the way from A to B. How many kilometers from A to B.
Solution using equation:
Let x km be the distance from A to B.
x/12h. - time from A to B
x/18h. - back time
Since he spent 15 minutes less on the way back, we will compose the equation
Answer: 9 km
Solving with Linear Function Graph:
1. Let us set the coordinate plane sOtc with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which we mark the distance.
2. Let's draw divisions on a scale: along the y-axis - in one cell 3 km; along the abscissa axis - one hour in 4 cells (in 1 cell - 15 min).
3. Let's build a line of movement there: mark the beginning of the movement with a dot (0; 0). The cyclist was traveling at a speed of 12 km/h, which means that the straight line must pass through the point (1; 12).
4. Let's build a line of movement back: mark the end of the line with a dot (; 0), because the cyclist spent 15 minutes less on the return trip. He was driving at a speed of 18km/h, which means that the next point of the line has the coordinate (;18).
5. Note (; 9) - the point of intersection of the lines: its ordinate will show the distance: s = 9
Answer: 9 km.
Task 2 (No. 757 in Yu.N. Makarychev's textbook "Algebra 7")
The distance between piers M and N is 162 km. A motor ship departed from pier M at a speed of 45 km/h. After 45 minutes, another motor ship departed from pier N towards him, the speed of which is 36 km/h. In how many hours after the departure of the first ship will they meet?
Solution using equation:
Let there be a meeting in x hours
162 -45(x+0.75)-36x=0
162-45x - 33.75 -36x = 0
81x=128.25
2) ![]()
Answer: 2 hours 20 minutes.
Solving with Linear Function Graph:
1. Set the coordinate plane sOt with the abscissa axis Ot, on which we mark the time intervals of movement, and the y-axis Os, on which
note the distance from pier M to pier N, equal to 162 km. the beginning
reference point is jetty M
2. Let's draw divisions on a scale: along the y-axis - in two cells 18 km; along the abscissa axis - one hour in 6 cells (in 1 cell - 10 min.), since The task condition specifies the time in minutes.
mark the point N (0; 162).
3. Let's build the line of movement of the first ship I: the beginning of its movement will be at the point with coordinates (0; 0). The first ship sailed at a speed of 45 km / h, which means that the straight line must pass through the point with coordinates (1; 45).
4. Let's build the line of movement of the second ship II: the beginning of the movement will be at the point c
coordinates (; 162), since he left point N, 162 km away from M, 45 min. later than the first, and 45 min. \u003d h. The second ship sailed at a speed of 36 km / h, which means that the straight line must pass through the point (; 126), since the second ship left in the direction of the point M: 162 - 36 \u003d 126 (km).
5. The point of intersection of lines I and II is point A (; 108). The abscissa of the point shows the time after which, after the departure of the first ship, they met: t =, |=h = 2h20min. - the time of the meeting of two ships after the departure of the first ship.
Answer: 2 hours 20 minutes.
Conclusion.
At the end of the study, I was able to identify the advantages and disadvantages of solving problems graphically.
Advantages:
Tasks can be briefly written down;
It is quite easy to work with small numbers.
Disadvantages:
It's hard to work with big numbers.
View presentation content
"project"

First level
Solving equations, inequalities, systems using function graphs. Visual Guide (2019)
Many tasks that we are used to calculating purely algebraically can be solved much easier and faster, using function graphs will help us with this. You say "how so?" to draw something, and what to draw? Trust me, sometimes it's more convenient and easier. Shall we start? Let's start with equations!
Graphical solution of equations
Graphical solution of linear equations
As you already know, the graph of a linear equation is a straight line, hence the name of this type. Linear equations are quite easy to solve algebraically - we transfer all unknowns to one side of the equation, everything that we know - to the other, and voila! We have found the root. Now I'll show you how to do it graphic way.
So you have an equation:
How to solve it?
Option 1, and the most common is to move the unknowns to one side, and the known to the other, we get:
And now we are building. What did you get?
What do you think is the root of our equation? That's right, the coordinate of the intersection point of the graphs:

Our answer is
That's the whole wisdom of the graphic solution. As you can easily check, the root of our equation is a number!
As I said above, this is the most common option, close to the algebraic solution, but you can solve it in another way. To consider an alternative solution, let's return to our equation:
This time we will not move anything from side to side, but will build graphs directly, as they are now:
Built? Look!

What is the solution this time? All right. The same is the coordinate of the point of intersection of the graphs:

And, again, our answer is .
As you can see, with linear equations, everything is extremely simple. It's time to consider something more complicated... For example, graphic solution of quadratic equations.
Graphical solution of quadratic equations
So, now let's start solving the quadratic equation. Let's say you need to find the roots of this equation:
Of course, you can now start counting through the discriminant, or according to the Vieta theorem, but many nerves make mistakes when multiplying or squaring, especially if the example is with large numbers, and, as you know, you won’t have a calculator on the exam ... Therefore, let's try to relax a bit and draw while solving this equation.
Graphically, solutions to this equation can be found in various ways. Consider the various options, and you yourself will choose which one you like best.
Method 1. Directly
We just build a parabola according to this equation:
To make it quick, I'll give you one little hint: it is convenient to start the construction by determining the vertex of the parabola. The following formulas will help determine the coordinates of the vertex of the parabola:
You say "Stop! The formula for is very similar to the formula for finding the discriminant "yes, it is, and this is a huge disadvantage of" direct "building a parabola to find its roots. However, let's count to the end, and then I'll show you how to make it much (much!) easier!
Did you count? What are the coordinates of the vertex of the parabola? Let's figure it out together:
Exactly the same answer? Well done! And now we already know the coordinates of the vertex, and to build a parabola, we need more ... points. What do you think, how many minimum points do we need? Correctly, .
You know that a parabola is symmetrical about its vertex, for example:

Accordingly, we need two more points along the left or right branch of the parabola, and in the future we will symmetrically reflect these points on the opposite side:

We return to our parabola. For our case, the point. We need two more points, respectively, can we take positive ones, but can we take negative ones? What are the best points for you? It is more convenient for me to work with positive ones, so I will calculate with and.
Now we have three points, and we can easily build our parabola by reflecting the last two points about its top:

What do you think is the solution to the equation? That's right, the points at which, that is, and. Because.
And if we say that, then it means that it must also be equal, or.
Just? We have finished solving the equation with you in a complex graphical way, or there will be more!
Of course, you can check our answer algebraically - you can calculate the roots through the Vieta theorem or the Discriminant. What did you get? The same? You see! Now let's see a very simple graphical solution, I'm sure you'll like it very much!
Method 2. Split into several functions
Let's take everything, too, our equation: , but we write it in a slightly different way, namely:
Can we write it like this? We can, since the transformation is equivalent. Let's look further.
Let's build two functions separately:
- - the graph is a simple parabola, which you can easily build even without defining the vertex using formulas and making a table to determine other points.
- - the graph is a straight line, which you can just as easily build by estimating the values and in your head without even resorting to a calculator.
Built? Compare with what I got:

Do you think that in this case are the roots of the equation? Correctly! Coordinates by, which are obtained by crossing two graphs and, that is:

Accordingly, the solution to this equation is:
What do you say? Agree, this solution method is much easier than the previous one and even easier than looking for roots through the discriminant! If so, try this method to solve the following equation:
What did you get? Let's compare our charts:

The graphs show that the answers are:
Did you manage? Well done! Now let's look at the equations a little bit more complicated, namely, the solution of mixed equations, that is, equations containing functions of different types.
Graphical solution of mixed equations
Now let's try to solve the following:
Of course, you can bring everything to a common denominator, find the roots of the resulting equation, while not forgetting to take into account the ODZ, but again, we will try to solve it graphically, as we did in all previous cases.
This time let's plot the following 2 graphs:
- - the graph is a hyperbola
- - a graph is a straight line that you can easily build by estimating the values and in your head without even resorting to a calculator.
Realized? Now start building.
Here's what happened to me:

Looking at this picture, what are the roots of our equation?
That's right, and. Here is the confirmation:

Try plugging our roots into the equation. Happened?
All right! Agree, graphically solving such equations is a pleasure!
Try to solve the equation yourself graphically:
I give you a hint: move part of the equation to the right so that both sides have the simplest functions to build. Got the hint? Take action!
Now let's see what you got:
Respectively:
- - cubic parabola.
- - an ordinary straight line.
Well, we are building:

As you wrote down for a long time, the root of this equation is -.
Having solved such a large number of examples, I'm sure you realized how you can easily and quickly solve equations graphically. It is time to figure out how to solve systems in this way.
Graphic solution of systems
The graphical solution of systems is essentially no different from the graphical solution of equations. We will also build two graphs, and their intersection points will be the roots of this system. One graph is one equation, the second graph is another equation. Everything is extremely simple!
Let's start with the simplest - solving systems of linear equations.
Solving systems of linear equations
Let's say we have the following system:
To begin with, we will transform it in such a way that on the left there is everything that is connected with, and on the right - what is connected with. In other words, we write these equations as a function in the usual form for us:
And now we just build two straight lines. What is the solution in our case? Correctly! The point of their intersection! And here you need to be very, very careful! Think why? I'll give you a hint: we're dealing with a system: the system has both, and... Got the hint?
All right! When solving the system, we must look at both coordinates, and not only, as when solving equations! Another important point is to write them down correctly and not confuse where we have the value and where the value is! Recorded? Now let's compare everything in order:

And answers: i. Make a check - substitute the found roots into the system and make sure that we solved it correctly in a graphical way?
Solving systems of nonlinear equations
But what if instead of one straight line, we have a quadratic equation? It's okay! You just build a parabola instead of a straight line! Do not believe? Try to solve the following system:
What is our next step? That's right, write it down so that it is convenient for us to build graphs:
And now it’s all about the small thing - I built it quickly and here’s the solution for you! Building:

Are the graphics the same? Now mark the solutions of the system in the picture and correctly write down the revealed answers!
I've done everything? Compare with my notes:

All right? Well done! You already click on such tasks like nuts! And if so, let's give you a more complicated system:
What are we doing? Correctly! We write the system so that it is convenient to build:
I’ll give you a little hint, since the system looks very complicated! When building graphs, build them "more", and most importantly, do not be surprised at the number of intersection points.
So let's go! Exhaled? Now start building!
Well, how? Beautiful? How many intersection points did you get? I have three! Let's compare our graphs:

Same way? Now carefully write down all the solutions of our system:
Now look at the system again:
Can you imagine that you solved it in just 15 minutes? Agree, mathematics is still simple, especially when looking at an expression, you are not afraid to make a mistake, but you take it and decide! You're a big lad!
Graphical solution of inequalities
Graphical solution of linear inequalities
After the last example, you are up to the task! Now exhale - compared to the previous sections, this one will be very, very easy!
We start, as usual, with a graphical solution of a linear inequality. For example, this one:
To begin with, we will carry out the simplest transformations - we will open the brackets of perfect squares and give similar terms:
The inequality is not strict, therefore - is not included in the interval, and the solution will be all points that are to the right, since more, more, and so on:

Answer:
That's all! Easily? Let's solve a simple inequality with two variables:
Let's draw a function in the coordinate system.

Do you have such a chart? And now we carefully look at what we have in inequality? Smaller? So, we paint over everything that is to the left of our straight line. What if there were more? That's right, then they would paint over everything that is to the right of our straight line. Everything is simple.

All solutions to this inequality are shaded in orange. That's it, the two-variable inequality is solved. This means that the coordinates and any point from the shaded area are the solutions.
Graphical solution of quadratic inequalities
Now we will deal with how to graphically solve quadratic inequalities.
But before we get straight to the point, let's recap some stuff about the square function.
What is the discriminant responsible for? That's right, for the position of the graph relative to the axis (if you don't remember this, then read the theory about quadratic functions for sure).
In any case, here's a little reminder for you:

Now that we have refreshed all the material in our memory, let's get down to business - we will graphically solve the inequality.
I will tell you right away that there are two options for solving it.
Option 1
We write our parabola as a function:
Using the formulas, we determine the coordinates of the vertex of the parabola (in the same way as when solving quadratic equations):
Did you count? What did you get?
Now let's take two more different points and calculate for them:
We begin to build one branch of the parabola:

We symmetrically reflect our points on another branch of the parabola:

Now back to our inequality.
We need it to be less than zero, respectively:

Since in our inequality there is a sign strictly less, we exclude the end points - we “poke out”.
Answer:
Long way, right? Now I will show you a simpler version of the graphical solution using the same inequality as an example:
Option 2

We return to our inequality and mark the intervals we need:

Agree, it's much faster.
Let's write down the answer now:
Let's consider another solution method that simplifies the algebraic part, but the main thing is not to get confused.
Multiply the left and right sides by:
Try to solve the following quadratic inequality on your own in any way you like: .
Did you manage?
See how my chart turned out:

Answer: .
Graphical solution of mixed inequalities
Now let's move on to more complex inequalities!
How do you like this:
Horrible, right? Honestly, I have no idea how to solve this algebraically ... But, it is not necessary. Graphically, there is nothing complicated in this! The eyes are afraid, but the hands are doing!
The first thing we start with is by building two graphs:
I will not write a table for everyone - I'm sure you can do it perfectly on your own (of course, there are so many examples to solve!).
Painted? Now build two graphs.
Let's compare our drawings?

Do you have the same? Fine! Now let's place the intersection points and determine with a color which graph we should have, in theory, should be larger, that is. Look what happened in the end:

And now we just look at where our selected chart is higher than the chart? Feel free to take a pencil and paint over this area! It will be the solution to our complex inequality!

At what intervals along the axis is we higher than? Right, . This is the answer!
Well, now you can handle any equation, and any system, and even more so any inequality!
BRIEFLY ABOUT THE MAIN
Algorithm for solving equations using function graphs:
- Express through
- Define the function type
- Let's build graphs of the resulting functions
- Find the intersection points of the graphs
- Correctly write down the answer (taking into account the ODZ and inequality signs)
- Check the answer (substitute the roots in the equation or system)
For more information about plotting function graphs, see the topic "".
Graphical solution of a quadratic equation To consolidate the ability to build graphs of various functions; To form the ability to solve quadratic equations graphically. Brdsk 2009 Municipal educational institution - Economic Lyceum Generalizing lesson on the topic "Quadratic function", algebra grade 8 teacher Fedoseeva T.M.
Plotting a quadratic function Determine the direction of the branches: a>0 branches up; a 0 branches up; a"> 0 branches up; a"> 0 branches up; a" title="(!LANG:Plotting a quadratic function Determine branch direction: a>0 branches up; a"> title="Plotting a quadratic function Determine the direction of the branches: a>0 branches up; a"> !}
0 branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. Find the point "title="(!LANG: Let's build a graph of the function y=x 2 -2x-3 using the algorithm: 1) a=1>0 the branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. Finding a point" class="link_thumb"> 3 !} Let's build a graph of the function y=x 2 -2x-3 using the algorithm: 1) a=1>0 branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. We find the points of intersection with the OX axis: x 1 \u003d -1; x 2 \u003d 3 1 way to solve the equation x 2 -2x-3 \u003d 0 y x Solve the equation x 2 +2x-3 \u003d 0 0 branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. We find the point "\u003e 0 the branches are directed upwards; 2) the top y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3) , (3; 0) and symmetrical about the x = 1 axis We build a parabola.Find the points of intersection with the OX axis: x 1 \u003d -1; x 2 \u003d 3 1 way to solve the equation x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Solve the equation x 2 + 2x-3 \u003d 0 "\u003e 0 branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. Find the point "title="(!LANG: Let's build a graph of the function y=x 2 -2x-3 using the algorithm: 1) a=1>0 the branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. Finding a point"> title="Let's build a graph of the function y=x 2 -2x-3 using the algorithm: 1) a=1>0 branches are directed upwards; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - the axis of the parabola Control points: (0: -3), (3; 0) and symmetrical to them about the x-axis = 1 We build a parabola. Finding a point"> !}
The second way: a). Let's divide the equation x 2 -2x-3=0 into parts x 2 = 2x+3 Let's write two functions y= x 2 ; y \u003d 2x + 3 We build graphs of these functions in one coordinate system. The abscissas of the intersection points are the roots of the equation. 0 1 x y Solve the equation x 2 +2x-3=0

The third way: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x We build graphs of these functions in one coordinate system. The abscissas of the intersection points are the roots of the equation. 0 1 x y Solve the equation x 2 +2x-3=0



DAGESTAN INSTITUTE FOR PROFESSIONAL DEVELOPMENT
PEDAGOGICAL STAFF
DEPARTMENT OF PHYSICAL AND MATHEMATICAL EDUCATION AND ICT
Project
on the topic:
« Construction and p reforms
function graphs
in school mathematics »
Rabadanova P.A.
mathematic teacher
MBOU "Kochubey secondary school"
Tarumovsky district
2015
1. Introduction……………………………………………………………….….3
2. Chapter I. Review of literature on the topic of the project………………………….….5
3. Chapter II. Empirical part:
3.1. Basic methods for converting function graphs……….….7
3.2. Plotting an evenandodd functions…………….. 10
3.3. Plotting an inverse function………………………... 11
3.4. Deformation (compression and tension) of graphs………………….12
3.5. Combination of transfer, reflection and deformation………………......13
4. Tasks for independent solution………………………..…...14
5.Conclusion…………………………………………………………………15
6. Conclusions…………………………………………………………..………17
INTRODUCTION
Transformation of function graphs is one of the fundamental mathematical concepts directly related to practical activities. The graphs reflect the variability and dynamism of the real world, the mutual relations of real objects and phenomena.
The functional line is the basic topic covered in the Basic and Unified State Examinations.Also, many mathematical concepts are considered by graphical methods. For example, toquadraticthe function is introduced and studied in close connection with quadratic equations and inequalities.Hence it follows thatteaching students how to build and transform graphs of a function is one of the main tasks of teaching mathematics at school.
The study of the function makes it possible to find aboutdomain of definition and scope of the function, scopeDecreasing or increasing rates, asymptotes, intervalssign constancy, etc. However, to build a graphkov many functions can beuse a number of methodsmake it easierbuilding. Therefore, students should have the competence to build graphs according to methodological schemes.
The above definesrelevance research topics.
Object of study is the study of the transformation of functional line graphs in school mathematics.
Subject of study - the process of constructing and transforming function graphs in a secondary school.
Purpose of the study: educational - consists in identifying a methodological scheme for constructing and converting graphs of a function;developing - development of abstract, algorithmic, logical thinking, spatial imagination;educational - education of the graphic culture of schoolchildren, the formation of mental skills.
The goals led to the decision of the followingtasks:
1. Analyze the educational and methodological on the problem under study.
2. Identify methodological schemestransformation of function graphs in the school course of mathematics.
3. Select the most effective methods and meansconstruction and transformation of function graphs in a secondary schoolcontributing to: meaningful assimilation of educational material; increasing the cognitive activity of students; development of their creative abilities.
HYPOTHESIS research: the formation of graphic skills in the process of studying the functions and the education of the graphic culture of students will effective if students have a methodical scheme for constructing and transforming function graphs in a school mathematics course.
CHAPTER I . REVIEW OF LITERATURE ON THE TOPIC OF THE PROJECT.
In preparation for the project, we studied the following literature:
Sivashinsky, I. Kh. Theorems and problems in algebra, elementary functions - M., 2002. - 115 p.
Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Functions and graphs (basic techniques) - M., 1985. - 120 s
V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Elementary Mathematics - M., 2010 (reissue). - 590 p.
Kuzmin, M. K. Construction of a graph of a function - J. Mathematics at school. - 2003. - No. 5. - S. 61-62.
Shilov G.E. How to build charts? - M., 1982.
Isaac Tanatar. Geometric transformations of graphs of functions - MTsNMO, 2012
ATIt is noted that the ability to “read” the behavior of a function on a certain set using a graph is used not only in the course of mathematics, but also in any practical activity of a person in which he has to deal with certain graphic representations of dependencies. Therefore, students should be able to determine some of its properties from the graph of a function.
The theoretical material for the transformation of graphs is strictly stated in. The technique is accompanied by illustrations with drawings, examples of varying complexity and their solutions, which makes it possible to deepen knowledge and plot complex functions.
Represents an electronic training course, the volume and content of which meet the requirements for a high school mathematics course. The theoretical material is supported by graphic animation illustrations that give a visual representation of the topic under study. The course includes three modules: a theoretical material study module, a self-examination module and a knowledge control module.
From , , methodical charting schemes, examples for independent work were used for the empirical part of the project.
Conclusions to chapter 1
The study of educational and methodical literature allowed:
1. Identify methodological schemestudying, constructing and transforming graphs of a function in a school mathematics course.
2. Select the most effective methods and meansconstruction and transformation of function graphs in school mathematics,contributing:
meaningful assimilation of educational material;
increasing the cognitive activity of students;
development of their creative abilities.
3. show that the functional line has a significant impact in the study of various concepts in mathematics.
Chapter 2. EMPIRICAL PART
In this chapter, we will consider the main methods for transforming function graphs, and give methodological schemes for constructing various combinations of graphs for various functions.
2.1. BASIC TECHNIQUES FOR FUNCTION GRAPH CONVERSION
Translation along the y-axis
f ( x ) f ( x )+ b .
Forplotting a functiony = f( x) + btraceem:
1. build a function graphy= f( x)
2. move axisabscissa on| b| units up atb>0 or at| b| eatprostrate down atb < 0. Obtained in the new systemdinat graph is the graph of a functiony = f( x) + b.
2. Transfer along axes abscissa
f ( x ) f ( x + a ) .
y = f( x+ a) traceem:

3. Plotting a function of the form y = f (- x )
f (x ) f (- x ).
To plot a functiony = f( - x) follows:
plot a functiony = f( x)
reflect it backrelative to the y-axis
the resulting graph isfunction graphy = f( - X).
4. Plotting a function of the form y= - f ( x )
f ( x ) - f ( x )
- f( x) follows:
plot a functiony= f( x)
reflect it about the x-axis

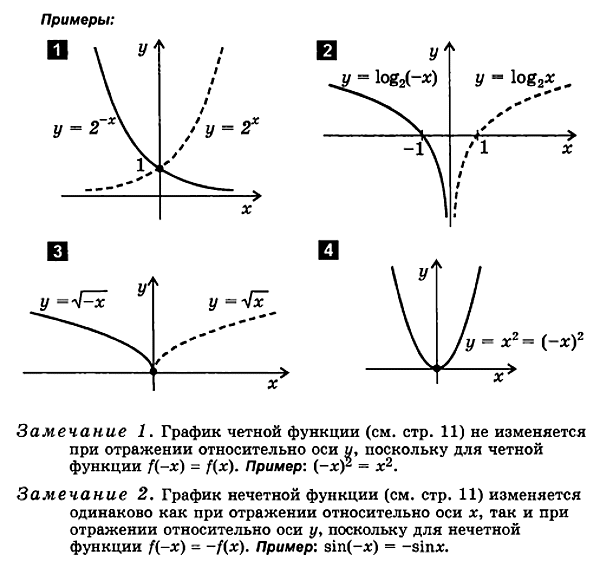
2.2. Plotting an even and odd features
When plottingFor even and odd functions, it is convenient to use the following properties:
1. Graph of an even function simmetricen relative to the y-axis.
2. The graph of an odd function is symmetrical about the origin.
To build graphs of an even and odd function, it is enough to plot only the right branch of the graph for positive values of the argument. The left branch is completed symmetrically about the origin for an odd function and about the y-axis for an even function.
To plot an even function y = f ( x ) after duet:
construct a branch of the graph of this function only inrange of positive values of the argument x≥0.
Otrace this branch about the y-axis

To plot an odd function y = f ( x ) follows:
build a graph branch of this function only inarea of positive values of the argument (х≥0).
Otrace this branch with respect to the originto the region of negative x values.

2.3. Plotting the inverse function
As already noted, the direct and inverse functionsshow the same relationship between variablesx and y, with the only difference that in the inverse function thesevariables have changed roles, which is equivalent to changingnotation of coordinate axes. Therefore, the graphthe inverse function is symmetrical to the graph of the direct functionabout the bisectorIandIIIcoordinate angles,i.e. relatively straighty = x. Thus, we getnext rule.
To plot the function y = (x) inverse to the functiony = f( x), should be builtscheduley = f( x) and reflect it with respect to the straight line y = x.

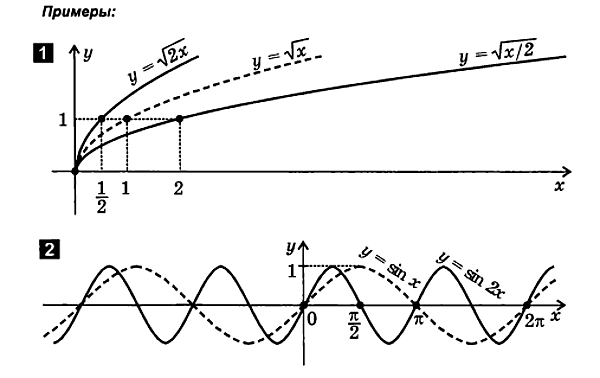
2.4. Deformation (compression and tension) of graphs
1. Compression (expansion) of the graph along the y-axis
f ( x ) A ∙ f ( x ).
To plot a functiony= A∙ f( x) follows:

8. Compression (expansion) of the graph along the x-axis
f( x)
To plot the function y= f( x) follows:
2.5. Combination of translation, reflection and deformation
Very often when plotting function graphs forchange the combination.
Consistent application of a number of such posture techniquesallows to significantly simplify the construction of a graph usingrunning function and often reduce it in the end toconstruction of one of the simplest elementary functionstions. Consider how, in view of the foregoing, it followsbuild function graphs.
Let us note that it is timeit is advisable to carry out the simplification dock in the next successorness.
Using parity orfunction oddness.
Axes transfer.
Reflection and deformation.
The construction of the graph is performed in the reverse order.
Example.
Plot a function![]()
The construction will be carried out in the following steps:
1. plot the natural logarithm:
2. squeezeto the axisOY2 times:;
3.
display symmetricallyabout the axisOY:
;
4. move along the axisOXon the(!!!) to the right:![]() :
:

5. display symmetrically about the axisOX:
;
6. movealong the axisOY3 units up:![]() :
:

EXAMPLES OF CONSTRUCTION AND CONVERSION OF FUNCTION GRAPHS
Example 1 Plot a function.
First, draw a sine graph, its period is equal to:

function graphobtained by compressing the graphtwice to the y-axis. log .
Plot a functionat = 2 cosX.
Plot a functiony = sinx .
CONCLUSION
During the work on the project work, various educational and methodological literature on this issue were analyzed. The results of the study made it possible to identify the most characteristic positive aspects of the study, construction and transformation of graphs of a function in a school mathematics course
The main goal of the project is to develop students' skills and abilities in reading and drawing drawings, in the formation of rational methods of independent activity.
The need to improve graphic education as a whole is dictated not only by modern production requirements, but also by the role of graphics in the development of technical thinking and cognitive abilities of students. A person's ability to process graphic information is one of the indicators of his mental development. Therefore, graphic training should become an integral element of general educational training.
findings
Thus, the developed project "Construction and transformation of function graphs", dedicated to one of the central concepts of mathematics - functional dependence, is focused on systematization and expansion of students' knowledge. The study of specific methods for transforming function graphs is carried out in an analytical and graphical way according to strict methodological schemes. The collected material can be used in the classroom and for self-training of students. A variety of forms and methods of organization and training can be used to conduct classes.
