There will also be tasks for an independent solution, to which you can see the answers.
Vector concept
Before you learn all about vectors and operations on them, tune in to solve a simple problem. There is a vector of your enterprise and a vector of your innovative abilities. The vector of entrepreneurship leads you to Goal 1, and the vector of innovative abilities - to Goal 2. The rules of the game are such that you cannot move in the directions of these two vectors at once and achieve two goals at once. Vectors interact, or, speaking mathematically, some operation is performed on vectors. The result of this operation is the "Result" vector, which leads you to Goal 3.
Now tell me: the result of which operation on the vectors "Enterprise" and "Innovative abilities" is the vector "Result"? If you can't say right away, don't be discouraged. As you study this lesson, you will be able to answer this question.
As we have seen above, the vector necessarily comes from some point A in a straight line to some point B. Consequently, each vector has not only a numerical value - length, but also a physical and geometric - direction. From this the first, simplest definition of a vector is derived. So, a vector is a directed segment going from a point A to the point B. It is marked like this:

And to start different vector operations , we need to get acquainted with one more definition of a vector.
A vector is a kind of representation of a point to be reached from some starting point. For example, a three-dimensional vector is usually written as (x, y, z) . Simply put, these numbers represent how far you have to go in three different directions to get to the point.
Let a vector be given. Wherein x = 3 (right hand points to the right) y = 1 (left hand points forward) z = 5 (under the point there is a ladder leading up). From this data, you will find the point by walking 3 meters in the direction indicated by the right hand, then 1 meter in the direction indicated by the left hand, and then a ladder awaits you and, climbing 5 meters, you will finally find yourself at the end point.
All other terms are refinements of the explanation presented above, necessary for various operations on vectors, that is, for solving practical problems. Let's go through these more rigorous definitions, dwelling on typical vector problems.
Physical examples vector quantities can be the displacement of a material point moving in space, the speed and acceleration of this point, as well as the force acting on it.

geometric vector represented in two-dimensional and three-dimensional space in the form directed segment. This is a segment that has a beginning and an end.
If a A is the beginning of the vector, and B is its end, then the vector is denoted by the symbol or a single lowercase letter . In the figure, the end of the vector is indicated by an arrow (Fig. 1)
Length(or module) of a geometric vector is the length of the segment that generates it
The two vectors are called equal , if they can be combined (when the directions coincide) by parallel translation, i.e. if they are parallel, point in the same direction and have equal lengths.
In physics, it is often considered pinned vectors, given by the application point, length, and direction. If the point of application of the vector does not matter, then it can be transferred, keeping the length and direction to any point in space. In this case, the vector is called free. We agree to consider only free vectors.
Linear operations on geometric vectors

Multiply a vector by a number
Vector product per number A vector is called a vector obtained from a vector by stretching (at ) or shrinking (at ) times, and the direction of the vector is preserved if , and reversed if . (Fig. 2)
It follows from the definition that the vectors and = are always located on one or parallel lines. Such vectors are called collinear. (You can also say that these vectors are parallel, but in vector algebra it is customary to say "collinear".) The converse is also true: if the vectors and are collinear, then they are related by the relation
Therefore, equality (1) expresses the condition of collinearness of two vectors.

Vector addition and subtraction
When adding vectors, you need to know that sum vectors and is called a vector whose beginning coincides with the beginning of the vector , and the end coincides with the end of the vector , provided that the beginning of the vector is attached to the end of the vector . (Fig. 3)

This definition can be distributed over any finite number of vectors. Let in space given n free vectors . When adding several vectors, their sum is taken as the closing vector, the beginning of which coincides with the beginning of the first vector, and the end with the end of the last vector. That is, if the beginning of the vector is attached to the end of the vector, and the beginning of the vector to the end of the vector, etc. and, finally, to the end of the vector - the beginning of the vector, then the sum of these vectors is the closing vector ![]() , whose beginning coincides with the beginning of the first vector , and whose end coincides with the end of the last vector . (Fig. 4)
, whose beginning coincides with the beginning of the first vector , and whose end coincides with the end of the last vector . (Fig. 4)
The terms are called the components of the vector, and the formulated rule is polygon rule. This polygon may not be flat.
When a vector is multiplied by the number -1, the opposite vector is obtained. The vectors and have the same length and opposite directions. Their sum gives null vector, whose length is zero. The direction of the null vector is not defined.
In vector algebra, there is no need to consider the operation of subtraction separately: to subtract a vector from a vector means to add the opposite vector to the vector, i.e. ![]()
Example 1 Simplify the expression:
![]() .
.
 ,
,
that is, vectors can be added and multiplied by numbers in the same way as polynomials (in particular, also problems for simplifying expressions). Usually, the need to simplify linearly similar expressions with vectors arises before calculating the products of vectors.
Example 2 The vectors and serve as diagonals of the parallelogram ABCD (Fig. 4a). Express in terms of and the vectors , , and , which are the sides of this parallelogram.

Decision. The intersection point of the diagonals of a parallelogram bisects each diagonal. The lengths of the vectors required in the condition of the problem are found either as half the sums of the vectors that form a triangle with the desired ones, or as half the differences (depending on the direction of the vector serving as a diagonal), or, as in the latter case, half the sum taken with a minus sign. The result is the vectors required in the condition of the problem:

There is every reason to believe that you now correctly answered the question about the "Enterprise" and "Innovative abilities" vectors at the beginning of this lesson. Correct answer: these vectors are subjected to an addition operation.
Solve problems on vectors on your own, and then look at the solutions
How to find the length of the sum of vectors?
This problem occupies a special place in operations with vectors, as it involves the use of trigonometric properties. Let's say you have a task like the following:
Given the length of vectors ![]() and the length of the sum of these vectors . Find the length of the difference of these vectors .
and the length of the sum of these vectors . Find the length of the difference of these vectors .
Solutions to this and other similar problems and explanations of how to solve them - in the lesson " Vector addition: the length of the sum of vectors and the cosine theorem ".
And you can check the solution of such problems on Online calculator "Unknown side of a triangle (vector addition and cosine theorem)" .
Where are the products of vectors?
The products of a vector by a vector are not linear operations and are considered separately. And we have lessons "Dot Product of Vectors" and "Vector and Mixed Product of Vectors".
Projection of a vector onto an axis
The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:
![]()
As is known, the projection of a point A on the line (plane) is the base of the perpendicular dropped from this point to the line (plane).

Let - an arbitrary vector (Fig. 5), and and - projections of its beginning (points A) and end (dots B) per axle l. (To build the projection of a point A) draw straight through the point A plane perpendicular to the line. The intersection of a line and a plane will determine the required projection.
Component of the vector on the l axis called such a vector lying on this axis, the beginning of which coincides with the projection of the beginning, and the end - with the projection of the end of the vector .
The projection of the vector onto the axis l called a number
![]() ,
,
equal to the length of the component vector on this axis, taken with a plus sign if the direction of the component coincides with the direction of the axis l, and with a minus sign if these directions are opposite.
The main properties of vector projections on the axis:
1. The projections of equal vectors on the same axis are equal to each other.
2. When a vector is multiplied by a number, its projection is multiplied by the same number.
3. The projection of the sum of vectors on any axis is equal to the sum of the projections on the same axis of the terms of the vectors.
4. The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:
![]()
 .
.

Decision. Let's project the vectors onto the axis l as defined in the theoretical reference above. From Fig.5a it is obvious that the projection of the sum of vectors is equal to the sum of the projections of vectors. We calculate these projections:

We find the final projection of the sum of vectors:
Relationship of a vector with a rectangular Cartesian coordinate system in space
Acquaintance with rectangular Cartesian coordinate system in space took place in the corresponding lesson, preferably open it in a new window.
In an ordered system of coordinate axes 0xyz axis Ox called x-axis, axis 0y – y-axis, and axis 0z – applicate axis.

with arbitrary point M space tie vector
called radius vector points M and project it onto each of the coordinate axes. Let us denote the values of the corresponding projections:
Numbers x, y, z called coordinates of point M, respectively abscissa, ordinate and applique, and are written as an ordered point of numbers: M(x; y; z)(Fig. 6).
A vector of unit length whose direction coincides with the direction of the axis is called unit vector(or ortom) axes. Denote by
Accordingly, the unit vectors of the coordinate axes Ox, Oy, Oz
![]()
Theorem. Any vector can be decomposed into the unit vectors of the coordinate axes:

![]() (2)
(2)
Equality (2) is called the expansion of the vector along the coordinate axes. The coefficients of this expansion are the projections of the vector onto the coordinate axes. Thus, the expansion coefficients (2) of the vector along the coordinate axes are the coordinates of the vector.
After choosing a certain coordinate system in space, the vector and the triple of its coordinates uniquely determine each other, so the vector can be written in the form
The vector representations in the form (2) and (3) are identical.
The condition of collinear vectors in coordinates
As we have already noted, vectors are called collinear if they are related by the relation
Let vectors ![]() . These vectors are collinear if the coordinates of the vectors are related by the relation
. These vectors are collinear if the coordinates of the vectors are related by the relation
![]() ,
,
that is, the coordinates of the vectors are proportional.
Example 6 Given vectors ![]() . Are these vectors collinear?
. Are these vectors collinear?
Decision. Let's find out the ratio of the coordinates of these vectors:
![]() .
.
The coordinates of the vectors are proportional, therefore, the vectors are collinear, or, what is the same, parallel.
Vector length and direction cosines
Due to the mutual perpendicularity of the coordinate axes, the length of the vector
![]()
is equal to the length of the diagonal of a rectangular parallelepiped built on the vectors
and is expressed by the equality
![]() (4)
(4)
A vector is completely defined by specifying two points (beginning and end), so the coordinates of the vector can be expressed in terms of the coordinates of these points.
Let the beginning of the vector in the given coordinate system be at the point
and the end is at the point


From equality
Follows that

or in coordinate form
Hence, the coordinates of the vector are equal to the differences of the coordinates of the same name of the end and beginning of the vector . Formula (4) in this case takes the form
The direction of the vector is determined direction cosines . These are the cosines of the angles that the vector makes with the axes Ox, Oy and Oz. Let's designate these angles respectively α , β and γ . Then the cosines of these angles can be found by the formulas
The direction cosines of a vector are also the coordinates of the vector's vector and thus the vector's vector
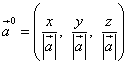
![]() .
.
Considering that the length of the vector vector is equal to one unit, that is,
![]() ,
,
we get the following equality for the direction cosines:
Example 7 Find the length of a vector x = (3; 0; 4).
Decision. The length of the vector is
![]()
Example 8 Given points:
Find out if the triangle built on these points is isosceles.
Decision. Using the vector length formula (6), we find the lengths of the sides and find out if there are two of them equal:

Two equal sides have been found, so there is no need to look for the length of the third side, and the given triangle is isosceles.
Example 9 Find the length of a vector and its direction cosines if ![]() .
.
Decision. The vector coordinates are given:
![]() .
.
The length of the vector is equal to the square root of the sum of the squares of the vector's coordinates:
![]() .
.
Finding direction cosines:

Solve the problem on vectors yourself, and then look at the solution
Operations on vectors given in coordinate form
Let two vectors and given by their projections be given:
![]()
![]()
Let us indicate actions on these vectors.
Page 1 of 2
Question 1. What is a vector? How are vectors defined?
Answer. We will call a directed segment a vector (Fig. 211). The direction of a vector is determined by specifying its beginning and end. In the drawing, the direction of the vector is marked with an arrow. To designate vectors, we will use lowercase Latin letters a, b, c, ... . You can also designate a vector by specifying its start and end. In this case, the beginning of the vector is placed in the first place. Instead of the word "vector", an arrow or a dash is sometimes placed above the letter designation of the vector. The vector in figure 211 can be denoted as follows:
\(\overline(a)\), \(\overrightarrow(a)\) or \(\overline(AB)\), \(\overrightarrow(AB)\).
Question 2. What vectors are called equally directed (oppositely directed)?
Answer. The vectors \(\overline(AB)\) and \(\overline(CD)\) are said to be equally directed if the half-lines AB and CD are equally directed.
The vectors \(\overline(AB)\) and \(\overline(CD)\) are called oppositely directed if the half-lines AB and CD are oppositely directed.
In Figure 212, the vectors \(\overline(a)\) and \(\overline(b)\) have the same direction, while the vectors \(\overline(a)\) and \(\overline(c)\) have opposite directions.

Question 3. What is the absolute value of a vector?
Answer. The absolute value (or modulus) of a vector is the length of the segment representing the vector. The absolute value of the vector \(\overline(a)\) is denoted by |\(\overline(a)\)|.
Question 4. What is a null vector?
Answer. The beginning of a vector can coincide with its end. Such a vector will be called a zero vector. The zero vector is denoted by zero with a dash (\(\overline(0)\)). No one talks about the direction of the zero vector. The absolute value of the zero vector is considered equal to zero.
Question 5. What vectors are called equal?
Answer. Two vectors are said to be equal if they are combined by a parallel translation. This means that there is a parallel translation that moves the beginning and end of one vector to the beginning and end of another vector, respectively.
Question 6. Prove that equal vectors have the same direction and are equal in absolute value. And vice versa: equally directed vectors that are equal in absolute value are equal.
Answer. With parallel translation, the vector retains its direction, as well as its absolute value. This means that equal vectors have the same direction and are equal in absolute value.
Let \(\overline(AB)\) and \(\overline(CD)\) be equally directed vectors equal in absolute value (Fig. 213). A parallel translation that takes point C to point A combines half-line CD with half-line AB, since they are equally directed. And since the segments AB and CD are equal, then the point D coincides with the point B, i.e. parallel translation translates the vector \(\overline(CD)\) into the vector \(\overline(AB)\). Hence, the vectors \(\overline(AB)\) and \(\overline(CD)\) are equal, as required.

Question 7. Prove that from any point one can draw a vector equal to the given vector, and only one.
Answer. Let CD be a line and the vector \(\overline(CD)\) be a part of line CD. Let AB be the line into which the line CD goes during parallel translation, \(\overline(AB)\) be the vector into which the vector \(\overline(CD)\) goes into during parallel translation, and hence the vectors \(\ overline(AB)\) and \(\overline(CD)\) are equal, and lines AB and CD are parallel (see Fig. 213). As we know, through a point not lying on a given line, it is possible to draw on the plane at most one line parallel to the given one (the axiom of parallel lines). Hence, through the point A one can draw one line parallel to the line CD. Since the vector \(\overline(AB)\) is part of the line AB, it is possible to draw one vector \(\overline(AB)\) through the point A, which is equal to the vector \(\overline(CD)\).
Question 8. What are vector coordinates? What is the absolute value of the vector with coordinates a 1 , a 2 ?
Answer. Let the vector \(\overline(a)\) start at point A 1 (x 1 ; y 1) and end at point A 2 (x 2 ; y 2). The coordinates of the vector \(\overline(a)\) will be the numbers a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . We will put the vector coordinates next to the letter designation of the vector, in this case \(\overline(a)\) (a 1 ; a 2) or just \((\overline(a 1 ; a 2 ))\). The zero vector coordinates are equal to zero.
From the formula expressing the distance between two points in terms of their coordinates, it follows that the absolute value of the vector with coordinates a 1 , a 2 is \(\sqrt(a^2 1 + a^2 2 )\).
Question 9. Prove that equal vectors have respectively equal coordinates, and vectors with respectively equal coordinates are equal.
Answer. Let A 1 (x 1 ; y 1) and A 2 (x 2 ; y 2) be the beginning and end of the vector \(\overline(a)\). Since the vector \(\overline(a")\) equal to it is obtained from the vector \(\overline(a)\) by parallel translation, then its beginning and end will be respectively A" 1 (x 1 + c; y 1 + d ), A" 2 (x 2 + c; y 2 + d). This shows that both vectors \(\overline(a)\) and \(\overline(a")\) have the same coordinates: x 2 - x 1 , y 2 - y 1 .
Let us now prove the converse assertion. Let the corresponding coordinates of the vectors \(\overline(A 1 A 2 )\) and \(\overline(A" 1 A" 2 )\) be equal. We prove that the vectors are equal.
Let x" 1 and y" 1 be the coordinates of the point A" 1, and x" 2, y" 2 be the coordinates of the point A" 2. By the condition of the theorem x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. Hence x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Parallel translation given by formulas
x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,
transfers point A 1 to point A" 1 , and point A 2 to point A" 2 , i.e. the vectors \(\overline(A 1 A 2 )\) and \(\overline(A" 1 A" 2 )\) are equal, as required.
Question 10. Define the sum of vectors.
Answer. The sum of the vectors \(\overline(a)\) and \(\overline(b)\) with coordinates a 1 , a 2 and b 1 , b 2 is the vector \(\overline(c)\) with coordinates a 1 + b 1 , a 2 + b a 2 , i.e.
\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).
Creation date: 2009-04-11 15:25:51
Last edited: 2012-02-08 09:19:45
For a long time I did not want to write this article - I thought about how to present the material. You also need to draw pictures. But, apparently, the stars have successfully formed today and there will be an article about vectors. Although, this is just a draft. In the future, I will break this article into several separate ones - there is enough material. Also, the article will gradually improve: I will make changes to it - because. in one sitting it will not be possible to reveal all aspects.
Vectors were introduced into mathematics in the nineteenth century to describe quantities that were difficult to describe using scalar values.
Vectors are heavily used in the development of computer games. They are used not only traditionally - to describe such quantities as force or speed, but also in areas that seem to have nothing to do with vectors: color storage, shadow creation.
Scalars and vectors
First, let me remind you what a scalar is and how it differs from a vector.
Scalar values store some value: mass, volume. That is, it is an entity that is characterized by only one number (for example, the amount of something).
A vector, unlike a scalar, is described using two values: magnitude and direction.
An important difference between vectors and coordinates: vectors are not tied to a specific location! Once again, the main thing in a vector is length and direction.
A vector is denoted by a bold letter of the Latin alphabet. For example: a, b, v.
In the first figure, you can see how the vector is denoted on the plane.
Vectors in space
In space, vectors can be expressed using coordinates. But first we need to introduce one concept:
Point radius vector
Let's take some point M(2,1) in space. The radius vector of a point is a vector that starts at the origin and ends at the point.
What we have here is nothing more than a vector OM. Vector start coordinates (0,0), end coordinates (2,1). Let's denote this vector as a.
In this case, the vector can be written as follows a = <2, 1>. This is the coordinate form of the vector a.
The coordinates of a vector are called its components relative to the axes. For example, 2 is a vector component a about the x-axis.
Let's once again dwell on what the coordinates of a point are. The coordinate of a point (for example, x) is the projection of the point onto the axis, i.e. the base of a perpendicular dropped from a point to an axis. In our example 2.
But back to the first picture. Here we have two points A and B. Let the coordinates of the points be (1,1) and (3,3). Vector v in this case it can be defined as v = <3-1, 3-1>. A vector lying at two points in three-dimensional space will look like this:
v =
I don't think there are any problems here.
Multiply a vector by a scalar
A vector can be multiplied by scalar values:
k v =
In this case, the scalar value is multiplied with each component of the vector.
If k > 1, then the vector will increase, if k is less than one but greater than zero, the vector will decrease in length. If k is less than zero, then the vector will change direction.
Unit vectors
Unit vectors are vectors whose length is equal to one. Note that the vector with coordinates<1,1,1>will not be equal to one! Finding the length of a vector is described below.
There are so-called orts - these are unit vectors that coincide in direction with the coordinate axes. i- unit vector of the x axis, j- unit vector of the y axis, k- unit vector of the z axis.
Wherein i = <1,0,0>, j = <0,1,0>, k = <0,0,1>.
Now we know what is the multiplication of a vector by a scalar and what are unit vectors. Now we can write v in vector form.
v= v x i+vy j+vz k, where v x , v y , v z are the corresponding components of the vector
Vector addition
To fully understand the previous formula, you need to understand how vector addition works.
Everything is simple here. Take two vectors v1 =
v1 + v2 =
We just add the corresponding components of the two vectors.
The difference is calculated in the same way.
It's about the mathematical form. For the sake of completeness, it's worth considering what adding and subtracting vectors would look like graphically.

To add two vectors a+b. We need to match the beginning of the vector b and the end of the vector a. Then, between the beginning of the vector a and the end of the vector b draw a new vector. For clarity, see the second figure (letter "a").
To subtract vectors, you need to combine the beginnings of two vectors and draw a new vector from the end of the second vector to the end of the first. The second picture (letter "b") shows what it looks like.
Vector length and direction
Let's look at the length first.
Length is the numeric value of the vector, regardless of direction.
The length is determined by the formula (for a three-dimensional vector):
the square root of the sum of the squares of the vector components.
Familiar formula, isn't it? In general, this is the formula for the length of a segment
The direction of the vector is determined by the direction cosines of the angles formed between the vector and the coordinate axes. To find the direction cosines, the appropriate components and length are used (the picture will be later).
Representing vectors in programs
Vectors can be represented in programs in a variety of ways. Both with the help of ordinary variables, which is inefficient, and with the help of arrays, classes and structures.
float vector3 = (1,2,3); // array for storing vector struct vector3 // structure for storing vectors ( float x,y,z; );
The greatest possibilities for storing vectors are provided by classes. In classes, we can describe not only the vector itself (variables), but also vector operations (functions).
Dot product of vectors
There are two types of vector multiplication: vector and scalar.
A distinctive feature of the scalar product is that the result will always be a scalar value, i.e. number.
Here it is worth paying attention to this moment. If the result of this operation is zero, then the two vectors are perpendicular - the angle between them is 90 degrees. If the result is greater than zero, the angle is less than 90 degrees. If the result is less than zero, the angle is greater than 90 degrees.
This operation is represented by the following formula:
a · b= a x * b x + a y * b y + a z * b z
The scalar product is the sum of the products of the corresponding components of two vectors. Those. We take x "s of two vectors, multiply them, then add them to the product of y" s and so on.
Cross product of vectors
The result of the cross product of two vectors will be a vector perpendicular to these vectors.
We will not discuss this formula in detail yet. Plus, it's pretty hard to remember. We will return to this point after getting acquainted with the determinants.
Well, for general development it is useful to know that the length of the resulting vector is equal to the area of the parallelogram built on vectors a and b.
Vector normalization
A normalized vector is a vector whose length is one.
The formula for finding a normalized vector is as follows - all components of the vector must be divided by its length:
v n= v/|v| =
Afterword
As you have probably seen, vectors are not difficult to understand. We have considered a number of operations on vectors.
In the following articles of the "mathematics" section, we will discuss matrices, determinants, systems of linear equations. It's all theory.
After that, we'll look at matrix transformations. It is then that you will understand how important mathematics is in creating computer games. This topic will just become a practice for all previous topics.
VECTORS. ACTIONSABOVEVECTORS. SCALAR,
VECTOR, MIXED PRODUCT OF VECTORS.
1. VECTORS, ACTIONS ON VECTORS.
Basic definitions.
Definition 1. A quantity that is fully characterized by its numerical value in the chosen system of units is called scalar or scalar .
(Body weight, volume, time, etc.)
Definition 2. A quantity characterized by a numerical value and direction is called vector or vector .
(Displacement, force, speed, etc.)
Designations: , or , .
A geometric vector is a directed segment.
For vector - point BUT- start point AT is the end of the vector.
Definition 3.Module vector is the length of segment AB.
Definition 4. A vector whose modulus is zero is called zero , is indicated.
Definition 5. Vectors located on parallel lines or on the same line are called collinear . If two collinear vectors have the same direction, then they are called co-directional .
Definition 6. Two vectors are considered equal , if they co-directed and are equal in modulus.
Actions on vectors.
1) Addition of vectors.
Def. 6.sum two vectors and is the diagonal of the parallelogram built on these vectors, coming from a common point of their application (parallelogram rule).

Fig.1.
Def. 7. The sum of three vectors , , is the diagonal of the parallelepiped built on these vectors (parallelepiped rule).
Def. eight. If a BUT, AT, With are arbitrary points, then + = (triangle rule).

fig.2
Addition properties.
1 about . + = + (displacement law).
2 about . + ( + ) = ( + ) + = ( + ) + (associative law).
3 about . + (– ) + .
2) Subtraction of vectors.
Def. nine. Under difference vectors and understand vector = - such that + = .
In a parallelogram, this is another diagonal SD (see fig. 1).
3) Multiplication of a vector by a number.
Def. ten. work vector to scalar k called vector
= k = k ,
long ka , and direction, which:
1. coincides with the direction of the vector if k > 0;
2. opposite to the direction of the vector if k < 0;
3. arbitrarily if k = 0.
Properties of multiplication of a vector by a number.
1 about . (k + l ) = k + l .
k ( + ) = k + k .
2 o . k (l ) = (kl ) .
3 o . 1 = , (–1) = – , 0 = .
Vector properties.
Def. eleven. Two vectors and are called collinear if they are located on parallel lines or at one straight line.
The zero vector is collinear to any vector.
Theorem 1. Two nonzero vectors and collinear, when they are proportional i.e.
= k , k - scalar.
Def. 12. Three vectors , , are called coplanar if they are parallel to some plane or lie in it.
Theorem 2. Three nonzero vectors , , coplanar, when one of them is a linear combination of the other two, i.e.
= k + l , k , l - scalars.
Projection of a vector onto an axis.
Theorem 3. Projection of a vector onto an axis (directed line) l is equal to the product of the length of the vector and the cosine of the angle between the direction of the vector and the direction of the axis, i.e. = a c os , = ( , l).

2. VECTOR COORDINATES
Def. thirteen. Vector projections on coordinate axes Oh, OU, Oz called vector coordinates. Designation: a x , a y , a z .
Vector length: ![]()
Example: Calculate the length of the vector .
Decision:
Distance between points ![]() and
and ![]() calculated by the formula: .
calculated by the formula: .
Example: Find the distance between points M (2,3,-1) and K (4,5,2).
Actions on vectors in coordinate form.
Given vectors = a x , a y , a z and = b x , b y , b z .
1. ( )= a x b x , a y b y , a z b z .
2. = a x , a y , a z, where - scalar.
Scalar product of vectors.
Definition: Under the scalar product of two vectors and
is understood as a number equal to the product of the lengths of these vectors and the cosine of the angle between them, i.e. = , - angle between vectors and .
Dot product properties:
1. =
2. ( + ) =
3.
4.
![]()
5. , where are scalars.
6. two vectors are perpendicular (orthogonal) if .
7. if and only if ![]() .
.
The scalar product in coordinate form has the form: ![]() ,
where and .
,
where and .
Example: Find the scalar product of vectors and
Decision:
Vector holding vectors.
Definition: The vector product of two vectors and is understood as a vector for which:
The module is equal to the area of the parallelogram built on these vectors, i.e. ![]() , where is the angle between the vectors and
, where is the angle between the vectors and
This vector is perpendicular to the multiplied vectors, i.e.
If the vectors are non-collinear, then they form a right triple of vectors.
Cross product properties:
1. When the order of the factors is changed, the vector product changes its sign to the opposite, preserving the module, i.e. ![]()
2 .Vector square is equal to zero-vector, i.e.
3
.The scalar factor can be taken out of the sign of the vector product, i.e. ![]()
4
.For any three vectors, the equality ![]()
5 .Necessary and sufficient condition for the collinearity of two vectors and :
Vector product in coordinate form.
If the coordinates of the vectors and , then their vector product is found by the formula:
 .
.
Then from the definition of a cross product it follows that the area of a parallelogram built on vectors and is calculated by the formula:
Example: Calculate the area of a triangle with vertices (1;-1;2), (5;-6;2), (1;3;-1).
Decision:  .
.
Then the area of the triangle ABC will be calculated as follows:
![]() ,
,

Mixed product of vectors.
Definition: A mixed (vector-scalar) product of vectors is a number determined by the formula: ![]() .
.
Mixed product properties:
1.
The mixed product does not change with a cyclic permutation of its factors, i.e. ![]() .
.
2. When two neighboring factors are interchanged, the mixed product changes its sign to the opposite, i.e. .
3 .Necessary and sufficient condition for three vectors to be coplanar : =0.
4 .The mixed product of three vectors is equal to the volume of the parallelepiped built on these vectors, taken with a plus sign if these vectors form a right triple, and with a minus sign if they form a left triple, i.e. .
If known coordinates vectors ,
then the mixed product is found by the formula: 
Example: Calculate the mixed product of vectors.
Decision: 
3. Basis of the system of vectors.
Definition. A system of vectors is understood as several vectors belonging to the same space R.
Comment. If the system consists of a finite number of vectors, then they are denoted by the same letter with different indices.
Example. 
Definition. Any vector of the form =  is called a linear combination of vectors. The numbers are the coefficients of the linear combination.
is called a linear combination of vectors. The numbers are the coefficients of the linear combination.
Example. ![]() .
.
Definition. If the vector is a linear combination of vectors , then we say that the vector is linearly expressed in terms of the vectors .
Definition. The system of vectors is called linearly independent, if none of the vectors of the system can be as a linear combination of the rest of the vectors. Otherwise, the system is called linearly dependent.
Example. Vector system ![]() linearly dependent, since the vector
linearly dependent, since the vector ![]() .
.
Basis definition. A system of vectors forms a basis if:
1) it is linearly independent,
2) any vector of space through it is linearly expressed.
Example 1 Space basis: .
2.
In the system of vectors ![]() vectors are the basis: , because
vectors are the basis: , because ![]() linearly expressed in terms of vectors .
linearly expressed in terms of vectors .
Comment. To find the basis of a given system of vectors, you need to:
1) write the coordinates of the vectors in the matrix,
2) using elementary transformations, bring the matrix to a triangular form,
3) non-zero rows of the matrix will be the basis of the system,
4) the number of vectors in the basis is equal to the rank of the matrix.
DEFINITION
Vector(from lat. " vector"-" bearing") - a directed segment of a straight line in space or on a plane.
Graphically, a vector is depicted as a directed straight line segment of a certain length. The vector whose beginning is at the point and the end at the point is denoted as (Fig. 1). Also, a vector can be denoted by a single small letter, for example, .
If a coordinate system is given in space, then the vector can be uniquely specified by a set of its coordinates. That is, a vector is understood as an object that has a value (length), direction and application point (beginning of the vector).
The beginnings of vector calculus appeared in works in 1831 in the works of the German mathematician, mechanic, physicist, astronomer and surveyor Johann Carl Friedrich Gauss (1777-1855). Works on operations with vectors were published by the Irish mathematician, mechanician and theoretical physicist, Sir William Rowan Hamilton (1805-1865) as part of his quaternion calculus. The scientist proposed the term "vector" and described some operations on vectors. Vector calculus was further developed thanks to the work on electromagnetism of the British physicist, mathematician and mechanic James Clerk Maxwell (1831-1879). In the 1880s, the book "Elements of Vector Analysis" by the American physicist, physicochemist, mathematician and mechanic Josiah Willard Gibbs (1839-1903) was published. Modern vector analysis was described in 1903 by the English self-taught scientist, engineer, mathematician and physicist Oliver Heaviside (1850-1925).
DEFINITION
Length or vector module is the length of the directed segment that defines the vector. Designated as .

Basic types of vectors
Zero vector is called a vector whose start point and end point are the same. The length of the null vector is zero.
Vectors that are parallel to the same line or lie on the same line are called collinear(Fig. 2).
co-directional if their directions are the same.
In Figure 2, these are the vectors and . The co-direction of vectors is denoted as follows: .
Two collinear vectors are called opposite directions if their directions are opposite.
In figure 3, these are the vectors and . Designation: .
