Oppitunnin tavoitteet:

Muodostaa tietoa, taitoja ja kykyjä soveltaa tehokkaasti yleistettyä intervallimenetelmää jatkuvien funktioiden ominaisuuden perusteella;

Muotoile toimintojen algoritmi, jotka johtavat vastaaviin muunnoksiin;

Opettele itsesi soveltamaan sitä eriarvoisuuksia ratkaiseessasi;

Toteuttaa tiedon, taitojen ja kykyjen siirto uusiin olosuhteisiin.

Kasvatus: tietojen, taitojen ja kykyjen systematisointi, lujittaminen, yleistäminen.

Koulutus: koulutus täysimittaisen johdonmukaisen argumentoinnin tarpeesta, tarkkuudesta, itsenäisyydestä.

Kehittäminen: matemaattisen logiikan kehittyminen, matemaattisen ajattelutavan muodostuminen (selkeä päättelyn kulku), kognitiivinen kiinnostus.

1) Johdanto, oppitunnin tavoitteen ja tavoitteiden asettaminen - 2 min.

2) Kotitehtävien tarkistaminen - 2 min. (etutyö, itsehillintä).

3) Epäyhtälöiden ratkaisun vaiheiden matemaattinen perustelu intervallimenetelmällä - 4 min (valmiit opiskelijavastaukset).

4) Epäyhtälöiden ominaisuuksien toisto - 2 min.

5) Valmistautuminen uuden oppimateriaalin omaksumiseen (tutkimiseen) toiston ja perustietojen päivittämisen kautta - 5 min. (frontaalityö, vastaukset kysymyksiin, ongelmatilanteet).

6) Yleistetty intervallimenetelmä epäyhtälöiden ratkaisemiseen, alkuymmärrys - 13 min. (Epäyhtälöiden kollektiivinen ratkaisu intervallimenetelmällä: taululla ja muistikirjoissa).

7) Tietoa läksyistä, ohjeet sen tekemiseen - 1 min.

8) Uuden tiedon lujittaminen - 15 min. (itsenäinen työskentely - vaihtoehto 1).

9) Oppitunnin yhteenveto, pohdiskelu - 1 min.

1) Johdanto, oppitunnin tavoitteen ja tavoitteiden asettaminen. (Opettajan tarina)

1) Tarve intervallimenetelmän laajemmalle soveltamiselle koulussa sanelee koko matematiikan opetusprosessin ideologia. Asia on siinä, että toiminnallinen linja (yksi tärkeimmistä matematiikan perusteiden tutkimuksessa) saa tehokkaan teknologisen tuen. Intervallimenetelmä perustuu sellaisiin tärkeisiin toiminnallisen riippuvuuden ominaisuuksiin kuin funktion nollia, sen vakiomerkin intervallit ja monotonisuus. Silloin yhtälöiden ja epäyhtälöiden funktionaalinen alkuperä sekä menetelmät niiden ratkaisemiseksi selkiytyvät. Funktion jatkuvuuskategoriat, sen graafin käyttäytyminen äärettömän epäjatkuvuuden pisteiden läheisyydessä, juuren lauseet, etumerkin pysyvyys, ääripisteet ja niiden tyypit tulevat visuaalisemmiksi. Ja kaikki tämä liittyy orgaanisesti yhdeksi toimivaksi kokonaisuudeksi.

Toisaalta myös käytettyjen tutkimuskohteiden geometrisointi on korvaamatonta, ts. esittää visuaalisesti, kuvaannollisesti kaikki käytetyt funktionaalisen riippuvuuden matemaattiset työkalut.

Intervallimenetelmän perusperiaatteet:

• toiminnallinen (yleistetty) lähestymistapa;
• toiminnallisten ominaisuuksien geometrisointiin luottaminen;
• tutkimuksen visualisointi.

Tämä johtaa menetelmän seuraaviin etuihin verrattuna muihin samanlaisissa tehtävissä käytettäviin: yksinkertaisuus ja tavoitteen saavuttamisen nopeus; näkyvyys (ja kyky hallita tai tarkistaa uudelleen); laskentaresurssien ja ajan säästäminen; koko tilanteen kattavuus, yleisen ajattelun ja analyysin taitojen muodostuminen ja kehittäminen sekä tähän liittyvät taidot tehdä loogisia johtopäätöksiä.

2) Kotitehtävien tarkistaminen.(Dia numero 4)

3) Tarina intervallimenetelmästä epäyhtälöiden ratkaisemiseksi. (Oppilas vastaa).

Epäyhtälöiden ratkaisun matemaattinen perustelu intervallimenetelmällä.

1) Tarkastellaan epäyhtälöitä: (x-2)(x-3)>0. (dia numero 5)

Voit ratkaista sen seuraavasti: Kahden tekijän tulo (osamäärä) on positiivinen silloin ja vain, jos molemmilla tekijöillä on sama etumerkki, ts. epätasa-arvo vastaa kahden järjestelmän yhdistelmää: (dia numero 6)

Ensimmäisestä järjestelmästä saadaan x >3, toisesta x< 2.

Ratkaisu on näiden kahden järjestelmän ratkaisujen liitto.

Vastaus:

Graafinen menetelmä (dia numero 7)

Toinen menetelmä on intervallimenetelmä(dia numero 8).

Hänen ajatuksensa on seuraava.

Merkitse reaaliviivalle polynomin (x-2)(x-3) nollat ​​(juuret)

epätasa-arvon vasemmalla puolella, ts. numerot 2 ja 3.

Kun x >3 (suuremman juuren oikealla puolella), niin (x-2)(x-3)>0, koska jokainen tekijä on positiivinen.

Jos liikutat akselia pitkin negatiiviseen suuntaan, kun kuljet pisteen x=3 läpi, tekijä (x-3) muuttaa etumerkkiä. Tuotteessa (x-2) (x-3) ilmestyy yksi negatiivinen tekijä, jonka seurauksena (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Nyt on helppo kirjoittaa epäyhtälön ratkaisu:

Johtopäätös: tuote voi vaihtaa etumerkkiä vain kulkiessaan pisteiden x=2 ja x=3 kautta

ja siksi säilyttää merkin jokaisella saadulla aikavälillä.

Tässä yksinkertaisessa esimerkissä intervallimenetelmän idea on helppo ymmärtää, mutta siinä ei ole havaittavia etuja.

Intervallimenetelmän rationaalisuutta, sen tehoa, tarkastelemme seuraavaa esimerkkiä (dia nro 9, 10,11, 12)

2) Ratkaise epäyhtälö (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)>0.

Tämän epätasa-arvon ratkaisemiseksi järjestelmäjoukon avulla olisi tarkasteltava 512 järjestelmän joukkoa, joissa kussakin järjestelmässä on 10 epäyhtälöä.

Käytetään intervallimenetelmää. Merkitsemme polynomin nollat ​​reaaliviivalle. Välillä x>10 polynomi on positiivinen, koska jokainen tekijä on positiivinen. Kulkiessaan jokaisen seuraavan juuren läpi polynomi vaihtaa etumerkkiä, koska tuloon ilmestyy ylimääräinen negatiivinen tekijä. Nyt on helppo kirjoittaa epäyhtälön ratkaisu etumerkkien vuorottelulla.

Intervallimenetelmän edut.

• tavoitteen saavuttamisen yksinkertaisuus ja nopeus;
• näkyvyys (ja kyky hallita tai tarkistaa uudelleen);
• laskennallisen työn ja ajan merkittävä väheneminen;
• koko tilanteen kattavuus;
• yleisen ajattelun ja analyysitaidon muodostuminen ja kehittäminen sekä niihin liittyvät loogisten johtopäätösten taidot.

Kommentti. On erittäin kätevää ratkaista epäyhtälöitä, joiden vasen puoli on kertoimella, koska nollia (juuria) ei ole vaikea löytää.

Tehtävä: Ratkaise epäyhtälö intervallimenetelmällä (x+3) 3 (x-4) 2 (x-5)>0(Dia 13)

4) Epäyhtälöiden ominaisuuksien toisto.

a) Kysymys: Mitä epäyhtälöitä kutsutaan ekvivalenteiksi?

(Kahta epäyhtälöä kutsutaan ekvivalentiksi, jos mikä tahansa ratkaisu ensimmäiseen epäyhtälöön on ratkaisu toiseen ja päinvastoin mikä tahansa ratkaisu toiseen on ratkaisu ensimmäiseen).

Tai: kahden epäyhtälön sanotaan olevan ekvivalentteja, jos niiden ratkaisujoukot ovat samat.

Dia 14. Epäyhtälöiden ominaisuuksien toisto.

Dia 15. Vastaa kysymykseen ja selitä.

Ovatko eriarvoisuudet tasa-arvoisia?

1) 4x-5<0 и 4х<5

2) -2x+5>0 ja 2x-5<0

3) -3x 2 +5x-7>0 ja 3x 2 -5x+7<0

4) (x+1)>0 ja (x 2 +5x+10) (x+1)>0

5) Suullinen frontaalityö uuden oppimateriaalin omaksumiseen (tutkimiseen) valmistautuessa toiston ja perustietojen päivittämisen kautta.

Dia 16. Pisteessä jatkuvan funktion määritelmä.

Dia 17. Jatkuvien funktioiden ominaisuus.

Dia 18. Etsi jatkuvuuden aukkoja.

Dia 19. Etsi virhe.

Dia 20. Ratkaise epäyhtälö suullisesti,
käyttämällä kaaviota.

Dia 21, 22. Epäyhtälön korvaaminen vastaavalla ehdolla.

Ratkaise epätasa-arvo

Tämä epäyhtälö vastaa ehtoa f(x) < 0 lasketaan

Siksi meidän on löydettävä kaikki x:n arvot, joille ehto f(x) < 0.

6) Yleistetty intervallimenetelmä epäyhtälöiden ratkaisemiseen, alkuymmärrys - 10 min. (Epäyhtälöiden kollektiivinen ratkaisu intervallimenetelmällä: taululla ja muistikirjoissa).

dia 23. Algoritmi. Yleistetty menetelmä epäyhtälöiden ratkaisemiseksi.

Epäyhtälöiden ratkaisu f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 intervallimenetelmällä. (Kaavio)

Dia 24 ja 25. Epäyhtälön ratkaiseminen algoritmilla. (Kommentit algoritmin kaikkiin kohtiin).

dia 26. Graafinen esitys tämän epäyhtälön ratkaisusta.

Dia 27. Ratkaise epäyhtälö taululla ja vihkoissa .

Dia 28. Graafinen esitys tämän epäyhtälön ratkaisusta.

Dia 29. Ratkaise epäyhtälö taululla ja vihkoissa

Dia 30. Graafinen esitys tämän epäyhtälön ratkaisusta.

Dia 31, 32. Ratkaise epäyhtälö suullisesti kuvan mukaan

7) Tietoja kotitehtävistä.(Ratkaise intervallimenetelmällä vaihtoehto numero 2)

8) Uuden tiedon lujittaminen (itsenäinen työskentely, vaihtoehto nro 1).

9) Oppitunnin yhteenveto, valmiiden ratkaisujen itsehallinta (diat 33, 34, 35), yleistetyn intervallimenetelmän algoritmin toisto ja sen soveltaminen.

10) Aineiston omaksumisen ja opiskelijoiden kiinnostuksen aihetta kohtaan analysointi. Tämä menetelmä on universaali kaikkien epäyhtälöiden ratkaisemisessa, mukaan lukien rationaalinen, modulo, irrationaalinen, eksponentiaalinen, logaritminen, koska intervallimenetelmä pelkistää epäyhtälöiden ratkaisun yhtälöiden ratkaisemiseen, funktion alueen ja arvon löytäminen pisteestä ei aiheuta vaikeuksia. Mutta minun piti antaa esimerkkejä epätasa-arvoista, joissa tämän menetelmän käyttö ei ole perusteltua, missä on järkevämpää soveltaa muita menetelmiä eriarvoisuuksien ratkaisemiseen.

Esitys “Jatkuvuuden soveltaminen eriarvoisuuksien ratkaisemisessa”. (35 diaa)

Määritelmä 4. Funktiota kutsutaan janan jatkuvaksi, jos se on jatkuva tämän janan jokaisessa pisteessä (pisteessä a se on jatkuva oikealla puolella, ts. ja pisteessä b se on jatkuva vasemmalla, ts.).

Kaikki peruselementtifunktiot ovat jatkuvia määrittelyalueellaan.

Segmentillä jatkuvien funktioiden ominaisuudet:

• 1) Jos funktio on jatkuva janalla, se on rajoitettu tähän segmenttiin (ensimmäinen Weierstrassin lause).
• 2) Jos funktio on jatkuva janalla, niin se saavuttaa tällä segmentillä minimi- ja maksimiarvonsa (toinen Weierstrassin lause) (katso kuva 2).
• 3) Jos funktio on jatkuva janalla ja ottaa sen päistään eri etumerkkien arvoja, niin janan sisällä on ainakin yksi piste siten, että (Bolzano-Cauchyn lause).

Toimintojen rajapisteet ja niiden luokittelu

funktion jatkuvuuspistesegmentti

Pisteitä, joissa jatkuvuusehto ei täyty, kutsutaan tämän funktion epäjatkuvuuspisteiksi. Jos on funktion epäjatkuvuuspiste, niin vähintään yksi kolmesta määritelmissä 1, 2 määritellyistä funktion jatkuvuuden ehdoista ei täyty siinä, nimittäin:

1) Funktio on määritelty pisteen läheisyydessä, mutta ei itse pisteessä. Esimerkin 2 a) funktiolla on siis tauko jossain pisteessä, koska sitä ei ole määritelty tässä pisteessä.

2) Funktio on määritelty pisteessä ja sen ympäristössä, on yksipuolisia rajoja ja, mutta ne eivät ole keskenään tasavertaisia: . Esimerkiksi esimerkin 2 b) funktio on määritelty pisteessä ja sen ympäristössä, mutta koska a.

3) Funktio on määritelty pisteessä ja sen ympäristössä, siinä on yksipuolisia rajoja ja ne ovat keskenään yhtä suuria, mutta eivät yhtä suuria kuin funktion arvo pisteessä: . Esimerkiksi toiminto. Tässä on katkaisukohta: tässä vaiheessa funktio on määritelty, on yksipuolisia ja keskenään tasavertaisia ​​rajoja, mutta ts.

Toimintojen keskeytyspisteet luokitellaan seuraavasti.

Määritelmä 5. Pistettä kutsutaan funktion ensimmäisen tyypin epäjatkuvuuspisteeksi, jos siinä on äärelliset rajat ja tässä pisteessä, mutta ne eivät ole keskenään samanarvoisia: . Suuruutta kutsutaan sitten funktion hyppyksi pisteessä.

Määritelmä 6. Pistettä kutsutaan funktion irrotettavan epäjatkuvuuden pisteeksi, jos tässä kohdassa on äärelliset rajat ja ne ovat keskenään yhtä suuret: , mutta itse funktiota ei ole määritelty pisteessä, tai se on määritelty, mutta.

Määritelmä 7. Pistettä kutsutaan funktion toisen tyypin epäjatkuvuuspisteeksi, jos tässä pisteessä ainakin yksi yksipuolisista rajoista (tai) ei ole olemassa tai on yhtä suuri kuin ääretön.

Esimerkki 3. Etsi seuraavien funktioiden katkaisupisteet ja määritä niiden tyyppi: a) b)

Ratkaisu. a) Funktio on määritelty ja jatkuva aikaväleillä u, koska jokaisella näillä aikaväleillä se annetaan jatkuvilla alkeisfunktioilla. Siksi tietyn funktion katkaisupisteitä voivat olla vain ne pisteet, joissa funktio muuttaa analyyttistä tehtäväänsä, ts. kohdat i. Etsitään funktion yksipuoliset rajat pisteestä:

Koska yksipuolisia rajoja on olemassa ja ne ovat äärellisiä, mutta eivät keskenään yhtä suuria, piste on ensimmäisen tyyppinen epäjatkuvuuspiste. Toimintohyppy:

Löydämme pisteen.

Funktion jatkuvuus intervallilla

Parametrin nimi	Merkitys
Artikkelin aihe:	Funktion jatkuvuus intervallilla
Otsikko (teemaattinen luokka)	Matematiikka

Määritelmä. Funktiota kutsutaan jatkuvaksi välissä, jos se on jatkuva tämän aikavälin jokaisessa pisteessä.

Jos funktio on määritetty X=a ja missä f(X) = f(a),

sitten he sanovat niin f(X) pisteessä ja jatkuva oikealla. Samoin jos f(X) = f(b), niin sanomme sen siinä vaiheessa b tämä toiminto jätetty jatkuvaksi.

Määritelmä. Funktiota kutsutaan yleensä jatkuvaksi välillä [ a, b], jos se on jatkuva kussakin pisteessään (pisteessä a jatkuva oikealla, pisteessä b on jatkuva vasemmalla).

korkein arvo toimintoja klo = f(x) segmentillä [ a, b f(x 1) tuo f(x) £ f(x 1) kaikille X Î [ a, b].

Alin arvo toimintoja klo = f(x) segmentillä [ a, b] on tapana kutsua sellaista sen arvoksi f(x 2) sitä f(x) ³ f(x 2) kaikille X Î [ a, b].

Intervalleilla jatkuvilla funktioilla on useita tärkeitä ominaisuuksia, jotka ilmaistaan ​​seuraavilla lauseilla.

Lause 3.3.1. Jatkuva funktio segmentillä [ a, b], saavuttaa minimiarvonsa siinä m ja suurin arvo M, eli sellaisia ​​kohtia on x 1 ja x 2 tästä segmentistä, joka f(x 1) = m, f(x 2) = M.

Lauseen geometrinen merkitys on yksinkertainen (ks. kuva 2).

Lause 3.3.2. Jos toiminto klo = f(x) on jatkuva aikavälillä [ a, b] ja ottaa päistään eriarvoisia arvoja f(a) = A, f(b) = B, A ¹ B, niin mikä tahansa luku C välillä A ja B, on piste Kanssa Î [ a, b] sellaista f(Kanssa) = C.

Lauseen geometrinen merkitys on esitetty kuvassa 3. Mikä tahansa suora viiva klo= C, missä A< C < B (или A >C > B), leikkaa funktion kuvaajan klo = f(x).

Seuraus. Jos funktio on jatkuva janalla ja ottaa sen päistään eri etumerkkien arvoja, niin tässä segmentissä on ainakin yksi piste, josta funktio katoaa.

Seurauksen geometrinen merkitys on esitetty kuvassa 4.

Kysymyksiä itsehillintää varten

1. Mitä funktiota kutsutaan jatkuvaksi pisteessä?

2. Anna vielä yksi vastaava määritelmä funktion ja argumenttien lisäyksen avulla.

3. Mitä voidaan sanoa kahden jatkuvan funktion summasta, erotuksesta, tulosta ja osamäärästä?

4. Millä argumentin arvoilla kaikki rationaaliset ja murto-rationaaliset funktiot ovat jatkuvia?

5. Milloin kompleksifunktio on jatkuva pisteessä?

6. Mitä kutsutaan yleisesti funktioiden murtumispisteeksi?

7. Mitä pisteitä kutsutaan ensimmäisen tyyppisiksi epäjatkuvuuspisteiksi?

8. Mitä arvoa kutsutaan yleensä funktiohypyksi?

9. Selitä "irrotettavan katkaisukohdan" käsitteet. Antaa esimerkkejä.

10. Mitä pisteitä kutsutaan toisen tyyppisiksi epäjatkuvuuspisteiksi? Antaa esimerkkejä.

11. Selitä käsitteet: ""jatkuvuus välissä"", ""jatkuvuus oikealla"", ""jatkuvuus vasemmalla"", ""jatkuvuus segmentillä"".

12. Määritä funktioiden suurimmat ja pienimmät arvot.

13. Muotoile lause jatkuvuuden suhteesta segmentillä, jolla on funktion suurin ja pienin arvo. Selitä se kuvalla.

14. Muotoile lause segmentin funktioiden jatkuvuuden ja funktioarvojen segmentin välisestä yhteydestä. Havainnollistaa sen geometrinen merkitys kuvassa.

15. Esitä seuraus yllä olevasta lauseesta ja sen geometrinen tulkinta.

LUENTO №4

Luennon aihe: Funktiojohdannainen

Luentosuunnitelma: Johdannan käsite, sen geometrinen ja fyysinen merkitys. Erottamisen perussäännöt. Monimutkaisen funktion johdannainen. Jotkut johdannaisen sovellukset.

4.1. Johdannan käsite, sen geometrinen ja fyysinen merkitys

Harkitse toimintoa klo = f(x) määritetty välissä ] a, b[. Päästää XÎ ] a, b[ ja X Î ] a, b[, sitten funktio kasvaa pisteessä X 0 ilmaistaan ​​kaavalla D klo = f(x 0+D X) – f(x 0).

Määritelmä. Funktion y derivaatta = f(x) pisteessä X 0:ta kutsutaan yleensä tämän funktion lisäyksen ja argumentin lisäyksen suhteen rajaksi, kun jälkimmäinen pyrkii nollaan:

f'(x 0) = tai y"(x 0) =.

Johdannan geometrinen merkitys: tämän funktion derivaatta pisteessä on yhtä suuri kuin Ox-akselin välisen kulman tangentti ja tämän funktion kaavion tangentti vastaavassa pisteessä (katso kuva 1):

f"(x 0) = rusketus a.

Määritelmä. Jos toiminto f(x) on määritelty aikavälillä [ a, b], on jatkuva intervallin ( a, b), pisteessä a jatkuva oikealla, pisteessä b on jatkuva vasemmalla, niin sanomme, että funktio f(x) jatkuva segmentillä [a, b].

Toisin sanoen funktio f(x) on jatkuva aikavälillä [ a, b], jos kolme ehtoa täyttyy:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Välillä jatkuville funktioille otetaan huomioon joitain ominaisuuksia, jotka muotoilemme seuraavien lauseiden muodossa ilman todisteita.

Lause 1. Jos toiminto f(x) on jatkuva aikavälillä [ a, b], niin se saavuttaa pienimmän ja suurimman arvonsa tällä segmentillä.

Tämä lause sanoo (kuva 1.15), että janalla [ a, b] on sellainen pointti x 1 tuo f(x 1) £ f(x) mille tahansa x alkaen [ a, b] ja että siinä on järkeä x 2 (x 2 О[ a, b]) sellainen, että " xÎ[ a, b] (f(x 2) ³ f(x)).

Merkitys f(x 1) on suurin annetulle funktiolle [ a, b], a f(x 2) - pienin. Merkitse: f(x 1) = M, f(x 2) =m. Koska varten f(x) seuraava epätasa-arvo pätee: " xÎ[ a, b] m£ f(x) £ M, niin saadaan seuraava johtopäätös lauseesta 1.

Seuraus. Jos toiminto f(x) on jatkuva janalla, niin se on rajoitettu tähän segmenttiin.

Lause 2. Jos toiminto f(x) on jatkuva aikavälillä [ a,b] ja ottaa eri merkkien arvot segmentin päistä, silloin on sellainen sisäpiste x 0 segmentti [ a, b], jossa funktio muuttuu 0:ksi, ts. $ x 0 Î ( a, b) (f(x 0) = 0).

Tämä lause sanoo, että funktion kuvaaja y=f(x), jatkuva aikavälillä [ a, b], ylittää akselin Härkä vähintään kerran, jos arvot f(a) ja f(b) on päinvastaisia ​​merkkejä. Joten (kuva 1.16) f(a) > 0, f(b) < 0 и функция f(x) katoaa kohdissa x 1 , x 2 , x 3 .

Lause 3. Anna toiminnon f(x) on jatkuva aikavälillä [ a, b], f(a) = A, f(b) = B ja A¹ B. (Kuva 1.17). Siis mille tahansa numerolle C, päättyi numeroiden väliin A ja B, siellä on sellainen sisäpiste x 0 segmentti [ a, b], mitä f(x 0) = C.

Seuraus. Jos toiminto f(x) on jatkuva aikavälillä [ a, b], m- pienin arvo f(x), M- funktion suurin arvo f(x) segmentillä [ a, b], silloin funktio ottaa (ainakin kerran) minkä tahansa arvon m välillä m ja M ja siksi segmentti [ m, M] on funktion kaikkien arvojen joukko f(x) segmentillä [ a, b].

Huomaa, että jos funktio on jatkuva aikavälillä ( a, b) tai on segmentissä [ a, b] epäjatkuvuuspisteestä, silloin lauseet 1, 2, 3 lakkaavat olemasta totta tällaiselle funktiolle.

Tarkastellaan lopuksi lausetta käänteisfunktion olemassaolosta.

Muista, että intervalli on segmentti, intervalli tai äärellinen tai ääretön puoliväli.

Lause 4. Päästää f(x) on jatkuva aikavälillä X, kasvaa (tai pienenee) X ja sillä on useita arvoja Y. Sitten toimintoon y=f(x) on käänteisfunktio x= j(y) määritetty aikavälillä Y, jatkuva ja kasvava (tai laskeva) päällä Y monella merkityksellä X.

Kommentti. Anna toiminnon x= j(y) on käänteinen funktiolle f(x). Koska argumentti on yleensä merkitty x, ja toiminto läpi y, niin kirjoitamme käänteisfunktion muodossa y=j(x).

Esimerkki 1. Toiminto y=x 2 (kuva 1.8, a) sarjassa X= jos se on jatkuva tämän janan kaikissa sisäpisteissä ja sen päissä, ts. kohdissa a ja b, on jatkuva oikealla ja vasemmalla.

Lause 1. Jatkuva funktio segmentillä [ a, b], ainakin yhdessä kohdassa tämän segmentin arvo on suurin ja ainakin yhdessä kohdassa pienin.

Lauseen mukaan jos funktio y = f(x) jatkuva segmentillä [ a, b], silloin on vähintään yksi piste x 1 Î [ a, b] siten, että funktion arvo f(x) tässä vaiheessa on suurin kaikista sen arvoista tällä segmentillä: f(x1) ≥ f(x). Vastaavasti on olemassa sellainen kohta x2, jossa funktion arvo on pienin kaikista segmentin arvoista: f(x 1) ≤ f(x).

On selvää, että tällaisia ​​pisteitä voi olla useita, esimerkiksi kuva osoittaa, että funktio f(x) ottaa pienimmän arvon kahdessa pisteessä x2 ja x 2 ".

Kommentti. Lauseen lauseesta voi tulla väärä, jos huomioidaan funktion arvo välillä ( a, b). Todellakin, jos tarkastelemme funktiota y=x päällä (0, 2), niin se on jatkuva tällä välillä, mutta ei saavuta maksimi- tai minimiarvojaan siinä: se saavuttaa nämä arvot intervallin päissä, mutta päät eivät kuulu meidän alueella.

Myös lause lakkaa olemasta totta epäjatkuville funktioille. Anna esimerkki.

Seuraus. Jos toiminto f(x) jatkuva [ a, b], niin se on rajoitettu tähän väliin.

Lause 2. Anna toiminnon y = f(x) jatkuva segmentillä [ a, b] ja ottaa eri etumerkkien arvot tämän segmentin päistä, silloin segmentin sisällä on vähintään yksi piste x=C, jossa funktio katoaa: f(C)= 0, missä a< C< b

Tällä lauseella on yksinkertainen geometrinen merkitys: jos jatkuvan funktion kaavion pisteet y = f(x), joka vastaa segmentin päitä [ a, b] sijaitsevat akselin vastakkaisilla puolilla Härkä, silloin tämä kuvaaja ainakin yhdessä janan pisteessä leikkaa akselin Härkä. Epäjatkuvilla toiminnoilla ei välttämättä ole tätä ominaisuutta.

Tämä lause hyväksyy seuraavan yleistyksen.

Lause 3 (väliarvojen lause). Anna toiminnon y = f(x) jatkuva segmentillä [ a, b] ja f(a) = A, f(b) = B. Siis mille tahansa numerolle C välillä A ja B, tämän segmentin sisällä on sellainen piste CÎ [ a, b], mitä f(c) = C.

Tämä lause on geometrisesti ilmeinen. Tarkastellaan funktion kuvaajaa y = f(x). Päästää f(a) = A, f(b) = B. Sitten mikä tahansa rivi y = C, missä C- mikä tahansa numero väliltä A ja B, leikkaa funktion kuvaajan ainakin yhdessä pisteessä. Leikkauspisteen abskissa on tämä arvo x=C, jossa f(c) = C.

Näin ollen jatkuva funktio, joka siirtyy arvostaan ​​toiseen, kulkee välttämättä kaikkien väliarvojen läpi. Erityisesti:

Seuraus. Jos toiminto y = f(x) on jatkuva jollakin aikavälillä ja ottaa suurimman ja pienimmän arvon, niin tällä välillä se ottaa ainakin kerran minkä tahansa arvon sen pienimmän ja suurimman arvojen väliltä.

JOHDANNAISSOVELLUKSET JA SEN SOVELLUKSET. JOHDANNAISMÄÄRITELMÄ

Tehdään jokin toiminto y=f(x), määritelty tietyllä aikavälillä. Jokaiselle argumentin arvolle x tästä intervallista funktio y=f(x) on tietty merkitys.

Harkitse kahta argumenttiarvoa: iniciaali x 0 ja uusi x.

Ero x–x 0 kutsutaan argumentin x lisäys pisteessä x 0 ja merkitty Δx. Tällä tavalla, ∆x = x – x 0 (argumentin lisäys voi olla joko positiivinen tai negatiivinen). Tästä tasa-arvosta seuraa se x=x 0 +Δx, eli muuttujan alkuarvo on saanut jonkin verran lisäystä. Sitten, jos pisteessä x 0 funktion arvo oli f(x 0 ), sitten uudessa kohdassa x funktio ottaa arvon f(x) = f(x 0 +∆x).

Ero y-y 0 = f(x) – f(x 0 ) nimeltään funktion lisäys y = f(x) pisteessä x 0 ja se on merkitty symbolilla Δy. Tällä tavalla,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Yleensä argumentin alkuarvo x 0 katsotaan kiinteäksi ja uudeksi arvoksi x-muuttuva. Sitten y 0 = f(x 0 ) osoittautuu jatkuvaksi ja y = f(x)-muuttuva. lisäyksiä Δy ja Δx on myös muuttujia ja kaava (1) osoittaa sen Dy on muuttujan funktio Δx.

Laadi funktion lisäyksen suhde argumentin kasvuun

Etsitään tämän suhteen raja kohdasta Δx→0. Jos tämä raja on olemassa, sitä kutsutaan tämän funktion derivaatiksi. f(x) pisteessä x 0 ja merkitse f "(x 0). Niin,

johdannainen tämä toiminto y = f(x) pisteessä x 0:ta kutsutaan funktion Δ lisäyssuhteen rajaksi y argumentin Δ lisäykseen x kun jälkimmäinen mielivaltaisesti pyrkii nollaan.

Huomaa, että saman funktion derivaatta eri pisteissä x voi saada erilaisia ​​arvoja, ts. derivaatta voidaan pitää argumentin funktiona x. Tämä toiminto on merkitty f "(x)

Johdannainen on merkitty symboleilla f "(x),y", . Johdannan erityinen arvo x = a merkitty f "(a) tai y "| x=a.

Toiminto funktion derivaatan löytämiseksi f(x) kutsutaan tämän funktion differentiaatioksi.

Voit etsiä johdannaisen suoraan määritelmän mukaan käyttämällä seuraavaa nyrkkisääntö:

Esimerkkejä.

JOHDANNAISEN MEKAANINEN MERKITYS

Fysiikasta tiedetään, että tasaisen liikkeen lailla on muoto s = v t, missä s- polku kuljettu ajankohtaan asti t, v on tasaisen liikkeen nopeus.

Kuitenkin, koska suurin osa luonnossa tapahtuvista liikkeistä on epätasaisia, sitten yleensä nopeus ja siten etäisyys s riippuu ajasta t, eli tulee olemaan ajan funktio.

Annetaan siis materiaalipisteen liikkua suoraan yhteen suuntaan lain mukaan s=s(t).

Huomaa hetki aikaa t 0 . Tässä vaiheessa piste on ohittanut polun s=s(t 0 ). Määritetään nopeus v aineellinen hetki t 0 .

Voit tehdä tämän harkitsemalla jotakin muuta hetkeä t 0 + Δ t. Se vastaa kuljettua matkaa s =s(t 0 + Δ t). Sitten aikavälille Δ t piste on kulkenut polun Δs =s(t 0 + Δ t)–s(t).

Mietitään suhdetta. Sitä kutsutaan keskinopeudeksi aikavälillä Δ t. Keskinopeus ei pysty kuvaamaan tarkasti pisteen liikenopeutta tällä hetkellä t 0 (koska liike on epätasainen). Jotta tämä todellinen nopeus voidaan ilmaista tarkemmin keskinopeudella, sinun on otettava pienempi aikaväli Δ t.

Eli liikkeen nopeus tiettynä ajankohtana t 0 (hetkellinen nopeus) on keskinopeuden raja aikavälillä alkaen t 0 - t 0 +Δ t kun Δ t→0:

,

nuo. epätasaisen liikkeen nopeus on kuljetun matkan johdannainen ajan suhteen.

JOHDANNAISEN GEOMETRIINEN MERKITYS

Otetaan ensin käyttöön käyrän tangentin määritelmä tietyssä pisteessä.

Olkoon meillä käyrä ja kiinteä piste siinä M 0(katso kuva) Harkitse toista kohtaa M tämä käyrä ja piirrä sekantti M 0 M. Jos kohta M alkaa liikkua käyrää ja pistettä pitkin M 0 pysyy paikallaan, sekantti muuttaa asentoaan. Jos, pisteen rajoittamattomalla approksimaatiolla M käyrästä pisteeseen M 0 millä tahansa puolella sekantti pyrkii ottamaan tietyn suoran paikan M 0 T, sitten suora viiva M 0 T kutsutaan käyrän tangentiksi annetussa pisteessä M 0.

Että., tangentti käyrään tietyssä pisteessä M 0 kutsutaan sekantin raja-asemaksi M 0 M kun piste M suuntautuu käyrää pitkin pisteeseen M 0.

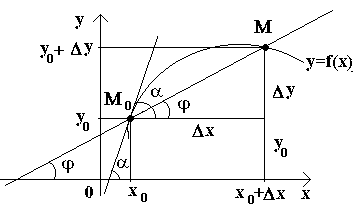
Harkitse nyt jatkuvaa funktiota y=f(x) ja tätä funktiota vastaava käyrä. Jollekin arvolle X 0-funktio ottaa arvon y0=f(x0). Nämä arvot x 0 ja y 0 käyrällä vastaa pistettä M 0 (x 0; y 0). Esitetään argumentti x0 lisäys Δ X. Argumentin uusi arvo vastaa funktion lisättyä arvoa y 0 +Δ y=f(x 0 –Δ x). Saamme pisteen M(x 0+Δ x; v 0+Δ y). Piirretään sekantti M 0 M ja merkitään φ:llä sekantin muodostama kulma akselin positiivisen suunnan kanssa Härkä. Tehdään suhde ja huomioidaan se.

Jos nyt Δ x→0, funktion Δ jatkuvuudesta johtuen klo→0, ja siksi piste M, liikkuu käyrää pitkin, lähestyy loputtomasti pistettä M 0. Sitten sekantti M 0 M on taipumus ottaa käyrän tangentin asema pisteessä M 0, ja kulma φ→α kohdassa Δ x→0, jossa α tarkoittaa tangentin ja akselin positiivisen suunnan välistä kulmaa Härkä. Koska funktio tg φ riippuu jatkuvasti φ:stä kohdassa φ≠π/2, niin kohdassa φ→α tg φ → tg α ja siksi tangentin kaltevuus on:

nuo. f"(x)= tgα.

Siis geometrisesti y "(x 0) edustaa tämän funktion kaavion tangentin jyrkkyyttä pisteessä x0, eli argumentin tietylle arvolle x, derivaatta on yhtä suuri kuin funktion kaavion tangentin muodostaman kulman tangentti f(x) vastaavassa kohdassa M 0 (x; y) positiivisella akselisuunnalla Härkä.

Esimerkki. Etsi käyrän tangentin kaltevuus y = x 2 kohdassa M(-1; 1).

Olemme jo nähneet sen ( x 2)" = 2X. Mutta käyrän tangentin kaltevuus on tg α = y"| x=-1 = -2.

TOIMINTOJEN ERILAITTAVUUS. ERITTYVÄN TOIMINNON JATKUVUUS

Toiminto y=f(x) nimeltään erottuva jossain vaiheessa x 0, jos sillä on tietty derivaatta tässä vaiheessa, ts. jos suhteen raja on olemassa ja on äärellinen.

Jos funktio on differentioituva jossakin segmentin [ a; b] tai intervalli ( a; b), sitten he sanovat sen erottuva segmentillä [ a; b] tai vastaavasti välissä ( a; b).

Pätee seuraava lause, joka muodostaa yhteyden differentioituvien ja jatkuvien funktioiden välille.

Lause. Jos toiminto y=f(x) erottuva jossain vaiheessa x0, niin se on jatkuva tässä vaiheessa.

Siten funktion erilaistuvuus merkitsee sen jatkuvuutta.

Todiste. Jos , sitten

,

jossa α on äärettömän pieni arvo, ts. määrä, joka pyrkii nollaan kohtaan Δ x→0. Mutta toisaalta

Δ y=f "(x0) Δ x+αΔ x=> Δ y→0 kohdassa Δ x→0, ts. f(x) – f(x0)→0 klo x→x 0, mikä tarkoittaa, että funktio f(x) jatkuva pisteessä x 0 . Q.E.D.

Siten epäjatkuvuuspisteissä funktiolla ei voi olla derivaattia. Käänteinen väite ei pidä paikkaansa: on jatkuvia funktioita, jotka eivät ole differentioituvia joissakin pisteissä (eli niillä ei ole derivaatta näissä pisteissä).

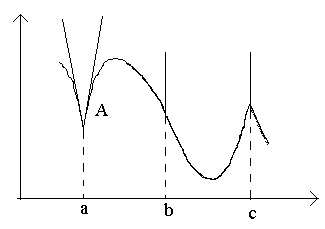
Harkitse kuvassa olevia kohtia a, b, c.

Pisteessä a klo Δ x→0 suhteella ei ole rajaa (koska yksipuoliset rajat ovat erilaiset Δ:lle x→0–0 ja Δ x→0+0). Pisteessä A kaaviossa ei ole määriteltyä tangenttia, mutta siinä on kaksi erilaista yksipuolista tangenttia, joissa on kulmakertoimet kohtaan 1 ja kohtaan 2. Tämän tyyppistä pistettä kutsutaan kulmapisteeksi.

Pisteessä b klo Δ x→0 suhde on vakiomerkkinen äärettömän suuri arvo . Funktiolla on ääretön derivaatta. Tässä vaiheessa kaaviolla on pystytangentti. Pistetyyppi - "käännepiste" pystytangentilla.

Pisteessä c yksipuoliset johdannaiset ovat äärettömän suuria määriä erilaisia ​​merkkejä. Tässä vaiheessa kaaviossa on kaksi yhdistettyä pystytangenttia. Tyyppi - "kärki" pystytangentilla - kulmapisteen erikoistapaus.