आव्यूह A के साथ, यदि ऐसी कोई संख्या l है कि AX = lX है।

इस मामले में, संख्या l कहा जाता है eigenvalueवेक्टर एक्स के अनुरूप ऑपरेटर (मैट्रिक्स ए)।

दूसरे शब्दों में, एक eigenvector एक वेक्टर है, जो एक रैखिक ऑपरेटर की कार्रवाई के तहत, एक कोलिनियर वेक्टर में बदल जाता है, अर्थात। बस कुछ संख्या से गुणा करें। इसके विपरीत, अनुचित वैक्टर को बदलना अधिक कठिन होता है।

हम eigenvector की परिभाषा को समीकरणों की एक प्रणाली के रूप में लिखते हैं:

आइए सभी शर्तों को बाईं ओर ले जाएं:

अंतिम प्रणाली को मैट्रिक्स रूप में निम्नानुसार लिखा जा सकता है:

(ए - एलई)एक्स \u003d ओ

परिणामी प्रणाली में हमेशा एक शून्य समाधान X = O होता है। ऐसे सिस्टम जिनमें सभी मुक्त शब्द शून्य के बराबर होते हैं, कहलाते हैं सजातीय. यदि ऐसी प्रणाली का मैट्रिक्स वर्गाकार है, और इसका निर्धारक शून्य के बराबर नहीं है, तो क्रैमर के सूत्रों के अनुसार, हमें हमेशा एक अनूठा समाधान मिलेगा - शून्य। यह साबित किया जा सकता है कि सिस्टम में गैर-शून्य समाधान हैं यदि और केवल अगर इस मैट्रिक्स का निर्धारक शून्य के बराबर है, अर्थात।

|ए - एलई| = = 0

अज्ञात l के साथ इस समीकरण को कहा जाता है विशेषता समीकरण (विशेषता बहुपद) मैट्रिक्स ए (रैखिक ऑपरेटर)।

यह सिद्ध किया जा सकता है कि एक रैखिक संकारक का अभिलक्षणिक बहुपद आधार के चुनाव पर निर्भर नहीं करता है।

उदाहरण के लिए, आइए मैट्रिक्स A = द्वारा दिए गए रैखिक ऑपरेटर के eigenvalues ​​​​और eigenvectors खोजें।

ऐसा करने के लिए, हम विशेषता समीकरण की रचना करते हैं |А - lЕ| = \u003d (1 - एल) 2 - 36 \u003d 1 - 2l + एल 2 - 36 \u003d एल 2 - 2l - 35 \u003d 0; डी \u003d 4 + 140 \u003d 144; eigenvalues ​​l 1 = (2 - 12)/2 = -5; एल 2 \u003d (2 + 12) / 2 \u003d 7.

eigenvectors खोजने के लिए, हम समीकरणों की दो प्रणालियों को हल करते हैं

(ए + 5ई) एक्स = ओ

(ए - 7ई) एक्स = ओ

उनमें से पहले के लिए, विस्तारित मैट्रिक्स रूप लेगा

,

जहां से x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, अर्थात्। एक्स (1) \u003d (- (2/3) एस; एस)।

उनमें से दूसरे के लिए, विस्तारित मैट्रिक्स रूप लेगा

,

जहां से x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; एक्स 1 \u003d (2/3) एस 1, यानी। एक्स (2) \u003d ((2/3) एस 1; एस 1)।

इस प्रकार, इस रैखिक संचालिका के eigenvectors फॉर्म के सभी वैक्टर हैं (-(2/3)c; c) eigenvalue (-5) के साथ और फॉर्म के सभी वैक्टर ((2/3)c 1 ; c 1) के साथ मूलांक 7 .

यह साबित किया जा सकता है कि ऑपरेटर ए का मैट्रिक्स इसके eigenvectors के आधार पर विकर्ण है और इसका रूप है:

,

जहां मैं इस मैट्रिक्स के आइजनवैल्यू हैं।

इसका विलोम भी सत्य है: यदि मैट्रिक्स A किसी आधार पर विकर्ण है, तो इस आधार के सभी सदिश इस मैट्रिक्स के eigenvectors होंगे।

यह भी साबित किया जा सकता है कि यदि एक रैखिक ऑपरेटर के पास n जोड़ीदार विशिष्ट eigenvalues ​​​​है, तो संबंधित eigenvectors रैखिक रूप से स्वतंत्र हैं, और इसी आधार पर इस ऑपरेटर के मैट्रिक्स का एक विकर्ण रूप है।

आइए इसे पिछले उदाहरण से समझाते हैं। आइए हम मनमाना गैर-शून्य मान c और c 1 लें, लेकिन ऐसे कि वैक्टर X (1) और X (2) रैखिक रूप से स्वतंत्र हों, अर्थात। आधार बनेगा। उदाहरण के लिए, चलो c \u003d c 1 \u003d 3, फिर X (1) \u003d (-2; 3), X (2) \u003d (2; 3)।

आइए हम इन वैक्टरों की रैखिक स्वतंत्रता को सत्यापित करें:

12 0. इस नए आधार में मैट्रिक्स A, A * = का रूप लेगा।

इसे सत्यापित करने के लिए, हम सूत्र A * = C -1 AC का उपयोग करते हैं। आइए पहले सी -1 खोजें।

सी -1 = ;

द्विघात रूप

द्विघात रूप n चरों से f (x 1, x 2, x n) को योग कहा जाता है, जिसका प्रत्येक पद या तो किसी एक चर का वर्ग होता है, या दो भिन्न चरों का गुणनफल होता है, जिसे एक निश्चित गुणांक के साथ लिया जाता है: f (x 1 , एक्स 2, एक्स एन) = (एक ij = एक जी)।

इन गुणांकों से बना मैट्रिक्स A कहलाता है आव्यूहद्विघात रूप। यह हमेशा के लिए है सममितमैट्रिक्स (यानी, मुख्य विकर्ण के बारे में एक मैट्रिक्स सममित, एक ij = a ji)।

मैट्रिक्स नोटेशन में, द्विघात रूप का रूप f(X) = X T AX होता है, जहां

वास्तव में

उदाहरण के लिए, आइए द्विघात रूप को मैट्रिक्स रूप में लिखें।

ऐसा करने के लिए, हम द्विघात रूप का एक मैट्रिक्स पाते हैं। इसके विकर्ण तत्व चर के वर्गों पर गुणांक के बराबर होते हैं, और शेष तत्व द्विघात रूप के संबंधित गुणांक के आधे के बराबर होते हैं। इसीलिए

मान लें कि चर X का आव्यूह-स्तंभ आव्यूह-स्तंभ Y के एक गैर-अपक्षयी रैखिक रूपांतरण द्वारा प्राप्त किया जाता है, अर्थात्। X = CY, जहाँ C क्रम n का एक अपक्षयी मैट्रिक्स है। तब द्विघात रूप f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y।

इस प्रकार, एक गैर-पतित रैखिक परिवर्तन सी के तहत, द्विघात रूप का मैट्रिक्स रूप लेता है: ए * = सी टी एसी।

उदाहरण के लिए, आइए द्विघात रूप f(y 1, y 2) को द्विघात रूप f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 से रैखिक रूपांतरण द्वारा प्राप्त किया गया है।

द्विघात रूप कहलाता है कैनन का(यह है विहित दृश्य) यदि इसके सभी गुणांक a ij = 0 i j के लिए, अर्थात।
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =।

इसका मैट्रिक्स विकर्ण है।

प्रमेय(सबूत यहां नहीं दिया गया है)। गैर-पतित रैखिक परिवर्तन का उपयोग करके किसी भी द्विघात रूप को एक विहित रूप में कम किया जा सकता है।

उदाहरण के लिए, आइए हम द्विघात रूप को विहित रूप में कम करें
एफ (एक्स 1, एक्स 2, एक्स 3) \u003d 2x 1 2 + 4x 1 एक्स 2 - 3x 2 2 - एक्स 2 एक्स 3।

ऐसा करने के लिए, पहले चर x 1 के लिए पूर्ण वर्ग का चयन करें:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3।

अब हम चर x 2 के लिए पूर्ण वर्ग का चयन करते हैं:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

फिर गैर-पतित रैखिक परिवर्तन y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 और y 3 \u003d x 3 इस द्विघात रूप को विहित रूप में लाता है f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 ।

ध्यान दें कि द्विघात रूप के विहित रूप को अस्पष्ट रूप से परिभाषित किया गया है (एक ही द्विघात रूप को विभिन्न तरीकों से विहित रूप में घटाया जा सकता है)। हालांकि, विभिन्न तरीकों से प्राप्त विहित रूपों में कई सामान्य गुण होते हैं। विशेष रूप से, द्विघात रूप के धनात्मक (ऋणात्मक) गुणांक वाले पदों की संख्या इस बात पर निर्भर नहीं करती है कि प्रपत्र को इस रूप में कैसे घटाया जाता है (उदाहरण के लिए, माना गया उदाहरण में हमेशा दो ऋणात्मक और एक धनात्मक गुणांक होगा)। इस संपत्ति को द्विघात रूपों की जड़ता का नियम कहा जाता है।

आइए हम एक ही द्विघात रूप को विहित रूप में एक अलग तरीके से कम करके इसे सत्यापित करें। आइए चर x 2 के साथ परिवर्तन शुरू करें:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, जहां y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 और y 3 = x 1। यहाँ, y 1 पर एक ऋणात्मक गुणांक -3 और y 2 और y 3 पर दो धनात्मक गुणांक 3 और 2 (और दूसरी विधि का उपयोग करके, हमें y 2 पर एक ऋणात्मक गुणांक (-5) और दो धनात्मक गुणांक प्राप्त हुए: 2 y 1 पर और y 3 के लिए 1/20)।

यह भी ध्यान दिया जाना चाहिए कि द्विघात रूप के एक मैट्रिक्स की रैंक, जिसे कहा जाता है द्विघात रूप की रैंक, विहित रूप के गैर-शून्य गुणांक की संख्या के बराबर है और रैखिक परिवर्तनों के तहत नहीं बदलता है।

द्विघात रूप f(X) कहलाता है सकारात्मक (नकारात्मक) निश्चित, यदि चर के सभी मानों के लिए जो एक साथ शून्य के बराबर नहीं हैं, तो यह धनात्मक है, अर्थात्। f(X) > 0 (ऋणात्मक, अर्थात्।
एफ (एक्स)< 0).

उदाहरण के लिए, द्विघात रूप f 1 (X) \u003d x 1 2 + x 2 2 धनात्मक निश्चित है, क्योंकि वर्गों का योग है, और द्विघात रूप f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 ऋणात्मक निश्चित है, क्योंकि प्रतिनिधित्व करता है इसे f 2 (X) \u003d - (x 1 - x 2) 2 के रूप में दर्शाया जा सकता है।

अधिकांश व्यावहारिक स्थितियों में, द्विघात रूप की संकेत-निश्चितता को स्थापित करना कुछ अधिक कठिन होता है, इसलिए इसके लिए निम्नलिखित प्रमेयों में से एक का उपयोग किया जाता है (हम उन्हें बिना प्रमाण के बनाते हैं)।

प्रमेय. एक द्विघात रूप धनात्मक (ऋणात्मक) निश्चित होता है यदि और केवल तभी जब इसके मैट्रिक्स के सभी eigenvalues ​​​​धनात्मक (ऋणात्मक) हों।

प्रमेय(सिलवेस्टर की कसौटी)। एक द्विघात रूप सकारात्मक निश्चित है यदि और केवल यदि इस रूप के मैट्रिक्स के सभी प्रमुख नाबालिग सकारात्मक हैं।

मेजर (कोने) माइनर n-वें क्रम के मैट्रिक्स A के k-वें क्रम को मैट्रिक्स का निर्धारक कहा जाता है, जो मैट्रिक्स A () की पहली k पंक्तियों और स्तंभों से बना होता है।

ध्यान दें कि ऋणात्मक-निश्चित द्विघात रूपों के लिए, मुख्य अवयस्कों के चिह्न वैकल्पिक होते हैं, और प्रथम-क्रम अवयस्क ऋणात्मक होने चाहिए।

उदाहरण के लिए, हम चिह्न-निश्चितता के लिए द्विघात रूप f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 की जांच करते हैं।

= (2 - एल)*
*(3 - एल) - 4 \u003d (6 - 2 एल - 3 एल + एल 2) - 4 \u003d एल 2 - 5 एल + 2 \u003d 0; डी = 25 - 8 = 17;
. इसलिए, द्विघात रूप सकारात्मक निश्चित है।

विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग A D 1 = a 11 = 2> 0. दूसरे क्रम का मुख्य नाबालिग D 2 = = 6 - 4 = 2> 0. इसलिए, सिल्वेस्टर मानदंड के अनुसार, द्विघात रूप सकारात्मक निश्चित है।

हम संकेत-निश्चितता के लिए एक और द्विघात रूप की जांच करते हैं, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2।

विधि 1. आइए द्विघात रूप = के एक मैट्रिक्स की रचना करें। विशेषता समीकरण का रूप होगा = (-2 - एल)*
*(-3 - एल) - 4 = (6 + 2 एल + 3 एल + एल 2) - 4 = एल 2 + 5 एल + 2 = 0; डी = 25 - 8 = 17;
. इसलिए, द्विघात रूप ऋणात्मक निश्चित है।

विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग ए डी 1 = ए 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. इसलिए, सिल्वेस्टर मानदंड के अनुसार, द्विघात रूप ऋणात्मक निश्चित है (प्रमुख अवयस्कों के चिन्ह वैकल्पिक रूप से, ऋण से प्रारंभ करते हुए)।

और एक अन्य उदाहरण के रूप में, हम साइन-निश्चितता के लिए द्विघात रूप f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 की जांच करते हैं।

विधि 1. आइए द्विघात रूप = के एक मैट्रिक्स की रचना करें। विशेषता समीकरण का रूप होगा = (2 - एल)*
*(-3 - एल) - 4 = (-6 - 2 एल + 3 एल + एल 2) - 4 = एल 2 + एल - 10 = 0; डी = 1 + 40 = 41;
.

इनमें से एक संख्या ऋणात्मक है और दूसरी धनात्मक है। eigenvalues ​​​​के संकेत अलग हैं। इसलिए, एक द्विघात रूप या तो ऋणात्मक या धनात्मक निश्चित नहीं हो सकता है, अर्थात। यह द्विघात रूप निश्चित चिह्न नहीं है (यह किसी भी चिन्ह का मान ले सकता है)।

विधि 2. मैट्रिक्स के पहले क्रम का मुख्य नाबालिग ए डी 1 = ए 11 = 2> 0. दूसरे क्रम का मुख्य नाबालिग डी 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

"। पहला भाग उन प्रावधानों को रेखांकित करता है जो कि केमोमेट्रिक्स को समझने के लिए न्यूनतम आवश्यक हैं, और दूसरे भाग में वे तथ्य शामिल हैं जिन्हें आपको बहुभिन्नरूपी विश्लेषण के तरीकों की गहरी समझ के लिए जानना आवश्यक है। प्रस्तुति को एक्सेल वर्कबुक में किए गए उदाहरणों द्वारा चित्रित किया गया है। मैट्रिक्स.एक्सएलएसजो इस दस्तावेज़ के साथ है।

उदाहरणों के लिंक टेक्स्ट में एक्सेल ऑब्जेक्ट के रूप में रखे जाते हैं। ये उदाहरण अमूर्त प्रकृति के हैं; वे किसी भी तरह से विश्लेषणात्मक रसायन विज्ञान की समस्याओं से बंधे नहीं हैं। केमोमेट्रिक्स में मैट्रिक्स बीजगणित के उपयोग के वास्तविक उदाहरणों की चर्चा विभिन्न रसायनमितीय अनुप्रयोगों के लिए समर्पित अन्य ग्रंथों में की गई है।

विश्लेषणात्मक रसायन विज्ञान में किए गए अधिकांश माप प्रत्यक्ष नहीं हैं लेकिन अप्रत्यक्ष. इसका अर्थ है कि प्रयोग में वांछित विश्लेषिकी C (एकाग्रता) के मान के स्थान पर एक और मान प्राप्त होता है एक्स(सिग्नल) से संबंधित है लेकिन सी के बराबर नहीं है, यानी। एक्स(सी) ≠ सी। एक नियम के रूप में, निर्भरता का प्रकार एक्स(सी) ज्ञात नहीं है, लेकिन सौभाग्य से विश्लेषणात्मक रसायन विज्ञान में अधिकांश माप आनुपातिक हैं। इसका मतलब है कि C in . की सांद्रता के रूप में एकसमय, सिग्नल एक्स उसी राशि से बढ़ जाएगा, अर्थात। एक्स(एकसी) = एक एक्स(सी)। इसके अलावा, संकेत भी योगात्मक होते हैं, जिससे कि सी 1 और सी 2 सांद्रता वाले दो पदार्थों वाले नमूने से संकेत प्रत्येक घटक से संकेतों के योग के बराबर होगा, अर्थात। एक्स(सी1 + सी2) = एक्स(सी1)+ एक्स(सी2)। आनुपातिकता और योगात्मकता एक साथ देते हैं रैखिकता. रैखिकता के सिद्धांत को स्पष्ट करने के लिए कई उदाहरण दिए जा सकते हैं, लेकिन यह दो सबसे महत्वपूर्ण उदाहरणों का उल्लेख करने के लिए पर्याप्त है - क्रोमैटोग्राफी और स्पेक्ट्रोस्कोपी। विश्लेषणात्मक रसायन विज्ञान में प्रयोग में निहित दूसरी विशेषता है मल्टी-चैनल. आधुनिक विश्लेषणात्मक उपकरण एक साथ कई चैनलों के लिए संकेतों को मापते हैं। उदाहरण के लिए, प्रकाश संचरण की तीव्रता को एक साथ कई तरंग दैर्ध्य के लिए मापा जाता है, अर्थात। स्पेक्ट्रम। इसलिए, प्रयोग में हम विभिन्न संकेतों के साथ काम कर रहे हैं एक्स 1 , एक्स 2 ,...., एक्स n अध्ययन के तहत प्रणाली में मौजूद पदार्थों के सांद्रता C 1, C 2, ..., C m के सेट की विशेषता है।

चावल। 1 स्पेक्ट्रा

तो, विश्लेषणात्मक प्रयोग को रैखिकता और बहुआयामीता की विशेषता है। इसलिए, प्रयोगात्मक डेटा को वैक्टर और मैट्रिक्स के रूप में मानना ​​​​और मैट्रिक्स बीजगणित के उपकरण का उपयोग करके उनमें हेरफेर करना सुविधाजनक है। इस उपागम की उपयोगिता को में दिखाए गए उदाहरण द्वारा दर्शाया गया है, जो 4000 से 4796 सेमी–1 तक 200 तरंग दैर्ध्य के लिए लिए गए तीन स्पेक्ट्रा को दर्शाता है। सबसे पहला ( एक्स 1) और दूसरा ( एक्स 2) स्पेक्ट्रा मानक नमूनों के लिए प्राप्त किए गए थे जिसमें दो पदार्थों ए और बी की सांद्रता ज्ञात है: पहले नमूने में [ए] = 0.5, [बी] = 0.1, और दूसरे नमूने में [ए] = 0.2, [ बी] = 0.6। एक नए, अज्ञात नमूने के बारे में क्या कहा जा सकता है, जिसके स्पेक्ट्रम का संकेत दिया गया है एक्स 3 ?

तीन प्रायोगिक स्पेक्ट्रा पर विचार करें एक्स 1 , एक्स 2 और एक्स 3 आयाम 200 के तीन वैक्टर के रूप में। रैखिक बीजगणित का उपयोग करके, कोई आसानी से दिखा सकता है कि एक्स 3 = 0.1 एक्स 1 +0.3 एक्स 2 , इसलिए तीसरे नमूने में स्पष्ट रूप से केवल पदार्थ A और B सांद्रता में हैं [A] = 0.5×0.1 + 0.2×0.3 = 0.11 और [B] = 0.1×0.1 + 0.6×0.3 = 0.19।

1. बुनियादी जानकारी

1.1 मैट्रिक्स

आव्यूहउदाहरण के लिए, संख्याओं की एक आयताकार तालिका कहलाती है

चावल। 2 मैट्रिक्स

मैट्रिसेस को बड़े अक्षरों में दर्शाया जाता है ( ए), और उनके तत्व - सूचकांकों के साथ संबंधित लोअरकेस अक्षरों के साथ, अर्थात। एकआई.जी. पहली अनुक्रमणिका पंक्तियों की संख्या और दूसरी संख्या स्तंभों को। केमोमेट्रिक्स में, इंडेक्स के अधिकतम मूल्य को इंडेक्स के समान अक्षर के साथ नामित करने की प्रथा है, लेकिन बड़े अक्षरों में। इसलिए, मैट्रिक्स एके रूप में भी लिखा जा सकता है ( एक आईजेयू , मैं = 1,..., मैं; जे = 1,..., जे) उदाहरण के लिए मैट्रिक्स मैं = 4, जे= 3 और एक 23 = −7.5.

संख्याओं की जोड़ी मैंतथा जेमैट्रिक्स का आयाम कहा जाता है और इसे के रूप में दर्शाया जाता है मैं× जे. केमोमेट्रिक्स में मैट्रिक्स का एक उदाहरण के लिए प्राप्त स्पेक्ट्रा का एक सेट है मैंनमूने पर जेतरंग दैर्ध्य।

1.2. मैट्रिसेस के साथ सबसे सरल ऑपरेशन

मैट्रिसेस कर सकते हैं संख्याओं से गुणा करें. इस मामले में, प्रत्येक तत्व को इस संख्या से गुणा किया जाता है। उदाहरण के लिए -

चावल। 3 किसी आव्यूह को किसी संख्या से गुणा करना

एक ही आयाम के दो आव्यूह तत्व-वार हो सकते हैं तहतथा घटाना. उदाहरण के लिए,

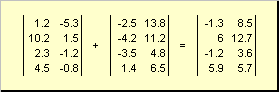
चावल। 4 मैट्रिक्स जोड़

एक संख्या और जोड़ से गुणा के परिणामस्वरूप, उसी आयाम का एक मैट्रिक्स प्राप्त होता है।

एक शून्य मैट्रिक्स एक मैट्रिक्स है जिसमें शून्य होता है। यह नामित है हे. जाहिर सी बात है ए+हे = ए, ए−ए = हेऔर 0 ए = हे.

मैट्रिक्स कर सकते हैं पक्षांतरित. इस ऑपरेशन के दौरान, मैट्रिक्स फ़्लिप किया जाता है, अर्थात। पंक्तियों और स्तंभों की अदला-बदली की जाती है। स्थानान्तरण एक डैश द्वारा इंगित किया गया है, ए"या अनुक्रमणिका एटी । इस प्रकार, यदि ए = {एक आईजेयू , मैं = 1,..., मैं; जे = 1,...,जे), फिर एटी = ( एक जी , जे = 1,...,जे; मैं = 1,..., मैं) उदाहरण के लिए

चावल। 5 मैट्रिक्स ट्रांसपोज़िशन

यह स्पष्ट है कि ( एटी) टी = ए, (ए+बी) टी = एटी+ बीटी ।

1.3. मैट्रिक्स गुणन

मैट्रिसेस कर सकते हैं गुणा, लेकिन केवल तभी जब उनके पास उपयुक्त आयाम हों। ऐसा क्यों है यह परिभाषा से स्पष्ट होगा। मैट्रिक्स उत्पाद ए, आयाम मैं× क, और मैट्रिक्स बी, आयाम क× जे, मैट्रिक्स कहा जाता है सी, आयाम मैं× जे, जिनके तत्व संख्याएं हैं

इस प्रकार उत्पाद के लिए अबयह आवश्यक है कि बाएं मैट्रिक्स में स्तंभों की संख्या एसही मैट्रिक्स में पंक्तियों की संख्या के बराबर था बी. मैट्रिक्स उत्पाद उदाहरण -

Fig.6 मैट्रिक्स का उत्पाद

मैट्रिक्स गुणन नियम निम्नानुसार तैयार किया जा सकता है। मैट्रिक्स का एक तत्व खोजने के लिए सीचौराहे पर खड़े मैं-वीं पंक्ति और जे-वां कॉलम ( सी आईजेयू) तत्व से गुणा किया जाना चाहिए मैं-पहले मैट्रिक्स की पंक्ति एपर जेदूसरे मैट्रिक्स का -वां कॉलम बीऔर सभी परिणाम जोड़ें। तो दिखाए गए उदाहरण में, तीसरी पंक्ति और दूसरे कॉलम से तत्व को तीसरी पंक्ति के तत्व-वार उत्पादों के योग के रूप में प्राप्त किया जाता है एऔर दूसरा कॉलम बी

Fig.7 मैट्रिक्स के उत्पाद का तत्व

आव्यूहों का गुणनफल क्रम पर निर्भर करता है, अर्थात्। अब ≠ बी ० ए, कम से कम आयामी कारणों से। इसे गैर-कम्यूटेटिव कहा जाता है। हालांकि, मैट्रिक्स का उत्पाद सहयोगी है। इसका मतलब है कि एबीसी = (अब)सी = ए(ईसा पूर्व) इसके अलावा, यह वितरणात्मक भी है, अर्थात। ए(बी+सी) = अब+एसी. जाहिर सी बात है एओ = हे.

1.4. स्क्वायर मैट्रिसेस

यदि किसी मैट्रिक्स के स्तंभों की संख्या उसकी पंक्तियों की संख्या के बराबर है ( मैं = जे = एन), तो ऐसे मैट्रिक्स को स्क्वायर कहा जाता है। इस भाग में हम केवल ऐसे आव्यूहों पर विचार करेंगे। इन आव्यूहों में से कोई विशेष गुण वाले आव्यूहों को अलग कर सकता है।

अकेलामैट्रिक्स (निरूपित) मैंऔर कभी - कभी इ) एक मैट्रिक्स है जिसमें सभी तत्व शून्य के बराबर होते हैं, केवल विकर्णों को छोड़कर, जो 1 के बराबर होते हैं, अर्थात।

स्पष्टतः ऐ = मैं एक = ए.

मैट्रिक्स कहा जाता है विकर्ण, यदि इसके सभी तत्व, विकर्णों को छोड़कर ( एक द्वितीय) शून्य के बराबर हैं। उदाहरण के लिए

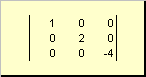
चावल। 8 विकर्ण मैट्रिक्स

आव्यूह एशीर्ष कहा जाता है त्रिकोणीय, यदि इसके विकर्ण के नीचे स्थित सभी तत्व शून्य के बराबर हैं, अर्थात। एक आईजेयू= 0, पर मैं>जे. उदाहरण के लिए

चावल। 9 ऊपरी त्रिकोणीय मैट्रिक्स

निचला त्रिकोणीय मैट्रिक्स इसी तरह परिभाषित किया गया है।

आव्यूह एबुलाया सममित, यदि एटी = ए. दूसरे शब्दों में एक आईजेयू = एक जी. उदाहरण के लिए

चावल। 10 सममित मैट्रिक्स

आव्यूह एबुलाया ओर्थोगोनल, यदि

एटी ए = आटी = मैं.

मैट्रिक्स कहा जाता है सामान्ययदि

1.5. ट्रेस और निर्धारक

निम्नलिखितवर्ग मैट्रिक्स ए(निरूपित ट्र( ए) या सपा ( ए)) इसके विकर्ण तत्वों का योग है,

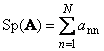
उदाहरण के लिए,

चावल। 11 मैट्रिक्स ट्रेस

जाहिर सी बात है

सपा(α ए) = α सपा ( ए) तथा

सपा ( ए+बी) = सपा ( ए)+ सपा ( बी).

यह दिखाया जा सकता है कि

सपा ( ए) = सपा ( एटी), सपा ( मैं) = एन,

और वो भी

सपा ( अब) = सपा ( बी ० ए).

एक वर्ग मैट्रिक्स की एक अन्य महत्वपूर्ण विशेषता इसकी है सिद्ध(det द्वारा निरूपित ( ए))। सामान्य मामले में निर्धारक की परिभाषा बल्कि जटिल है, इसलिए हम सबसे सरल विकल्प से शुरू करेंगे - मैट्रिक्स एआयाम (2×2)। फिर

एक (3×3) मैट्रिक्स के लिए, सारणिक बराबर होगा

मैट्रिक्स के मामले में ( एन× एन) सारणिक की गणना योग के रूप में की जाती है 1 2 3 ... एन= एन! पद, जिनमें से प्रत्येक बराबर है

सूचकांकों क 1 , क 2 ,..., कश्मीर नहींसभी संभव आदेशित क्रमपरिवर्तन के रूप में परिभाषित किया गया है आरसेट में संख्याएं (1, 2, ..., एन) मैट्रिक्स निर्धारक की गणना एक जटिल प्रक्रिया है, जो व्यवहार में विशेष कार्यक्रमों का उपयोग करके की जाती है। उदाहरण के लिए,

चावल। 12 मैट्रिक्स निर्धारक

हम केवल स्पष्ट गुणों पर ध्यान देते हैं:

डीईटी ( मैं) = 1, अलग ( ए) = पता ( एटी),

डीईटी ( अब) = पता ( ए) बी).

1.6. वैक्टर

यदि मैट्रिक्स में केवल एक कॉलम है ( जे= 1), तो ऐसी वस्तु कहलाती है वेक्टर. अधिक सटीक, एक कॉलम वेक्टर। उदाहरण के लिए

उदाहरण के लिए, एक पंक्ति वाले मैट्रिसेस पर भी विचार किया जा सकता है

यह वस्तु भी एक सदिश है, लेकिन पंक्ति वेक्टर. डेटा का विश्लेषण करते समय, यह समझना महत्वपूर्ण है कि हम किन वैक्टरों के साथ काम कर रहे हैं - कॉलम या पंक्तियाँ। तो एक नमूने के लिए लिए गए स्पेक्ट्रम को एक पंक्ति वेक्टर के रूप में माना जा सकता है। फिर सभी नमूनों के लिए कुछ तरंग दैर्ध्य पर वर्णक्रमीय तीव्रता के सेट को कॉलम वेक्टर के रूप में माना जाना चाहिए।

एक वेक्टर का आयाम उसके तत्वों की संख्या है।

यह स्पष्ट है कि किसी भी कॉलम वेक्टर को ट्रांसपोज़िशन द्वारा एक पंक्ति वेक्टर में बदला जा सकता है, अर्थात।

उन मामलों में जहां वेक्टर का रूप विशेष रूप से निर्दिष्ट नहीं है, लेकिन केवल एक वेक्टर कहा जाता है, तो उनका मतलब कॉलम वेक्टर होता है। हम भी इस नियम का पालन करेंगे। एक वेक्टर को लोअरकेस डायरेक्ट बोल्ड लेटर द्वारा दर्शाया जाता है। शून्य सदिश एक सदिश है जिसके सभी अवयव शून्य के बराबर होते हैं। यह दर्शाया गया है 0 .

1.7. वैक्टर के साथ सबसे सरल ऑपरेशन

वैक्टर को मैट्रिसेस की तरह ही संख्याओं से जोड़ा और गुणा किया जा सकता है। उदाहरण के लिए,

चावल। 13 वैक्टर के साथ संचालन

दो वैक्टर एक्सतथा आपबुलाया समरेख, यदि कोई संख्या α है, जैसे कि

1.8. वैक्टर के उत्पाद

एक ही आयाम के दो वैक्टर एनगुणा किया जा सकता है। माना दो सदिश हैं एक्स = (एक्स 1 , एक्स 2 ,...,एक्सएन) टी और आप = (आप 1 , आप 2 ,...,आपएन) टी। गुणन नियम "पंक्ति दर स्तंभ" द्वारा निर्देशित, हम उनसे दो उत्पाद बना सकते हैं: एक्सटी आपतथा xyटी । पहला काम

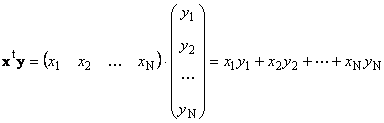
बुलाया अदिशया आंतरिक. इसका परिणाम एक संख्या है। यह संकेतन का भी उपयोग करता है ( एक्स,आप)= एक्सटी आप. उदाहरण के लिए,

चावल। 14 आंतरिक (स्केलर) उत्पाद

दूसरा काम

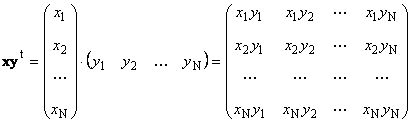
बुलाया बाहरी. इसका परिणाम एक आयाम मैट्रिक्स है ( एन× एन) उदाहरण के लिए,

चावल। 15 बाहरी उत्पाद

वे सदिश जिनका अदिश गुणनफल शून्य के बराबर होता है, कहलाते हैं ओर्थोगोनल.

1.9. वेक्टर मानदंड

एक सदिश का स्वयं के अदिश गुणनफल को अदिश वर्ग कहते हैं। यह मान

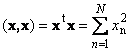
एक वर्ग को परिभाषित करता है लंबाईवेक्टर एक्स. लंबाई को दर्शाने के लिए (जिसे भी कहा जाता है) नियमवेक्टर) संकेतन का उपयोग किया जाता है

उदाहरण के लिए,

चावल। 16 वेक्टर मानदंड

इकाई लंबाई वेक्टर (|| एक्स|| = 1) सामान्यीकृत कहा जाता है। शून्येतर सदिश ( एक्स ≠ 0 ) को लंबाई से विभाजित करके सामान्यीकृत किया जा सकता है, अर्थात। एक्स = ||एक्स|| (एक्स/||एक्स||) = ||एक्स|| इ. यहां इ = एक्स/||एक्स|| सामान्यीकृत वेक्टर है।

वैक्टर को ऑर्थोनॉर्मल कहा जाता है यदि वे सभी सामान्यीकृत और जोड़ीदार ऑर्थोगोनल हैं।

1.10. वैक्टर के बीच का कोण

अदिश उत्पाद परिभाषित करता है और कोनादो वैक्टर के बीच एक्सतथा आप

यदि सदिश लंबकोणीय हैं, तो cosφ = 0 और φ = /2, और यदि वे संरेख हैं, तो cosφ = 1 और φ = 0.

1.11. एक मैट्रिक्स का वेक्टर प्रतिनिधित्व

प्रत्येक मैट्रिक्स एआकार मैं× जेवैक्टर के एक सेट के रूप में प्रतिनिधित्व किया जा सकता है

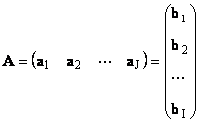
यहाँ प्रत्येक वेक्टर एक जेहै जे-वें स्तंभ और पंक्ति वेक्टर बी मैंहै मैं-मैट्रिक्स की पंक्ति ए

1.12. रैखिक रूप से निर्भर वैक्टर

समान आयाम के सदिश ( एन) को मैट्रिसेस की तरह एक संख्या से जोड़ा और गुणा किया जा सकता है। परिणाम एक ही आयाम का एक वेक्टर है। मान लीजिए कि एक ही आयाम के कई सदिश हैं एक्स 1 , एक्स 2 ,...,एक्स K और समान संख्याओं की संख्या α α 1 , α 2 ,...,α क. वेक्टर

आप= α 1 एक्स 1 + α 2 एक्स 2 +...+α क एक्स क

बुलाया रैखिक संयोजनवैक्टर एक्स क .

यदि ऐसी गैर-शून्य संख्याएं हैं α क ≠ 0, क = 1,..., क, क्या आप = 0 , तो वैक्टर का ऐसा सेट एक्स कबुलाया रैखिक रूप से आश्रित. अन्यथा, वैक्टर को रैखिक रूप से स्वतंत्र कहा जाता है। उदाहरण के लिए, वैक्टर एक्स 1 = (2, 2) टी और एक्स 2 = (−1, −1) t रैखिक रूप से निर्भर हैं, क्योंकि एक्स 1 +2एक्स 2 = 0

1.13. मैट्रिक्स रैंक

के एक सेट पर विचार करें कवैक्टर एक्स 1 , एक्स 2 ,...,एक्स कआयाम एन. वैक्टर की इस प्रणाली का रैंक रैखिक रूप से स्वतंत्र वैक्टर की अधिकतम संख्या है। उदाहरण के लिए सेट में

उदाहरण के लिए, केवल दो रैखिक रूप से स्वतंत्र वैक्टर हैं एक्स 1 और एक्स 2 है, इसलिए इसका रैंक 2 है।

जाहिर है, अगर सेट में उनके आयाम से अधिक वैक्टर हैं ( क>एन), तो वे अनिवार्य रूप से रैखिक रूप से निर्भर हैं।

मैट्रिक्स रैंक(रैंक द्वारा निरूपित ( ए)) वैक्टर की प्रणाली का रैंक है जिसमें यह शामिल है। हालांकि किसी भी मैट्रिक्स को दो तरह से दर्शाया जा सकता है (कॉलम वैक्टर या रो वैक्टर), यह रैंक वैल्यू को प्रभावित नहीं करता है, क्योंकि

1.14. उलटा मैट्रिक्स

वर्ग मैट्रिक्स एगैर-पतित कहा जाता है यदि इसमें एक अद्वितीय है उल्टाआव्यूह ए-1 , शर्तों द्वारा निर्धारित

आ −1 = ए −1 ए = मैं.

व्युत्क्रम मैट्रिक्स सभी मैट्रिक्स के लिए मौजूद नहीं है। गैर-अपक्षय के लिए एक आवश्यक और पर्याप्त शर्त है

डीईटी ( ए) 0 या रैंक ( ए) = एन.

मैट्रिक्स उलटा एक जटिल प्रक्रिया है जिसके लिए विशेष कार्यक्रम हैं। उदाहरण के लिए,

चावल। 17 मैट्रिक्स उलटा

हम सरलतम स्थिति के लिए सूत्र देते हैं - 2 × 2 . आव्यूह

यदि मैट्रिसेस एतथा बीगैर-पतित हैं, तो

(अब) −1 = बी −1 ए −1 .

1.15. छद्म उलटा मैट्रिक्स

यदि मैट्रिक्स एपतित है और उलटा मैट्रिक्स मौजूद नहीं है, तो कुछ मामलों में कोई इसका उपयोग कर सकता है छद्म प्रतिलोममैट्रिक्स, जिसे ऐसे मैट्रिक्स के रूप में परिभाषित किया गया है ए+ वह

आ + ए = ए.

छद्म उलटा मैट्रिक्स केवल एक ही नहीं है और इसका रूप निर्माण विधि पर निर्भर करता है। उदाहरण के लिए, एक आयताकार मैट्रिक्स के लिए, आप मूर-पेनरोज़ विधि का उपयोग कर सकते हैं।

यदि स्तंभों की संख्या पंक्तियों की संख्या से कम है, तो

ए + =(एटी ए) −1 एटी

उदाहरण के लिए,

चावल। 17a छद्म मैट्रिक्स उलटा

यदि स्तंभों की संख्या पंक्तियों की संख्या से अधिक है, तो

ए + =एटी ( आटी) −1

1.16. एक मैट्रिक्स द्वारा एक वेक्टर का गुणन

वेक्टर एक्सएक मैट्रिक्स द्वारा गुणा किया जा सकता है एउपयुक्त आयाम। इस मामले में, कॉलम वेक्टर को दाईं ओर गुणा किया जाता है कुल्हाड़ी, और वेक्टर स्ट्रिंग बाईं ओर है एक्सटी ए. यदि वेक्टर का आयाम जे, और मैट्रिक्स का आयाम मैं× जेतो परिणाम आयाम का एक वेक्टर है मैं. उदाहरण के लिए,

चावल। 18 वेक्टर-मैट्रिक्स गुणन

यदि मैट्रिक्स ए- वर्ग ( मैं× मैं), फिर वेक्टर आप = कुल्हाड़ीके समान आयाम हैं एक्स. जाहिर सी बात है

ए(α 1 एक्स 1 + α 2 एक्स 2) = α 1 कुल्हाड़ी 1 + α 2 कुल्हाड़ी 2 .

इसलिए मैट्रिक्स को वैक्टर के रैखिक परिवर्तन के रूप में माना जा सकता है। विशेष रूप से एक्स = एक्स, बैल = 0 .

2. अतिरिक्त जानकारी

2.1. रैखिक समीकरणों की प्रणाली

होने देना ए- मैट्रिक्स आकार मैं× जे, एक बी- आयाम वेक्टर जे. समीकरण पर विचार करें

कुल्हाड़ी = बी

वेक्टर के संबंध में एक्स, आयाम मैं. अनिवार्य रूप से, यह एक प्रणाली है मैंके साथ रैखिक समीकरण जेअनजान एक्स 1 ,...,एक्स जे. एक समाधान मौजूद है अगर और केवल अगर

पद( ए) = रैंक ( बी) = आर,

कहाँ पे बीसंवर्धित आयाम मैट्रिक्स है मैं×( जे+1) मैट्रिक्स से मिलकर ए, एक स्तंभ के साथ गद्देदार बी, बी = (ए बी) अन्यथा, समीकरण असंगत हैं।

यदि एक आर = मैं = जे, तो समाधान अद्वितीय है

एक्स = ए −1 बी.

यदि एक आर < मैं, तो कई अलग-अलग समाधान हैं जिन्हें रैखिक संयोजन के रूप में व्यक्त किया जा सकता है जे−आरवैक्टर सजातीय समीकरणों की प्रणाली कुल्हाड़ी = 0 एक वर्ग मैट्रिक्स के साथ ए (एन× एन) एक गैर तुच्छ समाधान है ( एक्स ≠ 0 ) अगर और केवल अगर अलग ( ए) = 0. अगर आर= रैंक ( ए)<एन, तो वहाँ हैं एन−आररैखिक स्वतंत्र समाधान।

2.2. द्विरेखीय और द्विघात रूप

यदि एक एएक वर्ग मैट्रिक्स है, और एक्सतथा आप- संबंधित आयाम के वैक्टर, फिर फॉर्म का अदिश उत्पाद एक्सटी एयबुलाया द्विरेखीयमैट्रिक्स द्वारा परिभाषित आकार ए. पर एक्स = आपअभिव्यक्ति एक्सटी कुल्हाड़ीबुलाया द्विघातप्रपत्र।

2.3. सकारात्मक निश्चित मैट्रिक्स

वर्ग मैट्रिक्स एबुलाया सकारात्मक रूप से निश्चित, यदि किसी शून्येतर सदिश के लिए एक्स ≠ 0 ,

एक्सटी कुल्हाड़ी > 0.

नकारात्मक (एक्सटी कुल्हाड़ी < 0), गैर नकारात्मक (एक्सटी कुल्हाड़ी 0) और गैर सकारात्मक (एक्सटी कुल्हाड़ी 0) कुछ मैट्रिक्स।

2.4. चोल्स्की अपघटन

यदि सममित मैट्रिक्स एसकारात्मक निश्चित है, तो एक अद्वितीय त्रिकोणीय मैट्रिक्स है यूसकारात्मक तत्वों के साथ, जिसके लिए

ए = यूटी यू.

उदाहरण के लिए,

चावल। 19 चोल्स्की अपघटन

2.5. ध्रुवीय अपघटन

होने देना एआयाम का एक गैर-डीजेनरेट वर्ग मैट्रिक्स है एन× एन. फिर होती है एक अनोखी ध्रुवीयप्रदर्शन

ए = एसआर,

कहाँ पे एसएक गैर-ऋणात्मक सममित मैट्रिक्स है, और आरएक ओर्थोगोनल मैट्रिक्स है। मैट्रिक्स एसतथा आरस्पष्ट रूप से परिभाषित किया जा सकता है:

एस 2 = आटी या एस = (आटी) ½ और आर = एस −1 ए = (आटी) -½ ए.

उदाहरण के लिए,

चावल। 20 ध्रुवीय अपघटन

यदि मैट्रिक्स एपतित है, तो अपघटन अद्वितीय नहीं है - अर्थात्: एसअभी भी अकेला, लेकिन आरकई हो सकते हैं। ध्रुवीय अपघटन एक मैट्रिक्स का प्रतिनिधित्व करता है एएक संपीड़न/खिंचाव संयोजन के रूप में एसऔर मोड़ आर.

2.6. eigenvectors और eigenvalues

होने देना एएक वर्ग मैट्रिक्स है। वेक्टर वीबुलाया खुद का वेक्टरमैट्रिक्स ए, यदि

ए वी = λ वी,

जहां संख्या कहा जाता है eigenvalueमैट्रिक्स ए. इस प्रकार, मैट्रिक्स द्वारा किया जाने वाला परिवर्तन एवेक्टर के ऊपर वी, एक कारक के साथ एक साधारण खिंचाव या संपीड़न के लिए कम हो जाता है। eigenvector निरंतर α 0 से गुणा करने के लिए निर्धारित किया जाता है, अर्थात। यदि वीएक eigenvector है, तो α वीएक आइजनवेक्टर भी है।

2.7. स्वदेशी मूल्य

मैट्रिक्स में ए, आयाम ( एन× एन) से बड़ा नहीं हो सकता एनस्वदेशी मूल्य वे संतुष्ट विशेषता समीकरण

डीईटी ( ए − λ मैं) = 0,

जो एक बीजीय समीकरण है एन-वें क्रम। विशेष रूप से, 2×2 मैट्रिक्स के लिए, विशेषता समीकरण का रूप होता है

उदाहरण के लिए,

चावल। 21 आइजनवैल्यू

eigenvalues ​​का सेट 1 ,..., एनमैट्रिक्स एबुलाया स्पेक्ट्रम ए.

स्पेक्ट्रम में विभिन्न गुण होते हैं। विशेष रूप से

डीईटी ( ए) = 1×...×λ एन, सपा ( ए) = 1 +...+λ एन.

एक मनमाना मैट्रिक्स के eigenvalues ​​जटिल संख्या हो सकते हैं, लेकिन यदि मैट्रिक्स सममित है ( एटी = ए), तो इसके प्रतिमान वास्तविक हैं।

2.8. आइजनवेक्टर

मैट्रिक्स में ए, आयाम ( एन× एन) से बड़ा नहीं हो सकता एन eigenvectors, जिनमें से प्रत्येक अपने स्वयं के मूल्य से मेल खाता है। eigenvector निर्धारित करने के लिए वी एनआपको सजातीय समीकरणों की एक प्रणाली को हल करने की आवश्यकता है

(ए − λ एन मैं)वी एन = 0 .

इसका एक गैर-तुच्छ समाधान है क्योंकि det( ए-λ एन मैं) = 0.

उदाहरण के लिए,

चावल। 22 आइजनवेक्टर

सममित मैट्रिक्स के eigenvectors ऑर्थोगोनल हैं।

एक वर्ग मैट्रिक्स का एक eigenvector वह होता है, जब किसी दिए गए मैट्रिक्स से गुणा किया जाता है, जिसके परिणामस्वरूप एक कोलिनियर वेक्टर होता है। सरल शब्दों में, जब एक मैट्रिक्स को एक eigenvector से गुणा किया जाता है, तो बाद वाला वही रहता है, लेकिन कुछ संख्या से गुणा किया जाता है।

परिभाषा

एक eigenvector एक गैर-शून्य वेक्टर V है, जिसे एक वर्ग मैट्रिक्स M से गुणा करने पर, स्वयं बन जाता है, कुछ संख्या से बढ़ जाता है। बीजीय संकेतन में, ऐसा दिखता है:

एम × वी = λ × वी,

जहाँ आव्यूह M का eigenvalue है।

आइए एक संख्यात्मक उदाहरण पर विचार करें। लिखने की सुविधा के लिए, मैट्रिक्स में संख्याओं को अर्धविराम द्वारा अलग किया जाएगा। मान लें कि हमारे पास एक मैट्रिक्स है:

• एम = 0; चार;
• 6; 10.

आइए इसे कॉलम वेक्टर से गुणा करें:

• वी = -2;

मैट्रिक्स को कॉलम वेक्टर से गुणा करते समय, हमें कॉलम वेक्टर भी मिलता है। सख्त गणितीय भाषा में, कॉलम वेक्टर द्वारा 2 × 2 मैट्रिक्स को गुणा करने का सूत्र इस तरह दिखेगा:

• एम × वी = एम11 × वी11 + एम12 × वी21;
• M21 x V11 + M22 x V21।

M11 का अर्थ मैट्रिक्स M का तत्व है, जो पहली पंक्ति और पहले कॉलम में खड़ा है, और M22 दूसरी पंक्ति और दूसरे कॉलम में स्थित तत्व है। हमारे मैट्रिक्स के लिए, ये तत्व M11 = 0, M12 = 4, M21 = 6, M22 10 हैं। एक कॉलम वेक्टर के लिए, ये मान V11 = -2, V21 = 1 हैं। इस सूत्र के अनुसार, हम निम्नलिखित प्राप्त करते हैं एक वेक्टर द्वारा एक वर्ग मैट्रिक्स के उत्पाद का परिणाम:

• एम × वी = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2।

सुविधा के लिए, हम कॉलम वेक्टर को एक पंक्ति में लिखते हैं। इसलिए, हमने वर्ग मैट्रिक्स को वेक्टर (-2; 1) से गुणा किया है, जिसके परिणामस्वरूप वेक्टर (4; -2) प्राप्त होता है। जाहिर है, यह वही वेक्टर है जिसे = -2 से गुणा किया जाता है। इस मामले में लैम्ब्डा मैट्रिक्स के एक eigenvalue को दर्शाता है।

मैट्रिक्स का eigenvector एक कोलिनियर वेक्टर है, यानी एक वस्तु जो मैट्रिक्स द्वारा गुणा करने पर अंतरिक्ष में अपनी स्थिति नहीं बदलती है। सदिश बीजगणित में संरेखता की अवधारणा ज्यामिति में समांतरता के पद के समान है। ज्यामितीय व्याख्या में, कोलिनियर वैक्टर विभिन्न लंबाई के समानांतर निर्देशित खंड होते हैं। यूक्लिड के समय से, हम जानते हैं कि एक एकल रेखा में अनंत संख्या में रेखाएँ होती हैं, इसलिए यह मान लेना तर्कसंगत है कि प्रत्येक मैट्रिक्स में अनंत संख्या में eigenvectors हैं।

पिछले उदाहरण से, यह देखा जा सकता है कि दोनों (-8; 4), और (16; -8), और (32, -16) eigenvectors हो सकते हैं। ये सभी eigenvalue = -2 के संगत संरेख सदिश हैं। इन वैक्टरों द्वारा मूल मैट्रिक्स को गुणा करते समय, हमें अभी भी एक वेक्टर मिलेगा, जो मूल से 2 गुना भिन्न होता है। इसलिए, जब एक आइजनवेक्टर खोजने के लिए समस्याओं को हल करते हैं, तो केवल रैखिक रूप से स्वतंत्र वेक्टर ऑब्जेक्ट खोजने की आवश्यकता होती है। सबसे अधिक बार, n × n मैट्रिक्स के लिए, eigenvectors की n-वें संख्या होती है। हमारे कैलकुलेटर को दूसरे क्रम के वर्ग मैट्रिक्स के विश्लेषण के लिए डिज़ाइन किया गया है, इसलिए परिणाम के रूप में लगभग हमेशा दो eigenvectors मिलेंगे, सिवाय इसके कि जब वे मेल खाते हों।

ऊपर के उदाहरण में, हम मूल मैट्रिक्स के आइजनवेक्टर को पहले से जानते थे और लैम्ब्डा संख्या को नेत्रहीन रूप से निर्धारित करते थे। हालांकि, व्यवहार में, सब कुछ दूसरे तरीके से होता है: शुरुआत में eigenvalues ​​होते हैं और उसके बाद ही eigenvectors होते हैं।

समाधान एल्गोरिथ्म

आइए मूल मैट्रिक्स M को फिर से देखें और इसके दोनों eigenvectors को खोजने का प्रयास करें। तो मैट्रिक्स इस तरह दिखता है:

• एम = 0; चार;
• 6; 10.

आरंभ करने के लिए, हमें eigenvalue निर्धारित करने की आवश्यकता है, जिसके लिए हमें निम्नलिखित मैट्रिक्स के निर्धारक की गणना करने की आवश्यकता है:

• (0 - ); चार;
• 6; (10 - )।

यह मैट्रिक्स मुख्य विकर्ण पर मौजूद तत्वों से अज्ञात घटाकर प्राप्त किया जाता है। निर्धारक मानक सूत्र द्वारा निर्धारित किया जाता है:

• डीटीए = एम11 × एम21 - एम12 × एम22
• डीटीए = (0 - ) × (10 - λ) - 24

चूँकि हमारा सदिश शून्य नहीं होना चाहिए, हम परिणामी समीकरण को रैखिक रूप से आश्रित मानते हैं और अपने सारणिक डेटा को शून्य के बराबर करते हैं।

(0 - ) × (10 - λ) - 24 = 0

आइए कोष्ठक खोलें और मैट्रिक्स का अभिलक्षणिक समीकरण प्राप्त करें:

2 - 10λ - 24 = 0

यह एक मानक द्विघात समीकरण है जिसे विवेचक के रूप में हल करने की आवश्यकता है।

डी \u003d बी 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

विभेदक की जड़ sqrt(D) = 14 है, इसलिए λ1 = -2, λ2 = 12. अब प्रत्येक लैम्ब्डा मान के लिए, हमें एक eigenvector खोजने की आवश्यकता है। आइए, = -2 के लिए निकाय के गुणांकों को व्यक्त करें।

• एम - × ई = 2; चार;
• 6; 12.

इस सूत्र में, E सर्वसमिका आव्यूह है। प्राप्त मैट्रिक्स के आधार पर, हम रैखिक समीकरणों की एक प्रणाली बनाते हैं:

2x + 4y = 6x + 12y

जहाँ x और y eigenvector के अवयव हैं।

आइए सभी X को बाईं ओर और सभी Y को दाईं ओर एकत्र करें। जाहिर है - 4x = 8y। व्यंजक को -4 से भाग दें और x = -2y प्राप्त करें। अब हम अज्ञात के किसी भी मान को लेकर मैट्रिक्स के पहले आइजेनवेक्टर को निर्धारित कर सकते हैं (रैखिक रूप से निर्भर ईजिनवेक्टरों की अनंतता के बारे में याद रखें)। आइए y = 1 लें, फिर x = -2। इसलिए, पहला eigenvector V1 = (-2; 1) जैसा दिखता है। लेख की शुरुआत पर लौटें। यह वेक्टर ऑब्जेक्ट था जिसे हमने एक eigenvector की अवधारणा को प्रदर्शित करने के लिए मैट्रिक्स को गुणा किया था।

आइए अब = 12 के लिए eigenvector खोजें।

• एम - × ई = -12; चार
• 6; -2.

आइए हम रैखिक समीकरणों की एक ही प्रणाली की रचना करें;

• -12x + 4y = 6x -2y
• -18x = -6y
• 3x = वाई।

अब चलिए x = 1 लेते हैं, इसलिए y = 3। इस प्रकार, दूसरा eigenvector V2 = (1; 3) जैसा दिखता है। इस वेक्टर द्वारा मूल मैट्रिक्स को गुणा करते समय, परिणाम हमेशा एक ही वेक्टर को 12 से गुणा किया जाएगा। यह समाधान एल्गोरिथ्म को पूरा करता है। अब आप जानते हैं कि मैट्रिक्स के आइजनवेक्टर को मैन्युअल रूप से कैसे परिभाषित किया जाए।

• निर्धारक;
• ट्रेस, यानी मुख्य विकर्ण पर तत्वों का योग;
• रैंक, यानी रैखिक रूप से स्वतंत्र पंक्तियों/स्तंभों की अधिकतम संख्या।

कार्यक्रम उपरोक्त एल्गोरिथम के अनुसार संचालित होता है, समाधान प्रक्रिया को न्यूनतम करता है। यह इंगित करना महत्वपूर्ण है कि कार्यक्रम में लैम्ब्डा को "सी" अक्षर द्वारा दर्शाया गया है। आइए एक संख्यात्मक उदाहरण देखें।

कार्यक्रम उदाहरण

आइए निम्नलिखित मैट्रिक्स के लिए eigenvectors को परिभाषित करने का प्रयास करें:

• एम = 5; 13;
• 4; 14.

आइए इन मानों को कैलकुलेटर की कोशिकाओं में दर्ज करें और निम्न रूप में उत्तर प्राप्त करें:

• मैट्रिक्स रैंक: 2;
• मैट्रिक्स निर्धारक: 18;
• मैट्रिक्स ट्रेस: ​​19;
• Eigenvector गणना: c 2 - 19.00c + 18.00 (विशेषता समीकरण);
• Eigenvector गणना: 18 (प्रथम लैम्ब्डा मान);
• Eigenvector गणना: 1 (दूसरा लैम्ब्डा मान);
• सदिश 1 के समीकरणों का निकाय: -13x1 + 13y1 = 4x1 - 4y1;
• वेक्टर 2 समीकरण प्रणाली: 4x1 + 13y1 = 4x1 + 13y1;
• आइजेनवेक्टर 1: (1; 1);
• आइजेनवेक्टर 2: (-3.25; 1)।

इस प्रकार, हमने दो रैखिक रूप से स्वतंत्र eigenvectors प्राप्त किए हैं।

निष्कर्ष

इंजीनियरिंग में किसी भी नए व्यक्ति के लिए रैखिक बीजगणित और विश्लेषणात्मक ज्यामिति मानक विषय हैं। बड़ी संख्या में वैक्टर और मैट्रिसेस भयानक हैं, और इस तरह की बोझिल गणनाओं में गलती करना आसान है। हमारा कार्यक्रम छात्रों को उनकी गणना की जांच करने या एक eigenvector खोजने की समस्या को स्वचालित रूप से हल करने की अनुमति देगा। हमारे कैटलॉग में अन्य रैखिक बीजगणित कैलकुलेटर हैं, उन्हें अपने अध्ययन या कार्य में उपयोग करें।

www.siteआपको खोजने की अनुमति देता है। साइट गणना करती है। कुछ ही सेकंड में सर्वर सही समाधान देगा। मैट्रिक्स के लिए विशेषता समीकरणसारणिक की गणना के लिए नियम द्वारा पाया जाने वाला एक बीजीय व्यंजक होगा मैट्रिक्स मैट्रिक्स, जबकि मुख्य विकर्ण पर विकर्ण तत्वों और चर के मूल्यों में अंतर होगा। गणना करते समय मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण, प्रत्येक तत्व मैट्रिक्ससंबंधित अन्य तत्वों से गुणा किया जाएगा मैट्रिक्स. मोड में खोजें ऑनलाइनकेवल वर्ग के लिए संभव मैट्रिक्स. ऑपरेशन खोजें मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणतत्वों के उत्पाद के बीजगणितीय योग की गणना करने के लिए कम कर देता है मैट्रिक्सनिर्धारक खोजने के परिणामस्वरूप मैट्रिक्स, केवल निर्धारित करने के उद्देश्य से मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण. यह ऑपरेशन सिद्धांत में एक विशेष स्थान रखता है मैट्रिक्स, आपको जड़ों का उपयोग करके eigenvalues ​​​​और वैक्टर खोजने की अनुमति देता है। कार्य ढूँढना मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणतत्वों को गुणा करना है मैट्रिक्सएक निश्चित नियम के अनुसार इन उत्पादों के बाद के योग के साथ। www.siteपाता मैट्रिक्स के लिए विशेषता समीकरणमोड में दिया गया आयाम ऑनलाइन. गणना मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणकिसी दिए गए आयाम के लिए, यह निर्धारक की गणना के लिए नियम द्वारा पाए गए संख्यात्मक या प्रतीकात्मक गुणांक वाले बहुपद को ढूंढ रहा है मैट्रिक्स- संबंधित तत्वों के उत्पादों के योग के रूप में मैट्रिक्स, केवल निर्धारित करने के उद्देश्य से मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण. एक वर्ग के लिए एक चर के संबंध में एक बहुपद ढूँढना मैट्रिक्स, परिभाषा के रूप में मैट्रिक्स के लिए विशेषता समीकरण, सिद्धांत में सामान्य मैट्रिक्स. बहुपद के मूलों का मान मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणके लिए eigenvectors और eigenvalues ​​​​को परिभाषित करने के लिए उपयोग किया जाता है मैट्रिक्स. हालांकि, अगर निर्धारक मैट्रिक्सशून्य होगा, तो मैट्रिक्स विशेषता समीकरणरिवर्स के विपरीत अभी भी मौजूद रहेगा मैट्रिक्स. गणना करने के लिए मैट्रिक्स के लिए विशेषता समीकरणया एक साथ कई खोजें मैट्रिक्स विशेषता समीकरण, आपको बहुत समय और प्रयास खर्च करने की ज़रूरत है, जबकि हमारा सर्वर मिल जाएगा ऑनलाइन मैट्रिक्स के लिए विशेषता समीकरण. इस मामले में, खोज द्वारा उत्तर मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणसही और पर्याप्त सटीकता के साथ होगा, भले ही संख्याएं खोजने पर मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणतर्कहीन होगा। स्थल पर www.siteतत्वों में वर्ण प्रविष्टियों की अनुमति है मैट्रिक्स, वह है ऑनलाइन मैट्रिक्स के लिए विशेषता समीकरणगणना करते समय एक सामान्य प्रतीकात्मक रूप में प्रतिनिधित्व किया जा सकता है विशेषता समीकरण मैट्रिक्स ऑनलाइन. खोजने की समस्या को हल करते समय प्राप्त उत्तर की जांच करना उपयोगी होता है मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरणसाइट का उपयोग करना www.site. बहुपद की गणना का संक्रिया करते समय - मैट्रिक्स की विशेषता समीकरण, इस समस्या को हल करने के लिए चौकस और अत्यंत एकाग्र होना आवश्यक है। बदले में, हमारी साइट इस विषय पर आपके निर्णय की जांच करने में आपकी सहायता करेगी विशेषता समीकरण मैट्रिक्स ऑनलाइन. यदि आपके पास हल की गई समस्याओं की लंबी जांच के लिए समय नहीं है, तो www.siteखोज और गणना करते समय जाँच के लिए निश्चित रूप से एक सुविधाजनक उपकरण होगा मैट्रिक्स ऑनलाइन के लिए विशेषता समीकरण.

परिभाषा 9.3.वेक्टर एक्स बुलाया खुद का वेक्टरमैट्रिक्स लेकिनअगर ऐसी कोई संख्या है λ, कि समानता रखती है: लेकिन एक्स= λ एक्स, अर्थात्, आवेदन करने का परिणाम एक्स मैट्रिक्स द्वारा दिया गया रैखिक परिवर्तन लेकिन, संख्या से इस सदिश का गुणन है λ . नंबर ही λ बुलाया अपना नंबरमैट्रिक्स लेकिन.

सूत्रों में प्रतिस्थापन (9.3) x` j = x j ,हम eigenvector के निर्देशांक निर्धारित करने के लिए समीकरणों की एक प्रणाली प्राप्त करते हैं:

. (9.5)

इस रैखिक सजातीय प्रणाली का एक गैर-तुच्छ समाधान तभी होगा जब इसका मुख्य निर्धारक 0 (क्रैमर का नियम) हो। इस शर्त को फॉर्म में लिखकर:

हमें eigenvalues ​​निर्धारित करने के लिए एक समीकरण मिलता है λ बुलाया विशेषता समीकरण. संक्षेप में, इसे निम्नानुसार दर्शाया जा सकता है:

| ए-λई | = 0, (9.6)

चूँकि इसका बायाँ भाग आव्यूह का निर्धारक है ए-λई. के संबंध में बहुपद | ए-λई| बुलाया विशेषता बहुपदमैट्रिसेस ए.

विशेषता बहुपद के गुण:

1) एक रैखिक परिवर्तन की विशेषता बहुपद आधार की पसंद पर निर्भर नहीं करता है। सबूत। (देखें (9.4)), लेकिन फलस्वरूप, । इस प्रकार, आधार की पसंद पर निर्भर नहीं करता है। इसलिए, और | ए-λई| नए आधार पर संक्रमण पर नहीं बदलता है।

2) यदि मैट्रिक्स लेकिनरैखिक परिवर्तन है सममित(वे। एक ij = एक जी), तो अभिलक्षणिक समीकरण (9.6) के सभी मूल वास्तविक संख्याएँ हैं।

eigenvalues ​​​​और eigenvectors के गुण:

1) यदि हम eigenvectors में से एक आधार चुनते हैं एक्स 1, एक्स 2, एक्स 3 eigenvalues ​​के अनुरूप 1 , 2 , 3मैट्रिक्स लेकिन, तो इस आधार पर रैखिक परिवर्तन ए में एक विकर्ण मैट्रिक्स है:

(9.7) इस गुण का प्रमाण eigenvectors की परिभाषा से मिलता है।

2) यदि परिवर्तन eigenvalues लेकिनभिन्न हैं, तो उनके संगत eigenvectors रैखिक रूप से स्वतंत्र हैं।

3) यदि आव्यूह का अभिलक्षणिक बहुपद लेकिनतीन अलग-अलग जड़ें हैं, तो किसी आधार पर मैट्रिक्स लेकिनएक विकर्ण आकार है।

आइए मैट्रिक्स के eigenvalues ​​​​और eigenvectors खोजें आइए विशेषता समीकरण बनाएं: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ - 7 λ + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

प्रत्येक पाए गए मान के अनुरूप eigenvectors के निर्देशांक खोजें λ. (9.5) से यह इस प्रकार है कि यदि एक्स (1) ={एक्स 1 , एक्स 2 , एक्स 3) के अनुरूप आइजनवेक्टर है λ 1 = -2, तब

एक सहयोगी लेकिन अनिश्चित प्रणाली है। इसका हल इस प्रकार लिखा जा सकता है एक्स (1) ={एक,0,-एक), जहां a कोई संख्या है। विशेष रूप से, यदि आपको इसकी आवश्यकता है | एक्स (1) |=1, एक्स (1) =

सिस्टम में प्रतिस्थापन (9.5) λ 2 = 3, हमें दूसरे eigenvector के निर्देशांक निर्धारित करने के लिए एक प्रणाली मिलती है - एक्स (2) ={y1,y2,y3}:

, कहाँ पे एक्स (2) ={बी,-बी,बी) या, प्रदान किया गया | एक्स (2) |=1, एक्स (2) =

के लिये λ 3 = 6 eigenvector खोजें एक्स (3) ={जेड1, जेड2, जेड3}:

, एक्स (3) ={सी,2सी, सी) या सामान्यीकृत संस्करण में

एक्स (3) = यह देखा जा सकता है एक्स (1) एक्स (2) = अब-अब= 0, एक्स (1) एक्स (3) = एसी-एसी= 0, एक्स (2) एक्स (3) = बीसी- 2बीसी + बीसी= 0. इस प्रकार, इस मैट्रिक्स के eigenvectors जोड़ीदार ओर्थोगोनल हैं।

व्याख्यान 10

द्विघात रूप और सममित मैट्रिक्स के साथ उनका संबंध। एक सममित मैट्रिक्स के eigenvectors और eigenvalues ​​​​के गुण। द्विघात रूप को विहित रूप में घटाना।

परिभाषा 10.1।द्विघात रूपवास्तविक चर एक्स 1, एक्स 2,…, एक्स एनइन चरों के संबंध में दूसरी डिग्री के बहुपद को कहा जाता है, जिसमें एक मुक्त शब्द और पहली डिग्री की शर्तें शामिल नहीं होती हैं।

द्विघात रूपों के उदाहरण:

(एन = 2),

(एन = 3). (10.1)

पिछले व्याख्यान में दी गई सममित मैट्रिक्स की परिभाषा को याद करें:

परिभाषा 10.2.वर्ग मैट्रिक्स को कहा जाता है सममित, यदि , अर्थात्, यदि मैट्रिक्स तत्व मुख्य विकर्ण के संबंध में सममित हैं, तो समान हैं।

सममित मैट्रिक्स के eigenvalues ​​​​और eigenvectors के गुण:

1) एक सममित मैट्रिक्स के सभी eigenvalues ​​​​वास्तविक हैं।

सबूत (के लिए एन = 2).

चलो मैट्रिक्स लेकिनकी तरह लगता है: . आइए विशेषता समीकरण बनाते हैं:

(10.2) विभेदक का पता लगाएं:

इसलिए, समीकरण के केवल वास्तविक मूल हैं।

2) सममित मैट्रिक्स के आइजेनवेक्टर ओर्थोगोनल होते हैं।

सबूत (के लिए एन= 2).

eigenvectors के निर्देशांक और समीकरणों को संतुष्ट करना चाहिए।