DEFINIÇÃO

As desigualdades trigonométricas são desigualdades que contêm uma variável sob o sinal de uma função trigonométrica.

Resolvendo inequações trigonométricas

A solução de desigualdades trigonométricas geralmente se resume a resolver as desigualdades trigonométricas mais simples da forma: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \ ), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \ leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg ) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)

As desigualdades trigonométricas mais simples são resolvidas graficamente ou usando um círculo trigonométrico unitário.

Por definição, o seno do ângulo \(\ \alpha \) é a ordenada do ponto \(\ P_(\alpha)(x, y) \) do círculo unitário (Fig. 1), e o cosseno é a abcissa deste ponto. Este fato é usado para resolver as desigualdades trigonométricas mais simples com cosseno e seno usando o círculo unitário.

Exemplos de solução de desigualdades trigonométricas

Exercício

Resolva a desigualdade \(\ \sin x \leq \frac(\sqrt(3))(2) \)

Solução

Como \(\ \left|\frac(\sqrt(3))(2)\right| , essa desigualdade tem solução e pode ser resolvida de duas maneiras

Primeira maneira. Vamos resolver essa desigualdade graficamente. Para fazer isso, construímos no mesmo sistema de coordenadas um gráfico do seno \(\ y=\sin x \) (Fig. 2) e a linha reta \(\ y=\frac(\sqrt(3))( 2)\)

Vamos selecionar os intervalos onde a senóide está localizada abaixo do gráfico da linha reta \(\ y=\frac(\sqrt(3))(2) \) . Encontre as abcissas \(\ x_(1) \) e \(\ x_(2) \) dos pontos de interseção desses gráficos: \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3) ))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Temos o intervalo \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) mas como a função \(\ y=\sin x \) é periódica e tem um período \(\ 2 \pi \) , então a resposta é a união de intervalos: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7) \pi)(3)+ 2 \pi k\right] \), \(\ k \in Z \)

A segunda maneira. Construa um círculo unitário e uma linha \(\ y=\frac(\sqrt(3))(2) \) , denote seus pontos de interseção \(\ P_(x_(1)) \) e \(\ P_(x_) (2))\) (Fig. 3). A solução para a desigualdade original será o conjunto de pontos de ordenadas que são menores que \(\ \frac(\sqrt(3))(2) \) . Vamos encontrar o valor de \(\ \boldsymbol(I)_(1) \) e \(\ \boldsymbol(I)_(2) \) indo no sentido anti-horário, \(\ x_(1) Fig. 3

\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

Levando em conta a periodicidade da função seno, finalmente obtemos os intervalos \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)

Answer\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\ k \ em Z \)

Exercício

Resolva a desigualdade \(\ \sin x>2 \)

Solução

O seno é uma função limitada: \(\ |\sin x| \leq 1 \) , e o lado direito dessa desigualdade é maior que um, então não há soluções.

Resposta: Não há soluções.

Exercício

Resolva a desigualdade \(\ \cos x>\frac(1)(2) \)

Solução

Essa desigualdade pode ser resolvida de duas maneiras: graficamente e usando um círculo unitário. Vamos considerar cada um dos métodos.

Primeira maneira. Vamos representar em um sistema de coordenadas as funções que descrevem as partes esquerda e direita da desigualdade, ou seja, \(\ y=\cos x \) e \(\ y=\frac(1)(2) \) . Vamos selecionar os intervalos onde o gráfico da função cosseno \(\ y=\cos x \) está localizado acima do gráfico da reta \(\ y=\frac(1)(2) \) (Fig. 4 ).

Encontre as abcissas dos pontos \(\ \boldsymbol(x)_(1) \) e \(\ x_(2) \) - os pontos de interseção dos gráficos das funções \(\ y=\cos x \ ) e \(\ y=\frac (1)(2) \) , que são as extremidades de um dos intervalos em que a desigualdade indicada é válida. \(\ x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3) \); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

Considerando que o cosseno é uma função periódica, com um período \(\ 2 \pi \) , a resposta é o valor \(\ x \) dos intervalos \(\ \left(-\frac(\pi)(3 )+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)

A segunda maneira. Vamos construir um círculo unitário e uma linha reta \(\ x=\frac(1)(2) \) (já que o eixo x corresponde aos cossenos no círculo unitário). Sejam \(\ P_(x_(1)) \) e \(\ P_(x_(2)) \) (Fig. 5) os pontos de interseção da reta e do círculo unitário. A solução da equação original será o conjunto de pontos de abcissas menores que \(\ \frac(1)(2) \) . Encontre o valor de \(\ x_(1) \) e \(\ 2 \) , fazendo um giro no sentido anti-horário para que \(\ x_(1) Levando em conta a periodicidade do cosseno, finalmente obtenhamos os intervalos \( \ \left(-\frac (\pi)(3)+2 \pi k ;\frac(\pi)(3)+2 \pi k\right) \),\(\ k \in Z \)

Resposta: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k\em Z\)

Exercício

Resolva a desigualdade \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)

Solução

Vamos traçar gráficos de funções \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) em um sistema de coordenadas

Vamos selecionar os intervalos onde o gráfico da função \(\ y=\operatorname(ctg) x \) não é maior que o gráfico da linha reta \(\ y=-\frac(\sqrt(3))(3 ) \) (Fig. 6) .

Encontre a abscissa do ponto \(\ x_(0) \) , que é o final de um dos intervalos em que a desigualdade \(\ x_(0)=\operatorname(arcctg)\left(-\frac(\ sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)(3 )=\frac(2 \pi)(3) \)

A outra extremidade dessa lacuna é o ponto \(\ \pi \) , e a função \(\ y=\operatorname(ctg) x \) é indefinida neste ponto. Assim, uma das soluções para esta desigualdade é o intervalo \(\ \frac(2 \pi)(3) \leq x

Resposta: \(\ x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\right) \), \(\ k \in Z \)

Desigualdades trigonométricas com argumento complexo

As desigualdades trigonométricas com um argumento complexo podem ser reduzidas às mais simples desigualdades trigonométricas usando uma substituição. Após resolvê-lo, a substituição inversa é feita e a incógnita original é expressa.

Exercício

Resolva a desigualdade \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

Solução

Expresse o cosseno do lado direito desta desigualdade: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

Realizamos a substituição \(\ t=2 x+100^(\circ) \) , após o que essa desigualdade é transformada na desigualdade mais simples \(\ \cos t \leq-\frac(1)(2) \ )

Vamos resolvê-lo usando o círculo unitário. Vamos construir um círculo unitário e uma linha \(\ x=-\frac(1)(2) \) . Vamos denotar \(\ P_(1) \) e \(\ P_(2) \) como os pontos de interseção da linha e do círculo unitário (Fig. 7).

A solução da desigualdade original será o conjunto de pontos de abcissas, que são no máximo \(\ -\frac(1)(2) \). O ponto \(\ P_(1) \) corresponde ao ângulo \(\ 120^(\circ) \) , e o ponto \(\ P_(2) \) . Assim, dado o período do cosseno, obtemos \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \ ), \(\ n \ em Z \)

Fazemos a substituição inversa \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n \), \(\ n \in Z \)

Expressamos \(\ \mathbf(x) \), para fazer isso, primeiro subtraia \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \ n\em Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)

e então, divida por 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^) (\circ)+360^(\circ) \cdot n)(2) \), \(\ n \in Z \); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)

Answer\(\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \), \ (\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\right) \)

Desigualdades trigonométricas duplas

Exercício

Resolva a dupla desigualdade trigonométrica \(\ \frac(1)(2)

Solução

Vamos introduzir a substituição \(\ t=\frac(x)(2) \) , então a desigualdade original terá a forma \(\ \frac(1)(2)

Vamos resolvê-lo usando o círculo unitário. Como o eixo das ordenadas corresponde ao seno no círculo unitário, selecionamos nele o conjunto de ordenadas que é maior que \(\ x=\frac(1)(2) \) e menor ou igual a \(\ \frac(\sqrt(2))(2) \) . Na Figura 8, esses pontos estarão localizados nos arcos \(\ P_(t_(1)) \), \(\ P_(t_(2)) \) e \(\ P_(t_(3)) \) , \( \ P_(t_(4)) \) . Vamos encontrar o valor \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) , fazendo um tour no sentido anti-horário, e \ (\ t_(1) \(\ t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3) \ pi)(4) \); \(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi ) (6)\)

Assim, obtemos dois intervalos, que, levando em conta a periodicidade da função seno, podem ser escritos da seguinte forma \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \) , \(\ \frac(3 \pi)(4)+2 \pi k Express \(\ \mathbf( x) \), para isso multiplicamos todos os lados de ambas as desigualdades por 2, obtemos \(\ \frac (\pi)(3)+4 \pi k \leq x

Resposta\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\right] \cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\right) \), \(\ k \in Z \)

As desigualdades são relações da forma a › b, onde a e b são expressões contendo pelo menos uma variável. As desigualdades podem ser estritas - ‹, › e não estritas - ≥, ≤.

As desigualdades trigonométricas são expressões da forma: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, em que F(x) é representado por uma ou mais funções trigonométricas .

Um exemplo da desigualdade trigonométrica mais simples é: sen x ‹ 1/2. É costume resolver tais problemas graficamente; dois métodos foram desenvolvidos para isso.

Método 1 - Resolvendo Desigualdades Plotando uma Função

Para encontrar um intervalo que satisfaça as condições da desigualdade sen x ‹ 1/2, você deve fazer o seguinte:

1. No eixo de coordenadas, construa uma senóide y = sin x.
2. No mesmo eixo, desenhe um gráfico do argumento numérico da desigualdade, ou seja, uma linha reta passando pelo ponto ½ da ordenada OY.
3. Marque os pontos de interseção dos dois gráficos.
4. Sombreie o segmento que é a solução do exemplo.

Quando há sinais fortes em uma expressão, os pontos de interseção não são soluções. Como o menor período positivo da senóide é 2π, escrevemos a resposta da seguinte forma:

Se os sinais da expressão não forem estritos, o intervalo de solução deve ser colocado entre colchetes - . A resposta para o problema também pode ser escrita como outra desigualdade:

Método 2 - Resolvendo desigualdades trigonométricas usando o círculo unitário

Problemas semelhantes são facilmente resolvidos com a ajuda de um círculo trigonométrico. O algoritmo de busca é muito simples:

1. Primeiro, desenhe um círculo unitário.
2. Então você precisa observar o valor da função arco do argumento do lado direito da desigualdade no arco do círculo.
3. É necessário traçar uma linha reta passando pelo valor da função arco paralela ao eixo x (OX).
4. Depois disso, resta apenas selecionar o arco de um círculo, que é o conjunto de soluções da desigualdade trigonométrica.
5. Escreva a resposta no formulário necessário.

Vamos analisar os passos da solução usando a desigualdade sen x › 1/2 como exemplo. Os pontos α e β estão marcados no círculo – os valores

Os pontos do arco localizados acima de α e β são o intervalo para resolver a desigualdade dada.

Se você precisar resolver um exemplo para cos, o arco de respostas estará localizado simetricamente ao eixo OX, e não OY. Você pode considerar a diferença entre os intervalos de solução para sen e cos nos diagramas abaixo no texto.

As soluções gráficas para desigualdades tangentes e cotangentes serão diferentes tanto do seno quanto do cosseno. Isto é devido às propriedades das funções.

O arco tangente e arcotangente são tangentes ao círculo trigonométrico, e o período positivo mínimo para ambas as funções é π. Para usar o segundo método de maneira rápida e correta, você precisa lembrar em qual eixo os valores de sin, cos, tg e ctg são plotados.

A tangente tangente corre paralela ao eixo OY. Se traçarmos o valor de arctg a no círculo unitário, o segundo ponto necessário estará localizado no quarto diagonal. cantos

Eles são pontos de interrupção para a função, pois o gráfico tende a eles, mas nunca os atinge.

No caso da cotangente, a tangente corre paralela ao eixo OX, e a função é interrompida nos pontos π e 2π.

Desigualdades trigonométricas complexas

Se o argumento da função de desigualdade é representado não apenas por uma variável, mas por uma expressão inteira contendo uma incógnita, então estamos falando de uma desigualdade complexa. O curso e a ordem de sua solução são um pouco diferentes dos métodos descritos acima. Suponha que precisamos encontrar uma solução para a seguinte desigualdade:

A solução gráfica prevê a construção de uma senóide ordinária y = sin x para valores de x escolhidos arbitrariamente. Vamos calcular uma tabela com as coordenadas dos pontos de referência do gráfico:

O resultado deve ser uma curva agradável.

Para facilidade de encontrar uma solução, substituímos o argumento da função complexa

A interseção de dois gráficos permite determinar a área dos valores desejados para os quais a condição de desigualdade é satisfeita.

O segmento encontrado é a solução para a variável t:

No entanto, o objetivo da tarefa é encontrar todas as variantes possíveis da desconhecida x:

Resolver a dupla desigualdade é bastante simples, você precisa mover π/3 para as partes extremas da equação e realizar os cálculos necessários:

Resposta para a tarefa será semelhante a um intervalo para desigualdade estrita:

Tais tarefas exigirão a experiência e habilidade dos alunos no manuseio de funções trigonométricas. Quanto mais tarefas de treinamento forem resolvidas no processo de preparação, mais fácil e rápido o aluno encontrará a resposta para a pergunta do exame.

Solução das equações trigonométricas mais simples

Primeiro, vamos relembrar as fórmulas para resolver as equações trigonométricas mais simples.

1. $sinx=a$

1. $cosx=a$

1. $tgx=a$

1. $ctgx=a$

Solução das desigualdades trigonométricas mais simples.

Para resolver as desigualdades trigonométricas mais simples, primeiro precisamos resolver a equação correspondente e, em seguida, usando o círculo trigonométrico, encontrar uma solução para a desigualdade. Considere as soluções das desigualdades trigonométricas mais simples por meio de exemplos.

Exemplo 1

$sinx\ge \frac(1)(2)$

Encontre uma solução para a desigualdade trigonométrica $sinx=\frac(1)(2)$

\ \

Figura 1. Solução da desigualdade $sinx\ge \frac(1)(2)$.

Como a desigualdade tem um sinal de “maior que ou igual”, a solução está no arco superior do círculo (em relação à solução da equação).

Resposta: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.

Exemplo 2

Encontre uma solução para a desigualdade trigonométrica $cosx=\frac(\sqrt(3))(2)$

\ \

Observe a solução no círculo trigonométrico

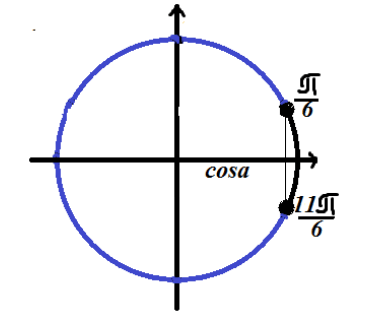
Como a desigualdade tem um sinal de “menor que”, a solução está no arco do círculo localizado à esquerda (em relação à solução da equação).

Resposta: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.

Exemplo 3

$tgx\le \frac(\sqrt(3))(3)$

Encontre uma solução para a desigualdade trigonométrica $tgx=\frac(\sqrt(3))(3)$

\ \

Aqui também precisamos de um domínio de definição. Como lembramos, a função tangente $x\ne \frac(\pi )(2)+\pi n,n\in Z$

Observe a solução no círculo trigonométrico

Figura 3. Solução da desigualdade $tgx\le \frac(\sqrt(3))(3)$.

Como a desigualdade tem um sinal de “menor ou igual a”, a solução está nos arcos do círculo marcado em azul na Figura 3.

Resposta: $\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\right.\left.\frac(7\pi )(6)+2\pi n\right]$

Exemplo 4

Encontre uma solução para a desigualdade trigonométrica $ctgx=\sqrt(3)$

\ \

Aqui também precisamos de um domínio de definição. Como lembramos, a função tangente $x\ne \pi n,n\in Z$

Observe a solução no círculo trigonométrico

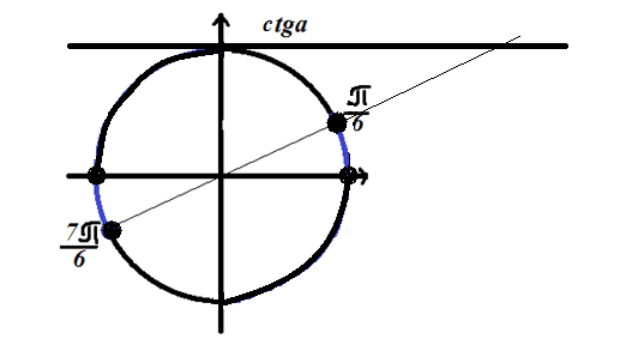
Figura 4. Solução da desigualdade $ctgx\le \sqrt(3)$.

Como a desigualdade tem um sinal de “maior que”, a solução está nos arcos do círculo marcado em azul na Figura 4.

Resposta: $\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\direita)$

MÉTODOS PARA RESOLVER DESIGUALDADES TRIGONOMETRICAS

Relevância. Historicamente, as equações e desigualdades trigonométricas têm tido um lugar especial no currículo escolar. Podemos dizer que a trigonometria é uma das seções mais importantes do curso escolar e de toda a ciência matemática em geral.

As equações e desigualdades trigonométricas ocupam um dos lugares centrais em um curso de matemática do ensino médio, tanto no que diz respeito ao conteúdo do material didático quanto aos métodos de atividade educacional e cognitiva que podem e devem ser formados durante seu estudo e aplicados na resolução de um grande problema. número de problemas de natureza teórica e aplicada.

A solução de equações e desigualdades trigonométricas cria os pré-requisitos para sistematizar os conhecimentos dos alunos relacionados a todo o material didático em trigonometria (por exemplo, as propriedades das funções trigonométricas, métodos para transformar expressões trigonométricas etc.) o material estudado em álgebra (equações, equivalência de equações, desigualdades, transformações idênticas de expressões algébricas, etc.).

Em outras palavras, a consideração de métodos para resolver equações e desigualdades trigonométricas envolve uma espécie de transferência dessas habilidades para um novo conteúdo.

O significado da teoria e suas inúmeras aplicações comprovam a relevância do tema escolhido. Isso, por sua vez, permite determinar as metas, objetivos e objeto de pesquisa do trabalho do curso.

Propósito do estudo: generalizar os tipos disponíveis de desigualdades trigonométricas, métodos básicos e especiais para sua solução, selecionar um conjunto de tarefas para resolver desigualdades trigonométricas por crianças em idade escolar.

Objetivos de pesquisa:

1. Com base na análise da literatura disponível sobre o tema da pesquisa, sistematize o material.

2. Dê um conjunto de tarefas necessárias para consolidar o tópico "Desigualdades trigonométricas".

Objeto de estudo são desigualdades trigonométricas no curso de matemática escolar.

Objeto de estudo: tipos de desigualdades trigonométricas e métodos para a sua solução.

Significado teórico é organizar o material.

Significado prático: aplicação de conhecimentos teóricos na resolução de problemas; análise dos principais métodos frequentemente encontrados para a resolução de inequações trigonométricas.

Métodos de pesquisa : análise da literatura científica, síntese e generalização dos conhecimentos adquiridos, análise da resolução de problemas, procura de métodos óptimos para a resolução de desigualdades.

§1. Tipos de desigualdades trigonométricas e métodos básicos para sua solução

1.1. As desigualdades trigonométricas mais simples

Duas expressões trigonométricas conectadas por um sinal ou > são chamadas de desigualdades trigonométricas.

Resolver uma desigualdade trigonométrica significa encontrar um conjunto de valores das incógnitas incluídas na desigualdade, sob os quais a desigualdade é satisfeita.

A parte principal das desigualdades trigonométricas é resolvida reduzindo-as para resolver as mais simples:

Este pode ser um método de fatoração, mudança de variável (
,
etc.), onde a desigualdade usual é resolvida primeiro e, em seguida, a desigualdade da forma
etc., ou outras formas.

As desigualdades mais simples são resolvidas de duas maneiras: usando o círculo unitário ou graficamente.

Deixarf(x  é uma das funções trigonométricas básicas. Para resolver a desigualdade
basta encontrar sua solução em um período, ou seja, em qualquer segmento cujo comprimento seja igual ao período da funçãof  x  . Então a solução da desigualdade original será encontradax , bem como aqueles valores que diferem daqueles encontrados por qualquer número inteiro de períodos da função. Nesse caso, é conveniente usar o método gráfico.

Vamos dar um exemplo de um algoritmo para resolver inequações
(
) e
.

Algoritmo para resolver a desigualdade
(
).

1. Formular a definição do seno de um númerox no círculo unitário.

3. No eixo y, marque um ponto com a coordenadauma .

4. Por este ponto, desenhe uma linha paralela ao eixo OX e marque os pontos de intersecção desta com o círculo.

5. Selecione um arco de círculo, todos os pontos dos quais têm uma ordenada menor queuma .

6. Especifique a direção do desvio (sentido anti-horário) e anote a resposta adicionando o período da função às extremidades do intervalo2πn ,
.

Algoritmo para resolver a desigualdade
.

1. Formular a definição da tangente de um númerox no círculo unitário.

2. Desenhe um círculo unitário.

3. Desenhe uma linha de tangentes e marque um ponto nela com uma ordenadauma .

4. Conecte este ponto à origem e marque o ponto de interseção do segmento resultante com o círculo unitário.

5. Selecione um arco de círculo, todos os pontos dos quais têm uma ordenada na linha tangente menor queuma .

6. Indique a direção da travessia e anote a resposta, levando em consideração o escopo da função, adicionando um pontopn ,
(o número do lado esquerdo do registro é sempre menor que o número do lado direito).

A interpretação gráfica das soluções das equações mais simples e as fórmulas para resolver as desigualdades de uma forma geral são fornecidas no apêndice (Apêndices 1 e 2).

Exemplo 1 Resolva a desigualdade
.

Desenhe uma linha no círculo unitário
, que intercepta o círculo nos pontos A e B.

Todos os valoresy no intervalo NM mais , todos os pontos do arco AMB satisfazem esta desigualdade. Em todos os ângulos de rotação, grandes , mas menor ,
assumirá valores superiores a (mas não mais de um).

Figura 1

Assim, a solução da inequação serão todos os valores no intervalo
, ou seja
. Para obter todas as soluções dessa desigualdade, basta adicionar às extremidades desse intervalo
, Onde
, ou seja
,
. Observe que os valores
e
são as raízes da equação
,

Essa.
;
.

Responda:
,
.

1.2. Método gráfico

Na prática, um método gráfico para resolver desigualdades trigonométricas geralmente é útil. Considere a essência do método no exemplo da desigualdade
:

1. Se o argumento for complexo (diferente deX ), então substituímos port .

2. Construímos em um plano coordenadotoOy gráficos de função
e
.

3. Encontramos taldois pontos adjacentes de intersecção de gráficos, entre os quaissinusóidesituadoacima de direto
. Encontre as abcissas desses pontos.

4. Escreva uma desigualdade dupla para o argumentot , considerando o período do cosseno (t estará entre as abcissas encontradas).

5. Faça uma substituição reversa (retorne ao argumento original) e expresse o valorX de uma dupla desigualdade, escrevemos a resposta como um intervalo numérico.

Exemplo 2 Resolva a desigualdade: .

Ao resolver inequações por um método gráfico, é necessário construir gráficos de funções com a maior precisão possível. Vamos transformar a desigualdade na forma:

Vamos construir gráficos de funções em um sistema de coordenadas
e
(Figura 2).

Figura 2

Gráficos de funções se cruzam em um pontoMAS com coordenadas
;
. Entre
pontos do gráfico
abaixo dos pontos do gráfico
. E quando
os valores da função são os mesmos. É por isso
no
.

Responda:
.

1.3. Método Algébrico

Muitas vezes, a desigualdade trigonométrica original, por uma substituição bem escolhida, pode ser reduzida a uma desigualdade algébrica (racional ou irracional). Esse método envolve transformar a desigualdade, introduzir uma substituição ou substituir uma variável.

Vamos considerar a aplicação deste método em exemplos concretos.

Exemplo 3 Redução à forma mais simples
.

(Fig. 3)

Fig.3

,
.

Responda:
,

Exemplo 4 Resolva a desigualdade:

ODZ:
,
.

Usando fórmulas:
,

escrevemos a desigualdade na forma:
.

Ou, supondo
após transformações simples obtemos

,

,

.

Resolvendo a última desigualdade pelo método intervalar, obtemos:

Fig.4

, respectivamente
. Então da Fig. 4 segue
, Onde
.

Fig.5

Responda:
,
.

1.4. Método de espaçamento

O esquema geral para resolver desigualdades trigonométricas pelo método intervalar:

Usando fórmulas trigonométricas, fatorize.

Encontre pontos de interrupção e zeros da função, coloque-os no círculo.

Pegue qualquer pontoPara (mas não encontrado anteriormente) e descubra o sinal do produto. Se o produto for positivo, coloque um ponto fora do círculo unitário no raio correspondente ao ângulo. Caso contrário, coloque o ponto dentro do círculo.

Se um ponto ocorre um número par de vezes, chamamos-lhe um ponto de multiplicidade par; se um número ímpar de vezes, chamamos-lhe um ponto de multiplicidade ímpar. Desenhe arcos da seguinte forma: comece a partir de um pontoPara , se o próximo ponto é de multiplicidade ímpar, então o arco intercepta o círculo neste ponto, mas se o ponto é de multiplicidade par, então ele não intercepta.

Arcos atrás de um círculo são lacunas positivas; dentro do círculo são intervalos negativos.

Exemplo 5 Resolva a desigualdade

,
.

Pontos da primeira série:
.

Pontos da segunda série:
.

Cada ponto ocorre um número ímpar de vezes, ou seja, todos os pontos de multiplicidade ímpar.

Descubra o sinal do produto em
: . Marcamos todos os pontos no círculo unitário (Fig. 6):

Arroz. 6

Responda:
,
;
,
;
,
.

Exemplo 6 . Resolva a desigualdade.

Solução:

Vamos encontrar os zeros da expressão .

Pegueaem :

,
;

,
;

,
;

,
;

No círculo unitário, os valores da sérieX 1 representado por pontos
. SeriesX 2 dá pontos
. Uma sérieX 3 ganhamos dois pontos
. Por fim, uma sérieX 4 representará pontos
. Colocamos todos esses pontos no círculo unitário, indicando entre parênteses ao lado de cada um de sua multiplicidade.

Agora deixe o número será igual. Fazemos uma estimativa pelo sinal:

Então o pontoUMA deve ser escolhido na viga que forma o ângulo com feixeOh, fora do círculo unitário. (Observe que o feixe auxiliarO UMA não precisa ser mostrado na imagem. PontoUMA selecionado aproximadamente.)

Agora do pontoUMA desenhamos uma linha contínua ondulada sequencialmente para todos os pontos marcados. E nos pontos
nossa linha passa de uma região para outra: se estava fora do círculo unitário, então passa para dentro dele. Aproximando-se do ponto , a reta retorna para a região interna, pois a multiplicidade desse ponto é par. Da mesma forma no ponto (com uma multiplicidade par) a linha deve ser girada para a região externa. Então, desenhamos uma certa imagem representada na Fig. 7. Ajuda a destacar as áreas desejadas no círculo unitário. Eles são marcados com um "+".

Fig.7

Resposta final:

Observação. Se a linha ondulada, depois de percorrer todos os pontos marcados no círculo unitário, não puder retornar ao pontoUMA , sem cruzar o círculo em um lugar “ilegal”, isso significa que houve um erro na solução, ou seja, um número ímpar de raízes foi omitido.

Responda: .

§2. Um conjunto de tarefas para resolver desigualdades trigonométricas

No processo de desenvolvimento da capacidade dos alunos de resolver desigualdades trigonométricas, também podem ser distinguidos 3 estágios.

1. preparatório,

2. formação de competências para resolver as mais simples desigualdades trigonométricas;

3. introdução de desigualdades trigonométricas de outros tipos.

O objetivo do estágio preparatório é que é necessário formar em crianças em idade escolar a capacidade de usar um círculo ou gráfico trigonométrico para resolver desigualdades, a saber:

Capacidade de resolver inequações simples da forma
,
,
,
, usando as propriedades das funções seno e cosseno;

Capacidade de fazer duplas desigualdades para arcos de um círculo numérico ou para arcos de gráficos de funções;

Capacidade de realizar várias transformações de expressões trigonométricas.

Recomenda-se implementar esta etapa no processo de sistematização do conhecimento dos escolares sobre as propriedades das funções trigonométricas. Os principais meios podem ser tarefas oferecidas aos alunos e realizadas sob a orientação de um professor ou de forma independente, bem como habilidades adquiridas na resolução de equações trigonométricas.

Aqui estão alguns exemplos de tais tarefas:

1 . Marcar um ponto no círculo unitário , E se

.

2. Em que quarto do plano coordenado está o ponto , E se é igual a:

3. Marcar pontos no círculo trigonométrico , E se:

4. Traga a expressão para funções trigonométricasEUquartos.

a)
, b)
, dentro)

5. Dado o arco MR.M - meioEUº trimestre,R - meioIIº trimestre. Restringir o valor de uma variávelt para: (compor uma dupla desigualdade) a) arco MP; b) arcos RM.

6. Escreva uma desigualdade dupla para as seções selecionadas do gráfico:

Arroz. 1

7. Resolver desigualdades
,
,
,
.

8. Converter expressão .

Na segunda etapa do aprendizado da resolução de desigualdades trigonométricas, podemos oferecer as seguintes recomendações relacionadas à metodologia para organizar as atividades dos alunos. Ao mesmo tempo, é necessário focar nas habilidades dos alunos para trabalhar com um círculo ou gráfico trigonométrico, que são formados durante a solução das equações trigonométricas mais simples.

Primeiro, é possível motivar a conveniência de obter um método geral para resolver as desigualdades trigonométricas mais simples referindo-se, por exemplo, a uma desigualdade da forma
. Usando os conhecimentos e habilidades adquiridos na fase preparatória, os alunos irão trazer a desigualdade proposta para a forma
, mas pode achar difícil encontrar um conjunto de soluções para a desigualdade resultante, uma vez que é impossível resolvê-lo usando apenas as propriedades da função seno. Essa dificuldade pode ser evitada consultando a ilustração apropriada (solução da equação graficamente ou usando um círculo unitário).

Em segundo lugar, o professor deve chamar a atenção dos alunos para as diferentes formas de completar a tarefa, dar um exemplo adequado de resolução da desigualdade tanto graficamente como usando o círculo trigonométrico.

Considere essas opções para resolver a desigualdade
.

1. Resolvendo a inequação usando o círculo unitário.

Na primeira lição sobre como resolver desigualdades trigonométricas, ofereceremos aos alunos um algoritmo de solução detalhado, que em uma apresentação passo a passo reflete todas as habilidades básicas necessárias para resolver a desigualdade.

Passo 1.Desenhe um círculo unitário, marque um ponto no eixo y e desenhe uma linha reta através dele paralela ao eixo x. Esta linha cruzará o círculo unitário em dois pontos. Cada um desses pontos representa números cujo seno é igual a .

Passo 2Esta linha reta dividiu o círculo em dois arcos. Vamos destacar aquele em que os números são exibidos que têm um seno maior que . Naturalmente, este arco está localizado acima da linha reta desenhada.

Arroz. 2

etapa 3Vamos escolher uma das extremidades do arco marcado. Vamos escrever um dos números que é representado por este ponto do círculo unitário .

Passo 4Para escolher um número correspondente à segunda extremidade do arco selecionado, "passamos" ao longo desse arco da extremidade nomeada à outra. Ao mesmo tempo, lembramos que ao se mover no sentido anti-horário, os números pelos quais passaremos aumentam (ao se mover na direção oposta, os números diminuiriam). Vamos escrever o número representado no círculo unitário na segunda extremidade do arco marcado .

Assim, vemos que a desigualdade
satisfaça os números para os quais a desigualdade
. Resolvemos a desigualdade para números localizados no mesmo período da função seno. Portanto, todas as soluções da inequação podem ser escritas como

Os alunos devem ser solicitados a considerar cuidadosamente a figura e descobrir por que todas as soluções para a desigualdade
pode ser escrito na forma
,
.

Arroz. 3

É necessário chamar a atenção dos alunos para o fato de que ao resolver as desigualdades para a função cosseno, traçamos uma linha reta paralela ao eixo y.

Forma gráfica de resolver a inequação.

Construindo gráficos
e
, dado que
.

Arroz. quatro

Então escrevemos a equação
e sua decisão
,
,
, encontrado usando fórmulas
,
,
.

(Dandon valores 0, 1, 2, encontramos três raízes da equação composta). Valores
são três abcissas consecutivas dos pontos de interseção dos gráficos
e
. Obviamente, sempre no intervalo
a desigualdade
, e no intervalo
- desigualdade
. Estamos interessados ​​no primeiro caso, e então adicionando às extremidades desse intervalo um número que é um múltiplo do período do seno, obtemos uma solução para a desigualdade
Como:
,
.

Arroz. 5

Resumir. Para resolver a desigualdade
, você precisa escrever a equação correspondente e resolvê-la. Da fórmula resultante encontre as raízes e , e escreva a resposta da inequação na forma: ,
.

Em terceiro lugar, o fato sobre o conjunto de raízes da desigualdade trigonométrica correspondente é muito claramente confirmado ao resolvê-lo graficamente.

Arroz. 6

É necessário demonstrar aos alunos que a bobina, que é a solução da inequação, se repete no mesmo intervalo, igual ao período da função trigonométrica. Você também pode considerar uma ilustração semelhante para o gráfico da função seno.

Em quarto lugar, é aconselhável realizar um trabalho de atualização dos métodos dos alunos de converter a soma (diferença) de funções trigonométricas em um produto, para chamar a atenção dos alunos para o papel dessas técnicas na resolução de desigualdades trigonométricas.

Tal trabalho pode ser organizado por meio do cumprimento independente pelos alunos das tarefas propostas pelo professor, dentre as quais destacamos as seguintes:

Quinto, os alunos devem ser solicitados a ilustrar a solução de cada inequação trigonométrica simples usando um gráfico ou um círculo trigonométrico. Certifique-se de prestar atenção à sua conveniência, especialmente ao uso de um círculo, pois ao resolver desigualdades trigonométricas, a ilustração correspondente serve como um meio muito conveniente de fixar o conjunto de soluções para uma determinada desigualdade

Conhecimento dos alunos com métodos para resolver desigualdades trigonométricas que não são as mais simples, é aconselhável realizar de acordo com o seguinte esquema: referindo-se a uma desigualdade trigonométrica específica referindo-se à equação trigonométrica correspondente busca conjunta (professor - alunos) para uma solução independente transferência da técnica encontrada para outras desigualdades do mesmo tipo.

Para sistematizar o conhecimento de trigonometria dos alunos, recomendamos selecionar especificamente tais desigualdades, cuja solução requer várias transformações que podem ser implementadas no processo de resolvê-la, concentrando a atenção dos alunos em suas características.

Como tais desigualdades produtivas, podemos propor, por exemplo, o seguinte:

Em conclusão, damos um exemplo de um conjunto de problemas para resolver desigualdades trigonométricas.

1. Resolva as desigualdades:

2. Resolva as desigualdades: 3. Encontre todas as soluções de inequações: 4. Encontre todas as soluções de inequações:

a)
, satisfazendo a condição
;

b)
, satisfazendo a condição
.

5. Encontre todas as soluções de inequações:

a) ;

b) ;

dentro)
;

G)
;

e)
.

6. Resolva as desigualdades:

a) ;

b) ;

dentro) ;

G)
;

e);

e);

e)
.

7. Resolva as desigualdades:

a)
;

b) ;

dentro) ;

G).

8. Resolva as desigualdades:

a) ;

b) ;

dentro) ;

G)
;

e)
;

e);

e)
;

h).

É aconselhável oferecer as tarefas 6 e 7 para alunos que estudam matemática em nível avançado, tarefa 8 - para alunos em aulas com estudo aprofundado de matemática.

§3. Métodos especiais para resolver desigualdades trigonométricas

Métodos especiais para resolver equações trigonométricas - isto é, aqueles métodos que só podem ser usados ​​para resolver equações trigonométricas. Esses métodos são baseados no uso das propriedades das funções trigonométricas, bem como no uso de várias fórmulas e identidades trigonométricas.

3.1. Método do Setor

Considere o método do setor para resolver desigualdades trigonométricas. Solução de inequações da forma

, OndeP ( x ) eQ ( x ) - funções trigonométricas racionais (senos, cossenos, tangentes e cotangentes entram nelas racionalmente), à ​​semelhança da solução de desigualdades racionais. É conveniente resolver desigualdades racionais pelo método dos intervalos no eixo real. Seu análogo na solução de desigualdades trigonométricas racionais é o método dos setores em um círculo trigonométrico, porsinx ecosx (
) ou um semicírculo trigonométrico paratgx ectgx (
).

No método intervalar, cada fator linear do numerador e denominador da forma
ponto no eixo numérico , e ao passar por este ponto
muda de sinal. No método do setor, cada multiplicador da forma
, Onde
- uma das funçõessinx oucosx e
, em um círculo trigonométrico correspondem dois ângulos e
, que dividem o círculo em dois setores. Ao passar por e função
muda de sinal.

O seguinte deve ser lembrado:

a) Multiplicadores da forma
e
, Onde
, retenha o sinal para todos os valores . Tais multiplicadores do numerador e denominador são descartados, mudando (se
) para cada rejeição, o sinal de desigualdade é invertido.

b) Multiplicadores da forma
e
também são descartados. Além disso, se estes são fatores do denominador, então as desigualdades da forma são adicionadas ao sistema equivalente de desigualdades
e
. Se estes são fatores do numerador, então no sistema equivalente de restrições eles correspondem às desigualdades
e
no caso de desigualdade inicial estrita, e igualdade
e
no caso de uma desigualdade inicial não estrita. Ao soltar o multiplicador
ou
o sinal de desigualdade é invertido.

Exemplo 1 Resolva as inequações: a)
, b)
. temos uma função, b). Resolva a desigualdade Temos

3.2. Método do círculo concêntrico

Este método é análogo ao método dos eixos numéricos paralelos na resolução de sistemas de desigualdades racionais.

Considere um exemplo de um sistema de desigualdades.

Exemplo 5 Resolver um sistema de inequações trigonométricas simples

Primeiro, resolvemos cada inequação separadamente (Figura 5). No canto superior direito da figura, indicaremos para qual argumento o círculo trigonométrico é considerado.

Fig.5

Em seguida, construímos um sistema de círculos concêntricos para o argumentoX . Desenhamos um círculo e sombreamos de acordo com a solução da primeira desigualdade, depois desenhamos um círculo de raio maior e sombreamos de acordo com a solução da segunda, depois construímos um círculo para a terceira desigualdade e um círculo de base . Desenhamos raios do centro do sistema até as extremidades dos arcos para que eles interceptem todos os círculos. Formamos uma solução no círculo base (Figura 6).

Fig.6

Responda:
,
.

Conclusão

Todos os objetivos do curso foram cumpridos. O material teórico é sistematizado: são apresentados os principais tipos de desigualdades trigonométricas e os principais métodos para sua solução (gráfico, algébrico, método dos intervalos, setoriais e método dos círculos concêntricos). Para cada método, foi dado um exemplo de resolução de uma inequação. A parte teórica foi seguida pela parte prática. Ele contém um conjunto de tarefas para resolver desigualdades trigonométricas.

Este curso pode ser usado pelos alunos para o trabalho independente. Os alunos podem verificar o nível de assimilação deste tópico, praticar na realização de tarefas de complexidade variável.

Tendo trabalhado na literatura relevante sobre este assunto, obviamente, podemos concluir que a capacidade e as habilidades para resolver desigualdades trigonométricas no curso escolar de álgebra e o início da análise são muito importantes, cujo desenvolvimento exige um esforço considerável por parte dos alunos. o professor de matemática.

Portanto, este trabalho será útil para professores de matemática, pois possibilita organizar efetivamente a formação dos alunos sobre o tema “Desigualdades trigonométricas”.

O estudo pode ser continuado expandindo-o para o trabalho de qualificação final.

Lista de literatura usada

Bogomolov, N. V. Coleção de problemas em matemática [Texto] / N.V. Bogomolov. – M.: Abetarda, 2009. – 206 p.

Vygodsky, M.Ya. Manual de matemática elementar [Texto] / M.Ya. Vygodsky. – M.: Abetarda, 2006. – 509 p.

Zhurbenko, L. N. Matemática em exemplos e tarefas [Texto] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.

Ivanov, O. A. Matemática elementar para alunos, alunos e professores [Texto] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.

Karp, A. P. Tarefas de álgebra e inícios de análise para a organização da repetição final e certificação no 11º ano [Texto] / A.P. Carpa. – M.: Iluminismo, 2005. – 79 p.

Kulanin, E. D. 3000 problemas competitivos em matemática [Texto] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.

Leibson, K. L. Coleção de tarefas práticas em matemática [Texto] / K.L. Leibson. – M.: Abetarda, 2010. – 182 p.

Cotovelo, V. V. Problemas com parâmetros e sua solução. Trigonometria: equações, desigualdades, sistemas. Grau 10 [Texto] / V.V. Cotovelo. – M.: ARKTI, 2008. – 64 p.

MANOVA, A. N. Matemáticas. Tutor expresso para se preparar para o exame: conta. subsídio [Texto] / A.N. Manova. - Rostov-on-Don: Phoenix, 2012. - 541 p.

Mordkovitch, A. G. Álgebra e início da análise matemática. 10-11 graus. Livro didático para alunos de instituições de ensino [Texto] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 p.

Novikov, A. I. Funções trigonométricas, equações e desigualdades [Texto] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 p.

Oganesyan, V. A. Métodos de ensino de matemática na escola secundária: Metodologia geral. Proc. bolsa para estudantes de física. - tapete. falso. ped. camarada. [Texto] / V.A. Oganesyan. – M.: Iluminismo, 2006. – 368 p.

Olechnik, S. N. Equações e desigualdades. Métodos de solução não padronizados [Texto] / S.N. Olekhnik. - M.: Editora Factorial, 1997. - 219 p.

Sevryukov, P.F. Equações e desigualdades trigonométricas, exponenciais e logarítmicas [Texto] / P.F. Sevryukov. – M.: Educação Nacional, 2008. – 352 p.

Sergeev, I. N. USO: 1000 tarefas com respostas e soluções em matemática. Todas as tarefas do grupo C [Texto] / I.N. Sergeev. – M.: Exame, 2012. – 301 p.

Sobolev, A. B. Matemática elementar [Texto] / A.B. Sobolev. - Ecaterimburgo: GOU VPO USTU-UPI, 2005. - 81 p.

Fenko, L. M. O método dos intervalos na resolução de inequações e no estudo de funções [Texto] / L.M. Fenko. – M.: Abetarda, 2005. – 124 p.

Friedman, L. M. Fundamentos teóricos da metodologia do ensino de matemática [Texto] / L.M. Friedman. - M.: Casa do livro "LIBROKOM", 2009. - 248 p.

Anexo 1

Interpretação gráfica de soluções para as desigualdades mais simples

Arroz. 1

Arroz. 2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Anexo 2

Soluções para as desigualdades mais simples

Na lição prática, repetiremos os principais tipos de tarefas do tópico "Trigonometria", analisaremos adicionalmente problemas de maior complexidade e consideraremos exemplos de resolução de várias desigualdades trigonométricas e seus sistemas.

Esta lição irá ajudá-lo a se preparar para um dos tipos de tarefas B5, B7, C1 e C3.

Vamos começar repetindo os principais tipos de tarefas que analisamos no tópico Trigonometria e resolvendo várias tarefas não padronizadas.

Tarefa nº 1. Converter ângulos em radianos e graus: a) ; b).

a) Use a fórmula para converter graus em radianos

Substitua o valor fornecido nele.

b) Aplique a fórmula para converter radianos em graus

Vamos fazer a substituição .

Responda. uma) ; b).

Tarefa nº 2. Calcule: a); b).

a) Como o ângulo está muito além da tabela, nós o reduzimos subtraindo o período do seno. Porque o ângulo é dado em radianos, então o período será considerado como .

b) Neste caso, a situação é semelhante. Como o ângulo é especificado em graus, consideraremos o período da tangente como .

O ângulo resultante, embora menor que o período, é maior, o que significa que não se refere mais à parte principal, mas à parte estendida da tabela. Para não treinar nossa memória mais uma vez memorizando uma tabela estendida de valores de função trigo, subtraímos o período tangente novamente:

Aproveitamos a estranheza da função tangente.

Responda. a) 1; b).

Tarefa nº 3. Calcular , E se .

Trazemos toda a expressão para tangentes dividindo o numerador e o denominador da fração por . Ao mesmo tempo, não podemos ter medo de que, porque neste caso, o valor da tangente não existiria.

Tarefa nº 4. Simplifique a expressão.

As expressões especificadas são convertidas usando fórmulas de conversão. É só que eles são escritos incomumente usando graus. A primeira expressão é geralmente um número. Simplifique todas as funções trigonométricas:

Porque , então a função muda para uma cofunção, ou seja, à cotangente, e o ângulo cai no segundo quarto, no qual o sinal da tangente original é negativo.

Pelas mesmas razões da expressão anterior, a função muda para uma cofunção, ou seja, à cotangente, e o ângulo cai no primeiro quarto, no qual a tangente inicial tem um sinal positivo.

Substituindo tudo em uma expressão simplificada:

Tarefa nº 5. Simplifique a expressão.

Vamos escrever a tangente do ângulo duplo de acordo com a fórmula correspondente e simplificar a expressão:

A última identidade é uma das fórmulas de substituição universal para cosseno.

Tarefa nº 6. Calcular .

O principal é não cometer um erro padrão e não responder que a expressão seja igual a . É impossível usar a propriedade principal da tangente do arco enquanto houver um fator na forma de dois próximo a ela. Para se livrar dele, escrevemos a expressão de acordo com a fórmula da tangente de um ângulo duplo, enquanto a tratamos como um argumento comum.

Agora já é possível aplicar a propriedade principal da tangente do arco, lembre-se que não há restrições quanto ao seu resultado numérico.

Tarefa nº 7. Resolva a equação.

Ao resolver uma equação fracionária que equivale a zero, é sempre indicado que o numerador é zero e o denominador não é, porque você não pode dividir por zero.

A primeira equação é um caso especial da equação mais simples, que é resolvida usando um círculo trigonométrico. Pense nessa solução você mesmo. A segunda desigualdade é resolvida como a equação mais simples usando a fórmula geral para as raízes da tangente, mas apenas com o sinal diferente.

Como podemos ver, uma família de raízes exclui outra exatamente da mesma família de raízes que não satisfaz a equação. Aqueles. não há raízes.

Responda. Não há raízes.

Tarefa nº 8. Resolva a equação.

Observe imediatamente que você pode tirar o fator comum e fazê-lo:

A equação foi reduzida a uma das formas padrão, quando o produto de vários fatores é igual a zero. Já sabemos que neste caso um deles é igual a zero, ou o outro, ou o terceiro. Escrevemos isso como um conjunto de equações:

As duas primeiras equações são casos especiais das mais simples, já encontramos equações semelhantes muitas vezes, por isso indicaremos imediatamente suas soluções. Reduzimos a terceira equação a uma função usando a fórmula de seno de ângulo duplo.

Vamos resolver a última equação separadamente:

Esta equação não tem raízes, porque o valor do seno não pode ir além .

Assim, apenas as duas primeiras famílias de raízes são a solução, elas podem ser combinadas em uma, o que é fácil de mostrar em um círculo trigonométrico:

Esta é uma família de todas as metades, ou seja,

Vamos passar para a resolução de desigualdades trigonométricas. Primeiro, vamos analisar a abordagem para resolver um exemplo sem usar fórmulas gerais de solução, mas com a ajuda de um círculo trigonométrico.

Tarefa nº 9. Resolva a desigualdade.

Desenhe uma linha auxiliar no círculo trigonométrico correspondente ao valor do seno igual a , e mostre o intervalo de ângulos que satisfazem a desigualdade.

É muito importante entender exatamente como especificar o intervalo de ângulo resultante, ou seja, qual é o seu começo e qual é o seu fim. O início da lacuna será o ângulo correspondente ao ponto em que entraremos no início da lacuna se nos movermos no sentido anti-horário. No nosso caso, este é o ponto que está à esquerda, porque movendo no sentido anti-horário e passando pelo ponto certo, ao contrário, saímos do intervalo de ângulo necessário. O ponto certo corresponderá, portanto, ao final do intervalo.

Agora precisamos entender os valores dos ângulos inicial e final da nossa lacuna de soluções para a desigualdade. Um erro típico é indicar imediatamente que o ponto direito corresponde ao ângulo , o esquerdo e dar a resposta. Isso não é verdade! Observe que acabamos de indicar o intervalo correspondente à parte superior do círculo, embora estejamos interessados ​​no inferior, ou seja, misturamos o início e o fim do intervalo de soluções que precisamos.

Para que o intervalo comece no canto do ponto direito e termine no canto do ponto esquerdo, o primeiro ângulo especificado deve ser menor que o segundo. Para fazer isso, teremos que medir o ângulo do ponto certo na direção de referência negativa, ou seja, no sentido horário e será igual a . Então, partindo dele no sentido horário positivo, chegaremos ao ponto direito após o ponto esquerdo e obteremos o valor do ângulo para ele. Agora, o início do intervalo de ângulos é menor que o final de , e podemos escrever o intervalo de soluções sem levar em conta o período:

Considerando que tais intervalos se repetirão um número infinito de vezes após qualquer número inteiro de rotações, obtemos a solução geral, levando em consideração o período do seno:

Colocamos colchetes porque a desigualdade é estrita e puncionamos os pontos do círculo que correspondem às extremidades do intervalo.

Compare sua resposta com a fórmula para a solução geral que demos na palestra.

Responda. .

Este método é bom para entender de onde vêm as fórmulas para soluções gerais das desigualdades trigonais mais simples. Além disso, é útil para quem tem preguiça de aprender todas essas fórmulas complicadas. No entanto, o método em si também não é fácil, escolha qual abordagem da solução é mais conveniente para você.

Para resolver desigualdades trigonométricas, você também pode usar os gráficos de funções nos quais a linha auxiliar é construída, de forma semelhante ao método mostrado usando o círculo unitário. Se você estiver interessado, tente entender essa abordagem para a solução por conta própria. A seguir, usaremos fórmulas gerais para resolver as desigualdades trigonométricas mais simples.

Tarefa nº 10. Resolva a desigualdade.

Usamos a fórmula geral da solução, levando em consideração que a desigualdade não é estrita:

Obtemos no nosso caso:

Responda.

Tarefa nº 11. Resolva a desigualdade.

Usamos a fórmula de solução geral para a desigualdade estrita correspondente:

Responda. .

Tarefa nº 12. Resolva as inequações: a) ; b).

Nessas desigualdades, não se deve se apressar em usar fórmulas para soluções gerais ou um círculo trigonométrico, basta lembrar o intervalo de valores de seno e cosseno.

a) Porque , então a desigualdade não tem sentido. Portanto, não há soluções.

b) Porque da mesma forma, o seno de qualquer argumento sempre satisfaz a desigualdade especificada na condição. Portanto, a desigualdade é satisfeita por todos os valores reais do argumento.

Responda. a) não há soluções; b).

Tarefa 13. Resolva a desigualdade .