Haverá também tarefas para uma solução independente, para as quais você poderá ver as respostas.

Conceito de vetor

Antes de aprender tudo sobre vetores e operações neles, sintonize para resolver um problema simples. Existe um vetor de sua empresa e um vetor de suas habilidades inovadoras. O vetor de empreendedorismo leva você ao Objetivo 1, e o vetor de habilidades inovadoras - ao Objetivo 2. As regras do jogo são tais que você não pode se mover na direção desses dois vetores ao mesmo tempo e atingir dois objetivos ao mesmo tempo. Vetores interagem, ou, falando matematicamente, alguma operação é realizada em vetores. O resultado dessa operação é o vetor "Resultado", que leva você ao Objetivo 3.

Agora me diga: o resultado de qual operação nos vetores "Empresa" e "Habilidades inovadoras" é o vetor "Resultado"? Se você não pode dizer imediatamente, não desanime. Ao estudar esta lição, você será capaz de responder a esta pergunta.

Como vimos acima, o vetor necessariamente vem de algum ponto UMA em linha reta até algum ponto B. Consequentemente, cada vetor tem não apenas um valor numérico - comprimento, mas também uma direção física e geométrica. A partir disso, a primeira definição mais simples de um vetor é derivada. Então, um vetor é um segmento direcionado que vai de um ponto UMA ao ponto B. Está marcado assim:

E para começar diferente operações vetoriais , precisamos nos familiarizar com mais uma definição de vetor.

Um vetor é um tipo de representação de um ponto a ser alcançado a partir de algum ponto de partida. Por exemplo, um vetor tridimensional geralmente é escrito como (x, y, z) . Simplificando, esses números representam a distância que você precisa percorrer em três direções diferentes para chegar ao ponto.

Seja dado um vetor. Em que x = 3 (a mão direita aponta para a direita) y = 1 (a mão esquerda aponta para a frente) z = 5 (sob o ponto há uma escada que leva para cima). A partir desses dados, você encontrará o ponto caminhando 3 metros na direção indicada pela mão direita, depois 1 metro na direção indicada pela mão esquerda, e então uma escada espera por você e, subindo 5 metros, você finalmente encontrará você mesmo no ponto final.

Todos os outros termos são refinamentos da explicação apresentada acima, necessários para várias operações em vetores, ou seja, para resolver problemas práticos. Vamos passar por essas definições mais rigorosas, nos concentrando em problemas vetoriais típicos.

Exemplos físicos quantidades vetoriais podem ser o deslocamento de um ponto material em movimento no espaço, a velocidade e a aceleração desse ponto, bem como a força que atua sobre ele.

vetor geométrico representado no espaço bidimensional e tridimensional na forma segmento direcionado. Este é um segmento que tem um começo e um fim.

Se um UMAé o início do vetor, e Bé o seu fim, então o vetor é denotado pelo símbolo ou por uma única letra minúscula . Na figura, o final do vetor é indicado por uma seta (Fig. 1)

Comprimento(ou módulo) de um vetor geométrico é o comprimento do segmento que o gera

Os dois vetores são chamados igual , se eles podem ser combinados (quando as direções coincidem) por translação paralela, ou seja, se eles são paralelos, apontam na mesma direção e têm comprimentos iguais.

Em física, muitas vezes é considerado vetores fixados, dado pelo ponto de aplicação, comprimento e direção. Se o ponto de aplicação do vetor não importa, então ele pode ser transferido, mantendo o comprimento e a direção para qualquer ponto no espaço. Neste caso, o vetor é chamado gratuitamente. Concordamos em considerar apenas vetores livres.

Operações lineares em vetores geométricos

Multiplicar um vetor por um número

Produto vetorial por número Um vetor é chamado de vetor obtido de um vetor esticando (at ) ou encolhendo (at ) vezes, e a direção do vetor é preservada se , e invertida se . (Figura 2)

Segue-se da definição que os vetores e = estão sempre localizados em uma ou em linhas paralelas. Esses vetores são chamados colinear. (Você também pode dizer que esses vetores são paralelos, mas em álgebra vetorial costuma-se dizer "colinear".) A recíproca também é verdadeira: se os vetores e são colineares, então eles estão relacionados pela relação

Portanto, a igualdade (1) expressa a condição de colinearidade de dois vetores.

Adição e subtração de vetores

Ao adicionar vetores, você precisa saber que soma vetores e é chamado de vetor cujo início coincide com o início do vetor , e o final coincide com o final do vetor , desde que o início do vetor esteja ligado ao final do vetor . (Fig. 3)

Esta definição pode ser distribuída por qualquer número finito de vetores. Deixe no espaço dado n vetores livres. Ao adicionar vários vetores, sua soma é tomada como vetor de fechamento, cujo início coincide com o início do primeiro vetor e o final com o final do último vetor. Ou seja, se o início do vetor estiver ligado ao final do vetor e o início do vetor ao final do vetor, etc. e, finalmente, até o final do vetor - o início do vetor, então a soma desses vetores é o vetor de fechamento , cujo início coincide com o início do primeiro vetor, e cujo final coincide com o final do último vetor. (Fig. 4)

Os termos são chamados de componentes do vetor, e a regra formulada é regra do polígono. Este polígono pode não ser plano.

Quando um vetor é multiplicado pelo número -1, o vetor oposto é obtido. Os vetores e têm o mesmo comprimento e direções opostas. Sua soma dá vetor nulo, cujo comprimento é zero. A direção do vetor nulo não está definida.

Em álgebra vetorial, não há necessidade de considerar a operação de subtração separadamente: subtrair um vetor de um vetor significa adicionar o vetor oposto ao vetor, ou seja,

Exemplo 1 Simplifique a expressão:

.

,

ou seja, vetores podem ser somados e multiplicados por números da mesma forma que polinômios (em particular, também problemas para simplificar expressões). Normalmente, surge a necessidade de simplificar expressões linearmente semelhantes com vetores antes de calcular os produtos de vetores.

Exemplo 2 Os vetores e servem como diagonais do paralelogramo ABCD (Fig. 4a). Expresse em termos de e os vetores , , e , que são os lados desse paralelogramo.

Solução. O ponto de interseção das diagonais de um paralelogramo corta cada diagonal. Os comprimentos dos vetores requeridos na condição do problema são encontrados ou como metade das somas dos vetores que formam um triângulo com os desejados, ou como metade das diferenças (dependendo da direção do vetor servindo como diagonal), ou, como neste último caso, metade da soma tomada com um sinal de menos. O resultado são os vetores necessários na condição do problema:

Há todos os motivos para acreditar que agora você respondeu corretamente à pergunta sobre os vetores "Empresa" e "Habilidades inovadoras" no início desta lição. Resposta correta: esses vetores são submetidos a uma operação de adição.

Resolva problemas em vetores por conta própria e, em seguida, veja as soluções

Como encontrar o comprimento da soma dos vetores?

Este problema ocupa um lugar especial nas operações com vetores, pois envolve o uso de propriedades trigonométricas. Digamos que você tenha uma tarefa como a seguinte:

Dado o comprimento dos vetores e o comprimento da soma desses vetores. Encontre o comprimento da diferença desses vetores.

Soluções para este e outros problemas semelhantes e explicações de como resolvê-los - na lição " Adição vetorial: o comprimento da soma dos vetores e o teorema do cosseno ".

E você pode conferir a solução de tais problemas em Calculadora online "Lado desconhecido de um triângulo (adição vetorial e teorema do cosseno)" .

Onde estão os produtos dos vetores?

Os produtos de um vetor por um vetor não são operações lineares e são considerados separadamente. E temos as aulas "Produto escalar de vetores" e "Vetor e produto misto de vetores".

Projeção de um vetor em um eixo

A projeção de um vetor sobre um eixo é igual ao produto do comprimento do vetor projetado pelo cosseno do ângulo entre o vetor e o eixo:

Como se sabe, a projeção de um ponto UMA na linha (plano) é a base da perpendicular baixada deste ponto para a linha (plano).

Seja - um vetor arbitrário (Fig. 5), e e - projeções de seu início (pontos UMA) e fim (pontos B) por eixo eu. (Para construir a projeção de um ponto UMA) desenhar direto pelo ponto UMA plano perpendicular à linha. A interseção de uma linha e um plano determinará a projeção necessária.

Componente do vetor no eixo l chamado tal vetor situado neste eixo, cujo início coincide com a projeção do início e o fim - com a projeção do final do vetor .

A projeção do vetor no eixo eu chamou um número

,

igual ao comprimento do vetor componente neste eixo, tomado com um sinal de mais se a direção do componente coincidir com a direção do eixo eu, e com um sinal de menos se essas direções forem opostas.

As principais propriedades das projeções vetoriais no eixo:

1. As projeções de vetores iguais no mesmo eixo são iguais entre si.

2. Quando um vetor é multiplicado por um número, sua projeção é multiplicada pelo mesmo número.

3. A projeção da soma dos vetores em qualquer eixo é igual à soma das projeções no mesmo eixo dos termos dos vetores.

4. A projeção de um vetor sobre um eixo é igual ao produto do comprimento do vetor projetado e o cosseno do ângulo entre o vetor e o eixo:

.

Solução. Vamos projetar os vetores no eixo eu conforme definido no referencial teórico acima. Da Fig.5a é óbvio que a projeção da soma dos vetores é igual à soma das projeções dos vetores. Calculamos essas projeções:

Encontramos a projeção final da soma dos vetores:

Relação de um vetor com um sistema de coordenadas cartesianas retangulares no espaço

Conhecimento com sistema de coordenadas cartesianas retangulares no espaço ocorreu na lição correspondente, de preferência abra-o em uma nova janela.

Em um sistema ordenado de eixos coordenados 0xyz eixo Boi chamado eixo x, eixo 0 ano – eixo y, e eixo 0z – aplicar eixo.

com ponto arbitrário M vetor de empate espacial

chamado vetor de raio pontos M e projetá-lo em cada um dos eixos coordenados. Vamos denotar os valores das projeções correspondentes:

Números x, y, z chamado coordenadas do ponto M, respectivamente abscissa, ordenado e aplique, e são escritos como um ponto ordenado de números: M(x; y; z)(Fig. 6).

Um vetor de comprimento unitário cuja direção coincide com a direção do eixo é chamado vetor de unidade(ou ortom) machados. Denotado por

Assim, os vetores unitários dos eixos coordenados Boi, Oi, Oz

Teorema. Qualquer vetor pode ser decomposto nos vetores unitários dos eixos coordenados:

(2)

A igualdade (2) é chamada de expansão do vetor ao longo dos eixos coordenados. Os coeficientes dessa expansão são as projeções do vetor sobre os eixos coordenados. Assim, os coeficientes de expansão (2) do vetor ao longo dos eixos coordenados são as coordenadas do vetor.

Depois de escolher um certo sistema de coordenadas no espaço, o vetor e o triplo de suas coordenadas se determinam de forma única, de modo que o vetor pode ser escrito na forma

As representações vetoriais na forma (2) e (3) são idênticas.

A condição de vetores colineares em coordenadas

Como já observamos, os vetores são chamados colineares se estiverem relacionados pela relação

Deixar vetores . Esses vetores são colineares se as coordenadas dos vetores estão relacionadas pela relação

,

ou seja, as coordenadas dos vetores são proporcionais.

Exemplo 6 Vetores dados . Esses vetores são colineares?

Solução. Vamos descobrir a razão entre as coordenadas desses vetores:

.

As coordenadas dos vetores são proporcionais, portanto, os vetores são colineares, ou, o que dá no mesmo, paralelos.

Cossenos de comprimento e direção do vetor

Devido à perpendicularidade mútua dos eixos coordenados, o comprimento do vetor

é igual ao comprimento da diagonal de um paralelepípedo retangular construído sobre os vetores

e é expresso pela igualdade

(4)

Um vetor é completamente definido especificando dois pontos (início e fim), de modo que as coordenadas do vetor podem ser expressas em termos das coordenadas desses pontos.

Seja o início do vetor no sistema de coordenadas dado no ponto

e o fim está no ponto

Da igualdade

Segue isso

ou em forma coordenada

Consequentemente, as coordenadas do vetor são iguais às diferenças das coordenadas de mesmo nome do final e início do vetor . A fórmula (4) neste caso assume a forma

A direção do vetor é determinada cossenos de direção . Estes são os cossenos dos ângulos que o vetor faz com os eixos Boi, Oi e Oz. Vamos designar esses ângulos respectivamente α , β e γ . Então os cossenos desses ângulos podem ser encontrados pelas fórmulas

Os cossenos de direção de um vetor também são as coordenadas do vetor do vetor e, portanto, o vetor do vetor

.

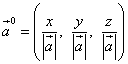
Considerando que o comprimento do vetor vetor é igual a uma unidade, ou seja,

,

obtemos a seguinte igualdade para os cossenos de direção:

Exemplo 7 Encontre o comprimento de um vetor x = (3; 0; 4).

Solução. O comprimento do vetor é

Exemplo 8 Pontos dados:

Descubra se o triângulo construído sobre esses pontos é isósceles.

Solução. Usando a fórmula do comprimento vetorial (6), encontramos os comprimentos dos lados e descobrimos se há dois deles iguais:

Dois lados iguais foram encontrados, então não há necessidade de procurar o comprimento do terceiro lado, e o triângulo dado é isósceles.

Exemplo 9 Encontre o comprimento de um vetor e seus cossenos de direção se .

Solução. As coordenadas vetoriais são dadas:

.

O comprimento do vetor é igual à raiz quadrada da soma dos quadrados das coordenadas do vetor:

.

Encontrando cossenos de direção:

Resolva o problema em vetores você mesmo e, em seguida, veja a solução

Operações em vetores dados em forma de coordenadas

Sejam dois vetores e dados por suas projeções:

Vamos indicar ações nesses vetores.

Pagina 1 de 2

Questão 1. O que é um vetor? Como os vetores são definidos?
Responda. Chamaremos um segmento direcionado de vetor (Fig. 211). A direção de um vetor é determinada especificando seu início e fim. No desenho, a direção do vetor é marcada com uma seta. Para designar vetores, usaremos letras latinas minúsculas a, b, c, ... . Você também pode designar um vetor especificando seu início e fim. Neste caso, o início do vetor é colocado em primeiro lugar. Em vez da palavra "vetor", às vezes é colocada uma seta ou um traço acima da designação da letra do vetor. O vetor na figura 211 pode ser denotado da seguinte forma:

\(\overline(a)\), \(\overrightarrow(a)\) ou \(\overline(AB)\), \(\overrightarrow(AB)\).

Questão 2. Que vetores são chamados igualmente direcionados (direcionados opostamente)?
Responda. Os vetores \(\overline(AB)\) e \(\overline(CD)\) são igualmente direcionados se as meias-linhas AB e CD forem igualmente direcionadas.
Os vetores \(\overline(AB)\) e \(\overline(CD)\) são chamados de direção oposta se as meias-linhas AB e CD forem de direção oposta.
Na Figura 212, os vetores \(\overline(a)\) e \(\overline(b)\) têm a mesma direção, enquanto os vetores \(\overline(a)\) e \(\overline(c) \) têm direções opostas.

Questão 3. Qual é o valor absoluto de um vetor?
Responda. O valor absoluto (ou módulo) de um vetor é o comprimento do segmento que representa o vetor. O valor absoluto do vetor \(\overline(a)\) é denotado por |\(\overline(a)\)|.

Pergunta 4. O que é um vetor nulo?
Responda. O início de um vetor pode coincidir com o seu fim. Tal vetor será chamado de vetor zero. O vetor zero é denotado por zero com um traço (\(\overline(0)\)). Ninguém fala sobre a direção do vetor zero. O valor absoluto do vetor zero é considerado igual a zero.

Pergunta 5. Que vetores são chamados iguais?
Responda. Dois vetores são ditos iguais se forem combinados por uma translação paralela. Isso significa que há uma translação paralela que move o início e o fim de um vetor para o início e o fim de outro vetor, respectivamente.

Pergunta 6. Prove que vetores iguais têm a mesma direção e são iguais em valor absoluto. E vice-versa: vetores igualmente direcionados que são iguais em valor absoluto são iguais.
Responda. Com a tradução paralela, o vetor mantém sua direção, bem como seu valor absoluto. Isso significa que vetores iguais têm a mesma direção e são iguais em valor absoluto.
Sejam \(\overline(AB)\) e \(\overline(CD)\) vetores igualmente direcionados iguais em valor absoluto (Fig. 213). Uma translação paralela que leva o ponto C ao ponto A combina meia linha CD com meia linha AB, uma vez que são igualmente direcionadas. E como os segmentos AB e CD são iguais, então o ponto D coincide com o ponto B, ou seja. a tradução paralela converte o vetor \(\overline(CD)\) no vetor \(\overline(AB)\). Portanto, os vetores \(\overline(AB)\) e \(\overline(CD)\) são iguais, conforme necessário.

Pergunta 7. Prove que de qualquer ponto pode-se desenhar um vetor igual ao vetor dado, e apenas um.
Responda. Seja CD uma linha e o vetor \(\overline(CD)\) uma parte da linha CD. Seja AB a linha na qual a linha CD vai durante a tradução paralela, \(\overline(AB)\) o vetor no qual o vetor \(\overline(CD)\) entra durante a tradução paralela e, portanto, os vetores \(\overline(AB)\) e \(\overline(CD)\) são iguais, e as linhas AB e CD são paralelas (veja a Fig. 213). Como sabemos, através de um ponto que não está em uma linha dada, é possível desenhar no plano no máximo uma linha paralela à dada (o axioma das linhas paralelas). Assim, através do ponto A pode-se traçar uma linha paralela à linha CD. Como o vetor \(\overline(AB)\) faz parte da reta AB, é possível traçar um vetor \(\overline(AB)\) passando pelo ponto A, que é igual ao vetor \(\overline (CD)\).

Pergunta 8. O que são coordenadas vetoriais? Qual é o valor absoluto do vetor com coordenadas a 1 , a 2 ?
Responda. Deixe o vetor \(\overline(a)\) começar no ponto A 1 (x 1 ; y 1) e terminar no ponto A 2 (x 2 ; y 2). As coordenadas do vetor \(\overline(a)\) serão os números a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . Vamos colocar as coordenadas do vetor ao lado da letra de designação do vetor, neste caso \(\overline(a)\) (a 1 ; a 2) ou apenas \((\overline(a 1 ; a 2 ))\ ). As coordenadas do vetor zero são iguais a zero.
Da fórmula que expressa a distância entre dois pontos em termos de suas coordenadas, segue-se que o valor absoluto do vetor com coordenadas a 1 , a 2 é \(\sqrt(a^2 1 + a^2 2 )\).

Pergunta 9. Prove que vetores iguais têm coordenadas respectivamente iguais e que vetores com coordenadas respectivamente iguais são iguais.
Responda. Sejam A 1 (x 1 ; y 1) e A 2 (x 2 ; y 2) o início e o fim do vetor \(\overline(a)\). Como o vetor \(\overline(a")\) igual a ele é obtido do vetor \(\overline(a)\) por tradução paralela, então seu início e fim serão respectivamente A" 1 (x 1 + c ; y 1 + d ), A" 2 (x 2 + c; y 2 ​​​​+ d). Isso mostra que ambos os vetores \(\overline(a)\) e \(\overline(a")\) têm as mesmas coordenadas: x 2 - x 1 , y 2 - y 1 .
Vamos agora provar a afirmação inversa. Sejam iguais as coordenadas correspondentes dos vetores \(\overline(A 1 A 2 )\) e \(\overline(A" 1 A" 2 )\). Provamos que os vetores são iguais.
Sejam x" 1 e y" 1 as coordenadas do ponto A" 1 e x" 2, y" 2 as coordenadas do ponto A" 2. Pela condição do teorema x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. Portanto, x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Tradução paralela dada por fórmulas

x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,

transfere o ponto A 1 para o ponto A" 1 e o ponto A 2 para o ponto A" 2 , ou seja, os vetores \(\overline(A 1 A 2 )\) e \(\overline(A" 1 A" 2 )\) são iguais, conforme necessário.

Pergunta 10. Defina a soma dos vetores.
Responda. A soma dos vetores \(\overline(a)\) e \(\overline(b)\) com as coordenadas a 1 , a 2 e b 1 , b 2 é o vetor \(\overline(c)\) com coordena a 1 + b 1 , a 2 + b a 2 , i.e.

\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).

Data de criação: 2009-04-11 15:25:51
Última edição: 2012-02-08 09:19:45

Por muito tempo eu não quis escrever este artigo - pensei em como apresentar o material. Você também precisa fazer desenhos. Mas, aparentemente, as estrelas se formaram com sucesso hoje e haverá um artigo sobre vetores. Embora, este seja apenas um rascunho. No futuro, dividirei este artigo em vários separados - há material suficiente. Além disso, o artigo melhorará gradualmente: farei alterações nele - porque. de uma só vez não será possível revelar todos os aspectos.

Os vetores foram introduzidos na matemática no século XIX para descrever quantidades que eram difíceis de descrever usando valores escalares.

Vetores são muito usados ​​no desenvolvimento de jogos de computador. Eles são usados ​​não apenas tradicionalmente - para descrever quantidades como força ou velocidade, mas também em áreas que parecem não ter nada a ver com vetores: armazenamento de cores, criação de sombras.

Escalares e vetores

Primeiro, deixe-me lembrá-lo o que é um escalar e como ele difere de um vetor.

Valores escalares armazenam algum valor: massa, volume. Ou seja, é uma entidade que se caracteriza por apenas um número (por exemplo, a quantidade de algo).

Um vetor, ao contrário de um escalar, é descrito usando dois valores: magnitude e direção.

Uma diferença importante entre vetores e coordenadas: os vetores não estão vinculados a um local específico! Mais uma vez, o principal em um vetor é o comprimento e a direção.

Um vetor é indicado por uma letra em negrito do alfabeto latino. Por exemplo: uma, b, v.

Na primeira figura, você pode ver como o vetor é denotado no plano.

Vetores no espaço

No espaço, os vetores podem ser expressos usando coordenadas. Mas primeiro precisamos introduzir um conceito:

Vetor de raio do ponto

Vamos tomar algum ponto M(2,1) no espaço. O vetor raio de um ponto é um vetor que começa na origem e termina no ponto.

O que temos aqui nada mais é do que um vetor OM. Coordenadas de início do vetor (0,0), coordenadas finais (2,1). Vamos denotar este vetor como uma.

Neste caso, o vetor pode ser escrito da seguinte forma uma = <2, 1>. Esta é a forma coordenada do vetor uma.

As coordenadas de um vetor são chamadas de seus componentes relativos aos eixos. Por exemplo, 2 é um componente vetorial uma sobre o eixo x.

Vamos mais uma vez nos debruçar sobre quais são as coordenadas de um ponto. A coordenada de um ponto (por exemplo, x) é a projeção do ponto no eixo, ou seja, a base de uma perpendicular baixada de um ponto a um eixo. Em nosso exemplo 2.

Mas voltando à primeira foto. Aqui temos dois pontos A e B. Sejam as coordenadas dos pontos (1,1) e (3,3). Vetor v neste caso pode ser definido como v = <3-1, 3-1>. Um vetor situado em dois pontos no espaço tridimensional terá a seguinte aparência:

v =

Acho que não há problemas aqui.

Multiplicar um vetor por um escalar

Um vetor pode ser multiplicado por valores escalares:

k v = =

Neste caso, o valor escalar é multiplicado por cada componente do vetor.

Se k > 1, o vetor aumentará, se k for menor que um, mas maior que zero, o vetor diminuirá em comprimento. Se k for menor que zero, então o vetor mudará de direção.

Vetores de unidade

Os vetores unitários são vetores cujo comprimento é igual a um. Observe que o vetor com coordenadas<1,1,1>não será igual a um! Encontrar o comprimento de um vetor é descrito abaixo.

Existem os chamados orts - são vetores unitários que coincidem em direção com os eixos coordenados. eu- vetor unitário do eixo x, j- vetor unitário do eixo y, k- vetor unitário do eixo z.

Em que eu = <1,0,0>, j = <0,1,0>, k = <0,0,1>.

Agora sabemos o que é a multiplicação de um vetor por um escalar e o que são vetores unitários. Agora podemos escrever v em forma de vetor.

v= vx eu+vy j+vz k, onde v x , v y , v z são os componentes correspondentes do vetor

Adição de vetor

Para entender completamente a fórmula anterior, você precisa entender como funciona a adição de vetores.

Tudo é simples aqui. Pegue dois vetores v1 = e v2 =

v1 + v2 =

Acabamos de somar os componentes correspondentes dos dois vetores.

A diferença é calculada da mesma forma.

É sobre a forma matemática. Por uma questão de completude, vale a pena considerar como a adição e a subtração de vetores ficariam graficamente.

Para adicionar dois vetores uma+b. Precisamos combinar o início do vetor b e o final do vetor uma. Então, entre o início do vetor uma e o final do vetor b desenhe um novo vetor. Para maior clareza, veja a segunda figura (letra "a").

Para subtrair vetores, você precisa combinar o início de dois vetores e desenhar um novo vetor do final do segundo vetor até o final do primeiro. A segunda foto (letra "b") mostra como é.

Comprimento e direção do vetor

Vejamos primeiro o comprimento.

Comprimento é o valor numérico do vetor, independentemente da direção.

O comprimento é determinado pela fórmula (para um vetor tridimensional):

a raiz quadrada da soma dos quadrados dos componentes do vetor.

Fórmula familiar, não é? Em geral, esta é a fórmula para o comprimento de um segmento

A direção do vetor é determinada pelos cossenos de direção dos ângulos formados entre o vetor e os eixos coordenados. Para encontrar os cossenos de direção, os componentes e o comprimento apropriados são usados ​​(a imagem será mais tarde).

Representando vetores em programas

Os vetores podem ser representados em programas de várias maneiras. Tanto com a ajuda de variáveis ​​comuns, o que é ineficiente, quanto com a ajuda de arrays, classes e estruturas.

vetor flutuante3 = (1,2,3); // array para armazenar vetor struct vector3 // estrutura para armazenar vetores ( float x,y,z; );

As maiores possibilidades para armazenar vetores são fornecidas por classes. Nas classes, podemos descrever não apenas o próprio vetor (variáveis), mas também as operações vetoriais (funções).

Produto escalar de vetores

Existem dois tipos de multiplicação vetorial: vetorial e escalar.

Uma característica distintiva do produto escalar é que o resultado será sempre um valor escalar, ou seja, número.

Aqui vale a pena prestar atenção a este momento. Se o resultado desta operação for zero, então os dois vetores são perpendiculares - o ângulo entre eles é de 90 graus. Se o resultado for maior que zero, o ângulo é menor que 90 graus. Se o resultado for menor que zero, o ângulo é maior que 90 graus.

Esta operação é representada pela seguinte fórmula:

uma · b= a x * b x + a y * b y + a z * b z

O produto escalar é a soma dos produtos das componentes correspondentes de dois vetores. Aqueles. Pegamos x "s de dois vetores, multiplicamos, depois os somamos ao produto de y" s e assim por diante.

Produto cruzado de vetores

O resultado do produto vetorial de dois vetores será um vetor perpendicular a esses vetores.

uma x b =

Não discutiremos essa fórmula em detalhes ainda. Além disso, é muito difícil de lembrar. Voltaremos a este ponto depois de nos familiarizarmos com os determinantes.

Bem, para o desenvolvimento geral, é útil saber que o comprimento do vetor resultante é igual à área do paralelogramo construído em vetores uma e b.

Normalização vetorial

Um vetor normalizado é um vetor cujo comprimento é um.

A fórmula para encontrar um vetor normalizado é a seguinte - todos os componentes do vetor devem ser divididos por seu comprimento:

v n= v/|v| =

Posfácio

Como você provavelmente já viu, os vetores não são difíceis de entender. Consideramos uma série de operações em vetores.

Nos próximos artigos da seção "matemática", discutiremos matrizes, determinantes, sistemas de equações lineares. É tudo teoria.

Depois disso, veremos as transformações de matrizes. É então que você entenderá a importância da matemática na criação de jogos de computador. Este tópico se tornará apenas uma prática para todos os tópicos anteriores.

VETORES. AÇÕESACIMA DEVETORES. ESCALAR,

VETOR, PRODUTO MISTURADO DE VETORES.

1. VETORES, AÇÕES SOBRE VETORES.

Definições básicas.

Definição 1. Uma quantidade que é totalmente caracterizada por seu valor numérico no sistema de unidades escolhido é chamada escalar ou escalar .

(peso corporal, volume, tempo, etc.)

Definição 2. Uma quantidade caracterizada por um valor numérico e direção é chamada vetor ou vetor .

(Deslocamento, força, velocidade, etc.)

Designações: , ou , .

Um vetor geométrico é um segmento direcionado.

Para vetor - ponto MAS- ponto de partida NOé o fim do vetor.

Definição 3.Módulo vetor é o comprimento do segmento AB.

Definição 4. Um vetor cujo módulo é zero é chamado zero , é indicado.

Definição 5. Vetores localizados em linhas paralelas ou na mesma linha são chamados colinear . Se dois vetores colineares têm a mesma direção, então eles são chamados co-direcional .

Definição 6. Dois vetores são considerados igual , se eles co-dirigido e são iguais em módulo.

Ações em vetores.

1) Adição de vetores.

Def. 6.soma dois vetores e é a diagonal do paralelogramo construído sobre esses vetores, vindo de um ponto comum de sua aplicação (regra do paralelogramo).

Figura 1.

Def. 7. A soma de três vetores , , é a diagonal do paralelepípedo construído sobre esses vetores (regra do paralelepípedo).

Def. oito. Se um MAS, NO, A PARTIR DE são pontos arbitrários, então + = (regra do triângulo).

Figura 2

Propriedades de adição.

1 cerca de . + = + (lei de deslocamento).

2 cerca de . + ( + ) = ( + ) + = ( + ) + (lei associativa).

3 cerca de . + (– ) + .

2) Subtração de vetores.

Def. 9. Debaixo diferença vetores e entenda o vetor = - tal que + = .

Em um paralelogramo, este é outro diagonal SD (ver fig. 1).

3) Multiplicação de um vetor por um número.

Def. dez. trabalhar vetor para escalar k chamado vetor

= k = k ,

grandes ka , e direção, que:

1. coincide com a direção do vetor se k > 0;

2. oposto à direção do vetor se k < 0;

3. arbitrariamente se k = 0.

Propriedades da multiplicação de um vetor por um número.

1 cerca de . (k + eu ) = k + eu .

k ( + ) = k + k .

2 o . k (eu ) = (kl ) .

3 o . 1  = , (–1)  = – , 0  = .

Propriedades do vetor.

Def. onze. Dois vetores e são chamados colinear se estiverem localizados linhas paralelas ou em uma linha reta.

O vetor zero é colinear a qualquer vetor.

Teorema 1. Dois vetores diferentes de zero e colinear,  quando são proporcionais, ou seja.

= k , k - escalar.

Def. 12. Três vetores , , são chamados coplanar se eles são paralelos a algum plano ou estão nele.

Teorema 2. Três vetores diferentes de zero , , coplanar,  quando um deles é uma combinação linear dos outros dois, ou seja,

= k + eu , k , eu - escalares.

Projeção de um vetor em um eixo.

Teorema 3. Projeção de um vetor em um eixo (linha direcionada) eué igual ao produto do comprimento do vetor pelo cosseno do ângulo entre a direção do vetor e a direção do eixo, ou seja. = uma  c SO  ,  = ( , eu).

2. COORDENADAS VETORIAIS

Def. 13. Projeções vetoriais em eixos de coordenadas Oh, UO, Oz chamado coordenadas vetoriais. Designação:  uma x , uma y , uma z .

Comprimento do vetor:

Exemplo: Calcule o comprimento do vetor .

Solução:

Distância entre pontos e calculado pela fórmula: .

Exemplo: Encontre a distância entre os pontos M (2,3,-1) e K (4,5,2).

Ações sobre vetores em forma de coordenadas.

Dados vetores = uma x , uma y , uma z e = b x , b y , b z .

1. (  )= uma x  b x , uma y  b y , uma z  b z .

2.  =   uma x ,  uma y ,  uma z, onde  - escalar.

Produto escalar de vetores.

Definição: Sob o produto escalar de dois vetores e

é entendido como um número igual ao produto dos comprimentos desses vetores e o cosseno do ângulo entre eles, ou seja, = , - ângulo entre vetores e .

Propriedades do produto escalar:

1.  =

2. ( + ) =

3.

4.

5. , onde são escalares.

6. dois vetores são perpendiculares (ortogonais) se .

7. se e somente se .

O produto escalar na forma de coordenadas tem a forma: , onde e .

Exemplo: Encontre o produto escalar de vetores e

Solução:

Vetor segurando vetores.

Definição: O produto vetorial de dois vetores e é entendido como um vetor para o qual:

O módulo é igual à área do paralelogramo construído sobre esses vetores, ou seja, , onde é o ângulo entre os vetores e

Este vetor é perpendicular aos vetores multiplicados, ou seja,

Se os vetores são não colineares, então eles formam um triplo direito de vetores.

Propriedades de produtos cruzados:

1. Quando a ordem dos fatores é alterada, o produto vetorial muda seu sinal para o contrário, preservando o módulo, ou seja

2 .O quadrado do vetor é igual ao vetor zero, ou seja.

3 .O fator escalar pode ser retirado do sinal do produto vetorial, ou seja.

4 . Para quaisquer três vetores, a igualdade

5 .Condição necessária e suficiente para a colinearidade de dois vetores e:

Produto vetorial em forma de coordenadas.

Se as coordenadas dos vetores e , então seu produto vetorial é encontrado pela fórmula:

.

Então, da definição de um produto vetorial, segue-se que a área de um paralelogramo é construída sobre vetores e é calculada pela fórmula:

Exemplo: Calcule a área de um triângulo com vértices (1;-1;2), (5;-6;2), (1;3;-1).

Solução: .

Então a área do triângulo ABC será calculada da seguinte forma:

,

Produto misto de vetores.

Definição: Um produto misto (vetor-escalar) de vetores é um número determinado pela fórmula: .

Propriedades do produto misto:

1. O produto misto não muda com uma permutação cíclica de seus fatores, ou seja, .

2. Quando dois fatores vizinhos são trocados, o produto misto muda seu sinal para o oposto, ou seja, .

3 . Condição necessária e suficiente para que três vetores sejam coplanares : =0.

4 .O produto misto de três vetores é igual ao volume do paralelepípedo construído sobre esses vetores, tomado com sinal de mais se esses vetores formarem um triplo à direita e com sinal de menos se formarem um triplo à esquerda, ou seja, .

Se conhecido coordenadas vetores , então o produto misto é encontrado pela fórmula:

Exemplo: Calcule o produto misto de vetores.

Solução:

3. Base do sistema de vetores.

Definição. Um sistema de vetores é entendido como vários vetores pertencentes ao mesmo espaço R.

Comente. Se o sistema consiste em um número finito de vetores, eles são denotados pela mesma letra com índices diferentes.

Exemplo.

Definição. Qualquer vetor da forma = é chamada de combinação linear de vetores. Os números são os coeficientes da combinação linear.

Exemplo. .

Definição. Se o vetor é uma combinação linear de vetores , então dizemos que o vetor é expresso linearmente em termos dos vetores .

Definição. O sistema de vetores é chamado Linearmente independente, se nenhum dos vetores do sistema pode ser uma combinação linear do resto dos vetores. Caso contrário, o sistema é chamado linearmente dependente.

Exemplo. Sistema vetorial linearmente dependente, uma vez que o vetor .

Definição de base. Um sistema de vetores forma uma base se:

1) é linearmente independente,

2) qualquer vetor de espaço através dele é expresso linearmente.

Exemplo 1 Base espacial: .

2. No sistema de vetores vetores são a base: , porque expresso linearmente em termos de vetores.

Comente. Para encontrar a base de um determinado sistema de vetores, você precisa:

1) escreva as coordenadas dos vetores na matriz,

2) usando transformações elementares, traga a matriz para uma forma triangular,

3) linhas diferentes de zero da matriz serão a base do sistema,

4) o número de vetores na base é igual ao posto da matriz.

DEFINIÇÃO

Vetor(de lat." vetor"-" rolamento") - um segmento direcionado de uma linha reta no espaço ou em um plano.

Graficamente, um vetor é representado como um segmento de linha reta direcionado de um determinado comprimento. O vetor cujo início está no ponto e o fim no ponto é denotado como (Fig. 1). Além disso, um vetor pode ser denotado por uma única letra minúscula, por exemplo, .

Se um sistema de coordenadas é dado no espaço, então o vetor pode ser especificado exclusivamente por um conjunto de suas coordenadas. Ou seja, um vetor é entendido como um objeto que possui um valor (comprimento), direção e ponto de aplicação (início do vetor).

Os primórdios do cálculo vetorial apareceram em trabalhos em 1831 nos trabalhos do matemático, mecânico, físico, astrônomo e agrimensor alemão Johann Carl Friedrich Gauss (1777-1855). Trabalhos sobre operações com vetores foram publicados pelo matemático, mecânico e físico teórico irlandês Sir William Rowan Hamilton (1805-1865) como parte de seu cálculo quaternion. O cientista propôs o termo "vetor" e descreveu algumas operações em vetores. O cálculo vetorial foi desenvolvido graças ao trabalho sobre eletromagnetismo do físico, matemático e mecânico britânico James Clerk Maxwell (1831-1879). Na década de 1880, foi publicado o livro "Elements of Vector Analysis" do físico, físico-químico, matemático e mecânico americano Josiah Willard Gibbs (1839-1903). A análise vetorial moderna foi descrita em 1903 pelo cientista, engenheiro, matemático e físico inglês autodidata Oliver Heaviside (1850-1925).

DEFINIÇÃO

Comprimento ou módulo vetorialé o comprimento do segmento direcionado que define o vetor. Designado como .

Tipos básicos de vetores

Vetor zeroé chamado de vetor cujo ponto inicial e final são os mesmos. O comprimento do vetor nulo é zero.

Os vetores que são paralelos à mesma linha ou estão na mesma linha são chamados colinear(Figura 2).

co-direcional se suas direções forem as mesmas.

Na Figura 2, esses são os vetores e . A co-direção de vetores é denotada como segue: .

Dois vetores colineares são chamados direções opostas se suas direções forem opostas.

Na figura 3, esses são os vetores e . Designação: .