Mai rămâne din ce în ce mai puțin timp până la promovarea examenului la matematică. Situația se încinge, nervii școlarilor, părinților, profesorilor și tutorilor sunt din ce în ce mai încordați. Cursurile zilnice aprofundate de matematică te vor ajuta să scapi de tensiunea nervoasă. La urma urmei, nimic, după cum știți, încarcă atât de pozitiv și nu ajută la promovarea examenelor, precum încrederea în abilitățile și cunoștințele cuiva. Astăzi, un profesor de matematică vă va spune despre rezolvarea sistemelor de inegalități logaritmice și exponențiale, sarcini care în mod tradițional provoacă dificultăți pentru mulți liceeni moderni.

Pentru a învăța cum să rezolvi problemele C3 de la Examenul Unificat de Stat la matematică, în calitate de tutor la matematică, îți recomand să fii atent la următoarele puncte importante.

1. Înainte de a trece la rezolvarea sistemelor de inegalități logaritmice și exponențiale, este necesar să învățați cum să rezolvați fiecare dintre aceste tipuri de inegalități separat. În special, pentru a înțelege cum se găsește aria valorilor admisibile, se efectuează transformări echivalente ale expresiilor logaritmice și exponențiale. Puteți înțelege câteva dintre secretele legate de aceasta studiind articolele „” și „”.

2. În același timp, este necesar să ne dăm seama că soluția unui sistem de inegalități nu se rezumă întotdeauna la rezolvarea separată a fiecărei inegalități și la traversarea golurilor rezultate. Uneori, cunoscând soluția unei inegalități a sistemului, soluția celei de-a doua este mult simplificată. În calitate de profesor de matematică care pregătește studenții pentru examenele finale în format USE, voi dezvălui câteva secrete legate de acest lucru în acest articol.

3. Este necesar să înțelegeți clar diferența dintre intersecția și unirea mulțimilor. Aceasta este una dintre cele mai importante cunoștințe matematice pe care un profesor profesionist cu experiență încearcă să le ofere elevului său încă de la primele lecții. O reprezentare vizuală a intersecției și unirii mulțimilor este dată de așa-numitele „cercuri Euler”.

Stabiliți intersecția O mulțime se numește o mulțime care conține doar acele elemente pe care le are fiecare dintre aceste mulțimi.

intersecție

Imaginea intersecției seturilor folosind „cercurile Euler”

Explicație cu degetul. Diana are un „set” în poșetă, format din ( pixuri, creion, conducători, caiete, piepteni). Alice are un „set” în poșetă, format din ( caiet, creion, oglinzi, caiete, cotleturile Kievului). Intersecția acestor două „mulțimi” va fi „mulțimea” formată din ( creion, caiete), deoarece atât Diana, cât și Alice au ambele aceste „elemente”.

Important de reținut! Dacă soluția inegalității este intervalul și soluția inegalității este intervalul, atunci soluția sistemelor:

este intervalul care este intersecție intervalele originale. Aici și mai josoricare dintre personaje title="(!LANG:Redată de QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">!} si sub este semnul opus.

Unirea de seturi se numeşte mulţimea care este formată din toate elementele mulţimilor originale.

Cu alte cuvinte, dacă sunt date două seturi și apoi lor asociere va fi un set de forma următoare:

Imagine a uniunii seturilor folosind „cercurile Euler”

Explicație cu degetul. Unirea „multimilor” luata in exemplul anterior va fi „multimea” formata din ( pixuri, creion, conducători, caiete, piepteni, caiet, oglinzi, cotleturile Kievului), deoarece este format din toate elementele „mulților” originale. O precizare care poate să nu fie de prisos. O multime de nu poti conţin aceleaşi elemente.

Important de reținut! Dacă soluția inegalității este intervalul și soluția inegalității este intervalul, atunci soluția mulțimii este:

este intervalul care este Uniune intervalele originale.

Să trecem direct la exemple.

Exemplul 1 Rezolvați sistemul de inegalități:

Rezolvarea problemei C3.

1. Rezolvăm prima inegalitate. Folosind substituția, trecem la inegalitatea:

2. Acum rezolvăm a doua inegalitate. Intervalul valorilor sale admisibile este determinat de inegalitatea:

Title="(!LANG:Redată de QuickLaTeX.com">!}

În intervalul acceptabil, având în vedere că baza logaritmului title="(!LANG:Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству:!}

Excluzând soluțiile care nu se încadrează în intervalul de valori admisibile, obținem intervalul

3. Raspunde la sistem inegalitățile vor intersecție

Lacunele rezultate pe linia numerică. Soluția este intersecția lor

Exemplul 2 Rezolvați sistemul de inegalități:

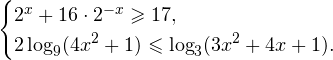
Rezolvarea problemei C3.

1. Rezolvăm prima inegalitate. Înmulțiți ambele părți prin title="(!LANG:Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству:!}

Să trecem la înlocuirea inversă:

2.

Title="(!LANG:Redată de QuickLaTeX.com">!}

Reprezentarea grafică a intervalului rezultat. Soluția sistemului - intersecția lor

Exemplul 3 Rezolvați sistemul de inegalități:

Rezolvarea problemei C3.

1. Rezolvăm prima inegalitate. Înmulțiți ambele părți ale acestuia prin title="(!LANG:Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство:!}

Folosind substituția, trecem la următoarea inegalitate:

Să trecem la înlocuirea inversă:

2. Acum rezolvăm a doua inegalitate. Să determinăm mai întâi intervalul de valori admisibile ale acestei inegalități:

ql-right-eqno">

Vă rugăm să rețineți că

Apoi, ținând cont de intervalul de valori admisibile, obținem:

3. Găsim soluția generală a inegalităților. Compararea valorilor iraționale obținute ale punctelor nodale nu este deloc o sarcină trivială în acest exemplu. Acest lucru se poate face în felul următor. La fel de

Title="(!LANG:Redată de QuickLaTeX.com">!}

apoi iar răspunsul final la sistem este:

Exemplul 4 Rezolvați sistemul de inegalități:

Rezolvarea problemei С3.

1. Să rezolvăm mai întâi a doua inegalitate:

2. Prima inegalitate a sistemului original este o inegalitate logaritmică de bază variabilă. O modalitate convenabilă de a rezolva astfel de inegalități este descrisă în articolul „Inegalități logaritmice complexe”, se bazează pe o formulă simplă:

În loc de semn, orice semn de inegalitate poate fi înlocuit, principalul lucru este ca acesta să fie același în ambele cazuri. Folosirea acestei formule simplifică foarte mult soluția inegalității:

Să determinăm acum intervalul de valori admisibile ale acestei inegalități. Este dat de următorul sistem:

Title="(!LANG:Redată de QuickLaTeX.com">!}

Title="(!LANG:Redată de QuickLaTeX.com">!}

Este ușor de observat că, în același timp, acest interval va fi și soluția inegalității noastre.

3. Răspunsul final la original sisteme inegalitățile vor intersecție intervale obţinute, adică

Exemplul 5 Rezolvați sistemul de inegalități:

Rezolvarea problemei C3.

1. Rezolvăm prima inegalitate. Folosim substituția Trecem la următoarea inegalitate pătratică:

2. Acum rezolvăm a doua inegalitate. Intervalul valorilor sale permise este determinat de sistem:

Title="(!LANG:Redată de QuickLaTeX.com">!}

Această inegalitate este echivalentă cu următorul sistem mixt:

În intervalul de valori valide, adică cu title="(!LANG:Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе:!}

Luând în considerare intervalul de valori admisibile, obținem:

3. Decizia finală a originalului sisteme este o

Rezolvarea problemei C3.

1. Rezolvăm prima inegalitate. Prin transformări echivalente îl aducem la forma:

2. Acum rezolvăm a doua inegalitate. Intervalul valorilor sale valide este determinat de intervalul: title="(!LANG:Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству:!}

Acest răspuns aparține în întregime gamei de valori acceptabile ale inegalității.

3. Încrucișând intervalele obținute în paragrafele precedente, obținem răspunsul final la sistemul de inegalități:

Astăzi am rezolvat sisteme de inegalități logaritmice și exponențiale. Sarcini de acest fel au fost oferite în versiuni de probă ale USE în matematică pe tot parcursul anului universitar curent. Cu toate acestea, în calitate de tutor de matematică cu experiență în pregătirea pentru USE, pot spune că acest lucru nu înseamnă deloc că sarcini similare vor fi în versiunile reale ale USE în matematică în iunie.

Permiteți-mi să exprim un avertisment, adresat în primul rând tutorilor și profesorilor implicați în pregătirea elevilor de liceu pentru USE în matematică. Este foarte periculos să pregătiți școlari pentru un examen strict pe subiecte date, deoarece în acest caz există riscul de a-l „umple” complet chiar și cu o ușoară modificare a formatului sarcinii menționat anterior. Educația la matematică trebuie să fie completă. Dragi colegi, vă rugăm să nu vă comparați studenții cu roboții prin așa-numitul „antrenament” pentru a rezolva un anumit tip de problemă. La urma urmei, nu există nimic mai rău decât formalizarea gândirii umane.

Succes tuturor și succes creativ!

Serghei Valerievici

Dacă încercați, atunci există două opțiuni: va funcționa sau nu va funcționa. Dacă nu încerci, există doar unul.
© Înțelepciunea populară

cererea numarul 3

Lecția 225 Inegalități raționale, iraționale, exponențiale și trigonometrice.

Data de:

Tip de lecție: lectie de generalizare si sistematizare a cunostintelor pe aceasta tema.

Obiectivele lecției:

generalizarea cunoştinţelor despre metodele de rezolvare a inegalităţilor exponenţiale. Pregătirea pentru examen;

formarea stimei de sine adecvate și a evaluării reciproce la elevi atunci când lucrează în grup;

dezvoltarea vorbirii matematice la comentarea unei soluții, la compilarea algoritmilor pentru finalizarea unei sarcini; capacitatea de a depăși dificultățile capacitatea de a lucra cu literatura de referință.

educație de ajutor reciproc.

Cunoștințe, abilități, aptitudini și calități care actualizează / dobândesc / consolidează / etc. elevii în timpul lecției:

sistematizează cunoștințele lor pe tema;

consolidarea cunoștințelor teoretice pe această temă;

să aplice cunoștințele într-o situație neobișnuită.

Echipamente și materiale necesare:

Laptopuri pentru testare individuala, proiector multimedia;

prezentare pentru lecție;

materiale de scris, fișe, fișe de autoevaluare.

Metode de predare: tehnologia învățării situaționale-problema folosind stadiul de caz.

Pașii lecției:

1. Moment org - 1 minut

2. formularea temei și a obiectivelor lecției 1 minut

3. Actualizarea cunoștințelor de bază. Sondaj Blitz. (3 min.)

4. Rezultatele sondajului blitz - 2 minute

5. Verificarea temelor. Notare. 3 minute

6. Teme de natură diferenţiată cu drept de alegere. 1 min

7. Repetarea teoriei și a inductorului (țintirea performanței) 2 min

8. Dezvoltarea abilităților de soluționare. Lucrați cu literatura de referință. 5 inegalități 10 min

9. Publicitate 2 minute

10. Gap. Sarcini nefamiliare - 2 min

11. rezolva aceste probleme 4 minute

12. Publicitate pentru rezolvarea unor probleme noi 4 min

13. Reflecție - 2 min

14. Autoevaluare 1 minut

Înainte de începerea lecției, elevii sunt așezați în conformitate cu cele trei niveluri de pregătire pe anumite rânduri. Rețineți că abilitățile pe tema luată în considerare nu fac parte din cerințele obligatorii pentru pregătirea studenților, prin urmare, doar studenții mai pregătiți (grupele 1 și 2) îl studiază cu mine.

Scopul lecției. Analizează modalități de rezolvare a inegalităților iraționale de complexitate medie și mare, dezvoltă scheme de sprijin.

Etapa 1 a lecției - organizatorică (1 min.)

Profesorul le spune elevilor tema lecției, scopul și le explică scopul fișei, care se află pe birouri.

Etapa 2 a lecției (5 min.)

Lucrare orală de repetare la rezolvarea celor mai simple probleme pe tema „Grad cu un indicator rațional”

Profesorul invită elevii să răspundă pe rând la întrebări, comentând răspunsul lor cu referire la faptul teoretic relevant.

Gradul cu exponent rațional

Simplificați: 1) 12m 4 /3m 8

2) 6s 3/7 + 4 (de la 1/7) 3

3) (32x 2) 1/5 x 3/5

4) 2 4,6a 2 -1,6a

5) 2x 0,2 x -1,2

6) 4x 3/5 x 1/10

8) 2x 4/5 3x 1/5

9) (3x 2/5) 2 + 2x 4/5

10) 3x 1/2 x 3/2

Calculați: 11) 4 3,2 m 4 -1,2 m , cu m = 1/4

12) 6 -5,6a 6 3,6a, la a = 1/2

13) 5 27 2/3 - 16 1/4

14) 3 4,4s 3 -6,4s, cu c = 1/2

15) 3x 2/5 x 3/5, la x = 2

Etapa 3 a lecției - învățarea unui subiect nou (20 min.), Prelegere

Profesorul invită grupa a 3-a de elevi să înceapă lucrul la repetarea cu fișe - consultanți pe tema „Ecuații trigonometrice simple” (întrucât materialul studiat este de un nivel crescut de complexitate și nu este obligatoriu). Elevii grupei a 3-a sunt, de regulă, elevi cu pregătire matematică slabă, școlari neglijați din punct de vedere pedagogic. După finalizarea sarcinii, cărțile sunt schimbate în cadrul grupului. Elevii mai pregătiți încep să analizeze un subiect nou.

Înainte de a analiza metodele de rezolvare a inegalităților iraționale, studenților trebuie să li se reamintească principalele fapte teoretice pe baza cărora se vor construi scheme de sprijin pentru tranziții echivalente. În funcție de nivelul de pregătire al elevilor, acestea pot fi fie răspunsuri orale la întrebările profesorului, fie munca comună a profesorului și elevilor, dar în orice caz, în lecție ar trebui auzite următoarele.

Definiția 1. Inegalitățile care au același set de soluții se numesc echivalente.

La rezolvarea inegalităților, această inegalitate este de obicei transformată într-una echivalentă.

De exemplu, inegalitatea (x - 3)/(x 2 + 1) sunt echivalente, deoarece au același set de soluții: X. inegalităților 2x / (x - 1) 1 și 2x x - 1 nu sunt echivalente, deoarece soluțiile primei sunt soluțiile x 1, iar soluțiile celei de-a doua sunt numerele x -1.

Definiția 2. Domeniul inegalității este mulțimea de valori x pentru care ambele părți ale inegalității au sens.

Motivația. Inegalitățile în sine sunt de interes pentru studiu, deoarece cu ajutorul lor, cele mai importante sarcini de cunoaștere a realității sunt scrise în limbaj simbolic. Inegalitatea servește adesea ca un instrument auxiliar important care permite cuiva să dovedească sau să infirme existența oricăror obiecte, să estimeze numărul lor, să le clasifice. Prin urmare, trebuie să ne confruntăm cu inegalitățile nu mai rar decât cu ecuațiile.

Definiție. O inegalitate care conține o variabilă sub semnul rădăcinii se numește irațională.

Exemplul 1√(5 - x)

Care este domeniul de aplicare al definiției inegalității?

Care este condiția ca ambele părți la pătrat pentru a produce o inegalitate echivalentă?

√(5 - x) 5 - x -11

Exemplul 2√10 + x - x 2 ≥ 2 10 + x - x 2 ≥ 0 10 + x - x 2 ≥ 4

10 + x - x 2 ≥ 4

deoarece fiecare soluție a celei de-a doua inegalități a sistemului este o soluție a primei inegalități.

Exemplul 3 Rezolvați inegalitățile

b) √2x 2 + 5x - 3 ≤ 0 2x 2 + 5x - 3 = 0

Să analizăm trei exemple tipice, din care va fi clar cum, la rezolvarea inegalităților, să se facă tranziții echivalente atunci când transformarea evidentă nu este echivalentă.

Exemplul 1√1 - 4x x + 11.

Ar fi de dorit, desigur, să pătrați ambele părți pentru a obține o inegalitate de pătrat. În acest caz, putem obține o inegalitate neechivalentă. Dacă luăm în considerare doar acele x pentru care ambele părți sunt nenegative (partea stângă este evident nenegativă), atunci pătratul va fi totuși posibil. Dar ce să faci cu acele x pentru care partea dreaptă este negativă? Și nu faceți nimic, deoarece niciunul dintre acești x nu va fi o soluție a inegalității: la urma urmei, pentru orice soluție a inegalității, partea dreaptă este mai mare decât stânga, care este un număr nenegativ și, prin urmare, este ea însăși. nu negativ. Deci, o consecință a inegalității noastre va fi un astfel de sistem

1 - 4x (x + 11) 2

Cu toate acestea, acest sistem nu trebuie să fie echivalent cu inegalitatea inițială. Domeniul de definire al sistemului rezultat este întreaga dreaptă numerică, în timp ce inegalitatea inițială este definită numai pentru acele x pentru care 1 - 4x ≥ 0. Deci, dacă dorim ca sistemul nostru să fie echivalent cu inegalitatea, trebuie să atribuim această condiție :

Răspuns: (- 6; ¼]

I se propune unui elev puternic să raționeze într-un mod general, rezultă că

√f(x) g (x) f (x) ( g(x)) 2

g(x) ≥ 0

f(x) ≥ 0.

Dacă inegalitatea originală avea semnul ≤ în loc de f (x) ≤ (g (x)) 2 .

Exemplul 2√x x - 2

Din nou, putem pătra acei x pentru care este îndeplinită condiția x - 2 ≥ 0. Cu toate acestea, acum nu mai este posibil să renunțăm la acele x pentru care partea dreaptă este negativă: până la urmă, în acest caz, partea dreaptă va fi mai mic decât partea stângă evident nenegativă, astfel încât toate aceste x vor fi soluții ale inegalităților. Cu toate acestea, nu toate, ci cele care sunt incluse în domeniul de aplicare al definiției inegalității, i.e. pentru care x ≥ 0. Ce cazuri ar trebui luate în considerare?

Cazul 1: dacă x - 2 ≥ 0, atunci inegalitatea noastră implică sistemul

2 caz: dacă x - 2

La analizarea cazurilor, apare o condiție compusă numită „set”. Obținem o mulțime de două sisteme echivalente cu inegalitatea

Un student puternic este invitat să raționeze într-un mod general, apoi se va dovedi astfel:

√f (x) g (x) f (x) (g (x)) 2

g(x) ≥ 0

f(x) ≥ 0

g(x).

Dacă inegalitatea inițială avea semnul ≥ în schimb, atunci f (x) ≥ (g (x)) 2 ar fi trebuit luată ca prima inegalitate a acestui sistem.

Exemplul 3√x 2 - 1 √x + 5.

Care sunt semnificațiile expresiilor din stânga și din dreapta?

Poate fi pătrat?

Care este domeniul de definire a inegalităților?

Obține x 2 - 1 x + 5

Care condiție este redundantă?

Astfel, obținem că această inegalitate este echivalentă cu sistemul

Un student puternic este invitat să conducă un raționament într-o formă generală, se va dovedi astfel:

√f (x) √g (x) f (x) g (x)

g(x) ≥ 0.

Gândiți-vă la ce se va schimba dacă în loc de inegalitatea inițială există un semn ≥, ≤ sau

Pe tablă sunt postate 3 scheme de rezolvare a inegalităților iraționale, se discută încă o dată principiul construcției lor.

Etapa 4 - consolidarea cunoștințelor (5 min.)

Elevii grupei a 2-a sunt invitați să indice care sistem sau combinația lor este echivalentă cu inegalitatea nr. 167 (Algebra și începutul analizei 10-11 celule. M, Enlightenment, 2005, Sh.A. Alimov)

Cei doi elevi cei mai pregătiți din această grupă sunt invitați să rezolve inegalitățile de pe tablă: Nr. 1. √x 2 - 1 1

Nr. 2. √25 - x 2

Elevii grupei I primesc o sarcină similară, dar de un nivel mai ridicat de complexitate Nr. 170 (Algebra și începutul analizei în clasele 10-11, M, Iluminism, 2005, Sh.A. Alimov)

unul dintre cei mai pregătiți elevi din această grupă este invitat să rezolve inegalitatea de pe tablă: √4x - x 2

În acest caz, toți studenții au voie să folosească rezumatul.

În acest moment, profesorul lucrează cu elevii grupei a 3-a: răspunde la întrebările lor, dacă este necesar, ajută; și controlează soluționarea problemelor de pe tablă.

La sfârșitul timpului, fiecărui grup i se dă o fișă de răspunsuri de verificat (puteți afișa răspunsurile pe ecran folosind un sistem multimedia).

Etapa 5 a lecției - discutarea soluțiilor la problemele prezentate pe tablă (7 min.)

Elevii care au finalizat sarcinile la tablă comentează deciziile lor, iar restul fac ajustări dacă este necesar și notează în caiete.

Etapa 6 a lecției - rezumarea lecției, comentarii la teme (2 min.)

3 schimb de cărți de grup în cadrul grupului.

2 grupa nr. 168 (3, 4)

1 grupa nr. 169 (5), nr. 170 (6)

Toate problemele B7 pe care le-am văzut au fost formulate aproape în același mod: rezolvarea unei ecuații. În acest caz, ecuațiile în sine aparțin unuia dintre cele trei tipuri:

1. logaritmică;
2. Demonstrativ;
3. Iraţional.

În general, un ghid complet pentru fiecare tip de ecuație va dura mai mult de o duzină de pagini, depășind cu mult domeniul de aplicare al examenului. Prin urmare, vom lua în considerare doar cazurile cele mai simple care necesită raționamente și calcule fără pretenții. Aceste cunoștințe vor fi suficiente pentru a rezolva orice problemă B7.

În matematică, termenul „rezolvarea unei ecuații” înseamnă a găsi mulțimea tuturor rădăcinilor unei ecuații date sau a demonstra că această mulțime este goală. Dar numai numere pot fi introduse în formularul USE - fără seturi. Prin urmare, dacă a existat mai mult de o rădăcină în sarcina B7 (sau, dimpotrivă, nici una) - a fost făcută o eroare în soluție.

Ecuații logaritmice

O ecuație logaritmică este orice ecuație care se reduce la forma log A f(X) = k, Unde A > 0, A≠ 1 este baza logaritmului, f(X) este o funcție arbitrară, k este o constantă.

O astfel de ecuație se rezolvă prin introducerea constantei k sub semnul logaritmului: k= jurnal A A k. Baza noului logaritm este egală cu baza originalului. Obținem jurnalul ecuației A f(X) = jurnal A A k, care se rezolvă prin eliminarea logaritmului.

Rețineți că, prin condiție A> 0, deci f(X) = A k> 0, adică logaritmul original există.

Sarcină. Rezolvați ecuația: log 7 (8 − X) = 2.

Decizie. log 7 (8 − X) = 2 ⇔ log 7 (8 − X) = log 7 7 2 ⇔ 8 − X = 49 ⇔ X = −41.

Sarcină. Rezolvați ecuația: log 0,5 (6 − X) = −2.

Decizie. log 0,5 (6 − X) = −2 ⇔ log 0,5 (6 − X) = log 0,5 0,5 −2 ⇔ 6 − X = 4 ⇔ X = 2.

Dar ce se întâmplă dacă ecuația inițială se dovedește a fi mai complicată decât jurnalul standard A f(X) = k? Apoi îl reducem la cel standard, adunând toți logaritmii într-o direcție, iar numerele în cealaltă.

Dacă există mai mult de un logaritm în ecuația originală, va trebui să căutați aria valorilor admisibile (ODV) a fiecărei funcții care se află sub logaritm. În caz contrar, pot apărea rădăcini suplimentare.

Sarcină. Rezolvați ecuația: log 5 ( X+ 1) + log 5 ( X + 5) = 1.

Deoarece există doi logaritmi în ecuație, găsim ODZ:

1. X + 1 > 0 ⇔ X > −1
2. X + 5 > 0 ⇔ X > −5

Obținem că ODZ este intervalul (−1, +∞). Acum rezolvăm ecuația:

jurnal 5 ( X+ 1) + log 5 ( X+ 5) = 1 ⇒ log 5 ( X + 1)(X+ 5) = 1 ⇔ log 5 ( X + 1)(X+ 5) = log 5 5 1 ⇔ ( X + 1)(X + 5) = 5 ⇔ X 2 + 6X + 5 = 5 ⇔ X (X + 6) = 0 ⇔ X 1 = 0, X 2 = −6.

Dar X 2 = -6 nu se califică pentru ODZ. Rămâne rădăcina X 1 = 0.

ecuații exponențiale

O ecuație exponențială este orice ecuație care se reduce la forma A f(X) = k, Unde A > 0, A≠ 1 - baza gradului, f(X) este o funcție arbitrară, k este o constantă.

Această definiție repetă aproape textual definiția unei ecuații logaritmice. Ecuatiile exponentiale se rezolva si mai usor decat cele logaritmice, deoarece aici nu se cere ca functia f(X) a fost pozitiv.

Pentru a rezolva acest lucru, facem înlocuirea k = A t, Unde tÎn general, logaritmul ( t= jurnal A k), dar în USE numerele Ași k va fi ales astfel încât să găsească t va fi usor. În ecuația rezultată A f(X) = A t bazele sunt egale, ceea ce înseamnă că exponenții sunt egali, adică. f(X) = t. Rezolvarea ultimei ecuații, de regulă, nu provoacă probleme.

Sarcină. Rezolvați ecuația: 7 X − 2 = 49.

Decizie. 7 X − 2 = 49 ⇔ 7 X − 2 = 7 2 ⇔ X − 2 = 2 ⇔ X = 4.

Sarcină. Rezolvați ecuația: 6 16 − X = 1/36.

Decizie. 6 16 - X = 1/36 ⇔ 6 16 − X = 6 −2 ⇔ 16 − X = −2 ⇔ X = 18.

Câteva despre transformarea ecuațiilor exponențiale. Dacă ecuația inițială este diferită de A f(X) = k , aplicăm regulile de lucru cu grade:

1. A n · A m = A n + m ,
2. A n / A m = A n − m ,
3. (A n) m = A n · m .

În plus, trebuie să cunoașteți regulile pentru înlocuirea rădăcinilor și fracțiilor cu grade cu un exponent rațional:

Astfel de ecuații sunt extrem de rare în USE, dar fără ele, analiza problemei B7 ar fi incompletă.

Sarcină. Rezolvați ecuația: (5/7) X− 2 (7/5) 2 X − 1 = 125/343

Observa asta:

1. (7/5) 2X − 1 = ((5/7) −1) 2X − 1 = (5/7) 1 − 2X ,
2. 125/343 = (5 3) /(7 3) = (5/7) 3 .

Avem: (5/7) X− 2 (7/5) 2 X − 1 = 125/343 ⇔ (5/7) X− 2 · (5/7) 1 − 2 X = (5/7) 3 ⇔ (5/7) X − 2 + 1 − 2X = (5/7) 3 ⇔ (5/7) −X − 1 = (5/7) 3 ⇔ −X − 1 = 3 ⇔ X = −4.

Ecuații iraționale

Irațional este înțeles ca orice ecuație care conține semnul rădăcinii. Dintre toată varietatea de ecuații iraționale, vom lua în considerare doar cel mai simplu caz, când ecuația are forma:

Pentru a rezolva această ecuație, pătram ambele părți. Obținem ecuația f(X) = A 2. În acest caz, cerința ODZ este îndeplinită automat: f(X) ≥ 0, deoarece A 2 ≥ 0. Rămâne de rezolvat o ecuație simplă f(X) = A 2 .

Sarcină. Rezolvați ecuația:

Punem la patrat ambele laturi si obtinem: 5 X − 6 = 8 2 ⇔ 5X − 6 = 64 ⇔ 5X = 70 ⇔ X = 14.

Sarcină. Rezolvați ecuația:

Mai întâi, ca și data trecută, pătrum ambele părți. Și apoi vom adăuga un semn minus la numărător. Noi avem:

Rețineți că atunci când X= −4 va exista un număr pozitiv sub rădăcină, adică. cerința ODZ a fost îndeplinită.