Să presupunem că Ahile aleargă de zece ori mai repede decât țestoasa și este la o mie de pași în spatele ei. În timpul în care Ahile parcurge această distanță, țestoasa se târăște o sută de pași în aceeași direcție. Când Ahile a alergat o sută de pași, țestoasa se va târa încă zece pași și așa mai departe. Procesul va continua la nesfârșit, Ahile nu va ajunge niciodată din urmă cu broasca țestoasă.
Acest raționament a devenit un șoc logic pentru toate generațiile următoare. Aristotel, Diogene, Kant, Hegel, Gilbert... Toți, într-un fel sau altul, au considerat aporii lui Zenon. Șocul a fost atât de puternic încât " ... discuțiile continuă în prezent, comunitatea științifică nu a reușit încă să ajungă la o opinie comună cu privire la esența paradoxurilor... în studiul problemei au fost implicate analiza matematică, teoria mulțimilor, noi abordări fizice și filozofice. ; niciunul dintre ele nu a devenit o soluție universal acceptată la problemă...„[Wikipedia,” Aporii lui Zeno „]. Toată lumea înțelege că sunt păcăliți, dar nimeni nu înțelege ce este înșelăciunea.
Din punctul de vedere al matematicii, Zenon în aporia sa a demonstrat clar trecerea de la valoare la. Această tranziție implică aplicarea în loc de constante. Din câte am înțeles, aparatul matematic pentru aplicarea unităților de măsură variabile fie nu a fost încă dezvoltat, fie nu a fost aplicat aporiei lui Zenon. Aplicarea logicii noastre obișnuite ne duce într-o capcană. Noi, prin inerția gândirii, aplicăm reciprocului unități constante de timp. Din punct de vedere fizic, se pare că timpul încetinește până la o oprire completă în momentul în care Ahile ajunge din urmă cu țestoasa. Dacă timpul se oprește, Ahile nu mai poate depăși țestoasa.
Dacă întoarcem logica cu care suntem obișnuiți, totul cade la locul său. Ahile aleargă cu o viteză constantă. Fiecare segment ulterior al traseului său este de zece ori mai scurt decât cel anterior. În consecință, timpul petrecut pentru depășirea acestuia este de zece ori mai mic decât cel precedent. Dacă aplicăm conceptul de „infinit” în această situație, atunci ar fi corect să spunem „Achile va depăși infinit rapid broasca țestoasă”.
Cum să eviți această capcană logică? Rămâneți în unități constante de timp și nu treceți la valori reciproce. În limbajul lui Zeno, arată astfel:
În timpul necesar lui Ahile pentru a alerga o mie de pași, țestoasa se târăște o sută de pași în aceeași direcție. În următorul interval de timp, egal cu primul, Ahile va alerga încă o mie de pași, iar țestoasa se va târa o sută de pași. Acum Ahile este cu opt sute de pași înaintea țestoasei.
Această abordare descrie în mod adecvat realitatea fără niciun paradox logic. Dar aceasta nu este o soluție completă la problemă. Afirmația lui Einstein despre insurmontabilitatea vitezei luminii este foarte asemănătoare cu aporia lui Zeno „Achile și broasca țestoasă”. Încă trebuie să studiem, să regândim și să rezolvăm această problemă. Iar soluția trebuie căutată nu în număr infinit de mare, ci în unități de măsură.
O altă aporie interesantă a lui Zeno spune despre o săgeată zburătoare:
O săgeată zburătoare este nemișcată, deoarece în fiecare moment de timp este în repaus și, deoarece este în repaus în fiecare moment de timp, este întotdeauna în repaus.
În această aporie, paradoxul logic este depășit foarte simplu - este suficient să clarificăm că în fiecare moment de timp săgeata zburătoare este în repaus în diferite puncte din spațiu, ceea ce, de fapt, este mișcare. Mai este un punct de remarcat aici. Dintr-o fotografie a unei mașini pe șosea, este imposibil să se determine nici faptul mișcării acesteia, nici distanța până la ea. Pentru a determina fapta mișcării mașinii, sunt necesare două fotografii realizate din același punct în momente diferite de timp, dar nu pot fi folosite pentru a determina distanța. Pentru a determina distanța până la mașină, aveți nevoie de două fotografii făcute din diferite puncte din spațiu în același timp, dar nu puteți determina faptul deplasării din ele (desigur, aveți nevoie de date suplimentare pentru calcule, trigonometria vă va ajuta) . Ceea ce vreau să subliniez în special este că două puncte în timp și două puncte în spațiu sunt două lucruri diferite care nu trebuie confundate, deoarece oferă oportunități diferite de explorare.
miercuri, 4 iulie 2018
Foarte bine diferențele dintre set și multiset sunt descrise în Wikipedia. Ne uitam.
După cum puteți vedea, „multimea nu poate avea două elemente identice”, dar dacă există elemente identice în set, un astfel de set se numește „multiset”. Ființele rezonabile nu vor înțelege niciodată o asemenea logică a absurdității. Acesta este nivelul papagalilor vorbitori și al maimuțelor dresate, în care mintea este absentă din cuvântul „complet”. Matematicienii acționează ca formatori obișnuiți, propovăduindu-ne ideile lor absurde.
Pe vremuri, inginerii care au construit podul se aflau într-o barcă sub pod în timpul testelor podului. Dacă podul s-a prăbușit, inginerul mediocru a murit sub dărâmăturile creației sale. Dacă podul putea rezista la sarcină, talentatul inginer a construit alte poduri.
Indiferent de cât de matematicieni se ascund în spatele expresiei „mind-mă, sunt în casă”, sau mai degrabă „matematica studiază concepte abstracte”, există un cordon ombilical care le leagă indisolubil de realitatea. Acest cordon ombilical este bani. Să aplicăm teoria mulțimilor matematicienilor înșiși.
Am studiat foarte bine matematica și acum stăm la casierie și plătim salarii. Aici vine un matematician la noi pentru banii lui. Numărăm întreaga sumă pentru el și o întindem pe masa noastră în grămezi diferite, în care punem bancnote de aceeași valoare. Apoi luăm câte o bancnotă din fiecare grămadă și îi dăm matematicianului „setul său de salariu matematic”. Explicăm la matematică că va primi restul bancnotelor doar atunci când demonstrează că mulțimea fără elemente identice nu este egală cu mulțimea cu elemente identice. Aici începe distracția.
În primul rând, logica deputaților va funcționa: „puteți aplica și altora, dar mie nu!” În plus, vor începe asigurările că există numere diferite de bancnote pe bancnotele de aceeași valoare nominală, ceea ce înseamnă că acestea nu pot fi considerate elemente identice. Ei bine, numărăm salariul în monede - nu există numere pe monede. Aici, matematicianul își va aminti frenetic de fizică: diferite monede au cantități diferite de murdărie, structura cristalină și aranjarea atomilor pentru fiecare monedă este unică...
Și acum am cea mai interesantă întrebare: unde este granița dincolo de care elementele unui multiset se transformă în elemente ale unui set și invers? O astfel de linie nu există - totul este decis de șamani, știința aici nu este nici măcar aproape.
Uite aici. Selectăm stadioane de fotbal cu aceeași suprafață de teren. Aria câmpurilor este aceeași, ceea ce înseamnă că avem un multiset. Dar dacă luăm în considerare numele acelorași stadioane, obținem multe, pentru că numele sunt diferite. După cum puteți vedea, același set de elemente este atât un set cât și un multiset în același timp. Cât de corect? Și aici matematicianul-șaman-shuller scoate un as de atu din mânecă și începe să ne vorbească fie despre un set, fie despre un multiset. În orice caz, ne va convinge că are dreptate.
Pentru a înțelege cum operează șamanii moderni cu teoria mulțimilor, legând-o de realitate, este suficient să răspundem la o întrebare: prin ce diferă elementele unui set de elementele altui set? Vă voi arăta, fără niciun „conceput ca nu un singur întreg” sau „neconceput ca un singur întreg”.
Duminică, 18 martie 2018
Suma cifrelor unui număr este un dans al șamanilor cu un tamburin, care nu are nimic de-a face cu matematica. Da, la lecțiile de matematică suntem învățați să găsim suma cifrelor unui număr și să o folosim, dar de aceea ei sunt șamani, pentru a-și învăța descendenții abilitățile și înțelepciunea, altfel șamanii pur și simplu vor muri.
Ai nevoie de dovezi? Deschideți Wikipedia și încercați să găsiți pagina „Suma cifrelor unui număr”. Ea nu există. Nu există o formulă în matematică prin care să poți găsi suma cifrelor oricărui număr. La urma urmei, numerele sunt simboluri grafice cu care scriem numere, iar în limbajul matematicii, sarcina sună astfel: „Găsiți suma simbolurilor grafice care reprezintă orice număr”. Matematicienii nu pot rezolva această problemă, dar șamanii o pot face în mod elementar.
Să ne dăm seama ce și cum facem pentru a găsi suma cifrelor unui număr dat. Și așa, să presupunem că avem numărul 12345. Ce trebuie făcut pentru a găsi suma cifrelor acestui număr? Să luăm în considerare toți pașii în ordine.
1. Notează numărul pe o foaie de hârtie. Ce am făcut? Am convertit numărul într-un simbol grafic numeric. Aceasta nu este o operație matematică.
2. Am tăiat o imagine primită în mai multe imagini care conțin numere separate. Decuparea unei imagini nu este o operație matematică.
3. Convertiți caracterele grafice individuale în numere. Aceasta nu este o operație matematică.
4. Adunați numerele rezultate. Acum asta e matematica.
Suma cifrelor numărului 12345 este 15. Acestea sunt „cursurile de tăiere și cusut” de la șamani folosite de matematicieni. Dar asta nu este tot.
Din punct de vedere al matematicii, nu contează în ce sistem de numere scriem numărul. Deci, în sisteme de numere diferite, suma cifrelor aceluiași număr va fi diferită. În matematică, sistemul numeric este indicat ca indice în dreapta numărului. Cu un număr mare de 12345, nu vreau să-mi păcălesc capul, luați în considerare numărul 26 din articolul despre. Să scriem acest număr în sisteme de numere binar, octal, zecimal și hexazecimal. Nu vom lua în considerare fiecare pas la microscop, am făcut-o deja. Să ne uităm la rezultat.
După cum puteți vedea, în diferite sisteme de numere, suma cifrelor aceluiași număr este diferită. Acest rezultat nu are nimic de-a face cu matematica. Este la fel ca și cum ați obține rezultate complet diferite atunci când determinați aria unui dreptunghi în metri și centimetri.
Zero în toate sistemele de numere arată la fel și nu are sumă de cifre. Acesta este un alt argument în favoarea faptului că . O întrebare pentru matematicieni: cum se notează în matematică ceea ce nu este un număr? Ce, pentru matematicieni, nu există decât numere? Pentru șamani, pot permite acest lucru, dar pentru oameni de știință, nu. Realitatea nu este doar despre cifre.
Rezultatul obținut ar trebui considerat ca o dovadă că sistemele numerice sunt unități de măsură ale numerelor. La urma urmei, nu putem compara numerele cu unități de măsură diferite. Dacă aceleași acțiuni cu unități de măsură diferite ale aceleiași mărimi duc la rezultate diferite după compararea lor, atunci acest lucru nu are nimic de-a face cu matematica.
Ce este matematica reală? Acesta este momentul în care rezultatul unei acțiuni matematice nu depinde de valoarea numărului, de unitatea de măsură folosită și de cine efectuează această acțiune.
Ai! Asta nu este toaleta femeilor?
- Femeie tânără! Acesta este un laborator pentru studierea sfințeniei nedefinite a sufletelor la înălțarea la cer! Nimbus în sus și săgeată în sus. Ce altă toaletă?
Femeie... Un halou deasupra și o săgeată în jos sunt masculin.
Dacă aveți o astfel de operă de artă de design fulgerând în fața ochilor dvs. de mai multe ori pe zi,
Atunci nu este surprinzător că găsiți brusc o pictogramă ciudată în mașina dvs.:
Personal, fac un efort pe mine însumi să văd minus patru grade la o persoană care face caca (o poză) (compunere din mai multe imagini: semnul minus, numărul patru, desemnarea grade). Și nu o consider pe fata asta o proastă care nu știe fizică. Ea are doar un arc stereotip al percepției imaginilor grafice. Și matematicienii ne învață asta tot timpul. Iată un exemplu.
1A nu este „minus patru grade” sau „unu a”. Acesta este „omul care face caca” sau numărul „douăzeci și șase” în sistemul numeric hexazecimal. Acei oameni care lucrează constant în acest sistem numeric percep automat numărul și litera ca un simbol grafic.
Tabelul de valori ale funcțiilor trigonometrice
Notă. Acest tabel de valori pentru funcțiile trigonometrice folosește semnul √ pentru a desemna rădăcina pătrată. Pentru a desemna o fracție - simbolul „/”.
Vezi si materiale utile:
Pentru determinarea valorii unei funcţii trigonometrice, găsiți-l la intersecția dreptei care indică funcția trigonometrică. De exemplu, un sinus de 30 de grade - căutăm o coloană cu titlul sin (sinus) și găsim intersecția acestei coloane a tabelului cu linia „30 de grade”, la intersecția lor citim rezultatul - unul al doilea. În mod similar, găsim cosinus 60 grade, sinus 60 grade (din nou, la intersecția coloanei sin (sinus) și rândul de 60 de grade, găsim valoarea sin 60 = √3/2), etc. În același mod, se găsesc valorile sinusurilor, cosinusurilor și tangentelor altor unghiuri „populare”.
Sinusul lui pi, cosinusul lui pi, tangenta lui pi și alte unghiuri în radiani
Tabelul de cosinus, sinusuri și tangente de mai jos este, de asemenea, potrivit pentru a afla valoarea funcțiilor trigonometrice al căror argument este dat în radiani. Pentru a face acest lucru, utilizați a doua coloană de valori unghiulare. Datorită acestui fapt, puteți converti valoarea unghiurilor populare de la grade la radiani. De exemplu, să găsim unghiul de 60 de grade în prima linie și să citim valoarea lui în radiani sub el. 60 de grade este egal cu π/3 radiani.
Numărul pi exprimă în mod unic dependența circumferinței unui cerc de măsura gradului unghiului. Deci pi radiani este egal cu 180 de grade.
Orice număr exprimat în termeni de pi (radian) poate fi ușor convertit în grade prin înlocuirea numărului pi (π) cu 180.
Exemple:
1. sine pi.
sin π = sin 180 = 0
astfel, sinusul lui pi este același cu sinusul de 180 de grade și este egal cu zero.
2. cosinus pi.
cos π = cos 180 = -1
astfel, cosinusul lui pi este același cu cosinusul de 180 de grade și este egal cu minus unu.
3. Tangenta pi
tg π = tg 180 = 0
astfel, tangenta lui pi este aceeași cu tangenta de 180 de grade și este egală cu zero.
Tabelul valorilor sinus, cosinus, tangente pentru unghiuri 0 - 360 de grade (valori frecvente)
|
unghiul α (grade) |
unghiul α (prin pi) |
păcat (sinus) |
cos (cosinus) |
tg (tangentă) |
ctg (cotangentă) |
sec (secantă) |
cauză (cosecant) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
Dacă în tabelul de valori ale funcțiilor trigonometrice, în loc de valoarea funcției, este indicată o liniuță (tangentă (tg) 90 de grade, cotangentă (ctg) 180 de grade), atunci pentru o anumită valoare a gradului de măsură a unghiul, funcția nu are o valoare definită. Dacă nu există liniuță, celula este goală, deci nu am introdus încă valoarea dorită. Suntem interesați de ce solicitări vin utilizatorii la noi și completăm tabelul cu noi valori, în ciuda faptului că datele actuale privind valorile cosinusurilor, sinusurilor și tangentelor celor mai comune valori unghiulare sunt suficiente pentru a rezolva cele mai multe Probleme.
Tabelul de valori ale funcțiilor trigonometrice sin, cos, tg pentru cele mai populare unghiuri
0, 15, 30, 45, 60, 90 ... 360 de grade
(valori numerice „conform tabelelor Bradis”)
| valoarea unghiului α (grade) | valoarea unghiului α în radiani | păcat (sinus) | cos (cosinus) | tg (tangent) | ctg (cotangent) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
În articol, vom înțelege pe deplin cum arată tabel de valori trigonometrice, sinus, cosinus, tangentă și cotangentă. Se consideră valoarea de bază a funcțiilor trigonometrice, dintr-un unghi de 0,30,45,60,90,...,360 de grade. Și să vedem cum să folosim aceste tabele în calcularea valorii funcțiilor trigonometrice.
Mai întâi luați în considerare tabelul cosinus, sinus, tangente și cotangente dintr-un unghi de 0, 30, 45, 60, 90,.. grade. Definirea acestor mărimi face posibilă determinarea valorii funcțiilor unghiurilor de 0 și 90 de grade:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, cotangenta lui 00 va fi nedefinită
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, tangenta lui 90 0 va fi nedefinită
Dacă luăm triunghiuri dreptunghiulare ale căror unghiuri sunt de la 30 la 90 de grade. Primim:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Reprezentăm toate valorile obținute în formular tabel trigonometric:
Tabel de sinusuri, cosinus, tangente și cotangente!
Dacă folosim formula de turnare, tabelul nostru va crește, se vor adăuga valori pentru unghiuri de până la 360 de grade. Va arata ca:

De asemenea, pe baza proprietăților periodicității, tabelul poate fi mărit dacă înlocuim unghiurile cu 0 0 +360 0 *z .... 330 0 +360 0 *z, în care z este un număr întreg. În acest tabel, este posibil să se calculeze valoarea tuturor unghiurilor corespunzătoare punctelor dintr-un singur cerc.
Să vedem clar cum să folosim tabelul în soluție.
Totul este foarte simplu. Deoarece valoarea de care avem nevoie se află în punctul de intersecție al celulelor de care avem nevoie. De exemplu, să luăm cos unui unghi de 60 de grade, în tabel va arăta astfel:

În tabelul final al principalelor valori ale funcțiilor trigonometrice, acționăm în același mod. Dar în acest tabel este posibil să aflăm cât de mult va fi tangenta dintr-un unghi de 1020 de grade, ea = -√3 Să verificăm 1020 0 = 300 0 +360 0 *2. Să găsim masa.

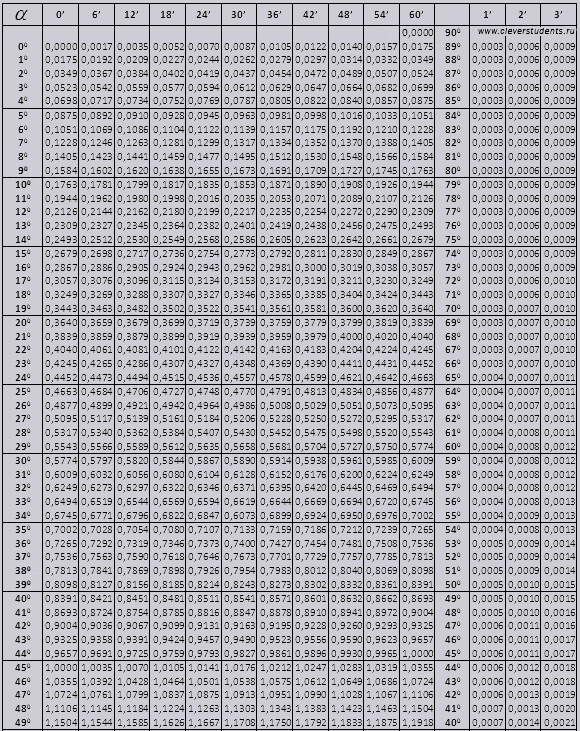
masa Bradis. Pentru sinus, cosinus, tangentă și cotangentă.
Tabelele lui Bradys sunt împărțite în mai multe părți, ele constau din tabele de cosinus și sinus, tangentă și cotangentă - care este împărțită în două părți (tg de un unghi de până la 90 de grade și ctg de unghiuri mici).
Sinus și cosinus


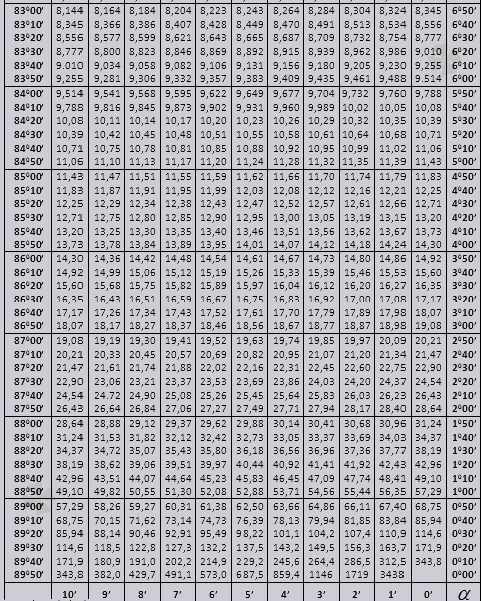
unghi tg de la 00 la 760, unghi ctg de la 140 la 900.

tg până la 900 și ctg unghiuri mici.

Să ne dăm seama cum să folosim tabelele Bradis în rezolvarea problemelor.
Să găsim denumirea sin (denumirea în coloana de la marginea din stânga) 42 de minute (denumirea este pe linia de sus). Prin trecere căutăm o desemnare, este = 0,3040.
Valorile minutelor sunt indicate cu un interval de șase minute, dacă valoarea de care avem nevoie se încadrează în acest interval. Să luăm 44 de minute și în tabel sunt doar 42. Luăm ca bază 42 și folosim coloanele suplimentare din partea dreaptă, luăm a 2-a corecție și adăugăm la 0,3040 + 0,0006 obținem 0,3046.
Cu sin 47 min, luăm 48 min ca bază și scădem 1 corecție din ea, adică 0,3057 - 0,0003 = 0,3054
Când calculăm cos, lucrăm similar cu sin, doar că luăm ca bază rândul de jos al tabelului. De exemplu cos 20 0 = 0,9397
Valorile tg ale unui unghi de până la 90 0 și cot ale unui unghi mic sunt corecte și nu există corecții în ele. De exemplu, găsiți tg 78 0 37min = 4,967 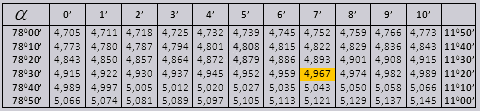
și ctg 20 0 13 min = 25,83 
Ei bine, aici am luat în considerare principalele tabele trigonometrice. Sperăm că aceste informații v-au fost extrem de utile. Întrebările tale de pe mese, dacă există, asigurați-vă că scrieți în comentarii!
Notă: Apărătoare de perete - o placă de protecție pentru protejarea pereților. Urmați link-ul pentru aripi fără perete și fără cadru (http://www.spi-polymer.ru/otboyniki/) și aflați mai multe.
Acest articol a adunat tabele de sinusuri, cosinus, tangente și cotangente. În primul rând, oferim un tabel cu principalele valori ale funcțiilor trigonometrice, adică un tabel cu sinusuri, cosinus, tangente și cotangente ale unghiurilor 0, 30, 45, 60, 90, ..., 360 de grade ( 0, π/6, π/4, π/3, π/2, …, 2π radian). După aceea, vom oferi un tabel de sinusuri și cosinus, precum și un tabel de tangente și cotangente de V. M. Bradis și vom arăta cum să folosiți aceste tabele atunci când găsiți valorile funcțiilor trigonometrice.
Navigare în pagină.
Tabel de sinusuri, cosinus, tangente și cotangente pentru unghiurile 0, 30, 45, 60, 90, ... grade
Bibliografie.
- Algebră: Proc. pentru 9 celule. medie scoala / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Iluminismul, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
- Bashmakov M.I. Algebra și începutul analizei: Proc. pentru 10-11 celule. medie şcoală - Ed. a 3-a. - M.: Iluminismul, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
- Algebră iar începutul analizei: Proc. pentru 10-11 celule. educatie generala instituții / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn și alții; Ed. A. N. Kolmogorova.- ed. a XIV-a- M.: Iluminismul, 2004.- 384 p.: ill.- ISBN 5-09-013651-3.
- Gusev V. A., Mordkovich A. G. Matematică (un manual pentru solicitanții la școlile tehnice): Proc. indemnizatie.- M.; Superior scoala, 1984.-351 p., ill.
- Bradis V. M. Tabele matematice din patru cifre: Pentru învățământul general. manual stabilimente. - Ed. a II-a. - M.: Butarda, 1999.- 96 p.: ill. ISBN 5-7107-2667-2
1. Funcții trigonometrice sunt funcţii elementare al căror argument este injecţie. Funcțiile trigonometrice descriu relația dintre laturile și unghiurile ascuțite dintr-un triunghi dreptunghic. Domeniile de aplicare a funcțiilor trigonometrice sunt extrem de diverse. Deci, de exemplu, orice proces periodic poate fi reprezentat ca o sumă de funcții trigonometrice (seria Fourier). Aceste funcții apar adesea la rezolvarea ecuațiilor diferențiale și funcționale.
2. Funcțiile trigonometrice includ următoarele 6 funcții: sinusului, cosinus, tangentă,cotangentă, secantăși cosecant. Pentru fiecare dintre aceste funcții, există o funcție trigonometrică inversă.
3. Este convenabil să se introducă definiția geometrică a funcțiilor trigonometrice folosind cerc unitar. Figura de mai jos prezintă un cerc cu raza r=1. Punctul M(x,y) este marcat pe cerc. Unghiul dintre vectorul rază OM și direcția pozitivă a axei Ox este α.
4. sinusului unghiul α este raportul dintre ordonata y a punctului M(x,y) și raza r:
sinα=y/r.
Deoarece r=1, atunci sinusul este egal cu ordonata punctului M(x,y).
5. cosinus unghiul α este raportul dintre abscisa x punctului M(x,y) și raza r:
cosα=x/r
6. tangentă unghiul α este raportul dintre ordonata y a punctului M(x,y) și abscisa sa x:
tanα=y/x,x≠0
7. Cotangentă unghiul α este raportul dintre abscisa x a punctului M(x,y) și ordonata y:
cotα=x/y,y≠0
8. Secantă unghiul α este raportul dintre raza r și abscisa x a punctului M(x,y):
secα=r/x=1/x,x≠0
9. Cosecant unghiul α este raportul dintre raza r și ordonata y a punctului M(x,y):
cscα=r/y=1/y,y≠0
10. În cercul unitar al proiecției x, y punctele M(x, y) și raza r formează un triunghi dreptunghic, în care x, y sunt catetele, iar r este ipotenuza. Prin urmare, definițiile de mai sus ale funcțiilor trigonometrice aplicate unui triunghi dreptunghic sunt formulate după cum urmează:
sinusului unghiul α este raportul dintre catetul opus și ipotenuză.
cosinus unghiul α este raportul dintre catetul adiacent și ipotenuză.
tangentă unghiul α se numește catete opus celui alăturat.
Cotangentă unghiul α se numește cateta adiacentă opusului.
Secantă unghiul α este raportul dintre ipotenuză și catetul adiacent.
Cosecant unghiul α este raportul dintre ipotenuză și catetul opus.
11. graficul funcției sinus
y=sinx, domeniu: x∈R, domeniu: −1≤sinx≤1
12. Graficul funcției cosinus
y=cosx, domeniu: x∈R, interval: −1≤cosx≤1
13. graficul funcției tangente 14. Graficul funcției cotangente 15. Graficul funcției secante
y=tanx, domeniu: x∈R,x≠(2k+1)π/2, domeniu: −∞ 
y=cotx, domeniu: x∈R,x≠kπ, domeniu: −∞ 
y=secx, domeniu: x∈R,x≠(2k+1)π/2, domeniu: secx∈(−∞,−1]∪∪)
