உங்கள் அருகில் பென்சில் உள்ளதா? அதன் பகுதியைப் பாருங்கள் - இது ஒரு வழக்கமான அறுகோணம் அல்லது, அறுகோணம் என்றும் அழைக்கப்படுகிறது. ஒரு கொட்டையின் குறுக்குவெட்டு, அறுகோண சதுரங்கம், சில சிக்கலான கார்பன் மூலக்கூறுகள் (உதாரணமாக, கிராஃபைட்), ஒரு ஸ்னோஃப்ளேக், ஒரு தேன்கூடு மற்றும் பிற பொருட்களும் இந்த வடிவத்தைக் கொண்டுள்ளன. ஒரு பிரம்மாண்டமான வழக்கமான அறுகோணம் சமீபத்தில் கண்டுபிடிக்கப்பட்டது. இயற்கையானது இந்த குறிப்பிட்ட வடிவத்தின் கட்டமைப்புகளை தனது படைப்புகளுக்கு அடிக்கடி பயன்படுத்துவது விசித்திரமாகத் தெரியவில்லையா? இன்னும் விரிவாகப் பார்ப்போம்.

ஒரு வழக்கமான அறுகோணம் என்பது ஆறு சம பக்கங்களும் சம கோணங்களும் கொண்ட பலகோணம். பள்ளி படிப்பிலிருந்து, இது பின்வரும் பண்புகளைக் கொண்டுள்ளது என்பதை நாங்கள் அறிவோம்:

• அதன் பக்கங்களின் நீளம் சுற்றப்பட்ட வட்டத்தின் ஆரம் ஒத்துள்ளது. எல்லாவற்றிலும், ஒரு வழக்கமான அறுகோணத்தில் மட்டுமே இந்த சொத்து உள்ளது.
• கோணங்கள் ஒன்றுக்கொன்று சமமாக இருக்கும், ஒவ்வொன்றின் அளவும் 120 ° ஆகும்.
• ஒரு அறுகோணத்தின் சுற்றளவு, அதைச் சுற்றி வளைக்கப்பட்ட வட்டத்தின் ஆரம் தெரிந்தால் Р=6*R அல்லது வட்டம் அதில் பொறிக்கப்பட்டிருந்தால் Р=4*√(3)*r என்ற சூத்திரத்தைப் பயன்படுத்திக் கண்டறியலாம். R மற்றும் r என்பது சுற்றப்பட்ட மற்றும் பொறிக்கப்பட்ட வட்டங்களின் ஆரங்கள்.
• வழக்கமான அறுகோணத்தால் ஆக்கிரமிக்கப்பட்ட பகுதி பின்வருமாறு தீர்மானிக்கப்படுகிறது: S=(3*√(3)*R 2)/2. ஆரம் தெரியவில்லை என்றால், அதற்குப் பதிலாக ஒரு பக்கத்தின் நீளத்தை மாற்றுகிறோம் - உங்களுக்குத் தெரிந்தபடி, இது சுற்றப்பட்ட வட்டத்தின் ஆரம் நீளத்திற்கு ஒத்திருக்கிறது.

வழக்கமான அறுகோணம் ஒரு சுவாரஸ்யமான அம்சத்தைக் கொண்டுள்ளது, இதன் காரணமாக இது இயற்கையில் மிகவும் பரவலாகிவிட்டது - இது விமானத்தின் எந்த மேற்பரப்பையும் ஒன்றுடன் ஒன்று மற்றும் இடைவெளிகள் இல்லாமல் நிரப்ப முடியும். பால் லெம்மா என்று அழைக்கப்படுபவை கூட உள்ளன, இதன் படி 1/√(3) க்கு சமமான ஒரு வழக்கமான அறுகோணம் ஒரு உலகளாவிய டயர் ஆகும், அதாவது, இது ஒரு அலகு விட்டம் கொண்ட எந்த தொகுப்பையும் மறைக்க முடியும்.

இப்போது ஒரு வழக்கமான அறுகோணத்தின் கட்டுமானத்தைக் கவனியுங்கள். பல வழிகள் உள்ளன, இதில் எளிதான திசைகாட்டி, பென்சில் மற்றும் ஆட்சியாளரின் பயன்பாடு அடங்கும். முதலில், ஒரு திசைகாட்டி மூலம் தன்னிச்சையான வட்டத்தை வரைகிறோம், பின்னர் இந்த வட்டத்தில் ஒரு தன்னிச்சையான இடத்தில் ஒரு புள்ளியை உருவாக்குகிறோம். திசைகாட்டியின் தீர்வை மாற்றாமல், இந்த கட்டத்தில் முனை வைத்து, வட்டத்தில் அடுத்த உச்சநிலையைக் குறிக்கவும், அனைத்து 6 புள்ளிகளையும் பெறும் வரை இந்த வழியில் தொடரவும். இப்போது அவற்றை நேரான பிரிவுகளுடன் ஒருவருக்கொருவர் இணைக்க மட்டுமே உள்ளது, மேலும் விரும்பிய எண்ணிக்கை மாறிவிடும்.

நடைமுறையில், நீங்கள் ஒரு பெரிய அறுகோணத்தை வரைய வேண்டிய நேரங்கள் உள்ளன. எடுத்துக்காட்டாக, இரண்டு நிலை பிளாஸ்டர்போர்டு உச்சவரம்பில், மத்திய சரவிளக்கின் இணைப்புப் புள்ளியைச் சுற்றி, நீங்கள் கீழ் மட்டத்தில் ஆறு சிறிய விளக்குகளை நிறுவ வேண்டும். இந்த அளவு திசைகாட்டி கண்டுபிடிக்க மிகவும் கடினமாக இருக்கும். இந்த வழக்கில் எவ்வாறு தொடர வேண்டும்? ஒரு பெரிய வட்டத்தை எப்படி வரைவது? மிகவும் எளிமையான. நீங்கள் விரும்பிய நீளத்தின் வலுவான நூலை எடுத்து பென்சிலுக்கு எதிரே அதன் முனைகளில் ஒன்றைக் கட்ட வேண்டும். நூலின் இரண்டாவது முனையை சரியான இடத்தில் உச்சவரம்புக்கு அழுத்தும் உதவியாளரைக் கண்டுபிடிப்பது மட்டுமே இப்போது உள்ளது. நிச்சயமாக, இந்த விஷயத்தில், சிறிய பிழைகள் சாத்தியமாகும், ஆனால் அவை வெளிநாட்டவருக்கு கவனிக்கப்பட வாய்ப்பில்லை.

பலகோணங்கள் என்ற தலைப்பு பள்ளி பாடத்திட்டத்தில் உள்ளடக்கப்பட்டுள்ளது, ஆனால் அவர்கள் அதில் போதுமான கவனம் செலுத்துவதில்லை. இதற்கிடையில், இது சுவாரஸ்யமானது, மேலும் இது ஒரு வழக்கமான அறுகோணம் அல்லது அறுகோணத்திற்கு குறிப்பாக உண்மை - எல்லாவற்றிற்கும் மேலாக, பல இயற்கை பொருட்கள் இந்த வடிவத்தைக் கொண்டுள்ளன. இதில் தேன்கூடு மற்றும் பல அடங்கும். இந்த வடிவம் நடைமுறையில் நன்றாகப் பயன்படுத்தப்படுகிறது.

வரையறை மற்றும் கட்டுமானம்

ஒரு வழக்கமான அறுகோணம் என்பது ஆறு பக்கங்களும் சமமான நீளமும் அதே எண்ணிக்கையிலான சம கோணங்களும் கொண்ட ஒரு விமான உருவமாகும்.

பலகோணத்தின் கோணங்களின் கூட்டுத்தொகைக்கான சூத்திரத்தை நாம் நினைவு கூர்ந்தால்

இந்த எண்ணிக்கையில் இது 720 ° க்கு சமம் என்று மாறிவிடும். சரி, உருவத்தின் அனைத்து கோணங்களும் சமமாக இருப்பதால், அவை ஒவ்வொன்றும் 120 ° க்கு சமம் என்பதைக் கணக்கிடுவது எளிது.

ஒரு அறுகோணத்தை வரைவது மிகவும் எளிது, உங்களுக்கு தேவையானது ஒரு திசைகாட்டி மற்றும் ஒரு ஆட்சியாளர்.

படிப்படியான வழிமுறைகள் இப்படி இருக்கும்:

விரும்பினால், சம ஆரம் கொண்ட ஐந்து வட்டங்களை வரைவதன் மூலம் ஒரு கோடு இல்லாமல் செய்யலாம்.

இவ்வாறு பெறப்பட்ட உருவம் வழக்கமான அறுகோணமாக இருக்கும், இதை கீழே நிரூபிக்கலாம்.

பண்புகள் எளிமையானவை மற்றும் சுவாரஸ்யமானவை

வழக்கமான அறுகோணத்தின் பண்புகளைப் புரிந்து கொள்ள, அதை ஆறு முக்கோணங்களாக உடைப்பது அர்த்தமுள்ளதாக இருக்கிறது:

இது எதிர்காலத்தில் அதன் பண்புகளை இன்னும் தெளிவாகக் காட்ட உதவும், அவற்றில் முக்கியமானது:

1. சுற்றப்பட்ட வட்டத்தின் விட்டம்;
2. பொறிக்கப்பட்ட வட்டத்தின் விட்டம்;
3. சதுரம்;
4. சுற்றளவு.

சுற்றப்பட்ட வட்டம் மற்றும் கட்டுமான சாத்தியம்

ஒரு அறுகோணத்தைச் சுற்றி ஒரு வட்டத்தை விவரிக்க முடியும், மேலும், ஒன்று மட்டுமே. இந்த எண்ணிக்கை சரியானது என்பதால், நீங்கள் அதை மிகவும் எளிமையாக செய்யலாம்: உள்ளே இரண்டு அடுத்தடுத்த கோணங்களில் இருந்து ஒரு இருசமயத்தை வரையவும். அவை புள்ளி O இல் வெட்டுகின்றன, மேலும் அவற்றுக்கிடையேயான பக்கத்துடன் சேர்ந்து ஒரு முக்கோணத்தை உருவாக்குகின்றன.

அறுகோணத்தின் பக்கத்திற்கும் இருபக்கங்களுக்கும் இடையே உள்ள கோணங்கள் ஒவ்வொன்றும் 60° ஆக இருக்கும், எனவே ஒரு முக்கோணம், எடுத்துக்காட்டாக, AOB ஐசோசெல்ஸ் என்று நாம் உறுதியாகக் கூறலாம். மூன்றாவது கோணமும் 60 ° க்கு சமமாக இருக்கும் என்பதால், அது சமபக்கமாகவும் இருக்கும். OA மற்றும் OB ஆகிய பிரிவுகள் சமமாக இருப்பதைப் பின்தொடர்கிறது, அதாவது அவை வட்டத்தின் ஆரமாக செயல்பட முடியும்.

அதன் பிறகு, நீங்கள் அடுத்த பக்கத்திற்குச் செல்லலாம், மேலும் புள்ளி C இல் உள்ள கோணத்திலிருந்து ஒரு இருசமயத்தையும் வரையலாம். இது மற்றொரு சமபக்க முக்கோணமாக மாறும், மேலும் AB பக்கமானது ஒரே நேரத்தில் இருவருக்கு பொதுவானதாக இருக்கும், மேலும் OS ஆனது அதே வட்டம் செல்லும் அடுத்த ஆரமாக இருக்கும். மொத்தத்தில் இதுபோன்ற ஆறு முக்கோணங்கள் இருக்கும், மேலும் அவை O புள்ளியில் பொதுவான உச்சியைக் கொண்டிருக்கும். அது வட்டத்தை விவரிக்க முடியும் என்று மாறிவிடும், அது ஒன்று மட்டுமே, அதன் ஆரம் அறுகோணத்தின் பக்கத்திற்கு சமமாக இருக்கும். :

அதனால்தான் திசைகாட்டி மற்றும் ஆட்சியாளரின் உதவியுடன் இந்த உருவத்தை உருவாக்க முடியும்.

சரி, இந்த வட்டத்தின் பரப்பளவு நிலையானதாக இருக்கும்:

பொறிக்கப்பட்ட வட்டம்

சுற்றப்பட்ட வட்டத்தின் மையம் பொறிக்கப்பட்ட ஒன்றின் மையத்துடன் ஒத்துப்போகிறது. இதை சரிபார்க்க, புள்ளி O இலிருந்து அறுகோணத்தின் பக்கங்களுக்கு செங்குத்தாக வரையலாம். அவை அறுகோணத்தை உருவாக்கும் அந்த முக்கோணங்களின் உயரமாக இருக்கும். ஐசோசெல்ஸ் முக்கோணத்தில், உயரமானது அது இருக்கும் பக்கத்தைப் பொறுத்தமட்டில் இடைநிலை ஆகும். எனவே, இந்த உயரம் செங்குத்தாக இருபக்கமாக உள்ளது, இது பொறிக்கப்பட்ட வட்டத்தின் ஆரம் ஆகும்.

ஒரு சமபக்க முக்கோணத்தின் உயரம் எளிமையாக கணக்கிடப்படுகிறது:

h²=a²-(a/2)²= a²3/4, h=a(√3)/2

R=a மற்றும் r=h என்பதால், அது மாறிவிடும்

r=R(√3)/2.

இவ்வாறு, பொறிக்கப்பட்ட வட்டம் ஒரு வழக்கமான அறுகோணத்தின் பக்கங்களின் மையங்கள் வழியாக செல்கிறது.

அதன் பரப்பளவு இருக்கும்:

S=3πa²/4,

அதாவது, அதில் முக்கால்வாசி விவரம்.

சுற்றளவு மற்றும் பரப்பளவு

சுற்றளவுடன் எல்லாம் தெளிவாக உள்ளது, இது பக்கங்களின் நீளங்களின் கூட்டுத்தொகை:

P=6a, அல்லது பி=6ஆர்

ஆனால் அறுகோணத்தை வகுக்கக்கூடிய அனைத்து ஆறு முக்கோணங்களின் கூட்டுத்தொகைக்கு சமமான பரப்பளவு இருக்கும். ஒரு முக்கோணத்தின் பரப்பளவு அடித்தளம் மற்றும் உயரத்தின் பாதிப் பொருளாகக் கணக்கிடப்படுவதால், பின்:

S \u003d 6 (a / 2) (a (√3) / 2) \u003d 6a² (√3) / 4 \u003d 3a² (√3) / 2அல்லது

S=3R²(√3)/2

பொறிக்கப்பட்ட வட்டத்தின் ஆரம் மூலம் இந்தப் பகுதியைக் கணக்கிட விரும்புவோர் இப்படிச் செய்யலாம்:

S=3(2r/√3)²(√3)/2=r²(2√3)

பொழுதுபோக்கு கட்டுமானங்கள்

ஒரு முக்கோணத்தை ஒரு அறுகோணத்தில் பொறிக்க முடியும், அதன் பக்கங்கள் ஒரு வழியாக செங்குத்துகளை இணைக்கும்:

மொத்தத்தில் அவர்களில் இருவர் இருப்பார்கள், அவர்கள் ஒருவருக்கொருவர் சுமத்துவது டேவிட் நட்சத்திரத்தை கொடுக்கும். இந்த முக்கோணங்கள் ஒவ்வொன்றும் சமபக்கமானது. இதைச் சரிபார்க்க எளிதானது. நீங்கள் ஏசி பக்கத்தைப் பார்த்தால், அது ஒரே நேரத்தில் இரண்டு முக்கோணங்களுக்கு சொந்தமானது - BAC மற்றும் AEC. அவற்றில் முதலாவது AB \u003d BC, மற்றும் அவற்றுக்கிடையேயான கோணம் 120 ° ஆக இருந்தால், மீதமுள்ள ஒவ்வொன்றும் 30 ° ஆக இருக்கும். இதிலிருந்து நாம் தர்க்கரீதியான முடிவுகளை எடுக்கலாம்:

1. sin30°=1/2 என்பதால், உச்சி B இலிருந்து ABCயின் உயரம் அறுகோணத்தின் பாதிப் பக்கத்திற்குச் சமமாக இருக்கும். இதை சரிபார்க்க விரும்புவோர் பித்தகோரியன் தேற்றத்தின்படி மீண்டும் கணக்கிடுமாறு அறிவுறுத்தலாம், அது இங்கே சரியாக பொருந்துகிறது.
2. AC பக்கமானது பொறிக்கப்பட்ட வட்டத்தின் இரண்டு ஆரங்களுக்கு சமமாக இருக்கும், இது மீண்டும் அதே தேற்றத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது. அதாவது, AC=2(a(√3)/2)=а(√3).
3. ABC, CDE மற்றும் AEF ஆகிய முக்கோணங்கள் இரண்டு பக்கங்களிலும் சமமாக இருக்கும் மற்றும் அவற்றுக்கிடையேயான கோணம், எனவே AC, CE மற்றும் EA ஆகிய பக்கங்களின் சமத்துவம் பின்வருமாறு.

ஒன்றோடொன்று குறுக்கிடும்போது, ​​முக்கோணங்கள் ஒரு புதிய அறுகோணத்தை உருவாக்குகின்றன, மேலும் இது வழக்கமானது. நிரூபிப்பது எளிது:

இவ்வாறு, உருவம் ஒரு வழக்கமான அறுகோணத்தின் அறிகுறிகளை சந்திக்கிறது - இது ஆறு சம பக்கங்களையும் கோணங்களையும் கொண்டுள்ளது. செங்குத்துகளில் உள்ள முக்கோணங்களின் சமத்துவத்திலிருந்து, புதிய அறுகோணத்தின் பக்கத்தின் நீளத்தைக் குறைப்பது எளிது:

d=а(√3)/3

அதைச் சுற்றி விவரிக்கப்பட்டுள்ள வட்டத்தின் ஆரமாகவும் இருக்கும். பொறிக்கப்பட்ட ஆரம் பெரிய அறுகோணத்தின் பாதி பக்கமாக இருக்கும், இது ஏபிசி முக்கோணத்தைக் கருத்தில் கொள்ளும்போது நிரூபிக்கப்பட்டது. அதன் உயரம் சரியாக பக்கத்தின் பாதி, எனவே, இரண்டாவது பாதி சிறிய அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரம்:

r₂=A/2

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

டேவிட் நட்சத்திரத்தின் உள்ளே உள்ள அறுகோணத்தின் பரப்பளவு நட்சத்திரம் பொறிக்கப்பட்ட பெரியதை விட மூன்று மடங்கு சிறியது என்று மாறிவிடும்.

கோட்பாட்டிலிருந்து நடைமுறைக்கு

அறுகோணத்தின் பண்புகள் இயற்கையிலும் மனித செயல்பாட்டின் பல்வேறு துறைகளிலும் மிகவும் தீவிரமாகப் பயன்படுத்தப்படுகின்றன. முதலாவதாக, இது போல்ட் மற்றும் கொட்டைகளுக்கு பொருந்தும் - முதல் மற்றும் இரண்டாவது தொப்பிகள் வழக்கமான அறுகோணத்தைத் தவிர வேறில்லை, நீங்கள் சேம்ஃபர்களை கணக்கில் எடுத்துக் கொள்ளாவிட்டால். குறடுகளின் அளவு பொறிக்கப்பட்ட வட்டத்தின் விட்டம் - அதாவது எதிர் முகங்களுக்கு இடையிலான தூரம்.

அதன் பயன்பாடு மற்றும் அறுகோண ஓடுகளைக் கண்டறிந்துள்ளது. இது ஒரு நாற்கரத்தை விட மிகவும் குறைவான பொதுவானது, ஆனால் அதை இடுவது மிகவும் வசதியானது: மூன்று ஓடுகள் ஒரு கட்டத்தில் சந்திக்கின்றன, நான்கு அல்ல. கலவைகள் மிகவும் சுவாரஸ்யமாக இருக்கலாம்:

கான்கிரீட் நடைபாதை அடுக்குகளும் தயாரிக்கப்படுகின்றன.

இயற்கையில் அறுகோணத்தின் பரவலானது எளிமையாக விளக்கப்பட்டுள்ளது. எனவே, வட்டங்கள் மற்றும் பந்துகள் ஒரே விட்டம் இருந்தால் விமானத்தில் இறுக்கமாக பொருத்துவது எளிதானது. இதன் காரணமாக, தேன்கூடுகள் அத்தகைய வடிவத்தைக் கொண்டுள்ளன.

தூரம் மற்றும் நீள அலகுகள் மாற்றி பகுதி அலகுகள் மாற்றி சேர் © 2011-2017 Mikhail Dovzhik பொருட்களை நகலெடுப்பது தடைசெய்யப்பட்டுள்ளது. ஆன்லைன் கால்குலேட்டரில், நீங்கள் அதே அளவீட்டு அலகுகளில் மதிப்புகளைப் பயன்படுத்தலாம்! அளவீட்டு அலகுகளை மாற்றுவதில் சிக்கல் இருந்தால், தொலைவு மற்றும் நீள அலகு மாற்றி மற்றும் பகுதி அலகு மாற்றியைப் பயன்படுத்தவும். நாற்கர பகுதி கால்குலேட்டரின் கூடுதல் அம்சங்கள்

• விசைப்பலகையில் வலது மற்றும் இடது விசைகளை அழுத்துவதன் மூலம் உள்ளீட்டு புலங்களுக்கு இடையில் செல்லலாம்.

கோட்பாடு. ஒரு நாற்கரத்தின் பரப்பளவு ஒரு நாற்கரமானது நான்கு புள்ளிகள் (செங்குத்துகள்) கொண்ட ஒரு வடிவியல் உருவமாகும், அவற்றில் மூன்று ஒரே நேர்கோட்டில் உள்ளன, மேலும் இந்த புள்ளிகளை ஜோடிகளாக இணைக்கும் நான்கு பிரிவுகள் (பக்கங்கள்). இந்த நாற்கரத்தின் ஏதேனும் இரண்டு புள்ளிகளை இணைக்கும் பிரிவு அதன் உள்ளே இருந்தால், ஒரு நாற்கரமானது குவிவு எனப்படும்.

பலகோணத்தின் பகுதியை எவ்வாறு கண்டுபிடிப்பது?

பலகோண AB இன் ஒவ்வொரு விளிம்பையும் எடுத்து, ABO முக்கோணத்தின் பரப்பளவை, O மூலையில் உள்ள உச்சியில், செங்குத்துகளின் ஒருங்கிணைப்புகள் மூலம் கணக்கிடுவதன் மூலம் பகுதியை நிர்ணயிப்பதற்கான சூத்திரம் தீர்மானிக்கப்படுகிறது. ஒரு பலகோணத்தைச் சுற்றி நடக்கும்போது, ​​பலகோணத்தின் உட்புறம் உட்பட முக்கோணங்கள் உருவாகின்றன மற்றும் அதற்கு வெளியே அமைந்துள்ளன. இந்த பகுதிகளின் கூட்டுத்தொகைக்கு இடையிலான வேறுபாடு பலகோணத்தின் பரப்பளவாகும்.

எனவே, "கார்ட்டோகிராபர்" தோற்றத்தில் இருப்பதால், சூத்திரம் சர்வேயர் ஃபார்முலா என்று அழைக்கப்படுகிறது; அது அந்தப் பகுதியை எதிரெதிர் திசையில் நடந்தால், அது இடதுபுறத்தில் இருந்தால் அந்தப் பகுதி சேர்க்கப்படும் மற்றும் தோற்றத்தின் அடிப்படையில் வலதுபுறம் இருந்தால் கழிக்கப்படும். குறுக்கிடாத (எளிய) பலகோணத்திற்கு பகுதி சூத்திரம் செல்லுபடியாகும், இது குவிந்த அல்லது குழிவானதாக இருக்கலாம். உள்ளடக்கம்

• 1 வரையறை
• 2 எடுத்துக்காட்டுகள்
• 3 மிகவும் சிக்கலான உதாரணம்
• 4 பெயர் விளக்கம்
• 5 பார்க்கவும்

பலகோணப் பகுதி

கவனம்

அவ்வாறு இருந்திருக்கலாம்:

• முக்கோணம்;
• நாற்புறம்;
• ஐந்து அல்லது அறுகோணம் மற்றும் பல.

அத்தகைய உருவம் நிச்சயமாக இரண்டு நிலைகளால் வகைப்படுத்தப்படும்:

1. அருகிலுள்ள பக்கங்களும் ஒரே கோட்டிற்கு சொந்தமானவை அல்ல.
2. அருகில் இல்லாதவற்றுக்கு பொதுவான புள்ளிகள் இல்லை, அதாவது அவை வெட்டுவதில்லை.

எந்த செங்குத்துகள் அருகில் உள்ளன என்பதைப் புரிந்து கொள்ள, அவை ஒரே பக்கத்தைச் சேர்ந்ததா என்பதை நீங்கள் பார்க்க வேண்டும். ஆம் எனில், அண்டை நாடு. இல்லையெனில், அவை ஒரு பகுதியால் இணைக்கப்படலாம், இது ஒரு மூலைவிட்டம் என்று அழைக்கப்பட வேண்டும். மூன்றுக்கும் மேற்பட்ட செங்குத்துகளைக் கொண்ட பலகோணங்களில் மட்டுமே அவற்றை வரைய முடியும்.

அவற்றில் என்ன வகைகள் உள்ளன? நான்கு மூலைகளுக்கு மேல் உள்ள பலகோணம் குவிந்த அல்லது குழிவானதாக இருக்கலாம். பிந்தையவற்றின் வேறுபாடு என்னவென்றால், அதன் சில முனைகள் பலகோணத்தின் தன்னிச்சையான பக்கத்தின் வழியாக வரையப்பட்ட ஒரு நேர்கோட்டின் வெவ்வேறு பக்கங்களில் இருக்கலாம்.

வழக்கமான மற்றும் ஒழுங்கற்ற அறுகோணத்தின் பகுதியை எவ்வாறு கண்டுபிடிப்பது?

• பக்கத்தின் நீளத்தை அறிந்து, அதை 6 ஆல் பெருக்கி, அறுகோணத்தின் சுற்றளவைப் பெறுங்கள்: 10 செ.மீ x 6 \u003d 60 செ.மீ.
• எங்கள் சூத்திரத்தில் முடிவுகளை மாற்றவும்:
பகுதி \u003d 1/2 * சுற்றளவு * அபோதீமா பகுதி \u003d ½ * 60cm * 5√3 தீர்க்கவும்: இப்போது சதுர வேர்களை அகற்றுவதற்கான பதிலை எளிமைப்படுத்தவும், சதுர சென்டிமீட்டரில் முடிவைக் குறிக்கவும் உள்ளது: ½ * 60 செ.மீ * 5 √3 cm \u003d 30 * 5√3 cm =150 √3 cm =259.8 cm² வழக்கமான அறுகோணத்தின் பரப்பளவை எவ்வாறு கண்டுபிடிப்பது என்பது குறித்த வீடியோ ஒழுங்கற்ற அறுகோணத்தின் பரப்பளவை தீர்மானிக்க பல விருப்பங்கள் உள்ளன:

• ட்ரேப்சாய்டு முறை.
• ஒருங்கிணைப்பு அச்சைப் பயன்படுத்தி ஒழுங்கற்ற பலகோணங்களின் பரப்பளவைக் கணக்கிடுவதற்கான ஒரு முறை.
• ஒரு அறுகோணத்தை மற்ற வடிவங்களாகப் பிரிக்கும் முறை.

உங்களுக்குத் தெரிந்த ஆரம்ப தரவைப் பொறுத்து, பொருத்தமான முறை தேர்ந்தெடுக்கப்படுகிறது.

முக்கியமான

சில ஒழுங்கற்ற அறுகோணங்கள் இரண்டு இணையான வரைபடங்களைக் கொண்டிருக்கும். ஒரு இணையான வரைபடத்தின் பகுதியைத் தீர்மானிக்க, அதன் நீளத்தை அதன் அகலத்தால் பெருக்கி, பின்னர் ஏற்கனவே அறியப்பட்ட இரண்டு பகுதிகளைச் சேர்க்கவும். பலகோணத்தின் பரப்பளவை எவ்வாறு கண்டறிவது என்பது குறித்த காணொளி ஒரு சமபக்க அறுகோணம் ஆறு சம பக்கங்களைக் கொண்டது மற்றும் வழக்கமான அறுகோணமாகும்.

ஒரு சமபக்க அறுகோணத்தின் பரப்பளவு முக்கோணங்களின் 6 பகுதிகளுக்கு சமம், அதில் வழக்கமான அறுகோண உருவம் பிரிக்கப்பட்டுள்ளது. ஒரு வழக்கமான அறுகோணத்தில் உள்ள அனைத்து முக்கோணங்களும் சமமானவை, எனவே அத்தகைய அறுகோணத்தின் பரப்பளவைக் கண்டுபிடிக்க, குறைந்தபட்சம் ஒரு முக்கோணத்தின் பரப்பளவை அறிந்தால் போதும். ஒரு சமபக்க அறுகோணத்தின் பகுதியைக் கண்டுபிடிக்க, மேலே விவரிக்கப்பட்ட வழக்கமான அறுகோணத்தின் பகுதிக்கான சூத்திரம் பயன்படுத்தப்படுகிறது.

404 கிடைக்கவில்லை

ஒரு வீட்டை அலங்கரித்தல், ஆடை, படங்கள் வரைதல் ஆகியவை வடிவவியலில் தகவல்களை உருவாக்குவதற்கும் குவிப்பதற்கும் பங்களித்தன, அந்தக் கால மக்கள் அனுபவபூர்வமாகப் பெற்றனர், பிட் பி பிட் மற்றும் தலைமுறையிலிருந்து தலைமுறைக்கு அனுப்பப்பட்டனர். இன்று, ஒரு கட்டர், ஒரு கட்டடம், ஒரு கட்டிடக் கலைஞர் மற்றும் அன்றாட வாழ்க்கையில் ஒவ்வொரு சாதாரண மனிதருக்கும் வடிவவியலின் அறிவு அவசியம். எனவே, வெவ்வேறு புள்ளிவிவரங்களின் பரப்பளவை எவ்வாறு கணக்கிடுவது என்பதை நீங்கள் கற்றுக் கொள்ள வேண்டும், மேலும் வழக்கமான அறுகோணத்திற்கான சூத்திரம் உட்பட ஒவ்வொரு சூத்திரங்களும் பின்னர் நடைமுறையில் பயனுள்ளதாக இருக்கும் என்பதை நினைவில் கொள்ளுங்கள்.
ஒரு அறுகோணம் என்பது பலகோண உருவம் ஆகும், இதன் மொத்த கோணங்களின் எண்ணிக்கை ஆறு. ஒரு வழக்கமான அறுகோணம் என்பது சம பக்கங்களைக் கொண்ட ஒரு அறுகோண உருவம். வழக்கமான அறுகோணத்தின் கோணங்களும் ஒன்றுக்கொன்று சமமாக இருக்கும்.
அன்றாட வாழ்க்கையில், வழக்கமான அறுகோண வடிவத்தைக் கொண்ட பொருட்களை நாம் அடிக்கடி காணலாம்.

பக்கவாட்டில் ஒழுங்கற்ற பலகோண பகுதி கால்குலேட்டர்

உனக்கு தேவைப்படும்

• - சில்லி;
• - மின்னணு ரேஞ்ச்ஃபைண்டர்;
• - ஒரு தாள் மற்றும் ஒரு பென்சில்;
• - கால்குலேட்டர்.

வழிமுறை 1 உங்களுக்கு அபார்ட்மெண்ட் அல்லது தனி அறையின் மொத்த பரப்பளவு தேவைப்பட்டால், அபார்ட்மெண்ட் அல்லது வீட்டின் தொழில்நுட்ப பாஸ்போர்ட்டைப் படிக்கவும், அது ஒவ்வொரு அறையின் காட்சிகளையும் அபார்ட்மெண்டின் மொத்த காட்சிகளையும் காட்டுகிறது. 2 ஒரு செவ்வக அல்லது சதுர அறையின் பரப்பளவை அளவிட, டேப் அளவீடு அல்லது மின்னணு ரேஞ்ச்ஃபைண்டர் எடுத்து சுவர்களின் நீளத்தை அளவிடவும். ரேஞ்ச்ஃபைண்டர் மூலம் தூரத்தை அளவிடும் போது, ​​பீம் திசையை செங்குத்தாக வைக்க வேண்டும், இல்லையெனில் அளவீட்டு முடிவுகள் சிதைந்து போகலாம். 3 பின்னர் அறையின் விளைவான நீளத்தை (மீட்டரில்) அகலத்தால் (மீட்டரில்) பெருக்கவும். இதன் விளைவாக மதிப்பு தரையில் இருக்கும், இது சதுர மீட்டரில் அளவிடப்படுகிறது.

காஸ் பகுதி சூத்திரம்

ஒரு ஐங்கோண அறை அல்லது ஒரு சுற்று வளைவு கொண்ட அறை போன்ற மிகவும் சிக்கலான கட்டமைப்பின் தரைப் பகுதியை நீங்கள் கணக்கிட வேண்டும் என்றால், ஒரு துண்டு காகிதத்தில் ஒரு திட்ட ஓவியத்தை வரையவும். பின்னர் சிக்கலான வடிவத்தை ஒரு சதுரம் மற்றும் ஒரு முக்கோணம் அல்லது ஒரு செவ்வகம் மற்றும் ஒரு அரை வட்டம் போன்ற பல எளிய வடிவங்களாக பிரிக்கவும். ஒரு டேப் அளவீடு அல்லது ரேஞ்ச்ஃபைண்டரைப் பயன்படுத்தி, பெறப்பட்ட உருவங்களின் அனைத்துப் பக்கங்களின் அளவையும் அளவிடவும் (ஒரு வட்டத்திற்கு, நீங்கள் விட்டம் தெரிந்து கொள்ள வேண்டும்) மற்றும் உங்கள் வரைபடத்தில் முடிவுகளை உள்ளிடவும்.

5 இப்போது ஒவ்வொரு வடிவத்தின் பகுதியையும் தனித்தனியாக கணக்கிடுங்கள். செவ்வகங்கள் மற்றும் சதுரங்களின் பரப்பளவு பக்கங்களைப் பெருக்குவதன் மூலம் கணக்கிடப்படுகிறது. ஒரு வட்டத்தின் பரப்பளவைக் கணக்கிட, விட்டத்தை அரை மற்றும் சதுரமாகப் பிரிக்கவும் (அதைத் தானே பெருக்கவும்), பின்னர் முடிவை 3.14 ஆல் பெருக்கவும்.
நீங்கள் வட்டத்தின் பாதியை மட்டுமே விரும்பினால், அதன் விளைவாக வரும் பகுதியை பாதியாக பிரிக்கவும். ஒரு முக்கோணத்தின் பரப்பளவைக் கணக்கிட, அனைத்து பக்கங்களின் கூட்டுத்தொகையை 2 ஆல் வகுத்து P ஐக் கண்டறியவும்.

ஒழுங்கற்ற பலகோணத்தின் பரப்பளவைக் கணக்கிடுவதற்கான சூத்திரம்

புள்ளிகள் எதிரெதிர் திசையில் வரிசையாக எண்ணப்பட்டால், மேலே உள்ள சூத்திரத்தில் உள்ள தீர்மானங்கள் நேர்மறை மற்றும் அதிலுள்ள மாடுலஸ் தவிர்க்கப்படலாம்; அவை கடிகார திசையில் எண்ணப்பட்டால், தீர்மானிப்பான்கள் எதிர்மறையாக இருக்கும். ஏனெனில் இந்த சூத்திரத்தை கிரீன் தேற்றத்தின் சிறப்பு நிகழ்வாகக் கருதலாம். சூத்திரத்தைப் பயன்படுத்த, கார்ட்டீசியன் விமானத்தில் உள்ள பலகோண முனைகளின் ஆயங்களை நீங்கள் அறிந்து கொள்ள வேண்டும்.

எடுத்துக்காட்டாக, ஆய ((2, 1), (4, 5), (7, 8)) கொண்ட முக்கோணத்தை எடுத்துக் கொள்வோம். முதல் உச்சியின் முதல் x-ஆயத்தை எடுத்து இரண்டாவது உச்சியின் y-கோர்டினேட்டால் பெருக்கவும், பின்னர் இரண்டாவது உச்சியின் x-கோர்டினேட்டை மூன்றாவது y-ஆயத்தால் பெருக்கவும். அனைத்து முனைகளிலும் இந்த நடைமுறையை நாங்கள் மீண்டும் செய்கிறோம். முடிவை பின்வரும் சூத்திரத்தால் தீர்மானிக்க முடியும்: A tri.

ஒழுங்கற்ற நாற்கரத்தின் பரப்பளவைக் கணக்கிடுவதற்கான சூத்திரம்

A) _(\text(tri.))=(1 \over 2)|x_(1)y_(2)+x_(2)y_(3)+x_(3)y_(1)-x_(2) y_(1)-x_(3)y_(2)-x_(1)y_(3)|) இதில் xi மற்றும் yi ஆகியவை தொடர்புடைய ஒருங்கிணைப்பைக் குறிக்கின்றன. வழக்கு n = 3க்கான பொதுவான சூத்திரத்தில் அடைப்புக்குறிகளைத் திறப்பதன் மூலம் இந்த சூத்திரத்தைப் பெறலாம். இந்த சூத்திரத்தைப் பயன்படுத்தி, ஒரு முக்கோணத்தின் பரப்பளவு 10 + 32 + 7 - 4 இன் பாதித் தொகைக்கு சமமாக இருப்பதைக் கண்டறியலாம். 35 - 16, இது 3. சூத்திரத்தில் உள்ள மாறிகளின் எண்ணிக்கை பலகோணத்தின் பக்கங்களின் எண்ணிக்கையைப் பொறுத்தது. எடுத்துக்காட்டாக, ஒரு பென்டகனின் பகுதிக்கான சூத்திரம் x5 மற்றும் y5 வரை மாறிகளைப் பயன்படுத்தும்: ஒரு பென்ட். = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 - x 2 y 1 - x 3 y 2 - x 4 y 3 - x 5 y 4 | 1 y 3 (\displaystyle \mathbf (A) _(\text(pent.))=(1 \over 2)|x_(1)y_(2)+x_(2)y_(3)+x_(3)y_(4 )+x_(4)y_(5)+x_(5)y_(1)-x_(2)y_(1)-x_(3)y_(2)-x_(4)y_(3)-x_(5) )y_(4)-x_(1)y_(5)|) ஒரு குவாட் - x4 மற்றும் y4 வரையிலான மாறிகள்: ஒரு குவாட்.

நான்கு மூலைகளுக்கு மேல் உள்ள மிகவும் பிரபலமான உருவம் வழக்கமான அறுகோணமாகும். வடிவவியலில், இது பெரும்பாலும் சிக்கல்களில் பயன்படுத்தப்படுகிறது. வாழ்க்கையில், தேன்கூடுகள் வெட்டப்பட்டவை.

இது எவ்வாறு தவறாக இருந்து வேறுபட்டது?

முதலில், ஒரு அறுகோணம் என்பது 6 செங்குத்துகளைக் கொண்ட ஒரு உருவம். இரண்டாவதாக, அது குவிந்த அல்லது குழிவானதாக இருக்கலாம். மற்ற இரண்டு வழியாக வரையப்பட்ட ஒரு நேர்கோட்டின் ஒரு பக்கத்தில் நான்கு செங்குத்துகள் அமைந்திருப்பதில் முதலாவது வேறுபடுகிறது.

மூன்றாவதாக, ஒரு வழக்கமான அறுகோணம் அதன் அனைத்து பக்கங்களும் சமமாக இருப்பதால் வகைப்படுத்தப்படுகிறது. மேலும், உருவத்தின் ஒவ்வொரு மூலையிலும் அதே மதிப்பு உள்ளது. அதன் அனைத்து கோணங்களின் கூட்டுத்தொகையைத் தீர்மானிக்க, நீங்கள் சூத்திரத்தைப் பயன்படுத்த வேண்டும்: 180º * (n - 2). இங்கே n என்பது உருவத்தின் முனைகளின் எண்ணிக்கை, அதாவது 6. ஒரு எளிய கணக்கீடு 720º மதிப்பைக் கொடுக்கிறது. எனவே ஒவ்வொரு கோணமும் 120 டிகிரி ஆகும்.

அன்றாட நடவடிக்கைகளில், ஒரு வழக்கமான அறுகோணம் ஒரு ஸ்னோஃப்ளேக் மற்றும் ஒரு கொட்டையில் காணப்படுகிறது. வேதியியலாளர்கள் பென்சீன் மூலக்கூறில் கூட அதைப் பார்க்கிறார்கள்.

சிக்கலைத் தீர்க்கும்போது என்ன பண்புகளை நீங்கள் தெரிந்து கொள்ள வேண்டும்?

மேலே கூறப்பட்டவற்றுடன் சேர்க்கப்பட வேண்டும்:

• உருவத்தின் மூலைவிட்டங்கள், மையத்தின் வழியாக வரையப்பட்டு, அதை ஆறு முக்கோணங்களாகப் பிரிக்கின்றன, அவை சமபக்கமாக உள்ளன;
• வழக்கமான அறுகோணத்தின் பக்கமானது அதைச் சுற்றியுள்ள வட்டத்தின் ஆரத்துடன் ஒத்துப்போகும் மதிப்பைக் கொண்டுள்ளது;
• அத்தகைய உருவத்தைப் பயன்படுத்தி, விமானத்தை நிரப்புவது சாத்தியமாகும், அவற்றுக்கிடையே இடைவெளிகளும் ஒன்றுடன் ஒன்றும் இருக்காது.

அறிமுகப்படுத்தப்பட்ட குறியீடு

பாரம்பரியமாக, வழக்கமான வடிவியல் உருவத்தின் பக்கமானது "a" என்ற லத்தீன் எழுத்தால் குறிக்கப்படுகிறது. சிக்கல்களைத் தீர்க்க, பகுதி மற்றும் சுற்றளவு தேவை, இவை முறையே S மற்றும் P ஆகும். ஒரு வட்டம் ஒரு வழக்கமான அறுகோணத்தில் பொறிக்கப்பட்டுள்ளது அல்லது அதைச் சுற்றி வளைக்கப்பட்டுள்ளது. பின்னர் அவற்றின் ஆரங்களுக்கான மதிப்புகள் உள்ளிடப்படுகின்றன. அவை முறையே r மற்றும் R என்ற எழுத்துக்களால் குறிக்கப்படுகின்றன.

சில சூத்திரங்களில், ஒரு உள் கோணம், ஒரு அரை-சுற்றளவு மற்றும் ஒரு அபோதெம் (இது பலகோணத்தின் மையத்திலிருந்து எந்தப் பக்கத்தின் நடுவிற்கும் செங்குத்தாக இருக்கும்) தோன்றும். அவற்றிற்கு எழுத்துக்கள் பயன்படுத்தப்படுகின்றன: α, p, m.

வடிவத்தை விவரிக்கும் சூத்திரங்கள்

பொறிக்கப்பட்ட வட்டத்தின் ஆரம் கணக்கிட, உங்களுக்கு இது தேவை: r= (a * √3) / 2, மற்றும் r = m. அதாவது, அதே ஃபார்முலா அபிநயத்திற்கும் இருக்கும்.

ஒரு அறுகோணத்தின் சுற்றளவு அனைத்து பக்கங்களின் கூட்டுத்தொகையாக இருப்பதால், அது பின்வருமாறு தீர்மானிக்கப்படும்: P = 6 * a. பக்கமானது சுற்றப்பட்ட வட்டத்தின் ஆரத்திற்கு சமமாக இருப்பதால், சுற்றளவுக்கு ஒரு வழக்கமான அறுகோணத்திற்கு அத்தகைய சூத்திரம் உள்ளது: P \u003d 6 * R. பொறிக்கப்பட்ட வட்டத்தின் ஆரத்திற்கு கொடுக்கப்பட்ட ஒன்றிலிருந்து, ஒரு இடையேயான உறவு மற்றும் r பெறப்பட்டது. பின்னர் சூத்திரம் பின்வரும் படிவத்தை எடுக்கும்: Р = 4 r * √3.

வழக்கமான அறுகோணத்தின் பகுதிக்கு, இது கைக்கு வரலாம்: S = p * r = (a 2 * 3 √3) / 2.

பணிகள்

எண் 1. நிபந்தனை.ஒரு வழக்கமான அறுகோண ப்ரிஸம் உள்ளது, அதன் ஒவ்வொரு விளிம்பும் 4 செ.மீ.க்கு சமமாக இருக்கும்.ஒரு சிலிண்டர் அதில் பொறிக்கப்பட்டுள்ளது, அதன் அளவு தீர்மானிக்கப்பட வேண்டும்.

தீர்வு.ஒரு சிலிண்டரின் அளவு அடித்தளத்தின் பரப்பளவு மற்றும் உயரத்தின் தயாரிப்பு என வரையறுக்கப்படுகிறது. பிந்தையது ப்ரிஸத்தின் விளிம்புடன் ஒத்துப்போகிறது. மேலும் இது ஒரு வழக்கமான அறுகோணத்தின் பக்கத்திற்கு சமம். அதாவது, சிலிண்டரின் உயரமும் 4 செ.மீ.

அதன் அடித்தளத்தின் பகுதியைக் கண்டுபிடிக்க, நீங்கள் அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரம் கணக்கிட வேண்டும். இதற்கான சூத்திரம் மேலே காட்டப்பட்டுள்ளது. எனவே r = 2√3 (cm). பின்னர் வட்டத்தின் பரப்பளவு: S \u003d π * r 2 \u003d 3.14 * (2√3) 2 \u003d 37.68 (cm 2).

பதில். வி \u003d 150.72 செமீ 3.

எண் 2. நிபந்தனை.வழக்கமான அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரம் கணக்கிடவும். அதன் பக்கம் √3 செ.மீ என்று அறியப்படுகிறது.அதன் சுற்றளவு என்னவாக இருக்கும்?

தீர்வு.இந்த பணிக்கு மேலே உள்ள இரண்டு சூத்திரங்களைப் பயன்படுத்த வேண்டும். மேலும், அவை மாற்றியமைக்கப்படாமல் பயன்படுத்தப்பட வேண்டும், பக்கத்தின் மதிப்பை மாற்றவும் மற்றும் கணக்கிடவும்.

இவ்வாறு, பொறிக்கப்பட்ட வட்டத்தின் ஆரம் 1.5 செ.மீ., சுற்றளவுக்கு, பின்வரும் மதிப்பு சரியாக இருக்கும்: 6√3 செ.மீ.

பதில். r = 1.5 செ.மீ., Р = 6√3 செ.மீ.

எண் 3. நிபந்தனை.சுற்றப்பட்ட வட்டத்தின் ஆரம் 6 செ.மீ. இந்த வழக்கில் வழக்கமான அறுகோணத்தின் பக்கத்தின் மதிப்பு என்ன?

தீர்வு.ஒரு அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரத்திற்கான சூத்திரத்திலிருந்து, பக்கத்தை கணக்கிட வேண்டிய ஒன்றை ஒருவர் எளிதாகப் பெறலாம். ஆரம் இரண்டால் பெருக்கப்பட்டு மூன்றின் மூலத்தால் வகுக்கப்படுகிறது என்பது தெளிவாகிறது. பகுத்தறிவில் உள்ள பகுத்தறிவின்மையைப் போக்க வேண்டும். எனவே, செயல்களின் முடிவு பின்வரும் வடிவத்தை எடுக்கும்: (12 √3) / (√3 * √3), அதாவது 4√3.

பதில். a = 4√3 செ.மீ.

வழக்கமான அறுகோணம் எப்படி இருக்கும் தெரியுமா?
இந்த கேள்வி தற்செயலாக கேட்கப்படவில்லை. 11 ஆம் வகுப்பு படிக்கும் பெரும்பாலான மாணவர்களுக்கு இதற்கான விடை தெரியாது.

ஒரு வழக்கமான அறுகோணம் என்பது அனைத்து பக்கங்களும் சமமாகவும் அனைத்து கோணங்களும் சமமாகவும் இருக்கும்..

இரும்பு கொட்டை. ஸ்னோஃப்ளேக். தேனீக்கள் வாழும் தேன்கூடுகளின் செல். பென்சீன் மூலக்கூறு. இந்த பொருட்களுக்கு பொதுவானது என்ன? - அவை அனைத்தும் வழக்கமான அறுகோண வடிவத்தைக் கொண்டுள்ளன என்பது உண்மை.

வழக்கமான அறுகோணத்திற்கான பணிகளைப் பார்க்கும்போது பல பள்ளிக் குழந்தைகள் தொலைந்து போகிறார்கள், மேலும் அவற்றைத் தீர்க்க சில சிறப்பு சூத்திரங்கள் தேவை என்று அவர்கள் நம்புகிறார்கள். அப்படியா?

வழக்கமான அறுகோணத்தின் மூலைவிட்டங்களை வரையவும். ஆறு சமபக்க முக்கோணங்களைப் பெற்றுள்ளோம்.

ஒரு சமபக்க முக்கோணத்தின் பரப்பளவு என்பது நமக்குத் தெரியும்.

பின்னர் ஒரு வழக்கமான அறுகோணத்தின் பரப்பளவு ஆறு மடங்கு பெரியது.

வழக்கமான அறுகோணத்தின் பக்கம் எங்கே.

வழக்கமான அறுகோணத்தில், அதன் மையத்திலிருந்து எந்த முனைகளுக்கும் உள்ள தூரம் வழக்கமான அறுகோணத்தின் பக்கத்திற்கு சமமாகவும் சமமாகவும் இருக்கும் என்பதை நினைவில் கொள்ளவும்.

இதன் பொருள் ஒரு வழக்கமான அறுகோணத்தைச் சுற்றியிருக்கும் வட்டத்தின் ஆரம் அதன் பக்கத்திற்குச் சமமாக இருக்கும்.
வழக்கமான அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரம் கண்டுபிடிக்க எளிதானது.
அவர் சமமானவர்.
வழக்கமான அறுகோணம் தோன்றும் எந்த பயன்பாட்டு சிக்கல்களையும் இப்போது நீங்கள் எளிதாக தீர்க்கலாம்.

பக்கவாட்டுடன் வழக்கமான அறுகோணத்தில் பொறிக்கப்பட்ட வட்டத்தின் ஆரத்தைக் கண்டறியவும்.

அத்தகைய வட்டத்தின் ஆரம்.

பதில்: .

6 ஆரம் கொண்ட வட்டத்தில் பொறிக்கப்பட்ட வழக்கமான அறுகோணத்தின் பக்கம் என்ன?

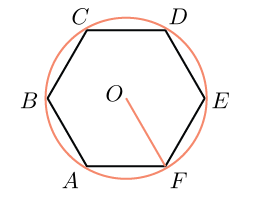
ஒரு வழக்கமான அறுகோணத்தின் பக்கமானது அதைச் சுற்றியுள்ள வட்டத்தின் ஆரத்திற்குச் சமம் என்பதை நாம் அறிவோம்.