Layunin ng Aralin:

Upang bumuo ng kaalaman, kasanayan at kakayahan ng epektibong aplikasyon ng pangkalahatang paraan ng mga agwat, batay sa pag-aari ng tuluy-tuloy na pag-andar;

Bumuo ng isang algorithm ng mga aksyon na humahantong sa mga katumbas na pagbabago;

Turuan ang iyong sarili na ilapat ito kapag nilulutas ang mga hindi pagkakapantay-pantay;

Upang maisakatuparan ang paglipat ng kaalaman, kasanayan at kakayahan sa mga bagong kondisyon.

Pang-edukasyon: systematization, consolidation, generalization ng kaalaman, kasanayan at kakayahan.

Pang-edukasyon: edukasyon ng pangangailangan para sa isang ganap na pare-parehong argumentasyon, katumpakan, pagsasarili.

Pagbuo: ang pagbuo ng matematikal na lohika, ang pagbuo ng isang matematikal na istilo ng pag-iisip (isang malinaw na pagkakahiwa-hiwalay ng kurso ng pangangatwiran), nagbibigay-malay na interes.

1) Panimula, pagtatakda ng layunin at layunin ng aralin - 2 min.

2) Pagsusuri ng takdang-aralin - 2 min. (pangharap na gawain, pagpipigil sa sarili).

3) Matematika na pagpapatibay ng mga yugto ng paglutas ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng agwat - 4 min (inihanda ang mga sagot ng mag-aaral).

4) Pag-uulit ng mga katangian ng hindi pagkakapantay-pantay - 2 min.

5) Paghahanda para sa asimilasyon (pag-aaral) ng bagong materyal na pang-edukasyon sa pamamagitan ng pag-uulit at pag-update ng pangunahing kaalaman - 5 min. (pangharap na gawain, mga sagot sa mga tanong, mga sitwasyon ng problema).

6) Pangkalahatang paraan ng agwat para sa paglutas ng mga hindi pagkakapantay-pantay, paunang pag-unawa - 13 min. (sama-samang solusyon ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng mga pagitan: sa pisara at sa mga notebook).

7) Impormasyon tungkol sa takdang-aralin, mga tagubilin para sa paggawa nito - 1 min.

8) Pagsasama-sama ng bagong kaalaman - 15 min. (independiyenteng trabaho - opsyon 1).

9) Pagbubuod ng aralin, pagninilay - 1 min.

1) Panimula, pagtatakda ng layunin at layunin ng aralin. (Kwento ng guro)

1) Ang pangangailangan para sa isang mas malawak na aplikasyon ng paraan ng mga pagitan sa paaralan ay idinidikta ng ideolohiya ng buong proseso ng pagtuturo ng matematika. Ang punto ay ang functional na linya (isa sa mga pangunahing sa pag-aaral ng mga pundasyon ng matematika) ay tumatanggap ng malakas na teknolohikal na suporta. Ang paraan ng mga agwat ay batay sa mga mahahalagang katangian ng functional dependence bilang mga zero ng isang function, mga agwat ng pare-parehong pag-sign at monotonicity nito. Pagkatapos ang functional na pinagmulan ng mga equation at hindi pagkakapantay-pantay, pati na rin ang mga pamamaraan para sa kanilang solusyon, ay nagiging mas malinaw. Ang mga kategorya ng pagpapatuloy ng isang function, ang pag-uugali ng graph nito sa paligid ng mga punto ng walang katapusang discontinuity, theorems sa root, constancy ng sign, extreme point at ang kanilang mga uri ay nagiging mas nakikita. At ang lahat ng ito ay organikong naka-link sa isang functional whole.

Sa kabilang banda, ang geometrization ng mga bagay ng pag-aaral na ginamit ay napakahalaga din, i.e. visually, figuratively present all the used mathematical tools of functional dependence.

Ang mga pangunahing prinsipyo na pinagbabatayan ng paraan ng agwat:

• functional (pangkalahatan) na diskarte;
• pag-asa sa geometrization ng mga functional na katangian;
• visualization ng pananaliksik.

Ito ay humahantong sa mga sumusunod na pakinabang ng pamamaraan kumpara sa iba pang ginagamit sa parehong uri ng mga gawain: pagiging simple at bilis ng pagkamit ng layunin; visibility (at ang kakayahang kontrolin o i-double-check); ekonomiya sa pagkalkula ng mga mapagkukunan at oras; lawak ng saklaw ng buong sitwasyon, ang pagbuo at pag-unlad ng mga kasanayan ng pangkalahatang pag-iisip at pagsusuri, pati na rin ang mga kasanayang nauugnay dito upang makagawa ng mga lohikal na konklusyon.

2) Sinusuri ang takdang-aralin.(Slide number 4)

3) Isang kwento tungkol sa paraan ng mga pagitan para sa paglutas ng mga hindi pagkakapantay-pantay. (Sagot ng mag-aaral).

Ang matematikal na pagpapatunay ng solusyon ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng mga pagitan.

1) Isaalang-alang ang mga hindi pagkakapantay-pantay: (x-2)(x-3)>0. (slide number 5)

Maaari mo itong lutasin tulad nito: Ang produkto (quotient) ng dalawang mga kadahilanan ay positibo kung at kung ang parehong mga kadahilanan ay may parehong tanda, i.e. ang hindi pagkakapantay-pantay ay katumbas ng kumbinasyon ng dalawang sistema: (slide number 6)

Mula sa unang sistema nakukuha namin ang x >3, mula sa pangalawang x< 2.

Ang solusyon ay ang unyon ng mga solusyon ng dalawang sistema.

Sagot:

Graphic na paraan (slide number 7)

Ang isa pang paraan ay paraan ng pagitan(slide number 8).

Ang kanyang ideya ay ang mga sumusunod.

Sa totoong linya, markahan ang mga zero (roots) ng polynomial (x-2)(x-3) na nakatayo

sa kaliwang bahagi ng hindi pagkakapantay-pantay, i.e. mga numero 2 at 3.

Kapag x >3 (sa kanan ng mas malaking ugat), pagkatapos ay (x-2)(x-3)>0, dahil positibo ang bawat salik.

Kung lumipat ka sa kahabaan ng axis sa isang negatibong direksyon, pagkatapos kapag dumaan ka sa puntong x=3, ang factor (x-3) ay magbabago ng sign. Sa produkto (x-2) (x-3) isang negatibong salik ang lilitaw, bilang resulta (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Ngayon ay madaling isulat ang solusyon ng hindi pagkakapantay-pantay:

Konklusyon: ang produkto ay maaaring magbago ng sign lamang kapag dumadaan sa mga puntos na x=2 at x=3

at, samakatuwid, pinapanatili ang tanda sa bawat isa sa mga nakuhang pagitan.

Sa simpleng halimbawang ito, madaling maunawaan ang ideya ng paraan ng agwat, ngunit hindi ito nagpapakita ng anumang kapansin-pansing mga pakinabang.

Ang pagiging makatwiran ng paraan ng agwat, ang kapangyarihan nito, isasaalang-alang natin ang sumusunod na halimbawa (slide No. 9, 10,11, 12))

2) Lutasin ang hindi pagkakapantay-pantay (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) ( x-10)>0.

Upang malutas ang hindi pagkakapantay-pantay na ito gamit ang isang hanay ng mga sistema, ang isa ay kailangang isaalang-alang ang isang hanay ng 512 mga sistema na may 10 hindi pagkakapantay-pantay sa bawat sistema.

Gamitin natin ang interval method. Minarkahan namin ang mga zero ng polynomial sa totoong linya. Sa pagitan ng x>10, ang polynomial ay magiging positibo, dahil ang bawat salik ay positibo. Kapag dumadaan sa bawat susunod na ugat, magbabago ang polynomial ng sign, dahil may lalabas na karagdagang negatibong salik sa produkto. Ngayon ay madaling isulat ang solusyon sa hindi pagkakapantay-pantay gamit ang paghahalili ng tanda.

Mga kalamangan ng paraan ng pagitan.

• pagiging simple at bilis ng pagkamit ng layunin;
• visibility (at ang kakayahang kontrolin o i-double-check);
• isang makabuluhang pagbawas sa dami ng computational work at oras;
• lawak ng saklaw ng buong sitwasyon;
• ang pagbuo at pag-unlad ng pangkalahatang pag-iisip at mga kasanayan sa pagsusuri, pati na rin ang mga kaugnay na kasanayan upang makagawa ng mga lohikal na konklusyon.

Magkomento. Ito ay napaka-maginhawa upang malutas ang mga hindi pagkakapantay-pantay, ang kaliwang bahagi nito ay naka-factor, dahil hindi mahirap makahanap ng mga zero (roots).

Gawain: Lutasin ang hindi pagkakapantay-pantay gamit ang interval method (x+3) 3 (x-4) 2 (x-5)>0(Slide 13)

4) Pag-uulit ng mga katangian ng hindi pagkakapantay-pantay.

a) Tanong: Anong mga hindi pagkakapantay-pantay ang tinatawag na katumbas?

(Dalawang hindi pagkakapantay-pantay ay sinasabing katumbas kung anumang solusyon sa unang hindi pagkakapantay-pantay ay solusyon sa pangalawa at, sa kabaligtaran, anumang solusyon sa pangalawa ay solusyon sa una).

O: ang dalawang hindi pagkakapantay-pantay ay sinasabing katumbas kung ang mga hanay ng kanilang mga solusyon ay pareho.

Slide 14. Pag-uulit ng mga katangian ng hindi pagkakapantay-pantay.

Slide 15. Sagutin ang tanong at ipaliwanag.

Pantay ba ang mga hindi pagkakapantay-pantay?

1) 4x-5<0 и 4х<5

2) -2x+5>0 at 2x-5<0

3) -3x 2 +5x-7>0 at 3x 2 -5x+7<0

4) (x+1)>0 at (x 2 +5x+10)(x+1)>0

5) Oral frontal work bilang paghahanda para sa asimilasyon (pag-aaral) ng bagong materyal na pang-edukasyon sa pamamagitan ng pag-uulit at pag-update ng pangunahing kaalaman.

Slide 16. Kahulugan ng isang function na tuloy-tuloy sa isang punto.

Slide 17. Pag-aari ng tuluy-tuloy na pag-andar.

Slide 18. Maghanap ng mga puwang ng pagpapatuloy.

Slide 19. Hanapin ang pagkakamali.

Slide 20. Lutasin ang hindi pagkakapantay-pantay sa salita,
gamit ang tsart.

Slide 21, 22. Pagpapalit ng hindi pagkakapantay-pantay ng katumbas na kondisyon.

Lutasin ang hindi pagkakapantay-pantay

Ang hindi pagkakapantay-pantay na ito ay katumbas ng kundisyon f(x) < 0 pagbibilang

Samakatuwid, kailangan nating hanapin ang lahat ng mga halaga ng x kung saan ang kundisyon f(x) < 0.

6) Pangkalahatang paraan ng agwat para sa paglutas ng mga hindi pagkakapantay-pantay, paunang pag-unawa - 10 min. (sama-samang solusyon ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng mga pagitan: sa pisara at sa mga notebook).

slide 23. Algorithm. Pangkalahatang pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay.

Solusyon ng mga hindi pagkakapantay-pantay f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 sa pamamagitan ng paraan ng pagitan. (Skema)

Slide 24 at 25. Paglutas ng hindi pagkakapantay-pantay sa pamamagitan ng algorithm. (Mga komento sa lahat ng mga punto ng algorithm).

slide 26. Graphical na paglalarawan ng solusyon sa hindi pagkakapantay-pantay na ito.

Slide 27. Lutasin ang hindi pagkakapantay-pantay sa pisara at sa mga kuwaderno .

Slide 28. Graphical na paglalarawan ng solusyon sa hindi pagkakapantay-pantay na ito.

Slide 29. Lutasin ang hindi pagkakapantay-pantay sa pisara at sa mga kuwaderno

Slide 30. Graphical na paglalarawan ng solusyon sa hindi pagkakapantay-pantay na ito.

Slide 31, 32. Lutasin ang hindi pagkakapantay-pantay sa salita, ayon sa larawan

7) Impormasyon tungkol sa takdang-aralin.(Lutasin sa pamamagitan ng paraan ng pagitan opsyon numero 2)

8) Pagsasama-sama ng bagong kaalaman (independiyenteng gawain, opsyon No. 1).

9) Pagbubuod ng aralin, pagpipigil sa sarili sa mga handa na solusyon (mga slide 33, 34, 35), pag-uulit ng algorithm ng pangkalahatang paraan ng mga agwat at aplikasyon nito.

10) Pagsusuri ng asimilasyon ng materyal at interes ng mga mag-aaral sa paksa. Ang pamamaraang ito ay unibersal para sa paglutas ng anumang mga hindi pagkakapantay-pantay, kabilang ang rational, na may modulus, irrational, exponential, logarithmic, dahil ang paraan ng agwat ay binabawasan ang solusyon ng mga hindi pagkakapantay-pantay sa paglutas ng mga equation, ang paghahanap ng domain ng kahulugan at ang halaga ng function sa isang punto ay hindi magdulot ng kahirapan. Ngunit kailangan kong magbigay ng mga halimbawa ng mga hindi pagkakapantay-pantay kung saan ang paggamit ng paraang ito ay hindi makatwiran, kung saan mas makatwiran na mag-aplay ng iba pang mga pamamaraan para sa paglutas ng mga hindi pagkakapantay-pantay.

Paglalahad "Paglalapat ng pagpapatuloy sa paglutas ng mga hindi pagkakapantay-pantay". (35 slide)

Depinisyon 4. Ang isang function ay tinatawag na tuloy-tuloy sa isang segment kung ito ay tuloy-tuloy sa bawat punto ng segment na ito (sa punto a ito ay tuloy-tuloy sa kanan, ibig sabihin, at sa punto b ito ay tuloy-tuloy sa kaliwa, ibig sabihin).

Ang lahat ng mga pangunahing pag-andar ng elementarya ay tuloy-tuloy sa kanilang domain ng kahulugan.

Mga katangian ng mga function na tuloy-tuloy sa isang segment:

• 1) Kung ang isang function ay tuloy-tuloy sa isang segment, ito ay bounded sa segment na ito (ang unang Weierstrass theorem).
• 2) Kung ang isang function ay tuloy-tuloy sa isang segment, pagkatapos ay sa segment na ito naabot nito ang pinakamababang halaga at ang pinakamataas na halaga nito (ang pangalawang Weierstrass theorem) (tingnan ang Fig. 2).
• 3) Kung ang isang function ay tuluy-tuloy sa isang segment at kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo nito, kung gayon mayroong hindi bababa sa isang punto sa loob ng segment tulad na (ang Bolzano-Cauchy theorem).

Mga breakpoint ng function at ang kanilang pag-uuri

segment ng pagpapatuloy ng function

Ang mga punto kung saan hindi natutugunan ang kondisyon ng pagpapatuloy ay tinatawag na mga discontinuity point ng function na ito. Kung ito ay isang discontinuity point ng isang function, kung gayon hindi bababa sa isa sa tatlong kundisyon para sa pagpapatuloy ng function na tinukoy sa Definition 1, 2 ay hindi nasiyahan dito, ibig sabihin:

1) Ang function ay tinukoy sa paligid ng punto, ngunit hindi tinukoy sa mismong punto. Kaya ang function na isinasaalang-alang sa halimbawa 2 a) ay may pahinga sa isang punto, dahil hindi ito tinukoy sa puntong ito.

2) Ang function ay tinukoy sa isang punto at sa kapitbahayan nito, may isang panig na mga limitasyon at, ngunit hindi sila pantay sa isa't isa: . Halimbawa, ang function mula sa halimbawa 2 b) ay tinukoy sa isang punto at kapitbahayan nito, ngunit, dahil, a.

3) Ang function ay tinukoy sa punto at sa paligid nito, may isang panig na mga limitasyon at, sila ay katumbas ng bawat isa, ngunit hindi katumbas ng halaga ng function sa puntong: . Halimbawa, function. Narito ang break point: sa puntong ito ang function ay tinukoy, may isang panig na mga limitasyon at katumbas ng bawat isa, ngunit, ibig sabihin.

Ang mga breakpoint ng function ay inuri bilang mga sumusunod.

Depinisyon 5. Ang isang punto ay tinatawag na isang discontinuity point ng unang uri ng isang function kung may mga finite limit at sa puntong ito, ngunit hindi sila pantay sa isa't isa: . Ang dami ay tinatawag na jump ng function sa punto.

Kahulugan 6 . Ang isang punto ay tinatawag na isang punto ng isang naaalis na discontinuity ng isang function kung sa puntong ito ay may mga hangganan na limitasyon at, sila ay katumbas ng bawat isa: , ngunit ang function mismo ay hindi tinukoy sa punto, o tinukoy, ngunit.

Depinisyon 7. Ang isang punto ay tinatawag na isang discontinuity point ng pangalawang uri ng isang function kung sa puntong ito kahit isa sa mga one-sided na limitasyon (o) ay wala o katumbas ng infinity.

Halimbawa 3. Maghanap ng mga break point ng mga sumusunod na function at tukuyin ang kanilang uri: a) b)

Solusyon. a) Ang function ay tinukoy at tuloy-tuloy sa mga pagitan u, dahil sa bawat isa sa mga pagitan na ito ay ibinibigay ng tuluy-tuloy na elementarya na pag-andar. Samakatuwid, ang mga breakpoint ng isang ibinigay na function ay maaari lamang ang mga punto kung saan binabago ng function ang analytical assignment nito, i.e. puntos i. Hanapin natin ang isang panig na limitasyon ng function sa punto:

Dahil ang isang panig na mga limitasyon ay umiiral at may hangganan, ngunit hindi katumbas ng bawat isa, ang punto ay isang discontinuity point ng unang uri. Function jump:

Para sa isang puntong nahanap natin.

Pagpapatuloy ng isang function sa isang pagitan

Pangalan ng parameter	Ibig sabihin
Paksa ng artikulo:	Pagpapatuloy ng isang function sa isang pagitan
Rubric (temang kategorya)	Math

Kahulugan. Ang isang function ay tinatawag na tuloy-tuloy sa isang pagitan kung ito ay tuloy-tuloy sa bawat punto ng pagitan na ito.

Kung ang function ay tinukoy para sa X=a at kung saan f(X) = f(a),

tapos sasabihin nila yan f(X) sa punto at tuloy-tuloy sa kanan. Katulad nito, kung f(X) = f(b), pagkatapos ay sasabihin namin iyon sa punto b function na ito naiwang tuloy-tuloy.

Kahulugan. Ang function ay karaniwang tinatawag na tuloy-tuloy sa segment [ a, b], kung ito ay tuloy-tuloy sa bawat punto nito (sa punto a tuloy-tuloy sa kanan, sa isang punto b ay tuloy-tuloy sa kaliwa).

pinakamataas na halaga mga function sa = f(x) sa segment [ a, b f(x 1) iyon f(x) £ f(x 1) para sa lahat X Î [ a, b].

Pinakamababang halaga mga function sa = f(x) sa segment [ a, b] nakaugalian na ang tawag sa ganoong halaga f(x 2) iyon f(x) ³ f(x 2) para sa lahat X Î [ a, b].

Ang mga function na tuluy-tuloy sa isang pagitan ay may ilang mahahalagang katangian, na ipinahayag ng mga sumusunod na theorems.

Teorama 3.3.1. Isang function na tuloy-tuloy sa segment [ a, b], umabot sa pinakamababang halaga nito m at ang pinakamalaking halaga M, ibig sabihin, may mga ganyang punto x 1 at x 2 ng segment na ito, na f(x 1) = m, f(x 2) = M.

Ang theorem ay may simpleng geometric na kahulugan (tingnan ang Fig. 2).

Teorama 3.3.2. Kung sakaling ang function sa = f(x) ay tuloy-tuloy sa pagitan [ a, b] at kumukuha ng hindi pantay na halaga sa mga dulo nito f(a) = A, f(b) = B, A ¹ B, kung gayon anuman ang bilang C sa pagitan ng A at B, mayroong isang punto Sa Î [ a, b] ganyan f(Sa) = C.

Ang geometric na kahulugan ng theorem ay inilalarawan sa Fig.3. Anumang tuwid na linya sa= C, kung saan ang A< C < B (или A >C > B), intersects ang graph ng function sa = f(x).

Bunga. Kung ang function ay tuloy-tuloy sa isang segment at kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo nito, pagkatapos ay mayroong hindi bababa sa isang punto sa segment na ito kung saan nawala ang function.

Ang geometric na kahulugan ng kinahinatnan ay inilalarawan sa Fig.4.

Mga tanong para sa pagpipigil sa sarili

1. Anong function ang tinatawag na tuluy-tuloy sa isang punto?

2. Magbigay ng isa pang katumbas na kahulugan sa mga tuntunin ng pag-andar at argumento na mga pagdaragdag.

3. Ano ang masasabi tungkol sa kabuuan, pagkakaiba, produkto at quotient ng dalawang tuluy-tuloy na function?

4. Para sa anong mga halaga ng argumento ang buong rational at fractional-rational function na tuluy-tuloy?

5. Kailan tuloy-tuloy ang isang kumplikadong function sa isang punto?

6. Ano ang karaniwang tinatawag na breaking point ng mga function?

7. Anong mga punto ang tinatawag na mga discontinuity point ng unang uri?

8. Anong halaga ang karaniwang tinatawag na function jump?

9. Ipaliwanag ang mga konsepto ng "removable break point". Magbigay ng halimbawa.

10. Anong mga punto ang tinatawag na mga discontinuity point ng pangalawang uri? Magbigay ng halimbawa.

11. Ipaliwanag ang mga konsepto: ""continuity on the interval"", ""continuity on the right"", ""continuity on the left"", ""continuity on the segment"".

12. Tukuyin ang pinakamalaki at pinakamaliit na halaga ng mga function.

13. Bumuo ng isang teorama sa relasyon ng pagpapatuloy sa isang segment na may pinakamalaki at pinakamaliit na halaga ng function. Ipaliwanag ito gamit ang isang larawan.

14. Bumuo ng teorama sa koneksyon sa pagitan ng pagpapatuloy ng mga function sa isang segment at ng segment ng mga halaga ng function. Ilarawan ang geometric na kahulugan nito sa figure.

15. Magbigay ng kahihinatnan ng teorama sa itaas at ang geometric na interpretasyon nito.

LECTURE №4

Paksa ng lecture: Derivative ng function

Plano ng lecture: Ang konsepto ng isang derivative, ang geometriko at pisikal na kahulugan nito. Mga pangunahing tuntunin ng pagkita ng kaibhan. Derivative ng isang kumplikadong function. Ang ilang mga aplikasyon ng derivative.

4.1. Ang konsepto ng isang derivative, ang geometriko at pisikal na kahulugan nito

Isaalang-alang ang function sa = f(x) na tinukoy sa pagitan ] a, b[. Hayaan XÎ ] a, b[at X Î ] a, b[, pagkatapos ay ang pagdaragdag ng function sa punto X Ang 0 ay ipinahayag ng formula D sa = f(x 0+D X) – f(x 0).

Kahulugan. Ang derivative ng function na y = f(x) sa punto X 0 ay karaniwang tinatawag na limitasyon ng ratio ng pagtaas ng function na ito sa pagtaas ng argumento kapag ang huli ay may posibilidad na zero:

f'(x 0) = o y"(x 0) =.

Ang geometric na kahulugan ng derivative: ang derivative ng function na ito sa isang punto ay katumbas ng tangent ng anggulo sa pagitan ng Ox axis at ng tangent sa graph ng function na ito sa kaukulang punto (tingnan ang Fig. 1):

f"(x 0) = kayumanggi a.

Kahulugan. Kung ang function f(x) ay tinukoy sa pagitan [ a, b], ay tuloy-tuloy sa bawat punto ng pagitan ( a, b), sa punto a tuloy-tuloy sa kanan, sa isang punto b ay tuloy-tuloy sa kaliwa, pagkatapos ay sinasabi namin na ang function f(x) tuloy-tuloy sa segment [a, b].

Sa madaling salita, ang function f(x) ay tuloy-tuloy sa pagitan [ a, b] kung ang tatlong kundisyon ay natutugunan:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Para sa mga function na tuluy-tuloy sa isang pagitan, isinasaalang-alang namin ang ilang mga katangian, na aming binabalangkas sa anyo ng mga sumusunod na theorems na walang mga patunay.

Teorama 1. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], pagkatapos ay maabot nito ang pinakamaliit at pinakamalaking halaga nito sa segment na ito.

Ang teorama na ito ay nagsasaad (Larawan 1.15) na sa segment [ a, b] may ganyang punto x 1 iyon f(x 1) £ f(x) para sa alinman x mula sa [ a, b] at mayroong isang punto x 2 (x 2 О[ a, b]) ganyan" xÎ[ a, b] (f(x 2) ³ f(x)).

Ibig sabihin f(x 1) ay ang pinakamalaking para sa ibinigay na function sa [ a, b], a f(x 2) - ang pinakamaliit. Ipahiwatig: f(x 1) = M, f(x 2) =m. Dahil para sa f(x) ang sumusunod na hindi pagkakapantay-pantay ay pinanghahawakan: " xÎ[ a, b] m£ f(x) £ M, pagkatapos ay makuha natin ang sumusunod na corollary mula sa Theorem 1.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa isang segment, pagkatapos ay nakatali ito sa segment na ito.

Teorama 2. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a,b] at kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo ng segment, pagkatapos ay mayroong isang panloob na punto x 0 segment [ a, b], kung saan ang function ay nagiging 0, i.e. $ x 0 Î ( a, b) (f(x 0) = 0).

Ang theorem na ito ay nagsasaad na ang graph ng isang function y=f(x), tuloy-tuloy sa segment [ a, b], tumatawid sa axis baka kahit isang beses kung ang mga halaga f(a) at f(b) may magkasalungat na mga palatandaan. Kaya, (Larawan 1.16) f(a) > 0, f(b) < 0 и функция f(x) naglalaho sa mga punto x 1 , x 2 , x 3 .

Teorama 3. Hayaan ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], f(a) = A, f(b) = B at A¹ B. (Larawan 1.17). Pagkatapos ay para sa anumang numero C, natapos sa pagitan ng mga numero A at B, may ganoong interior point x 0 segment [ a, b], Ano f(x 0) = C.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa pagitan [ a, b], m- ang pinakamaliit na halaga f(x), M- ang pinakamalaking halaga ng function f(x) sa segment [ a, b], pagkatapos ang function ay tumatagal (kahit isang beses) ng anumang halaga m sa pagitan m at M, at samakatuwid ang segment [ m, M] ay ang set ng lahat ng value ng function f(x) sa segment [ a, b].

Tandaan na kung ang function ay tuloy-tuloy sa pagitan ( a, b) o mayroon sa segment [ a, b] ng discontinuity point, pagkatapos ang Theorems 1, 2, 3 ay titigil na totoo para sa naturang function.

Sa konklusyon, isaalang-alang ang theorem sa pagkakaroon ng isang inverse function.

Alalahanin na ang isang agwat ay isang segment, isang agwat, o isang may hangganan o walang katapusang kalahating pagitan.

Teorama 4. Hayaan f(x) ay tuloy-tuloy sa pagitan X, tumataas (o bumababa) ng X at may hanay ng mga halaga Y. Pagkatapos ay para sa pag-andar y=f(x) mayroong isang kabaligtaran na pag-andar x= j(y) na tinukoy sa pagitan Y, tuloy-tuloy at tumataas (o bumababa) sa Y na may maraming kahulugan X.

Magkomento. Hayaan ang function x= j(y) ay kabaligtaran para sa function f(x). Dahil ang argumento ay karaniwang tinutukoy ng x, at ang function sa pamamagitan ng y, pagkatapos ay isinusulat namin ang inverse function bilang y=j(x).

Halimbawa 1. Function y=x 2 (Larawan 1.8, a) sa set X= kung ito ay tuloy-tuloy sa lahat ng panloob na punto ng segment na ito, at sa mga dulo nito, i.e. sa mga punto a at b, ay tuloy-tuloy sa kanan at kaliwa, ayon sa pagkakabanggit.

Teorama 1. Isang function na tuloy-tuloy sa segment [ a, b], hindi bababa sa isang punto ng segment na ito ay tumatagal ng pinakamalaking halaga at hindi bababa sa isang punto - ang pinakamaliit.

Ang theorem ay nagsasaad na kung ang function y = f(x) tuloy-tuloy sa segment [ a, b], pagkatapos ay mayroong kahit isang punto x 1 Î [ a, b] na ang halaga ng function f(x) sa puntong ito ay magiging pinakamalaki sa lahat ng mga halaga nito sa segment na ito: f(x1) ≥ f(x). Katulad nito, may ganoong punto x2, kung saan ang halaga ng function ang magiging pinakamaliit sa lahat ng value sa segment: f(x 1) ≤ f(x).

Ito ay malinaw na maaaring mayroong ilang mga naturang punto, halimbawa, ang figure ay nagpapakita na ang function f(x) kumukuha ng pinakamaliit na halaga sa dalawang punto x2 at x 2 ".

Magkomento. Ang pahayag ng theorem ay maaaring maging mali kung isasaalang-alang natin ang halaga ng function sa pagitan ( a, b). Sa katunayan, kung isasaalang-alang natin ang pag-andar y=x sa (0, 2), pagkatapos ito ay tuloy-tuloy sa agwat na ito, ngunit hindi maabot ang pinakamataas o pinakamababang halaga nito: naabot nito ang mga halagang ito sa mga dulo ng agwat, ngunit ang mga dulo ay hindi kabilang sa aming rehiyon.

Gayundin, ang teorama ay tumigil na maging totoo para sa mga di-tuloy na pag-andar. Magbigay ng halimbawa.

Bunga. Kung ang function f(x) tuloy-tuloy sa [ a, b], pagkatapos ito ay nakatali sa pagitan na ito.

Teorama 2. Hayaan ang function y = f(x) tuloy-tuloy sa segment [ a, b] at kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo ng segment na ito, pagkatapos ay mayroong kahit isang punto sa loob ng segment x=C, kung saan nawawala ang function: f(C)= 0, kung saan a< C< b

Ang theorem na ito ay may isang simpleng geometric na kahulugan: kung ang mga punto ng graph ng isang tuluy-tuloy na function y = f(x), naaayon sa mga dulo ng segment [ a, b] nakahiga sa magkabilang panig ng axis baka, pagkatapos ang graph na ito ay nagsa-intersect sa axis kahit man lang sa isang punto ng segment baka. Maaaring walang ganitong katangian ang mga hindi tuluy-tuloy na function.

Ang teorama na ito ay umamin sa sumusunod na paglalahat.

Theorem 3 (teorem sa mga intermediate na halaga). Hayaan ang function y = f(x) tuloy-tuloy sa segment [ a, b] at f(a) = A, f(b) = B. Pagkatapos ay para sa anumang numero C sa pagitan A at B, may ganoong punto sa loob ng segment na ito CÎ [ a, b], Ano f(c) = C.

Ang teorama na ito ay geometrically obvious. Isaalang-alang ang graph ng function y = f(x). Hayaan f(a) = A, f(b) = B. Tapos kahit anong linya y=C, saan C- anumang numero sa pagitan A at B, nag-intersect sa graph ng function kahit man lang sa isang punto. Ang abscissa ng intersection point ay ang halagang iyon x=C, Kung saan f(c) = C.

Kaya, ang isang tuluy-tuloy na pag-andar, na dumadaan mula sa isa sa mga halaga nito patungo sa isa pa, ay kinakailangang dumaan sa lahat ng mga intermediate na halaga. Sa partikular:

Bunga. Kung ang function y = f(x) ay tuluy-tuloy sa ilang pagitan at tumatagal sa pinakamalaki at pinakamaliit na halaga, pagkatapos ay sa pagitan na ito ay tumatagal, kahit isang beses, anumang halaga sa pagitan ng pinakamaliit at pinakamalaking halaga nito.

DERIVATIVE AT MGA APLIKASYON NITO. DERIVATIVE DEFINITION

Magkaroon tayo ng ilang function y=f(x), tinukoy sa ilang pagitan. Para sa bawat halaga ng argumento x mula sa pagitan na ito ang function y=f(x) may tiyak na kahulugan.

Isaalang-alang ang dalawang halaga ng argumento: inisyal x 0 at bago x.

Pagkakaiba x–x 0 ang tinatawag pagtaas ng argumento x sa punto x 0 at denote Δx. Sa ganitong paraan, ∆x = x – x 0 (maaaring positibo o negatibo ang pagtaas ng argumento). Mula sa pagkakapantay-pantay na ito ay sinusundan iyon x=x 0 +Δx, ibig sabihin. ang paunang halaga ng variable ay nakatanggap ng ilang pagtaas. Pagkatapos, kung sa punto x 0 ang halaga ng function noon f(x 0 ), pagkatapos ay sa bagong punto x kukunin ng function ang halaga f(x) = f(x 0 +∆x).

Pagkakaiba y-y 0 = f(x) – f(x 0 ) tinawag pagtaas ng function y = f(x) sa punto x 0 at ipinapahiwatig ng simbolo Δy. Sa ganitong paraan,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Karaniwan ang paunang halaga ng argumento x 0 ay itinuturing na naayos at ang bagong halaga x- variable. Pagkatapos y 0 = f(x 0 ) lumalabas na pare-pareho at y = f(x)- variable. mga dagdag Δy at Δx magiging mga variable din at ang formula (1) ay nagpapakita na Dy ay isang function ng variable Δx.

Buuin ang ratio ng pagtaas ng function sa pagtaas ng argumento

Hanapin natin ang limitasyon ng kaugnayang ito sa Δx→0. Kung umiiral ang limitasyong ito, kung gayon ito ay tinatawag na derivative ng function na ito. f(x) sa punto x 0 at tukuyin f "(x 0). Kaya,

derivative function na ito y = f(x) sa punto x Ang 0 ay tinatawag na limitasyon ng increment ratio ng function na Δ y sa pagtaas ng argumentong Δ x kapag ang huli ay arbitraryo ay nagiging zero.

Tandaan na para sa parehong function ang derivative sa iba't ibang mga punto x maaaring tumagal sa iba't ibang mga halaga, i.e. ang derivative ay maaaring isipin bilang isang function ng argumento x. Ang function na ito ay tinutukoy f "(x)

Ang derivative ay tinutukoy ng mga simbolo f "(x), y", . Ang tiyak na halaga ng derivative sa x = a denoted f "(a) o y "| x=a.

Ang operasyon ng paghahanap ng derivative ng isang function f(x) ay tinatawag na pagkakaiba-iba ng function na ito.

Upang direktang mahanap ang derivative ayon sa kahulugan, maaari mong ilapat ang sumusunod pamantayan:

Mga halimbawa.

MEKANIKAL NA KAHULUGAN NG DERIVATIVE

Ito ay kilala mula sa pisika na ang batas ng unipormeng paggalaw ay may anyo s = v t, saan s- landas na nilakbay hanggang sa punto ng oras t, v ay ang bilis ng pare-parehong paggalaw.

Gayunpaman, dahil karamihan sa mga paggalaw na nagaganap sa kalikasan ay hindi pantay, pagkatapos ay sa pangkalahatang kaso, ang bilis, at, dahil dito, ang distansya s ay depende sa oras t, ibig sabihin. magiging function ng oras.

Kaya, hayaan ang materyal na punto na lumipat sa isang tuwid na linya sa isang direksyon ayon sa batas s=s(t).

Tandaan sandali sa oras t 0 . Sa puntong ito, ang punto ay lumipas na sa landas s=s(t 0 ). Tukuyin natin ang bilis v materyal na punto sa oras t 0 .

Upang gawin ito, isaalang-alang ang ilang iba pang sandali sa oras t 0 + Δ t. Ito ay tumutugma sa layo na nilakbay s =s(t 0 + Δ t). Pagkatapos para sa agwat ng oras Δ t ang punto ay naglakbay sa landas na Δs =s(t 0 + Δ t)–s(t).

Isaalang-alang natin ang relasyon. Ito ay tinatawag na average na bilis sa pagitan ng oras Δ t. Ang average na bilis ay hindi maaaring tumpak na makilala ang bilis ng paggalaw ng isang punto sa sandaling ito t 0 (dahil hindi pantay ang paggalaw). Upang mas tumpak na maipahayag ang totoong bilis na ito gamit ang average na bilis, kailangan mong kumuha ng mas maliit na agwat ng oras Δ t.

Kaya, ang bilis ng paggalaw sa isang naibigay na oras t 0 (madaliang bilis) ay ang limitasyon ng average na bilis sa pagitan mula sa t 0 hanggang t 0 +Δ t kapag Δ t→0:

,

mga. bilis ng hindi pantay na paggalaw ay ang derivative ng distansyang nilakbay na may kinalaman sa oras.

GEOMETRIK NA KAHULUGAN NG DERIVATIVE

Ipakilala muna natin ang kahulugan ng isang tangent sa isang kurba sa isang naibigay na punto.

Hayaan tayong magkaroon ng isang kurba at isang nakapirming punto dito M 0(tingnan ang figure) Isaalang-alang ang isa pang punto M curve na ito at gumuhit ng secant M 0 M. Kung punto M nagsisimulang gumalaw kasama ang kurba, at ang punto M 0 nananatiling nakatigil, nagbabago ang posisyon ng secant. Kung, na may walang limitasyong pagtatantya ng punto M kurba sa punto M 0 sa anumang panig, ang secant ay may posibilidad na kunin ang posisyon ng isang tiyak na tuwid na linya M 0 T, pagkatapos ay ang tuwid na linya M 0 T ay tinatawag na padaplis sa kurba sa ibinigay na punto M 0.

yun., padaplis sa kurba sa isang naibigay na punto M 0 tinatawag na limitasyon na posisyon ng secant M 0 M kapag ang punto M tends along the curve to a point M 0.

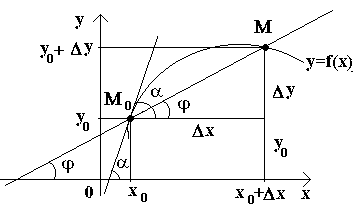
Isaalang-alang ngayon ang tuluy-tuloy na pag-andar y=f(x) at ang curve na naaayon sa function na ito. Para sa ilang halaga X 0 function ay tumatagal ng isang halaga y0=f(x0). Ang mga halagang ito x 0 at y 0 sa curve ay tumutugma sa isang punto M 0 (x 0; y 0). Magbigay tayo ng argumento x0 pagtaas Δ X. Ang bagong value ng argument ay tumutugma sa incremented value ng function y 0 +Δ y=f(x 0 –Δ x). Nakakakuha tayo ng punto M(x 0+Δ x; y 0+Δ y). Gumuhit tayo ng secant M 0 M at tukuyin sa pamamagitan ng φ ang anggulo na nabuo ng secant na may positibong direksyon ng axis baka. Gumawa tayo ng isang relasyon at tandaan na .

Kung ngayon Δ x→0, pagkatapos, dahil sa pagpapatuloy ng function na Δ sa→0, at samakatuwid ang punto M, gumagalaw sa kahabaan ng kurba, walang katiyakan na lumalapit sa punto M 0. Tapos yung secant M 0 M ay may posibilidad na kunin ang posisyon ng isang padaplis sa kurba sa punto M 0, at ang anggulo φ→α sa Δ x→0, kung saan ang α ay tumutukoy sa anggulo sa pagitan ng tangent at ng positibong direksyon ng axis baka. Dahil ang function na tg φ ay patuloy na nakasalalay sa φ sa φ≠π/2, pagkatapos ay sa φ→α tg φ → tg α at, samakatuwid, ang slope ng tangent ay magiging:

mga. f"(x)= tgα .

Kaya, geometrically y "(x 0) kumakatawan sa slope ng tangent sa graph ng function na ito sa punto x0, ibig sabihin. para sa isang ibinigay na halaga ng argumento x, ang derivative ay katumbas ng tangent ng anggulo na nabuo ng tangent sa graph ng function f(x) sa kaukulang punto M 0 (x; y) na may positibong direksyon ng axis baka.

Halimbawa. Hanapin ang slope ng tangent sa curve y = x 2 sa punto M(-1; 1).

nakita na natin yan ( x 2)" = 2X. Ngunit ang slope ng padaplis sa kurba ay tg α = y"| x=-1 = - 2.

PAGKAKAIBA NG MGA FUNCTION. PAGPAPATULOY NG ISANG NAIIBA NA FUNCTION

Function y=f(x) tinawag naiba-iba sa isang punto x 0 kung mayroon itong tiyak na derivative sa puntong ito, i.e. kung ang limitasyon ng relasyon ay umiiral at may hangganan.

Kung ang isang function ay naiba-iba sa bawat punto ng ilang segment [ a; b] o pagitan ( a; b), pagkatapos ay sinasabi nila na ito naiba-iba sa segment [ a; b] o, ayon sa pagkakabanggit, sa pagitan ( a; b).

Ang sumusunod na theorem ay wasto, na nagtatatag ng koneksyon sa pagitan ng naiba-iba at tuluy-tuloy na mga pag-andar.

Teorama. Kung ang function y=f(x) naiba sa isang punto x0, pagkatapos ito ay tuloy-tuloy sa puntong ito.

Kaya, ang pagkakaiba-iba ng isang function ay nagpapahiwatig ng pagpapatuloy nito.

Patunay. Kung ang , pagkatapos

,

kung saan ang α ay isang infinitesimal na halaga, i.e. dami na umaabot sa zero sa Δ x→0. Ngunit pagkatapos

Δ y=f "(x0) Δ x+αΔ x=> Δ y→0 sa Δ x→0, ibig sabihin. f(x) – f(x0)→0 sa x→x 0 , na nangangahulugan na ang function f(x) tuloy-tuloy sa punto x 0 . Q.E.D.

Kaya, sa mga discontinuity point, hindi maaaring magkaroon ng derivative ang function. Ang kabaligtaran na pahayag ay hindi totoo: may mga tuluy-tuloy na pag-andar na hindi naiba sa ilang mga punto (iyon ay, wala silang derivative sa mga puntong ito).

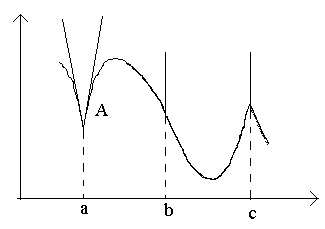
Isaalang-alang ang mga punto sa figure a, b, c.

Sa punto a sa Δ x→0 ang kaugnayan ay walang limitasyon (dahil ang mga one-sided na limitasyon ay iba para sa Δ x→0–0 at Δ x→0+0). Sa punto A ang graph ay walang tinukoy na tangent, ngunit mayroong dalawang magkaibang one-sided tangent na may mga slope sa 1 at sa 2. Ang ganitong uri ng punto ay tinatawag na corner point.

Sa punto b sa Δ x→0 ang ratio ay pare-pareho ang sign na walang hanggan malaking halaga . Ang function ay may walang katapusang derivative. Sa puntong ito, ang graph ay may patayong padaplis. Uri ng punto - "inflection point" na may patayong padaplis.

Sa punto c Ang mga one-sided derivatives ay walang katapusang malalaking dami ng iba't ibang mga palatandaan. Sa puntong ito, ang graph ay may dalawang pinagsamang patayong tangent. Uri - "cusp" na may vertical tangent - isang espesyal na kaso ng isang sulok na punto.