Ang function na y=f(x) ay tinatawag na differentiable sa ilang punto x 0 kung mayroon itong tiyak na derivative sa puntong ito, i.e. kung ang limitasyon ng relasyon ay umiiral at may hangganan.

Kung ang isang function ay naiba-iba sa bawat punto ng isang partikular na segment [a; b] o pagitan (a; b), pagkatapos ay sinasabi namin na ito ay naiba sa pagitan [a; b] o, ayon sa pagkakabanggit, sa pagitan (a; b).

Ang sumusunod na theorem ay wasto, na nagtatatag ng koneksyon sa pagitan ng naiba at tuluy-tuloy na mga pag-andar.

Teorama. Kung ang function na y=f(x) ay naiba sa isang punto x 0, kung gayon ito ay tuloy-tuloy sa puntong ito.

Kaya, mula sa pagkakaiba-iba ng isang function, ang pagpapatuloy nito ay sumusunod.

Patunay. Kung, kung gayon

kung saan ang b ay isang infinitesimal na dami, i.e. isang dami na umaabot sa zero kapag Dx>0. Ngunit pagkatapos

Dy=f "(x 0) Dx+bDx => Dy>0 sa Dx>0, ibig sabihin, f(x) - f(x 0)>0 sa x>x 0,

at nangangahulugan ito na ang function na f(x) ay tuloy-tuloy sa puntong x 0 . Q.E.D.

Kaya, hindi maaaring magkaroon ng derivative ang function sa mga discontinuity point. Ang kabaligtaran ay hindi totoo: may mga tuluy-tuloy na pag-andar na hindi naiba-iba sa ilang mga punto (iyon ay, walang derivative sa mga puntong ito).

Tingnan natin ang mga punto a, b, c sa figure.

Sa punto a para sa Dx>0, ang ratio ay walang limitasyon (dahil ang mga one-sided na limitasyon ay iba para sa Dx>0-0 at Dx>0+0). Sa puntong A ng graph ay walang tiyak na tangent, ngunit mayroong dalawang magkaibang one-way na tangent na may mga slope na 1 at 2. Ang ganitong uri ng punto ay tinatawag na corner point.

Sa punto b para sa Dx>0, ang ratio ay pare-pareho ang tanda at walang katapusan na malaki. Ang function ay may walang katapusang derivative. Sa puntong ito ang graph ay may patayong padaplis. Uri ng punto - "inflection point" na may patayong tangent.

Sa punto c, ang mga one-sided derivatives ay walang katapusang malalaking dami ng iba't ibang mga palatandaan. Sa puntong ito ang graph ay may dalawang pinagsamang vertical tangent. Uri - "return point" na may vertical tangent - isang espesyal na kaso ng isang corner point.

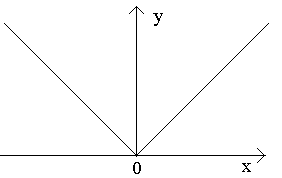
1. Isaalang-alang ang function na y=|x|. Ang function na ito ay tuloy-tuloy sa punto

Ipakita natin na wala itong derivative sa puntong ito.

f(0+Dx) = f(Dx) = |Dx|. Samakatuwid, Дy = f(Дx) - f(0) = |Дx|

Ngunit pagkatapos ay sa Dx< 0 (т.е. при Дx стремящемся к 0 слева)

At kapag Dx > 0

Kaya, ang ratio para sa Dx> 0 sa kanan at kaliwa ay may iba't ibang mga limitasyon, na nangangahulugan na ang ratio ay walang limitasyon, i.e. derivative ng function na y=|x| ay wala sa puntong x= 0. Sa geometrically, nangangahulugan ito na sa puntong x = 0 ang "curve" na ito ay walang tiyak na tangent (sa puntong ito ay may dalawa).

2. Ang function ay tinukoy at tuloy-tuloy sa buong linya ng numero. Alamin natin kung ang function na ito ay may derivative sa x= 0.

Dahil dito, ang function na isinasaalang-alang ay hindi naiba-iba sa puntong x= 0. Ang tangent sa curve sa puntong ito ay bumubuo ng isang anggulo p/2 na may abscissa axis, i.e. coincides sa Oy axis.

3 Kahulugan ng derivative ng isang function sa isang punto Hayaang tukuyin ang function na f(x) sa ilang kapitbahayan ng point x 0. KAHULUGAN. Kung mayroong isang (finite) na limitasyon ng kaugnayan kung gayon ang f(x) ay tinatawag na differentiable point x 0, at ang limit mismo ay tinatawag na derivative ng function na f(x) sa puntong x 0 at ipinapahiwatig ng f " (x 0), ibig sabihin, Tukuyin natin ang x = x – x 0 ay ang pagtaas ng argumento kapag lumilipat mula sa punto x 0 patungo sa puntong x, at ang y = f(x 0 + x) – f(x 0) ay ang katumbas na pagtaas ng function. Pagkatapos ay ang derivative ng function na f(x) sa puntong x 0 ay ang limitasyon ng ratio ng pagtaas ng function sa argument increment na naging sanhi nito, kapag ang argument increment ay may posibilidad na zero.

4 Halimbawa 1. Magbigay tayo ng mga halimbawa ng pagkalkula ng mga derivatives ng ilan sa mga pinakasimpleng elementary function, batay sa kahulugan ng derivative. y = a x (0 0. Ipagpalagay na ang | x | 0 ay isang arbitrary na punto, kung gayon 0.Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, kung gayon">

0.Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya (sinx) = cosx, x R." title=" 5 Halimbawa 3. Kunin natin ang x 0 > 0. Ipagpalagay na ang | x | 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya ( sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Halimbawa 3. Kunin ang x 0 > 0. Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: So (sinx) = cosx, x R. 0.Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya (sinx) = cosx, x R."> 0. Ipagpalagay na | x | 0 – arbitrary point, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya (sinx) = cosx, x R."> 0. Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya (sinx) = cosx, x R." title=" 5 Halimbawa 3. Kunin natin ang x 0 > 0. Ipagpalagay na ang | x | 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: Kaya ( sinx) = cosx, x R."> title="5 Halimbawa 3. Kunin ang x 0 > 0. Ipagpalagay na | x | Ang 0 ay isang arbitrary na punto, pagkatapos Halimbawa 4. y = sinx, x R. Kunin ang x 0 R at kalkulahin ang pagtaas ng function sa puntong ito: So (sinx) = cosx, x R."> !}

6 TEOREM. Kung ang isang function na f(x) ay naiba-iba sa isang punto x 0, kung gayon ito ay tuluy-tuloy sa puntong iyon. Patunay. Let there exist Then Mula dito makuha natin na f (x) – f (x 0) = f "(x 0) (x – x 0) + (x – x 0)α(x) para sa x x 0. Ibig sabihin, f(x) ay tuloy-tuloy sa puntong x 0. Continuity ng differentiable function (1)

7 TANDAAN. Ang pagpapatuloy ng isang function sa isang punto ay hindi isang sapat na kundisyon para sa pagkakaroon ng isang derivative sa puntong iyon. Halimbawa 5. f(x) = x. Pag-aralan natin ang pag-uugali ng f (x) sa paligid ng x 0 = 0. Dito f (x) f (0) = 0 sa x 0. Iyon ay ang function ay tuloy-tuloy sa puntong x 0 = 0. Isaalang-alang ang x y 0 Ang limitasyon ay wala, dahil Kaya, ang function na f (x) = x ay walang derivative sa puntong x = 0, bagama't ito ay tuloy-tuloy sa ganito punto

8 Halimbawa x y 0 sa x 0. sa x 0. Ibig sabihin Ang f(x) ay tuloy-tuloy sa puntong x = 0. Ibig sabihin, Ang f(x) ay walang derivative sa puntong x = 0 at, samakatuwid, ay hindi naiba-iba sa puntong ito. Pag-aralan natin ang pag-uugali ng f (x) sa paligid ng puntong x = 0.

9 Hayaang maging differentiable ang function na y = f(x) sa puntong x 0. Pagkatapos, ayon sa (1), ang pagtaas nito sa puntong x 0 ay maaaring isulat bilang y = f(x 0 + x) – f(x 0) = f ( x 0) x + o(x) sa x. Ang pagkakaiba ng function na f (x 0) x ay ang pangunahing linear na nauugnay sa x bahagi ng pagtaas ng function na y = f(x) sa puntong x 0 ay tinatawag na differential ng function sa punto x 0 na may increment x at ay denoted df(x 0 ; x) o df(x 0 ) o df o dу. y = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) sa x. DEPINISYON. Ang pangunahing bahagi ng pagtaas, linear na may paggalang sa x. Isang infinitesimal ng isang mas mataas na order kaysa sa x. Ngayon ang pagtaas ng function ay maaaring isulat tulad nito:

10 TANDAAN. Ang increment x ay madalas na tinutukoy ng simbolo na dx at tinatawag na differential ng independent variable. Kaya, ang kaugalian ng isang function sa puntong x 0 ay maaaring isulat sa anyong df(x 0) = f "(x 0) dx. Kung ang isang function ay naiba-iba sa bawat punto ng isang tiyak na pagitan, ang differential dy nito ay isang function ng x at dx: dy = f "(x)dx. Mula rito, sa partikular, nakakakuha tayo ng expression para sa derivative. Ibig sabihin, ang derivative ay maaaring ituring bilang ratio ng differential ng isang function sa differential ng independent variable.

11 Geometric na kahulugan ng derivative at differential Hayaang tukuyin ang function na y = f(x) sa U(x 0) at differentiable sa puntong x 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L – secant L 0 – tangent x y = f(x 0 + x) – f(x 0) sa x dahil sa continuity ng function. Ang padaplis sa graph ng function na y = f(x) sa punto M 0 ay ang naglilimitang posisyon ng secant L sa x. y Kung ang function ay differentiable sa punto x 0, pagkatapos ay sa secant equation y/ x f (x 0) sa x at ang tangent equation ay may anyo na y = y 0 + f (x 0) (x – x 0).

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) para sa x 0 L0L0 tg = f (x 0) Kung y/ x para sa x, ang tuwid na linyang x = x 0 na nagreresulta mula sa secant equation ay tinatawag na vertical tangent sa graph ng function sa point M 0. Mula sa tangent equation ay nakukuha natin ang y – y 0 = f (x 0) (x – x 0) = df (x 0) – pagtaas ng ordinate ng tangent kapag lumilipat mula sa point x 0 hanggang point x. Ang normal sa graph ng isang function sa point M 0 ay isang tuwid na linya na patayo sa tangent na dumadaan sa point M 0. Ang equation nito ay may anyong y = y 0 – 1/f (x 0) (x – x 0). L 1 – normal

13 Mga pisikal na aplikasyon ng derivative at differential Kung ang S(t) ay ang landas na dinaanan ng isang materyal na punto sa oras t, kung gayon ang S "(t) ay ang agarang bilis ng materyal na punto, at ang dS = S "(t)dt ay ang distansya na lalakbayin ng materyal na punto para sa tagal ng panahon mula t hanggang t + dt, kung ito ay gumagalaw sa bilis na katumbas ng agarang bilis sa sandaling t. Kung ang Q(t) ay ang dami ng kuryente na dumadaloy sa cross section ng conductor sa oras t, kung gayon ang Q "(t) = I ay ang kasalukuyang lakas. Kung ang N(t) ay ang dami ng substance na nabuo sa oras t sa panahon isang kemikal na reaksyon, pagkatapos ay N "(t) - rate ng reaksyong kemikal.

Kung ang function y = f(x) ay naiba sa isang punto x = x 0, pagkatapos ito ay tuloy-tuloy sa puntong ito.

Kaya, hindi maaaring magkaroon ng derivative ang function sa mga discontinuity point. Ang kabaligtaran na konklusyon ay hindi tama, i.e. mula sa katotohanan na sa ilang mga punto x = x 0 function y = f(x) ay tuloy-tuloy ay hindi nangangahulugan na ito ay naiba sa puntong ito. Halimbawa, ang function y = |x| tuloy-tuloy para sa lahat x (–< X < ), но в точке x= 0 ay walang derivative. Sa puntong ito ay walang padaplis sa graph. Mayroong kanang padaplis at kaliwang padaplis, ngunit hindi sila nagtutugma.

21 Paghahanap ng mga panuntunan produksyon mga halaga

Panuntunan 1. Kung ang mga function na y = f(x) at y = g(x) ay may derivative sa point x, kung gayon ang sum nila ay mayroon ding derivative sa point x, at ang derivative ng sum ay katumbas ng sum ng derivatives:
(f(x) + 8(x))" =f (x)+ (x).
Sa pagsasagawa, ang panuntunang ito ay nabuo nang mas maikli: ang derivative ng isang kabuuan ay katumbas ng kabuuan ng mga derivatives nito.
Halimbawa,
Panuntunan 2. Kung ang function na y = f(x) ay may derivative sa point x, ang function na y = kf(x) ay mayroon ding derivative sa point x, at:

Sa pagsasagawa, ang panuntunang ito ay nabuo nang mas maikli: ang pare-parehong kadahilanan ay maaaring alisin sa tanda ng hinalaw. Halimbawa,

Panuntunan 3. Kung ang mga function na y=f(x) at y =g(x) ay may derivative sa point x, kung gayon ang kanilang produkto ay mayroon ding derivative sa point x, at:

Sa pagsasagawa, ang panuntunang ito ay binabalangkas tulad ng sumusunod: ang derivative ng produkto ng dalawang function ay katumbas ng kabuuan ng dalawang termino. Ang unang termino ay ang produkto ng derivative ng unang function at ang pangalawang function, at ang pangalawang termino ay ang produkto ng unang function at ang derivative ng pangalawang function.
Halimbawa:
Panuntunan 4. Kung ang mga function na y = f(x) at y=g(x) ay may derivative kung gayon ang quotient ay may derivative sa puntong x, at:

Talaan ng mga kumplikadong derivatives

22 Diff. functional sa punto

Function y=f(x) ay sinasabing differentiable sa punto x 0 kung ang pagtaas nito ay Δ y(x 0,Δ x) ay maaaring katawanin bilang

Δ y(x 0,Δ x)=AΔ x+o(Δ x).

Pangunahing linear na bahagi AΔ x mga dagdag Δ y ay tinatawag na kaugalian ng function na ito sa punto x 0, na tumutugma sa pagtaas ng Δ x, at ipinapahiwatig ng simbolo dy(x 0,Δ x).

Para sa pag-andar y=f(x) ay naiba sa punto x 0, ito ay kinakailangan at sapat para umiral ang derivative f′( x 0), at ang pagkakapantay-pantay ay totoo A=f′( x 0).

Ang expression para sa kaugalian ay may anyo

dy(x 0,dx)=f′( x 0)dx,

saan dx=Δ x.

23 Prod. Kumplikado Function

Derivative ng isang kumplikadong function. Derivative ng isang function na tinukoy sa parametrically

Hayaan y - kumplikadong pag-andar x, ibig sabihin. y = f(u), u = g(x), o

Kung g(x) At f(u) – naiba-iba ang mga function ng kanilang mga argumento, ayon sa pagkakabanggit, sa mga punto x At u = g(x), pagkatapos ay ang kumplikadong function ay din differentiable sa punto x at matatagpuan sa pamamagitan ng formula

Derivative ng isang function na ibinigay parametrically.

24 Prod at diff. Pinakamataas na pagkakasunud-sunod

Ngayon hayaan ang derivative ng ika-order na tukuyin sa isang tiyak na kapitbahayan ng punto at maging differentiable. Pagkatapos

Kung ang isang function ay may partial derivative na may kinalaman sa isa sa mga variable sa ilang domain D, kung gayon ang nasabing derivative, na mismo ay isang function ng, ay maaaring magkaroon ng partial derivatives na may kinalaman sa pareho o anumang iba pang variable sa ilang mga punto. Para sa orihinal na function, ang mga derivative na ito ay magiging second-order partial derivatives (o second partial derivatives).

Ang pangalawa o mas mataas na order na partial derivative na kinuha na may kinalaman sa iba't ibang variable ay tinatawag na mixed partial derivative. Halimbawa,

Differential ng order n, Saan n > 1, ng isang function sa ilang punto ay tinatawag na differential sa puntong ito ng order differential (n - 1), yan ay

Para sa isang function na nakadepende sa isang variable, ganito ang hitsura ng pangalawa at pangatlong differential:

Mula dito maaari nating makuha ang isang pangkalahatang pagtingin sa pagkakaiba n ika-utos mula sa function:

25 Theorems ng Fermat, Rolle, Langrange

v Teorama ni Fermat: Hayaang tukuyin ang function at maabot ang maximum at minimum na mga halaga nito ( M At m) sa ilan sa mga . Kung mayroong isang derivative sa , kung gayon ito ay kinakailangang katumbas ng 0.

Patunay: Umiiral. Mayroong dalawang posibleng kaso:

1) , => , => .

2) , => , => .

Mula sa 1) at 2) ito ay sumusunod na

v Rolle's theorem (tungkol sa mga ugat ng derivative): Hayaang tuluy-tuloy at naiba-iba ang function at kunin ang parehong mga halaga sa mga dulo ng segment: . Pagkatapos ay mayroong kahit isang punto mula sa , ang derivative kung saan .

v Patunay: Ang patuloy na pag-abot sa M At m. Pagkatapos ay posible ang dalawang kaso:

2) ang pinakamalaking halaga ay nakamit sa loob ng pagitan ayon sa teorama ni Fermat.

v Ang teorama ni Langrage (tungkol sa mga huling pagtaas): Hayaang tuluy-tuloy ang function at naiba-iba sa . Pagkatapos ay mayroong hindi bababa sa isa sa , kung saan ang sumusunod na pagkakapantay-pantay ay nagtataglay: .

Patunay: Ipakilala natin ang function . (continuous on at differentiable on ).

Ang isang function ay nakakatugon sa Rolle's Theorem ay umiiral , kung saan: , , , .

· ang function ay tinatawag mahigpit na tumataas sa kung

· ang function ay tinatawag bumababa sa kung

· ang function ay tinatawag mahigpit na bumababa sa kung

Kahulugan: Ang derivative ng isang function sa isang punto ay ang limitasyon kung saan ang ratio ng pagtaas nito sa puntong iyon sa katumbas na pagtaas ng argument ay may posibilidad kapag ang huli ay may posibilidad na zero:

Iyon ay, kung tinukoy sa, pagkatapos

Teorama 1:

Ang graph ng isang function ay may non-vertical tangent kung at kung mayroong finite value ng derivative ng function na iyon sa isang partikular na punto.

Patunay:

Hayaang magkaroon ng value f'()-finite, kung gayon

Hayaang magkaroon ng non-vertical tangent => mayroong isang may hangganan.

Ang secant ay may gawi sa padaplis.

Ang teorama ay napatunayan.

Ticket 2 Continuity ng isang function na may derivative.

Ang isang function na f (x), na tinukoy sa ilang kapitbahayan ng isang punto a, ay tinatawag na tuloy-tuloy sa puntong ito kung

Teorama: (isang kinakailangang kondisyon para sa pagkakaroon ng isang derivative)

Kung ang isang function ay may hangganan sa isang punto, hindi ito tuloy-tuloy sa punto.

Patunay:

Samakatuwid, ito ay tuloy-tuloy sa isang punto.

Ang teorama ay napatunayan.

Magkomento : ang kabaligtaran na pahayag ay hindi totoo, kung ang isang function ay tuloy-tuloy sa isang punto, kung gayon hindi ito sumusunod na mayroon itong hinango sa puntong iyon.

Pahayag : Kung ang isang function ay may kanan at kaliwang derivatives sa isang punto, ito ay tuloy-tuloy sa parehong kanan at kaliwa.

Ticket 3

Derivative ng isang kabuuan, produkto, quotient.

Derivative ng inverse function.

Kahulugan ng isang naiba-iba na function. Kinakailangan at sapat na kondisyon para sa pagkakaiba-iba.

Hayaang magkaroon ng derivative ang function sa isang punto (finite): .

Pagkatapos, para sa mga sapat na maliliit, maaari naming isulat ito bilang isang kabuuan at ilang function, na tinutukoy namin ng, na may posibilidad na maging zero kasama ng:,

at ang pagtaas sa isang punto ay maaaring isulat bilang:

o (1) ,

pagkatapos ng lahat, ang expression ay nauunawaan bilang isang function na ang ratio nito ay may posibilidad na zero kasama ng.

Paliwanag:

Kahulugan .

Ang isang function ay sinasabing naiba-iba sa isang punto kung ang pagtaas nito ay maaaring katawanin bilang: (2),

kung saan ang A ay hindi nakasalalay sa, ngunit sa pangkalahatan ay nakasalalay sa.

Teorama 1:

Upang maging differentiable ang isang function sa isang punto, kinakailangan at sapat na mayroon itong finite derivative sa puntong iyon.

Patunay:

Sapat ng kondisyon ay napatunayan sa itaas: mula sa pagkakaroon ng isang finite derivative sinundan nito ang posibilidad ng representasyon sa anyo (1), kung saan maaari nating ilagay.

Kondisyon ng pangangailangan . Hayaang maging differentiable ang function sa isang punto. Pagkatapos mula sa (2), sa pag-aakalang, nakuha namin.

Ang limitasyon ng kanang bahagi sa ay umiiral at katumbas ng A:.

Nangangahulugan ito na mayroong derivative. Ang teorama ay napatunayan.

Ticket 6 Differential ng isang function, ang geometric na kahulugan nito.

Kung ang function f may derivative f΄(x o ) sa punto x o, pagkatapos ay mayroong limitasyon kung saan ang Δ f=f(x o + Δ x)-f(x o ) ,,o, saan A=f΄(x o ) .

Kahulugan:

Function f differentiable sa punto x o, kung ang pagtaas nito ay maaaring katawanin bilang:

saan AΔ x=df. (*)

Ang kaugalian ay ang pangunahing linear na bahagi ng pagtaas ng function.

Kung may finite derivative f΄(x o ) sa punto x o, pagkatapos ay ang function f(x) ay differentiable sa puntong ito.

Ang kabaligtaran ay totoo rin: kung ang function f differentiable sa punto x o, ibig sabihin. ang increment nito ay maaaring katawanin sa anyo (*), pagkatapos ay mayroon itong derivative sa punto x o, katumbas ng A:

Geometric na kahulugan ng kaugalian:

A At B– mga graph point f(x), naaayon sa mga halaga x o At (x o + Δ x) malayang baryabol. Ordinasyon ng mga puntos A At B ayon sa pagkakapantay-pantay f(x o ) At f(x o + Δ x). Pagtaas ng function Δ f=f(x o + Δ x)-f(x o ) sa punto x o katumbas ng haba ng segment BD at maaaring katawanin bilang kabuuan Δ f=BD=DC+CB, Saan DC=tgαΔ x=f΄(x o ) Δ x At α ay ang anggulo sa pagitan ng padaplis sa punto A sa graph at ang positibong direksyon ng axis x. Mula dito ay malinaw na DC may differential function f sa punto x o :

DC=df=f΄(x o ) Δ x.

Kasabay nito, ang bahagi ng pangalawang miyembro C.B. mga dagdag Δ f account para sa halaga. Ang halagang ito, sa malaking Δ x, maaaring mas malaki pa kaysa sa pangunahing termino, ngunit ito ay isang infinitesimal ng isang mas mataas na order kaysa sa Δ x, kapag Δ x→0.

MGA KATANGIAN NG MGA TUNGKULIN NA PATULOY SA ISANG PANAYAM

Isaalang-alang natin ang ilang mga katangian ng mga function na tuloy-tuloy sa isang pagitan. Ipinakita namin ang mga katangiang ito nang walang patunay.

Function y = f(x) tinawag tuloy-tuloy sa segment [a, b], kung ito ay tuloy-tuloy sa lahat ng panloob na punto ng segment na ito, at sa mga dulo nito, i.e. sa mga punto a At b, ay tuloy-tuloy sa kanan at kaliwa, ayon sa pagkakabanggit.

Teorama 1. Isang function na tuloy-tuloy sa pagitan [ a, b], hindi bababa sa isang punto ng segment na ito ay tumatagal ng pinakamalaking halaga at hindi bababa sa isang punto ang pinakamaliit.

Ang theorem ay nagsasaad na kung ang isang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b], pagkatapos ay mayroong kahit isang punto x 1 Î [ a, b] na ang halaga ng function f(x) sa puntong ito ay magiging pinakamalaki sa lahat ng mga halaga nito sa segment na ito: f(x 1) ≥ f(x). Katulad nito, may ganoong punto x 2, kung saan ang value ng function ang magiging pinakamaliit sa lahat ng value sa segment: f(x 1) ≤ f(x).

Ito ay malinaw na maaaring mayroong ilang mga tulad na mga punto, halimbawa, ang figure ay nagpapakita na ang function f(x) kumukuha ng pinakamaliit na halaga sa dalawang punto x 2 At x 2 ".

Magkomento. Ang pahayag ng theorem ay maaaring maging mali kung isasaalang-alang natin ang halaga ng function sa pagitan ( a, b). Sa katunayan, kung isasaalang-alang natin ang pag-andar y = x sa (0, 2), pagkatapos ito ay tuloy-tuloy sa agwat na ito, ngunit hindi maabot ang alinman sa pinakamalaki o pinakamaliit na halaga dito: naabot nito ang mga halagang ito sa mga dulo ng agwat, ngunit ang mga dulo ay hindi nabibilang sa aming domain.

Gayundin, ang teorama ay tumigil na maging totoo para sa mga di-tuloy na pag-andar. Magbigay ng halimbawa.

Bunga. Kung ang function f(x) ay tuloy-tuloy sa [ a, b], kung gayon ito ay limitado sa segment na ito.

Teorama 2. Hayaan ang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b] at sa mga dulo ng segment na ito ay kumukuha ng mga halaga ng iba't ibang mga palatandaan, pagkatapos ay mayroong hindi bababa sa isang punto sa loob ng segment x = C, kung saan ang function ay napupunta sa zero: f(C)= 0, kung saan a< C< b

Ang theorem na ito ay may isang simpleng geometric na kahulugan: kung ang mga punto ng graph ng isang tuluy-tuloy na function y = f(x), naaayon sa mga dulo ng segment [ a, b] nakahiga sa magkabilang panig ng axis baka, pagkatapos ay i-intersect ng graph na ito ang axis kahit man lang isang punto ng segment baka. Maaaring walang ganitong katangian ang mga hindi tuluy-tuloy na function.

Ang teorama na ito ay umamin sa sumusunod na paglalahat.

Theorem 3 (intermediate value theorem). Hayaan ang function y = f(x) ay tuloy-tuloy sa pagitan [ a, b] At f(a) = A, f(b) = B. Pagkatapos ay para sa anumang numero C, nagtapos sa pagitan ng A At B, may ganoong punto sa loob ng segment na ito CÎ [ a, b], Ano f(c) = C.

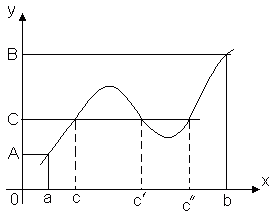
Ang teorama na ito ay geometrically obvious. Isaalang-alang ang graph ng function y = f(x). Hayaan f(a) = A, f(b) = B. Pagkatapos ng anumang tuwid na linya y = C, Saan C– anumang numero sa pagitan A At B, ay mag-intersect sa graph ng function kahit man lang sa isang punto. Ang abscissa ng intersection point ay ang halagang iyon x = C, Kung saan f(c) = C.

Kaya, ang isang tuluy-tuloy na pag-andar, na lumilipat mula sa isang halaga patungo sa isa pa, ay kinakailangang dumaan sa lahat ng mga intermediate na halaga. Sa partikular:

Bunga. Kung ang function y = f(x) ay tuloy-tuloy sa isang partikular na pagitan at kumukuha ng pinakamalaki at pinakamaliit na halaga, pagkatapos ay sa pagitan na ito ay tumatagal ng kahit isang beses ang anumang halaga na nasa pagitan ng pinakamaliit at pinakamalaking halaga nito.

DERIVATIVE AT MGA APLIKASYON NITO. KAHULUGAN NG DERIVATIVE

Magkaroon tayo ng ilang function y=f(x), tinukoy sa ilang pagitan. Para sa bawat halaga ng argumento x mula sa pagitan na ito ang function y=f(x) may tiyak na kahulugan.

Isaalang-alang ang dalawang halaga ng argumento: inisyal x 0 at bago x.

Pagkakaiba x–x 0 ang tinatawag sa pamamagitan ng pagdaragdag ng argumento x sa punto x 0 at ipinapahiwatig Δx. kaya, Δx = x – x 0 (ang pagtaas ng argumento ay maaaring maging positibo o negatibo). Mula sa pagkakapantay-pantay na ito ay sinusundan iyon x=x 0 +Δx, ibig sabihin. ang paunang halaga ng variable ay nakatanggap ng ilang pagtaas. Pagkatapos, kung sa punto x 0 ang halaga ng function noon f(x 0 ), pagkatapos ay sa isang bagong punto x kukunin ng function ang halaga f(x) = f(x 0 +Δx).

Pagkakaiba y–y 0 = f(x) – f(x 0 ) tinawag pagtaas ng function y = f(x) sa punto x 0 at ipinahiwatig ng simbolo Δy. kaya,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Karaniwan ang paunang halaga ng argumento x 0 ay itinuturing na naayos, at ang bagong halaga x– variable. Pagkatapos y 0 = f(x 0 ) lumalabas na pare-pareho, at y = f(x)– variable. Mga dagdag Δy At Δx magiging mga variable din at ang formula (1) ay nagpapakita na Dy ay isang function ng isang variable Δx.

Gawin natin ang ratio ng increment ng function sa increment ng argument

Hanapin natin ang limitasyon ng ratio na ito sa Δx→0. Kung umiiral ang limitasyong ito, kung gayon ito ay tinatawag na derivative ng function na ito f(x) sa punto x 0 at tukuyin f "(x 0). Kaya,

Derivative function na ito y = f(x) sa punto x Ang 0 ay tinatawag na limitasyon ng ratio ng pagtaas ng function na Δ y sa argumentong pagtaas Δ x, kapag ang huli ay arbitraryong nagiging zero.

Tandaan na para sa parehong function ang derivative sa iba't ibang mga punto x maaaring tumagal sa iba't ibang mga halaga, i.e. ang derivative ay maaaring ituring bilang isang function ng argumento x. Ang function na ito ay itinalaga f "(x)

Ang derivative ay tinutukoy ng mga simbolo f "(x), y", . Ang tiyak na halaga ng derivative sa x = a denoted f "(a) o y "| x=a.

Ang operasyon ng paghahanap ng derivative ng isang function f(x) ay tinatawag na pagkita ng kaibhan ng function na ito.

Upang direktang mahanap ang derivative ayon sa kahulugan, maaari mong gamitin ang sumusunod: pamantayan:

Mga halimbawa.

MECHANICAL SENSE OF DERIVATIVE

Ito ay kilala mula sa pisika na ang batas ng unipormeng paggalaw ay may anyo s = v t, Saan s– ang landas ay naglakbay patungo sa sandali ng panahon t, v- bilis ng pare-parehong paggalaw.

Gayunpaman, dahil Karamihan sa mga paggalaw na nagaganap sa kalikasan ay hindi pantay, pagkatapos ay sa pangkalahatan ang bilis, at, dahil dito, ang distansya. s ay depende sa oras t, ibig sabihin. magiging function ng oras.

Kaya, hayaan ang isang materyal na punto na lumipat sa isang tuwid na linya sa isang direksyon ayon sa batas s=s(t).

Markahan natin ang isang tiyak na punto ng oras t 0 . Sa puntong ito ang punto ay lumipas na sa landas s=s(t 0 ). Tukuyin natin ang bilis v materyal na punto sa isang sandali sa oras t 0 .

Upang gawin ito, isaalang-alang natin ang ilang iba pang punto sa oras t 0 + Δ t. Ito ay tumutugma sa nilakbay na landas s =s(t 0 + Δ t). Pagkatapos sa isang yugto ng panahon Δ t ang punto ay naglakbay sa landas na Δs =s(t 0 + Δ t)–s(t).

Isaalang-alang natin ang saloobin. Ito ay tinatawag na average na bilis sa pagitan ng oras Δ t. Ang average na bilis ay hindi maaaring tumpak na makilala ang bilis ng paggalaw ng isang punto sa sandaling ito t 0 (dahil hindi pantay ang paggalaw). Upang mas tumpak na maipahayag ang totoong bilis na ito gamit ang average na bilis, kailangan mong kumuha ng mas maikling panahon Δ t.

Kaya, ang bilis ng paggalaw sa isang naibigay na sandali sa oras t 0 (madaliang bilis) ay ang limitasyon ng average na bilis sa pagitan mula sa t 0 hanggang t 0 +Δ t, kapag Δ t→0:

,

mga. hindi pantay na bilis ito ang derivative ng distansyang nilakbay patungkol sa oras.

HEOMETRICAL MEANING NG DERIVATIVE

Ipakilala muna natin ang kahulugan ng isang tangent sa isang kurba sa isang naibigay na punto.

Magkaroon tayo ng isang kurba at isang nakapirming punto dito M 0(tingnan ang figure) Isaalang-alang ang isa pang punto M curve na ito at gumuhit ng secant M 0 M. Kung ang punto M nagsisimulang gumalaw kasama ang kurba, at ang punto M 0 nananatiling hindi gumagalaw, pagkatapos ay nagbabago ang secant ng posisyon nito. Kung, na may walang limitasyong pagtatantya ng punto M kasama ang isang kurba sa isang punto M 0 sa anumang panig ang secant ay may posibilidad na sumakop sa posisyon ng isang tiyak na tuwid na linya M 0 T, pagkatapos ay diretso M 0 T tinatawag ang padaplis sa kurba sa isang naibigay na punto M 0.

yun., padaplis sa kurba sa isang naibigay na punto M 0 tinatawag na limitasyon ng posisyon ng secant M 0 M kapag point M tends along the curve to a point M 0.

Isaalang-alang natin ngayon ang tuluy-tuloy na pag-andar y=f(x) at ang curve na naaayon sa function na ito. Sa ilang halaga X 0 function ay tumatagal ng halaga y 0 =f(x 0). Ang mga halagang ito x 0 at y 0 sa curve ay tumutugma sa isang punto M 0 (x 0 ; y 0). Ibigay natin ang argumento x 0 pagtaas Δ X. Ang bagong value ng argument ay tumutugma sa incremented value ng function y 0 +Δ y=f(x 0 –Δ x). Nakukuha namin ang punto M(x 0+Δ x; y 0+Δ y). Gumuhit tayo ng secant M 0 M at tukuyin sa pamamagitan ng φ ang anggulo na nabuo ng isang secant na may positibong direksyon ng axis baka. Gumawa tayo ng isang relasyon at pansinin na .

Kung ngayon Δ x→0, pagkatapos ay dahil sa pagpapatuloy ng function na Δ sa→0, at samakatuwid ang punto M, gumagalaw sa isang kurba, lumalapit sa puntong walang limitasyon M 0. Tapos yung secant M 0 M ay may posibilidad na kunin ang posisyon ng isang padaplis sa kurba sa punto M 0, at ang anggulo φ→α sa Δ x→0, kung saan ang α ay tumutukoy sa anggulo sa pagitan ng tangent at ng positibong direksyon ng axis baka. Dahil ang function na tan φ ay patuloy na nakasalalay sa φ para sa φ≠π/2, kung gayon para sa φ→α tan φ → tan α at, samakatuwid, ang slope ng tangent ay magiging:

mga. f "(x)= tg α .

Kaya, geometrically y "(x 0) kumakatawan sa slope ng tangent sa graph ng function na ito sa punto x 0, ibig sabihin. para sa isang ibinigay na halaga ng argumento x, ang derivative ay katumbas ng tangent ng anggulo na nabuo ng tangent sa graph ng function f(x) sa angkop na punto M 0 (x; y) na may positibong direksyon ng axis baka.

Halimbawa. Hanapin ang slope ng tangent sa curve y = x 2 sa punto M(-1; 1).

Nakita na natin kanina na ( x 2)" = 2X. Ngunit ang angular coefficient ng tangent sa curve ay tan α = y"| x=-1 = – 2.

PAGKAKAIBA NG MGA FUNCTION. PAGPAPATULOY NG NAIIBA NA FUNCTION

Function y=f(x) tinawag naiba-iba sa isang punto x 0 kung mayroon itong tiyak na derivative sa puntong ito, i.e. kung ang limitasyon ng relasyon ay umiiral at may hangganan.

Kung ang isang function ay naiba-iba sa bawat punto ng isang partikular na segment [ A; b] o pagitan ( A; b), pagkatapos ay sinasabi nila na siya naiba-iba sa segment [ A; b] o, ayon sa pagkakabanggit, sa pagitan ( A; b).

Ang sumusunod na theorem ay wasto, na nagtatatag ng koneksyon sa pagitan ng naiba at tuluy-tuloy na mga pag-andar.

Teorama. Kung ang function y=f(x) naiba sa isang punto x 0, pagkatapos ito ay tuloy-tuloy sa puntong ito.

Kaya, mula sa pagkakaiba-iba ng isang function, ang pagpapatuloy nito ay sumusunod.

Patunay. Kung , Iyon

,

kung saan ang α ay isang infinitesimal na dami, i.e. isang dami na may posibilidad na zero bilang Δ x→0. Ngunit pagkatapos

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 sa Δ x→0, ibig sabihin. f(x) – f(x 0)→0 sa x→x 0 , na nangangahulugan na ang function f(x) tuloy-tuloy sa isang punto x 0 . Q.E.D.

Kaya, hindi maaaring magkaroon ng derivative ang function sa mga discontinuity point. Ang kabaligtaran ay hindi totoo: may mga tuluy-tuloy na pag-andar na hindi naiba-iba sa ilang mga punto (iyon ay, walang derivative sa mga puntong ito).

Isaalang-alang ang mga punto sa figure a, b, c.

Sa punto a sa Δ x→0 ang ratio ay walang limitasyon (dahil ang mga one-sided na limitasyon ay iba para sa Δ x→0–0 at Δ x→0+0). Sa punto A graph walang tinukoy na tangent, ngunit mayroong dalawang magkaibang one-way na tangent na may mga slope Upang 1 at Upang 2. Ang ganitong uri ng punto ay tinatawag na corner point.

Sa punto b sa Δ x Ang →0 ratio ay isang pare-parehong tanda na walang katapusang malaking dami. Ang function ay may walang katapusang derivative. Sa puntong ito ang graph ay may patayong padaplis. Uri ng punto - "inflection point" ng isang patayong padaplis.

Sa punto c Ang mga one-sided derivatives ay walang katapusang malalaking dami ng iba't ibang mga palatandaan. Sa puntong ito ang graph ay may dalawang pinagsamang vertical tangent. Uri – “return point” na may vertical tangent – ​​isang espesyal na case ng isang corner point.