- die Determinante der Matrix A wird berechnet;
- durch algebraische Additionen wird die inverse Matrix A -1 gefunden;
- eine Lösungsvorlage wird in Excel erstellt;
Anweisung. Um eine Lösung nach der inversen Matrixmethode zu erhalten, ist es notwendig, die Dimension der Matrix anzugeben. Füllen Sie als Nächstes im neuen Dialogfeld die Matrix A und den Ergebnisvektor B aus.
Siehe auch Lösung von Matrixgleichungen.Lösungsalgorithmus
- Die Determinante der Matrix A wird berechnet. Wenn die Determinante Null ist, dann das Ende der Lösung. Das System hat unendlich viele Lösungen.
- Wenn die Determinante von Null verschieden ist, wird die inverse Matrix A -1 durch algebraische Additionen gefunden.
- Der Entscheidungsvektor X = (x 1 , x 2 , ..., x n ) wird durch Multiplizieren der inversen Matrix mit dem Ergebnisvektor B erhalten.
Algebraische Additionen.
| A 1,1 = (-1) 1+1 |
| ∆ 1,1 = (1 (-2)-0 2) = -2 |
| A 1,2 = (-1) 1+2 |
| ∆ 1,2 = -(3 (-2)-1 2) = 8 |
| A 1,3 = (-1) 1+3 |
| ∆ 1,3 = (3 0-1 1) = -1 |
| A 2,1 = (-1) 2+1 |
| ∆ 2,1 = -(-2 (-2)-0 1) = -4 |
| A 2,2 = (-1) 2+2 |
| ∆ 2,2 = (2 (-2)-1 1) = -5 |
| A 2,3 = (-1) 2+3 |
| ∆ 2,3 = -(2 0-1 (-2)) = -2 |
| A 3,1 = (-1) 3+1 |
| ∆ 3,1 = (-2 2-1 1) = -5 |
| 3 |
| -2 |
| -1 |
XT = (1,0,1)
x 1 = -21 / -21 = 1
x 2 = 0 / -21 = 0
x 3 = -21 / -21 = 1
Untersuchung:
2 1+3 0+1 1 = 3
-2 1+1 0+0 1 = -2
1 1+2 0+-2 1 = -1
Thema 2. SYSTEME LINEARER ALGEBRAISCHER GLEICHUNGEN.
Grundlegendes Konzept.
Bestimmung 1. System m lineare Gleichungen mit n unbekannt ist ein System der Form:
wo und Zahlen sind.
Bestimmung 2. Die Lösung des Systems (I) ist eine solche Menge von Unbekannten, in der jede Gleichung dieses Systems zu einer Identität wird.
Bestimmung 3. System (I) wird aufgerufen gemeinsam wenn es mindestens eine Lösung hat und unvereinbar wenn es keine Lösungen hat. Das gemeinsame System heißt sicher wenn es eine eindeutige Lösung hat, und unsicher sonst.
Bestimmung 4. Gleichung eingeben
genannt Null, und eine Gleichung der Form
genannt unvereinbar. Offensichtlich ist ein Gleichungssystem, das eine inkonsistente Gleichung enthält, inkonsistent.
Bestimmung 5. Die beiden linearen Gleichungssysteme werden aufgerufen gleichwertig wenn jede Lösung eines Systems eine Lösung eines anderen und umgekehrt jede Lösung des zweiten Systems eine Lösung des ersten ist.
Matrixschreibweise für ein System linearer Gleichungen.
Betrachten Sie System (I) (siehe §1).
Bezeichnen:
Koeffizientenmatrix für Unbekannte
Matrix - Spalte der freien Mitglieder
Matrix - Spalte von Unbekannten
.
Bestimmung 1. Die Matrix wird aufgerufen die Hauptmatrix des Systems(I), und die Matrix ist die erweiterte Matrix des Systems (I).
Durch die Definition der Matrixgleichheit entspricht System (I) der Matrixgleichheit:
.
Die rechte Seite dieser Gleichheit durch die Definition des Produkts von Matrizen ( siehe Definition 3 § 5 Kapitel 1) kann faktorisiert werden:
, d.h.
Gleichberechtigung (2) genannt Matrixschreibweise des Systems (I).
Lösen eines linearen Gleichungssystems nach Cramers Methode.
Einlasssystem (I) (siehe §1) m=n, d.h. die Anzahl der Gleichungen ist gleich der Anzahl der Unbekannten, und die Hauptmatrix des Systems ist nicht entartet, d.h. . Dann hat System (I) aus §1 eine eindeutige Lösung
wo ∆ = det A Haupt genannt Systemdeterminante(I), ∆ ich erhält man aus der Determinante Δ durch Ersetzen ich-te Spalte zur Spalte der freien Mitglieder des Systems (I).
Beispiel: Lösen Sie das System nach Cramers Methode:
.
Durch Formeln (3)
.
Wir berechnen die Determinanten des Systems:
,
,
.
Um die Determinante zu erhalten, haben wir die erste Spalte in der Determinante durch eine Spalte mit freien Elementen ersetzt; indem wir die 2. Spalte in der Determinante durch eine Spalte mit freien Elementen ersetzen, erhalten wir ; In ähnlicher Weise erhalten wir, wenn wir die dritte Spalte in der Determinante durch eine Spalte mit freien Elementen ersetzen, . Systemlösung:
Lösen von linearen Gleichungssystemen mit einer inversen Matrix.
Einlasssystem (I) (siehe §1) m=n und die Hauptmatrix des Systems ist nicht entartet. Wir schreiben System (I) in Matrixform ( siehe §2):
Weil Matrix EIN nicht ausgeartet ist, dann hat sie eine inverse Matrix ( siehe Theorem 1 §6 von Kapitel 1). Multiplizieren Sie beide Seiten der Gleichung (2) dann zur Matrix
Per Definition der inversen Matrix . Von der Gleichberechtigung (3) wir haben
Lösen Sie das System mit der inversen Matrix
.
Bezeichnen
Im Beispiel (§ 3) haben wir die Determinante berechnet, also die Matrix EIN hat eine inverse Matrix. Dann in Kraft (4) , d.h.
. (5)
Finden Sie die Matrix ( siehe §6 Kapitel 1)
, 
, 
,
, 
, 
,
,
.
Gauss-Methode.
Gegeben sei das lineare Gleichungssystem:
. (ICH)
Es ist erforderlich, alle Lösungen des Systems (I) zu finden oder sicherzustellen, dass das System inkonsistent ist.
Bestimmung 1.Nennen wir die elementare Transformation des Systems(I) eine der drei Aktionen:
1) Streichung der Nullgleichung;
2) Hinzufügen der entsprechenden Teile der anderen Gleichung zu beiden Teilen der Gleichung, multipliziert mit der Zahl l;
3) Vertauschen von Termen in den Gleichungen des Systems, so dass Unbekannte mit denselben Zahlen in allen Gleichungen dieselben Stellen einnehmen, d.h. Wenn wir zum Beispiel in der 1. Gleichung den 2. und 3. Term geändert haben, dann muss das gleiche in allen Gleichungen des Systems gemacht werden.
Das Gauss-Verfahren besteht darin, dass das System (I) mit Hilfe elementarer Transformationen auf ein äquivalentes System reduziert wird, dessen Lösung direkt gefunden oder dessen Unlösbarkeit festgestellt wird.
Wie in §2 beschrieben, ist System (I) eindeutig durch seine erweiterte Matrix bestimmt, und jede elementare Transformation von System (I) entspricht einer elementaren Transformation der erweiterten Matrix:
.
Transformation 1) entspricht dem Löschen der Nullzeile in der Matrix , Transformation 2) ist äquivalent dem Hinzufügen der anderen Zeile der Matrix zu der entsprechenden Zeile der Matrix, multipliziert mit der Zahl l, Transformation 3) ist äquivalent dem Neuanordnen der Spalten in der Matrix .
Es ist leicht einzusehen, dass im Gegenteil jeder elementaren Transformation der Matrix eine elementare Transformation des Systems (I) entspricht. Im Hinblick auf das Gesagte werden wir anstelle von Operationen mit dem System (I) mit der erweiterten Matrix dieses Systems arbeiten.
In der Matrix besteht die 1. Spalte aus Koeffizienten bei x 1, 2. Spalte - von den Koeffizienten bei x 2 usw. Bei der Umordnung von Spalten ist zu berücksichtigen, dass diese Bedingung verletzt wird. Wenn wir zum Beispiel die 1. und 2. Spalte vertauschen, dann gibt es jetzt in der 1. Spalte Koeffizienten bei x 2, und in der 2. Spalte - Koeffizienten bei x 1.
Wir werden das System (I) mit der Gauß-Methode lösen.
1. Streiche alle Nullzeilen in der Matrix, falls vorhanden (d. h. streiche alle Nullgleichungen im System (I).
2. Prüfen Sie, ob es unter den Zeilen der Matrix eine Zeile gibt, in der alle Elemente außer dem letzten gleich Null sind (nennen wir eine solche Zeile inkonsistent). Offensichtlich entspricht eine solche Linie einer inkonsistenten Gleichung in System (I), daher hat System (I) keine Lösungen, und hier endet der Prozess.
3. Die Matrix möge keine inkonsistenten Zeilen enthalten (System (I) enthält keine inkonsistenten Gleichungen). Wenn ein a 11 = 0, dann finden wir in der 1. Zeile ein Element (außer dem letzten), das von Null verschieden ist, und ordnen die Spalten so an, dass in der 1. Zeile keine Null an erster Stelle steht. Das nehmen wir jetzt an (d.h. wir vertauschen die entsprechenden Terme in den Gleichungen des Systems (I)).
4. Multiplizieren Sie die 1. Reihe mit und addieren Sie das Ergebnis zur 2. Reihe, dann multiplizieren Sie die 1. Reihe mit und addieren Sie das Ergebnis zur 3. Reihe usw. Offensichtlich ist dieser Prozess gleichbedeutend mit der Eliminierung des Unbekannten x 1 aus allen Gleichungen des Systems (I), außer der 1. In der neuen Matrix erhalten wir Nullen in der 1. Spalte unter dem Element eine 11:
.
5. Streichen Sie alle Nullzeilen in der Matrix, falls vorhanden, prüfen Sie, ob es eine inkonsistente Zeile gibt (wenn ja, dann ist das System inkonsistent und die Lösung endet dort). Lassen Sie uns prüfen, ob a 22 / =0, wenn ja, dann finden wir in der 2. Zeile ein von Null verschiedenes Element und ordnen die Spalten so um, dass . Als nächstes multiplizieren wir die Elemente der 2. Reihe mit 
und addiere mit den entsprechenden Elementen der 3. Reihe, dann - die Elemente der 2. Reihe an und addiere mit den entsprechenden Elementen der 4. Reihe, usw., bis wir Nullen darunter bekommen a 22 /
.
Die durchgeführten Handlungen sind gleichbedeutend mit der Beseitigung des Unbekannten x 2 aus allen Gleichungen des Systems (I), außer der 1. und 2. Da die Anzahl der Zeilen endlich ist, erhalten wir also nach endlich vielen Schritten, dass entweder das System inkonsistent ist, oder wir kommen zu einer Schrittmatrix ( siehe Definition 2 §7 Kapitel 1) :
,
Schreiben wir das der Matrix entsprechende Gleichungssystem auf. Dieses System entspricht dem System (I)
.
Aus der letzten Gleichung drücken wir aus; wir setzen in die vorherige Gleichung ein, finden usw., bis wir erhalten.
Bemerkung 1. Wenn wir also das System (I) nach dem Gauß-Verfahren lösen, gelangen wir zu einem der folgenden Fälle.
1. System (I) ist inkonsistent.
2. System (I) hat eine eindeutige Lösung, wenn die Anzahl der Zeilen in der Matrix gleich der Anzahl der Unbekannten ist ().
3. System (I) hat unendlich viele Lösungen, wenn die Anzahl der Zeilen in der Matrix kleiner ist als die Anzahl der Unbekannten ().
Daher gilt der folgende Satz.
Satz. Das lineare Gleichungssystem ist entweder inkonsistent oder hat eine eindeutige Lösung, oder es gibt eine unendliche Menge von Lösungen.
Beispiele. Lösen Sie das Gleichungssystem nach dem Gauß-Verfahren oder beweisen Sie seine Widersprüchlichkeit:
b) 
;
a) Schreiben wir das gegebene System um in die Form:
.
Wir haben die 1. und 2. Gleichung des ursprünglichen Systems vertauscht, um die Berechnungen zu vereinfachen (statt mit Brüchen werden wir mit einer solchen Permutation nur mit ganzen Zahlen operieren).
Wir erstellen eine erweiterte Matrix:
.
Es gibt keine Nullzeilen; keine inkompatiblen Zeilen, ; wir schließen die 1. Unbekannte aus allen Gleichungen des Systems außer der 1. aus. Dazu multiplizieren wir die Elemente der 1. Reihe der Matrix mit „-2“ und addieren sie zu den entsprechenden Elementen der 2. Reihe, was gleichbedeutend damit ist, die 1. Gleichung mit „-2“ zu multiplizieren und zu addieren 2. Gleichung. Dann multiplizieren wir die Elemente der 1. Reihe mit „-3“ und addieren sie zu den entsprechenden Elementen der dritten Reihe, also multipliziere die 2. Gleichung des gegebenen Systems mit "-3" und addiere es zur 3. Gleichung. Erhalten
.
Die Matrix entspricht einem Gleichungssystem). - (siehe Definition 3 § 7 von Kapitel 1).
System von m linearen Gleichungen mit n Unbekannten ein System der Form genannt
wo aij und b ich (ich=1,…,m; b=1,…,n) sind einige bekannte Zahlen, und x 1 ,…,x n- Unbekannt. In der Notation der Koeffizienten aij erster Index ich bezeichnet die Nummer der Gleichung, und die zweite j ist die Zahl der Unbekannten, bei der dieser Koeffizient steht.
Die Koeffizienten für die Unbekannten werden in Form einer Matrix geschrieben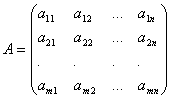 
, die wir anrufen werden Systemmatrix.
Die Zahlen auf der rechten Seite der Gleichungen b 1 ,…,b m genannt freie Mitglieder.
Aggregat n Zahlen c 1 ,…,c n genannt Entscheidung dieses Systems, wenn jede Gleichung des Systems eine Gleichheit wird, nachdem Zahlen darin eingesetzt wurden c 1 ,…,c n anstelle der entsprechenden Unbekannten x 1 ,…,x n.
Unsere Aufgabe wird es sein, Lösungen für das System zu finden. In diesem Fall können drei Situationen auftreten:
Ein lineares Gleichungssystem, das mindestens eine Lösung hat, heißt gemeinsam. Ansonsten, d.h. hat das System keine Lösungen, so wird es aufgerufen unvereinbar.
Überlegen Sie, wie Sie Lösungen für das System finden können.
MATRIX-METHODE ZUM LÖSEN VON SYSTEMEN VON LINEAREN GLEICHUNGEN
Matrizen ermöglichen es, ein lineares Gleichungssystem kurz aufzuschreiben. Gegeben sei ein System aus 3 Gleichungen mit drei Unbekannten:
Betrachten Sie die Matrix des Systems 
und Matrixspalten von unbekannten und freien Mitgliedern 
Lassen Sie uns das Produkt finden
diese. als Ergebnis des Produkts erhalten wir die linken Seiten der Gleichungen dieses Systems. Dann kann dieses System unter Verwendung der Definition der Matrixgleichheit geschrieben werden als
oder kürzer EIN∙X=B.
Hier Matrizen EIN und B bekannt sind, und die Matrix X Unbekannt. Sie muss gefunden werden, weil. seine Elemente sind die Lösung dieses Systems. Diese Gleichung heißt Matrixgleichung.
Die Matrixdeterminante sei von Null verschieden | EIN| ≠ 0. Dann wird die Matrixgleichung wie folgt gelöst. Multiplizieren Sie beide Seiten der Gleichung auf der linken Seite mit der Matrix A-1, die Inverse der Matrix EIN: . Weil die A -1 A = E und E∙X=X, dann erhalten wir die Lösung der Matrixgleichung in der Form X = A -1 B .
Beachten Sie, dass, da die inverse Matrix nur für quadratische Matrizen gefunden werden kann, die Matrixmethode nur solche Systeme lösen kann, in denen Die Anzahl der Gleichungen ist gleich der Anzahl der Unbekannten. Allerdings ist auch die Matrixschreibweise des Systems möglich, falls die Anzahl der Gleichungen ungleich der Anzahl der Unbekannten ist, dann die Matrix EIN ist nicht quadratisch und daher ist es unmöglich, eine Lösung für das System in der Form zu finden X = A -1 B.
Beispiele. Gleichungssysteme lösen.
CRAMERS REGEL
Stellen Sie sich ein System aus 3 linearen Gleichungen mit drei Unbekannten vor:
Determinante dritter Ordnung entsprechend der Matrix des Systems, d.h. zusammengesetzt aus Koeffizienten bei Unbekannten,
genannt Systemdeterminante.
Wir setzen drei weitere Determinanten wie folgt zusammen: Wir ersetzen nacheinander 1, 2 und 3 Spalten in der Determinante D durch eine Spalte mit freien Termen
Dann können wir folgendes Ergebnis beweisen.
Satz (Cramers Regel). Wenn die Determinante des Systems Δ ≠ 0 ist, dann hat das betrachtete System genau eine Lösung, und
Nachweisen. Stellen Sie sich also ein System von 3 Gleichungen mit drei Unbekannten vor. Multipliziere die 1. Gleichung des Systems mit dem algebraischen Komplement Eine 11 Element eine 11, 2. Gleichung - an A21 und 3. - auf A 31:
Fügen wir diese Gleichungen hinzu:
Betrachten Sie jede der Klammern und die rechte Seite dieser Gleichung. Durch den Satz über die Erweiterung der Determinante nach den Elementen der 1. Spalte
Ebenso kann gezeigt werden, dass und .
Schließlich ist es leicht zu sehen 
Damit erhalten wir die Gleichheit: .
Folglich, .
Die Gleichheiten und werden auf ähnliche Weise hergeleitet, woraus die Behauptung des Satzes folgt.
Wir stellen also fest, dass, wenn die Determinante des Systems Δ ≠ 0 ist, das System eine eindeutige Lösung hat und umgekehrt. Wenn die Determinante des Systems gleich Null ist, dann hat das System entweder eine unendliche Menge von Lösungen oder keine Lösungen, d.h. unvereinbar.
Beispiele. Lösen Sie ein Gleichungssystem
GAUSS-METHODE
Mit den bisher betrachteten Methoden können nur solche Systeme gelöst werden, bei denen die Anzahl der Gleichungen mit der Anzahl der Unbekannten übereinstimmt und die Determinante des Systems von Null verschieden sein muss. Das Gaußsche Verfahren ist universeller und eignet sich für Systeme mit beliebig vielen Gleichungen. Es besteht in der sukzessiven Eliminierung von Unbekannten aus den Gleichungen des Systems.
Betrachten wir wieder ein System aus drei Gleichungen mit drei Unbekannten:
.
Wir lassen die erste Gleichung unverändert, und von der 2. und 3. schließen wir die enthaltenden Terme aus x 1. Dazu dividieren wir die zweite Gleichung durch a 21 und multipliziere mit - a 11 und addiere dann mit der 1. Gleichung. In ähnlicher Weise teilen wir die dritte Gleichung in a 31 und multipliziere mit - a 11 und füge es dann dem ersten hinzu. Als Ergebnis wird das ursprüngliche System die Form annehmen:
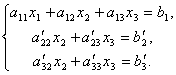
Nun eliminieren wir aus der letzten Gleichung den Term enthaltend x2. Teilen Sie dazu die dritte Gleichung durch , multiplizieren Sie mit und addieren Sie sie zur zweiten. Dann haben wir ein Gleichungssystem:
Daher ist es aus der letzten Gleichung leicht zu finden x 3, dann aus der 2. Gleichung x2 und schließlich vom 1. - x 1.
Bei Anwendung der Gauß-Methode können die Gleichungen ggf. vertauscht werden.
Anstatt ein neues Gleichungssystem zu schreiben, beschränken sie sich oft darauf, die erweiterte Matrix des Systems zu schreiben:
und dann durch elementare Transformationen in eine Dreiecks- oder Diagonalform bringen.
Zu elementare Transformationen Matrizen enthalten die folgenden Transformationen:
- Permutation von Zeilen oder Spalten;
- Multiplizieren einer Zeichenfolge mit einer Zahl ungleich Null;
- Zu einer Zeile weitere Zeilen hinzufügen.
Beispiele: Lösen Sie Gleichungssysteme mit der Gauß-Methode.
Das System hat also unendlich viele Lösungen.
In Betracht ziehen System linearer algebraischer Gleichungen(LANGSAM) bzgl n Unbekannt x 1 , x 2 , ..., x n :
Dieses System in "gefalteter" Form kann wie folgt geschrieben werden:
S n i=1 a ij x j = b ich , i=1,2, ..., n.
Nach der Regel der Matrizenmultiplikation lässt sich das betrachtete lineare Gleichungssystem einschreiben Matrixform ax=b, wo
,
,.
Matrix EIN, deren Spalten die Koeffizienten für die entsprechenden Unbekannten und die Zeilen die Koeffizienten für die Unbekannten in der entsprechenden Gleichung sind, heißt Systemmatrix. Spaltenmatrix b, deren Elemente die rechten Teile der Gleichungen des Systems sind, heißt die Matrix des rechten Teils oder einfach rechte Seite des Systems. Spaltenmatrix x , dessen Elemente unbekannte Unbekannte sind, heißt Systemlösung.
Das System der linearen algebraischen Gleichungen geschrieben als ax=b, ist Matrixgleichung.
Wenn die Matrix des Systems nicht entartet, dann hat es eine inverse Matrix und dann die Lösung des Systems ax=b ergibt sich aus der Formel:
x=A -1 b.
Beispiel Löse das System 
Matrix-Methode.
Lösung Finden Sie die inverse Matrix für die Koeffizientenmatrix des Systems
Berechnen Sie die Determinante, indem Sie über die erste Zeile expandieren:
Weil die Δ ≠ 0 , dann EIN -1 existiert.
Die inverse Matrix wird korrekt gefunden.
Lassen Sie uns eine Lösung für das System finden 
Folglich, x 1 = 1, x 2 = 2, x 3 = 3 .
Untersuchung: 
7. Der Satz von Kronecker-Capelli über die Kompatibilität eines Systems linearer algebraischer Gleichungen.
System linearer Gleichungen sieht aus wie:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.1)
ein m1 x 1 + ein m1 x 2 +... + ein mn x n = b m .
Hier sind a i j und b i (i = ; j = ) gegeben, und x j sind unbekannte reelle Zahlen. Unter Verwendung des Konzepts eines Produkts von Matrizen können wir System (5.1) in die Form umschreiben:
wobei A = (a i j) die Matrix ist, die aus den Koeffizienten der Unbekannten des Systems (5.1) besteht, das aufgerufen wird Systemmatrix, X = (x 1 , x 2 , ..., x n) T , B = (b 1 , b 2 , ..., b m) T - Spaltenvektoren, die jeweils aus unbekannten x j und freien Termen b i zusammengesetzt sind.
Bestellte Abholung n reelle Zahlen (c 1 , c 2 ,..., c n) genannt Systemlösung(5.1) wenn infolge der Substitution dieser Zahlen anstelle der entsprechenden Variablen x 1 , x 2 ,..., x n jede Gleichung des Systems zu einer arithmetischen Identität wird; mit anderen Worten, wenn es einen Vektor C= (c 1 , c 2 ,..., c n) T gibt, so dass AC B.
System (5.1) wird aufgerufen gemeinsam, oder lösbar wenn es mindestens eine Lösung gibt. Das System wird aufgerufen unvereinbar, oder unlöslich wenn es keine Lösungen hat.
,
gebildet durch Zuweisung einer Spalte freier Terme zur Matrix A auf der rechten Seite, heißt Erweitertes Matrixsystem.
Die Frage der Kompatibilität des Systems (5.1) wird durch den folgenden Satz gelöst.
Satz von Kronecker-Capelli . Das lineare Gleichungssystem ist genau dann konsistent, wenn die Ränge der Matrizen A und A übereinstimmen, d.h. r(A) = r(A) = r.
Für die Lösungsmenge M des Systems (5.1) gibt es drei Möglichkeiten:
1) M = (in diesem Fall ist das System inkonsistent);
2) M besteht aus einem Element, d.h. das System hat eine eindeutige Lösung (in diesem Fall heißt das System sicher);
3) M besteht aus mehr als einem Element (dann heißt das System unsicher). Im dritten Fall hat System (5.1) unendlich viele Lösungen.
Das System hat nur dann eine eindeutige Lösung, wenn r(A) = n. In diesem Fall ist die Anzahl der Gleichungen nicht kleiner als die Anzahl der Unbekannten (mn); wenn m > n, dann sind m-n Gleichungen Folgen des Rests. Wenn 0 Um ein beliebiges lineares Gleichungssystem zu lösen, muss man Systeme lösen können, bei denen die Anzahl der Gleichungen gleich der Anzahl der Unbekannten ist, die sogenannten Systeme vom Cramer-Typ: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 , a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.3) ...
... ... ...
... ... ein n1 x 1 + ein n1 x 2 +... + ein nn x n = b n . Systeme (5.3) werden auf eine der folgenden Arten gelöst: 1) durch das Gauß-Verfahren oder durch das Verfahren der Eliminierung von Unbekannten; 2) nach Cramers Formeln; 3) nach der Matrixmethode. Beispiel 2.12. Untersuchen Sie das Gleichungssystem und lösen Sie es, wenn es kompatibel ist: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x1 + x2 + 4x3 - 2x4 = 1, x 1 - 3 x 2 - 6 x 3 + 5 x 4 = 0. Lösung. Wir schreiben die erweiterte Matrix des Systems auf:
Berechnen wir den Rang der Hauptmatrix des Systems. Es ist offensichtlich, dass zum Beispiel das Moll zweiter Ordnung in der oberen linken Ecke = 7 0; die Minderjährigen dritter Ordnung, die es enthalten, sind gleich Null: Daher ist der Rang der Hauptmatrix des Systems 2, d.h. r(A) = 2. Um den Rang der erweiterten Matrix A zu berechnen, betrachte den angrenzenden Minor daher ist der Rang der erweiterten Matrix r(A) = 3. Da r(A) r(A) ist, ist das System inkonsistent. (manchmal wird diese Methode auch als Matrixmethode oder inverse Matrixmethode bezeichnet) erfordert eine vorherige Vertrautheit mit einem solchen Konzept wie der Matrixform des Schreibens von SLAE. Das Verfahren der inversen Matrix ist zum Lösen solcher Systeme linearer algebraischer Gleichungen gedacht, für die die Determinante der Systemmatrix ungleich Null ist. Dies impliziert natürlich, dass die Matrix des Systems quadratisch ist (das Konzept der Determinante existiert nur für quadratische Matrizen). Das Wesen der inversen Matrixmethode kann in drei Punkten ausgedrückt werden: Jede SLAE kann in Matrixform als $A\cdot X=B$ geschrieben werden, wobei $A$ die Matrix des Systems ist, $B$ die Matrix der freien Terme ist, $X$ die Matrix der Unbekannten ist. Lassen Sie die Matrix $A^(-1)$ existieren. Multipliziere beide Seiten der Gleichheit $A\cdot X=B$ mit der Matrix $A^(-1)$ links: $$A^(-1)\cdot A\cdot X=A^(-1)\cdot B.$$ Da $A^(-1)\cdot A=E$ ($E$ ist die Identitätsmatrix) wird die oben geschriebene Gleichheit zu: $$E\cdot X=A^(-1)\cdot B.$$ Da $E\cdot X=X$, dann: $$X=A^(-1)\cdot B.$$ Beispiel 1 Lösen Sie die SLAE $ \left \( \begin(aligned) & -5x_1+7x_2=29;\\ & 9x_1+8x_2=-11. \end(aligned) \right.$ mit der inversen Matrix. $$ A=\left(\begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right);\; B=\left(\begin(array) (c) 29\\ -11 \end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \end(array)\right). $$ Finden wir die inverse Matrix zur Matrix des Systems, d.h. Berechnen Sie $A^(-1)$. In Beispiel #2 $$ A^(-1)=-\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right) . $$ Lassen Sie uns nun alle drei Matrizen ($X$, $A^(-1)$, $B$) in die Gleichung $X=A^(-1)\cdot B$ einsetzen. Dann führen wir eine Matrixmultiplikation durch $$ \left(\begin(array) (c) x_1\\ x_2 \end(array)\right)= -\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right)\cdot \left(\begin(array) (c) 29\\ -11 \end(array)\right)=\\ =-\frac (1)(103)\cdot \left(\begin(array) (c) 8\cdot 29+(-7)\cdot (-11)\\ -9\cdot 29+(-5)\cdot (- 11) \end(array)\right)= -\frac(1)(103)\cdot \left(\begin(array) (c) 309\\ -206 \end(array)\right)=\left( \begin(array) (c) -3\\ 2\end(array)\right). $$ Also haben wir $\left(\begin(array) (c) x_1\\ x_2 \end(array)\right)=\left(\begin(array) (c) -3\\ 2\end(array )\ rechts)$. Aus dieser Gleichheit haben wir: $x_1=-3$, $x_2=2$. Antworten: $x_1=-3$, $x_2=2$. Beispiel #2 Löse SLAE $ \left\(\begin(aligned) & x_1+7x_2+3x_3=-1;\\ & -4x_1+9x_2+4x_3=0;\\ & 3x_2+2x_3=6. \end(aligned)\right .$ nach der Methode der inversen Matrix. Schreiben wir die Matrix des Systems $A$, die Matrix der freien Terme $B$ und die Matrix der Unbekannten $X$ auf. $$ A=\left(\begin(array) (ccc) 1 & 7 & 3\\ -4 & 9 & 4 \\0 & 3 & 2\end(array)\right);\; B=\left(\begin(array) (c) -1\\0\\6\end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right). $$ Jetzt ist es an der Zeit, die inverse Matrix der Systemmatrix zu finden, d.h. Finde $A^(-1)$. In Beispiel 3 auf der Seite zum Finden inverser Matrizen wurde die inverse Matrix bereits gefunden. Lassen Sie uns das fertige Ergebnis verwenden und $A^(-1)$ schreiben: $$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array)\right). $$ Nun setzen wir alle drei Matrizen ($X$, $A^(-1)$, $B$) in die Gleichheit $X=A^(-1)\cdot B$ ein, danach führen wir rechts eine Matrixmultiplikation durch Seite dieser Gleichheit. $$ \left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)= \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \end(array) \right)\cdot \left(\begin(array) (c) -1\\0\ \6\end(array)\right)=\\ =\frac(1)(26)\cdot \left(\begin(array) (c) 6\cdot(-1)+(-5)\cdot 0 +1\cdot 6 \\ 8\cdot (-1)+2\cdot 0+(-16)\cdot 6 \\ -12\cdot (-1)+(-3)\cdot 0+37\cdot 6 \end(array)\right)=\frac(1)(26)\cdot \left(\begin(array) (c) 0\\-104\\234\end(array)\right)=\left( \begin(array) (c) 0\\-4\\9\end(array)\right) $$ Also haben wir $\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)=\left(\begin(array) (c) 0\\-4\ \9 \end(array)\right)$. Aus dieser Gleichheit haben wir: $x_1=0$, $x_2=-4$, $x_3=9$.
.
