Formulierung des Problems

Die Aufgabe besteht darin, den Benutzer mit den Grundkonzepten numerischer Verfahren, wie der Determinante und der inversen Matrix, und verschiedenen Berechnungsmethoden vertraut zu machen. In diesem theoretischen Bericht werden in einer einfachen und zugänglichen Sprache zunächst die grundlegenden Konzepte und Definitionen eingeführt, auf deren Grundlage weitere Forschungen durchgeführt werden. Der Benutzer hat möglicherweise keine speziellen Kenntnisse auf dem Gebiet der numerischen Methoden und der linearen Algebra, kann die Ergebnisse dieser Arbeit jedoch problemlos verwenden. Zur Verdeutlichung wird ein Programm zum Berechnen der Matrixdeterminante durch mehrere Verfahren, geschrieben in der Programmiersprache C++, angegeben. Das Programm dient als Laborständer zur Erstellung von Illustrationen für den Bericht. Außerdem wird eine Untersuchung von Methoden zur Lösung von Systemen linearer algebraischer Gleichungen durchgeführt. Die Nutzlosigkeit der Berechnung der inversen Matrix ist bewiesen, daher bietet das Papier optimalere Möglichkeiten, Gleichungen zu lösen, ohne sie zu berechnen. Es wird erklärt, warum es so viele verschiedene Methoden zur Berechnung von Determinanten und inversen Matrizen gibt und deren Mängel analysiert. Dabei werden auch Fehler bei der Berechnung der Determinante berücksichtigt und die erreichte Genauigkeit abgeschätzt. Neben russischen Begriffen werden auch deren englische Entsprechungen in der Arbeit verwendet, um zu verstehen, unter welchen Namen in Bibliotheken nach numerischen Verfahren gesucht werden muss und was ihre Parameter bedeuten.

Grundlegende Definitionen und einfache Eigenschaften

Bestimmend

Lassen Sie uns die Definition der Determinante einer quadratischen Matrix beliebiger Ordnung einführen. Diese Definition wird wiederkehrend, das heißt, um festzustellen, was die Determinante der Ordnungsmatrix ist, müssen Sie bereits wissen, was die Determinante der Ordnungsmatrix ist. Beachten Sie auch, dass die Determinante nur für quadratische Matrizen existiert.

Die Determinante einer quadratischen Matrix wird mit oder det bezeichnet.

Bestimmung 1. bestimmend quadratische Matrix zweite Ordnungsnummer aufgerufen wird .

bestimmend quadratische Matrix der Ordnung , heißt die Zahl

wobei die Determinante der Ordnungsmatrix ist, die man aus der Matrix erhält, indem man die erste Zeile und die Spalte mit der Nummer löscht.

Zur Verdeutlichung schreiben wir auf, wie man die Determinante einer Matrix vierter Ordnung berechnen kann:

Kommentar. In Ausnahmefällen wird die eigentliche Berechnung von Determinanten für Matrizen oberhalb dritter Ordnung aufgrund der Definition verwendet. In der Regel erfolgt die Berechnung nach anderen Algorithmen, auf die später eingegangen wird und die weniger Rechenaufwand erfordern.

Kommentar. In Definition 1 wäre es genauer zu sagen, dass die Determinante eine Funktion ist, die auf der Menge der quadratischen Ordnungsmatrizen definiert ist und Werte in der Menge der Zahlen annimmt.

Kommentar. In der Literatur wird anstelle des Begriffs "Determinante" auch der Begriff "Determinante" verwendet, der die gleiche Bedeutung hat. Aus dem Wort „Determinante“ entstand die Bezeichnung det.

Betrachten wir einige Eigenschaften von Determinanten, die wir in Form von Aussagen formulieren.

Aussage 1. Beim Transponieren einer Matrix ändert sich die Determinante nicht, also .

Aussage 2. Die Determinante des Produkts quadratischer Matrizen ist gleich dem Produkt der Determinanten der Faktoren, dh .

Erklärung 3. Wenn zwei Zeilen in einer Matrix vertauscht werden, ändert ihre Determinante das Vorzeichen.

Erklärung 4. Wenn eine Matrix zwei identische Zeilen hat, dann ist ihre Determinante Null.

In Zukunft müssen wir Zeichenketten addieren und eine Zeichenkette mit einer Zahl multiplizieren. Wir werden diese Operationen auf Zeilen (Spalten) auf die gleiche Weise wie Operationen auf Zeilenmatrizen (Spaltenmatrizen) ausführen, d. h. Element für Element. Das Ergebnis ist eine Zeile (Spalte), die in der Regel nicht mit den Zeilen der ursprünglichen Matrix übereinstimmt. Bei Operationen zum Addieren von Zeilen (Spalten) und Multiplizieren mit einer Zahl können wir auch von Linearkombinationen von Zeilen (Spalten) sprechen, dh Summen mit numerischen Koeffizienten.

Erklärung 5. Wenn eine Zeile einer Matrix mit einer Zahl multipliziert wird, wird ihre Determinante mit dieser Zahl multipliziert.

Erklärung 6. Wenn die Matrix eine Nullzeile enthält, dann ist ihre Determinante Null.

Erklärung 7. Wenn eine der Zeilen der Matrix gleich der anderen multipliziert mit einer Zahl ist (die Zeilen sind proportional), dann ist die Determinante der Matrix Null.

Erklärung 8. Lassen Sie die i-te Zeile in der Matrix so aussehen. Dann , wobei die Matrix aus der Matrix erhalten wird, indem die i-te Zeile durch die Zeile ersetzt wird, und die Matrix durch Ersetzen der i-ten Zeile durch die Zeile erhalten wird.

Erklärung 9. Wenn eine der Zeilen der Matrix zu einer anderen addiert und mit einer Zahl multipliziert wird, ändert sich die Determinante der Matrix nicht.

Erklärung 10. Wenn eine der Zeilen einer Matrix eine Linearkombination ihrer anderen Zeilen ist, dann ist die Determinante der Matrix Null.

Bestimmung 2. Algebraische Addition zu einem Matrixelement heißt eine Zahl gleich , wobei die Determinante der Matrix ist, die aus der Matrix durch Löschen der i-ten Zeile und der j-ten Spalte erhalten wird. Das algebraische Komplement zu einem Matrixelement wird mit bezeichnet.

Beispiel. Lassen . Dann

Kommentar. Unter Verwendung algebraischer Additionen kann die Definition von 1 Determinante wie folgt geschrieben werden:

Erklärung 11. Zerlegung der Determinante in einen beliebigen String.

Die Matrixdeterminante erfüllt die Formel

Beispiel. Berechnung .

Entscheidung. Lassen Sie uns die Erweiterung in der dritten Zeile verwenden, es ist rentabler, weil in der dritten Zeile zwei von drei Zahlen Nullen sind. Werden

Erklärung 12. Für eine quadratische Matrix der Ordnung bei haben wir die Beziehung .

Erklärung 13. Alle für Zeilen formulierten Eigenschaften der Determinante (Aussagen 1 - 11) gelten auch für Spalten, insbesondere gilt die Erweiterung der Determinante in der j-ten Spalte und Gleichberechtigung beim .

Erklärung 14. Die Determinante einer Dreiecksmatrix ist gleich dem Produkt der Elemente ihrer Hauptdiagonale.

Folge. Die Determinante der Identitätsmatrix ist gleich eins, .

Fazit. Die oben aufgeführten Eigenschaften ermöglichen es, mit relativ geringem Rechenaufwand Determinanten von Matrizen ausreichend hoher Ordnung zu finden. Der Berechnungsalgorithmus ist der folgende.

Algorithmus zum Erstellen von Nullen in einer Spalte. Es sei erforderlich, die Ordnungsdeterminante zu berechnen. Wenn , dann vertausche die erste Zeile und jede andere Zeile, in der das erste Element nicht Null ist. Als Ergebnis ist die Determinante gleich der Determinante der neuen Matrix mit dem entgegengesetzten Vorzeichen. Wenn das erste Element jeder Zeile gleich Null ist, dann hat die Matrix eine Null-Spalte und nach den Anweisungen 1, 13 ist ihre Determinante gleich Null.

Wir berücksichtigen das also bereits in der ursprünglichen Matrix . Lassen Sie die erste Zeile unverändert. Fügen wir zur zweiten Zeile die erste Zeile hinzu, multipliziert mit der Zahl . Dann ist das erste Element der zweiten Zeile gleich .

Die verbleibenden Elemente der neuen zweiten Reihe werden mit , bezeichnet. Die Determinante der neuen Matrix nach Aussage 9 ist gleich . Multipliziere die erste Zeile mit der Zahl und addiere sie zur dritten. Das erste Element der neuen dritten Zeile ist gleich

Die verbleibenden Elemente der neuen dritten Reihe werden mit , bezeichnet. Die Determinante der neuen Matrix nach Aussage 9 ist gleich .

Wir werden den Prozess fortsetzen, Nullen anstelle der ersten Elemente von Zeichenfolgen zu erhalten. Schließlich multiplizieren wir die erste Zeile mit einer Zahl und addieren sie zur letzten Zeile. Das Ergebnis ist eine Matrix, bezeichnet mit , die die Form hat

und . Um die Determinante der Matrix zu berechnen, verwenden wir die Erweiterung in der ersten Spalte

Seit damals

Die Determinante der Ordnungsmatrix steht auf der rechten Seite. Wir wenden denselben Algorithmus darauf an, und die Berechnung der Determinante der Matrix wird auf die Berechnung der Determinante der Ordnungsmatrix reduziert. Der Vorgang wird wiederholt, bis wir die Determinante zweiter Ordnung erreichen, die per Definition berechnet wird.

Wenn die Matrix keine spezifischen Eigenschaften hat, dann ist es nicht möglich, den Berechnungsaufwand gegenüber dem vorgeschlagenen Algorithmus wesentlich zu reduzieren. Eine weitere gute Seite dieses Algorithmus ist, dass es einfach ist, ein Programm für einen Computer zu schreiben, um die Determinanten von Matrizen großer Ordnungen zu berechnen. In Standardprogrammen zur Berechnung von Determinanten wird dieser Algorithmus mit geringfügigen Änderungen verwendet, die mit der Minimierung der Auswirkungen von Rundungsfehlern und Eingabedatenfehlern bei Computerberechnungen verbunden sind.

Beispiel. Matrixdeterminante berechnen .

Entscheidung. Die erste Zeile bleibt unverändert. Zur zweiten Zeile addieren wir die erste, multipliziert mit der Zahl:

Die Determinante ändert sich nicht. Zur dritten Zeile addieren wir die erste, multipliziert mit der Zahl:

Die Determinante ändert sich nicht. Zur vierten Zeile addieren wir die erste, multipliziert mit der Zahl:

Die Determinante ändert sich nicht. Als Ergebnis erhalten wir

Mit dem gleichen Algorithmus berechnen wir die Determinante einer Matrix der Ordnung 3, die rechts steht. Wir lassen die erste Zeile unverändert, zur zweiten Zeile addieren wir die erste, multipliziert mit der Zahl :

Zur dritten Zeile addieren wir die erste, multipliziert mit der Zahl :

Als Ergebnis erhalten wir

Antworten. .

Kommentar. Obwohl bei den Berechnungen Brüche verwendet wurden, war das Ergebnis eine ganze Zahl. In der Tat könnten Operationen mit Brüchen vermieden werden, wenn man die Eigenschaften von Determinanten und die Tatsache nutzt, dass die ursprünglichen Zahlen ganze Zahlen sind. Aber in der Ingenieurpraxis sind Zahlen äußerst selten ganze Zahlen. Daher werden die Elemente der Determinante in der Regel Dezimalbrüche sein und es ist nicht ratsam, irgendwelche Tricks anzuwenden, um Berechnungen zu vereinfachen.

inverse Matrix

Bestimmung 3. Die Matrix wird aufgerufen inverse Matrix für eine quadratische Matrix, wenn .

Aus der Definition folgt, dass die inverse Matrix eine quadratische Matrix der gleichen Ordnung wie die Matrix sein wird (andernfalls wäre eines der Produkte oder nicht definiert).

Die inverse Matrix für eine Matrix wird mit bezeichnet. Also, wenn existiert, dann .

Aus der Definition einer inversen Matrix folgt, dass die Matrix die Inverse der Matrix ist, also . Man kann sagen, dass Matrizen und zueinander invers oder gegenseitig invers sind.

Wenn die Determinante einer Matrix Null ist, dann existiert ihre Inverse nicht.

Da es für die Bestimmung der inversen Matrix wichtig ist, ob die Determinante der Matrix gleich Null ist oder nicht, führen wir die folgenden Definitionen ein.

Bestimmung 4. Nennen wir die quadratische Matrix degenerieren oder spezielle Matrix, Wenn nicht entartet oder nichtsinguläre Matrix, Wenn .

Erklärung. Wenn eine inverse Matrix existiert, dann ist sie eindeutig.

Erklärung. Wenn eine quadratische Matrix nicht entartet ist, existiert ihre Umkehrung und (1) wo sind algebraische Additionen zu Elementen .

Satz. Eine inverse Matrix für eine quadratische Matrix existiert genau dann, wenn die Matrix nichtsingulär ist, die inverse Matrix eindeutig ist und Formel (1) gültig ist.

Kommentar. Besonderes Augenmerk sollte auf die Stellen gelegt werden, die algebraische Additionen in der inversen Matrixformel einnehmen: Der erste Index zeigt die Zahl Säule, und die zweite ist die Zahl Linien, in die das berechnete algebraische Komplement geschrieben werden soll.

Beispiel. .

Entscheidung. Determinante finden

Seit , dann ist die Matrix nicht entartet, und die Inverse dafür existiert. Algebraische Additionen finden:

Wir setzen die inverse Matrix zusammen, indem wir die gefundenen algebraischen Additionen so platzieren, dass der erste Index der Spalte und der zweite der Zeile entspricht: (2)

Die resultierende Matrix (2) ist die Lösung des Problems.

Kommentar. Im vorherigen Beispiel wäre es genauer, die Antwort so zu schreiben:
(3)

Allerdings ist die Notation (2) kompakter und es ist bequemer, eventuelle weitere Berechnungen damit durchzuführen. Daher ist es vorzuziehen, die Antwort in der Form (2) zu schreiben, wenn die Elemente der Matrizen ganze Zahlen sind. Und umgekehrt, wenn die Elemente der Matrix Dezimalbrüche sind, dann ist es besser, die inverse Matrix ohne Faktor davor zu schreiben.

Kommentar. Wenn Sie die inverse Matrix finden, müssen Sie ziemlich viele Berechnungen und eine ungewöhnliche Regel zum Anordnen algebraischer Additionen in der endgültigen Matrix durchführen. Daher besteht eine hohe Fehlerwahrscheinlichkeit. Um Fehler zu vermeiden, sollten Sie eine Überprüfung durchführen: Berechnen Sie das Produkt der ursprünglichen Matrix mit der endgültigen in der einen oder anderen Reihenfolge. Wenn das Ergebnis eine Identitätsmatrix ist, dann wird die inverse Matrix korrekt gefunden. Andernfalls müssen Sie nach einem Fehler suchen.

Beispiel. Finden Sie die Inverse einer Matrix .

Entscheidung. - bestehen.

Antworten: .

Fazit. Das Finden der inversen Matrix durch Formel (1) erfordert zu viele Berechnungen. Für Matrizen der vierten Ordnung und höher ist dies nicht akzeptabel. Der eigentliche Algorithmus zum Auffinden der inversen Matrix wird später angegeben.

Berechnung der Determinante und inversen Matrix nach der Gauß-Methode

Die Gauß-Methode kann verwendet werden, um die Determinante und die inverse Matrix zu finden.

Die Matrixdeterminante ist nämlich gleich det.

Die inverse Matrix wird durch Lösen von linearen Gleichungssystemen mit der Gaußschen Eliminationsmethode gefunden:

Wo die j-te Spalte der Identitätsmatrix ist, ist der erforderliche Vektor.

Die resultierenden Lösungsvektoren - bilden offensichtlich die Spalten der Matrix, da .

Formeln für die Determinante

1. Wenn die Matrix nichtsingulär ist, dann und (das Produkt der führenden Elemente).

Da es für die Bestimmung der inversen Matrix wichtig ist, ob die Determinante der Matrix gleich Null ist oder nicht, führen wir die folgenden Definitionen ein.

Definition 14.9 Nennen wir die quadratische Matrix degenerieren oder spezielle Matrix, Wenn nicht entartet oder nichtsinguläre Matrix, Wenn .

Angebot 14.21 Wenn eine inverse Matrix existiert, dann ist sie eindeutig.

Nachweisen. Seien zwei Matrizen und die Umkehrung der Matrix . Dann

Somit, .

Cramersche Regel.

Lassen Sie die Matrixgleichung AX=B

Woher ; ist die aus der Determinante erhaltene Determinante D Ersatz ich-te Spalte durch die Spalte der freien Mitglieder der Matrix B:

Nachweisen Das Theorem gliedert sich in drei Teile:

1. Die Lösung von System (1) existiert und ist eindeutig.

2. Gleichheiten (2) sind eine Folge der Matrixgleichung (1).

3. Gleichheiten (2) führen zu einer Matrixgleichung (1).

Da existiert auch eine eindeutige inverse Matrix.
Multiplizieren wir beide Teile der Matrixgleichung (1) links mit , erhalten wir die Lösung dieser Gleichung:

Einzigartigkeit inverse Matrix beweist den ersten Teil des Theorems.

Kommen wir zum Beweis Eins-zu-Eins-Korrespondenz zwischen den Formeln (1) und (2).

Unter Verwendung von Formel (4) erhalten wir einen Ausdruck für ich-tes Element. Dazu müssen Sie multiplizieren ich-te Zeile der Matrix

pro Spalte B.

Angesichts dessen ich-te Zeile der zugehörigen Matrix aus algebraischen Additionen zusammengesetzt ist, erhalten wir folgendes Ergebnis:

Die Herleitung der Cramerschen Formeln ist abgeschlossen. Zeigen wir nun, dass die Ausdrücke

Ändern wir die Reihenfolge der Summierung auf der rechten Seite des resultierenden Ausdrucks:

wo ist das Delta-Kronecker-Symbol.

Da das Delta-Symbol die Summation über einen der Indizes entfernt, erhalten wir das erforderliche Ergebnis:

Komplexe Zahlen: Die Idee ist, neue Objekte mit Hilfe bekannter zu definieren. Reelle Zahlen liegen auf einer Geraden. Beim Übergang zum Flugzeug erhalten wir komplexe Zahlen. Definition: Eine komplexe Zahl ist ein Paar reeller Zahlen z = (a,b). Die Zahl a = Re z heißt Realteil und b = Im z Imaginärteil der komplexen Zahl z .

Operationen mit komplexen Zahlen: Die komplexen Zahlen z1 z2 sind Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Zusatz: Z=z1+z2. ⇔Rez=Rez1+Rez2 & Imz1+ Imz2. Die Zahl (0,0) wird mit 0 bezeichnet. Dies ist das neutrale Element. Es wird nachgewiesen, dass die Addition komplexer Zahlen ähnliche Eigenschaften wie die Addition reeller Zahlen hat. (1. Z1+ z2 = z2 + z1 – Kommutativität; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – Assoziativität; 3. Z1 + 0 = z1 – Existenz von Null (neutrales Element); 4. z + (−z) = 0 - die Existenz des entgegengesetzten Elements). Multiplikation: z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. Eine komplexe Zahl z liegt auf der reellen Achse, wenn Imz = 0 ist. Die Ergebnisse von Operationen mit solchen Zahlen stimmen mit den Ergebnissen von Operationen mit gewöhnlichen reellen Zahlen überein. Die Multiplikation komplexer Zahlen hat die Eigenschaften der Schließung, Kommutativität und Assoziativität. Die Zahl (1,0) wird mit 1 bezeichnet und stellt durch Multiplikation ein neutrales Element dar. Wenn a∈ R, z ∈C , dann ist Re(az) = aRe z, Im(az) = a Imz . Definition Die Zahl (0,1) wird mit bezeichnet ich und heißt imaginäre Einheit. In dieser Notation erhalten wir die Darstellung einer komplexen Zahl in algebraischer Form: z = a + ib, a,b∈ R. i=-1.(a,b)=(a,0)+(0,b) ;(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-b1b2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z!=0; a 2 + b 2 > 0 (a + ib) (a-ib / a 2 + b 2) = 1. Die Nummer wird angerufen konjugieren zu z wenn Re = Re z ; Ich bin =- Ich bin z.

= + ; = ; z =(a+ib)(a-ib)=a 2 + b 2 Der Betrag einer Zahl z ist eine reelle Zahl| z |= . Faire Formel| z| 2 = z Aus der Definition folgt, dass z ≠ 0⇔| z|≠ 0. z-1 = /|z| 2 (1)

Trigonometrische Form einer komplexen Zahl: a=rcos(t); b=r sin(t). Z=a+ib=r(cos(t)+isin(t))(2) t-Argument einer komplexen Zahl. Z1=z2 =>|z1|=|z2|

arg(z1)-arg(z2)=2pk.

Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)( ein)

Arg(z1z2)=arg(z1)+arg(z2) (2)

Z!=0 z -1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))

R(cos(t)-isin(t))

Definition: Die Wurzel des Grades n aus Eins ist die Lösung der Gleichung z n =1 Vorschlag. Es gibt n verschiedene n-te Einheitswurzeln. Sie werden geschrieben als z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 . Satz. In der Menge der komplexen Zahlen hat die Gleichung immer n Lösungen Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-Ganzzahlen. K gehört zu Z. k=2=E 2 =E n-1 E n ; En = 1; E n+p = E p . Somit ist bewiesen, dass die Lösungen der Gleichung die Ecken eines regulären n-Ecks sind und eine der Ecken mit 1 zusammenfällt.

n-te Wurzel von z 0. Zk \u003d Z 0; Z0 =0=>Z=0; Z 0 !=0;Z=r(cos(t)-isin(t)); Z 0 \u003d r 0 (cos (t0) + isin (t0)); r0!=0; Z n \u003d r n (cos (nt) + isin (nt))

r n \u003d r 0, nt-t 0 \u003d 2pk; r=; t=(2пk+t0)/n; z= (cos((2pk+t0)/n)+isin((2pk+t0)/n)= (cos t0/n+isin t0/n)(cos(2pk/n)+isin(2pk/n) )=Z 1 E k ;z=z 1 E k ;Z 1 n =z 0, k=0, n=1

Matrizen. Definition: Eine m × n-Matrix ist eine rechteckige Tabelle mit m Zeilen und n Spalten, deren Elemente reelle oder komplexe Zahlen sind. Matrixelemente haben doppelte Indizes.

Wenn m = n, dann ist es eine quadratische Matrix der Ordnung m, und Elemente mit demselben Index bilden die Hauptdiagonale der Matrix.

Matrixoperationen: Definition: Zwei Matrizen A, B werden aufgerufen

gleich, wenn ihre Größen gleich sind und A = B,1≤ i ≤ m,1≤ j ≤ n

Zusatz. Matrizen gleicher Größe werden berücksichtigt. Definition:C = A + B ⇔ C = A + B, ∀i, j Angebot. Die Matrixaddition ist kommutativ, assoziativ, es gibt ein neutrales Element und für jede Matrix gibt es ein entgegengesetztes Element.

Das neutrale Element ist die Nullmatrix, deren alle Elemente gleich 0 sind. Sie wird mit Θ bezeichnet.

Multiplikation. Eine m × n-Matrix A wird mit Amn bezeichnet . Definition: C mk = A mn B nk ó

C= Beachten Sie, dass die Multiplikation im Allgemeinen nicht kommutativ ist. Geschlossenheit gilt für eine quadratische Matrix fester Größe. Gegeben seien drei Matrizen Amn, Bnk, Ckr. Dann ist (AB)C = A(BC). Existiert ein Produkt aus 3 Matrizen, so ist es assoziativ.

Das Kronecker-Symbol δij . Es ist 1, wenn die Indizes übereinstimmen, andernfalls 0. Definition. Die Identitätsmatrix I n ist eine quadratische Matrix der Ordnung n, für die die Gleichheiten n I n [ i | j] = δij Angebot. Gleichheiten I m A mn =A mn I n =A mn

Die Addition und Multiplikation von Matrizen ist durch die Gesetze der Distributivität verbunden. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +

Matrixtransposition. Eine transponierte Matrix ist eine Matrix, die aus der ursprünglichen erhalten wird, indem Zeilen durch Spalten ersetzt werden.

(A+B) T = A T + B T

(AB) T \u003d B T EIN T; (AB) T \u003d (AB) \u003d \u003d (B T EIN T)

Multiplizieren einer Matrix mit einer Zahl. Das Produkt aus der Zahl a und der Matrix Amn heißt die neue Matrix B=aA

1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;

A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)

linearer Raum(L) über dem Körper F heißt Vektormenge L=(α,β..)

1.α+β=β+α(Kommutativität) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(Assoziativität) 3.α+θ=α, α∙1=α(Existenz von Neutral) 4.α+(-α)=θ (Existenz von Gegenteil)

a(α+β)=aα+aβ, (a+b)α=aα+bα. Dokumentation (|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a und b>0, |a +b|=a+b,|a|=a,|b|=b.) aα+(-a)α=θ, (a+0)α=aα

Ein Beispiel für einen linearen Raum ist ein Satz von Matrizen fester Größe mit Additions- und Multiplikationsoperationen mit einer Zahl.

Das System der linearen Vektoren heißt linear abhängig, wenn 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ Wenn das System nicht linear abhängig ist, dann ist es linear unabhängig. Betrachten Sie 1. n=1 α 1 hängen ab. a 1 ≠0, a 1 α 1 =θ, a 1 -1 (a 1 α 1)= a 1 -1∙ θ=θ, (a 1 -1 a 1)α 1 =1∙α 1 =α 1 ; 2. n=2 α 1 , α 2 abhängen. a 1 ≠ 0, a 1 α 1 + a 2 α 2 = θ, α 1 = –a 1 –1 a 2 α 2 = b 2 α 2; 3.n≥2 α 1 ..α n abhängen. a 1 ≠ 0, α 1 = Σ k = 2 n b k α k , 1 α 1 – Σ k = 2 n b k α k = θ, (1, b 2 ... b n) ≠ 0

Angebot: Ein System von Vektoren, das mehr als einen Vektor enthält, ist linear abhängig, dann ist ein Vektor des Systems eine Linearkombination der anderen.

Wenn ein Vektorsystem ein linear abhängiges Teilsystem enthält, dann ist das gesamte System linear abhängig. Dokumentation: (α 1 ..α n abhängig. System: α 1 ..α n ;α n +1 ..α m , a 1 α 1 +..+a n α n +0α n +1 +.. +0α m =θ, a 1 ..a n ,0..0≠0.) Wenn das System einen Nullvektor enthält, dann ist es linear abhängig. Linearer Raumsatz: (Gegeben seien 2 Vektorsysteme α 1 ..α m , β 1 ..β n . Das Vektorsystem α wird durch β ausgedrückt, wenn jeder Vektor α eine Linearkombination β α i = Σ k =1 ist n a ik β k , (α ) ( (β), (β) ( (γ)→ (α) ( (γ)) Satz: Bei 2 Vektorsystemen ist α unabhängig und (α) ( (β)→m≤n Beweisen wir, dass α 1 ..α m +1 β 1 ..β m (α) ( (β)→(α ) abhängt (Beweisen wir per Induktion. m=1: α 1 =a 11 β 1 , α 2 =a 21 β 1. a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 = θ α 1 = a 11 β 1 +.. a 1 n -1 β n -1 .. α n = a n 1 β 1 + .. a nn -1 β n - 1 Wenn alle Koeffizienten =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ ist das ganze System linear abhängig a 1 n -1 ≠0 α 2 ′= α 2 – с 2 α 1 =b 21 β 1 +..+b 2 n -2 β n -2 , c 2 =a 2 n -1 / a 1 n -1 , α 3 ′= α 3 –с 3 α 1 . .α n ′= α n –с n α 1. Durch Präinduktion existiert eine von Null verschiedene Menge von Zahlen d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 ( α 2 –с 2 α 1)+d 3 (α 3 –с 3 α 1)+.. d n (α n –с n α 1)=θ , (α) ( (β) , m>n →(α )abhängig wenn (α) unabhängig →m≤n)

MLNP-max.leitungsunabhängiges.Subsystem. Gegeben sei ein System von Vektoren α 1 ...α n eines Teilsystems. α i 1 ..α in heißt MLIS falls 1. α 1 ..α n unabhängig ist2. α i 1 .. α ir , α ij abhängig. Jeder Vektor des Systems ist eine lineare Kombination von MLLM-Vektoren. ( α i 1 .. α ir , α ij abhängig a i 1 α i 1 +.. a ir α ir + a ij α ij = θ

a i 1 ..a ir , a ij ≠0 if a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 Widerspruch a ij ≠0 α ij = a ij - 1 (-a i 1 α i 1 -.. Luft ir α ir) (α 1 ..α n) ( (α i 1 ..α ir)

Folge: Beliebige 2 MLIS aus einem Vektorsystem enthalten die gleiche Anzahl von Vektoren (α i 1 ..α ir) ( (α j 1 ..α jk) , (α j 1 ..α jk) ( (α i 1 . .α ir ) k≤r, r≤k →r=k Man nennt die Anzahl der MLLM-Vektoren Rang ursprüngliches System. Im Fall eines linearen Raums (ein Vektorsystem besteht aus allen Vektoren im Raum) ist das MLLM mb entweder endlich oder unendlich. Wir betrachten den letzten Fall. Die Anzahl der Vektoren (Rang) ist die Dimension des linearen Raums. MLNP-Basis. Der Raum gerichteter Segmente. Zwei nicht kollineare Vektoren bilden sich Base im Raum der Vektoren in der Ebene. α 3 = α 1 '+ α 2 ' = ein 1 α 1 + ein 2 α 2 . 3 linear abhängige Vektoren α 3 = a 1 α 1 + a 2 α 2 . Komplanarität – 3 Vektoren sind parallel zur gleichen Ebene α 4 = α 4 ′ + α 5 ′ , α 4 ′ = a 1 α 1 + a 2 α 2 , α 5 ′ = a 3 α 3 , α 4 = a 1 α 1 + ein 2 α 2 + ein 3 α 3 . Leerzeichen von Zeichenketten der Länge n. α= Angebot: Der Raum von Zeichenketten der Länge n hat die Dimension n. ( ξ 1 =<1…0>ξ2 =<0,1…0>.. n =<0…1>, ein 1 ξ 1 + ein 2 ξ 2 +.. ein n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (lineare Unabhängigkeit) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →der Raum von Zeichenketten der Länge n hat die Dimension und n.

Matrix-Rang.

Zwei Systeme von Vektoren α und β heißen äquivalent, wenn jeder Vektor

α( β(ausgedrückt) und β( α.

Angebot. Die Reihen äquivalenter Systeme fallen zusammen.

α ich 1 , α ich 2 ,…, α ir – MLLM α , β ich 1 , β ich 2 ,…, β ik – MLLM β , α ich 1 , α ich 2 ,…, α ir< β < β i 1 , β i 2 ,…, β ik → r<=k

Vertauschung von α- und β-Stellen → r>=k >>> Also r=k.

Definition. Sei die Matrix A=

α ich =

Matrix-Rang A heißt der Rang des Vektorsystems α1, α2,…, αm, das sich aus dieser Matrix >>Rang(A)-Rang zusammensetzt

Aus der Definition geht hervor, dass sich beim Umordnen der Spalten der Rang nicht ändert. Zeigen wir, dass sich auch der Rang nicht ändert, wenn die Spalten neu angeordnet werden.

A'=

α'i=

Linear abhängig:

b 1 α 1 + b 2 α 2 +…+ b m α m =θ, b 1 a 11 +b 2 a 21 +…+b m ein m 1=0, b 1 α' 1 + b 2 α' 2 +…+ b m α' m , b 1 ein 11 +b 2 ein 21 +…+b m ein m 1=0

Es ist gleich der Summe der Produkte der Elemente einer Reihe oder Spalte und ihrer algebraischen Komplemente, d.h. , wobei i 0 festgelegt ist.
Der Ausdruck (*) heißt Zerlegung der Determinante D in die Elemente der Zeile mit der Nummer i 0 .

Dienstzuweisung. Dieser Service dient dazu, die Determinante der Matrix online zu finden, wobei die gesamte Lösung im Word-Format ausgeführt wird. Zusätzlich wird eine Lösungsvorlage in Excel erstellt.

Anweisung. Wählen Sie die Dimension der Matrix aus und klicken Sie auf Weiter.

Matrixdimension 2 3 4 5 6 7 8 9 10

Es gibt zwei Möglichkeiten, die Determinante zu berechnen: a-priorat und Zerlegung nach Zeile oder Spalte. Wenn Sie die Determinante finden möchten, indem Sie Nullen in einer der Zeilen oder Spalten erstellen, können Sie diesen Rechner verwenden.

Algorithmus zum Finden der Determinante

1. Für Matrizen der Ordnung n=2 wird die Determinante nach folgender Formel berechnet: Δ=a 11 *a 22 -a 12 *a 21
2. Für Matrizen der Ordnung n=3 wird die Determinante durch algebraische Additionen oder berechnet Sarrus-Methode.
3. Eine Matrix mit einer Dimension größer als drei wird in algebraische Additionen zerlegt, für die ihre Determinanten (Minoren) berechnet werden. Zum Beispiel, Matrixdeterminante 4. Ordnung wird durch Erweiterung in Zeilen oder Spalten gefunden (siehe Beispiel).

Zur Berechnung der Determinanten enthaltenden Funktionen in der Matrix werden Standardmethoden verwendet. Berechnen Sie beispielsweise die Determinante einer Matrix 3. Ordnung:

Lassen Sie uns die erste Zeilenerweiterung verwenden.
Δ = sin(x)× + 1× = 2sin(x)cos(x)-2cos(x) = sin(2x)-2cos(x)

Methoden zur Berechnung von Determinanten

Bestimmung der Determinante durch algebraische Additionen ist eine gängige Methode. Ihre vereinfachte Version ist die Berechnung der Determinante nach der Sarrus-Regel. Bei einer großen Matrixdimension werden jedoch die folgenden Methoden verwendet:

1. Berechnung der Determinante durch Ordnungsreduktion
2. Berechnung der Determinante nach der Gaußschen Methode (durch Reduzierung der Matrix auf eine Dreiecksform).

In Excel wird zur Berechnung der Determinante die Funktion = MOPRED (Zellenbereich) verwendet.

Angewandte Verwendung von Determinanten

Die Determinanten werden in der Regel für ein bestimmtes System in Form einer quadratischen Matrix berechnet. Betrachten Sie einige Arten von Aufgaben auf Matrixdeterminante finden. Manchmal ist es erforderlich, einen unbekannten Parameter a zu finden, für den die Determinante gleich Null wäre. Dazu ist es notwendig, eine Gleichung für die Determinante aufzustellen (z Dreiecksregel) und, gleichgesetzt mit 0, den Parameter a berechnen.
Zerlegung nach Spalten (nach der ersten Spalte):
Minor für (1,1): Löschen Sie die erste Zeile und die erste Spalte aus der Matrix.
Lassen Sie uns die Determinante für diesen Moll finden. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6.

Bestimmen wir den Moll für (2,1): Dazu löschen wir die zweite Zeile und die erste Spalte aus der Matrix.

Lassen Sie uns die Determinante für diesen Moll finden. ∆ 2,1 = (0 (-2)-2 (-2)) = 4 . Minor für (3,1): Lösche die 3. Zeile und 1. Spalte aus der Matrix.
Lassen Sie uns die Determinante für diesen Moll finden. ∆ 3,1 = (0 1-2 (-2)) = 4
Die Hauptdeterminante ist: ∆ = (1 (-6)-3 4+1 4) = -14

Lassen Sie uns die Determinante finden, indem wir die Erweiterung nach Zeilen (nach der ersten Zeile) verwenden:
Minor für (1,1): Löschen Sie die erste Zeile und die erste Spalte aus der Matrix.

Lassen Sie uns die Determinante für diesen Moll finden. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6. Minor für (1,2): Löschen Sie die 1. Zeile und 2. Spalte aus der Matrix. Lassen Sie uns die Determinante für dieses Moll berechnen. ∆ 1,2 \u003d (3 (-2) -1 1) \u003d -7. Und um den Moll für (1,3) zu finden, löschen wir die erste Zeile und die dritte Spalte aus der Matrix. Lassen Sie uns die Determinante für diesen Moll finden. ∆ 1,3 = (3 2-1 2) = 4
Wir finden die Hauptdeterminante: ∆ \u003d (1 (-6) -0 (-7) + (-2 4)) \u003d -14

System von m linearen Gleichungen mit n Unbekannten ein System der Form genannt

wo aij und b ich (ich=1,…,m; b=1,…,n) sind einige bekannte Zahlen, und x 1 ,…,x n- Unbekannt. In der Notation der Koeffizienten aij erster Index ich bezeichnet die Nummer der Gleichung, und die zweite j ist die Zahl der Unbekannten, bei der dieser Koeffizient steht.

Die Koeffizienten für die Unbekannten werden in Form einer Matrix geschrieben , die wir anrufen werden Systemmatrix.

Die Zahlen auf der rechten Seite der Gleichungen b 1 ,…,b m namens freie Mitglieder.

Aggregat n Zahlen c 1 ,…,c n namens Entscheidung dieses Systems, wenn jede Gleichung des Systems eine Gleichheit wird, nachdem Zahlen darin eingesetzt wurden c 1 ,…,c n anstelle der entsprechenden Unbekannten x 1 ,…,x n.

Unsere Aufgabe wird es sein, Lösungen für das System zu finden. In diesem Fall können drei Situationen auftreten:

Ein lineares Gleichungssystem, das mindestens eine Lösung hat, heißt gemeinsam. Ansonsten, d.h. hat das System keine Lösungen, so wird es aufgerufen unvereinbar.

Überlegen Sie, wie Sie Lösungen für das System finden können.

MATRIX-METHODE ZUM LÖSEN VON SYSTEMEN VON LINEAREN GLEICHUNGEN

Matrizen ermöglichen es, ein lineares Gleichungssystem kurz aufzuschreiben. Gegeben sei ein System aus 3 Gleichungen mit drei Unbekannten:

Betrachten Sie die Matrix des Systems 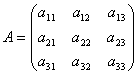und Matrixspalten von unbekannten und freien Mitgliedern

Lassen Sie uns das Produkt finden

jene. als Ergebnis des Produkts erhalten wir die linken Seiten der Gleichungen dieses Systems. Dann kann dieses System unter Verwendung der Definition der Matrixgleichheit geschrieben werden als

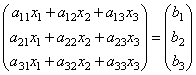oder kürzer EIN∙X=B.

Hier Matrizen EIN und B bekannt sind, und die Matrix X Unbekannt. Sie muss gefunden werden, weil. seine Elemente sind die Lösung dieses Systems. Diese Gleichung heißt Matrixgleichung.

Die Matrixdeterminante sei von Null verschieden | EIN| ≠ 0. Dann wird die Matrixgleichung wie folgt gelöst. Multiplizieren Sie beide Seiten der Gleichung auf der linken Seite mit der Matrix A-1, die Inverse der Matrix EIN: . Soweit A -1 A = E und E∙X=X, dann erhalten wir die Lösung der Matrixgleichung in der Form X = A -1 B .

Beachten Sie, dass, da die inverse Matrix nur für quadratische Matrizen gefunden werden kann, die Matrixmethode nur solche Systeme lösen kann, in denen Die Anzahl der Gleichungen ist gleich der Anzahl der Unbekannten. Allerdings ist auch die Matrixschreibweise des Systems möglich, falls die Anzahl der Gleichungen ungleich der Anzahl der Unbekannten ist, dann die Matrix EIN ist nicht quadratisch und daher ist es unmöglich, eine Lösung für das System in der Form zu finden X = A -1 B.

Beispiele. Gleichungssysteme lösen.

CRAMERS REGEL

Stellen Sie sich ein System aus 3 linearen Gleichungen mit drei Unbekannten vor:

Determinante dritter Ordnung entsprechend der Matrix des Systems, d.h. zusammengesetzt aus Koeffizienten bei Unbekannten,

namens Systemdeterminante.

Wir setzen drei weitere Determinanten wie folgt zusammen: Wir ersetzen nacheinander 1, 2 und 3 Spalten in der Determinante D durch eine Spalte mit freien Termen

Dann können wir folgendes Ergebnis beweisen.

Satz (Cramers Regel). Wenn die Determinante des Systems Δ ≠ 0 ist, dann hat das betrachtete System genau eine Lösung, und

Nachweisen. Stellen Sie sich also ein System von 3 Gleichungen mit drei Unbekannten vor. Multipliziere die 1. Gleichung des Systems mit dem algebraischen Komplement Eine 11 Element eine 11, 2. Gleichung - an A21 und 3. - auf A 31:

Fügen wir diese Gleichungen hinzu:

Betrachten Sie jede der Klammern und die rechte Seite dieser Gleichung. Durch den Satz über die Erweiterung der Determinante nach den Elementen der 1. Spalte

Ebenso kann gezeigt werden, dass und .

Schließlich ist es leicht zu sehen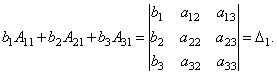

Damit erhalten wir die Gleichheit: .

Somit, .

Die Gleichheiten und werden auf ähnliche Weise hergeleitet, woraus die Behauptung des Satzes folgt.

Wir stellen also fest, dass, wenn die Determinante des Systems Δ ≠ 0 ist, das System eine eindeutige Lösung hat und umgekehrt. Wenn die Determinante des Systems gleich Null ist, dann hat das System entweder eine unendliche Menge von Lösungen oder keine Lösungen, d.h. unvereinbar.

Beispiele. Lösen Sie ein Gleichungssystem

GAUSS-METHODE

Mit den bisher betrachteten Methoden können nur solche Systeme gelöst werden, bei denen die Anzahl der Gleichungen mit der Anzahl der Unbekannten übereinstimmt und die Determinante des Systems von Null verschieden sein muss. Das Gaußsche Verfahren ist universeller und eignet sich für Systeme mit beliebig vielen Gleichungen. Es besteht in der sukzessiven Eliminierung von Unbekannten aus den Gleichungen des Systems.

Betrachten wir wieder ein System aus drei Gleichungen mit drei Unbekannten:

.

Wir lassen die erste Gleichung unverändert, und von der 2. und 3. schließen wir die enthaltenden Terme aus x 1. Dazu dividieren wir die zweite Gleichung durch a 21 und multipliziere mit - a 11 und addiere dann mit der 1. Gleichung. In ähnlicher Weise teilen wir die dritte Gleichung in a 31 und multipliziere mit - a 11 und füge es dann dem ersten hinzu. Als Ergebnis wird das ursprüngliche System die Form annehmen:

Nun eliminieren wir aus der letzten Gleichung den Term enthaltend x2. Teilen Sie dazu die dritte Gleichung durch , multiplizieren Sie mit und addieren Sie sie zur zweiten. Dann haben wir ein Gleichungssystem:

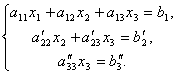
Daher ist es aus der letzten Gleichung leicht zu finden x 3, dann aus der 2. Gleichung x2 und schließlich vom 1. - x 1.

Bei Anwendung der Gauß-Methode können die Gleichungen ggf. vertauscht werden.

Anstatt ein neues Gleichungssystem zu schreiben, beschränken sie sich oft darauf, die erweiterte Matrix des Systems zu schreiben:

und dann durch elementare Transformationen in eine Dreiecks- oder Diagonalform bringen.

Zu elementare Transformationen Matrizen enthalten die folgenden Transformationen:

1. Permutation von Zeilen oder Spalten;
2. Multiplizieren einer Zeichenfolge mit einer Zahl ungleich Null;
3. Zu einer Zeile weitere Zeilen hinzufügen.

Beispiele: Lösen Sie Gleichungssysteme mit der Gauß-Methode.

Das System hat also unendlich viele Lösungen.

2.Ist │A│=0, dann ist die Matrix A entartet und die inverse Matrix A -1 existiert nicht.

Ist die Determinante der Matrix A ungleich Null, so existiert die inverse Matrix.

3. Finden Sie A T transponiert zu A.

4. Finde die algebraischen Komplemente der Elemente der transponierten Matrix und bilde daraus die adjungierte Matrix. 5. Wir berechnen die inverse Matrix nach der Formel: 6. Überprüfen Sie die Richtigkeit der Berechnung der inversen Matrix anhand ihrer Definition A -1 ∙A = A ∙A -1 = E.

· №28

· In einer m x n-Matrix kann man durch Löschen beliebiger Zeilen und Spalten quadratische Teilmatrizen der k-ten Ordnung auswählen, wobei k ≤ min (m; n). Die Determinanten solcher Untermatrizen werden Minoren k-ter Ordnung der Matrix A genannt.

· Der Rang einer Matrix A ist die höchste Ordnung von Nicht-Null-Minoren dieser Matrix.

· Der Rang einer Matrix A wird mit rang A oder r(A) bezeichnet.

· Aus der Definition folgt:

· 1) der Rang einer Matrix der Größe m x n überschreitet nicht die kleinste ihrer Größen, d.h. r(A) ≤ min(m;n).

· 2) r(A)=0 genau dann, wenn alle Elemente der Matrix gleich Null sind, d.h. A=0.

· 3) Für eine quadratische Matrix n-ter Ordnung gilt r(A) = n genau dann, wenn die Matrix A nichtsingulär ist.

· Im allgemeinen Fall ist die Bestimmung des Rangs einer Matrix durch Aufzählung aller Minoren ziemlich mühsam. Um diese Aufgabe zu erleichtern, werden elementare Transformationen verwendet, die den Rang der Matrix erhalten:

· 1) Ablehnung der Nullzeile (Spalte).

· 2) Multiplikation aller Elemente einer Zeile (Spalte) einer Matrix mit einer Zahl ungleich Null.

· 3) Ändern der Reihenfolge der Zeilen (Spalten) der Matrix.

· 4) Addieren zu jedem Element einer Zeile (Spalte) die entsprechenden Elemente einer anderen Zeile (Spalte), multipliziert mit einer beliebigen Zahl.

· 5) Matrixtransposition.

· Satz. Der Rang einer Matrix ändert sich bei elementaren Transformationen der Matrix nicht.

№31

— Die Anzahl der Gleichungen im System (1) sei gleich der Anzahl der Variablen, d.h. m=n. Dann ist die Matrix des Systems quadratisch, und ihre Determinante Δ=│А│ heißt Determinante des Systems.

— Angenommen, dass │А│ ungleich Null ist, dann gibt es eine inverse Matrix A -1 .

— Multipliziert man die beiden Teile der Matrixgleichheit links mit der inversen Matrix A -1, erhält man:

— A -1 (AX) \u003d A -1 B.

Die Lösung des Gleichungssystems nach der inversen Matrixmethode ist die Spaltenmatrix:

X \u003d A -1 B.

(A -1 A)X \u003d EX \u003d X

— Satz von Cramer. Sei Δ die Determinante der Matrix des Systems A und Δ j die Determinante der Matrix, die man aus der Matrix erhält, indem man die j-te Spalte durch eine Spalte mit freien Termen ersetzt. Wenn Δ dann nicht gleich Null ist, hat das System eine eindeutige Lösung, die durch die Cramer-Formeln definiert ist:

wobei j=1..n.

№33

—
Die Gauß-Methode - die Methode der sukzessiven Eliminierung von Variablen - besteht darin, dass das Gleichungssystem mit Hilfe elementarer Transformationen auf ein äquivalentes System vom Stufen- oder Dreieckstyp reduziert wird.

— Betrachten Sie die Matrix:

— diese Matrix wird als erweiterte Matrix des Systems (1) bezeichnet, da sie neben der Matrix des Systems A zusätzlich eine Spalte mit freien Mitgliedern enthält.

№26

— Ein N-dimensionaler Vektor ist ein geordneter Satz von n reellen Zahlen, geschrieben als X=(x 1,x 2,...x n) , wobei x i die i-te Komponente des Vektors X ist.

— Zwei n-dimensionale Vektoren sind genau dann gleich, wenn ihre jeweiligen Komponenten gleich sind, d.h. X=Y wenn x i = y i , i=1…n.

Der Satz von Vektoren mit reellen Komponenten, in dem die Operationen zum Addieren von Vektoren und zum Multiplizieren eines Vektors mit einer Zahl definiert sind, die die obigen Eigenschaften erfüllen, wird als Vektorraum bezeichnet.

— Ein Vektorraum R heißt n-dimensional, wenn es n linear unabhängige Vektoren in ihm gibt und alle n + 1 Vektoren bereits abhängig sind. Die Zahl n heißt Dimension des Vektorraums R und wird mit dim(R) bezeichnet.

№29

Lineare Operatoren

— Definition. Wenn ein Gesetz (Regel) gegeben ist, nach dem jedem Vektor x des Raums ein einziger Vektor y des Raums zugeordnet ist

dann sagen sie: dass der Operator (Transformation, Abbildung) A(x) gegeben ist, wirkend von bis und

schreibe y=A(x).

— Ein Operator heißt linear, wenn er für beliebige Vektoren x und y des Raums gilt

und jeder Zahl λ gelten die folgenden Beziehungen:

№37

— Sei À eine Menge bestehend aus endlich vielen Elementen a 1 , a 2 , a 3 …a n . Aus verschiedenen Elementen der Menge A können Gruppen gebildet werden. Wenn jede Gruppe die gleiche Anzahl von Elementen m (m aus n) enthält, dann sagt man, dass sie Verbindungen von n Elementen mit jeweils m bilden. Es gibt drei Arten von Verbindungen: Platzierungen, Kombinationen und Permutationen.

— Verbindungen, die jeweils alle n Elemente der Menge A enthalten und sich daher nur in der Reihenfolge der Elemente voneinander unterscheiden, nennt man Permutationen von n Elementen. Die Anzahl solcher Permutationen wird durch das Symbol Р n bezeichnet.

№35

Die klassische Definition der Wahrscheinlichkeit basiert auf dem Konzept der Äquiwahrscheinlichkeit von Ereignissen.

Äquivalenz von Ereignissen bedeutet, dass es keinen Grund gibt, eines von ihnen anderen vorzuziehen.

Betrachten wir einen Test, bei dem Ereignis A eintreten kann.Jedes Ergebnis, bei dem Ereignis A eintritt, wird als günstiges Ereignis A bezeichnet.

Die Wahrscheinlichkeit eines Ereignisses A (bezeichnet mit P(A)) ist das Verhältnis der Anzahl der für das Ereignis A günstigen Ergebnisse (bezeichnet mit k) zur Anzahl aller Testergebnisse – N, d. h. P(A)=k/N.

— Aus der klassischen Definition der Wahrscheinlichkeit folgen folgende Eigenschaften:

— Die Wahrscheinlichkeit eines Ereignisses liegt zwischen null und eins.

— Die Wahrscheinlichkeit für ein bestimmtes Ereignis ist gleich eins.

— Die Wahrscheinlichkeit eines unmöglichen Ereignisses ist null

№39, 40

— Additionssatz. Wenn A und B inkonsistent sind, dann ist P(A + B) = P(A) + P(B)