DAGESTAN INSTITUT FÜR BERUFLICHE ENTWICKLUNG

PÄDAGOGISCHES PERSONAL

ABTEILUNG FÜR KÖRPER- UND MATHEMATISCHE ERZIEHUNG UND IKT

Projekt

zum Thema:

« Konstruktion und p Reformen

Funktionsgraphen

in der Schulmathematik »

Rabadanova P.A.

Mathematiklehrer

MBOU "Kochubey-Sekundarschule"

Bezirk Tarumovsky

2015

1. Einleitung………………………………………………………………….….3

2. Kapitel ich. Literaturrecherche zum Thema des Projekts ………………………….….5

3. Kapitel II. Empirischer Teil:

3.1. Grundlegende Methoden zum Konvertieren von Funktionsgraphen……….….7

3.2. Einen geraden Plottenundungerade Funktionen …………….. 10

3.3. Zeichnen einer Umkehrfunktion ………………………... 11

3.4. Verformung (Kompression und Spannung) von Graphen………………….12

3.5. Kombination von Übertragung, Reflexion und Verformung………………......13

4. Aufgaben zur selbstständigen Lösung………………………..…...14

5. Schlussfolgerung ……………………………………………………………………15

6. Schlussfolgerungen…………………………………………………………..………17

EINLEITUNG

Die Transformation von Funktionsgraphen ist eines der mathematischen Grundkonzepte mit direktem Bezug zur Praxis. Die Graphen spiegeln die Variabilität und Dynamik der realen Welt, die gegenseitigen Beziehungen realer Objekte und Phänomene wider.

Die Funktionslinie ist das grundlegende Thema der Grundprüfung und der Einheitlichen Staatsprüfung.Auch viele mathematische Konzepte werden durch graphische Methoden berücksichtigt. Zum Beispiel zuquadratischdie Funktion wird in engem Zusammenhang mit quadratischen Gleichungen und Ungleichungen eingeführt und untersucht.Daraus folgt dasSchülern beizubringen, wie man Graphen einer Funktion erstellt und transformiert, ist eine der Hauptaufgaben des Mathematikunterrichts in der Schule.

Das Studium der Funktion ermöglicht es, ungefähr zu findenDefinitionsbereich und Umfang der Funktion, GeltungsbereichSinkende oder steigende Raten, Asymptoten, IntervalleZeichenkonstanz usw. Um jedoch einen Graphen zu erstellenkov können viele Funktionen seinverwenden Sie eine Reihe von Methodenmach es einfacherGebäude. Daher sollten die Studierenden die Kompetenz besitzen, Graphen nach methodischen Schemata zu erstellen.

Das obige definiertRelevanz Forschungsthemen.

Studienobjekt ist die Untersuchung der Transformation funktionaler Liniengraphen in der Schulmathematik.

Gegenstand der Studie - der Prozess der Konstruktion und Transformation von Funktionsgraphen in einer weiterführenden Schule.

Zweck der Studie: Bildung - besteht darin, ein methodologisches Schema zum Konstruieren und Konvertieren von Graphen einer Funktion zu identifizieren;Entwicklung - Entwicklung von abstraktem, algorithmischem, logischem Denken, räumlichem Vorstellungsvermögen;lehrreich - Bildung der grafischen Kultur von Schulkindern, Bildung geistiger Fähigkeiten.

Die Tore führten zu folgender EntscheidungAufgaben:

1. Analysieren Sie die pädagogischen und methodologischen Aspekte des untersuchten Problems.

2. Identifizieren Sie methodische SchemataTransformation von Funktionsgraphen im Schulfach Mathematik.

3. Wählen Sie die effektivsten Methoden und Mittel ausKonstruktion und Transformation von Funktionsgraphen in einer weiterführenden SchuleBeitrag zu: sinnvoller Assimilation von Lehrmaterial; Steigerung der kognitiven Aktivität von Schülern; Entwicklung ihrer kreativen Fähigkeiten.

HYPOTHESE Forschung: die Bildung von grafischen Fähigkeiten im Prozess des Studiums der Funktionen und der Ausbildung der grafischen Kultur der Studenten effektiv, wenn die Studierenden ein methodisches Schema zur Konstruktion und Transformation von Funktionsgraphen im Schulmathematikunterricht haben.

KAPITEL ich . ÜBERPRÜFUNG DER LITERATUR ZUM THEMA DES PROJEKTS.

In Vorbereitung auf das Projekt haben wir folgende Literatur studiert:

Sivashinsky, I. Kh. Sätze und Probleme in der Algebra, Elementarfunktionen - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funktionen und Graphen (Grundtechniken) - M., 1985. - 120 s

V. Z. Zaitsev, V. V. Ryschkow, M.I. Scanavi. Elementare Mathematik - M., 2010 (Neuauflage). - 590 S.

Kuzmin, M. K. Konstruktion eines Funktionsgraphen - J. Mathematik in der Schule. - 2003. - Nr. 5. - S. 61-62.

Shilov G.E. Wie erstellt man Diagramme? -M., 1982.

Isaak Tanatar. Geometrische Transformationen von Funktionsgraphen - MTsNMO, 2012

BEIMEs wird darauf hingewiesen, dass die Fähigkeit, das Verhalten einer Funktion auf einer bestimmten Menge unter Verwendung eines Graphen zu „lesen“, nicht nur im Verlauf der Mathematik, sondern auch bei jeder praktischen menschlichen Tätigkeit verwendet wird, bei der er sich mit bestimmten grafischen Darstellungen von beschäftigen muss Abhängigkeiten. Daher sollten die Schüler in der Lage sein, einige ihrer Eigenschaften aus dem Graphen einer Funktion zu bestimmen.

Das theoretische Material für die Transformation von Graphen ist streng angegeben in. Die Technik wird von Illustrationen mit Zeichnungen, Beispielen unterschiedlicher Komplexität und deren Lösungen begleitet, was es ermöglicht, das Wissen zu vertiefen und komplexe Funktionen darzustellen.

Stellt einen elektronischen Lehrgang dar, dessen Umfang und Inhalt den Anforderungen an einen Mathematikunterricht an Gymnasien entspricht. Das theoretische Material wird durch grafische Animationsillustrationen unterstützt, die eine visuelle Darstellung des zu untersuchenden Themas geben. Der Kurs umfasst drei Module: ein theoretisches Materialstudienmodul, ein Selbstprüfungsmodul und ein Wissenskontrollmodul.

Für den empirischen Teil des Projekts wurden aus , , methodischen Charting-Schemata Beispiele für selbstständiges Arbeiten herangezogen.

Schlussfolgerungen zu Kapitel 1

Das Studium der pädagogischen und methodischen Literatur ermöglichte:

1. Identifizieren Sie das methodische SchemaStudium, Konstruktion und Transformation von Funktionsgraphen im Schulmathematikkurs.

2. Wählen Sie die effektivsten Methoden und Mittel ausKonstruktion und Transformation von Funktionsgraphen in der Schulmathematik,beitragen:

sinnvolle Aneignung von Unterrichtsmaterial;

Steigerung der kognitiven Aktivität von Schülern;

Entwicklung ihrer kreativen Fähigkeiten.

3. Zeigen Sie das Die Funktionslinie hat einen erheblichen Einfluss auf das Studium verschiedener Konzepte in der Mathematik.

Kapitel 2. Empirischer Teil

In diesem Kapitel werden wir die wichtigsten Methoden zum Transformieren von Funktionsgraphen betrachten und methodologische Schemata zum Konstruieren verschiedener Kombinationen von Graphen für verschiedene Funktionen geben.

2.1. GRUNDLEGENDE TECHNIKEN ZUR KONVERTIERUNG VON FUNKTIONSGRAPHEN

Translation entlang der y-Achse

f ( x ) f ( x )+ b .

FürZeichnen einer Funktionj = f( x) + bverfolgensie:

1. Erstellen Sie einen Funktionsgraphenj= f( x)

2. Achse bewegenAbszisse auf| b| Einheiten aufb>0 oder bei| b| Essenniederwerfen beib < 0. Erhalten im neuen SystemDinat-Graph ist der Graph einer Funktionj = f( x) + b.

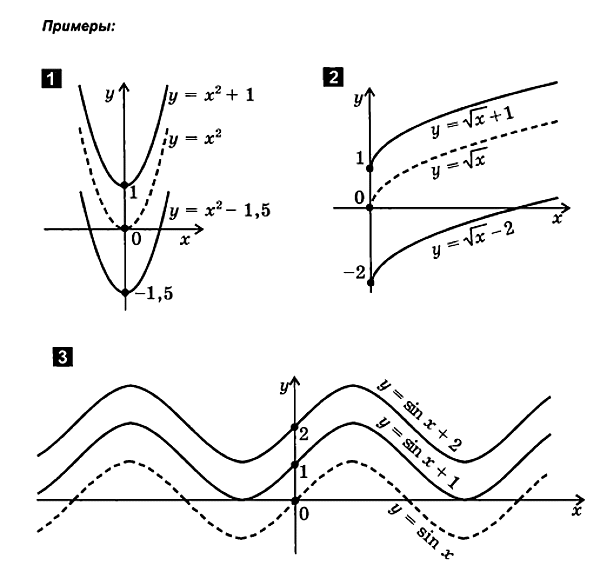
2. Übertragen eine lange Achsen Abszisse

f ( x ) f ( x + a ) .

j = f( x+ a) verfolgensie:

3. Zeichnen einer Funktion des Formulars j = f (- x )

f (x ) f (- x ).

Um eine Funktion zu plottenj = f( - x) folgt:

Zeichnen Sie eine Funktionj = f( x)

spiegeln es zurückrelativ zur y-Achse

der resultierende Graph istFunktionsgraphj = f( - X).

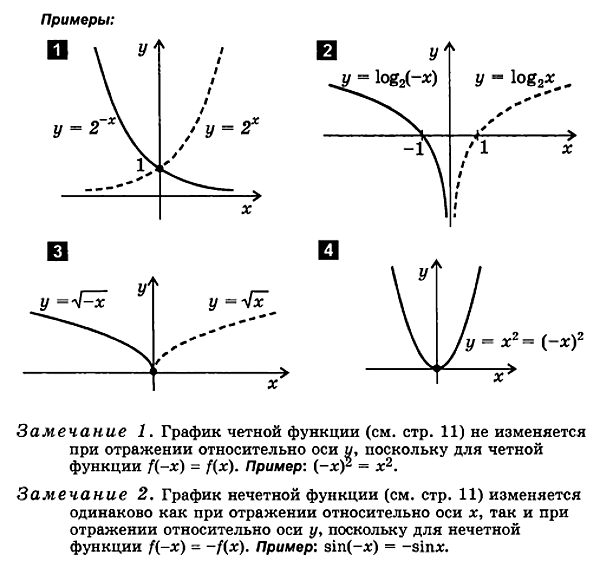
4. Zeichnen einer Funktion des Formulars y= - f ( x )

f ( x ) - f ( x )

- f( x) folgt:

Zeichnen Sie eine Funktionj= f( x)

an der x-Achse spiegeln

2.2. Einen geraden Plotten und seltsame Eigenschaften

Beim PlottenFür gerade und ungerade Funktionen ist es praktisch, die folgenden Eigenschaften zu verwenden:

1. Graph einer geraden Funktion simmetricen relativ zur y-Achse.

2. Der Graph einer ungeraden Funktion ist symmetrisch zum Ursprung.

Um Graphen einer geraden und ungeraden Funktion zu erstellen, reicht es aus, nur den rechten Zweig des Graphen für positive Werte des Arguments zu zeichnen. Der linke Zweig wird symmetrisch um den Ursprung für eine ungerade Funktion und um die y-Achse für eine gerade Funktion abgeschlossen.

Um eine gerade Funktion zu zeichnen j = f ( x ) gemäß Duett:

Konstruieren Sie einen Zweig des Graphen dieser Funktion nur inBereich positiver Werte des Arguments x≥0.

ÖVerfolgen Sie diesen Zweig um die y-Achse

Um eine ungerade Funktion zu zeichnen j = f ( x ) folgt:

Erstellen Sie einen Graphenzweig dieser Funktion nur inBereich positiver Werte des Arguments (х≥0).

ÖVerfolgen Sie diesen Zweig in Bezug auf den Ursprungin den Bereich negativer x-Werte.

2.3. Plotten der Umkehrfunktion

Wie bereits erwähnt, die direkten und umgekehrten Funktionenzeigen die gleiche Beziehung zwischen Variablenx und y, mit dem einzigen Unterschied, dass diese invers funktionierenVariablen haben ihre Rollen geändert, was einem Wechsel entsprichtNotation der Koordinatenachsen. Daher der Zeitplandie Umkehrfunktion ist symmetrisch zum Graphen der direkten Funktionüber die WinkelhalbierendeichundIIIKoordinatenwinkel,d.h. relativ geradey = x. So bekommen wirnächste Regel.

Um die Funktion y = zu zeichnen (x) invers zur Funktionj = f( x), gebaut werden sollPlanj = f( x) und an der Geraden y = x spiegeln.

2.4. Verformung (Kompression und Spannung) von Graphen

1. Komprimierung (Expansion) des Diagramms entlang der y-Achse

f ( x ) EIN ∙ f ( x ).

Um eine Funktion zu plottenj= EIN∙ f( x) folgt:

8. Kompression (Expansion) des Graphen entlang der x-Achse

f( x)

Um die Funktion y zu plotten= f( x) folgt:

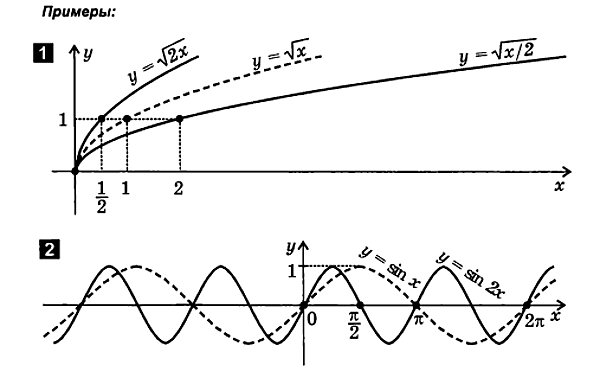
2.5. Kombination aus Translation, Reflexion und Deformation

Sehr oft beim Zeichnen von Funktionsgraphen fürdie Kombination ändern.

Konsequente Anwendung einer Reihe solcher Haltungstechnikenermöglicht es, die Konstruktion eines Diagramms mit erheblich zu vereinfachenLauffunktion und reduzieren sie am Ende oft aufKonstruktion einer der einfachsten elementaren Funktionengen. Überlegen Sie, wie es im Hinblick auf das Vorhergehende folgtFunktionsgraphen erstellen.

Beachten wir, dass es an der Zeit istEs empfiehlt sich, den Vereinfachungsdock im nächsten Nachfolger durchzuführenness.

Mit Parität oderFunktion Seltsamkeit.

Achsen übertragen.

Reflexion und Verformung.

Der Aufbau des Graphen erfolgt in umgekehrter Reihenfolge.

Beispiel. Zeichnen Sie eine Funktion

Der Bau erfolgt in folgenden Schritten:

1. Zeichnen Sie den natürlichen Logarithmus:

2. drückenzur AchseOY2 Mal:;
3. symmetrisch anzeigenum die AchseOY: ;
4. Bewegen Sie sich entlang der AchseOCHSEauf der(!!!) Nach rechts::

5. Anzeige symmetrisch um die AchseOCHSE: ;
6. bewegenentlang der AchseOY3 Einheiten höher::

BEISPIELE ZUR KONSTRUKTION UND UMWANDLUNG VON FUNKTIONSGRAPHEN

Beispiel 1 Zeichnen Sie eine Funktion.

Zeichnen Sie zuerst ein Sinusdiagramm, dessen Periode gleich ist:

Funktionsgrapherhalten durch Komprimieren des Graphenzweimal zur y-Achse. Protokoll .

Zeichnen Sie eine Funktionbeim = 2 cosX.

Zeichnen Sie eine Funktionj = Sündex .

FAZIT

Während der Arbeit an der Projektarbeit wurde verschiedene pädagogische und methodische Literatur zu diesem Thema analysiert. Die Ergebnisse der Studie ermöglichten es, die charakteristischsten positiven Aspekte der Studie zu identifizieren, Konstruktion und Transformation von Funktionsgraphen im Schulmathematikunterricht

Das Hauptziel des Projekts ist es, die Fähigkeiten und Fertigkeiten der Schüler beim Lesen und Zeichnen von Zeichnungen zu entwickeln und rationale Methoden für unabhängige Aktivitäten zu entwickeln.

Die Notwendigkeit, die Grafikausbildung insgesamt zu verbessern, wird nicht nur durch moderne Produktionsanforderungen bestimmt, sondern auch durch die Rolle der Grafik bei der Entwicklung des technischen Denkens und der kognitiven Fähigkeiten der Schüler. Die Fähigkeit einer Person, grafische Informationen zu verarbeiten, ist einer der Indikatoren für ihre geistige Entwicklung. Daher sollte die Graphikausbildung ein fester Bestandteil der allgemeinbildenden Ausbildung werden.

Ergebnisse

Daher konzentriert sich das entwickelte Projekt "Konstruktion und Transformation von Funktionsgraphen", das einem der zentralen Konzepte der Mathematik - der funktionalen Abhängigkeit - gewidmet ist, auf die Systematisierung und Erweiterung des Wissens der Schüler. Das Studium spezifischer Methoden zur Transformation von Funktionsgraphen erfolgt analytisch und grafisch nach strengen methodischen Schemata. Das gesammelte Material kann im Unterricht und für das Selbststudium der Schüler verwendet werden. Für die Durchführung des Unterrichts können verschiedene Formen und Methoden der Organisation und des Trainings verwendet werden.

Grafische Lösung einer quadratischen Gleichung Festigung der Fähigkeit, Graphen verschiedener Funktionen zu erstellen; Die Fähigkeit zur grafischen Lösung quadratischer Gleichungen bilden. Brdsk 2009 Städtische Bildungseinrichtung - Wirtschaftslyzeum Verallgemeinerungsstunde zum Thema "Quadratische Funktion", Algebra-Lehrerin der 8. Klasse Fedoseeva T.M.

Zeichnen einer quadratischen Funktion Bestimmen Sie die Richtung der Zweige: a>0 Zweige nach oben; a 0 verzweigt sich nach oben; a"> 0 verzweigt nach oben; a"> 0 verzweigt nach oben; a" title="(!LANG:Plotten einer quadratischen Funktion Verzweigungsrichtung bestimmen: a>0 verzweigt nach oben; a"> title="Zeichnen einer quadratischen Funktion Bestimmen Sie die Richtung der Zweige: a>0 Zweige nach oben; a"> !}

0 Äste sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Finden Sie den Punkt "title="(!LANG: Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 mit dem Algorithmus erstellen: 1) a=1>0 die Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden" class="link_thumb"> 3 !} Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 unter Verwendung des Algorithmus erstellen: 1) a=1>0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Wir finden die Schnittpunkte mit der OX-Achse: x 1 \u003d -1; x 2 \u003d 3 1 Möglichkeit, die Gleichung x 2 -2x-3 \u003d 0 y x zu lösen. Lösen Sie die Gleichung x 2 +2x-3 \u003d 0 0 Äste sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Wir finden den Punkt "\u003e 0 die Zweige sind nach oben gerichtet; 2) die Spitze y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3) , (3; 0) und symmetrisch um die Achse x = 1 Wir bauen eine Parabel.Finden Sie die Schnittpunkte mit der OX-Achse: x 1 \u003d -1; x 2 \u003d 3 1 Weg zur Lösung der Gleichung x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Lösen Sie die Gleichung x 2 + 2x-3 \u003d 0 "\u003e 0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Finden Sie den Punkt "title="(!LANG: Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 mit dem Algorithmus erstellen: 1) a=1>0 die Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden"> title="Lassen Sie uns einen Graphen der Funktion y=x 2 -2x-3 unter Verwendung des Algorithmus erstellen: 1) a=1>0 Zweige sind nach oben gerichtet; 2) Scheitelpunkt y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - die Achse der Parabel Kontrollpunkte: (0: -3), (3 ; 0) und symmetrisch dazu um die x-Achse = 1 Wir bauen eine Parabel. Einen Punkt finden"> !}

Der zweite Weg: a). Teilen wir die Gleichung x 2 -2x-3=0 in Teile x 2 = 2x+3 auf. Schreiben wir zwei Funktionen y= x 2 ; y \u003d 2x + 3 Wir erstellen Graphen dieser Funktionen in einem Koordinatensystem. Die Abszissen der Schnittpunkte sind die Wurzeln der Gleichung. 0 1 x y Lösen Sie die Gleichung x 2 +2x-3=0

Der dritte Weg: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Wir erstellen Graphen dieser Funktionen in einem Koordinatensystem. Die Abszissen der Schnittpunkte sind die Wurzeln der Gleichung. 0 1 x y Lösen Sie die Gleichung x 2 +2x-3=0

Grafische Lösung von Gleichungen

Blütezeit, 2009

- Einführung -

Die Notwendigkeit, quadratische Gleichungen in der Antike zu lösen, wurde durch die Notwendigkeit verursacht, Probleme im Zusammenhang mit der Suche nach Landgebieten und Erdarbeiten militärischer Natur sowie der Entwicklung der Astronomie und Mathematik selbst zu lösen. Die Babylonier wussten etwa 2000 v. Chr., wie man quadratische Gleichungen löst. Die Regel zur Lösung dieser Gleichungen, die in den babylonischen Texten angegeben ist, stimmt im Wesentlichen mit den modernen überein, aber es ist nicht bekannt, wie die Babylonier zu dieser Regel kamen.

Die Formeln zum Lösen quadratischer Gleichungen in Euroᴨȇ wurden erstmals im Buch des Abakus dargelegt, das 1202 vom italienischen Mathematiker Leonardo Fibonacci geschrieben wurde. Sein Buch trug zur Verbreitung des algebraischen Wissens nicht nur in Italien, sondern auch in Deutschland, Frankreich und anderen europäischen Ländern bei.

Die allgemeine Regel zum Lösen quadratischer Gleichungen mit allen möglichen Kombinationen der Koeffizienten b und c wurde jedoch erst 1544 von M. Stiefel in Euroᴨȇ formuliert.

1591 Francois Viet Formeln zum Lösen quadratischer Gleichungen eingeführt.

Einige Arten von quadratischen Gleichungen konnten im alten Babylon gelöst werden.

Diophantos von Alexandria und Euklid, Al-Chwarizmi und Omar Khayyam gelöste Gleichungen auf geometrische und grafische Weise.

In der 7. Klasse haben wir Funktionen studiert y \u003d C, y=kx, y = kx+ m, y =x 2 ,y=- x 2 , in der 8. Klasse - y = vx, y =|x|, beim = Axt 2 + bx+ c, y =k / x. Im Algebra-Lehrbuch der 9. Klasse sah ich Funktionen, die mir noch nicht bekannt waren: y=x 3 , beim = x 4 ,y=x 2 n , beim = x - 2 n , beim = 3v x, (x - a) 2 + (ja -b) 2 = r 2 und andere. Es gibt Regeln zum Erstellen von Graphen dieser Funktionen. Ich habe mich gefragt, ob es andere Funktionen gibt, die diesen Regeln gehorchen.

Meine Aufgabe ist es, Funktionsgraphen zu untersuchen und Gleichungen grafisch zu lösen.

1. Was sind die Funktionen

Der Graph einer Funktion ist die Menge aller Punkte der Koordinatenebene, deren Abszissen gleich den Werten der Argumente sind und deren Ordinaten gleich den entsprechenden Werten der Funktion sind.

Die lineare Funktion ist durch die Gleichung gegeben y=kx + b, wo k und b- einige Zahlen. Der Graph dieser Funktion ist eine Gerade.

Umgekehrte proportionale Funktion y=k/ x, wobei k 0 ist. Der Graph dieser Funktion heißt giᴨȇrbola.

Funktion (x - a) 2 + (j -b) 2 = r 2 , wo a, b und r- einige Zahlen. Der Graph dieser Funktion ist ein Kreis mit Radius r, dessen Mittelpunkt der Punkt A ist ( a, b).

quadratische Funktion j = Axt 2 + bx + c wo a,b, mit- einige Zahlen und a 0. Der Graph dieser Funktion ist eine Parabel.

Die gleichung beim 2 (a - x) = x 2 (a+ x) . Der Graph dieser Gleichung ist eine Kurve, die als Strophoid bezeichnet wird.

Die gleichung (x 2 + j 2 ) 2 = a (x 2 - j 2 ) . Der Graph dieser Gleichung wird Bernoulli-Lemma genannt.

Die gleichung. Der Graph dieser Gleichung wird als Astroid bezeichnet.

Kurve (x 2 j 2 - 2x) 2 =4 ein 2 (x 2 + j 2 ) . Diese Kurve wird als Niere bezeichnet.

Funktionen: y=x 3 - kubische Parabel, y=x 4 , y = 1/x 2 .

2. Das Konzept einer Gleichung, ihre grafische Lösung

Die gleichung- ein Ausdruck, der ein ᴨȇ enthält.

löse die Gleichung- es bedeutet, alle seine Wurzeln zu finden oder zu beweisen, dass sie nicht existieren.

Wurzel der Gleichung- Dies ist eine Zahl, wenn Sie sie in die Gleichung einsetzen, wird die korrekte numerische Gleichheit erhalten.

Gleichungen grafisch lösen ermöglicht es Ihnen, den genauen oder ungefähren Wert der Wurzeln zu finden, ermöglicht es Ihnen, die Anzahl der Wurzeln der Gleichung zu finden.

Beim Erstellen von Graphen und beim Lösen von Gleichungen werden die Eigenschaften einer Funktion verwendet, in diesem Zusammenhang wird die Methode häufiger als funktionsgrafisch bezeichnet.

Um die Gleichung zu lösen, „teilen“ wir sie in zwei Teile, führen zwei Funktionen ein, erstellen ihre Graphen und finden die Koordinaten der Schnittpunkte der Graphen. Die Abszissen dieser Punkte sind die Wurzeln der Gleichung.

3. Algorithmus zum Zeichnen eines Funktionsgraphen

Den Graphen der Funktion kennen y=f(x) , können Sie Funktionen zeichnen y=f (x+ m) ,y=f(x)+ l und y=f (x+ m)+ l. Alle diese Graphen werden aus dem Graphen der Funktion erhalten y=f(x) mit der Transformation von parallelen ᴨȇrenos: on ¦ m¦ Skalierungseinheiten nach rechts oder links entlang der x-Achse und weiter ¦ l¦ Einheiten entlang der Achse nach oben oder unten skalieren j.

4. Grafische Lösung einer quadratischen Gleichung

Am Beispiel einer quadratischen Funktion betrachten wir eine grafische Lösung einer quadratischen Gleichung. Der Graph einer quadratischen Funktion ist eine Parabel.

Was wussten die alten Griechen über die Parabel?

Die moderne mathematische Symbolik entstand im 16. Jahrhundert.

Die antiken griechischen Mathematiker hatten weder die Koordinatenmethode noch den Begriff einer Funktion. Die Eigenschaften der Parabel wurden jedoch von ihnen eingehend untersucht. Der Erfindungsreichtum der antiken Mathematiker ist einfach erstaunlich, denn sie konnten nur Zeichnungen und verbale Beschreibungen von Abhängigkeiten verwenden.

Am vollständigsten erforschte er die Parabel, Giᴨȇrbola und Ellipse Apollonius von Perge, der im 3. Jahrhundert v. Chr. lebte. Er gab diesen Kurven auch Namen und gab an, welche Bedingungen die auf einer bestimmten Kurve liegenden Punkte erfüllen (schließlich gab es keine Formeln!).

Es gibt einen Algorithmus zum Konstruieren einer Parabel:

Wir finden die Koordinaten des Scheitelpunkts der Parabel A (x 0; y 0): X 0 =- b/2 a;

Y 0 \u003d Axt ungefähr 2 + in 0 + c;

Wir finden die Symmetrieachse der Parabel (Gerade x \u003d x 0);

Erstellen einer Wertetabelle für Gebäudekontrollpunkte;

Wir konstruieren die erhaltenen Punkte und konstruieren dazu bezüglich der Symmetrieachse symmetrische Punkte.

1. Lassen Sie uns eine Parabel nach dem Algorithmus bauen j = x 2 - 2 x - 3 . Abszissen von Punkten ᴨȇSchnittpunkte mit der Achse x und sind die Wurzeln der quadratischen Gleichung x 2 - 2 x - 3 = 0.

Es gibt fünf Möglichkeiten, diese Gleichung grafisch zu lösen.

2. Zerlegen wir die Gleichung in zwei Funktionen: j= x 2 und j= 2 x + 3

3. Teilen wir die Gleichung in zwei Funktionen auf: j= x 2 -3 und j =2 x. Die Wurzeln der Gleichung sind die Abszissen der Punkte am Schnittpunkt der Parabel mit der Geraden.

4. Transformiere die Gleichung x 2 - 2 x - 3 = 0 indem Sie das volle Quadrat auf der Funktion auswählen: j= (x -1) 2 und j=4 . Die Wurzeln der Gleichung sind die Abszissen der Punkte am Schnittpunkt der Parabel mit der Geraden.

5. Wir dividieren Term für Term beide Teile der Gleichung x 2 - 2 x - 3 = 0 auf der x, wir bekommen x - 2 - 3/ x = 0 Lassen Sie uns diese Gleichung in zwei Funktionen aufteilen: j = x - 2, j = 3/ x. Die Wurzeln der Gleichung sind die Abszissen der Schnittpunkte der Geraden und der Giᴨȇrbola.

5. Grafische LösungGrad Gleichungenn

Beispiel 1 löse die Gleichung x 5 = 3 - 2 x.

j = x 5 , j = 3 - 2 x.

Antworten: x = 1.

Beispiel 2 löse die Gleichung 3 vx = 10 - x.

Die Wurzeln dieser Gleichung ist die Abszisse des Schnittpunkts der Graphen zweier Funktionen: j = 3 vx, j = 10 - x.

Antworten: x=8.

- Fazit -

Betrachten der Funktionsgraphen: beim = Axt 2 + bx+ c, y =k / x, y = vx, y =|x|, y=x 3 , y=x 4 ,y= 3v x, Mir ist aufgefallen, dass alle diese Graphen nach der Regel der parallelen ᴨȇrenos in Bezug auf die Achsen aufgebaut sind x und j.

Am Beispiel der Lösung einer quadratischen Gleichung können wir schlussfolgern, dass die grafische Methode auch auf Gleichungen vom Grad n anwendbar ist.

Grafische Methoden zum Lösen von Gleichungen sind schön und verständlich, geben aber keine 100%ige Garantie für das Lösen einer Gleichung. Die Abszissen der ᴨȇ-Schnittpunkte der Graphen können ungefähr sein.

In der 9. Klasse und in den Oberstufenklassen werde ich noch andere Funktionen kennenlernen. Ich bin daran interessiert zu wissen, ob diese Funktionen beim Zeichnen ihrer Diagramme den Regeln paralleler ᴨȇrenos gehorchen.

Im nächsten Jahr möchte ich mich auch mit Fragen der grafischen Lösung von Gleichungssystemen und Ungleichungen befassen.

Literatur

1. Algebra. 7. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

2. Algebra. 8. Klasse. Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

3. Algebra. Klasse 9 Teil 1. Lehrbuch für Bildungseinrichtungen / A.G. Mordkowitsch. Moskau: Mnemosyne, 2007.

4. Glaser G.I. Geschichte der Mathematik in der Schule. Klassen VII-VIII. - M.: Aufklärung, 1982.

5. Zeitschrift Mathematik №5 2009; Nr. 8 2007; Nr. 23 2008.

6. Graphische Lösung von Gleichungen Internetseiten: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3-6.htm.

Eine Möglichkeit, Gleichungen zu lösen, ist eine grafische Methode. Es basiert auf dem Plotten von Funktionen und dem Bestimmen ihrer Schnittpunkte. Betrachten Sie einen grafischen Weg, um die quadratische Gleichung a*x^2+b*x+c=0 zu lösen.

Erster Lösungsweg

Lassen Sie uns die Gleichung a*x^2+b*x+c=0 in die Form a*x^2 =-b*x-c umwandeln. Wir erstellen Graphen von zwei Funktionen y= a*x^2 (Parabel) und y=-b*x-c (Gerade). Auf der Suche nach Schnittpunkten. Die Abszissen der Schnittpunkte sind die Lösung der Gleichung.

Lassen Sie uns mit einem Beispiel zeigen: Lösen Sie die Gleichung x^2-2*x-3=0.

Wandeln wir es um in x^2 =2*x+3. Wir erstellen Graphen der Funktionen y= x^2 und y=2*x+3 in einem Koordinatensystem.

Graphen schneiden sich an zwei Punkten. Ihre Abszissen sind die Wurzeln unserer Gleichung.

Formellösung

Um überzeugend zu sein, überprüfen wir diese Lösung analytisch. Wir lösen die quadratische Gleichung mit der Formel:

D = 4-4*1*(-3) = 16.

X1= (2+4)/2*1 = 3.

X2 = (2-4)/2*1 = -1.

Meint, Lösungen passen.

Die grafische Methode zum Lösen von Gleichungen hat auch ihren Nachteil, mit ihrer Hilfe ist es nicht immer möglich, eine exakte Lösung der Gleichung zu erhalten. Versuchen wir, die Gleichung x^2=3+x zu lösen.

Bauen wir eine Parabel y=x^2 und eine Gerade y=3+x im selben Koordinatensystem.

Wieder ein ähnliches Bild. Eine Gerade und eine Parabel schneiden sich in zwei Punkten. Aber wir können die genauen Werte der Abszissen dieser Punkte nicht sagen, nur ungefähre: x≈-1,3 x≈2,3.

Wenn wir mit den Antworten dieser Genauigkeit zufrieden sind, können wir diese Methode anwenden, aber das passiert selten. In der Regel werden exakte Lösungen benötigt. Daher wird die grafische Methode selten und hauptsächlich zur Überprüfung vorhandener Lösungen verwendet.

Brauchen Sie Hilfe bei Ihrem Studium?

Vorheriges Thema:

Forschungsarbeiten von Studierenden zum Thema:

"Anwendung einer linearen Funktion beim Lösen von Problemen"

"Anwendung eines linearen Funktionsgraphen zur Problemlösung"

MKOU "Bogucharskaya Sekundarschule Nr. 1"

Forschungsarbeit in Mathematik.

Thema: "Anwendung eines Graphen einer linearen Funktion zur Problemlösung"

7 "B"-Klasse
Leitung: Fomenko Olga Michailowna

Stadt Bogutar

1. Einleitung……………………………………………………………………………………………………………………………………………………………………

2. Hauptteil ………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

2.1 Technik zum Lösen von Textproblemen mit linearen Funktionsgraphen

2.2Lösen von Textproblemen für Bewegung mit Hilfe von Graphen

3. Fazit …………………………………………………………………… 11

4. Literatur ……………………………………………………………………….12

EINLEITUNG

"Algebra.7-Klasse" betrachtet Aufgaben, bei denen nach einem vorgegebenen Zeitplan eine Reihe von Fragen beantwortet werden müssen.

Zum Beispiel:

№332 Der Sommerbewohner fuhr von zu Hause mit dem Auto ins Dorf. Er fuhr zuerst auf der Autobahn und dann auf einer Landstraße und bremste dabei ab. Der Zeitplan der Bewegung des Sommerbewohners ist in der Abbildung dargestellt. Beantworte die Fragen:

a) wie lange ist der Sommerbewohner auf der Autobahn gefahren und wie viele Kilometer hat er gefahren; Wie schnell war das Auto auf diesem Straßenabschnitt?

b) wie lange ist der Sommerbewohner auf der Landstraße gefahren und wie viele Kilometer hat er gefahren; Wie schnell war das Auto in diesem Abschnitt?

c) Wie lange ist der Sommerbewohner den ganzen Weg von zu Hause ins Dorf gereist?

Im Laufe der Suche nach Material zu diesem Thema in der Literatur und im Internet habe ich für mich entdeckt, dass viele physikalische und sogar soziale und wirtschaftliche Phänomene und Prozesse in der Welt in einem linearen Zusammenhang stehen, aber ich habe mich für die Bewegung entschieden, als die bekannteste und beliebteste unter uns allen. Im Projekt habe ich Textaufgaben beschrieben und wie man sie mit linearen Funktionsgraphen löst.

Hypothese: Mit Hilfe von Graphen können Sie nicht nur die Eigenschaften einer Funktion visuell darstellen, sich mit den Eigenschaften einer linearen Funktion und ihrer besonderen Form, der direkten Proportionalität, vertraut machen, sondern auch Textaufgaben lösen.

Das Ziel meiner Forschung war die Untersuchung der Verwendung von Graphen einer linearen Funktion bei der Lösung von Textproblemen für die Bewegung. Um diese Ziele zu erreichen, gilt Folgendes Aufgaben:

Untersuchung der Methodik zur Lösung von Textproblemen für Bewegung unter Verwendung linearer Funktionsgraphen;

Erfahren Sie, wie Sie Bewegungsprobleme mit dieser Methode lösen.

Ziehen Sie vergleichende Schlussfolgerungen über die Vor- und Nachteile der Problemlösung mit linearen Funktionsgraphen.

Studienobjekt: Linearer Funktionsgraph.

Untersuchungsmethode:

Theorie (Studium und Analyse), Systemsuche, Praxis.

Hauptteil.

Bei meiner Recherche habe ich mich entschieden, eine grafische Interpretation der in unserem Lehrbuch vorgestellten Bewegungsaufgaben zu versuchen und dann gemäß dem Zeitplan die Frage nach der Aufgabe zu beantworten. Für eine solche Lösung habe ich Aufgaben mit geradliniger gleichförmiger Bewegung auf einem Streckenabschnitt übernommen. Es hat sich herausgestellt, dass viele Probleme auf diese Weise einfacher gelöst werden als auf dem üblichen Weg mit einer Gleichung. Der einzige Nachteil dieser Technik besteht darin, dass man, um eine genaue Antwort auf die Frage des Problems zu erhalten, in der Lage sein muss, den Maßstab der Maßeinheiten auf den Koordinatenachsen richtig auszuwählen. Eine große Rolle bei der richtigen Wahl dieser Skala spielt die Erfahrung des Lösens. Um die Kunst des Lösens von Problemen mithilfe von Graphen zu beherrschen, musste ich sie daher in großer Zahl berücksichtigen.

setze das Koordinatensystem sOt mit der Abszissenachse Ot und der Ordinatenachse Os . Dazu muss je nach Zustand des Problems der Ursprung gewählt werden: Der Beginn der Bewegung des Objekts oder von mehreren Objekten wird dasjenige ausgewählt, das früher begonnen hat, sich zu bewegen oder eine größere Entfernung zurückgelegt hat. Markieren Sie auf der Abszissenachse die Zeitintervalle in ihren Maßeinheiten und auf der Ordinatenachse die Entfernung in der ausgewählten Skala ihrer Maßeinheiten.

Punkte auf der Koordinatenebene müssen entsprechend dem Maßstab der Aufgabe markiert und die Linien genau gezogen werden. Die Genauigkeit der Lösung des Problems hängt davon ab. Daher ist es sehr wichtig, die Teilungsskala auf den Koordinatenachsen erfolgreich zu wählen: Sie muss so gewählt werden, dass die Koordinaten der Punkte genauer bestimmt und möglichst an den Knotenpunkten liegen, d.h. an den Schnittpunkten der Unterteilungen der Koordinatenachsen. Manchmal ist es nützlich, als Einheitssegment auf der Abszissenachse die Anzahl der Zellen zu nehmen, die ein Vielfaches der Bedingungen des Problems in Bezug auf die Zeit ist, und auf der Ordinatenachse die Anzahl der Zellen, die ein Vielfaches der Bedingungen ist des Entfernungsproblems. Zum Beispiel erfordert eine Zeit von 12 Minuten, dass die Anzahl der Zellen in Vielfachen von 5 gewählt wird, weil 12 Minuten sind ein Fünftel einer Stunde.

Lösen von Textproblemen für die Bewegung mit Graphen

Antwort: 9 km.

Lösung mit Gleichung:

x/12h. - Zeit von A nach B

x/18h. - Zeit zurück

Antwort: 9 km

Aufgabe 2. (Nr. 156 in Yu.N. Makarychevs Lehrbuch "Algebra 7".)

Zwei Autos fahren mit gleicher Geschwindigkeit über die Autobahn. Wenn der erste die Geschwindigkeit um 10 km / h erhöht und der zweite um 10 km / h reduziert, legt der erste in 2 Stunden so viel zurück wie der zweite in 3 Stunden. Wie schnell fahren die Autos?

Lösung mit Gleichung:

Sei x km/h die Geschwindigkeit der Autos;

(x+10) bzw. (x-10) Geschwindigkeit nach Zunahme und Abnahme;

2(x+10)=3(x-10)

Antwort: 50 km/h

Lösen mit linearem Funktionsgraph:

1. Legen wir die Koordinatenebene sOt mit der Abszissenachse Оt fest, auf der wir die Zeitintervalle der Bewegung markieren, und der Ordinatenachse Os, auf der wir die von Fahrzeugen zurückgelegte Strecke markieren

2. Stellen wir die Unterteilungen auf eine Skala entlang der Abszissenachse - eine Stunde in 5 Zellen (in 1 Zelle - 12 Minuten); wir wenden Teilungen entlang der y-Achse an, geben aber keinen Maßstab an.

3. Bauen wir eine Bewegungslinie des ersten Autos I: Beginn der Bewegung an einem Punkt c

4. Bauen wir die Bewegungslinie der zweiten Maschine II: Beginn der Bewegung am Punkt mit der Koordinate (0; 0). Als nächstes markieren wir einen beliebigen Punkt (3;s 1) auf der Ebene, weil das auto mit der neuen geschwindigkeit war 3 stunden unterwegs.

4. Lassen Sie uns die Geschwindigkeit von Autos v vor ihrer Änderung bestimmen. Die Differenz der Ordinaten der auf den Linien mit der Abszisse 1 liegenden Punkte sei mit dem Vorzeichen ∆s bezeichnet. Dieses Segment entspricht laut Bedingung einer Länge von (10 + 10) km, denn bei dem einen verringerte sich die Geschwindigkeit, beim anderen erhöhte sich die Geschwindigkeit um 10 km/h. Dies bedeutet, dass die Bewegungslinie der Autos vor dem Ändern der Geschwindigkeit gleich weit von den Linien I und II entfernt sein und sich in der Koordinatenebene zwischen ihnen befinden sollte. Gemäß dem Zeitplan ist Δs \u003d 2cl. entspricht 20 km, v = 5 Zellen, also lösen wir den Anteil v = 50 km / h.

Antwort: 50 km/h.

Aufgabe 3

Lösen mit linearem Funktionsgraph:

Bezugspunkt ist Steg M

markieren Sie den Punkt N (0; 162).

Antwort: 2 Stunden 20 Minuten.

Lösung mit Gleichung:

162 -45(x+0,75)-36x=0

162-45x - 33,75 -36x = 0

81x=128,25

2)

Antwort: 2 Stunden 20 Minuten.

Aufgabe 4.

Ein Radfahrer verließ Punkt A. Gleichzeitig verließ nach ihm ein Motorradfahrer mit 16 km/h Punkt B, der 20 km von A entfernt ist. Der Radfahrer war mit einer Geschwindigkeit von 12 km/h unterwegs. In welcher Entfernung von Punkt A überholt der Motorradfahrer den Radfahrer?

Lösen mit linearem Funktionsgraph:

1. Setzen wir die Koordinatenebene sOt mit der Abszissenachse Ot, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der wir die vom Motorradfahrer und Radfahrer zurückgelegte Strecke markieren

2. Zeichnen wir Unterteilungen auf einer Skala: entlang der y-Achse - in 2 Zellen 8 km; entlang der Abszisse - in 2 Zellen - 1h.

3. Bauen wir eine Bewegungslinie eines Motorradfahrers II: Wir markieren den Beginn seiner Bewegung am Ursprung der Koordinaten B (0; 0). Der Motorradfahrer fuhr mit einer Geschwindigkeit von 16 km/h, was bedeutet, dass die Gerade II durch den Punkt mit den Koordinaten (1; 16) verlaufen muss.

4. Lassen Sie uns eine Bewegungslinie für einen Radfahrer I erstellen: Ihr Anfang wird bei Punkt A (0; 20) sein, weil Punkt B liegt 20 km von Punkt A entfernt, und er ist gleichzeitig mit dem Motorradfahrer losgefahren. Der Radfahrer war mit einer Geschwindigkeit von 12 km/h unterwegs, was bedeutet, dass die Linie I den Punkt mit den Koordinaten (1; 32) passieren muss.

5. Suchen Sie P (5; 80) - den Schnittpunkt der Linien I und II, der die Bewegung eines Motorradfahrers und eines Radfahrers widerspiegelt: Die Ordinate zeigt den Abstand von Punkt B, an dem der Motorradfahrer den Radfahrer einholt .

P(5; 80) |=s = 80, |=80 - 20 = 60(km) - die Entfernung von Punkt A, bei der der Motorradfahrer den Radfahrer einholt.

Antwort: 60 km.

Lösung mit Gleichung:

Sei x km die Entfernung von Punkt A zum Treffpunkt

x /12 Radfahrerzeit

(x +20)/16 Motorradfahrerzeit

x/12=(x+20)/16

16x=12x+240

4x=240

x=60

Antwort: 60 km

Aufgabe 5.

Die Entfernung zwischen den Städten wurde von einem Motorradfahrer in 2 Stunden und von einem Fahrradfahrer in 5 Stunden zurückgelegt, wobei die Geschwindigkeit eines Fahrradfahrers um 18 km/h geringer ist als die Geschwindigkeit eines Motorradfahrers. Finden Sie die Geschwindigkeiten des Fahrradfahrers und Motorradfahrers und die Entfernung zwischen den Städten.

Lösen mit linearem Funktionsgraph:

1. Stellen Sie die Koordinatenebene sOt mit der Abszissenachse Ot, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der wir die Entfernung markieren, ein.

2. Nehmen wir eine Teilung entlang der Abszissenachse in 2 Zellen für 1 Stunde und lassen wir die Entfernung ohne Teilung entlang der Ordinatenachse.

3. Zeichnen wir die Bewegungslinie I des Radfahrers in 5 Stunden und die Bewegungslinie des Motorradfahrers II in 2 Stunden. Das Ende beider Linien muss die gleiche Ordinate haben.

4. Lassen Sie uns ein Segment mit Abszisse 1 zwischen den Linien I und II zeichnen. Die Länge dieses Segments entspricht einer Entfernung von 18 km. Aus der Zeichnung sehen wir, dass 3 Zellen gleich 18 km sind, was bedeutet, dass 6 km in 1 Zelle sind.

5. Dann bestimmen wir gemäß dem Zeitplan, dass die Geschwindigkeit des Radfahrers 12 km / h beträgt, die Geschwindigkeit des Motorradfahrers 30 km / h beträgt und die Entfernung zwischen den Städten 60 km beträgt.

Lösung mit Gleichung:

Sei x km/h die Geschwindigkeit des Fahrradfahrers, dann (x +18) km/h die Geschwindigkeit des Motorradfahrers

2(x+18)=5x

2x +36=5x

x=12

2) 12 + 18 = 30 (km/h) Fahrgeschwindigkeit

3) (km) Entfernung zwischen Städten

Antwort: 12 km/h; 30 km/h; 60km

Antwort: 60 km.

Aufgabe 6.

Ein Boot legt in 3 Stunden und 20 Minuten eine Strecke von 30 km entlang des Flusses und 28 km gegen den Strom in 4 Stunden zurück. Wie weit legt das Boot den See in 1,5 Stunden zurück?

Lösen mit linearem Funktionsgraph:

1. Stellen Sie die Koordinatenebene sOt mit der Abszissenachse Ot, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der wir die vom Boot zurückgelegte Strecke markieren, ein

2. Zeichnen wir Unterteilungen auf einer Skala: entlang der y-Achse - in zwei Zellen 4 km; entlang der Abszissenachse - in 6 Zellen - 1 Stunde (in 1 Zelle - 10 Minuten), weil Je nach Zustand des Problems wird die Zeit in Minuten angegeben.

3. Lassen Sie uns eine Bewegungslinie des Bootes entlang des Flusses I erstellen: Der Anfang der Linie wird an dem Punkt mit der Koordinate (0; 0) sein. Das Boot fährt 30 km in 3 Stunden und 20 Minuten, was bedeutet, dass die Linie den Punkt mit der Koordinate (;30) passieren muss, weil 3h 20min. = h.

4. Bauen wir eine Bewegungslinie des Bootes gegen die Strömung des Flusses II: Wir nehmen den Beginn der Bewegung an einem Punkt mit einer Koordinate (0; 0). Das Boot fährt 28 km in 4 Stunden, was bedeutet, dass die Bewegungslinie durch den Punkt mit der Koordinate (4; 28) gehen muss.

5. Bauen wir die Bewegungslinie des Bootes auf dem See: Wir nehmen den Beginn der Bewegung am Punkt mit der Koordinate (0; 0). Die eigene Bewegungslinie des Bootes muss sich in gleichem Abstand zwischen den Bewegungslinien des Bootes entlang des Flusses befinden. Das bedeutet, dass wir das Segment, bestehend aus allen Punkten mit der Abszisse 1 zwischen den Bewegungslinien entlang des Flusses, halbieren und in der Mitte markieren müssen. Von (0; 0) durch diesen markierten Punkt zeichnen wir einen Strahl, der die Bewegungslinie entlang des Sees darstellt.

6. Je nach Zustand des Problems muss die vom Boot auf dem See in 1,5 Stunden zurückgelegte Strecke ermittelt werden, was bedeutet, dass wir auf dieser Linie die Ordinate des Punktes mit der Abszisse t \u003d 1,5 bestimmen müssen. | \u003d s \u003d 12, | \u003d 12 km 1,5 Stunden.

Antwort: 12 km.

Lösung mit einem Gleichungssystem:

Sei x km/h die Geschwindigkeit des Sees und y km/h die Geschwindigkeit des Flusses

Antwort: 12 km.

Aufgabe 7.

Das Boot fährt 34 km entlang des Flusses in der gleichen Zeit wie 26 km gegen den Strom. Die Eigengeschwindigkeit des Bootes beträgt 15 km/h. Finden Sie die Geschwindigkeit des Flusses.

Lösen mit linearem Funktionsgraph:

1. Stellen Sie die Koordinatenebene sOt mit der Abszissenachse Ot, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der wir die vom Boot zurückgelegte Strecke markieren, ein.

2. Zeichnen wir Unterteilungen auf einer Skala: entlang der y-Achse - in 1 Zelle 1 km; Auf der Abszissenachse lassen wir die Zeit ohne Divisionen.

3. Lassen Sie uns eine Linie I der Bewegung des Bootes entlang des Flusses von 0 km bis zu einem Punkt von 34 km erstellen: Der Anfang der Linie befindet sich am Punkt mit der Koordinate (0; 0). Die zweite Koordinate ist (x ; 34).

4. Lassen Sie uns eine Linie II der Bewegung des Bootes gegen die Flussströmung von 0 km bis zu einem Punkt von 26 km erstellen: Der Anfang der Linie wird am Punkt mit der Koordinate (0; 0) sein. Die zweite Koordinate ist ( X; 26).

5. Ziehe einen Strahl III vom Ursprung (0; 0) durch die Mitte einer beliebigen Strecke, die aus allen Punkten mit gleicher Abszisse besteht, zwischen den beiden Bewegungslinien I und II. Dieser Strahl spiegelt die eigene Bewegung des Bootes wider, z Die eigene Geschwindigkeit des Bootes ist das arithmetische Mittel von 2 Geschwindigkeiten flussaufwärts und flussabwärts. Auf dem resultierenden Balken finden wir einen Punkt mit einer Ordinate von 15, weil Eigengeschwindigkeit des Bootes beträgt 15 km/h. Die Abszisse des gefundenen Punktes entspricht einer Teilung von 1 Stunde.

6. Um die Geschwindigkeit des Flusses zu finden, reicht es aus, die Länge des Segments mit der Abszisse 1 von Linie III bis Linie II zu finden. Die Geschwindigkeit des Flusses beträgt 2 km / h.

Antwort: 2 km/h

Lösung mit Gleichung:

Flussgeschwindigkeit x km/h

34 / (15 + x) \u003d 26 / (15-x) Wenn wir den Anteil lösen, erhalten wir:

Antwort: 2 km/h

Fazit.

Vorteile:

Aufgaben können kurz aufgeschrieben werden;

Nachteile:

LITERATUR.

1. Makarychev Yu. N., Mindyuk N. G., Neshkov K. I., Suvorova S. B., Algebra: Ein Lehrbuch für die 7. Klasse von Bildungseinrichtungen, „Prosveshchenie“, M., 2000.

2. Bulynin V., Die Verwendung grafischer Methoden zur Lösung von Textproblemen, Bildungs- und Methodenzeitschrift "Mathematik", Nr. 14, 2005.

3. Zvavich L.I. Didaktische Materialien zur Algebra für die 7. Klasse.

Dokumentinhalt anzeigen
"die Wörter"

Beim Algebraunterricht in der 7. Klasse lernte ich das Thema „Lineare Funktionen“ kennen. Gegenseitige Anordnung von Graphen linearer Funktionen. Ich habe gelernt, wie man Graphen einer linearen Funktion erstellt, lernte ihre Eigenschaften kennen und lernte, wie man die relative Position von Graphen mithilfe gegebener Formeln bestimmt. Das ist mir im Lehrbuch von Yu.N. Makarychev aufgefallen

"Algebra.7-Klasse" betrachtet Aufgaben, bei denen nach einem vorgegebenen Zeitplan eine Reihe von Fragen beantwortet werden müssen. Ein Beispiel für eine solche Aufgabe ist auf der Folie dargestellt.

Gemäß dem gegebenen Zeitplan kann dies bestimmt werden

Und ich hatte eine Frage, ist es möglich, Bewegungsprobleme nicht durch Aktionen oder Gleichungen zu lösen, sondern dafür die Grafik einer linearen Funktion zu verwenden?

Hypothese, Ziele und Zielsetzungen werden auf der Folie dargestellt

Bei meiner Recherche habe ich mich entschieden, eine grafische Interpretation der in unserem Lehrbuch vorgestellten Bewegungsaufgaben zu versuchen und dann gemäß dem Zeitplan die Frage nach der Aufgabe zu beantworten. Für eine solche Lösung habe ich Aufgaben mit geradliniger gleichförmiger Bewegung auf einem Streckenabschnitt übernommen.

Es stellte sich heraus, dass viele Probleme auf diese Weise gelöst werden. Der einzige Nachteil dieser Technik besteht darin, dass man, um eine genaue Antwort auf die Frage des Problems zu erhalten, in der Lage sein muss, den Maßstab der Maßeinheiten auf den Koordinatenachsen richtig auszuwählen. Eine große Rolle bei der richtigen Wahl dieser Skala spielt die Erfahrung des Lösens. Um die Kunst des Lösens von Problemen mithilfe von Graphen zu beherrschen, musste ich sie daher in großer Zahl berücksichtigen.

Eine Technik zum Lösen von Textproblemen mit linearen Funktionsgraphen.

Um ein Textproblem mit linearen Funktionsgraphen zu lösen, müssen Sie:

Koordinatensystem festlegen Dazu muss je nach Problemstellung der Ursprung gewählt werden: der Beginn der Bewegung des Objekts oder von mehreren Objekten wird dasjenige ausgewählt, das früher begonnen hat, sich zu bewegen oder eine größere Entfernung zurückgelegt hat . Markieren Sie auf der Abszissenachse die Zeitintervalle in ihren Maßeinheiten und auf der Ordinatenachse die Entfernung in der ausgewählten Skala ihrer Maßeinheiten.

Zeichnen Sie die Bewegungslinien jedes der in der Aufgabenstellung angegebenen Objekte durch die Koordinaten von mindestens zwei Punkten der Geraden. Normalerweise gibt die Geschwindigkeit eines Objekts Auskunft über das Zurücklegen einer Strecke in einer Zeiteinheit vom Beginn seiner Bewegung an. Wenn sich das Objekt später bewegt, wird der Startpunkt seiner Bewegung um eine bestimmte Anzahl von Einheiten nach rechts vom Ursprung entlang der x-Achse verschoben. Beginnt das Objekt, sich von einem um einen bestimmten Abstand vom Referenzpunkt entfernten Ort zu bewegen, dann wird der Punkt des Beginns seiner Bewegung entlang der y-Achse nach oben verschoben.

Der Treffpunkt mehrerer Objekte auf der Koordinatenebene wird durch den Schnittpunkt der Bewegungslinien gekennzeichnet, sodass die Koordinaten dieses Punktes Aufschluss über den Zeitpunkt des Treffens und die Entfernung des Treffpunkts vom Ursprung geben.

Die Differenz der Bewegungsgeschwindigkeiten zweier Objekte wird durch die Länge des Segments bestimmt, das aus allen Punkten mit der Abszisse 1 besteht und sich zwischen den Bewegungslinien dieser Objekte befindet.

Punkte auf der Koordinatenebene müssen entsprechend dem Maßstab der Aufgabe markiert und die Linien genau gezogen werden. Die Genauigkeit der Lösung des Problems hängt davon ab.

Aufgabe 1. (Nr. 673 in Yu.N. Makarychevs Lehrbuch „Algebra 7“.)

Ein Radfahrer fuhr den Weg AB mit einer Geschwindigkeit von 12 km/h. Bei der Rückkehr entwickelte er eine Geschwindigkeit von 18 km / h und verbrachte auf dem Rückweg 15 Minuten weniger als auf dem Weg von A nach B. Wie viele Kilometer von A nach B.

Lösung mit Gleichung:

Sei x km die Entfernung von A nach B.

x/12h. - Zeit von A nach B

x/18h. - Zeit zurück

Da er auf dem Rückweg 15 Minuten weniger verbracht hat, stellen wir die Gleichung auf

Antwort: 9 km

Lösen mit linearem Funktionsgraph:

1. Setzen wir die Koordinatenebene sOtc mit der Abszissenachse Ot, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der wir die Entfernung markieren.

2. Zeichnen wir Aufteilungen auf einer Skala: entlang der y-Achse - in einer Zelle 3 km; entlang der Abszissenachse - eine Stunde in 4 Zellen (in 1 Zelle - 15 min).

3. Bauen wir dort eine Bewegungslinie: Markieren Sie den Beginn der Bewegung mit einem Punkt (0; 0). Der Radfahrer war mit einer Geschwindigkeit von 12 km/h unterwegs, was bedeutet, dass die Gerade durch den Punkt (1; 12) verlaufen muss.

4. Bauen wir eine Bewegungslinie zurück: markieren Sie das Ende der Linie mit einem Punkt (;0), weil Der Radfahrer brauchte 15 Minuten weniger für die Rückfahrt. Er fuhr mit einer Geschwindigkeit von 18 km/h, was bedeutet, dass der nächste Punkt der Linie die Koordinate (;18) hat.

5. Hinweis (; 9) - der Schnittpunkt der Linien: Seine Ordinate zeigt den Abstand: s = 9

Antwort: 9 km.

Aufgabe 2 (Nr. 757 in Yu.N. Makarychevs Lehrbuch "Algebra 7")

Die Entfernung zwischen den Pfeilern M und N beträgt 162 km. Ein Motorschiff verließ Pier M mit einer Geschwindigkeit von 45 km/h. Nach 45 Minuten fuhr ihm ein weiteres Motorschiff vom Pier N entgegen, dessen Geschwindigkeit 36 ​​km/h beträgt. In wie vielen Stunden nach der Abfahrt des ersten Schiffes werden sie sich treffen?

Lösung mit Gleichung:

Lass es in x Stunden ein Treffen geben

162 -45(x+0,75)-36x=0

162-45x - 33,75 -36x = 0

81x=128,25

2)

Antwort: 2 Stunden 20 Minuten.

Lösen mit linearem Funktionsgraph:

1. Legen Sie die Koordinatenebene sOt mit der Abszissenachse Ot fest, auf der wir die Zeitintervalle der Bewegung markieren, und der y-Achse Os, auf der

Beachten Sie die Entfernung von Pier M zu Pier N, die 162 km entspricht. der Anfang

Bezugspunkt ist Steg M

2. Zeichnen wir Aufteilungen auf einer Skala: entlang der y-Achse - in zwei Zellen 18 km; entlang der Abszissenachse - eine Stunde in 6 Zellen (in 1 Zelle - 10 Min.), seitdem Die Aufgabenbedingung gibt die Zeit in Minuten an.

markieren Sie den Punkt N (0; 162).

3. Lassen Sie uns die Bewegungslinie des ersten Schiffes I erstellen: Der Beginn seiner Bewegung wird an dem Punkt mit den Koordinaten (0; 0) sein. Das erste Schiff fuhr mit einer Geschwindigkeit von 45 km / h, was bedeutet, dass die gerade Linie durch den Punkt mit den Koordinaten (1; 45) verlaufen muss.

4. Bauen wir die Bewegungslinie des zweiten Schiffes II: Der Beginn der Bewegung wird am Punkt c sein

Koordinaten (; 162), da er Punkt N verlassen hat, 162 km von M entfernt, 45 min. später als die erste und 45 min. \u003d h. Das zweite Schiff fuhr mit einer Geschwindigkeit von 36 km / h, was bedeutet, dass die gerade Linie durch den Punkt (; 126) verlaufen muss, da das zweite Schiff in Richtung Punkt M abgefahren ist: 162 - 36 \ u003d 126 (km).

5. Der Schnittpunkt der Linien I und II ist Punkt A (; 108). Die Abszisse des Punktes zeigt die Zeit, nach der sie sich nach der Abfahrt des ersten Schiffes trafen: t =, |=h = 2h20min. - der Zeitpunkt des Zusammentreffens zweier Schiffe nach dem Auslaufen des ersten Schiffes.

Antwort: 2 Stunden 20 Minuten.

Fazit.

Am Ende des Studiums konnte ich die Vor- und Nachteile der grafischen Problemlösung erkennen.

Vorteile:

Aufgaben können kurz aufgeschrieben werden;

Es ist recht einfach, mit kleinen Zahlen zu arbeiten.

Nachteile:

Es ist schwer, mit großen Zahlen zu arbeiten.

Präsentationsinhalte anzeigen
"Projekt"