Zeichnen Sie ein Polygon auf kariertes Papier. Zum Beispiel wie in Abbildung 1 gezeigt.

Versuchen wir jetzt, seine Fläche zu berechnen. Wie kann man das machen? Am einfachsten ist es wohl, es in rechtwinklige Dreiecke und Rechtecke zu zerlegen, deren Flächen sich bereits leicht berechnen lassen und die Ergebnisse zu addieren. Die von mir verwendete Methode ist einfach, aber sehr umständlich und außerdem nicht für alle Polygone geeignet.

Stellen Sie sich ein nicht entartetes einfaches ganzzahliges Polygon vor (d. h. es ist verbunden - zwei beliebige seiner Punkte können durch eine durchgehende Kurve verbunden werden, die vollständig darin enthalten ist, und alle seine Scheitelpunkte haben ganzzahlige Koordinaten, seine Grenze ist eine verbundene Polylinie ohne Selbstüberschneidungen, und es hat ein Nicht-Null-Quadrat). Um die Fläche eines solchen Polygons zu berechnen, können Sie den folgenden Satz verwenden:

Satz von Pick. Sei die Anzahl der ganzzahligen Punkte innerhalb des Polygons, sei die Anzahl der ganzzahligen Punkte auf seiner Grenze und sei seine Fläche. Dann Picks Formel:

Beispiel. Für das Polygon in Abbildung 1 (gelbe Punkte), (blaue Punkte, Ecken nicht vergessen!), also quadratische Einheiten.

Beweis des Satzes von Pick. Beachten Sie zunächst, dass die Formel von Pick für das Einheitsquadrat gilt. Tatsächlich haben wir in diesem Fall

Stellen Sie sich ein Rechteck vor, dessen Seiten auf den Gitterlinien liegen. Die Seitenlängen seien gleich und. Wir haben in diesem Fall und nach der Pick-Formel

Betrachten Sie nun ein rechtwinkliges Dreieck, dessen Schenkel auf den Koordinatenachsen liegen. Ein solches Dreieck erhält man aus einem Rechteck mit Seiten und, wie im vorherigen Fall betrachtet, durch diagonales Schneiden. Lassen Sie ganzzahlige Punkte auf der Diagonalen liegen. Dann bekommen wir das für diesen Fall

Betrachten Sie nun ein beliebiges Dreieck. Sie erhält man, indem man von einem Rechteck mehrere rechtwinklige Dreiecke und ggf. ein Rechteck abschneidet (siehe Abbildungen 2 und 3). Da die Formel von Pick sowohl für ein Rechteck als auch für ein rechtwinkliges Dreieck gilt, erhalten wir, dass sie auch für ein beliebiges Dreieck gilt.

Es bleibt noch der letzte Schritt: von Dreiecken zu Polygonen übergehen. Jedes Polygon kann in Dreiecke unterteilt werden (z. B. durch Diagonalen). Daher müssen wir nur beweisen, dass beim Hinzufügen eines beliebigen Dreiecks zu einem beliebigen Polygon die Formel von Pick wahr bleibt.

Das Vieleck und das Dreieck haben eine gemeinsame Seite. Nehmen wir an, dass die Formel von Pick gültig ist, und wir werden beweisen, dass sie auch für das aus der Addition erhaltene Polygon gilt. Da und eine gemeinsame Seite haben, werden alle auf dieser Seite liegenden ganzzahligen Punkte mit Ausnahme von zwei Eckpunkten zu inneren Punkten des neuen Polygons. Scheitelpunkte werden Grenzpunkte sein. Lassen Sie uns die Anzahl gemeinsamer Punkte mit und bezeichnen

Die Anzahl der inneren ganzzahligen Punkte des neuen Polygons,

Die Anzahl der Grenzpunkte für das neue Polygon.

Aus diesen Gleichheiten erhalten wir

Da wir angenommen haben, dass der Satz für und für getrennt gilt, dann

Damit ist die Pick-Formel bewiesen.

Diese Formel wurde 1899 vom österreichischen Mathematiker Peak Georg Aleksandrov (1859 - 1943) entdeckt. Zusätzlich zu dieser Formel entdeckte Georg Pick die Pick-, Pick-Julia-, Pick-Nevalina-Theoreme und bewies die Schwarz-Pick-Ungleichung. BEI Anhang 1 Sie können die nicht standardmäßigen Aufgaben sehen, die ich für die Anwendung der Pick-Formel in Betracht gezogen habe.

Peak-Formel

1. Einleitung

2. Spitzenformel. Beweis I.

Beweis II.

Der Beweis von Sh.

3. Aufgaben.

4. Die Formel für die Fläche eines Polygons in Bezug auf die Koordinaten der Eckpunkte.

5. Aufgaben.

6. Literatur

Peak-Formel.

1. Einleitung.

Wir schöpfen Weisheit aus der Geschichte,

in Poesie - Witz,

in Mathematik - Einsicht.

F. Speck

Die Handlung entfaltet sich auf einem normalen Stück kariertem Papier.

Die Linien, die entlang der Seiten der Zellen verlaufen, bilden ein Gitter, und die Eckpunkte der Zellen sind die Knoten dieses Gitters. Lassen Sie uns ein Polygon mit Scheitelpunkten an den Knoten auf das Blatt zeichnen und seine Fläche ermitteln.

Sie können auf verschiedene Arten danach suchen. Sie können beispielsweise ein Polygon in ziemlich einfache Formen schneiden, ihre Flächen finden und sie addieren.

Aber hier stecken wir in einer Menge Ärger. Die Figur lässt sich leicht in Rechtecke, Trapeze und Dreiecke zerlegen, und ihre Fläche wird mühelos berechnet.

Obwohl das Polygon einfach genug aussieht, wird es viel Arbeit erfordern, seine Fläche zu berechnen. Was wäre, wenn das Polygon schicker aussehen würde? Es stellt sich heraus, dass die Flächen von Polygonen, deren Ecken an den Knoten des Gitters liegen, viel einfacher berechnet werden können: Es gibt eine Formel, die ihre Fläche mit der Anzahl der Knoten in Beziehung setzt, die innerhalb und auf dem Rand des Polygons liegen. Diese wunderbare und einfache Formel wird Picks Formel genannt.

2. Spitzenformel.

Die Eckpunkte eines Polygons (nicht unbedingt konvex) befinden sich an den Knoten eines ganzzahligen Gitters. Darin liegen B-Knoten des Gitters und an der Grenze G-Knoten. Lassen Sie uns beweisen, dass seine Fläche B + ist – 1 (Peak-Formel).

Beweis I.

Stellen Sie sich ein Polygon vor, dessen Scheitelpunkte an den Knoten eines ganzzahligen Gitters liegen, dh sie haben ganzzahlige Koordinaten.

Wir teilen das Polygon in Dreiecke mit Ecken an den Knoten des Gitters, die weder innen noch an den Seiten Knoten enthalten.

Bezeichnen:

n ist die Anzahl der Seiten des Polygons,

m ist die Anzahl der Dreiecke mit Ecken an den Knoten des Gitters, die weder innen noch an den Seiten Knoten enthalten,

B ist die Anzahl der Knoten innerhalb des Polygons,

Г ist die Anzahl der Knoten an den Seiten, einschließlich der Eckpunkte.

Die Flächen aller dieser Dreiecke sind gleich und gleich.

Daher ist die Fläche des Polygons
.

180 0 m .

Lassen Sie uns diese Summe nun auf eine andere Weise finden.

Die Summe der Winkel mit einem Scheitelpunkt an einem beliebigen inneren Knoten beträgt 360 0 .

Dann ist die Summe der Winkel mit Scheitelpunkten an allen inneren Knoten 360 0 V.

Die Gesamtsumme der Winkel an den Knoten an den Seiten, aber nicht an den Ecken, ist 180 0 (G - n).

Die Summe der Winkel an den Eckpunkten des Vielecks ist 180 0 ( n – 2) .

Die Gesamtsumme der Winkel aller Dreiecke ist 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Also 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

woraus wir den Ausdruck für die Fläche S des Polygons erhalten:

S= B + – 1 ,

bekannt als Picksche Formel.

In der Abbildung: V = 24, D = 9, alsoS = 24 + – 1 = 27,5.

Finden Sie die Fläche des ersten Polygons mit der Peak-Formel:

B = 28 (grüne Punkte);

D = 20 (blaue Punkte).

Wir erhalten, S =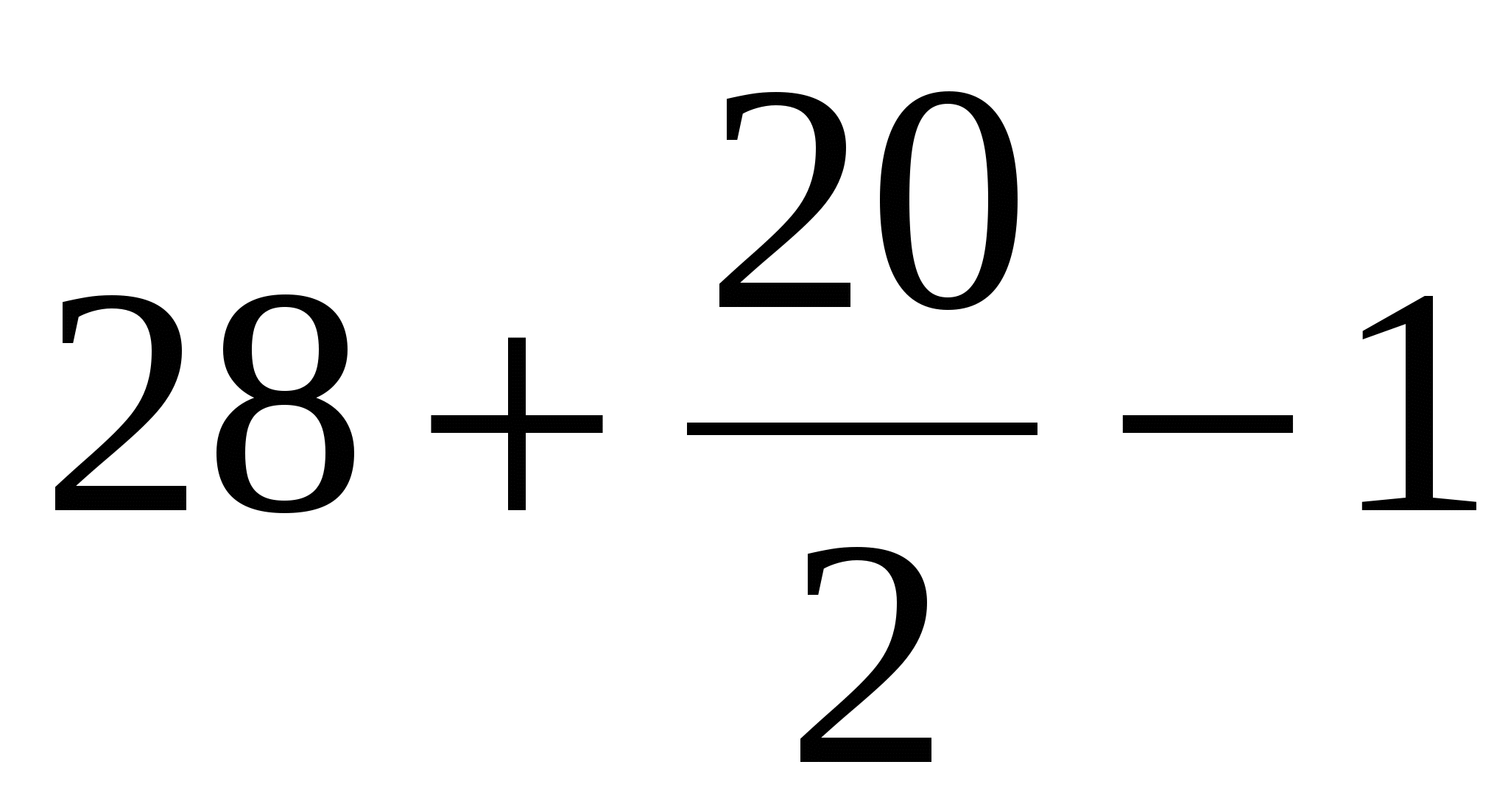
= 37 Quadrateinheiten

Beweis II.

Jedem Polygon M mit Ecken an den Knoten eines ganzzahligen Gitters ordnen wir die Zahl f (M) = zu
, wobei über alle zu M gehörenden Gitterknoten summiert wird, und dem Winkel ist wie folgt definiert: =
für einen inneren Punkt eines Polygons, =
für einen anderen Grenzpunkt als einen Scheitelpunkt, und – Winkel am Scheitelpunkt, wenn der gegebene Knoten ein Scheitelpunkt ist. Es ist leicht zu sehen, dass f (M) =
+
= B + – 1. Es bleibt zu prüfen, ob die Zahl f (M) gleich der Fläche des Polygons M ist.

Das Polygon M sei in Polygone M 1 und M 2 mit Spitzen an den Knoten des Gitters geschnitten. Dann gilt f(M) = f(M 1) + f(M 2), denn für jeden Knoten addieren sich die Winkel. Wenn also die Formel von Pick für zwei der Polygone M, M 1 und M 2 gilt, dann gilt sie auch für das dritte.

Wenn M ein Rechteck mit Seiten ist p und q, entlang der Gitterlinien gerichtet, dann

f (M) = (p – 1)(q – 1) +
= pq.

In diesem Fall gilt die Formel von Pick. Indem man das Rechteck M diagonal in Dreiecke M 1 und M 2 zerschneidet und die Tatsache nutzt, dass f (M) = f (M 1) + f (M 2) und f (M 1) = f (M 2), ist es einfach um die Gültigkeit der Formel von Pick für jedes rechtwinklige Dreieck zu beweisen, dessen Schenkel entlang der Linien des Gitters gerichtet sind. Durch Abschneiden mehrerer solcher Dreiecke von einem Rechteck kann ein beliebiges Dreieck erhalten werden.

Um den Beweis der Formel von Pick zu vervollständigen, bleibt noch anzumerken, dass jedes Polygon durch sich nicht schneidende Diagonalen in Dreiecke geschnitten werden kann.

Der Beweis von Sh.

Der Zusammenhang zwischen der Fläche einer Figur und der Anzahl der Knoten, die in diese Figur fallen, wird bei einem Rechteck besonders deutlich.

Lassen A B C D- ein Rechteck mit Eckpunkten an den Knoten und Seiten, die entlang der Gitterlinien verlaufen.

Bezeichne mit BEI die Anzahl der Knoten, die innerhalb des Rechtecks ​​liegen, und durch G ist die Anzahl der Knoten auf seiner Grenze. Verschieben Sie das Raster um eine halbe Zelle nach rechts und eine halbe Zelle nach unten.

Dann kann das Gebiet des Rechtecks ​​wie folgt zwischen den Knoten "verteilt" werden: jeder von BEI Knoten "steuert" die gesamte Zelle des verschobenen Gitters, jeder von ihnen G- 4 Begrenzungsknoten, die keine Eckpunkte sind - die Hälfte der Zelle, und jeder der Eckpunkte - ein Viertel der Zelle. Daher ist die Fläche des Rechtecks ​​S

Für Rechtecke mit Scheitelpunkten an Knoten und Seiten, die entlang von Gitterlinien verlaufen, haben wir also die Formel aufgestellt

Lassen Sie uns beweisen, dass diese Formel nicht nur für Rechtecke gilt, sondern auch für beliebige Polygone mit Scheitelpunkten an den Gitterknoten.

Bezeichne mit S m PolygonflächeM mit Scheitelpunkten an Knoten und durchP m - Wert
, woBEI m ist die Anzahl der Knoten darinM, a G m ist die Anzahl der Knoten auf der Grenze. Dann kann die Pick-Formel geschrieben werden als
.

Wir teilen den Beweis der Formel in mehrere Schritte auf.

Schritt 1.

Wenn PolygonM mit Eckpunkten an Gitterknoten, die in 2 Polygone geschnitten sindM 1 und M 2 , dann auch Scheitelpunkte nur an den Gitterknoten haben
. Lassen Sie das PolygonM in Polygone schneidenM 1 und M 2 mit Scheitelpunkten an Knoten durch ein Segment AB. Alle Knoten, außer denen, die auf das Segment fallenAB, Geben Sie dem linken und rechten Teil der Formel den gleichen Beitrag. Betrachten Sie die Knoten, die auf dem Segment AB liegen.

Liegt ein solcher Knoten zwischen A und B (z. B. C), dann für ein PolygonM es ist intern und für PolygoneM 1 und M 2 - Grenze. Daher sein Beitrag zuP m gleich 1 ist, und in jedem der Ausdrücke
und
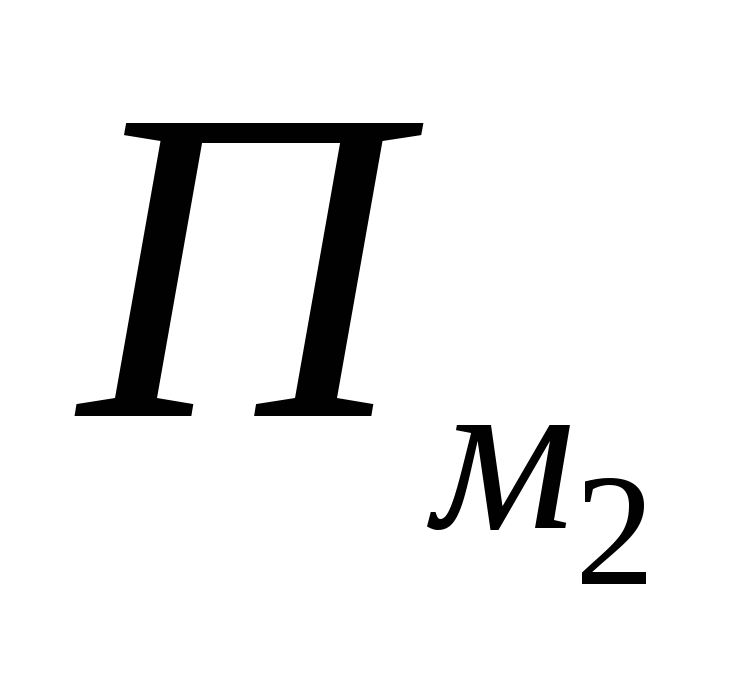– je 0,5, also die Beiträge eines solchen Knotens zuP m und
sind gleich.

Betrachten Sie die Knoten A und B. Sie sind beide Grenzen für M, und für M 1 , M 2 .

Daher fällt der Beitrag jedes dieser Knoten anP m beträgt 0,5 a
- Einheit. Dies bedeutet, dass der Gesamtbeitrag der Knoten A und B zuP m gleich 1 ist, was 1 weniger ist als ihr Beitrag zu
. Aber
, a .

Aus dem gesamten "Beitrag" aller Knoten P m 1 wird abgezogen
2 wird subtrahiert, und dies kompensiert die Differenz in den Beiträgen der Knoten A und B.

So,
.

Schritt 2

Wenn Polygon M mit Eckpunkten an den Gitterknoten, die in zwei Polygone geschnitten sind M 1 und M 2 (auch mit Eckpunkten an Knoten) und die Formel gilt für einige zwei der Polygone MM 1 , M 2 , dann gilt es auch für das dritte Polygon.

Lassen Sie zum Beispiel, es ist wahr fürM 1 und M 2 , also
. Dann (im ersten Schritt), aber weiter erster Schritt), der letzte Ausdruck ist gleichP m , und Gleichberechtigung
und es gibt die Pick-Formel.

Schritt 3

Beweisen wir Picks Formel für ein rechtwinkliges Dreieck mit Ecken an den Gitterknoten und Schenkeln, die auf den Gitterlinien liegen.

Dreieck ABC zu einem Rechteck aufbauen A B C D .

Für Rechtecke ist die Formel von Pick korrekt: S A B C D = P A B C D . Nach dem ersten Schritt P A B C D = P ABC + S ACD , P ABC = P ACD , Also P A B C D = 2P ABC . Aber S A B C D = 2 S ABC . Deshalb S ABC = P ABC .

Schritt 4

Picks Formel ist korrekt für ein beliebiges Dreieck mit Scheitelpunkten an den Gitterknoten.

Nach der Untersuchung der Abbildung ist es leicht zu verstehen: Jedes solche Dreieck kann durch „Abschneiden“ von einem Rechteck mit entlang der Gitterlinien verlaufenden Seiten, mehreren Rechtecken und rechtwinkligen Dreiecken mit Beinen auf den Gitterlinien erhalten werden. Und da Picks Formel für Rechtecke und rechtwinklige Dreiecke gilt, gilt sie (erinnern Sie sich an Schritt 2) auch für das ursprüngliche Dreieck.

Wir haben bewiesen, dass, wenn ein Polygon in Dreiecke mit Scheitelpunkten an den Knoten des Gitters geschnitten werden kann, die Formel von Pick dafür gilt.

3. Aufgaben.

Finden Sie den Bereich der Figuren:

1
.

B=9

G = 4

B=9

G = 5

Berechnung der Fläche einer Figur.

Pick-Methode

Die Arbeit eines Schülers der Klasse 5B der MBOU-Sekundarschule Nr. 23 in Irkutsk

Balsukova Alexandra

Leiter: Khodyreva T.G.

2014

Berechnung der Fläche einer Figur. Pick-Methode

Studienobjekt : Aufgaben auf kariertem Papier

Gegenstand der Studie : Probleme zur Berechnung der Fläche eines Polygons auf kariertem Papier, Methoden und Techniken zu ihrer Lösung.

Forschungsmethoden Schlüsselwörter: Vergleich, Verallgemeinerung, Analogie, Studium von Literatur und Internetquellen, Informationsanalyse.

Zweck der Studie:

Wählen Sie die wichtigsten, interessanten und verständlichen Informationen aus

Analysieren und organisieren Sie die erhaltenen Informationen

Finden Sie verschiedene Methoden und Techniken zum Lösen von Problemen auf kariertem Papier

Überprüfen Sie die Formeln zur Berechnung der Flächen geometrischer Formen mit der Peak-Formel

Erstellen Sie eine elektronische Präsentation der Arbeit, um das gesammelte Material zu präsentieren

Geometrie ist das mächtigste Werkzeug zur Verfeinerung unserer geistigen Fähigkeiten und ermöglicht es uns, richtig zu denken und zu argumentieren.

(G. Galilei)

Relevanz des Themas

Die Leidenschaft für Mathematik beginnt oft damit, dass man über ein Problem nachdenkt. Beim Studium des Themas „Flächen von Polygonen“ stellt sich also die Frage, ob es Aufgaben gibt, die sich von den im Lehrbuch betrachteten Aufgaben unterscheiden. Solche Aufgaben umfassen Aufgaben auf kariertem Papier. Was ist die Besonderheit solcher Probleme, gibt es spezielle Methoden und Techniken zur Lösung von Problemen auf kariertem Papier. In einer Mathestunde hat uns die Lehrerin eine interessante Methode zur Berechnung von Polygonen vorgestellt. Ich begann, die Literatur und Internetquellen zu diesem Thema zu studieren. Es scheint, dass faszinierende Dinge auf einer karierten Ebene zu finden sind, dh auf einem endlosen Blatt Papier, das in identische Quadrate liniert ist. Es stellt sich heraus, dass die Aufgaben rund um kariertes Papier sehr vielfältig sind. Ich habe gelernt, die Flächen von Polygonen zu berechnen, die auf einem karierten Blatt Papier gezeichnet sind. Für viele Aufgaben auf dem Papier in einem Käfig gibt es keine allgemeine Regel für die Lösung, bestimmte Methoden und Techniken. Dies ist ihre Eigenschaft, die ihren Wert für die Entwicklung nicht einer bestimmten pädagogischen Fähigkeit oder Fähigkeit bestimmt, sondern im Allgemeinen der Fähigkeit zu denken, zu reflektieren, zu analysieren, nach Analogien zu suchen, dh diese Aufgaben entwickeln Denkfähigkeiten im weitesten Sinne.

Und ich habe auch erfahren, dass solche Aufgaben in den Kontroll- und Messmaterialien des GIA und der Einheitlichen Staatsprüfung berücksichtigt werden. Daher halte ich das Studium dieses Materials für nützlich, um es nicht nur im weiteren Bildungsprozess anzuwenden, sondern auch um nicht standardmäßige Olympiade-Probleme zu lösen.

2.Das Gebietskonzept

Quadrat- Numerisches Merkmal einer zweidimensionalen geometrischen Figur, das die Größe dieser Figur zeigt. Historisch wurde Flächenberechnung genannt . Eine Figur, die Fläche hat, heißt quadrieren .

Die Fläche einer flachen Figur in Bezug auf die Geometrie

1. Quadrat- das Maß einer flachen Figur in Bezug auf die Standardfigur, die ein Quadrat mit einer Seite gleich einer Länge ist.

2. Quadrat- ein numerisches Merkmal, das flachen Figuren einer bestimmten Klasse (z. B. Polygonen) zugeordnet wird. Die Fläche eines Quadrats mit einer Seite, die einer Längeneinheit entspricht, gleich einer Flächeneinheit

3. Quadrat- ein positiver Wert, dessen Zahlenwert folgende Eigenschaften hat:

 Gleiche Figuren haben gleiche Flächen;

 Wenn eine Figur in Teile unterteilt wird, die einfache Figuren sind (dh solche, die in eine endliche Anzahl flacher Dreiecke unterteilt werden können), entspricht die Fläche dieser Figur der Summe ihrer Flächen Teile;

 Die Fläche eines Quadrats mit einer Seite gleich der Maßeinheit ist gleich eins.

Daraus können wir schließen, dass die Fläche kein spezifischer Wert ist, sondern nur eine bedingte Eigenschaft einer flachen Figur angibt. Um die Fläche einer beliebigen Figur zu finden, muss man bestimmen, wie viele Quadrate mit einer Seite gleich einer Länge sie enthält. Nehmen wir zum Beispiel ein Rechteck, in das ein Quadratzentimeter genau 6 mal passt. Das bedeutet, dass die Fläche des Rechtecks ​​6 cm2 beträgt.

Die Wahl der Fläche eines Quadrats mit einer Seite gleich der Maßeinheit als Mindestmaßeinheit für alle Flächen ist kein Zufall. Dies ist das Ergebnis einer Übereinkunft zwischen Menschen, die im Zuge der „natürlichen“ jahrhundertealten Selektion entstanden ist. Darüber hinaus gab es weitere Vorschläge für eine Maßeinheit. So wurde beispielsweise vorgeschlagen, die Fläche eines gleichseitigen Dreiecks als solche Einheit zu nehmen (d. h. jede flache Figur könnte als „Summe“ einer bestimmten Anzahl gleichseitiger Dreiecke dargestellt werden), was zu a führen würde Änderung der numerischen Darstellung von Flächen.

So tauchten Formeln zur Berechnung von Flächen in der Mathematik auf und wurden von einer Person nicht sofort realisiert - dies viele Wissenschaftler, die in verschiedenen Epochen und verschiedenen Ländern leben. (Falsche Formeln fanden keinen Platz in der Wissenschaft und gerieten in Vergessenheit). Die wahren Formeln wurden über Jahrtausende ergänzt, korrigiert und begründet, bis sie uns in ihrer modernen Form erreichten.

Na sicher Flächenmessung besteht darin, die Fläche einer bestimmten Figur mit der Fläche einer Figur als Maßeinheit zu vergleichen. Als Ergebnis des Vergleichs wird eine bestimmte Zahl erhalten - der numerische Wert der Fläche der angegebenen Figur. Diese Zahl zeigt an, wie oft die Fläche einer bestimmten Figur größer (oder kleiner) ist als die Fläche der Figur, die als Flächeneinheit genommen wird.

T Daraus können wir schließen, dass die Fläche eine künstliche Größe ist, die historisch vom Menschen eingeführt wurde, um eine Eigenschaft einer flachen Figur zu messen. Die Notwendigkeit, einen solchen Wert einzugeben, war auf das wachsende Bedürfnis zurückzuführen, zu wissen, wie groß dieses oder jenes Territorium ist, wie viel Getreide benötigt wird, um ein Feld zu säen, oder um die Bodenfläche für die Dekoration von Zierfliesen zu berechnen.

Peak-Formel

Um die Fläche eines Polygons auf kariertem Papier abzuschätzen, reicht es aus, zu berechnen, wie viele Zellen dieses Polygon bedeckt (wir nehmen die Fläche der Zelle als Einheit). Genauer gesagt, wennS ist die Fläche des Polygons, B ist die Anzahl der Zellen, die vollständig innerhalb des Polygons liegen, und G ist die Anzahl der Zellen, die einen Innenraum haben. Wir betrachten nur solche Polygone, deren Eckpunkte alle an den Knoten des karierten Papiers liegen – also an solchen, bei denen die Polygongitterlinien mindestens einen gemeinsamen Punkt schneiden.

Die Fläche eines beliebigen auf kariertes Papier gezeichneten Dreiecks kann leicht berechnet werden, indem man sie als Summe oder Differenz der Flächen von rechtwinkligen Dreiecken und Rechtecken darstellt, deren Seiten den Gitterlinien folgen, die durch die Eckpunkte des gezeichneten Dreiecks verlaufen.

Um die Fläche eines solchen Polygons zu berechnen, können Sie den folgenden Satz verwenden:

Satz . Lassen - die Anzahl der ganzzahligen Punkte innerhalb des Polygons, - die Anzahl der ganzzahligen Punkte auf seiner Grenze, - sein Bereich. DannPicks Formel:

Beispiel. Für das Polygon in der AbbildungL = 7 (rote Punkte), 9 (grüne Punkte), alsoS = 7+ 9/2 -1 = 10,5 quadratische Einheiten.

Satz von Pick- klassisches Ergebnis und .

Die Fläche eines Dreiecks mit Eckpunkten an den Knoten und ohne Knoten innerhalb oder an den Seiten (außer den Eckpunkten) ist gleich 1/2. Dieser Fakt.

3. Geschichte

Picks Formel wurde von dem österreichischen Mathematiker Georg Alexander (1859-1942) in entdeckt . Mit 16 Jahren beendete Georg die Schule und trat ein. Mit 20 Jahren erhielt er die Lehrbefugnis für Physik und Mathematik. 1884 ging Peak nach zu . Dort traf er einen anderen Schüler von Klein,. Später, 1885, kehrte er zurückwo er den Rest seiner wissenschaftlichen Laufbahn verbrachte.

Georg Pick war mit Einstein befreundet. Pick und Einstein teilten nicht nur wissenschaftliche Interessen, sondern waren auch musikbegeistert. Pick, der in einem Quartett spielte, das aus Universitätsprofessoren bestand, machte Einstein mit den wissenschaftlichen und musikalischen Gesellschaften Prags bekannt.

Der Kreis der mathematischen Interessen von Peak war extrem breit. Insbesondere hat er mehr als 50 wissenschaftliche Arbeiten. Picks Satz, der 1899 von ihm entdeckt wurde, war weithin bekannt für die Berechnung der Fläche eines Polygons. In Deutschland steht dieses Theorem in den Schulbüchern.

4.Anwendungen der Pick-Formel

Die Pick-Formel wird nicht nur zur Berechnung der Flächen von Polygonen verwendet, sondern auch zur Lösung vieler Probleme des Olympiade-Levels.

Einige Beispiele für die Verwendung der Pick-Formel beim Lösen von Problemen:

1) Der Schachkönig ging um das Brett von 8 × 8 Zellen herum, nachdem er jede besucht hatte

Heimfeld genau einmal und mit dem letzten Zug zurück zum Original

aufstellen. Eine unterbrochene Linie, die die Mittelpunkte der Felder in Reihe verbindet

der König bestanden hat, hat keine Selbstüberschneidungen. Welcher Bereich kann

diese unterbrochene Linie begrenzen? (Die Seite der Zelle ist 1.)

Aus der Pick-Formel folgt unmittelbar, dass die durch die Lo-

Mana ist 64/2 − 1 = 31; hier sind die Gitterknoten die Mittelpunkte 64

Felder und liegen nach Annahme alle auf der Grenze des Polygons. So

So gibt es zwar ziemlich viele solcher "Trajektorien" des Königs, aber alle

Polygone mit gleichen Flächen begrenzen.

Aufgaben aus den Kontroll- und Messmitteln des GIA und der Einheitlichen Staatsprüfung

Aufgabe B3

Finden Sie den Bereich der abgebildeten Figur auf kariertem Papier mit einer Zellengröße von 1 cm 1 cm (siehe Abb.). Geben Sie Ihre Antwort in Quadratzentimetern an.

4. Fazit

Während der Forschung habe ich Nachschlagewerke und populärwissenschaftliche Literatur studiert. Ich erfuhr, dass das Problem, die Fläche eines Polygons mit Eckpunkten an den Knoten des Gitters zu finden, den österreichischen Mathematiker Pick 1899 dazu inspirierte, die wunderbare Pick-Formel zu beweisen.

Als Ergebnis meiner Arbeit erweiterte ich mein Wissen über das Lösen von Problemen auf kariertem Papier, bestimmte die Einordnung der zu untersuchenden Probleme für mich und überzeugte mich von ihrer Vielfalt.

Ich habe gelernt, die Flächen von Polygonen zu berechnen, die auf einem karierten Blatt gezeichnet sind.Die betrachteten Aufgaben haben unterschiedliche Schwierigkeitsgrade - von einfach bis Olympiade. Jeder kann darunter Aufgaben mit einem machbaren Schwierigkeitsgrad finden, von denen aus es möglich ist, schwierigere zu lösen.

Ich kam zu dem Schluss, dass das Thema, das mich interessiert, sehr facettenreich ist, die Aufgaben auf kariertem Papier vielfältig sind, die Methoden und Techniken zu ihrer Lösung ebenfalls vielfältig sind. Daher hat sich unser Ich entschieden, in dieser Richtung weiterzuarbeiten.

5. Verwendete Literatur:

1. N. B. Vasil’ev, „Around the Pick formula“, Kvant. - 1974. - Nr. 12

2. Kokse Prasolov VV Aufgaben in der Planimetrie. - M.: MTsNMO, 2006.t e r G.S.M. Einführung in die Geometrie. -M.: Nauka, 1966

3. Roslova L.O., Sharygin I.F. Messungen. - M.: Hrsg. „Offene Welt“, 2005.

Internet-Ressourcen:

:

Feedback zur Arbeit

„Berechnung der Flächen von ebenen Figuren. Pick-Methode"

Die Berücksichtigung dieses Themas wird die kognitive Aktivität des Schülers erhöhen, der später im Geometrieunterricht die Harmonie der Zeichnung zu sehen beginnt und die Geometrie (und Mathematik im Allgemeinen) nicht mehr als langweilige Wissenschaft wahrnimmt.

Bewertet von Mathelehrer

Chodyreva Tatyana Georgievna

Es gibt eine wunderbare Formel, mit der Sie zählen können Polygonfläche auf dem Koordinatengitter nahezu fehlerfrei. Es ist nicht einmal eine Formel, es ist real Satz. Auf den ersten Blick mag es kompliziert erscheinen. Aber es reicht aus, um ein paar Aufgaben zu lösen - und Sie werden verstehen, wie cool diese Funktion ist. Mach weiter!

Beginnen wir mit einer neuen Definition:

Ein Koordinatenstapelknoten ist ein beliebiger Punkt, der am Schnittpunkt der vertikalen und horizontalen Linien dieses Gitters liegt.

Bezeichnung:

Im ersten Bild sind die Knoten überhaupt nicht markiert. Der zweite hat 4 Knoten. Im dritten Bild schließlich sind alle 16 Knoten markiert.

Was hat das mit Aufgabe B5 zu tun? Tatsache ist, dass die Eckpunkte des Polygons bei solchen Problemen auftreten stets liegen an den Knoten des Gitters. Als Konsequenz gilt für sie der folgende Satz:

Satz. Betrachten Sie ein Polygon auf einem Koordinatengitter, dessen Eckpunkte an den Knoten dieses Gitters liegen. Dann ist die Fläche des Polygons:

wobei n die Anzahl der Knoten innerhalb des gegebenen Polygons ist, k die Anzahl der Knoten ist, die auf seiner Grenze liegen (Randknoten).

Betrachten Sie als Beispiel ein gewöhnliches Dreieck auf einem Koordinatengitter und versuchen Sie, die inneren und Randknoten zu markieren.

Das erste Bild zeigt ein gewöhnliches Dreieck. Auf dem zweiten Bild sind seine inneren Knoten markiert, deren Anzahl n = 10 ist. Auf dem dritten Bild sind die am Rand liegenden Knoten markiert, es gibt insgesamt k = 6 davon.

Vielleicht verstehen viele Leser nicht, wie man die Zahlen n und k zählt. Beginnen Sie mit internen Knoten. Hier ist alles offensichtlich: Wir übermalen das Dreieck mit einem Bleistift und sehen, wie viele Knoten schattiert sind.

Bei Randknoten ist es etwas komplizierter. Polygon-Grenze - geschlossene unterbrochene Linie, die das Koordinatengitter an vielen Stellen schneidet. Am einfachsten ist es, einen "Startpunkt" zu markieren und dann den Rest zu umgehen.

Grenzknoten sind nur die Punkte auf der Polylinie, an denen sie sich gleichzeitig schneiden drei Zeilen:

1. Eigentlich eine unterbrochene Linie;
2. Horizontale Gitterlinie;
3. vertikale Linie.

Mal sehen, wie das alles bei echten Problemen funktioniert.

Eine Aufgabe. Finden Sie die Fläche eines Dreiecks, wenn die Zellengröße 1 x 1 cm beträgt:

Zuerst markieren wir die Knoten, die innerhalb des Dreiecks liegen, sowie an seinem Rand:

Es stellt sich heraus, dass es nur einen inneren Knoten gibt: n = 1. Es gibt sechs Randknoten: drei stimmen überein mit Dreiecksecken, und drei weitere liegen an den Seiten. Gesamt k = 6.

Nun berechnen wir die Fläche mit der Formel:

Das ist alles! Problem gelöst.

Eine Aufgabe. Finden Sie die Fläche eines auf kariertem Papier abgebildeten Vierecks mit einer Zellengröße von 1 cm x 1 cm und geben Sie Ihre Antwort in Quadratzentimetern an.

Wieder markieren wir die internen und Randknoten. Es gibt n = 2 interne Knoten Grenzknoten: k = 7, davon 4 Ecken des Vierecks, und 3 weitere liegen an den Seiten.

Es bleibt, die Zahlen n und k in der Flächenformel zu ersetzen:

Achten Sie auf das letzte Beispiel. Dieses Problem wurde tatsächlich bei der Diagnosearbeit im Jahr 2012 vorgeschlagen. Wenn Sie nach dem Standardschema arbeiten, müssen Sie viele zusätzliche Konstruktionen durchführen. Und durch die Knotenmethode wird alles fast mündlich gelöst.

Wichtiger Hinweis zu den Bereichen

Aber die Formel ist nicht alles. Lassen Sie uns die Formel ein wenig umschreiben und die Terme auf die rechte Seite bringen auf einen gemeinsamen Nenner. Wir bekommen:

Die Zahlen n und k sind die Anzahl der Knoten, sie sind immer ganze Zahlen. Der ganze Zähler ist also auch eine ganze Zahl. Wir teilen es durch 2, was eine wichtige Tatsache impliziert:

Die Fläche wird immer ausgedrückt ganze Zahl oder Bruch. Außerdem stehen am Ende des Bruchs immer „fünf Zehntel“: 10,5; 17,5 usw.

Daher wird die Fläche in Aufgabe B5 immer als ganze Zahl oder als Bruchteil der Form ***,5 ausgedrückt. Wenn die Antwort anders ist, bedeutet dies, dass irgendwo ein Fehler gemacht wurde. Denken Sie daran, wenn Sie die eigentliche Prüfung in Mathematik ablegen!

Um die Vorschau von Präsentationen zu verwenden, erstellen Sie ein Google-Konto (Konto) und melden Sie sich an: https://accounts.google.com

Beschriftungen der Folien:

Abgeschlossen von einem Schüler der Sekundarschule Nr. 7 8 "A" -Klasse Yunosheva Ksenia Instruktorin: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"

Ziele der Arbeit: Ermittlung der Existenz einer anderen, vom Schullehrplan abweichenden Formel zur Ermittlung der Fläche eines Gitterpolygons. Anwendungsbereiche der gewünschten Rezeptur.

Einführung. Die mathematische Bildung an allgemeinbildenden Schulen ist ein wesentlicher Bestandteil der Allgemeinbildung und der allgemeinen Kultur des modernen Menschen. Das Schulsystem ist zu diesem Zeitpunkt auf eine elfjährige Ausbildung ausgelegt. Alle Schülerinnen und Schüler müssen am Ende der elften Klasse das Einheitliche Staatsexamen ablegen, das den schulischen Wissensstand zeigt. Aber der Schullehrplan bietet nicht immer die rationalsten Wege, um Probleme zu lösen. Betrachtet man beispielsweise die Ergebnisse des USE im Jahr 2010, so zeigt sich, dass viele Studierende aufgrund der Aufgabe B6 Punkte verlieren. Ich machte mich auf den Weg, um herauszufinden, wie ich Zeit sparen und dieses Problem richtig lösen kann.

Aufgabe B6. Figuren werden auf kariertem Papier mit Zellen dargestellt, die 1 cm mal 1 cm messen (siehe Abbildung). Berechne ihre Fläche in Quadratzentimetern.

Um diese Aufgabe noch zu lösen, muss ich also die Formeln zur Flächenfindung anwenden, die wir in der 8. Klasse lernen. Aber es wird viel Zeit in Anspruch nehmen, und ich muss die Frage so schnell wie möglich beantworten, weil die Prüfungszeit ist streng begrenzt. Daher habe ich nach Recherchen herausgefunden, dass es den Satz von Pick gibt, der im Lehrplan der Schule nicht behandelt wird, mir aber dabei helfen wird, die Aufgabe schneller zu bewältigen.

Geschichtlicher Bezug. Georg Alexander Pick (10. August 1859 – 26. Juli 1942) war ein österreichischer Mathematiker. Er starb im Konzentrationslager Theresienstadt. Es ist heute bekannt wegen Picks Formel zur Bestimmung der Fläche eines Gitters aus Polygonen. Er veröffentlichte seine Formel 1899 in einer Abhandlung, sie wurde populär, als Hugo Steinhaus sie 1969 in eine Ausgabe von Mathematical Pictures aufnahm. Pick studierte an der Universität Wien und promovierte 1880. Nach seiner Promotion wurde er Assistent von Ernest Mach an der Scherl-Ferdinand-Universität in Prag. 1881 wurde er dort Lehrer. 1884 von der Universität beurlaubt, begann er bei Felix Klein an der Universität Leipzig zu arbeiten. Er blieb in Prag bis zu seiner Pensionierung 1927, als er nach Wien zurückkehrte. Pick leitete das Komitee an der (damaligen) Deutschen Universität Prag, das Albert Einstein 1911 zum Professor für mathematische Physik ernannte. Pick wurde zum Mitglied der Tschechischen Akademie der Wissenschaften und Künste gewählt, aber nach der Übernahme Prags durch die Nazis ausgeschlossen. Nach seiner Pensionierung 1927 kehrte Pick in seine Geburtsstadt Wien zurück. Nach dem Anschluss, als die Nazis am 12. März 1938 in Österreich einmarschierten, kehrte Pieck nach Prag zurück. Im März 1939 überfielen die Nazis die Tschechoslowakei. Georg wurde am 13. Juli 1942 in das Konzentrationslager Theresienstadt gebracht. Er starb zwei Wochen später.

Satz von Pick. Der Satz von Pick ist ein klassisches Ergebnis der kombinatorischen Geometrie und der Geometrie der Zahlen. Die Fläche eines Polygons mit ganzzahligen Eckpunkten ist gleich der Summe B + D/2 - 1, wobei B die Anzahl der ganzzahligen Punkte innerhalb des Polygons und D die Anzahl der ganzzahligen Punkte an der Grenze des Polygons ist.

Ein schmeichelhafter Beweis des Satzes von Pick. Jedes solche Polygon kann leicht in Dreiecke mit Scheitelpunkten an den Knoten des Gitters unterteilt werden, die weder innen noch an den Seiten Knoten enthalten. Es kann gezeigt werden, dass die Flächen aller dieser Dreiecke gleich und gleich 1/2 sind, und daher ist die Fläche des Polygons gleich der Hälfte ihrer Zahl T. Um diese Zahl zu finden, bezeichnen wir sie mit n die Anzahl der Seiten des Polygons, durch i - die Anzahl der Knoten darin und durch b - die Anzahl der Knoten an den Seiten, einschließlich der Eckpunkte. Die Gesamtsumme der Winkel aller Dreiecke ist πТ. Lassen Sie uns diese Summe nun auf eine andere Weise finden. Die Summe der Winkel mit einem Scheitelpunkt an einem beliebigen inneren Knoten ist 2 π , d. h. die Gesamtsumme solcher Winkel ist 2 π i ; die Gesamtsumme der Winkel an den Knoten auf den Seiten, aber nicht an den Ecken, ist (b - n) π, und die Summe der Winkel an den Ecken des Polygons ist (n - 2) π. Somit ist π T \u003d 2i π + (b - n) π + (n - 2) π, woraus wir einen Ausdruck für die Fläche S eines Polygons erhalten, der als Pick-Formel bekannt ist. In der Abbildung ist beispielsweise b = 9, i = 24, und daher beträgt die Fläche des Polygons 27,5.

Anwendung. Also zurück zu Aufgabe B6. Jetzt, da wir die neue Formel kennen, können wir die Fläche dieses Vierecks leicht finden. Da B 5 ist; D - 14, dann 5 + 14: 2-1 \u003d 11 (cm²) Die Fläche dieses Vierecks beträgt 11 cm².

Mit der gleichen Formel können wir die Fläche eines Dreiecks finden. Da B-14, G-10, dann 14+10:2-1=18 (Quadratzentimeter) Die Fläche dieses Dreiecks beträgt 18 Quadratzentimeter.

Wenn B-9, D-12, dann: 9+12:2-1=14 (cm²) Die Fläche dieses Vierecks beträgt 14 cm².

Geltungsbereich der Formel. Abgesehen davon, dass die Formel in verschiedenen Arten von Prüfungen, Aufgaben usw. verwendet wird, begleitet sie die ganze Welt um uns herum.

Nach Peaks Formel S = B + ½ G-1 1) Körper B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) Schwanz B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

Nach der Peak-Formel S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10,5-1 \u003d 45,5

Fazit. Als Ergebnis kam ich zu dem Schluss, dass es viele verschiedene Möglichkeiten gibt, Bereichsprobleme zu lösen, die nicht im Schullehrplan behandelt werden, und zeigte sie am Beispiel der Pick-Formel auf.

Verzeichnis. Ein Polygon ohne Selbstüberschneidungen wird als Gitterpolygon bezeichnet, wenn alle seine Eckpunkte an Punkten mit ganzzahligen Koordinaten (im kartesischen Koordinatensystem) liegen. Ein Punkt in der Koordinatenebene heißt ganzzahlig, wenn beide Koordinaten ganzzahlig sind.