In this lesson, we will talk about exponential and logarithmic functions. They are usually studied together, as they are mutually inverse. We will talk about the use of these functions, about why these functions are selected for study.

The exponential function is used to describe all the phenomena that we call avalanche processes. To put it more clearly, these are processes where the change in magnitude is proportional to the amount of magnitude already present (the more, the more it changes; the less, the less it changes).

An example of such a process is the reproduction of bacteria. Let's consider such a task. There is one bacterium in the glass. Every second it divides into two bacteria, new bacteria also divide into two every second, and so on. Within a minute, the entire glass was filled with bacteria. How many bacteria were in the glass a second before?

I would like to say that a little less than a whole glass was filled, somewhere, but the correct answer is: half a glass. If half a glass is filled, then in a second each bacterium will divide into parts, and they will fill the entire glass. As you can see, the first half of the glass was filled in seconds, and the second half was filled in only a second.

Melting glaciers

Surely everyone has heard about the problem of melting ice on the planet. Why do such processes of glaciation and, conversely, warming occur? They were before, although now they say that human activity has a key influence on their speed. There are various hypotheses, but this is not so important.

More importantly, reducing the amount of ice increases the amount of absorbed solar energy. That is, the less ice becomes, the faster it will melt. The process is exponential, or, in other words, self-invoking, self-feeding.

Such a process is described exponential function (or exponential): (Fig. 1). - base, , , and - exponent, changing value.

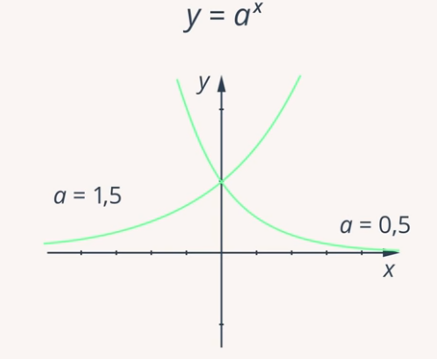
Rice. 1. Graph of a function

Another example of an exponential function that is familiar to many is compound interest. If we put money in the bank at a fixed percentage, while we do not withdraw money, and interest is charged on the entire amount available, then the amount that we will receive through periods: , where is the initial deposit, is the interest rate, is the number of periods (years, months, etc.) passed. At first, the amount will grow slowly, but then the growth will accelerate.

Another good example. If we raise to a power, then we get approximately, but in a power, it is practically. If we present this example in the form of interest, then in the first case it is charged per day, then the amount will increase by a factor of a year. And in the second case, one percent per day is withdrawn, then in a year there will be almost nothing left.

At the same time, one of the characteristic features of the exponential function is that under such a scheme, the sum cannot decrease. A similar example from nuclear physics is the half-life. Radioactive elements have a half-life, for example, over the years the mass of a substance will decrease by half (Fig. 2).

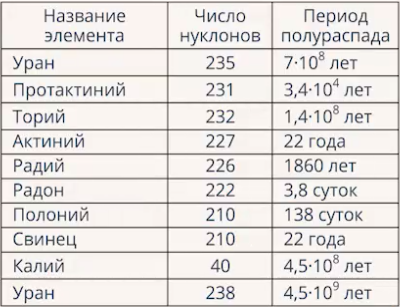
Rice. 2. Table of half-lives of some elements

That is, if we had a kilogram of substance, then in the first years a gram of substance (quite a lot) will go away, and in the next years - already a gram, etc. And then there will be a period where about a gram of a substance will go over the years. This is an example of a decreasing exponent.

If we consider the set of all functions and select among them those that have the following property: , then it will be satisfied for exponential functions: .