Newton Leibniz is a German philosopher who was born on July 1, 1646. In addition to philosophy, he was fascinated by the exact sciences. He distinguished himself in logic, mathematics, mechanics, physics, history, diplomacy, and mechanics. Newton is also considered to be an inventor, as well as a linguist. He was the founder and the first to be able to head the Academy of Sciences in Berlin. Leibniz took an honorary place in the French Academy of Sciences as a foreign member.
The most important scientific achievements of Leibniz are considered:
Creation of mathematical analysis. The calculus is differential and integral, which he based on infinitesimals.
With its help, the foundation of mathematical logic was laid.
The science of combinatorics.
Binary number system with numbers 0 and 1. Now all modern technology is based on them.
For psychology, there was a very important contribution, like the concept of unconscious small perceptions. In addition, the doctrine of the unconscious mental life appeared.
He revealed the law of conservation of energy and introduced the concept of manpower.
Newton is considered the finalist of the philosophy of the 17th century. He became the ancestor of a new system and gave it a name - monadology. In addition to achievements in philosophy, he was able to identify the doctrine of synthesis and analysis. Leibniz formulated it as the law of sufficient reason. As he noted, all this did not start only from thinking and logic, but also from being and ontology. The philosopher can be credited with the authorship of the modern formulation of the law of identity. It was he who brought to the world the understanding of the term "model".
In his writings, Leibniz wrote about the diversity of machine simulation possibilities in the human brain. As it turned out, it has a large number of functions. It was this scientist who first exposed the world to the idea that some types of energy can be transferred to others. These studies have made a great contribution to physics. Of course, the most important and famous work of his life was the formula. They called it the Newton-Leibniz formula.
Newton Leibniz formula
Let some continuous function f be given on some segment of the Ox axis. We assume that this function does not change its sign on the entire interval.
If f is a continuous and non-negative function on a certain segment, and F is some of its antiderivatives on this segment, then the area of the curvilinear trapezoid S is equal to the increment of the antiderivative on this segment.
This theorem can be written in the following formula:
S = F(b) – F(a)
The integral of the function f(x) from a to b will be equal to S. Here and below, to denote the definite integral of some function f(x), with integration limits from a to b, we will use the following notation (a;b)∫f( x). Below is an example of how it would look.
So we can equate these two results. We get: (a;b)∫f(x)dx = F(b) - F(a), provided that F is an antiderivative for the function f on . This formula is called the Newton-Leibniz formula. It will be true for any continuous function f on the interval.
The Newton-Leibniz formula is used to calculate integrals. Let's look at a few examples:
Example 1: calculate the integral. We find the antiderivative for the integrand x2. One of the antiderivatives will be the function (x3)/3.
Now we use the Newton-Leibniz formula:
(-1;2)∫x2dx = (23)/3 – ((-1)3)/3 = 3
Answer: (-1;2)∫x2dx = 3.
Example 2: calculate the integral (0;pi)∫sin(x)dx.
Find the antiderivative for the integrand sin(x). One of the antiderivatives will be the –cos(x) function. Let's use the Newton-Leibniz formula:
(0;pi)∫cos(x)dx = -cos(pi) + cos(0) = 2.
Answer: (0;pi)∫sin(x)dx=2
Sometimes, for simplicity and convenience of notation, the increment of the function F on the segment (F(b)-F(a)) is written as follows:
Using this notation for increment, the Newton-Leibniz formula can be rewritten as follows:
As noted above, this is just an abbreviation for ease of recording, nothing else is affected by this recording. This notation and the formula (a;b)∫f(x)dx = F(b) - F(a) will be equivalent.
This formula is still used by a large number of scientists and calculators. With its help, Leibniz brought development to many sciences.
Let some continuous function f be given on some segment of the Ox axis. We assume that this function does not change its sign on the entire interval.
If f is a continuous and non-negative function on a certain segment, and F is some of its antiderivatives on this segment, then the area of the curvilinear trapezoid S is equal to the increment of the antiderivative on this segment.
This theorem can be written in the following formula:
S = F(b) - F(a)
The integral of the function f(x) from a to b will be equal to S. Here and below, to denote the definite integral of some function f(x), with integration limits from a to b, we will use the following notation (a;b)∫f( x). Below is an example of how it would look.
Newton-Leibniz formula
So we can equate these two results. We get: (a;b)∫f(x)dx = F(b) - F(a), provided that F is an antiderivative for the function f on . This formula is called Newton-Leibniz formulas. It will be true for any continuous function f on the interval.
The Newton-Leibniz formula is used to calculate integrals. Let's look at a few examples:
Example 1: calculate the integral. Find the antiderivative for the integrand x 2 . One of the antiderivatives will be the function (x 3)/3.
Now we use the Newton-Leibniz formula:
(-1;2)∫x 2 dx = (2 3)/3 - ((-1) 3)/3 = 3
Answer: (-1;2)∫x 2 dx = 3.
Example 2: calculate the integral (0;pi)∫sin(x)dx.
Find the antiderivative for the integrand sin(x). One of the antiderivatives will be the -cos(x) function. Let's use the Newton-Leibniz formula:
(0;pi)∫cos(x)dx = -cos(pi) + cos(0) = 2.
Answer: (0;pi)∫sin(x)dx=2
Sometimes, for simplicity and convenience of notation, the increment of the function F on the segment (F(b)-F(a)) is written as follows:
![]()
Using this notation for increment, the Newton-Leibniz formula can be rewritten as follows:
![]()
As noted above, this is just an abbreviation for ease of recording, nothing else is affected by this recording. This notation and the formula (a;b)∫f(x)dx = F(b) - F(a) will be equivalent.
definite integral from a continuous function f(x) on the finite interval [ a, b] (where ) is the increment of some of its antiderivatives on this segment. (In general, understanding will be noticeably easier if you repeat the topic of the indefinite integral) In this case, the notation
As can be seen in the graphs below (the increment of the antiderivative function is indicated by ), The definite integral can be either positive or negative.(It is calculated as the difference between the value of the antiderivative in the upper limit and its value in the lower limit, i.e. as F(b) - F(a)).

Numbers a and b are called the lower and upper limits of integration, respectively, and the interval [ a, b] is the segment of integration.
Thus, if F(x) is some antiderivative function for f(x), then, according to the definition,
![]() (38)
(38)
Equality (38) is called Newton-Leibniz formula . Difference F(b) – F(a) is briefly written like this:
Therefore, the Newton-Leibniz formula will be written as follows:
![]() (39)
(39)
Let us prove that the definite integral does not depend on which antiderivative of the integrand is taken when calculating it. Let F(x) and F( X) are arbitrary antiderivatives of the integrand. Since these are antiderivatives of the same function, they differ by a constant term: Ф( X) = F(x) + C. That's why

Thus, it is established that on the segment [ a, b] increments of all antiderivatives of the function f(x) match.
Thus, to calculate the definite integral, it is necessary to find any antiderivative of the integrand, i.e. First you need to find the indefinite integral. Constant FROM excluded from subsequent calculations. Then the Newton-Leibniz formula is applied: the value of the upper limit is substituted into the antiderivative function b , further - the value of the lower limit a and calculate the difference F(b) - F(a) . The resulting number will be a definite integral..
At a = b accepted by definition
Example 1
Solution. Let's find the indefinite integral first:
Applying the Newton-Leibniz formula to the antiderivative
(at FROM= 0), we get
![]()
However, when calculating a definite integral, it is better not to find the antiderivative separately, but immediately write the integral in the form (39).
Example 2 Calculate a definite integral
Solution. Using the formula
![]()
![]()
Properties of the Definite Integral
Theorem 2.The value of the definite integral does not depend on the designation of the integration variable, i.e.
![]() (40)
(40)
Let F(x) is antiderivative for f(x). For f(t) the antiderivative is the same function F(t), in which the independent variable is denoted differently. Consequently,
![]()
Based on formula (39), the last equality means the equality of the integrals
Theorem 3.The constant factor can be taken out of the sign of a definite integral, i.e.
![]() (41)
(41)
Theorem 4.The definite integral of the algebraic sum of a finite number of functions is equal to the algebraic sum of the definite integrals of these functions, i.e.
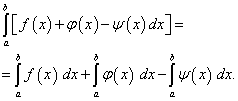 (42)
(42)
Theorem 5.If the integration segment is divided into parts, then the definite integral over the entire segment is equal to the sum of the definite integrals over its parts, i.e. if
![]() (43)
(43)
Theorem 6.When rearranging the limits of integration, the absolute value of the definite integral does not change, but only its sign changes, i.e.
![]() (44)
(44)
Theorem 7(mean value theorem). The definite integral is equal to the product of the length of the integration segment and the value of the integrand at some point inside it, i.e.
![]() (45)
(45)
Theorem 8.If the upper integration limit is greater than the lower one and the integrand is non-negative (positive), then the definite integral is also non-negative (positive), i.e. if

Theorem 9.If the upper limit of integration is greater than the lower limit and the functions and are continuous, then the inequality
can be integrated term by term, i.e.
![]() (46)
(46)
The properties of the definite integral allow us to simplify the direct calculation of integrals.
Example 5 Calculate a definite integral
![]()
Using Theorems 4 and 3, and when finding antiderivatives - tabular integrals (7) and (6), we obtain

Definite integral with variable upper limit
Let f(x) is continuous on the segment [ a, b] function, and F(x) is its prototype. Consider the definite integral
![]() (47)
(47)
and through t the integration variable is denoted so as not to confuse it with the upper bound. When it changes X the definite integral (47) also changes, i.e., it is a function of the upper limit of integration X, which we denote by F(X), i.e.
![]() (48)
(48)
Let us prove that the function F(X) is antiderivative for f(x) = f(t). Indeed, differentiating F(X), we get
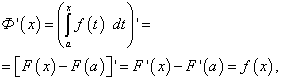
because F(x) is antiderivative for f(x), a F(a) is a constant value.
Function F(X) is one of the infinite set of antiderivatives for f(x), namely the one that x = a goes to zero. This statement is obtained if in equality (48) we put x = a and use Theorem 1 of the previous section.
Calculation of definite integrals by the method of integration by parts and the method of change of variable
![]()
where, by definition, F(x) is antiderivative for f(x). If in the integrand we make the change of variable
then, in accordance with formula (16), we can write
In this expression
antiderivative function for
Indeed, its derivative, according to the rule of differentiation of a complex function, is equal to

Let α and β be the values of the variable t, for which the function
takes respectively the values a and b, i.e.

But, according to the Newton-Leibniz formula, the difference F(b) – F(a) there is
The solution of applied problems is reduced to the calculation of the integral, but it is not always possible to do this accurately. Sometimes it is necessary to know the value of a definite integral with some degree of accuracy, for example, to a thousandth.
There are tasks when it would be necessary to find the approximate value of a certain integral with the required accuracy, then numerical integration is used such as the Simposn method, trapezoids, rectangles. Not all cases allow us to calculate it with a certain accuracy.
This article considers the application of the Newton-Leibniz formula. This is necessary for the exact calculation of the definite integral. Detailed examples will be given, the change of variable in the definite integral will be considered, and we will find the values of the definite integral when integrating by parts.
Yandex.RTB R-A-339285-1
Newton-Leibniz formula
Definition 1When the function y = y (x) is continuous from the segment [ a ; b ], and F (x) is one of the antiderivatives of the function of this segment, then Newton-Leibniz formula considered fair. Let's write it like this ∫ a b f (x) d x = F (b) - F (a) .
This formula is considered the basic formula of integral calculus.
To prove this formula, it is necessary to use the concept of an integral with the available variable upper limit.
When the function y = f (x) is continuous from the segment [ a ; b ] , then the value of the argument x ∈ a ; b , and the integral has the form ∫ a x f (t) d t and is considered a function of the upper limit. It is necessary to accept the notation of the function will take the form ∫ a x f (t) d t = Φ (x) , it is continuous, and the inequality of the form ∫ a x f (t) d t " = Φ " (x) = f (x) is valid for it.
We fix that the increment of the function Φ (x) corresponds to the increment of the argument ∆ x , it is necessary to use the fifth main property of a definite integral and obtain
Φ (x + ∆ x) - Φ x = ∫ a x + ∆ x f (t) d t - ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) x + ∆ x - x = f(c) ∆x
where value c ∈ x ; x + ∆x .
We fix the equality in the form Φ (x + ∆ x) - Φ (x) ∆ x = f (c) . By definition of the derivative of a function, it is necessary to pass to the limit as ∆ x → 0, then we get a formula of the form located on [ a ; b ] Otherwise, the expression can be written
F (x) = Φ (x) + C = ∫ a x f (t) d t + C , where the value of C is constant.
Let's calculate F (a) using the first property of the definite integral. Then we get that
F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C , hence C = F (a) . The result is applicable when calculating F (b) and we get:
F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a) , in other words, F (b) = ∫ a b f (t) d t + F ( a) . Equality proves the Newton-Leibniz formula ∫ a b f (x) d x + F (b) - F (a) .
The increment of the function is taken as F x a b = F (b) - F (a) . With the help of notation, the Newton-Leibniz formula becomes ∫ a b f (x) d x = F x a b = F (b) - F (a) .
To apply the formula, it is necessary to know one of the antiderivatives y = F (x) of the integrand y = f (x) from the segment [ a ; b ] , calculate the increment of the antiderivative from this segment. Consider a few examples of calculations using the Newton-Leibniz formula.
Example 1
Calculate the definite integral ∫ 1 3 x 2 d x using the Newton-Leibniz formula.
Solution
Consider that the integrand of the form y = x 2 is continuous from the interval [ 1 ; 3 ] , then and is integrable on this interval. According to the table of indefinite integrals, we see that the function y \u003d x 2 has a set of antiderivatives for all real values \u200b\u200bof x, which means that x ∈ 1; 3 will be written as F (x) = ∫ x 2 d x = x 3 3 + C . It is necessary to take the antiderivative with C \u003d 0, then we get that F (x) \u003d x 3 3.
Let's use the Newton-Leibniz formula and get that the calculation of the definite integral will take the form ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 - 1 3 3 = 26 3 .
Answer:∫ 1 3 x 2 d x = 26 3
Example 2
Calculate the definite integral ∫ - 1 2 x · e x 2 + 1 d x using the Newton-Leibniz formula.
Solution
The given function is continuous from the segment [ - 1 ; 2 ], which means that it is integrable on it. It is necessary to find the value of the indefinite integral ∫ x e x 2 + 1 d x using the method of summing under the differential sign, then we get ∫ x e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d (x 2 + 1) = 1 2 e x 2+1+C.
Hence we have a set of antiderivatives of the function y = x · e x 2 + 1 , which are valid for all x , x ∈ - 1 ; 2.
It is necessary to take the antiderivative at C = 0 and apply the Newton-Leibniz formula. Then we get an expression of the form
∫ - 1 2 x e x 2 + 1 d x = 1 2 e x 2 + 1 - 1 2 = = 1 2 e 2 2 + 1 - 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 - 1)
Answer:∫ - 1 2 x e x 2 + 1 d x = 1 2 e 2 (e 3 - 1)
Example 3
Calculate the integrals ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x and ∫ - 1 1 4 x 3 + 2 x 2 d x .
Solution
Segment - 4; - 1 2 says that the function under the integral sign is continuous, which means that it is integrable. From here we find the set of antiderivatives of the function y = 4 x 3 + 2 x 2 . We get that
∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x - 2 d x = 2 x 2 - 2 x + C
It is necessary to take the antiderivative F (x) \u003d 2 x 2 - 2 x, then, applying the Newton-Leibniz formula, we obtain the integral, which we calculate:
∫ - 4 - 1 2 4 x 3 + 2 x 2 d x = 2 x 2 - 2 x - 4 - 1 2 = 2 - 1 2 2 - 2 - 1 2 - 2 - 4 2 - 2 - 4 = 1 2 + 4 - 32 - 1 2 = - 28
We make the transition to the calculation of the second integral.
From the segment [ - 1 ; 1 ] we have that the integrand is considered unbounded, because lim x → 0 4 x 3 + 2 x 2 = + ∞ , then it follows from this that a necessary condition for integrability from the segment. Then F (x) = 2 x 2 - 2 x is not an antiderivative for y = 4 x 3 + 2 x 2 from the interval [ - 1 ; 1 ] , since the point O belongs to the segment, but is not included in the domain of definition. This means that there is a definite integral of Riemann and Newton-Leibniz for the function y = 4 x 3 + 2 x 2 from the interval [ - 1 ; one ] .
Answer: ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x \u003d - 28, there is a definite integral of Riemann and Newton-Leibniz for the function y = 4 x 3 + 2 x 2 from the interval [ - 1 ; one ] .
Before using the Newton-Leibniz formula, you need to know exactly about the existence of a definite integral.
Change of variable in a definite integral
When the function y = f (x) is defined and continuous from the segment [ a ; b ] , then the existing set [ a ; b ] is considered to be the range of the function x = g (z) defined on the interval α ; β with the existing continuous derivative, where g (α) = a and g β = b , hence we get that ∫ a b f (x) d x = ∫ α β f (g (z)) g " (z) d z .
This formula is used when it is necessary to calculate the integral ∫ a b f (x) d x , where the indefinite integral has the form ∫ f (x) d x , we calculate using the substitution method.
Example 4
Calculate a definite integral of the form ∫ 9 18 1 x 2 x - 9 d x .
Solution
The integrand is considered continuous on the integration interval, which means that the definite integral exists. Let's give the notation that 2 x - 9 = z ⇒ x = g (z) = z 2 + 9 2 . The value x \u003d 9 means that z \u003d 2 9 - 9 \u003d 9 \u003d 3, and for x \u003d 18 we get that z \u003d 2 18 - 9 \u003d 27 \u003d 3 3, then g α \u003d g (3) \u003d 9 , g β = g 3 3 = 18 . Substituting the obtained values into the formula ∫ a b f (x) d x = ∫ α β f (g (z)) g "(z) d z, we obtain that
∫ 9 18 1 x 2 x - 9 d x = ∫ 3 3 3 1 z 2 + 9 2 z z 2 + 9 2 "d z = = ∫ 3 3 3 1 z 2 + 9 2 z z d z = ∫ 3 3 3 2 z 2 + 9 d z
According to the table of indefinite integrals, we have that one of the antiderivatives of the function 2 z 2 + 9 takes the value 2 3 a r c t g z 3 . Then, applying the Newton-Leibniz formula, we obtain that
∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 - 2 3 a r c t g 3 3 = 2 3 a r c t g 3 - a r c t g 1 = 2 3 π 3 - π 4 = π 18
The finding could be done without using the formula ∫ a b f (x) d x = ∫ α β f (g (z)) g " (z) d z .
If the replacement method uses an integral of the form ∫ 1 x 2 x - 9 d x , then we can arrive at the result ∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C .
From here we will perform calculations using the Newton-Leibniz formula and calculate the definite integral. We get that
∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 18 - 9 3 - a r c t g 2 9 - 9 3 = = 2 3 a r c t g 3 - a r c t g 1 = 2 3 π 3 - π 4 \u003d π 18
The results matched.
Answer: ∫ 9 18 2 x 2 x - 9 d x = π 18
Integration by parts in the calculation of a definite integral
If on the segment [ a ; b ] the functions u (x) and v (x) are defined and continuous, then their first-order derivatives v " (x) u (x) are integrable, so from this interval for the integrable function u " (x) v ( x) the equality ∫ a b v " (x) u (x) d x = (u (x) v (x)) a b - ∫ a b u " (x) v (x) d x is true.
The formula can be used then, it is necessary to calculate the integral ∫ a b f (x) d x , and ∫ f (x) d x it was necessary to find it using integration by parts.
Example 5
Calculate the definite integral ∫ - π 2 3 π 2 x · sin x 3 + π 6 d x .
Solution
The function x sin x 3 + π 6 is integrable on the segment - π 2; 3 π 2 , so it is continuous.
Let u (x) \u003d x, then d (v (x)) \u003d v "(x) d x \u003d sin x 3 + π 6 d x, and d (u (x)) \u003d u "(x) d x \u003d d x, and v (x) = - 3 cos π 3 + π 6 . From the formula ∫ a b v "(x) u (x) d x = (u (x) v (x)) a b - ∫ a b u " (x) v (x) d x we get that
∫ - π 2 3 π 2 x sin x 3 + π 6 d x = - 3 x cos x 3 + π 6 - π 2 3 π 2 - ∫ - π 2 3 π 2 - 3 cos x 3 + π 6 d x \u003d \u003d - 3 3 π 2 cos π 2 + π 6 - - 3 - π 2 cos - π 6 + π 6 + 9 sin x 3 + π 6 - π 2 3 π 2 \u003d 9 π 4 - 3 π 2 + 9 sin π 2 + π 6 - sin - π 6 + π 6 = 9 π 4 - 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2
The solution of the example can be done in another way.
Find the set of antiderivatives of the function x sin x 3 + π 6 using integration by parts using the Newton-Leibniz formula:
∫ x sin x x 3 + π 6 d x = u = x, d v = sin x 3 + π 6 d x ⇒ d u = d x , v = - 3 cos x 3 + π 6 = = - 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = - 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ - π 2 3 π 2 x sin x 3 + π 6 d x = - 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 - - - 3 - π 2 cos - π 6 + π 6 + 9 sin - π 6 + π 6 = = 9 π 4 + 9 3 2 - 3 π 2 - 0 = 3 π 4 + 9 3 2
Answer: ∫ x sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
If you notice a mistake in the text, please highlight it and press Ctrl+Enter






























1 out of 30
Presentation on the topic: Newton-Leibniz formula
slide number 1

Description of the slide:
slide number 2

Description of the slide:
slide number 3

Description of the slide:
slide number 4

Description of the slide:
Newton and Leibniz From the surviving documents, historians of science have found out that Newton discovered the differential and integral calculus as early as 1665-1666, but did not publish it until 1704. Leibniz developed his version of analysis independently (since 1675), although the initial impetus to his thought probably came from rumors that Newton already had such a calculus, as well as thanks to scientific conversations in England and correspondence with Newton. Unlike Newton, Leibniz immediately published his version, and later, together with Jacob and Johann Bernoulli, widely promoted this landmark discovery throughout Europe. Most scientists on the Continent had no doubt that Leibniz had discovered analysis.
slide number 5

Description of the slide:
Heeding the persuasion of friends who appealed to his patriotism, Newton in the 2nd book of his "Principles" (1687) said: In letters that I exchanged about ten years ago with a very skilled mathematician, Mr. a method for determining maxima and minima, drawing tangents and solving similar questions, equally applicable to both rational and irrational terms, and I hid the method by rearranging the letters of the following sentence: “when an equation is given containing any number of current quantities, find fluxions and back". The most famous husband answered me that he also attacked such a method and communicated to me his method, which turned out to be scarcely different from mine, and then only in terms and formulas.
slide number 6

Description of the slide:
In 1693, when Newton finally published the first summary of his version of the analysis, he exchanged friendly letters with Leibniz. Newton said: Our Wallis has attached to his "Algebra", which has just appeared, some of the letters that I wrote to you in my time. At the same time, he demanded of me that I openly state the method that I at that time hid from you by rearranging the letters; I made it as short as I could. I hope that I did not write anything that was unpleasant for you, but if this happened, then please let me know, because my friends are dearer to me than mathematical discoveries.
slide number 7

Description of the slide:
After the appearance of the first detailed publication of Newtonian analysis (a mathematical supplement to "Optics", 1704), an anonymous review appeared in Leibniz's journal "Acta eruditorum" with offensive allusions to Newton. The review clearly indicated that the author of the new calculus was Leibniz. Leibniz himself vehemently denied that the review was written by him, but historians have been able to find a draft written in his handwriting. Newton ignored Leibniz's article, but his students responded indignantly, after which a pan-European priority war broke out, "the most shameful squabble in the entire history of mathematics."
slide number 8

Description of the slide:
On January 31, 1713, the Royal Society received a letter from Leibniz containing a conciliatory wording: he agrees that Newton came to analysis on his own, "on general principles like ours." An angry Newton demanded the creation of an international commission to clarify the priority. The commission did not take much time: a month and a half later, having studied Newton's correspondence with Oldenburg and other documents, it unanimously recognized Newton's priority, moreover, in a wording that was insulting to Leibniz this time. The decision of the commission was printed in the proceedings of the Society with all supporting documents attached.
slide number 9

Description of the slide:
In response, from the summer of 1713 Europe was flooded with anonymous pamphlets that defended Leibniz's priority and asserted that "Newton appropriates to himself the honor that belongs to another." The pamphlets also accused Newton of stealing the results of Hooke and Flamsteed. Newton's friends, for their part, accused Leibniz himself of plagiarism; according to them, during his stay in London (1676), Leibniz got acquainted with the unpublished works and letters of Newton at the Royal Society, after which Leibniz published the ideas expressed there and passed them off as his own. The war did not weaken until December 1716, when the abbot Conti informed Newton: "Leibniz is dead - the dispute is over
slide number 10

Description of the slide:
slide number 11

Description of the slide:
slide number 12

Description of the slide:
Set an arbitrary value x € (a.b) and define a new function. It is defined for all values x € (a.b) , because we know that if there is an integral of ʄ on (a,b) , then there is also an integral of ʄ on (a ,b) , where Recall that we assume by definition
slide number 13

Description of the slide:
slide number 14

Description of the slide:
Thus F is continuous on (a,b) whether or not ʄ has discontinuities; it is important that ʄ is integrable on (a,b) The figure shows the graph of ʄ . The area of the variable figure aABx is equal to F (X) Its increment F (X+h)-F(x) is equal to the area of the figure xBC(x+h) , which, due to the Boundedness of ʄ, obviously tends to zero as h → 0, regardless of whether whether x will be a point of continuity or discontinuity ʄ e.g. point x-d
slide number 15

Description of the slide:
slide number 16

Description of the slide:
slide number 17

Description of the slide:
Passing to the limit in as h→0 shows the existence of the derivative of F at the point and the validity of the equality. For x=a,b, we are talking about the right and left derivatives, respectively. If the function ʄ is continuous on (a,b) , then, based on the above, the corresponding function has a derivative equal to Therefore, the function F(x) is the antiderivative for ʄ (a,b)
slide number 18

Description of the slide:
We have proved that an arbitrary continuous function ʄ on the segment (a,b) has an antiderivative on this segment defined by equality. This proves the existence of an antiderivative for any function continuous on an interval. Now let there be an arbitrary antiderivative of the function ʄ(x) on (a,b) . We know that Where C is some constant. Assuming in this equality x=a and taking into account that F(a)=0 we get Ф(a)=C Thus, But
slide number 19

Description of the slide:
slide number 20

Description of the slide:
Integral The integral of a function is a natural analogue of the sum of a sequence. According to the fundamental theorem of analysis, integration is the operation inverse to differentiation. The process of finding an integral is called integration. There are several different definitions of the operation of integration, differing in technical details. However, they are all compatible, that is, any two integration methods, if they can be applied to a given function, will give the same result.
slide number 21

Description of the slide:
slide number 22

Description of the slide:
History The signs for the integral ʃ of the derivation dx were first used by Leibniz at the end of the 17th century. The symbol of the integral was formed from the letter S - an abbreviation of the word lat. summa (sum). The Integral in Antiquity Integration can be traced back to ancient Egypt, around 1800 BC. e., the Moscow Mathematical Papyrus demonstrates knowledge of the formula for the volume of a truncated pyramid. The first known method for calculating integrals is the method of exhaustion by Eudoxus (c. 370 BC), who tried to find areas and volumes by breaking them into an infinite number of parts for which the area or volume is already known. This method was picked up and developed by Archimedes, and was used to calculate the areas of parabolas and approximate the area of a circle. Similar methods were developed independently in China in the 3rd century AD by Liu Hui, who used them to find the area of a circle. This method was subsequently used by Ju Chongshi to find the volume of a sphere.
slide number 23

Description of the slide:
Historical significance and philosophical meaning of the Newton-Leibniz formula One of the most important research tools of this series is the Newton-Leibniz formula, and the method behind it for finding the antiderivative function by integrating its derivative. The historical significance of the formula is in the use of infinitesimal quantities and in the absolutely exact answer to the question posed. The advantages of using this method for solving mathematical, physical and other natural science problems, for example, the classical problem of squaring a circle - building a square of equal size to a given circle, are well known. The philosophical meaning - in the possibility of obtaining information about the whole from its infinitesimal part, noted earlier - is clearly realized in medicine and biology, an example of which can be the success of genetic engineering in cloning - the creation of mutually similar living beings. History remains a rare exception in the list of sciences that have used the Newton-Leibniz formula. The impossibility of presenting information from historical sources in the form of numbers - formula arguments - is traditional. Thus, until now, the philosophical meaning of the formula is not entirely philosophical, since it is realized only in natural science knowledge, leaving social and humanitarian knowledge without such a powerful tool. Although, if one adheres to the traditional features of social and humanitarian knowledge, its weaknesses, so to speak, then it is on its case.
slide number 24

Description of the slide:
But further scientific analysis in our time gives a new, different picture of the ongoing process. The atomistic views that are now dominant in science decompose matter into a bunch of tiny particles or regularly located centers of forces that are in eternal various movements. In the same way, the ether penetrating matter is constantly excited and oscillates in waves. All these motions of matter and ether are in the closest and continuous connection with the world space, which is infinite for us. Such a representation, inaccessible to our concrete imagination, follows from the data of physics.
slide number 25

Description of the slide:
Even mystical and magical currents must reckon with this position, although they can, by giving a different meaning to the concept of time, completely destroy the significance of this fact in the general world outlook. Thus, as long as the question concerns phenomena perceived by the senses, even these areas of philosophy and religion, which are the most remote from exact knowledge, must reckon with the scientifically proven fact, as they should reckon with the fact that twice two is four in the area that is subject to the senses. and mind.
slide number 26

Description of the slide:
At the same time, the amount of knowledge accumulated by mankind is already quite enough to break this tradition. Indeed, there is no need in a Pythagorean way to look for a digital correspondence to the statements “Peter I visited Venice during the Great Embassy” and “Peter I was not in Venice during the Great Embassy”, when these expressions themselves can easily serve as arguments of George Boole’s algebra of logic. The result of every historical research is essentially a set of such arguments. Thus, in my opinion, it is justified to use a set of historical studies as an integrand function, presented in the form of arguments of the algebra of logic, with the aim of obtaining the most probable reconstruction of the historical event under study as an antiderivative. There are many challenges along the way. In particular: the representation of a specific historical study - a derivative of a reconstructed event - in the form of a set of logical expressions - the operation is obviously more complicated than, for example, the electronic cataloging of a simple library archive. However, the information breakthrough of the late 20th - early 21st century (an extremely high degree of integration of the element base and an increase in the power of information) makes the fulfillment of such a task quite real.
slide number 27

Description of the slide:
In the light of the foregoing, at the present stage, historical analysis is a mathematical analysis with the theory of probability and the algebra of logic, and the desired antiderivative function is the probability of a historical event, which in general is quite consistent and even complements the idea of science at the present stage, because the replacement of the concept of essence by the concept of function - the main thing in the understanding of science in modern times - is complemented by an assessment of this function. Consequently, the modern historical significance of the formula is in the possibility of realizing Leibniz's dream "about the time when, instead of endless disputes, two philosophers, like two mathematicians, will take pens in their hands and, sitting down at the table, replace the dispute with calculation" . Each historical research-conclusion has the right to exist, reflects a real event and complements the informational historical picture. The danger of the degeneration of historical science into a set of colorless phrases-statements - the result of the application of the proposed method, is no more than the danger of music degenerating into a set of sounds, and painting into a set of colors at the present stage of human development. This is how I see the new philosophical meaning of the Newton-Leibniz formula, given for the first time at the end of the 17th - beginning of the 18th centuries.
slide number 28

Description of the slide:
In fact, the formula, in view of the peculiarity of the perception of mathematical symbols by carriers of social and humanitarian knowledge, expressed in a panic fear by these carriers of any representation of such signs, will be given in verbal form: a definite integral of the derivative of a function is the antiderivative of this function. Some formal difference between the given example of the problem of squaring a circle from the usual educational and mathematical example of calculating the area located under an arbitrary curve in the Cartesian coordinate system does not, of course, change the essence.
slide number 29

Description of the slide:
USED LITERATURE: 1. Brodsky I.A. Works in four volumes. T.3. SPb., 1994. 2. Vernadsky V.I. Biosphere and noosphere. M., 2003. 3. Wundt, Wilhelm. Introduction to philosophy. M., 2001. 4. Gaidenko P.P. The evolution of the concept of science. M., 1980. 5. Descartes, Rene. Reflections on Primitive Philosophy. SPb., 1995. 6. Karpov G.M. The Great Embassy of Peter I. Kaliningrad, 1998. 7. Kunzman P., Burkard F.-P., Vidman F. Philosophy: dtv-Atlas. M., 2002. 8. Malakhovskiy V.S. Selected chapters of the history of mathematics. Kaliningrad, 2002. 9. Natanson I.P. A short course in higher mathematics. SPb., 2001. 10. Engels F. Anti-Dühring. M., 1988. 11. Sheremetevsky V.P. Essays on the history of mathematics. M., 2004 Internet resources http://ru.wikipedia.org
slide number 30

Description of the slide:
