Solved problems from the textbook PHYSICS. Methodical instructions and control tasks. Edited by A. G. Chertov
Below are the conditions of the problems and scanned sheets with solutions. The page may take some time to load.
109. Along the edge of a uniformly rotating with an angular velocity ω \u003d 1 rad / s platform is coming person and bypasses the platform in time t = 9.9 s. What is the greatest acceleration a of human motion relative to the Earth? Take platform radius R = 2m.
119. How much will a boat with a length L = 3.5 m and a mass M = 200 kg move relative to the shore if a person standing at the stern with a mass m = 80 kg moves to the bow of the boat? (Consider the boat perpendicular to the shore.
129. A gun that did not have a recoil device was fired in a horizontal direction. When the gun was fixed, the projectile was fired at a speed of V1 = 600 m/s, and when the gun was allowed to roll back freely, the projectile was fired at a speed of V2 = 580 m/s. With what speed did the gun roll back?
139. A chain with a length of L = 2 m lies on the table, hanging from the table at one end. If the length of the hanging part exceeds 1/3L, the chain will slide off the table. Determine the speed V of the chain at the moment it leaves the table.
149. A block is attached to the edge of the table. A weightless and inextensible thread is thrown through the block, to the ends of which weights are attached. One load moves along the surface of the table, and the other moves down along the vertical. Determine the coefficient μ of friction between the surfaces of the load and the table, if the masses of each load and the mass of the block are the same and the loads move with an acceleration a = 0.56m/s2. Ignore the slippage of the thread along the block and the friction force acting on the block.
159. A horizontal platform with a mass of M=150 kg revolves around vertical axis passing through the center of the platform, with a frequency of ν2=8 min-1. A person weighing m = 70 kg stands at the same time on the edge of the platform. With what angular velocity ω1 will the platform begin to rotate if the person moves from the edge of the platform to its center? Consider the platform as a round, homogeneous disk, and the person as a material point.
169. What is the mass of the Earth if it is known that the Moon makes 13 revolutions around the Earth during the year and the distance from the Earth to the Moon is 3.84 × 108 m?
179. On a smooth horizontal table lies a ball of mass m2 = 200 g, attached to a horizontally located light spring with a stiffness of k = 500 N/m. A bullet of mass m1=10 g, flying at a speed of V=300 m/s, hits the ball and gets stuck in it. Neglecting the movement of the ball during the impact and air resistance, determine the amplitude A and the period T of the ball's oscillations.






Page 3 of 3
160. Man of mass m = 60 kg standing edge horizontal platform mass M = 120 kg, rotating by inertia around a fixed vertical axis with a frequency n 1 = 10 mni -1 , goes to its center. Considering the platform as a round homogeneous disk, and the person as a point mass, determine with what frequency n 2 will be then rotate the platform.
161. The platform, which has the form of a solid homogeneous disk, can rotate by inertia around a fixed vertical axis. On the edge of the platform stands a man whose mass is 3 times less mass platforms. Determine how and how many times the angular velocity of the platform will change if the person moves closer to the center at a distance equal to half the radius of the platform.

162. A person with a mass m = 60 kg, standing on the edge of a horizontal platform with a radius R = 1 m, and a mass M = 120 kg, rotating by inertia around a fixed vertical axis with a frequency n 1 = 10 min ^ -1, goes to its center. Considering the platform as a round homogeneous disk, and the person as a point mass, determine the work done by the person when moving from the edge of the platform to its center.
![]()
164. A load weighing m = 110 kg is suspended from a carbon steel wire with a length l = 1.5 m and a diameter d = 2.1 mm. Bearing for steel Young's modulus E= 216 GPa and proportionality limit σ n = 330 MPa, determine: 1) what fraction of the initial length is the wire elongation under this load; 2) exceeds the applied voltage or not proportional limit.
![]()
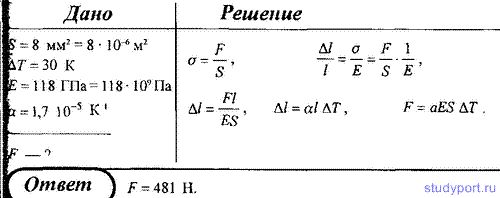
165. A copper wire with a cross section S \u003d 8 mm 2 under the action of a tensile force elongated by as much as it elongates when heated by 30 K. Taking the Young's modulus for copper E\u003d 118 GPa and linear expansion coefficient a \u003d 1.7 * 10 -5 K -1, determine numerical value this strength.
166. A rubber cord 40 cm long and an inner diameter of 8 mm is stretched so that it lengthens by 8 cm. Taking the Poisson's ratio for rubber equal to 0.5, determine the inner diameter of the stretched cord.

167. Determine the work that must be expended to compress the spring by 15 cm, if it is known that the force is proportional to the deformation and under the action of a force of 20 N the spring is compressed by 1 cm.
168. Determine the relative elongation of an aluminum rod if work A \u003d 6.9 J was spent during its stretching. The length of the rod l \u003d 1 m, area cross section S = 1 mm 2, Young's modulus for aluminum E= 69 GPa.
A person standing on the edge of a rotating horizontal platform moves from the edge to the center. With what speed will the platform begin to rotate if its mass is 100 kg, the mass of a person is 60 kg and it did 10 rpm. Consider the platform as a round homogeneous disk, and the person as a point mass.
A platform in the form of a disk with a radius of 1 m and a mass of 200 kg rotates by inertia around a vertical axis, making 1 rev / sec. A man of mass 50 kg is standing on the edge of the platform. How many revolutions per second will the platform make if the person moves half a meter closer to the center.
A copper ball with a radius of 10 cm rotates at a speed of 2 rpm around an axis passing through its center. What work must be done to double the angular velocity of the ball?
A hoop and a disk of the same mass roll without sliding at the same linear speed v. The kinetic energy of the hoop is 4 kgf*m. Find the kinetic energy of the disk.
A disk with a mass of 1 kg and a diameter of 60 cm rotates around an axis passing through the center perpendicular to its plane, making 2 rpm. What work must be done to stop the disk.
Find the kinetic energy of a cyclist traveling at a speed of 9 km/h. The mass of the cyclist together with the bicycle is 78 kg, and the wheels account for 3 kg. Consider bicycle wheels as hoops.
A boy rolls a hoop along a horizontal road at a speed of 7.2 km/h. How far can the hoop roll up the hill due to its kinetic energy? The slope of the slide is 10 m for every 100 m of the path.
The flywheel rotates constant speed, corresponding to the frequency n=10 rpm; its kinetic energy W to = 7.85 kJ. How long will the torque M = 50 N * m applied to this flywheel increase angular velocity flywheel twice?
A man stands on Zhukovsky's bench and catches a ball of mass m=0.4 kg, flying in a horizontal direction with a speed v=20 m/s. The trajectory of the ball passes at a distance r = 0.8 m from the vertical axis of rotation of the bench. With what angular velocity w will Zhukovsky's bench begin to rotate with the person who caught the ball, if the total moment of inertia J of the person and the bench is 6 kgm 2?
On the edge of a horizontal platform having the shape of a disk with a radius R=2 m stands a person weighing m 1 =80 kg. The mass of 2 platforms is 240 kg. The platform can rotate around a vertical axis passing through its center. Neglecting friction, find with what angular velocity w the platform will rotate if a person walks along its edge with a speed v = 2 m/s relative to the platform.
The disc-shaped platform can rotate around a vertical axis. On the edge of the platform stands a man with mass m 1 =60 kg. At what angle will the platform turn if a person walks along the edge of the platform and, having bypassed it, returns to starting point on the platform? The mass of 2 platforms is 240 kg. Calculate the moment of inertia J of a person as for a material point.
The platform in the form of a disk with a radius R=1 m rotates by inertia with a frequency of n 1 =6 min -1 . On the edge of the platform stands a man whose mass m is 80 kg. With what frequency n will the platform rotate if a person moves to its center? The moment of inertia J of the platform is 120 kgm 2 . Calculate the moment of inertia of a person as for a material point.
A man stands in the center of the Zhukovsky bench and holds in his hands a rod with a length of l = 2.4 m and a mass of m = 8 kg, located vertically along the axis of rotation of the bench. The bench with the person rotates with frequency n 1 =1c -1 . With what frequency n 2 will the bench with the person rotate if he turns the rod to a horizontal position? The total moment of inertia J of a person and a bench is 6 kgm 2.
A man stands on a Zhukovsky bench and holds in his hands a rod located vertically along the axis of rotation of the bench. The rod serves as the axis of rotation of the wheel located at the upper end of the rod. The bench is motionless, the wheel rotates with a frequency of n=10 s -1 . The radius R of the wheel is 20 cm, its mass is m = 3 kg. Determine the frequency of rotation n 2 benches if a person turns the rod through an angle of 180 0? The total moment of inertia J of a person and a bench is 6 kgm 2. The mass of the wheel can be considered uniformly distributed over the rim.
From a pulley with a diameter of d \u003d 0.48 m, power N \u003d 9 kW is transmitted through the belt. The pulley rotates with a frequency of n=240 min -1. The tension force T 1 of the driving branch of the belt is twice the tension force T 2 of the driven branch. Find the tension forces of both branches of the belt.
The flywheel in the form of a disk with mass m=80 kg and radius R= 30 cm is at rest. What work A 1 needs to be done to tell the flywheel the frequency n = 10 s -1 ? What work A 2 would have to be done if, with the same mass, the disk had a smaller thickness but twice the radius?
Kinetic energy T of a rotating flywheel is 1 kJ. Under the action of a constant braking torque, the flywheel began to rotate equally slowly, and, having made N \u003d 80 revolutions, it stopped. Determine the moment of braking force M.
A solid cylinder of mass m=4 kg rolls without slipping on a horizontal surface. The linear velocity v of the cylinder axis is 1 m/s. Determine the total kinetic energy T of the cylinder.
A hoop and a solid cylinder having the same mass m=2 kg roll without sliding at the same speed v=5 m/s. Find the kinetic energies T 1 and T 2 of these bodies.
A thin straight rod l = 1 m long is attached to horizontal axis passing through its end. The rod was deflected at an angle =60 0 from the equilibrium position and released. Determine the linear velocity v of the lower end of the rod at the moment of passing through the equilibrium position.
Determine the linear velocity v of the center of a ball rolling without sliding from inclined plane height h=1 m.
How much time t will the hoop roll down without slipping from an inclined plane with a length l = 1 m and a height h = 10 cm?
A bullet weighing m=10 g flies with a speed v=800 m/s, rotating about the longitudinal axis with a frequency n=3000 s -1 . Taking the bullet as a cylinder with a diameter of d = 8 mm, determine the total kinetic energy T of the bullet.
The flywheel, whose moment of inertia J is equal to 40 kgm 2, began to rotate uniformly accelerated from a state of rest under the action of a moment of force M = 20 Nm. The rotation continued for t=10 s. Determine the kinetic energy T acquired by the flywheel.
To determine the power of the motor, a tape was thrown on its pulley with a diameter of d \u003d 20 cm. A dynamometer is attached to one end of the tape, and a weight P is hung from the other. Find the motor power N, if the motor rotates with a frequency n=24 s -1, the mass m of the load is 1 kg and the dynamometer reading is F=24 N.
The armature of the motor rotates with a frequency of n=1500 min -1 . Determine the torque M if the motor develops power N = 500 W
