In this article I will talk about how to apply the ability to find to the study of a function: to find its largest or smallest value. And then we will solve several problems from Task B15 from the Open Task Bank for .

As usual, let's start with the theory first.

At the beginning of any study of a function, we find it

To find the largest or smallest value of the function, you need to investigate on which intervals the function increases and on which it decreases.

To do this, you need to find the derivative of the function and study its intervals of sign constancy, that is, the intervals on which the derivative retains its sign.

The intervals on which the derivative of a function is positive are intervals of increasing function.

The intervals on which the derivative of a function is negative are intervals of decreasing function.

one . Let's solve task B15 (No. 245184)

To solve it, we will follow the following algorithm:

a) Find the domain of the function

b) Find the derivative of the function .

c) Set it equal to zero.

d) Let us find the intervals of constant sign of the function.

e) Find the point at which the function takes the greatest value.

f) Find the value of the function at this point.

I tell the detailed solution of this task in the VIDEO LESSON:

Probably your browser is not supported. To use the "Unified State Examination Hour" simulator, try downloading
Firefox

2. Let's solve task B15 (No. 282862)

Find the largest value of a function on the segment

It is obvious that the function takes the greatest value on the segment at the maximum point, at x=2. Find the value of the function at this point:

Answer: 5

3 . Let's solve task B15 (No. 245180):

Find the largest value of a function

1.title="(!LANG:ln5>0">, , т.к. title="5>1">, поэтому это число не влияет на знак неравенства.!}

2. Since the scope of the original function title="(!LANG:4-2x-x^2>0">, следовательно знаменатель дроби всегда больще нуля и дробь меняет знак только в нуле числителя.!}

3. The numerator is zero at . Let's check if the ODZ belongs to the function. To do this, check if the condition title="(!LANG:4-2x-x^2>0"> при .!}

Title="4-2(-1)-((-1))^2>0">,

so the point belongs to the ODZ of the function

We examine the sign of the derivative to the right and left of the point:

We see that the function takes the greatest value at the point . Now let's find the value of the function at :

Note 1. Note that in this problem we did not find the domain of the function: we only fixed the constraints and checked whether the point at which the derivative is equal to zero belongs to the domain of the function. In this problem, this turned out to be enough. However, this is not always the case. It depends on the task.

Remark 2. When studying the behavior of a complex function, one can use the following rule:

• if the outer function of a compound function is increasing, then the function takes on its greatest value at the same point at which the inner function takes on its greatest value. This follows from the definition of an increasing function: the function increases on the interval I if the larger value of the argument from this interval corresponds to the larger value of the function.
• if the outer function of a complex function is decreasing, then the function takes on the largest value at the same point at which the inner function takes on the smallest value . This follows from the definition of a decreasing function: the function decreases on the interval I if the larger value of the argument from this interval corresponds to the smaller value of the function

In our example, the outer function - increases over the entire domain of definition. Under the sign of the logarithm is an expression - a square trinomial, which, with a negative senior coefficient, takes the largest value at the point . Next, we substitute this value of x into the equation of the function and find its largest value.

Let the function y=f(X) continuous on the segment [ a, b]. As is known, such a function reaches its maximum and minimum values ​​on this segment. The function can take these values ​​either at an interior point of the segment [ a, b], or on the boundary of the segment.

To find the largest and smallest values ​​of a function on the segment [ a, b] necessary:

1) find the critical points of the function in the interval ( a, b);

2) calculate the values ​​of the function at the found critical points;

3) calculate the values ​​of the function at the ends of the segment, that is, for x=a and x = b;

4) from all the calculated values ​​of the function, choose the largest and smallest.

Example. Find the largest and smallest values ​​of a function

on the segment.

Finding critical points:

These points lie inside the segment ; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;

at the point x= 3 and at the point x= 0.

Investigation of a function for convexity and an inflection point.

Function y = f (x) called convexup in between (a, b) , if its graph lies under a tangent drawn at any point of this interval, and is called convex down (concave) if its graph lies above the tangent.

The point at the transition through which the convexity is replaced by concavity or vice versa is called inflection point.

Algorithm for studying for convexity and inflection point:

1. Find the critical points of the second kind, that is, the points at which the second derivative is equal to zero or does not exist.

2. Put critical points on the number line, breaking it into intervals. Find the sign of the second derivative on each interval; if , then the function is convex upwards, if, then the function is convex downwards.

3. If, when passing through a critical point of the second kind, it changes sign and at this point the second derivative is equal to zero, then this point is the abscissa of the inflection point. Find its ordinate.

Asymptotes of the graph of a function. Investigation of a function into asymptotes.

Definition. The asymptote of the graph of a function is called straight, which has the property that the distance from any point of the graph to this line tends to zero with an unlimited removal of the graph point from the origin.

There are three types of asymptotes: vertical, horizontal and inclined.

Definition. Direct called vertical asymptote function graph y = f(x), if at least one of the one-sided limits of the function at this point is equal to infinity, that is

where is the discontinuity point of the function, that is, it does not belong to the domain of definition.

Example.

D( y) = (‒ ∞; 2) (2; + ∞)

x= 2 - breaking point.

Definition. Straight y=A called horizontal asymptote function graph y = f(x) at , if

Example.

x
y

Definition. Straight y=kx +b (k≠ 0) is called oblique asymptote function graph y = f(x) at , where

General scheme for the study of functions and plotting.

Function research algorithmy = f(x) :

1. Find the domain of the function D (y).

2. Find (if possible) the points of intersection of the graph with the coordinate axes (with x= 0 and at y = 0).

3. Investigate for even and odd functions ( y (‒ x) = y (x) ‒ parity; y(‒ x) = ‒ y (x) ‒ odd).

4. Find the asymptotes of the graph of the function.

5. Find intervals of monotonicity of the function.

6. Find the extrema of the function.

7. Find the intervals of convexity (concavity) and inflection points of the graph of the function.

8. On the basis of the conducted research, construct a graph of the function.

Example. Investigate the function and plot its graph.

1) D (y) =

x= 4 - breaking point.

2) When x = 0,

(0; – 5) – point of intersection with oy.

At y = 0,

3) y(‒ x)= general function (neither even nor odd).

4) We investigate for asymptotes.

a) vertical

b) horizontal

c) find oblique asymptotes where

‒oblique asymptote equation

5) In this equation, it is not required to find intervals of monotonicity of the function.

6)

These critical points partition the entire domain of the function on the interval (˗∞; ˗2), (˗2; 4), (4; 10) and (10; +∞). It is convenient to present the obtained results in the form of the following table.

Let's see how to explore a function using a graph. It turns out that looking at the graph, you can find out everything that interests us, namely:

• function scope
• function range
• function zeros
• periods of increase and decrease
• high and low points
• the largest and smallest value of the function on the interval.

Let's clarify the terminology:

Abscissa is the horizontal coordinate of the point.
Ordinate- vertical coordinate.
abscissa- the horizontal axis, most often called the axis.
Y-axis- vertical axis, or axis.

Argument is an independent variable on which the values ​​of the function depend. Most often indicated.
In other words, we ourselves choose , substitute in the function formula and get .

Domain functions - the set of those (and only those) values ​​of the argument for which the function exists.
Denoted: or .

In our figure, the domain of the function is a segment. It is on this segment that the graph of the function is drawn. Only here this function exists.

Function range is the set of values ​​that the variable takes. In our figure, this is a segment - from the lowest to the highest value.

Function zeros- points where the value of the function is equal to zero, i.e. . In our figure, these are the points and .

Function values ​​are positive where . In our figure, these are the intervals and .
Function values ​​are negative where . We have this interval (or interval) from to.

The most important concepts - increasing and decreasing function on some set. As a set, you can take a segment, an interval, a union of intervals, or the entire number line.

Function increases

In other words, the more , the more , that is, the graph goes to the right and up.

Function decreasing on the set if for any and belonging to the set the inequality implies the inequality .

For a decreasing function, a larger value corresponds to a smaller value. The graph goes right and down.

In our figure, the function increases on the interval and decreases on the intervals and .

Let's define what is maximum and minimum points of the function.

Maximum point- this is an internal point of the domain of definition, such that the value of the function in it is greater than in all points sufficiently close to it.
In other words, the maximum point is such a point, the value of the function at which more than in neighboring ones. This is a local "hill" on the chart.

In our figure - the maximum point.

Low point- an internal point of the domain of definition, such that the value of the function in it is less than in all points sufficiently close to it.
That is, the minimum point is such that the value of the function in it is less than in neighboring ones. On the graph, this is a local “hole”.

In our figure - the minimum point.

The point is the boundary. It is not an interior point of the domain of definition and therefore does not fit the definition of a maximum point. After all, she has no neighbors on the left. In the same way, there can be no minimum point on our chart.

The maximum and minimum points are collectively called extremum points of the function. In our case, this is and .

But what if you need to find, for example, function minimum on the cut? In this case, the answer is: because function minimum is its value at the minimum point.

Similarly, the maximum of our function is . It is reached at the point .

We can say that the extrema of the function are equal to and .

Sometimes in tasks you need to find the largest and smallest values ​​of the function on a given segment. They do not necessarily coincide with extremes.

In our case smallest function value on the interval is equal to and coincides with the minimum of the function. But its largest value on this segment is equal to . It is reached at the left end of the segment.

In any case, the largest and smallest values ​​of a continuous function on a segment are achieved either at the extremum points or at the ends of the segment.

How to find the largest and smallest values ​​of a function on a segment?

For this we follow the well-known algorithm:

1 . We find ODZ functions.

2 . Finding the derivative of a function

3 . Equate the derivative to zero

4 . We find the intervals on which the derivative retains its sign, and from them we determine the intervals of increase and decrease of the function:

If on the interval I the derivative of the function 0" title="(!LANG:f^(prime)(x)>0">, то функция !} increases over this interval.

If on the interval I the derivative of the function , then the function decreases over this interval.

5 . We find maximum and minimum points of the function.

AT the function maximum point, the derivative changes sign from "+" to "-".

AT minimum point of the functionderivative changes sign from "-" to "+".

6 . We find the value of the function at the ends of the segment,

• then we compare the value of the function at the ends of the segment and at the maximum points, and choose the largest of them if you need to find the largest value of the function
• or we compare the value of the function at the ends of the segment and at the minimum points, and choose the smallest of them if you need to find the smallest value of the function

However, depending on how the function behaves on the interval, this algorithm can be significantly reduced.

Consider the function . The graph of this function looks like this:

Let's consider several examples of solving problems from the Open Task Bank for

one . Task B15 (#26695)

On the cut.

1. The function is defined for all real values ​​of x

Obviously, this equation has no solutions, and the derivative is positive for all values ​​of x. Therefore, the function increases and takes on the largest value at the right end of the interval, that is, at x=0.

Answer: 5.

2 . Task B15 (No. 26702)

Find the largest value of a function on the segment.

1.ODZ function title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

The derivative is zero at , however, at these points it does not change sign:

Therefore, title="(!LANG:3/(cos^2(x))>=3">, значит, title="3/(cos^2(x))-3>=0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} increases and takes the greatest value at the right end of the interval, at .

To make it clear why the derivative does not change sign, we transform the expression for the derivative as follows:

Title="(!LANG:y^(prime)=3/(cos^2(x))-3=(3-3cos^2(x))/(cos^2(x))=(3sin^2 (x))/(cos^2(x))=3tg^2(x)>=0">!}

Answer: 5.

3 . Task B15 (#26708)

Find the smallest value of the function on the interval .

1. ODZ functions: title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

Let's place the roots of this equation on a trigonometric circle.

The interval contains two numbers: and

Let's put up the signs. To do this, we determine the sign of the derivative at the point x=0: . When passing through the points and the derivative changes sign.

Let's depict the change of signs of the derivative of the function on the coordinate line:

Obviously, the point is a minimum point (where the derivative changes sign from "-" to "+"), and in order to find the smallest value of the function on the segment, you need to compare the function values ​​at the minimum point and at the left end of the segment, .

The process of finding the smallest and largest values ​​of a function on a segment is reminiscent of a fascinating flight around an object (a graph of a function) on a helicopter with firing from a long-range cannon at certain points and choosing from these points very special points for control shots. Points are selected in a certain way and according to certain rules. By what rules? We will talk about this further.

If the function y = f(x) continuous on the segment [ a, b] , then it reaches on this segment least and highest values . This can either happen in extremum points or at the ends of the segment. Therefore, to find least and the largest values ​​of the function , continuous on the interval [ a, b] , you need to calculate its values ​​in all critical points and at the ends of the segment, and then choose the smallest and largest of them.

Let, for example, it is required to determine the maximum value of the function f(x) on the segment [ a, b] . To do this, find all its critical points lying on [ a, b] .

critical point is called the point at which function defined, and her derivative is either zero or does not exist. Then you should calculate the values ​​of the function at critical points. And, finally, one should compare the values ​​of the function at critical points and at the ends of the segment ( f(a) and f(b) ). The largest of these numbers will be the largest value of the function on the segment [a, b] .

The problem of finding the smallest values ​​of the function .

We are looking for the smallest and largest values ​​​​of the function together

Example 1. Find the smallest and largest values ​​of a function on the segment [-1, 2] .

Decision. We find the derivative of this function. Equate the derivative to zero () and get two critical points: and . To find the smallest and largest values ​​of a function on a given segment, it is enough to calculate its values ​​at the ends of the segment and at the point , since the point does not belong to the segment [-1, 2] . These function values ​​are the following: , , . It follows that smallest function value(marked in red on the graph below), equal to -7, is reached at the right end of the segment - at the point , and greatest(also red on the graph), is equal to 9, - at the critical point .

If the function is continuous in a certain interval and this interval is not a segment (but is, for example, an interval; the difference between an interval and a segment: the boundary points of the interval are not included in the interval, but the boundary points of the segment are included in the segment), then among the values ​​of the function there may not be be the smallest and largest. So, for example, the function depicted in the figure below is continuous on ]-∞, +∞[ and does not have the largest value.

However, for any interval (closed, open, or infinite), the following property of continuous functions holds.

Example 4. Find the smallest and largest values ​​of a function on the segment [-1, 3] .

Decision. We find the derivative of this function as the derivative of the quotient:

.

We equate the derivative to zero, which gives us one critical point: . It belongs to the interval [-1, 3] . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Let's compare these values. Conclusion: equal to -5/13, at the point and the greatest value equal to 1 at the point .

We continue to search for the smallest and largest values ​​​​of the function together

There are teachers who, on the topic of finding the smallest and largest values ​​of a function, do not give students examples more complicated than those just considered, that is, those in which the function is a polynomial or a fraction, the numerator and denominator of which are polynomials. But we will not limit ourselves to such examples, since there are teachers among teachers who like to make students think in full (table of derivatives). Therefore, the logarithm and the trigonometric function will be used.

Example 6. Find the smallest and largest values ​​of a function on the segment .

Decision. We find the derivative of this function as derivative of the product :

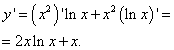
We equate the derivative to zero, which gives one critical point: . It belongs to the segment. To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

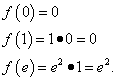
The result of all actions: the function reaches its minimum value, equal to 0, at a point and at a point and the greatest value equal to e² , at the point .

Example 7. Find the smallest and largest values ​​of a function on the segment .

Decision. We find the derivative of this function:

Equate the derivative to zero:

The only critical point belongs to the segment . To find the smallest and largest values ​​of a function on a given segment, we find its values ​​at the ends of the segment and at the found critical point:

Conclusion: the function reaches its minimum value, equal to , at the point and the greatest value, equal to , at the point .

In applied extremal problems, finding the smallest (greatest) values ​​of a function, as a rule, comes down to finding the minimum (maximum). But it is not the minima or maxima themselves that are of greater practical interest, but the values ​​of the argument at which they are achieved. When solving applied problems, an additional difficulty arises - the compilation of functions that describe the phenomenon or process under consideration.

Example 8 A tank with a capacity of 4, having the shape of a parallelepiped with a square base and open at the top, must be tinned. What should be the dimensions of the tank in order to cover it with the least amount of material?

Decision. Let be x- base side h- tank height, S- its surface area without cover, V- its volume. The surface area of ​​the tank is expressed by the formula , i.e. is a function of two variables. To express S as a function of one variable, we use the fact that , whence . Substituting the found expression h into the formula for S:

Let us examine this function for an extremum. It is defined and differentiable everywhere in ]0, +∞[ , and

.

We equate the derivative to zero () and find the critical point. In addition, when the derivative does not exist, but this value is not included in the domain of definition and therefore cannot be an extremum point. So, - the only critical point. Let's check it for the presence of an extremum using the second sufficient sign. Let's find the second derivative. When the second derivative is greater than zero (). This means that when the function reaches a minimum . Because this minimum - the only extremum of this function, it is its smallest value. So, the side of the base of the tank should be equal to 2 m, and its height.

Example 9 From paragraph A, located on the railway line, to the point With, at a distance from it l, goods must be transported. The cost of transporting a weight unit per unit distance by rail is equal to , and by highway it is equal to . To what point M railroad line should be held highway to transport cargo from BUT in With was the most economical AB railroad is assumed to be straight)?