ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under corner between two planes we mean one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . So . Because and , then

.

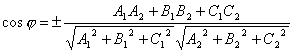Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

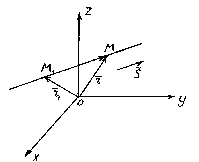
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y and z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

Let be M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, and is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

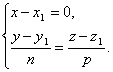
However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox and Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors and . Therefore, for the direction vector of the straight line l you can take the cross product of normal vectors:

.

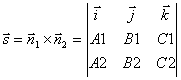Example. Give the general equations of the straight line to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

. Hence, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get

a. Let two lines be given. These lines, as it was indicated in Chapter 1, form various positive and negative angles, which can be either acute or obtuse. Knowing one of these angles, we can easily find any other.

By the way, for all these angles, the numerical value of the tangent is the same, the difference can only be in the sign

Equations of lines. The numbers are the projections of the directing vectors of the first and second lines. The angle between these vectors is equal to one of the angles formed by straight lines. Therefore, the problem is reduced to determining the angle between the vectors, We get

For simplicity, we can agree on an angle between two straight lines to understand an acute positive angle (as, for example, in Fig. 53).

Then the tangent of this angle will always be positive. Thus, if a minus sign is obtained on the right side of formula (1), then we must discard it, i.e., keep only the absolute value.

Example. Determine the angle between lines

By formula (1) we have

with. If it is indicated which of the sides of the angle is its beginning and which is its end, then, counting always the direction of the angle counterclockwise, we can extract something more from formulas (1). As is easy to see from Fig. 53 the sign obtained on the right side of the formula (1) will indicate which one - acute or obtuse - the angle forms the second line with the first.

(Indeed, from Fig. 53 we see that the angle between the first and second direction vectors is either equal to the desired angle between the lines, or differs from it by ±180°.)

d. If the lines are parallel, then their direction vectors are also parallel. Applying the condition of parallelism of two vectors, we get!

This is a necessary and sufficient condition for two lines to be parallel.

Example. Direct

are parallel because

e. If the lines are perpendicular, then their direction vectors are also perpendicular. Applying the condition of perpendicularity of two vectors, we obtain the condition of perpendicularity of two lines, namely

Example. Direct

perpendicular because

In connection with the conditions of parallelism and perpendicularity, we will solve the following two problems.

f. Draw a line parallel to a given line through a point

The decision is made like this. Since the desired line is parallel to the given one, then for its directing vector we can take the same one as that of the given line, i.e., a vector with projections A and B. And then the equation of the desired line will be written in the form (§ 1)

Example. Equation of a straight line passing through a point (1; 3) parallel to a straight line

will be next!

g. Draw a line through a point perpendicular to the given line

Here, it is no longer suitable to take a vector with projections A and as a directing vector, but it is necessary to win a vector perpendicular to it. The projections of this vector must therefore be chosen according to the condition that both vectors are perpendicular, i.e., according to the condition

This condition can be fulfilled in an infinite number of ways, since here there is one equation with two unknowns. But the easiest way is to take it. Then the equation of the desired straight line will be written in the form

Example. Equation of a line passing through a point (-7; 2) in a perpendicular line

will be the following (according to the second formula)!

h. In the case when the lines are given by equations of the form

rewriting these equations differently, we have

I will be brief. The angle between two lines is equal to the angle between their direction vectors. Thus, if you manage to find the coordinates of the direction vectors a \u003d (x 1; y 1; z 1) and b \u003d (x 2; y 2; z 2), you can find the angle. More precisely, the cosine of the angle according to the formula:

Let's see how this formula works on specific examples:

Task. Points E and F are marked in the cube ABCDA 1 B 1 C 1 D 1 - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AE and BF.

Since the edge of the cube is not specified, we set AB = 1. We introduce a standard coordinate system: the origin is at point A, and the x, y, z axes are directed along AB, AD, and AA 1, respectively. The unit segment is equal to AB = 1. Now let's find the coordinates of the direction vectors for our lines.

Find the coordinates of the vector AE. To do this, we need points A = (0; 0; 0) and E = (0.5; 0; 1). Since the point E is the middle of the segment A 1 B 1 , its coordinates are equal to the arithmetic mean of the coordinates of the ends. Note that the origin of the vector AE coincides with the origin, so AE = (0.5; 0; 1).

Now let's deal with the BF vector. Similarly, we analyze the points B = (1; 0; 0) and F = (1; 0.5; 1), because F - the middle of the segment B 1 C 1 . We have:
BF = (1 - 1; 0.5 - 0; 1 - 0) = (0; 0.5; 1).

So, the direction vectors are ready. The cosine of the angle between the lines is the cosine of the angle between the direction vectors, so we have:

Task. In a regular trihedral prism ABCA 1 B 1 C 1 , all edges of which are equal to 1, points D and E are marked - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AD and BE.

We introduce a standard coordinate system: the origin is at point A, the x-axis is directed along AB, z - along AA 1 . We direct the y axis so that the OXY plane coincides with the ABC plane. The unit segment is equal to AB = 1. Find the coordinates of the direction vectors for the desired lines.

First, let's find the coordinates of the AD vector. Consider the points: A = (0; 0; 0) and D = (0.5; 0; 1), because D - the middle of the segment A 1 B 1 . Since the beginning of the vector AD coincides with the origin, we get AD = (0.5; 0; 1).

Now let's find the coordinates of the vector BE. Point B = (1; 0; 0) is easy to calculate. With point E - the middle of the segment C 1 B 1 - a little more complicated. We have:

It remains to find the cosine of the angle:

Task. In a regular hexagonal prism ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , all edges of which are equal to 1, the points K and L are marked - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AK and BL.

We introduce a standard coordinate system for a prism: we place the origin of coordinates at the center of the lower base, direct the x-axis along FC, the y-axis through the midpoints of segments AB and DE, and the z-axis vertically upwards. The unit segment is again equal to AB = 1. Let us write out the coordinates of the points of interest to us:

Points K and L are the midpoints of the segments A 1 B 1 and B 1 C 1, respectively, so their coordinates are found through the arithmetic mean. Knowing the points, we find the coordinates of the direction vectors AK and BL:

Now let's find the cosine of the angle:

Task. In a regular quadrangular pyramid SABCD, all edges of which are equal to 1, points E and F are marked - the midpoints of the sides SB and SC, respectively. Find the angle between lines AE and BF.

We introduce a standard coordinate system: the origin is at point A, the x and y axes are directed along AB and AD, respectively, and the z axis is directed vertically upwards. The unit segment is equal to AB = 1.

Points E and F are the midpoints of the segments SB and SC, respectively, so their coordinates are found as the arithmetic mean of the ends. We write down the coordinates of the points of interest to us:
A = (0; 0; 0); B = (1; 0; 0)

Knowing the points, we find the coordinates of the direction vectors AE and BF:

The coordinates of the vector AE coincide with the coordinates of point E, since point A is the origin. It remains to find the cosine of the angle:

Definition. If two lines are given y = k 1 x + b 1 , y = k 2 x + b 2 , then the acute angle between these lines will be defined as

Two lines are parallel if k 1 = k 2 . Two lines are perpendicular if k 1 = -1/ k 2 .

Theorem. The straight lines Ax + Vy + C \u003d 0 and A 1 x + B 1 y + C 1 \u003d 0 are parallel when the coefficients A 1 \u003d λA, B 1 \u003d λB are proportional. If also С 1 = λС, then the lines coincide. The coordinates of the point of intersection of two lines are found as a solution to the system of equations of these lines.

Equation of a line passing through a given point

Perpendicular to this line

Definition. The line passing through the point M 1 (x 1, y 1) and perpendicular to the line y \u003d kx + b is represented by the equation:

Distance from point to line

Theorem. If a point M(x 0, y 0) is given, then the distance to the line Ax + Vy + C \u003d 0 is defined as

.

Proof. Let the point M 1 (x 1, y 1) be the base of the perpendicular dropped from the point M to the given line. Then the distance between points M and M 1:

(1)

The x 1 and y 1 coordinates can be found as a solution to the system of equations:

The second equation of the system is the equation of a straight line passing through a given point M 0 perpendicular to a given straight line. If we transform the first equation of the system to the form:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

then, solving, we get:

Substituting these expressions into equation (1), we find:

The theorem has been proven.

Example. Determine the angle between the lines: y = -3 x + 7; y = 2 x + 1.

k 1 \u003d -3; k2 = 2; tgφ = ; φ= p /4.

Example. Show that the lines 3x - 5y + 7 = 0 and 10x + 6y - 3 = 0 are perpendicular.

Decision. We find: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, therefore, the lines are perpendicular.

Example. The vertices of the triangle A(0; 1), B (6; 5), C (12; -1) are given. Find the equation for the height drawn from vertex C.

Decision. We find the equation of the side AB: ; 4 x = 6 y - 6;

2x – 3y + 3 = 0;

The desired height equation is: Ax + By + C = 0 or y = kx + b. k = . Then y = . Because the height passes through point C, then its coordinates satisfy this equation: whence b = 17. Total: .

Answer: 3x + 2y - 34 = 0.

Equation of a line passing through a given point in a given direction. Equation of a straight line passing through two given points. Angle between two lines. Condition of parallelism and perpendicularity of two lines. Determining the point of intersection of two lines

1. Equation of a line passing through a given point A(x 1 , y 1) in a given direction, determined by the slope k,

y - y 1 = k(x - x 1). (1)

This equation defines a pencil of lines passing through a point A(x 1 , y 1), which is called the center of the beam.

2. Equation of a straight line passing through two points: A(x 1 , y 1) and B(x 2 , y 2) is written like this:

The slope of a straight line passing through two given points is determined by the formula

3. Angle between straight lines A and B is the angle by which the first straight line must be rotated A around the point of intersection of these lines counterclockwise until it coincides with the second line B. If two lines are given by slope equations

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

then the angle between them is determined by the formula

It should be noted that in the numerator of the fraction, the slope of the first straight line is subtracted from the slope of the second straight line.

If the equations of a straight line are given in general form

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

the angle between them is determined by the formula

4. Conditions for parallelism of two lines:

a) If the lines are given by equations (4) with a slope, then the necessary and sufficient condition for their parallelism is the equality of their slopes:

k 1 = k 2 . (8)

b) For the case when the lines are given by equations in general form (6), the necessary and sufficient condition for their parallelism is that the coefficients at the corresponding current coordinates in their equations are proportional, i.e.

5. Conditions for perpendicularity of two lines:

a) In the case when the lines are given by equations (4) with a slope, the necessary and sufficient condition for their perpendicularity is that their slopes are reciprocal in magnitude and opposite in sign, i.e.

This condition can also be written in the form

k 1 k 2 = -1. (11)

b) If the equations of straight lines are given in general form (6), then the condition for their perpendicularity (necessary and sufficient) is to fulfill the equality

A 1 A 2 + B 1 B 2 = 0. (12)

6. The coordinates of the point of intersection of two lines are found by solving the system of equations (6). Lines (6) intersect if and only if

1. Write the equations of the lines passing through the point M, one of which is parallel and the other is perpendicular to the given line l.

Oh-oh-oh-oh-oh ... well, it's tinny, as if you read the sentence to yourself =) However, then relaxation will help, especially since today I bought suitable accessories. Therefore, let's proceed to the first section, I hope, by the end of the article I will keep a cheerful mood.

Mutual arrangement of two straight lines

The case when the hall sings along in chorus. Two lines can:

1) match;

2) be parallel: ;

3) or intersect at a single point: .

Help for dummies : please remember the mathematical sign of the intersection , it will occur very often. The entry means that the line intersects with the line at the point.

How to determine the relative position of two lines?

Let's start with the first case:

Two lines coincide if and only if their respective coefficients are proportional, that is, there is such a number "lambda" that the equalities

Let's consider straight lines and compose three equations from the corresponding coefficients: . From each equation it follows that, therefore, these lines coincide.

Indeed, if all the coefficients of the equation multiply by -1 (change signs), and reduce all the coefficients of the equation by 2, you get the same equation: .

The second case when the lines are parallel:

Two lines are parallel if and only if their coefficients at the variables are proportional: , but.

As an example, consider two straight lines. We check the proportionality of the corresponding coefficients for the variables :

However, it is clear that .

And the third case, when the lines intersect:

Two lines intersect if and only if their coefficients of the variables are NOT proportional, that is, there is NOT such a value of "lambda" that the equalities are fulfilled

So, for straight lines we will compose a system:

From the first equation it follows that , and from the second equation: , hence, the system is inconsistent(no solutions). Thus, the coefficients at the variables are not proportional.

Conclusion: lines intersect

In practical problems, the solution scheme just considered can be used. By the way, it is very similar to the algorithm for checking vectors for collinearity, which we considered in the lesson. The concept of linear (non) dependence of vectors. Vector basis. But there is a more civilized package:

Example 1

Find out the relative position of the lines:

Decision based on the study of directing vectors of straight lines:

a) From the equations we find the direction vectors of the lines: .

, so the vectors are not collinear and the lines intersect.

Just in case, I will put a stone with pointers at the crossroads:

The rest jump over the stone and follow on, straight to Kashchei the Deathless =)

b) Find the direction vectors of the lines:

The lines have the same direction vector, which means they are either parallel or the same. Here the determinant is not necessary.

Obviously, the coefficients of the unknowns are proportional, while .

Let's find out if the equality is true:

Thus,

c) Find the direction vectors of the lines:

Let's calculate the determinant, composed of the coordinates of these vectors:
, therefore, the direction vectors are collinear. The lines are either parallel or coincide.

The proportionality factor "lambda" is easy to see directly from the ratio of collinear direction vectors. However, it can also be found through the coefficients of the equations themselves: .

Now let's find out if the equality is true. Both free terms are zero, so:

The resulting value satisfies this equation (any number generally satisfies it).

Thus, the lines coincide.

Answer:

Very soon you will learn (or even have already learned) to solve the considered problem verbally literally in a matter of seconds. In this regard, I see no reason to offer something for an independent solution, it is better to lay one more important brick in the geometric foundation:

How to draw a line parallel to a given one?

For ignorance of this simplest task, the Nightingale the Robber severely punishes.

Example 2

The straight line is given by the equation . Write an equation for a parallel line that passes through the point.

Decision: Denote the unknown line by the letter . What does the condition say about it? The line passes through the point. And if the lines are parallel, then it is obvious that the directing vector of the line "ce" is also suitable for constructing the line "de".

We take out the direction vector from the equation:

Answer:

The geometry of the example looks simple:

Analytical verification consists of the following steps:

1) We check that the lines have the same direction vector (if the equation of the line is not properly simplified, then the vectors will be collinear).

2) Check if the point satisfies the resulting equation.

Analytical verification in most cases is easy to perform orally. Look at two equations and many of you will quickly figure out how parallel lines are without any drawing.

Examples for self-solving today will be creative. Because you still have to compete with Baba Yaga, and she, you know, is a lover of all kinds of riddles.

Example 3

Write an equation for a line passing through a point parallel to the line if

There is a rational and not very rational way to solve. The shortest way is at the end of the lesson.

We did a little work with parallel lines and will return to them later. The case of coinciding lines is of little interest, so let's consider a problem that is well known to you from the school curriculum:

How to find the point of intersection of two lines?

If straight intersect at the point , then its coordinates are the solution systems of linear equations

How to find the point of intersection of lines? Solve the system.

Here's to you geometric meaning of a system of two linear equations with two unknowns are two intersecting (most often) straight lines on a plane.

Example 4

Find the point of intersection of lines

Decision: There are two ways to solve - graphical and analytical.

The graphical way is to simply draw the given lines and find out the point of intersection directly from the drawing:

Here is our point: . To check, you should substitute its coordinates into each equation of a straight line, they should fit both there and there. In other words, the coordinates of a point are the solution of the system . In fact, we considered a graphical way to solve systems of linear equations with two equations, two unknowns.

The graphical method, of course, is not bad, but there are noticeable disadvantages. No, the point is not that seventh graders decide this way, the point is that it will take time to make a correct and EXACT drawing. In addition, some lines are not so easy to construct, and the intersection point itself can be somewhere in the thirtieth kingdom outside the notebook sheet.

Therefore, it is more expedient to search for the intersection point by the analytical method. Let's solve the system:

To solve the system, the method of termwise addition of equations was used. To develop the relevant skills, visit the lesson How to solve a system of equations?

Answer:

The verification is trivial - the coordinates of the intersection point must satisfy each equation of the system.

Example 5

Find the point of intersection of the lines if they intersect.

This is a do-it-yourself example. The task can be conveniently divided into several stages. Analysis of the condition suggests that it is necessary:
1) Write the equation of a straight line.
2) Write the equation of a straight line.
3) Find out the relative position of the lines.
4) If the lines intersect, then find the point of intersection.

The development of an action algorithm is typical for many geometric problems, and I will repeatedly focus on this.

Full solution and answer at the end of the tutorial:

A pair of shoes has not yet been worn out, as we got to the second section of the lesson:

Perpendicular lines. The distance from a point to a line.
Angle between lines

Let's start with a typical and very important task. In the first part, we learned how to build a straight line parallel to the given one, and now the hut on chicken legs will turn 90 degrees:

How to draw a line perpendicular to a given one?

Example 6

The straight line is given by the equation . Write an equation for a perpendicular line passing through a point.

Decision: It is known by assumption that . It would be nice to find the direction vector of the straight line. Since the lines are perpendicular, the trick is simple:

From the equation we “remove” the normal vector: , which will be the directing vector of the straight line.

We compose the equation of a straight line by a point and a directing vector:

Answer:

Let's unfold the geometric sketch:

Hmmm... Orange sky, orange sea, orange camel.

Analytical verification of the solution:

1) Extract the direction vectors from the equations and with the help dot product of vectors we conclude that the lines are indeed perpendicular: .

By the way, you can use normal vectors, it's even easier.

2) Check if the point satisfies the resulting equation .

Verification, again, is easy to perform verbally.

Example 7

Find the point of intersection of perpendicular lines, if the equation is known and dot.

This is a do-it-yourself example. There are several actions in the task, so it is convenient to arrange the solution point by point.

Our exciting journey continues:

Distance from point to line

Before us is a straight strip of the river and our task is to reach it in the shortest way. There are no obstacles, and the most optimal route will be movement along the perpendicular. That is, the distance from a point to a line is the length of the perpendicular segment.

The distance in geometry is traditionally denoted by the Greek letter "ro", for example: - the distance from the point "em" to the straight line "de".

Distance from point to line is expressed by the formula

Example 8

Find the distance from a point to a line

Decision: all you need is to carefully substitute the numbers into the formula and do the calculations:

Answer:

Let's execute the drawing:

The distance found from the point to the line is exactly the length of the red segment. If you make a drawing on checkered paper on a scale of 1 unit. \u003d 1 cm (2 cells), then the distance can be measured with an ordinary ruler.

Consider another task according to the same drawing:

The task is to find the coordinates of the point , which is symmetrical to the point with respect to the line . I propose to perform the actions on your own, however, I will outline the solution algorithm with intermediate results:

1) Find a line that is perpendicular to a line.

2) Find the point of intersection of the lines: .

Both actions are discussed in detail in this lesson.

3) The point is the midpoint of the segment. We know the coordinates of the middle and one of the ends. By formulas for the coordinates of the middle of the segment find .

It will not be superfluous to check that the distance is also equal to 2.2 units.

Difficulties here may arise in calculations, but in the tower a microcalculator helps out a lot, allowing you to count ordinary fractions. Have advised many times and will recommend again.

How to find the distance between two parallel lines?

Example 9

Find the distance between two parallel lines

This is another example for an independent solution. A little hint: there are infinitely many ways to solve. Debriefing at the end of the lesson, but better try to guess for yourself, I think you managed to disperse your ingenuity well.

Angle between two lines

Whatever the corner, then the jamb:


In geometry, the angle between two straight lines is taken as the SMALLER angle, from which it automatically follows that it cannot be obtuse. In the figure, the angle indicated by the red arc is not considered to be the angle between intersecting lines. And its “green” neighbor or oppositely oriented crimson corner.

If the lines are perpendicular, then any of the 4 angles can be taken as the angle between them.

How are the angles different? Orientation. First, the direction of "scrolling" the corner is fundamentally important. Secondly, a negatively oriented angle is written with a minus sign, for example, if .

Why did I say this? It seems that you can get by with the usual concept of an angle. The fact is that in the formulas by which we will find the angles, a negative result can easily be obtained, and this should not take you by surprise. An angle with a minus sign is no worse, and has a very specific geometric meaning. In the drawing for a negative angle, it is imperative to indicate its orientation (clockwise) with an arrow.

How to find the angle between two lines? There are two working formulas:

Example 10

Find the angle between lines

Decision and Method one

Consider two straight lines given by equations in general form:

If straight not perpendicular, then oriented the angle between them can be calculated using the formula:

Let's pay close attention to the denominator - this is exactly scalar product direction vectors of straight lines:

If , then the denominator of the formula vanishes, and the vectors will be orthogonal and the lines will be perpendicular. That is why a reservation was made about the non-perpendicularity of the lines in the formulation.

Based on the foregoing, the solution is conveniently formalized in two steps:

1) Calculate the scalar product of directing vectors of straight lines:
so the lines are not perpendicular.

2) We find the angle between the lines by the formula:

Using the inverse function, it is easy to find the angle itself. In this case, we use the oddness of the arc tangent (see Fig. Graphs and properties of elementary functions):

Answer:

In the answer, we indicate the exact value, as well as the approximate value (preferably both in degrees and in radians), calculated using a calculator.

Well, minus, so minus, it's okay. Here is a geometric illustration:

It is not surprising that the angle turned out to be of a negative orientation, because in the condition of the problem the first number is a straight line and the “twisting” of the angle began precisely from it.

If you really want to get a positive angle, you need to swap the straight lines, that is, take the coefficients from the second equation , and take the coefficients from the first equation . In short, you need to start with a direct .