Движение тела, брошенного под углом к горизонту
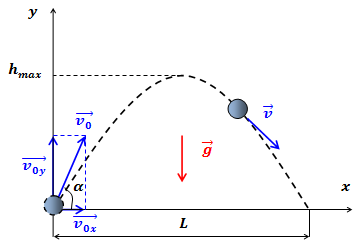
Рассмотрим движение тела, брошенного со скоростью V 0 , вектор которой направлен под угломα к горизонту, в плоскости XOY, расположив тело в момент бросания в начало координат, как это изображено на рисунке 1.
В отсутствии сил сопротивления, движение тела, брошенного под углом к горизонту, можно рассматривать как частный случай криволинейного движения под действием силы тяжести. Применяя 2 - ой закон Ньютона
∑ F i | ||||||||||
получаем | ||||||||||
mg = ma, | ||||||||||
a = g | ||||||||||
Проекции вектора ускорения a на оси ОХ и ОУ равны: | ||||||||||
= −g | ||||||||||
где g =const - это | ускорение свободного падения, | которого всегда |
||||||||
направлен вертикально вниз, | численное значение g = 9,8м/с2 ; | = −g | т.к. ось ОУ на |
|||||||
рисунке 1 направлена вверх, в случае, когда ось OY направлена вниз, то проекция вектора
2 a на ось ОУ будет положительна (читая условия задач, выбирайте сами направление осей, если это не прописано в условии).
Значения проекций вектора ускорения a на оси ОХ и ОУ дают основание сделать
следующий вывод:
∙ тело, брошенное под углом к горизонту, одновременно участвует в двух движениях - равномерном по горизонтали и равнопеременном по
вертикали. | ||||||
Скорость тела в таком случае | ||||||
V = Vx + Vy | ||||||
Скорость тела в начальный момент времени (в момент бросания тела) | ||||||
V 0= V 0x | V 0 y . | |||||
Проекции вектора начальной скорости на оси ОХ и ОУ равны | ||||||
V cosα | ||||||
V 0y | V 0 sin α | |||||
Для равнопеременного движения зависимости скорости и перемещения от времени задаются уравнениями:
V 0 +at | ||||||||||||
S 0 +V 0 t + | ||||||||||||
и S 0 - это скорость и перемещение тела в начальный момент времени, |
||||||||||||
и S t - это скорость и перемещение тела в момент времени t. |
||||||||||||
Проекции векторного уравнения (8) на оси ОХ и ОУ равны |
||||||||||||
V 0 x | Ax t, | |||||||||||
V ty= V 0 y+ a yt | ||||||||||||
Const | ||||||||||||||||
V 0 y -gt | ||||||||||||||||
Проекции векторного уравнения (9) на оси ОХ и ОУ равны | ||||||||||||||||
S ox+ V oxt + | ||||||||||||||||
a y t2 |
||||||||||||||||
S 0 y | V oy t + | |||||||||||||||
с учетом равенств (4), получаем | ||||||||||||||||
S 0 y | V oy t - | gt 2 | ||||||||||||||
где Sox и Soy - | координаты тела | в начальный момент времени, | а Stx и Sty - |
|||||||||||||
координаты тела в момент времени t.
За время своего движения t (от момента бросания до момента падения на тот же
уровень) тело поднимается на максимальную высоту hmax , спускается с неё и отлетает от места бросания на расстояние L (дальность полета) - см. рисунок 1.
1) Время движения тела t можно найти, учитывая значения координат тела Sy в
начальный момент времени и в момент времени t (см. рис.1)
Решением уравнения (15) для момента падения тела на тот же уровень, с которого его бросили, будет значение
подставив значения Vox и (17) в первое уравнение системы (13), получаем
L = V 0 cosα× t , | |||||||||||
откуда, с учетом (16), получаем | |||||||||||
L = V cosα× | 2V sin α | ||||||||||
3) Максимальную высоту подъёма тела h max можно найти, учитывая значение
скорости тела V в точке максимального подъёма тела
V 0 x | Т.к. в этой точке V y | |||||||||||||||
Используя вторые уравнения систем (11) и (13) , | значение Voу , а также тот факт, |
|||||||||||||||
что в точке максимального подъёма тела Sy = hmax , получаем |
||||||||||||||||
0 = V 0 sin α- g × t под | ||||||||||||||||
gt под2 | ||||||||||||||||
V 0 sin α× t - | ||||||||||||||||
h max | ||||||||||||||||
где tпод - время подъёма - время движения на высоту максимального подъёма тела. |
||||||||||||||||
Решая эту систему, получаем | ||||||||||||||||
t под= | V 0 sin α | |||||||||||||||
sin 2 α | ||||||||||||||||
Сравнение значений (16) и (22), даёт основание сделать вывод
· время движения на высоту максимального подъёма тела (t под ) равно времени спуска тела (tсп ) с этой высоты и равно половине времени всего движения тела от момента бросания до момента падения на тот же уровень
t под | T сп | |||||

Изучать движение тела, брошенного со скоростью V 0 , вектор которой направлен под угломα к горизонту, в плоскости XOY, очень наглядно на компьютерной модели
"Свободное падение тел" в сборнике компьютерных моделей "Открытая физика"
компании ФИЗИКОН. В этой модели можно задавать разные начальные условия.
Например, рассмотренный нами случай нужно задавать (команда "Очистить") при начальном условии h = 0 и выбранных V0 и α. Команда "Старт" продемонстрирует движение тела и даст картинку траектории движения и направление векторов скорости тела в фиксированные моменты времени.
Рис.2. Диалоговое окно компьютерной модели "Свободное падение тел" в разделе
"Механика"; тело движется из точки начала координат и падает на том же уровне .
Если условие задачи отличается от рассмотренного нами случая, то необходимо
для решения задачи, выбрав направление осей, разместить тело в начальный момент
времени, изобразить траекторию движения тела до точки падения, таким образом
определив координаты тела в начальный и конечный моменты времени. Затем
использовать уравнения (3), (5), (8) и (9) как основу для решения и рассмотренный выше
алгоритм решения задачи.
Рассмотрим частные случаи.

6 1. Тело бросили со скоростью V 0 , вектор которой направлен под углом α к
горизонту, с высоты h и оно упало на расстоянии L от места бросания. y в начальный
Soy = h, |
а значения остальных координат будут выбраны так же, как мы выбирали.
Рис.3. Диалоговое окно компьютерной модели "Свободное падение тел" в разделе
"Механика"; тело движется из точки h = 50м и падает на нулевой уровень .
2. Тело бросили горизонтально со скоростьюV 0 , с высоты h и оно упало на расстоянии L от места бросания.Отличие от рассмотренного нами случая заключается в том, значения координат тела S y в начальный момент определится так же уравнением (25),
а значения остальных координат будут выбраны так же, как мы выбирали. Но в этом случае начальная скорость тела в проекции на ось ОУ равна нулю (так как α = 0), т.е.
проекции вектора начальной скорости на оси ОХ и ОУ равны
V 0y | ||||

Рис.4. Диалоговое окно компьютерной модели "Свободное падение тел" в разделе
"Механика"; тело, брошенное горизонтально, движется из точки h = 50м и падает на нулевой уровень .
Курсовая работа по дисциплине
Высокоуровневые методы информатики и программирования
на тему:
Движение тела, брошенного под углом к горизонту: программное обеспечение
Введение
1. Описание предметной области
1.1 Предметная область
1.1.1 Развитие направления
1.1.2 Движение тела, брошенного под углом к горизонту
2. Рабочий проект
2.1 Общие сведения о работе программе (на чем написано, какие технологии использованы)
2.2 Основные процедуры/классы системы
2.3 Инсталляция программного продукта
2.4 Руководство пользователя
2.5 Сообщения системы
2.6 Требования к техническому и программному обеспечению
2.6.1 Требования к программному обеспечению
2.6.2 Требования к техническому обеспечению
2.7 Тестирование системы
Заключение
Список литературы
Приложение 1. Блок-схема
Приложение 2. Программа на оптическом носителе
Целью данной курсовой работы является закрепление практических навыков программирования и разработка программы, реализующей модель движения тела, брошенного под углом к горизонту.
Практической значимостью данной работы является автоматизация расчетов физических величин движения тела, брошенного под углом к горизонту и, как следствие, экономия времени преподавателей или студентов при решении указанной задачи.
движение тело программный обеспечение
1. Описание предметной области
1.1 Предметная область
Меха́ника (греч. μηχανική - искусство построения машин) - область физики, изучающая движение материальных объектов и взаимодействие между ними. Важнейшими разделами механики являются классическая механика и квантовая механика.
Движение тела, брошенного под углом к горизонту, необходимо рассматривать, как криволинейное движение, которое в свою очередь является одним из разделов механики.
1.1.1 Развитие направления
Изучение особенностей такого движения началось довольно давно, еще в XVI веке и было связано с появлением и совершенствованием артиллерийских орудий.
Представления о траектории движения артиллерийских снарядов в те времена были довольно забавными. Считалось, что траектория эта состоит из трех участков: А - насильственного движения, В - смешанного движения и С - естественного движения, при котором ядро падает на солдат противника сверху (рис. 1.1).
Рис. 1.1. Траектория движения артиллерийских снарядов
Законы полета метательных снарядов не привлекали особого внимания ученых до тех пор, пока не были изобретены дальнобойные орудия, которые посылали снаряд через холмы или деревья - так, что стреляющий не видел их полета.
Сверхдальняя стрельба из таких орудий на первых порах использовалась в основном для деморализации и устрашения противника, а точность стрельбы не играла вначале особенно важной роли.
Близко к правильному решению о полете пушечных ядер подошел итальянский математик Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге "Новая наука" были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века.
Однако, полное решение проблем, связанных с движением тел брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей. В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия. Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы.Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая.
Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха. Появилась и новая наука – баллистика. Прошло много-много лет, и теперь снаряды движутся столь быстро, что даже простое сравнение вида траекторий их движения подтверждает возросшее влияние сопротивления воздуха.
На рисунке 1.2 идеальная траектория движения тяжелого снаряда, вылетевшего из ствола пушки с большой начальной скоростью, показана пунктиром, а сплошной линией - действительная траектория полета снаряда при тех же условиях выстрела.

В современной баллистике для решения подобных задач используется электронно-вычислительная техника - компьютеры, а мы пока ограничимся простым случаем - изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений.
1.1.2 Движение тела, брошенного под углом к горизонту
Точное описание характера движения тела, брошенного под углом к горизонту возможно только при рассмотрении некоторой идеальной ситуации. Будем считать, что влиянием воздуха на движение можно пренебречь.
На рисунке 1.3 показана траектория движения шарика, брошенного под некоторым углом к горизонту. Траекторией движения называется кривая, отображающая положение тела в любой момент движения этого тела в выбранной системе координат. Как покажет дальнейший анализ, это знакомая из алгебры кривая, называемая параболой .

Рис. 1.3. Траектория тела, брошенного под углом а к горизонту
Если пренебречь влиянием воздуха на тело, то на тело, брошенное под углом к горизонту, как и на тело, свободно падающее, или на тело, получившую начальную скорость, направленную вертикально, действует только сила тяжести. Как бы тело не двигалось, сила тяжести может сообщить ему только ускорение g , направленное вниз. Этим и определяются и траектория движения тела, и характер его движения.
Пусть из некоторой точки O брошено тело с начальной скоростью v0, направленной под углом α к горизонту. Примем за начало отсчета координат точку, из которой брошено тело. Ось X направим горизонтально, а ось Y – вертикально вверх. Из рисунка видно, что проекции вектора v0 на оси X и Y соответственно равны v0cosα и v0sinα:
Так как на тело действует только сила тяжести, то при движении тела будет изменяться только проекция скорости v0y. Проекция же v0x изменяться не будет так же, как при прямолинейном равномерном движении:
(1)Координата же y изменяется так же, как при прямолинейном равномерном движении:
(2)Чтобы найти траекторию движения тела, надо подставить в уравнения последовательно увеличивающиеся значения t и вычислить координаты x и y и для каждого значения t при известных значениях модуля начальной скорости v0 и угла α. По полученным данным значениям x и y нанести точки, изображающие последовательное положение тела. Соединив их плавной кривой, мы и получим траекторию движения тела. Она окажется подобной той, что изображена на рисунке 1.1. Уравнение траектории можно очень просто получить из выражений (1) и (2). Подставив выражение для времени, полученное из выражения (1) в выражение (2), легко получаем уравнение траектории движения шарика, которая оказывается параболической:
2. Рабочий проект
2.1 Общие сведения о работе программе (на чем написано, какие технологии использованы)
Программа написана на языке высокого уровня VisualBasic.
При разработке были использованы следующие технологии:
· работа с массивами данных;
· работа с таблицей DataGridView;
· работа с библиотекой ZedGraph.dllи компонентом ZedGrarh, используемого для вывода графиков на экран;
· работа с компонентом MenuStrip, используемого для создания меню программы.
2.2 Основные процедуры/классы системы
В программе используются следующие основные процедуры:
1. Вычисление координат Xи Yв момент времени tи заполнение списка координат list1 данными:
Dim t As New Integer
Dim Vx, Vy, x, y, g, rad, b, a1 As Double
rad = Math.PI / 180
Dim list1 As New ZedGraph.PointPairList
Dim ex As New Boolean
While ex = False
Vx = V * Math.Cos(a * rad)
Vy = V * Math.Sin(a * rad)
y = Vy * t - g * t * t / 2
If y < 0 Then
Dim x1, x2, y1, y2 As Double
x1 = Vx * (t - 1)
y1 = Vy * (t-1) - g * (t-1) * (t-1) / 2
a1 = (x2 - x1) / (y2 - y1)
b = y1 - a1 * x1
CreateGraph(zg1, list1)
2. Вывод графика на экран
Private Sub CreateGraph(
ByVal zg As ZedGraph.ZedGraphControl,
ByVal list1 As ZedGraph.PointPairList)
Dim myPane As ZedGraph.GraphPane
myPane = zg1.GraphPane
myPane.Title.Text= "Движение тела, брошенного
под углом к горизонту"
myPane.XAxis.Title.Text= "X(м)"
myPane.YAxis.Title.Text = "Y(м)"
myPane.CurveList.Clear()
myPane.AddCurve("График функции", list1,
Color.DarkGray, ZedGraph.SymbolType.VDash)
myPane.Chart.Fill = New ZedGraph.Fill(
Color.WhiteSmoke, Color.Azure, 45.0F)
myPane.Fill = New ZedGraph.Fill(Color.White,
Color.FromArgb(220, 220, 255), 45.0F)
zg1.AxisChange()
Создание новых классов для реализации в программе методов движения тела, брошенного под углом к горизонту, не потребовалось.
2.3 Инсталляция программного продукта
Программа не требует предварительной установки. Необходимо лишь скопировать исполняемый файл «Движение тела, брошенного под углом к горизонту.exe» в папку «Programfiles» и запустить его двойным нажатием мыши на значке приложения.. При этом гарантируется полноценная работа данного приложением, даже если оно запущено не от имени администратора ПК.
При выдачи сообщения (рис. 2.1) об необходимо установить на компьютер microsoft.net framework 3.0. Для этого необходимо запустить файл «dotnetfx.exe» с диска и далее следовать указаниям инсталлятора.

Рис. 2.1. Сообщение об ошибке
2.4 Руководство пользователя
Тут вы пишете как пользоваться вашей программой. В общем виде должно быть написано следующее. Запустили экзешник удивили форму(рис. Х1). На форме есть такие то такие то поля и нужны они для того то. Далее идет скриншот формы. После этого мы заполняем поля значениями и жмем кнопку. После этого на форме появляется решение (рис. Х2). Скриншот формы с решением. После этого мы выбиравем пункт меню такой то, видим то то (рис Х3). Далее выбираем пункт выход и программа завершает свою работу
После запуска программы «Движение тела, брошенного под углом к горизонту.exe» в папку «Programfiles» вниманию пользователя предоставляется удобное и понятное в использовании окно программы (рис. 2.2).
В указанном окне есть поля «Начальная скорость» и «Угол к горизонту», предназначенные для задания основных параметров программы. Необходимо указать соответствующие параметры брошенного к горизонту тела. Программа автоматически выполнит необходимые вычисления и выведет график на экран. В таблице в правой части экрана выводятся значения высоты, угла движения к горизонту, времени полета при изменении дальности полета по оси Xна 1 м (рис. 2.3).

Рис. 2.2. Главное окно программы

Рис. 2.3. Вывод в таблицу промежуточных значений
При выделении любой строки в таблице, соответствующая точка подсветится красным цветом (рис. 2.4).

Рис. 2.4. Выделение точки на графике
2.5 Сообщения системы
При первом запуске программа может выдать ошибку, представленную на рисунке 2.1. Порядок ее устранения описан в п. 2.3.
Никаких других сообщений система не выдает, диапазоны вводимых данных контролируются автоматически.
2.6 Требования к техническому и программному обеспечению
Разрабатываемая программа должна соответствовать следующим минимальным требованиям, обусловленным заданием к проекту.
2.6.1 Требования к программному обеспечению
· ОС- Windows NT/2000/XP/2003/Vista;
· Microsoft.net framework 3.0.
2.6.2 Требования к техническому обеспечению
· IBM-совместимый компьютер с МП Intel Pentium III или AMD K6 с тактовой частотой 500 МГц и выше;
· 64 MB ОЗУ;
· НЖМД со свободным пространством 1 МБ;
· Клавиатура;
2.7 Тестирование системы
Программа тестировалась на предмет наличия ошибок. На бумаге были рассчитаны эталонные значения высоты, угла и времени полета тела, брошенного под углов к горизонту, при заданных параметрах V0=10 и a=30. Полученные результаты представлены в таблице 2.1.
Таблица 2.1.Эталонные значения
| Длина полета (м) | Высота полета (м) | Угол наклона к горизонту | Время полета (с) |
| 0 | 0 | 30 | 0 |
| 1 | 0,512 | 27,1112 | 0,1155 |
| 2 | 0,8932 | 20,8677 | 0,2309 |
| 3 | 1,1437 | 14,0612 | 0,3464 |
| 4 | 1,2634 | 6,8262 | 0,4619 |
| 5 | 1,2523 | 179,367 | 0,5774 |
| 6 | 1,1105 | 171,929 | 0,6928 |
| 7 | 0,8379 | 164,7538 | 0,8083 |
| 8 | 0,4346 | 158,0351 | 0,9238 |
Программа показала идентичные результаты.
1.В.В. Лабор «Visual Basic: создание приложений для Windows. Практическое пособие для новичков и профессионалов» Минск, «Харвест», 2003 г.
2.Ч. Петцольд «Программирование для Microsoft Windows на Basic, Пер. с англ. – М,: издательско-торговый дом «Русская Редакция», 2002 г.
3.Алешкевич В.А. Деденко Л.Г. Караваев В.А., «Механика», Академия 2004.
Блок-схема
 Тема урока: «Движение тела, брошенного под углом к горизонту»
Тема урока: «Движение тела, брошенного под углом к горизонту»
Цели урока:
Д идактическая:
рассмотреть с обучающимися одно из сложных видов движения под действием силы тяжести, когда тело брошено под углом к горизонту. Сформировать умения находить характеристики такого движения. Учить мыслить, исследовать, видеть связь между физическими процессами и математическими описаниями. Ознакомить с использованием теоретических выводов на практике, в оборонной технике.
Развивающая:
развивать умения находить решение проблемы, творчески применять знания, развивать умения взаимодействия с другими участниками учебного процесса, развивать мышление, продолжить развитие познавательного интереса, навыков самообразования.
Воспитательная:
Воспитывать культуру речи, аккуратность при выполнении самостоятельных заданий.
Задачи урока:
Обучающиеся должны знать:
Что представляет собой понятие «баллистическое движение»;
Каковы особенности движения тела, как выглядит график движения, как изменяется скорость, координаты тела, брошенного под углом к горизонту.
Должны уметь:
Применять полученные знания к решению задач.
Метод работы: групповой, индивидуальный.
ТСО : мультимедийный проектор, экран.
Дидактические средства: листы с рисунками и текстами заданий, компьютерная презентация, учебник (В.В.Белага Физика 9 класс М., «Просвещение», 2016г.).
Демонстрации: опыт со струёй воды или баллистическим пистолетом.
Структура урока:
1.Организационный этап 2 мин.
2. Проверка домашнего задания. Актуализация знаний 5 мин.
3. Изучение нового материала с элементами поисковой работы 26 мин. (из них физкультминутка 2 минуты)
4. Самостоятельная работа 10 мин.
5. Домашнее задание 2 мин.
План урока:
1. Организационный этап:
Я шла на работу и наблюдала за облаками, за свободно падающими листочками. Думаю, что вы тоже успели полюбоваться красивой природой и у вас хорошее настроение. Давайте улыбнемся друг другу. И от этих улыбок пусть все станут еще добрее, счастливее, веселее. И тогда мы с удовольствием будем совершать удивительные открытия на уроке.
2. Проверка домашнего задания
Актуализация знаний
Если тело брошено горизонтально, то…
1. Как направлена скорость тела в любой точке траектории?
2. Какой будет линия движения?
3. Как оно движется вдоль оси ОХ, ОУ?
4..Запишите значения координат X и Y в зависимости от времени;
5.Из какой формулы можно определить время падения тела?
6.Где встречается такой вид движения?
3. Изучение нового материала
Слово учителя:
Сегодня мы будем знакомиться с понятием «баллистика». Простейшие метательные орудия - праща, лук со стрелами - были известны человеку с глубокой древности. Довольно высокая меткость этих орудий обеспечивалась навыками и искусством стрелка. Появления тяжелых баллист и катапульт совершенствовали эмпирические правила наведения орудий на цель.
Первую попытку осмыслить законы движущегося в воздухе тела сделали философы античности в своем стремлении создать общую картину мироздания. Аристотель (384-322 гг. до н. э.) . Архимед (287-212 гг. до н. э.) - творец совершеннейших по тому времени военных метательных машин - первым дал конкретное представление о форме траектории снаряда. Он считал, что брошенное под углом к горизонту тело движется по спирали. Несмотря на созерцательный характер мировоззрения авторов античности, их исследования в области механики и геометрии явились тем фундаментом, на котором много веков спустя развились наиболее плодотворные идеи механики и, в частности, баллистики.
На протяжении всей истории человечества, враждующие стороны в многочисленных войнах, доказывая свое превосходство, использовали сначала камни, копья и стрелы, а затем и ядра, снаряды и бомбы. При этом точный бросок камня, поражение противника летящим копьем или стрелой фиксировалось воином визуально.
До XVI века артиллеристы пользовались таблицами, в которых на основе практических наблюдений были указаны углы, ветер, дальность полета, но меткость попадания была очень низкой. Возникла проблема научного предсказания - как достигнуть высокой меткости попадания снаряда (слайд 2, 3). Баллистикой занимались такие выдающиеся ученые, как Галилей, Торричелли, Мерсен, Ломоносов, Эйлер, Бернулли.
Великий астроном и физик Галилео Галилею, исследования которого стимулировали появление баллистики (от греческого слова ballo - бросаю). Баллистика - раздел механики, изучающий движение тел в поле силы тяжести Земли (слайд 4).
Ученый показал, что тело, брошенное под углом к горизонту, будет лететь по параболе. Им был предложен метод расчёта траекторий движения тела при различных углах вылета и начальных скоростей. Он вычислил таблицы для артиллерийской стрельбы. Из них следует, что наиболее эффективная стрельба будет при выбросе тела под углом 45° к горизонту.
Учитель: Как вы думаете, какие факторы влияют на такое движение?
(Предполагаемые ответы обучающихся: скорость, трение, угол вылета).
Для простоты пренебрежем силой сопротивления тела о воздух. Обратимся к опыту.
Демонстрация:
Выводы из наблюдений делают ребята:
1.Характер полета струи воды зависит от угла наклона и скорости вытекания воды;
2. Тело, брошенное под углом к горизонту, движется по параболе (параболу нарисовать заранее). Это движение похоже на движение тела, которое брошено горизонтально.
Учитель:
(рисунок выполнен на доске заранее)
– Встречали ли вы на практике такой вид движения?
(слайд5,6).
– Как, по вашему мнению, движется тело, брошенное под углом к горизонту?
– Какой будет цель нашего урока
(слайд 7,8)?
–Какими, на ваш взгляд, величинами можно охарактеризовать такой вид движения?
Вместе с обучающимися делаем выводы: Движение тела, брошенного под углом к горизонту можно охарактеризовать временем полета, дальностью полета и высотой подъема.
Пояснения для ребят : для описания кинематики движения тела удобно одну из осей системы координат ось OY направить вертикально вверх, а другую ось OX – расположить горизонтально (слайд 9).
Обучающиеся работают с Заданием №1 по предложенному алгоритму, заполняют таблицу (см. Лист учащегося). Частично-поисковая работа в группах по 2 человека.
Делаем выводы : движение тела, брошенного под углом к горизонту:
Происходит по криволинейной траектории. Эта траектория представляет собой параболу.
Можно представить как сумму двух движений: равномерного прямолинейного движения вдоль оси OX и движения с ускорением свободного падения вдоль оси OY.
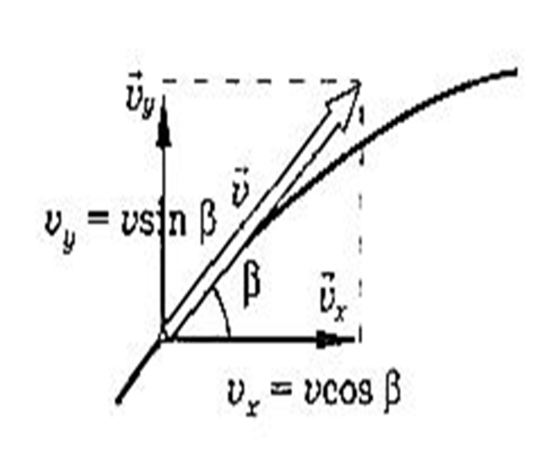
На рисунке изображен вектор начальной скорости тела и его проекции на координатные оси. Ученики делают записи в тетради.
Так как ускорение свободного падения с течение времени не меняется, то движение тела будет описываться уравнениями:
ОХ: х = х 0 + υ 0х t + а х t 2 /2, υ 0 x = υ 0,* cos α, a x = 0 ;
ОУ: у = у 0 + υ 0у t + а у t 2 /2 , υ 0 y = υ 0* sin α, a y = – g ,
время движения до высшей точки равно времени движения от неё до точки падения на землю, т. е. время полета тела t = 2t подъема на мах высоту
Физкультурная минутка
Комплекс упражнений: гимнастики для глаз.
Самостоятельная работа обучающихся в группах по 4 человека (Выполнение задания№2: вывод формул для расчета времени полёта, высоты полёта, дальности полёта). Учитель оказывает помощь по мере необходимости, затем проходит проверка результатов деятельности (слайд 10,11,12).
Слово учителя:
Реальное движение тел в земной атмосфере происходит по баллистической траектории. Тело, движущееся с большой скоростью, испытывает гораздо большее сопротивление, чем при движении с маленькими скоростями. Траектория в таком случае значительно отличается от параболы (слайд 13). Опыты показывают, что в воздухе максимальная дальность полета снарядов и пуль достигается при угле вылета 30 0 - 40 0 . Если бы стрельба осуществлялась в вакууме (на Луне, к примеру), то теоретические выводы давали бы правильные результаты. При описании движения тел в атмосфере учет сопротивления воздуха требует достаточно громоздкого математического расчета. Эти серьёзные, трудные и важные задачи решаются в институтах.
В наше неспокойное время для повышения обороноспособности любой страны требуются различные виды вооружений. Как показали недавние события в Сирии, большую роль в деле защиты играют ракеты. Но при проектировании ракет возникает множество задач (слайд14).
Задание№3. Решение задачи.
Обучающимся предлагается решить одно задание а), б) или в) в тетради Им по предложенному алгоритму.
Задача: Спортсмен, толкающий ядро, сообщает ему начальную скорость 25 м/с, направленную под углом а) 30градусов.; б) 45градусов; в) 60градусов к горизонту.
Вычислите время полёта ядра.
Вычислите дальность полета ядра.
Вычислите максимальную высоту подъема ядра над землей.
Рефлексия
Что изучает баллистика?
Охарактеризуйте движение в точках 0,1,2. Чему равна скорость в точке 2? (слайд 15).
Каков характер движения тела при баллистическом движении по горизонтали? (слайд 16)
Каков характер движения тела при баллистическом движении по вертикали?
Что является баллистической траекторией?
Под каким углом к горизонту нужно бросить тело, чтобы дальность полета была максимальной?
Что было не понятным?
Что вы узнали сегодня на уроке?
Чему вы научились?
Что понравилось?
Домашнее задание
1.Напишите уравнение координаты y(x) для тела, брошенного под углом к горизонту.
2
.
Докажите
, что максимальная дальность полета достигается, если начальная скорость тела направлена под углом 45о к горизонту
(по желанию).
Алгоритм решения типовой задачи:
1. Кратко запишите условие задачи.
2. Изобразите графически движение в произвольной системе отсчета, указав траекторию пути, вектора перемещения, скорости, ускорения.
3. Скорректируйте и обозначьте на рисунке систему отсчета, введя начало отсчета времени и уточнив оси координат для движения, скорости и ускорения. Лучше направить их вдоль одного из перемещений, а отсчет времени начните в момент нахождения точки в нуле координат.
4. Запишите уравнения движения и скорости. Уравнения движения и скорости - это зависимости перемещения (пути) и скорости от времени.
5. Решите уравнения в общем виде.
6. Подставьте величины в общее решение, вычислите.
7. Запишите ответ.
Условие задачи: Спортсмен, толкающий ядро, сообщает ему начальную скорость 25 м/с, направленную под углом а) 30o; б) 45o; в) 60o к горизонту
Найдите проекции начальной скорости на горизонтальное и вертикальное направление.
Определите время движения снаряда до высшей точки подъёма.
Вычислите время движения ядра до земли.
Сделайте расчет максимальной высоты подъема ядра над землей.
Движение тела, брошенного под углом к горизонту
Основные формулы криволинейного движения
1 . Скорость движения материальной точки
\(\vec V=\frac{d\vec r}{dt}\) ,
где \(\vec r\) - радиус-вектор точки.
2 . Ускорение материальной точки
\(\vec a=\frac{d\vec V}{dt}=\frac{d^2\vec r}{dt^2}\) ,
\(a=\sqrt{a^2_{\tau}+a^2_n}\) ,
где \(a_{\tau}\) - тангенциальное ускорение, \(a_n\) - нормальное ускорение.
3 . Тангенциальное ускорение
\(a_{\tau}=\frac{dV}{dt}=\frac{d^2s}{dt^2}\)
4 . Нормальное ускорение
\(a_n=\frac{V^2}{R}\) ,
где \(R\) - радиус кривизны траектории.
5 . для равнопеременного движения
\(S=V_0t+\frac{at^2}{2}\)
\(V=V_0+at\)
Выразив из второго равенства \(t\) и подставив в первое, получим полезную формулу
\(2aS=V^2-V_0^2\)
Примеры решения задач
В задачах о движении тела в поле силы тяжести будем полагать \(a=g=9.8\) м/с 2 .
Задача 1.
Снаряд вылетает из орудия с начальной скоростью 490 м/с под углом 30 0 к горизонту. Найти высоту, дальность и время полета снаряда, не учитывая его вращение и сопротивление воздуха.
Решение задачи
Найти: \(h, S, t\)
\(V_0=490\) м/с
\(\alpha=30^0\)
Свяжем ИСО с орудием.
Составляющие скорости по осям Ox и Oy в начальный момент времени равны:
\(V_{0x}=V_0\cos\alpha\) - остается неизменной во все время полета снаряда,
\(V_{0y}=V_0\sin\alpha\) - меняется согласно уравнению равнопеременного движения
\(V_y=V_0\sin\alpha-gt\) .
В наивысшей точке подъема \(V_y=V_0\sin\alpha-gt_1=0\) , откуда
\(t_1=\frac{V_0\sin\alpha}{g}\)
Полное время полета снаряда
\(t=2t_1=\frac{2V_0\sin\alpha}{g}=50\) c.
Высоту подъема снаряда определим из формулы пути равно замедленного движения
\(h=V_{0y}t_1-\frac{gt_1^2}{2}=\frac{V_0^2\sin^2\alpha}{2g}=3060\) м.
Дальность полета определим как
\(S=V_{0x}t=\frac{V_0^2\sin{2\alpha}}{g}=21000\) м.
Задача 2 .
Из точки А свободно падает тело. Одновременно из точки В под углом \(\alpha\) к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол \(\alpha\) не зависит от начальной скорости \(V_0\) тела, брошенного из точки В, и определить этот угол, если \(\frac{H}{S}=\sqrt3\) . Сопротивлением воздуха пренебречь.
Решение задачи.
Найти: \(\alpha\)
Дано: \(\frac{H}{S}=\sqrt3\)
Свяжем ИСО с точкой В.

Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим скорость \(V_0\) тела, брошенного из точки В, на горизонтальную и вертикальную составляющие:
\(V_{0x}=V_0\cos\alpha\) ; \(V_{0y}=V_0\sin\alpha\) .
Пусть от начала движения до момента встречи пройдет время
\(t=\frac{S}{V_{0x}}=\frac{S}{V_0\cos\alpha}\) .
За это время тело из точки А опуститься на величину
\(H-h=\frac{gt^2}{2}\) ,
а тело из точки В поднимется на высоту
\(h=V_{0y}t-\frac{gt^2}{2}=V_0\sin\alpha{t}-\frac{gt^2}{2}\) .
Решая последние два уравнения совместно, находим
\(H=V_0\sin\alpha{t}\) .
Подставляя сюда ранее найденное время, получим
\(\tan\alpha=\frac{H}{S}=\sqrt3\) ,
т.е. угол бросания не зависит от начальной скорости.
\(\alpha=60^0\)
Задача 3.
С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Решение задачи.
Найти: \(\alpha\)
Дано: \(V_0=40\) м/с. \(t=3\) c.
Свяжем ИСО с башней.

Тело одновременно участвует в двух движениях: равномерно в горизонтальном направлении со скоростью \(V_0\) и в свободном падении со скоростью \(V_y=gt\) . Тогда полная скорость тела есть
\(V=\sqrt{V_0^2+g^2t^2}=50 м/с.\)
Направление вектора скорости определяется углом \(\alpha\) . Из рисунка видим, что
\(\cos\alpha=\frac{V_0}{V}=\frac{V_0}{\sqrt{V_0^2+g^2t^2}}=0.8\)
\(\alpha=37^0\)
Задача 4.
Два тела брошены вертикально вверх из одной точки одно вслед за другим с интервалом времени, равным \(\Delta{t}\) , с одинаковыми скоростями \(V_0\) . Через какое время \(t\) после бросания первого тела они встретятся?
Решение задачи.
Найти: \(t\)
Дано: \(V_0\) , \(\Delta{t}\)
Из анализа условия задачи, ясно, что первое тело поднимется на максимальную высоту и на спуске встретится со вторым телом. Запишем законы движения тел:
\(h_1=V_0t-\frac{gt^2}{2}\)
\(h_2=V_0(t-\Delta{t})-\frac{g(t-\Delta{t})^2}{2}\) .
В момент встречи \(h_1=h_2\) , откуда сразу получаем
\(t=\frac{V_0}{g}+\frac{\Delta{t}}{2}\)
