Tämä on melko mielenkiintoinen matematiikan osa, jonka kohtaavat ehdottomasti kaikki jatko-opiskelijat ja opiskelijat. Kaikki eivät kuitenkaan pidä matanista. Jotkut eivät ymmärrä edes perusasioita, kuten näennäisesti tavanomaista toimintotutkimusta. Tämän artikkelin tarkoituksena on korjata tämä virhe. Haluatko oppia lisää funktioanalyysistä? Haluatko tietää, mitä ääripisteet ovat ja miten ne löytää? Sitten tämä artikkeli on sinua varten.
Funktion graafin tutkiminen
Aluksi on syytä ymmärtää, miksi kaaviota on ylipäänsä tarpeen analysoida. On yksinkertaisia toimintoja, jotka on helppo piirtää. Näyttävä esimerkki tällaisesta funktiosta on paraabeli. Hänen kaavionsa piirtäminen ei ole vaikeaa. Tarvitset vain yksinkertaisen muunnoksen avulla löytää luvut, joilla funktio saa arvon 0. Ja periaatteessa tämä on kaikki mitä sinun tarvitsee tietää paraabelikuvaajan piirtämiseksi.
Mutta entä jos funktio, joka meidän on piirrettävä, on paljon monimutkaisempi? Koska monimutkaisten funktioiden ominaisuudet ovat melko epäselviä, on tarpeen suorittaa koko analyysi. Vasta sitten funktio voidaan esittää graafisesti. Kuinka tehdä se? Löydät vastauksen tähän kysymykseen tästä artikkelista.
Toiminnan analysointisuunnitelma
Ensimmäinen asia on suorittaa funktion pinnallinen tutkimus, jonka aikana löydämme määritelmäalueen. Joten aloitetaan järjestyksessä. Määritelmäalue on joukko niitä arvoja, joilla funktio määritellään. Yksinkertaisesti sanottuna nämä ovat numeroita, joita voidaan käyttää funktiossa x:n sijasta. Laajan määrittämiseksi sinun tarvitsee vain tarkastella merkintää. Esimerkiksi on selvää, että funktiolla y (x) \u003d x 3 + x 2 - x + 43 on määritelmäalue - reaalilukujen joukko. No, funktiolla, kuten (x 2 - 2x) / x, kaikki on hieman erilaista. Koska nimittäjässä olevan luvun ei pitäisi olla 0, tämän funktion toimialue on kaikki reaaliluvut, paitsi nolla.
Seuraavaksi sinun on löydettävä funktion niin sanotut nollat. Nämä ovat argumentin arvoja, joiden koko funktio saa arvon nolla. Tätä varten funktio on rinnastettava nollaan, harkittava sitä yksityiskohtaisesti ja suoritettava joitain muunnoksia. Otetaan jo tuttu funktio y(x) = (x 2 - 2x)/x. Koulukurssilta tiedämme, että murtoluku on 0, kun osoittaja on nolla. Siksi hylkäämme nimittäjän ja alamme työskennellä osoittajan kanssa samastaen sen nollaan. Saamme x 2 - 2x \u003d 0 ja poistamme x:n suluista. Tästä syystä x (x - 2) \u003d 0. Tämän seurauksena huomaamme, että funktiomme on yhtä suuri kuin nolla, kun x on 0 tai 2.
Tutkiessaan funktion kuvaajaa monet kohtaavat ongelman ääripisteiden muodossa. Ja se on outoa. Loppujen lopuksi äärimmäisyydet ovat melko yksinkertainen aihe. Etkö usko? Katso itse lukemalla tämän osan artikkelista, jossa puhumme vähimmäis- ja enimmäispisteistä.

Aluksi on syytä ymmärtää, mikä ääripää on. Ekstreemi on raja-arvo, jonka funktio saavuttaa kaaviossa. Tästä käy ilmi, että on olemassa kaksi ääriarvoa - maksimi ja minimi. Selvyyden vuoksi voit katsoa yllä olevaa kuvaa. Tutkitulla alueella piste -1 on funktion y (x) \u003d x 5 - 5x maksimi ja vastaavasti piste 1 minimi.
Älä myöskään sekoita käsitteitä keskenään. Funktion ääripisteet ovat argumentteja, joissa annettu funktio saa ääriarvot. Ekstreemi puolestaan on funktion minimien ja maksimien arvo. Harkitse esimerkiksi yllä olevaa kuvaa uudelleen. -1 ja 1 ovat funktion ääripisteitä, ja 4 ja -4 ovat itse ääripäät.
Ääripisteiden löytäminen

Mutta miten löydät funktion ääripisteet? Kaikki on melko yksinkertaista. Ensimmäinen asia on löytää yhtälön derivaatta. Oletetaan, että saimme tehtävän: "Etsi funktion y (x) ääripisteet, x on argumentti. Otetaan selvyyden vuoksi funktio y (x) \u003d x 3 + 2x 2 + x + 54. Erotetaan ja saa seuraavan yhtälön: 3x 2 + 4x + 1. Tuloksena saimme standardin toisen asteen yhtälön. Ainoa mitä tarvitsee tehdä on rinnastaa se nollaan ja löytää juuret. Koska diskriminantti on suurempi kuin nolla (D \u003d 16 - 12 \u003d 4), tämä yhtälö määräytyy kahdella juurilla. Löydämme ne ja saamme kaksi arvoa: 1/3 ja -1. Nämä ovat funktion ääripisteet. Miten voit kuitenkin määrittää kuka on kuka? Mikä piste on maksimi ja mikä minimi? Tätä varten sinun on otettava viereinen piste ja selvitettävä sen arvo. Otetaan esimerkiksi numero -2, joka on vasemmalla koordinaattia pitkin Korvaamme tämän arvon yhtälössämme y (-2) = 12 - 8 + 1 = 5. Tuloksena saimme positiivisen luvun, mikä tarkoittaa, että välillä 1/3 - -1 funktio kasvaa, mikä puolestaan tarkoittaa, että aikaväleillä min äärettömästä arvoon 1/3 ja -1:stä plus äärettömään, funktio pienenee. Siten voidaan päätellä, että luku 1/3 on funktion minimipiste tutkitulla aikavälillä ja -1 on maksimipiste.

On myös syytä huomata, että tentti ei edellytä vain ääripisteiden löytämistä, vaan myös jonkinlaisen toimenpiteen suorittamista niillä (lisää, kerro jne.). Tästä syystä on syytä kiinnittää erityistä huomiota ongelman olosuhteisiin. Loppujen lopuksi huomaamattomuuden vuoksi voit menettää pisteitä.
Tästä artikkelista lukija oppii, mikä on toiminnallisen arvon ääriarvo, sekä sen käytännön ominaisuuksista. Tällaisen käsitteen tutkiminen on erittäin tärkeää korkeamman matematiikan perusteiden ymmärtämiseksi. Tämä aihe on olennainen kurssin syvemmälle tutkimiselle.
Yhteydessä
Mikä on ääripää?
Koulukurssilla annetaan monia määritelmiä "äärimmäisyyden" käsitteelle. Tämän artikkelin tarkoituksena on antaa syvin ja selkein käsitys termistä niille, jotka eivät tiedä asiasta. Joten termillä tarkoitetaan sitä, missä määrin toiminnallinen intervalli saa minimi- tai maksimiarvon tietyssä joukossa.
Ekstreemi on sekä funktion minimi- että maksimiarvo samanaikaisesti. On minimipiste ja maksimipiste, eli kaavion argumentin ääriarvot. Tärkeimmät tieteet, joissa tätä käsitettä käytetään:
- tilastot;
- koneen ohjaus;
- ekonometria.
Ääripisteillä on tärkeä rooli tietyn funktion järjestyksen määrittämisessä. Kuvaajan koordinaattijärjestelmä näyttää parhaimmillaan ääriasennon muutoksen toiminnallisuuden muutoksesta riippuen.
Johdannaisen funktion ääriarvo
On myös sellainen asia kuin "johdannainen". On tarpeen määrittää ääripiste. On tärkeää olla sekoittamatta minimi- tai maksimipisteitä suurimpaan ja pienimpään arvoon. Nämä ovat erilaisia käsitteitä, vaikka ne saattavat näyttää samanlaisilta.
Funktion arvo on tärkein tekijä määritettäessä, kuinka maksimipiste löydetään. Johdannaista ei muodosteta arvoista, vaan yksinomaan sen ääriasemasta tavalla tai toisella.
Itse derivaatta määritetään ääripisteiden tietojen perusteella, ei suurimman tai pienimmän arvon perusteella. Venäläisissä kouluissa näiden kahden käsitteen välistä rajaa ei vedetä selkeästi, mikä vaikuttaa tämän aiheen ymmärtämiseen yleisesti.
Tarkastellaanpa nyt sellaista asiaa kuin "terävä ääripää". Tähän mennessä on olemassa akuutti minimiarvo ja akuutti maksimiarvo. Määritelmä on annettu venäläisen funktion kriittisten pisteiden luokituksen mukaisesti. Ääripisteen käsite on perusta kriittisten pisteiden löytämiselle kaaviosta.

Sellaisen käsitteen määrittelemiseen käytetään Fermatin lausetta. Se on tärkein ääripisteiden tutkimuksessa ja antaa selkeän kuvan niiden olemassaolosta muodossa tai toisessa. Äärimmäisyyden varmistamiseksi on tärkeää luoda tietyt edellytykset kaavion pienenemiselle tai nousulle.
Jotta voit vastata tarkasti kysymykseen "miten löytää maksimipiste", sinun on noudatettava näitä säännöksiä:
- Tarkan määritelmäalueen löytäminen kaaviosta.
- Hae funktion ja ääripisteen derivaatta.
- Ratkaise perusepäyhtälöt argumentin alueelle.
- Pystyy todistamaan missä funktioissa kuvaajan piste on määritelty ja jatkuva.

Huomio! Funktion kriittisen pisteen etsintä on mahdollista vain, jos on olemassa vähintään toisen asteen derivaatta, jonka takaa suuri osa ääripisteen läsnäolosta.
Toiminnon ääripään välttämätön ehto
Jotta ääriarvo olisi olemassa, on tärkeää, että siinä on sekä minimi- että maksimipisteet. Jos tätä sääntöä noudatetaan vain osittain, ääripään olemassaolon ehtoa rikotaan.

Jokainen toiminto missä tahansa asennossa on eriytettävä, jotta sen uudet merkitykset voidaan tunnistaa. On tärkeää ymmärtää, että tapaus, jossa piste katoaa, ei ole pääperiaate erotettavissa olevan pisteen löytämisessä.
Terävä ääriarvo, kuten myös funktiominimi, on erittäin tärkeä näkökohta matemaattisen ongelman ratkaisemisessa ääriarvoja käyttämällä. Tämän komponentin ymmärtämiseksi paremmin on tärkeää viitata funktion määrittämisessä oleviin taulukkoarvoihin.
| Täydellinen merkityksen tutkiminen | Arvon piirtäminen |
| 1. Arvojen nousu- ja laskupisteiden määrittäminen. 2. Murtopisteiden, ääripisteiden ja koordinaattiakseleiden leikkauspisteiden löytäminen. 3. Prosessi kaavion sijainnin muutosten määrittämiseksi. 4. Kuperuuden ja kuperuuden indeksin ja suunnan määrittäminen ottaen huomioon asymptoottien esiintyminen. 5. Yhteenvetotaulukon luominen tutkimuksesta sen koordinaattien määrittämiseksi. 6. Äärimmäisten ja akuuttien pisteiden kasvu- ja laskuvälien löytäminen. 7. Käyrän kuperuuden ja koveruuden määritys. 8. Tutkimuksen perusteella kaavion rakentaminen mahdollistaa minimi- tai maksimiarvon. |
Pääelementti, kun on tarpeen työskennellä ääripäiden kanssa, on sen kaavion tarkka rakenne. Koulujen opettajat eivät usein kiinnitä suurta huomiota niin tärkeään näkökohtaan, joka on koulutusprosessin törkeä rikkomus. Kaavion rakentaminen tapahtuu vain funktionaalisten tietojen tutkimuksen tulosten, terävien ääriarvojen määrittämisen sekä kaavion pisteiden perusteella. Funktion derivaatan terävät ääripäät näytetään tarkkojen arvojen kaaviossa käyttämällä tavallista asymptootien määrittämismenettelyä. |
Tarkastellaan jatkuvan funktion kuvaajaa y=f(x) näkyy kuvassa.
Funktioarvo pisteessä x 1 on suurempi kuin funktion arvot kaikissa vierekkäisissä pisteissä sekä vasemmalla että oikealla x yksi . Tässä tapauksessa funktiolla sanotaan olevan pisteessä x 1 max. Pisteessä x 3-funktiolla on ilmeisesti myös maksimi. Jos ajattelemme asiaa x 2, silloin funktion arvo siinä on pienempi kuin kaikki naapuriarvot. Tässä tapauksessa funktiolla sanotaan olevan pisteessä x 2 vähintään. Samoin pisteen osalta x 4 .
Toiminto y=f(x) pisteessä x 0 on enimmäismäärä, jos funktion arvo tässä pisteessä on suurempi kuin sen arvot jonkin pisteen sisältävän välin kaikissa kohdissa x 0 eli jos pisteen lähistöllä on sellainen x 0, joka on kaikille x≠x 0 , kuuluessamme tähän naapurustoon, meillä on epätasa-arvo f(x)<f(x 0 ) .
Toiminto y=f(x) Sillä on minimi pisteessä x 0 , jos pisteen lähistöllä on sellainen x 0 , mikä on kaikille x≠x 0 kuuluvat tähän naapurustoon, meillä on epätasa-arvo f(x)>f(x0.
Pisteitä, joissa funktio saavuttaa maksimi- ja minimipisteensä, kutsutaan ääripisteiksi, ja funktion arvot näissä kohdissa ovat funktion ääripisteitä.
Kiinnitetään huomiota siihen, että janalle määritelty funktio voi saavuttaa maksiminsa ja miniminsä vain tarkasteltavana olevan segmentin sisällä olevissa pisteissä.
Huomaa, että jos funktiolla on maksimi jossain pisteessä, tämä ei tarkoita, että tässä vaiheessa funktiolla on maksimiarvo koko alueella. Yllä käsitellyssä kuvassa funktio pisteessä x 1:llä on maksimi, vaikka on pisteitä, joissa funktion arvot ovat suurempia kuin pisteessä x 1 . Erityisesti, f(x 1) < f(x 4) eli funktion minimi on suurempi kuin maksimi. Maksimin määritelmästä seuraa vain, että tämä on funktion suurin arvo pisteissä, jotka ovat riittävän lähellä maksimipistettä.
Lause 1. (Edellytys ääripään olemassaololle.) Jos erottuva toiminto y=f(x) on pisteessä x=x 0 ääripää, niin sen derivaatta tässä vaiheessa katoaa.
Todiste. Olkoon varmuuden vuoksi paikalla x 0 funktiolla on maksimi. Sitten riittävän pienillä lisäyksillä Δ x meillä on f(x 0 + Δ x)
Siirretään nämä epäyhtälöt rajaan muodossa Δ x→ 0 ja ottaen huomioon, että derivaatta f "(x 0) on olemassa, joten vasemmalla oleva raja ei riipu siitä, kuinka Δ x→ 0, saamme: Δ:lle x → 0 – 0 f"(x 0) ≥ 0 ja kohdassa Δ x → 0 + 0 f"(x 0) ≤ 0. Alkaen f"(x 0) määrittelee luvun, niin nämä kaksi epäyhtälöä ovat yhteensopivia vain jos f"(x 0) = 0.
Todistetussa lauseessa sanotaan, että maksimi- ja minimipisteet voivat olla vain niiden argumentin arvojen joukossa, joiden derivaatta katoaa.
Olemme tarkastelleet tapausta, jossa funktiolla on derivaatta tietyn segmentin kaikissa kohdissa. Mitä tapahtuu, kun johdannaista ei ole olemassa? Harkitse esimerkkejä.
Esimerkkejä.
- y=|x|.
Funktiolla ei ole derivaattia pisteessä x=0 (tässä vaiheessa funktion kuvaajalla ei ole varmaa tangenttia), mutta tässä vaiheessa funktiolla on minimi, koska y(0) = 0 ja kaikille x≠ 0y > 0.
- Päästää x< x
0 . Sitten c< x
0 ja f "(c)> 0.
Siksi f "(c)(x-x 0)<
0 ja siksi
f(x) - f(x 0 )< 0 eli f(x)< f(x 0 ).
- Päästää x > x 0 . Sitten c> x 0 ja f"(c)< 0. Keinot f "(c)(x-x 0)< 0. Siksi f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Etsi funktion laajuus f(x).
- Etsi funktion ensimmäinen derivaatta f"(x).
- Määritä kriittiset pisteet tätä varten:
- löytää yhtälön todelliset juuret f"(x)=0;
- löytää kaikki arvot x jonka alla johdannainen f"(x) ei ole olemassa.
- Määritä derivaatan etumerkki kriittisen pisteen vasemmalla ja oikealla puolella. Koska derivaatan etumerkki pysyy vakiona kahden kriittisen pisteen välillä, riittää, että määritetään derivaatan etumerkki missä tahansa pisteessä kriittisen pisteen vasemmalla ja yhdessä pisteessä oikealla.
- Laske funktion arvo ääripisteissä.
- Etsi kaikki funktion kriittiset pisteet välillä ( a, b) ja laske funktioarvot näissä kohdissa.
- Laske funktion arvot segmentin päissä x=a, x=b.
- Valitse kaikista saaduista arvoista suurin ja pienin.
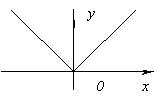
Funktiolla ei ole derivaattia at x=0, koska se menee äärettömään milloin x=0. Mutta tässä vaiheessa funktiolla on maksimi.

Funktiolla ei ole derivaattia at x=0 koska ![]() klo x→0. Tässä vaiheessa funktiolla ei ole maksimi- eikä minimiarvoa. Todella, f(x)=0 ja at x<0f(x)<0, а при x>0f(x)>0.
klo x→0. Tässä vaiheessa funktiolla ei ole maksimi- eikä minimiarvoa. Todella, f(x)=0 ja at x<0f(x)<0, а при x>0f(x)>0.

Siten annetuista esimerkeistä ja formuloidusta lauseesta on selvää, että funktiolla voi olla ääriarvo vain kahdessa tapauksessa: 1) pisteissä, joissa derivaatta on olemassa ja on yhtä suuri kuin nolla; 2) kohdassa, jossa johdannaista ei ole olemassa.
Jos kuitenkin jossain vaiheessa x 0 tiedämme sen f"(x 0 ) =0, niin tästä ei voida päätellä, että pisteessä x 0 funktiolla on ääriarvo.
Esimerkiksi. ![]() .
.

Mutta pointti x=0 ei ole ääripiste, koska tämän pisteen vasemmalla puolella funktion arvot sijaitsevat akselin alapuolella Härkä, ja ylhäällä oikealla.
Argumentin arvoja funktion alueelta, jolle funktion derivaatta katoaa tai ei ole olemassa, kutsutaan kriittiset kohdat.
Kaikesta edellä olevasta seuraa, että funktion ääripisteet ovat kriittisten pisteiden joukossa, eikä jokainen kriittinen piste ole kuitenkaan ääripiste. Siksi funktion ääripään löytämiseksi sinun on löydettävä kaikki funktion kriittiset pisteet ja tutkittava sitten jokainen näistä pisteistä erikseen maksimi- ja minimipisteiden suhteen. Tätä varten palvelee seuraava lause.
Lause 2. (Riittävä ehto ääripään olemassaololle.) Olkoon funktio jatkuva jollain kriittisen pisteen sisältävällä aikavälillä x 0 , ja se on differentioituva tämän intervallin kaikissa pisteissä (paitsi ehkä itse pisteen x 0). Jos derivaatta vaihtaa etumerkkiä plussasta miinusmerkkiin siirtyessään vasemmalta oikealle tämän pisteen läpi, niin pisteessä x = x 0 funktiolla on maksimi. Jos läpi kulkiessa x 0 vasemmalta oikealle, derivaatta muuttaa etumerkin miinuksesta plussaan, niin funktiolla on tässä vaiheessa minimi.
Eli jos
Todiste. Oletetaan ensin, että kun kuljemme läpi x 0, derivaatta muuttaa etumerkin plussasta miinusmerkkiin, ts. kaikille x lähellä kohtaa x 0 f "(x)> 0 puolesta x< x 0 , f"(x)< 0 puolesta x > x 0 . Sovelletaan Lagrangen lausetta eroon f(x) - f(x 0 ) = f "(c)(x-x 0), missä c on välillä x ja x 0 .
Siis kaikille arvoille x tarpeeksi lähellä x 0 f(x)< f(x 0 ) . Ja tämä tarkoittaa sitä pisteessä x 0 funktiolla on maksimi.
Minimilauseen toinen osa todistetaan samalla tavalla.

Havainnollistetaan tämän lauseen merkitys kuvassa. Päästää f"(x 1 ) =0 ja mille tahansa x, tarpeeksi lähellä x 1, epätasa-arvo
f"(x)< 0 klo x< x 1 , f "(x)> 0 klo x > x 1 .
Sitten pisteen vasemmalle puolelle x 1 funktio kasvaa ja oikealla pienenee, siis milloin x = x 1-funktio siirtyy kasvavasta laskevaan, eli sillä on maksimi.
Samoin voidaan tarkastella kohtia x 2 ja x 3 .

Kaavamaisesti kaikki edellä mainitut voidaan kuvata kuvassa:
Sääntö funktion y=f(x) tutkimiseksi ääripäälle
Esimerkkejä. Tutustu minimi- ja maksimitoimintoihin.
SUURIMMAT JA VÄHIMMÄIMÄT TOIMINTOARVOT SIIRTYMISESSA
suurin funktion arvo segmentillä on suurin kaikista sen arvoista tällä segmentillä, ja vähiten on pienin kaikista arvoistaan.
Harkitse toimintoa y=f(x) jatkuva aikavälillä [ a, b]. Kuten tiedetään, tällainen funktio saavuttaa maksimi- ja minimiarvonsa joko segmentin rajalla tai sen sisällä. Jos funktion maksimi- tai minimiarvo saavutetaan segmentin sisäisessä pisteessä, tämä arvo on funktion maksimi tai minimi, eli se saavutetaan kriittisissä pisteissä.
Siten saamme seuraavan sääntö funktion suurimman ja pienimmän arvojen löytämiseksi segmentistä [ a, b] :
>> Äärimmäisyydet
Toiminnan ääripää
Määritelmä ääripää
Toiminto y = f(x) kutsutaan lisääntyy (hiipumassa) jossain välissä, jos x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).
Jos segmentin differentioituva funktio y \u003d f (x) kasvaa (vähenee), niin sen derivaatta tässä segmentissä f " (x )> 0
(f"(x)< 0).
Piste x noin nimeltään paikallinen maksimipiste (minimi) funktiosta f (x ), jos pisteellä on lähialue x o, jonka kaikissa pisteissä epäyhtälö f (x)≤ f (x o) (f (x)≥ f (x o )).
Maksimi- ja minimipisteet kutsutaan ääripisteet, ja funktion arvot näissä kohdissa ovat sen äärimmäinen.
ääripisteet
Ekstreemin välttämättömät olosuhteet . Jos kohta x noin on funktion f (x) ääripiste, sitten joko f " (x o ) = 0 tai f(x o ) ei ole olemassa. Tällaisia pisteitä kutsutaan kriittinen, jossa funktio itse määritellään kriittisessä pisteessä. Funktion ääripäät tulisi etsiä sen kriittisten pisteiden joukosta.
Ensimmäinen riittävä ehto. Päästää x noin - Kriittinen piste. Jos f" (x ) kulkiessaan pisteen läpi x noin muuttaa plusmerkin miinusmerkiksi ja sitten kohtaan x o funktiolla on maksimi, muuten sillä on minimi. Jos derivaatta ei muuta etumerkkiä kulkiessaan kriittisen pisteen läpi, niin pisteessä x noin ei ole ääripäätä.
Toinen riittävä ehto.
Olkoon funktiolla f(x).
f" (x ) pisteen läheisyydessä x
noin
ja toinen derivaatta aivan pisteessä x o. Jos f"(x o) = 0, >0 ( <0), то точка x o on funktion f(x) paikallinen minimi (maksimi) piste. Jos =0, tulee joko käyttää ensimmäistä riittävää ehtoa tai ottaa käyttöön korkeammat.
Jaksolla funktio y \u003d f (x) voi saavuttaa pienimmän tai suurimman arvon joko kriittisissä pisteissä tai segmentin päissä.
Esimerkki 3.22.
Ratkaisu. Koska f " (
Tehtävät funktion ääripään löytämiseksi
Esimerkki 3.23. a
Ratkaisu. x ja y y
0
≤ x≤
> 0, kun x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
toimintoja sq.
yksiköitä).
Esimerkki 3.24. p ≈
Ratkaisu. s
S"
R = 2, H = 16/4 = 4.
Esimerkki 3.22.Etsi funktion f (x) = 2x 3 - 15x 2 + 36x - 14 ääripää.
Ratkaisu. Koska f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), sitten funktion kriittiset pisteet x 1 \u003d 2 ja x 2 \u003d 3. Ääripisteet voivat olla vain näissä pisteitä. Koska pisteen x 1 \u003d 2 läpi kulkiessaan derivaatta muuttaa etumerkin plussasta miinukseen, niin tässä vaiheessa funktiolla on maksimi. Kulkiessaan pisteen x 2 \u003d 3 läpi derivaatta muuttaa etumerkin miinuksesta plussiksi, joten pisteessä x 2 \u003d 3 funktiolla on minimi. Laske funktion arvot pisteinä
x 1 = 2 ja x 2 = 3, löydämme funktion ääripäät: maksimi f (2) = 14 ja minimi f (3) = 13.
Esimerkki 3.23.Kivimuurien lähelle on rakennettava suorakaiteen muotoinen alue siten, että se on aidattu metalliverkolla kolmelta sivulta ja se on seinän vieressä neljänneltä puolelta. Tätä varten on a verkon lineaarimetrit. Millä kuvasuhteella sivustolla on suurin pinta-ala?
Ratkaisu.Merkitse sivuston sivut läpi x ja y. Kohteen pinta-ala on yhtä suuri kuin S = xy. Päästää y on seinän vieressä olevan sivun pituus. Sitten ehdon mukaan yhtälön 2x + y = a on oltava voimassa. Siksi y = a - 2x ja S = x (a - 2x), missä
0
≤ x≤ a /2 (tyynyn pituus ja leveys eivät voi olla negatiivisia). S "= a - 4x, a - 4x = 0, kun x = a/4, mistä
y \u003d a - 2 × a / 4 \u003d a / 2. Koska x = a /4 on ainoa kriittinen piste, tarkistetaan muuttuuko derivaatan etumerkki tämän pisteen läpi kulkiessa. x a /4 S "> 0, kun x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
toimintoja S(a/4) = a/4(a - a/2) = a 2 /8 (sq.
yksiköitä).
Koska S on jatkuva päällä ja sen arvot S(0) ja S(a /2) päissä ovat nolla, niin löydetty arvo on funktion suurin arvo. Siten paikan suotuisin kuvasuhde annetuissa ongelman olosuhteissa on y = 2x.
Esimerkki 3.24.Vaaditaan suljettu sylinterimäinen säiliö, jonka tilavuus on V=16 p ≈ 50 m3. Mitkä pitäisi olla säiliön mitat (säde R ja korkeus H), jotta sen valmistukseen kuluisi mahdollisimman vähän materiaalia?
Ratkaisu.Sylinterin kokonaispinta-ala on S = 2 p R(R+H). Tiedämme sylinterin tilavuuden V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Joten S(R) = 2 p (R2+16/R). Löydämme tämän funktion johdannaisen:
S"(R) = 2 p (2R-16 / R 2) = 4 p (R-8 / R 2). S" (R) = 0, kun R3 = 8, siksi
R = 2, H = 16/4 = 4.
Funktiot, ei ole ollenkaan välttämätöntä tietää ensimmäisen ja toisen derivaatan olemassaolosta ja ymmärtää niiden fyysistä merkitystä. Ensin sinun on ymmärrettävä seuraavat asiat:
- funktion ääripäät maksimoivat tai päinvastoin minimoivat funktion arvon mielivaltaisen pienellä alueella;
- ääripisteessä toiminnon ei pitäisi olla epäjatkuvuutta.
Ja nyt sama asia, vain yksinkertaisin sanoin. Katso kuulakärkikynän kärkeä. Jos kynä asetetaan pystysuoraan kirjoituspään ollessa ylöspäin, pallon ääripiste - korkein kohta - on aivan keskellä. Tässä tapauksessa puhumme maksimista. Jos nyt käännät kynän kirjoituspää alaspäin, pallon keskellä on jo toiminto minimi. Tässä esitetyn kuvan avulla voit kuvitella luetellut paperitavarakynän käsittelyt. Joten funktion ääripäät ovat aina kriittisiä pisteitä: sen maksimit tai minimit. Kaavion viereinen osa voi olla mielivaltaisen terävä tai sileä, mutta sen on oltava molemmilla puolilla, vain tässä tapauksessa piste on ääripää. Jos kaavio on vain toisella puolella, tämä piste ei ole ääriarvo, vaikka ääripään ehdot täyttyisivät sen toisella puolella. Tutkitaan nyt funktion ääripäitä tieteellisestä näkökulmasta. Jotta pisteen katsottaisiin olevan ääriarvo, on välttämätöntä ja riittävää, että:
- ensimmäinen derivaatta oli nolla tai sitä ei ollut olemassa pisteessä;
- ensimmäinen derivaatta muuttaa merkkiä tässä vaiheessa.

Ehtoa tulkitaan hieman eri tavalla korkeamman asteen derivaattojen näkökulmasta: pisteessä differentioituvalle funktiolle riittää, että on olemassa pariton derivaatta, joka ei ole yhtä suuri kuin nolla, kun taas kaikki alemman kertaluvun derivaatat on olemassa ja olla yhtä suuri kuin nolla. Tämä on yksinkertaisin tulkinta oppikirjoista, mutta tavallisimmille ihmisille tämä on syytä selittää esimerkillä. Perustana on tavallinen paraabeli. Tee varaus heti, nollapisteessä sillä on minimi. Vähän matematiikkaa:
- ensimmäinen derivaatta (X 2) | = 2X, nollapisteelle 2X = 0;
- toinen johdannainen (2X) | = 2, nollapisteelle 2 = 2.

Tällä yksinkertaisella tavalla havainnollistetaan ehdot, jotka määrittävät funktion ääriarvot sekä ensimmäisen kertaluvun derivaateille että korkeamman asteen derivaateille. Voimme lisätä tähän, että toinen derivaatta on vain sama pariton derivaatta, joka ei ole yhtä suuri kuin nolla, josta keskusteltiin hieman korkeammalla. Kun kyse on kahden muuttujan funktion ääriarvoista, ehtojen on täytyttävä molemmille argumenteille. Kun yleistäminen tapahtuu, osittaiset derivaatat tulevat peliin. Toisin sanoen ääripään olemassaololle pisteessä on välttämätöntä, että molemmat ensimmäisen kertaluvun derivaatat ovat yhtä suuria kuin nolla, tai ainakin yhtä niistä ei ole olemassa. Ekstreemumin olemassaolon riittävyyden vuoksi tutkitaan lauseke, joka on toisen kertaluvun derivaatan tulon ja funktion sekoitetun toisen kertaluvun derivaatan neliön erotus. Jos tämä lauseke on suurempi kuin nolla, on olemassa ääriarvo, ja jos on yhtäläisyys nollaan, kysymys jää avoimeksi ja lisätutkimusta tarvitaan.
