Järjestelmän sisäisten voimien tekemien töiden summa on yleensä eri kuin nolla.

Jos materiaalijärjestelmä on ehdottoman kiinteä kappale, niin sisäisten voimien tekemän työn summa on nolla.

Minkä tahansa voiman tekemä työ on nolla, jos voima kohdistetaan paikallaan olevaan pisteeseen, jonka nopeus on nolla tietyllä hetkellä.

Joustavien venymättömien kaapelien, köysien jne. sisäisten jännitysvoimien työ. yhtä suuri kuin nolla.

Painovoiman työ on yhtä suuri kuin materiaalijärjestelmän painon ja massakeskipisteen pystysiirtymän tulo plus-merkillä, jos massakeskipiste laskeutuu, ja miinusmerkillä, jos massakeskipiste nousee: A = ±Mgh c, missä M on materiaalijärjestelmän massa, kg; h c– massakeskuksen pystysuuntainen liike, m; g - painovoiman kiihtyvyys, neiti 2 .

Akselin ympäri pyörivään ehdottoman jäykään kappaleeseen kohdistetun voiman työ , on yhtä suuri kuin: A=±M P (φ-φ 0 ) , Missä M P- parin kehoon kohdistuvan voiman momentti, Nm; φ-φ 0 – rungon lopullisen kiertokulman arvo.

Kitkavoiman työ : A= -F tr · S, Missä S- liikkuva, m. Kitkavoiman tekemä työ on aina negatiivista.

Jousen elastisten voimien työ : A=0.5s∙(λ 2 0 - λ 2 1 ) , Missä Kanssa- jousen jäykkyyskerroin; λ - jousipidennys, m. Työ on positiivista, kun λ 0 > λ 1 ja negatiivinen klo λ 0 < λ 1 .

5.3.3. Tehtävä d -2. Kineettisen energian muutosta koskevan lauseen soveltaminen mekaanisen järjestelmän liikkeen tutkimukseen

Annettu. Mekaaninen järjestelmä koostuu rullista 1 Ja 2 (tai rulla ja liikkuva lohko), askelpyörä 3 askelsäteillä R 3 = 0,3 m,r 3 = 0,1 m ja pyörimissäde suhteessa pyörimisakseliin ρ 3 = 0,2 m, lohko 4 säde R 4 = 0,2 m ja rahtia 5 Ja 6 (Kuva D 2.0 – D 2.9, Taulukko D-2); kehon 1 Ja 2 katsotaan kiinteiksi homogeenisiksi sylintereiksi ja lohkon massa 4 – jakautuu tasaisesti reunaa pitkin. Kuormien ja tason välinen kitkakerroin f =0,1 . Järjestelmän rungot on yhdistetty toisiinsa kierteillä, jotka on heitetty lohkojen läpi ja kierretty hihnapyörälle 3 (tai hihnapyörällä ja telalla); kierteiden osat ovat samansuuntaisia ​​vastaavien tasojen kanssa. Jousi, jolla on jäykkyyskerroin, on kiinnitetty yhteen rungoista Kanssa .

Voiman alla F = f ( s ), riippuen sen sovelluspisteen siirtymästä s, järjestelmä alkaa liikkua lepotilasta; jousen muodonmuutos liikehetkellä on nolla. Kun liikutaan hihnapyörällä 3 on jatkuva vääntömomentti M vastusvoimat (laakerien kitkasta).

Kaikki rullat rullaavat koneilla luistamatta.

Jos määrätyn kuormamassan mukaan 5 Ja 6 tai rullien massaa 1 (Kuva E 2.0-2.4) ja 2 (Kuva D 2.5-2.9) ovat nolla, silloin niitä ei voida esittää piirustuksessa.

Määritellä: halutun määrän arvo liikkeen hetkellä s tulee tasa-arvoiseksi s 1 = 0,2 m. Haluttu arvo ilmoitetaan taulukon D 2 sarakkeessa "Etsi", jossa se on merkitty: ω 3 – kappaleen kulmanopeus 3 ; ε 4 – kehon kulmakiihtyvyys 4 ; v 5 – kehon nopeus 5 ; ja c2 on kehon massakeskipisteen kiihtyvyys 2 ja niin edelleen.

Ohjeet. Kun ratkaiset ongelman, ota huomioon, että järjestelmän liike-energia on yhtä suuri kuin kaikkien järjestelmään kuuluvien kappaleiden liike-energioiden summa; tämä energia tulee ilmaista nopeudella (lineaarinen tai kulma), joka on määritettävä tehtävässä. Energiaa laskettaessa käytetään hetkellistä nopeuskeskiötä määrittämään suhde tasossa yhdensuuntaisesti liikkuvan kappaleen pisteiden nopeuksien välillä tai sen kulmanopeuden ja massakeskuksen nopeuden välillä. Työtä laskettaessa on välttämätöntä ilmaista kaikki liikkeet tietyn liikkeen kautta s 1 , ottaen huomioon, että liikkeiden välinen suhde on tässä sama kuin vastaavien nopeuksien välillä.

Alla käsitellyt esimerkit tarjoavat tuloksia, joita voidaan käyttää suoraan ongelmien ratkaisemisessa.

1. Painovoiman työ. Liikkukoon piste M, johon painovoima P vaikuttaa paikasta toiseen. Valitaan koordinaattiakselit siten, että akseli on suunnattu pystysuunnassa ylöspäin (kuva 231). Sitten . Korvaamalla nämä arvot kaavaan (44), saamme ottaen huomioon, että integrointimuuttuja on:

Jos piste on korkeampi, niin , jossa h on pisteen pystysuuntainen liike; jos piste on pisteen alapuolella, niin .

Lopulta saamme

Näin ollen painovoiman tekemä työ on yhtä suuri kuin plus- tai miinusmerkillä otetun voiman suuruuden ja sen kohdistamispisteen pystysuuntaisen siirtymän tulo. Teos on positiivinen, jos aloituspiste on korkeampi kuin lopetuspiste, ja negatiivinen, jos aloituspiste on alempi kuin loppupiste.

Saadusta tuloksesta seuraa, että painovoiman työ ei riipu sen liikeradan tyypistä, jota pitkin sen sovelluspiste liikkuu. Voimia, joilla on tämä ominaisuus, kutsutaan potentiaalisiksi (katso § 126).

2. Kimmovoiman työ. Tarkastellaan vaakatasossa olevaa kuormaa M, joka on kiinnitetty jousen vapaaseen päähän (kuva 232, a). Merkitse tasolle pisteellä O jousen päätypaikka, kun se ei ole jännittynyt - jännittämättömän jousen pituus) ja ota tämä piste koordinaattien origoksi. Jos nyt vedetään kuormaa tasapainoasennosta O venyttäen jousi arvoon I, niin jousi saa venymän ja pisteeseen O kohdistuva kimmovoima F vaikuttaa kuormaan. Koska meidän tapauksessamme niin kaavaan (6) 76 §:stä

Viimeinen yhtälö pätee myös (kuorma on pisteen O vasemmalla puolella); silloin voima F suunnataan oikealle ja tulos on sellainen kuin sen pitääkin olla,

Etsitään kimmovoiman tekemä työ siirrettäessä kuormaa asennosta asentoon

Koska tässä tapauksessa korvaamalla nämä arvot kaavaan (44), löydämme

(Sama tulos saadaan F:n riippuvuuden kuvaajasta (kuva 232, b), laskemalla piirustuksessa varjostetun puolisuunnikkaan pinta-ala a ja huomioiden työn etumerkki.) Tuloksena olevassa kaavassa , edustaa jousen alkuvenymää - jousen lopullista pidennystä.

eli kimmovoiman työ on yhtä suuri kuin puolet jäykkyyskertoimen ja jousen alku- ja loppuvenymän (tai puristuksen) neliöiden tulosta.

Työ on positiivinen, kun eli kun jousen pää siirtyy kohti tasapainoasemaa, ja negatiivinen, kun eli kun jousen pää siirtyy pois tasapainoasennosta.

Voidaan osoittaa, että kaava (48) pysyy voimassa, kun pisteen M liike ei ole suoraviivaista. Siten käy ilmi, että voiman F työ riippuu vain pisteen M arvoista ja ei riipu pisteen M liikeradan tyypistä. Näin ollen kimmovoima on myös potentiaalinen.

3. Kitkavoiman työ. Tarkastellaan pistettä, joka liikkuu jotakin karkeaa pintaa (kuva 233) tai käyrää pitkin. Pisteeseen vaikuttava kitkavoima on suuruudeltaan yhtä suuri kuin missä f on kitkakerroin ja N on pinnan normaalireaktio. Kitkavoima on suunnattu vastapäätä pisteen liikettä. Näin ollen ja kaavan (44) mukaisesti

Jos kitkavoima on numeerisesti vakio, niin missä s on käyrän kaaren pituus, jota pitkin piste liikkuu.

Siten kitkavoiman liukumisen aikana tekemä työ on aina negatiivinen. Koska tämä työ riippuu kaaren pituudesta, kitkavoima on ei-potentiaalinen voima.

4. Painovoiman työ Jos maapalloa (planeettaa) pidetään homogeenisena pallona (tai homogeenisista samankeskisistä kerroksista koostuvana pallona), niin pisteessä M, jonka massa sijaitsee pallon ulkopuolella etäisyyden päässä sen keskustasta (tai pallon pintaan), tapahtuu painovoiman F vaikutus, joka on suunnattu kohti keskustaa O (kuva 234), jonka arvo määräytyy kaavalla (5) §:stä 76. Esitetään tämä kaava muodossa

n määritämme kertoimen k ehdosta, että kun piste on maan pinnalla (r = R, missä R on maan säde), painovoima on mg, missä g on maapallon kiihtyvyys. painovoima (tarkemmin sanottuna painovoima) maan pinnalla. Sitten sen täytyy olla

Huomaa, että työllä ja energialla on samat mittayksiköt. Tämä tarkoittaa, että työ voidaan muuntaa energiaksi. Esimerkiksi kehon nostamiseksi tietylle korkeudelle, sillä on potentiaalienergiaa, tarvitaan voima, joka tekee tämän työn. Nostovoiman tekemä työ muuttuu potentiaalienergiaksi.

Sääntö työn määrittämiseksi riippuvuusgraafin F(r) mukaan: työ on numeerisesti yhtä suuri kuin voiman ja siirtymän kaavion alla olevan kuvan ala.

Voimavektorin ja siirtymän välinen kulma

1) Määritä oikein työn tekevän voiman suunta; 2) Kuvaamme siirtymävektorin; 3) Siirrämme vektorit yhteen pisteeseen ja saamme halutun kulman.

Kuvassa kehoon vaikuttavat painovoima (mg), tuen reaktio (N), kitkavoima (Ftr) ja köyden F jännitysvoima, jonka vaikutuksesta kappale liikkuu r.

Painovoiman työ

Maareaktiotyö

Kitkavoiman työ

Työ tehdään köyden kiristämällä

Työ tehdään tuloksena olevalla voimalla

Resultanttivoiman tekemä työ voidaan löytää kahdella tavalla: 1. menetelmä - kaikkien kehoon vaikuttavien voimien työn summana (ottaen huomioon "+" tai "-" -merkit) kaikkien kehoon vaikuttavien voimien summa.
Menetelmä 2 - etsi ensin resultanttivoima, sitten suoraan sen työ, katso kuva

Joustovoiman työ

Joustovoiman tekemän työn löytämiseksi on otettava huomioon, että tämä voima muuttuu, koska se riippuu jousen venymisestä. Hooken laista seuraa, että kun absoluuttinen venymä kasvaa, voima kasvaa.

Laskeaksesi elastisen voiman työn jousen (rungon) siirtyessä epämuodostuneesta tilasta epämuodostuneeseen tilaan, käytä kaavaa

Tehoa

Skalaarisuure, joka luonnehtii työn nopeutta (analogia voidaan vetää kiihtyvyyteen, joka kuvaa nopeuden muutosnopeutta). Määritetään kaavalla

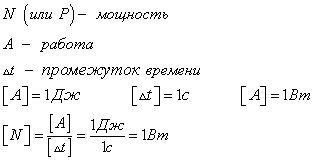
Tehokkuus

Tehokkuus on koneen tekemän hyödyllisen työn suhde kaikkeen samana aikana käytettyyn työhön (toimitettuun energiaan)

Tehokkuus ilmaistaan ​​prosentteina. Mitä lähempänä tämä luku on 100 %, sitä parempi on koneen suorituskyky. Tehokkuus ei voi olla suurempi kuin 100, koska on mahdotonta tehdä enemmän työtä pienemmällä energialla.

Kaltevan tason hyötysuhde on painovoiman tekemän työn suhde kaltevaa tasoa pitkin liikkumiseen kuluvaan työhön.

Tärkein asia muistaa

1) Kaavat ja mittayksiköt;
2) Työ suoritetaan väkisin;
3) Osaa määrittää voima- ja siirtymävektorin välinen kulma

Jos voiman tekemä työ liikutettaessa kappaletta suljettua polkua pitkin on nolla, niin tällaisia ​​voimia kutsutaan konservatiivinen tai potentiaalia. Kitkavoiman tekemä työ liikutettaessa kappaletta suljettua reittiä pitkin ei ole koskaan yhtä suuri kuin nolla. Kitkavoima, toisin kuin painovoima tai elastinen voima, on ei-konservatiivinen tai ei-potentiaalinen.

On ehtoja, joissa kaavaa ei voida käyttää
Jos voima on muuttuva, jos liikerata on kaareva viiva. Tässä tapauksessa polku jaetaan pieniin osiin, joille nämä ehdot täyttyvät, ja jokaisella näistä osista lasketaan perustyö. Kokonaistyö tässä tapauksessa on yhtä suuri kuin perustöiden algebrallinen summa:

Tietyn voiman tekemän työn arvo riippuu vertailujärjestelmän valinnasta.

30.2.1. Gravitaatiotyö jatkuu

sen käyttökohdan lopullinen liike

Anna materiaalin osoittaa
liikkuu asennosta
asentoon
mielivaltaista rataa pitkin - katso kuva 3.

Kuva 30.3

.

Yleisesti kutsuttu: - pisteen alkuaseman geodeettinen korkeus; - pisteen lopullisen sijainnin geodeettinen korkeus;
- ero geodeettisissa korkeuksissa. Täten:

- painovoiman tekemä työ ei riipu sen soveltamispisteen liikeradan muodosta ja on yhtä suuri kuin painovoimamoduulin ja tämän pisteen alku- ja loppuaseman geodeettisten korkeuksien eron tulo.

30.2.2. Elastisen voiman työ sen kohdistamispisteen lopullisessa siirtymässä

Kuvassa 30.4:
- kappale, johon kohdistetaan elastinen voima ; - kehon asento, joka vastaa jousen epämuodostunutta tilaa;

- koordinoida

Johtaa kaava kimmovoiman työn laskemiseksi

ata, joka määrittää jonkin kehon nykyisen asennon
.

SISÄÄN
Hooken lain mukaan
, Missä - jousen jäykkyys, - sen muodonmuutoksen suuruus. Kuvassa 30.4 esitettyä kolmiota kutsutaan kimmovoimadiagrammiksi.

Kimmovoiman työ siirrettäessä kappaletta tietystä koordinaatin määrittämästä epämuodostuneesta tilasta , muotoutumattomaksi (
), kutsutaan kimmovoiman kokonaistyöksi.

Kuva 30.4

kimmovoiman kokonaistyö (kun elastinen elementti siirretään muotoutumattomaan tilaan) määritetään kaavalla

.

Epätäydellinen elastisen voiman työ (hyväksyttävä lyhenne: "kimmovoiman työ") on työtä, jonka elastinen elementti suorittaa siirtyessään yhdestä epämuodostuneesta tilastaan ​​toiseen. On selvää, että:

kimmovoiman työ on yhtä suuri kuin sen kolmiokaavion sen osan pinta-ala, joka sijaitsee niiden koordinaattien välissä, jotka erottavat elastisen elementin yhden epämuodostuneen tilan toisesta.

30.2.3. Gravitaatiovoiman työ

N

Johda kaava gravitaatiovoiman työn laskemiseksi

ja kuva 30.5:
- houkutteleva keskus (maa, aurinko jne.); - veti massaa; - Newtonin lain määräämä vetovoima:
. Akseli alkaa
, - jokin lopullinen koordinaattiarvo .

Painovoiman tekemä kokonaistyö (
) on työ, jonka se tekee siirtäessään vetämää massaa äärettömyydestä etäisyyden määräämään asentoon . Johdetaan sille kaava

Kuva 30.5

laskelmat:

gravitaatiovoiman tekemä kokonaistyö (sen suorittama vetäytyneen massan siirtyessä äärettömyydestä etäisyyden määräämään asentoon vetokeskuksesta) määritetään kaavalla
.

Hanki tulos itse:

painovoiman työ, joka kuluu vedetyn massan siirtämiseen paikasta V määräytyy kaavan mukaan

.

30.3. Kaavat kiinteisiin kappaleisiin vaikuttavien voimien kokonaistehojen laskemiseksi

30.3.1. Translaatioliikkeen tapaus

Yksittäisten voimien kehittämät voimat:

Koska keho liikkuu sitten eteenpäin

Vain .

Siksi kokonaisteho:

translaationaalisesti liikkuvaan kappaleeseen kohdistettujen voimien kokonaisteho määritellään yksittäisen voiman tehoksi, joka on yhtä suuri kuin tähän kappaleeseen vaikuttavien voimien päävektori ja jonka kohdistamispiste liikkuu kappaleen nopeuden mukana.

8.3.2. Tapaus pallomaisesta liikkeestä

pallomaisesti liikkuvaan kappaleeseen kohdistettujen voimien kokonaisteho määritellään tähän kappaleeseen kohdistuvan erillisen voimaparin tehona, jonka momentti on yhtä suuri kuin kappaleeseen vaikuttavien ulkoisten voimien päämomentti.

30.3.3. Pyörimisliikkeen tapaus

Pyörivä liike on pallomaisen liikkeen erikoistapaus.

Olkoon pyörimisakseli . Sitten

pyörivästi liikkuvaan kappaleeseen kohdistettujen voimien kokonaisteho määritellään ulkoisten voimien päämomentin tulona suhteessa pyörimisakseliin ja kulmanopeuden projektion samalle akselille.

Konkreettisia ongelmia ratkaistaessa joudutaan usein käsittelemään jatkuvia voimien momentteja ja samalla määrittämään niiden toiminta äärellisillä siirtymillä. Tässä tapauksessa meillä on:

(integraation jälkeen)
, eli:

kappaleen lopulliseen kiertoon kohdistuvien voimien kokonaistyö määritellään ulkoisten voimien päämomentin tulona suhteessa pyörimisakseliin ja siitä johtuvan kulmakoordinaatin lisäyksen tulona.

Tunnettu kaava fysiikasta A = Fs Voiman työn määrittämiseen voidaan käyttää vain silloin, kun kehoon vaikuttaa liikkeen suuntaan suunnattu vakiovoima. Usein on kuitenkin tarpeen määrittää työ, kun voima muuttuu kuljetun matkan mukaan. Esimerkiksi jousen venyttämiseksi sinun on käytettävä voimaa, joka on verrannollinen kuljettuun matkaan - jousen venymiseen.

Anna kehon liikkua segmenttiä [ a, b] akselit Härkä, kun taas voimavektorin projektio akselille Härkä on toiminto F(x) Perustelu x. Voit määrittää voiman tekemän työn jakamalla segmentin [ a, b] päällä n osia pisteillä a = x0 < x 1 < x 2 < ...x n= b . Näin ollen koko kehon liike alkaen a V b sisältää n polun osia.

Käytetty voima A on yhtä suuri kuin perustöiden summa, joka suoritetaan siirrettäessä kehoa polun kutakin osaa pitkin.

Esimerkki 1. Puristus S kierrejousi verrannollinen käytettyyn voimaan F. Laske voiman tekemä työ F kun jousta puristetaan 5 cm, jos tarvitaan 1 kg:n voima sen puristamiseen 1 cm.

Ratkaisu. Pakottaa F ja liikkuvat S ehdollisesti riippuvuudesta F=kS, Missä k- vakio. Me ilmaisemme S metreissä, F- kilogrammoina. klo S=0,01 F=1, eli 1= k*0,01, mistä k=100, F=100S.

Kaavan (1) avulla määritämme voiman työn:

Esimerkki 2. Pakottaa F, jolla sähkövaraus e 1 hylkii latauksen e 2 (saman merkin), joka sijaitsee etäisyyden päässä siitä r, ilmaistaan ​​kaavalla

Missä k- vakio.

Laske voiman tekemä työ F siirrettäessä latausta e 2 pisteestä A 1, kaukana e 1 etäisyydellä r 1, asiaan A 2, erillään e 1 etäisyydellä r 2, olettaen, että maksu e 1 sijoitettu pisteeseen A 0, otettu lähtöpisteeksi.

Ratkaisu. Laskemme kaavan (1) avulla voiman työn:

.

Kun saamme

.

Kun saamme. Viimeistä suuruutta kutsutaan varauksen synnyttämän kentän potentiaaliksi e 1 .

Esimerkki 3. Laske työ, joka on tehtävä 9 g:n massapallon poistamiseksi tynnyristä, jonka korkeus on 3 m.