पाठ मकसद:

निरंतर कार्यों की संपत्ति के आधार पर, अंतराल की सामान्यीकृत विधि के प्रभावी अनुप्रयोग के ज्ञान, कौशल और क्षमताओं का निर्माण करना;

समान परिवर्तनों की ओर ले जाने वाली क्रियाओं का एक एल्गोरिथम तैयार करना;

असमानताओं को हल करते समय खुद को इसे लागू करना सिखाएं;

नई परिस्थितियों में ज्ञान, कौशल और क्षमताओं के हस्तांतरण को अंजाम देना।

शैक्षिक: व्यवस्थितकरण, समेकन, ज्ञान, कौशल और क्षमताओं का सामान्यीकरण।

शैक्षिक: एक पूर्ण सुसंगत तर्क, सटीकता, स्वतंत्रता की आवश्यकता की शिक्षा।

विकासशील: गणितीय तर्क का विकास, सोच की गणितीय शैली का निर्माण (तर्क के पाठ्यक्रम का एक स्पष्ट विच्छेदन), संज्ञानात्मक रुचि।

1) पाठ का परिचय, लक्ष्य और उद्देश्य निर्धारित करना - 2 मि.

2) गृहकार्य की जाँच करना - 2 मिनट। (ललाट काम, आत्म-नियंत्रण)।

3) अंतराल विधि द्वारा असमानताओं को हल करने के चरणों की गणितीय पुष्टि - 4 मिनट (छात्रों के उत्तर तैयार)।

4) असमानताओं के गुणों की पुनरावृत्ति - 2 मिनट।

5) बुनियादी ज्ञान के दोहराव और अद्यतन के माध्यम से नई शैक्षिक सामग्री के आत्मसात (अध्ययन) की तैयारी - 5 मिनट। (सामने का काम, सवालों के जवाब, समस्या की स्थिति)।

6) असमानताओं को हल करने के लिए सामान्यीकृत अंतराल विधि, प्रारंभिक समझ - 13 मिनट। (अंतराल की विधि द्वारा असमानताओं का सामूहिक समाधान: बोर्ड पर और नोटबुक में)।

7) गृहकार्य की जानकारी, उसे करने के निर्देश - 1 मिनट।

8) नए ज्ञान का समेकन - 15 मिनट। (स्वतंत्र कार्य - विकल्प 1)।

9) पाठ का सारांश, प्रतिबिंब - 1 मिनट।

1) पाठ का परिचय, लक्ष्य और उद्देश्य निर्धारित करना। (शिक्षक की कहानी)

1) स्कूल में अंतराल की पद्धति के व्यापक अनुप्रयोग की आवश्यकता गणित पढ़ाने की पूरी प्रक्रिया की विचारधारा से निर्धारित होती है। मुद्दा यह है कि कार्यात्मक रेखा (गणित की नींव के अध्ययन में मुख्य में से एक) को शक्तिशाली तकनीकी सहायता प्राप्त होती है। अंतराल की विधि कार्यात्मक निर्भरता की ऐसी महत्वपूर्ण विशेषताओं पर आधारित होती है जैसे किसी फ़ंक्शन के शून्य, इसके निरंतर संकेत के अंतराल और एकरसता। तब समीकरणों और असमानताओं की कार्यात्मक उत्पत्ति, साथ ही उनके समाधान के तरीके अधिक स्पष्ट हो जाते हैं। किसी फलन की निरंतरता की श्रेणियां, अनंत असंततता के बिंदुओं के आसपास उसके ग्राफ का व्यवहार, मूल पर प्रमेय, संकेत की निरंतरता, चरम बिंदु और उनके प्रकार अधिक दृश्य बन जाते हैं। और यह सब व्यवस्थित रूप से एक कार्यात्मक पूरे में जुड़ा हुआ है।

दूसरी ओर, उपयोग की जाने वाली अध्ययन की वस्तुओं का ज्यामितीयकरण भी अमूल्य है, अर्थात। कार्यात्मक निर्भरता के सभी उपयोग किए गए गणितीय उपकरणों को नेत्रहीन, आलंकारिक रूप से प्रस्तुत करते हैं।

अंतराल विधि के मूल सिद्धांत:

• कार्यात्मक (सामान्यीकृत) दृष्टिकोण;
• कार्यात्मक गुणों के ज्यामितीयकरण पर निर्भरता;
• अनुसंधान दृश्य।

यह एक ही तरह के कार्यों में उपयोग किए जाने वाले अन्य की तुलना में विधि के निम्नलिखित लाभों की ओर जाता है: लक्ष्य को प्राप्त करने की सादगी और गति; दृश्यता (और नियंत्रित करने या दोबारा जांच करने की क्षमता); संसाधनों और समय की गणना में अर्थव्यवस्था; पूरी स्थिति के कवरेज की चौड़ाई, सामान्यीकृत सोच और विश्लेषण के कौशल का गठन और विकास, साथ ही तार्किक निष्कर्ष निकालने के लिए इससे जुड़े कौशल।

2) गृहकार्य की जाँच करना।(स्लाइड नंबर 4)

3) असमानताओं को हल करने के लिए अंतराल की विधि के बारे में एक कहानी। (छात्र उत्तर)।

अंतराल की विधि द्वारा असमानताओं के समाधान की गणितीय पुष्टि।

1) असमानताओं पर विचार करें: (x-2)(x-3)>0। (स्लाइड नंबर 5)

आप इसे इस प्रकार हल कर सकते हैं: दो कारकों का गुणनफल (भागफल) धनात्मक होता है यदि और केवल तभी जब दोनों कारकों का एक ही चिन्ह हो, अर्थात। असमानता दो प्रणालियों के संयोजन के बराबर है: (स्लाइड संख्या 6)

पहली प्रणाली से हम x >3 प्राप्त करते हैं, दूसरे x . से< 2.

समाधान दो प्रणालियों के समाधान का मिलन है।

जवाब:

ग्राफिक विधि (स्लाइड नंबर 7)

एक और तरीका है अंतराल विधि(स्लाइड नंबर 8)।

उनका विचार इस प्रकार है।

वास्तविक रेखा पर, बहुपद (x-2)(x-3) खड़े होने के शून्य (मूल) को चिह्नित करें

असमानता के बाईं ओर, अर्थात्। नंबर 2 और 3.

जब x >3 (बड़े मूल के दायीं ओर), तब (x-2)(x-3)>0, क्योंकि प्रत्येक गुणनखंड धनात्मक होता है।

यदि आप अक्ष के अनुदिश ऋणात्मक दिशा में चलते हैं, तो बिंदु x=3 से गुजरने पर गुणनखंड (x-3) संकेत बदल जाएगा। उत्पाद (x-2) (x-3) में एक नकारात्मक कारक दिखाई देगा, जिसके परिणामस्वरूप (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

अब असमानता का समाधान लिखना आसान है:

निष्कर्ष: x=2 और x=3 . बिंदुओं से गुजरने पर ही गुणन चिह्न बदल सकता है

और, इसलिए, प्रत्येक प्राप्त अंतराल पर चिन्ह को सुरक्षित रखता है।

इस सरल उदाहरण में, अंतराल विधि के विचार को समझना आसान है, लेकिन यह कोई ध्यान देने योग्य लाभ नहीं दिखाता है।

हम निम्नलिखित उदाहरण में अंतराल विधि की तर्कसंगतता, इसकी शक्ति पर विचार करेंगे (स्लाइड संख्या 9, 10,11, 12))

2) असमानता को हल करें (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (एक्स-10)>0.

सिस्टम के एक सेट का उपयोग करके इस असमानता को हल करने के लिए, प्रत्येक सिस्टम में 10 असमानताओं के साथ 512 सिस्टम के एक सेट पर विचार करना होगा।

आइए अंतराल विधि का उपयोग करें। हम बहुपद के शून्यकों को वास्तविक रेखा पर अंकित करते हैं। अंतराल x>10 पर बहुपद धनात्मक होगा, क्योंकि प्रत्येक गुणनखंड धनात्मक है। प्रत्येक अगली जड़ से गुजरने पर, बहुपद चिन्ह बदल जाएगा, क्योंकि उत्पाद में एक अतिरिक्त ऋणात्मक कारक दिखाई देगा। अब साइन अल्टरनेशन का उपयोग करके असमानता का हल लिखना आसान है।

अंतराल विधि के लाभ।

• लक्ष्य प्राप्त करने की सादगी और गति;
• दृश्यता (और नियंत्रित करने या दोबारा जांच करने की क्षमता);
• कम्प्यूटेशनल कार्य और समय की मात्रा में उल्लेखनीय कमी;
• पूरी स्थिति के कवरेज की चौड़ाई;
• सामान्यीकृत सोच और विश्लेषण कौशल का गठन और विकास, साथ ही तार्किक निष्कर्ष निकालने के लिए संबंधित कौशल।

टिप्पणी। असमानताओं को हल करना बहुत सुविधाजनक है, जिनमें से बाईं ओर का कारक है, क्योंकि शून्य (मूल) को खोजना मुश्किल नहीं है।

कार्य: अंतराल विधि का उपयोग करके असमानता को हल करें (एक्स+3) 3 (एक्स-4) 2 (एक्स-5)>0(स्लाइड 13)

4) असमानताओं के गुणों की पुनरावृत्ति।

क) प्रश्न: किन असमानताओं को समतुल्य कहा जाता है?

(दो असमानताओं को समतुल्य कहा जाता है यदि पहली असमानता का कोई समाधान दूसरी का समाधान है और इसके विपरीत, दूसरी का कोई भी समाधान पहले का समाधान है)।

या: दो असमानताओं को समतुल्य कहा जाता है यदि उनके समाधान के समुच्चय समान हों।

स्लाइड 14. असमानताओं के गुणों की पुनरावृत्ति।

स्लाइड 15. प्रश्न का उत्तर दें और समझाएं।

क्या असमानताएँ समान हैं?

1) 4x-5<0 и 4х<5

2) -2x+5>0 और 2x-5<0

3) -3x 2 +5x-7>0 और 3x 2 -5x+7<0

4) (x+1)>0 और (x 2 +5x+10)(x+1)>0

5) बुनियादी ज्ञान की पुनरावृत्ति और अद्यतन के माध्यम से नई शैक्षिक सामग्री के आत्मसात (अध्ययन) की तैयारी में मौखिक ललाट कार्य।

स्लाइड 16. एक बिंदु पर सतत फलन की परिभाषा।

स्लाइड 17. निरंतर कार्यों की संपत्ति।

स्लाइड 18. निरंतरता के अंतराल खोजें।

स्लाइड 19. गलती का पता लगाएं।

स्लाइड 20. असमानता को मौखिक रूप से हल करें,
एक चार्ट का उपयोग करना।

स्लाइड 21, 22. असमानता को एक समान स्थिति से बदलना।

असमानता को हल करें

यह असमानता शर्त f(x) के बराबर है < 0 गिनती

इसलिए, हमें x के सभी मानों को खोजने की आवश्यकता है जिसके लिए शर्त f(x) < 0.

6) असमानताओं को हल करने के लिए सामान्यीकृत अंतराल विधि, प्रारंभिक समझ - 10 मिनट। (अंतराल की विधि द्वारा असमानताओं का सामूहिक समाधान: बोर्ड पर और नोटबुक में)।

स्लाइड 23. कलन विधि। असमानताओं को हल करने के लिए सामान्यीकृत विधि।

असमानताओं का हल f(x)>0, f(x) > 0, एफ (एक्स)<0, f(x)< 0 अंतराल विधि द्वारा। (योजना)

स्लाइड 24 और 25। एल्गोरिथम द्वारा असमानता को हल करना। (एल्गोरिदम के सभी बिंदुओं पर टिप्पणियाँ)।

स्लाइड 26. इस असमानता के समाधान का चित्रमय चित्रण।

स्लाइड 27. बोर्ड और नोटबुक में असमानता को हल करें .

स्लाइड 28. इस असमानता के समाधान का चित्रमय चित्रण।

स्लाइड 29. बोर्ड और नोटबुक में असमानता को हल करें

स्लाइड 30. इस असमानता के समाधान का चित्रमय चित्रण।

स्लाइड 31, 32. असमानता को मौखिक रूप से हल करें, चित्र के अनुसार

7) गृहकार्य की जानकारी।(अंतराल विधि से हल करें विकल्प संख्या 2)

8) नए ज्ञान का समेकन (स्वतंत्र कार्य, विकल्प संख्या 1)।

9) पाठ को सारांशित करना, तैयार किए गए समाधानों पर आत्म-नियंत्रण (स्लाइड्स 33, 34, 35), अंतराल की सामान्यीकृत विधि और इसके आवेदन के एल्गोरिदम की पुनरावृत्ति।

10) विषय में सामग्री और छात्रों की रुचि को आत्मसात करने का विश्लेषण।तर्कसंगत, मॉड्यूलो, अपरिमेय, घातीय, लॉगरिदमिक सहित किसी भी असमानता को हल करने में यह विधि सार्वभौमिक है, क्योंकि अंतराल विधि समीकरणों को हल करने के लिए असमानताओं के समाधान को कम करती है, एक बिंदु पर डोमेन और फ़ंक्शन के मूल्य को खोजने से कठिनाइयों का कारण नहीं बनता है। लेकिन मुझे असमानताओं का उदाहरण देना था जहां इस पद्धति का उपयोग उचित नहीं है, जहां असमानताओं को हल करने के लिए अन्य तरीकों को लागू करना अधिक तर्कसंगत है।

प्रस्तुति "असमानताओं को हल करने में निरंतरता का अनुप्रयोग"। (35 स्लाइड्स)

परिभाषा 4. किसी फलन को खंड पर निरंतर कहा जाता है यदि यह इस खंड के प्रत्येक बिंदु पर निरंतर है (बिंदु a पर यह दाईं ओर निरंतर है, अर्थात, और बिंदु b पर यह बाईं ओर निरंतर है, अर्थात)।

परिभाषा के अपने क्षेत्र में सभी बुनियादी प्राथमिक कार्य निरंतर हैं।

एक खंड पर निरंतर कार्यों के गुण:

• 1) यदि कोई फलन किसी खंड पर सतत है, तो वह इस खंड (पहला वीयरस्ट्रैस प्रमेय) पर आबद्ध है।
• 2) यदि कोई फलन किसी खंड पर निरंतर है, तो इस खंड पर यह अपने न्यूनतम मान और इसके अधिकतम मान (दूसरा वीयरस्ट्रैस प्रमेय) तक पहुँच जाता है (चित्र 2 देखें)।
• 3) यदि कोई फलन किसी खंड पर निरंतर है और उसके सिरों पर विभिन्न चिह्नों के मान लेता है, तो खंड के अंदर कम से कम एक बिंदु ऐसा होता है (बोलजानो-कॉची प्रमेय)।

फंक्शन ब्रेकप्वाइंट और उनका वर्गीकरण

फ़ंक्शन निरंतरता बिंदु खंड

जिन बिंदुओं पर निरंतरता की स्थिति संतुष्ट नहीं होती है, उन्हें इस फ़ंक्शन के असंततता बिंदु कहा जाता है। यदि किसी फ़ंक्शन का एक असंततता बिंदु है, तो परिभाषा 1, 2 में निर्दिष्ट फ़ंक्शन की निरंतरता के लिए तीन शर्तों में से कम से कम एक इसमें संतुष्ट नहीं है, अर्थात्:

1) फ़ंक्शन को बिंदु के आस-पास परिभाषित किया गया है, लेकिन बिंदु पर ही परिभाषित नहीं किया गया है। तो उदाहरण 2 ए में माना गया फ़ंक्शन एक बिंदु पर एक विराम है, क्योंकि यह इस बिंदु पर परिभाषित नहीं है।

2) फ़ंक्शन को एक बिंदु और उसके पड़ोस पर परिभाषित किया गया है, एक तरफा सीमाएं हैं और, लेकिन वे एक दूसरे के बराबर नहीं हैं:। उदाहरण के लिए, उदाहरण 2 बी) से फ़ंक्शन एक बिंदु और उसके पड़ोस पर परिभाषित किया गया है, लेकिन, चूंकि, ए।

3) फ़ंक्शन को बिंदु और उसके आस-पास परिभाषित किया गया है, एक तरफा सीमाएं हैं और वे एक दूसरे के बराबर हैं, लेकिन बिंदु पर फ़ंक्शन के मान के बराबर नहीं हैं:। उदाहरण के लिए, फ़ंक्शन। यहां विराम बिंदु है: इस बिंदु पर फ़ंक्शन परिभाषित किया गया है, एक तरफा सीमाएं हैं और एक दूसरे के बराबर हैं, लेकिन, यानी।

फ़ंक्शन ब्रेकप्वाइंट को निम्नानुसार वर्गीकृत किया गया है।

परिभाषा 5. एक बिंदु को पहले प्रकार के फलन का असंततता बिंदु कहा जाता है यदि परिमित सीमाएं हैं और इस बिंदु पर, लेकिन वे एक दूसरे के बराबर नहीं हैं:। तब मात्रा को बिंदु पर फलन की छलांग कहा जाता है।

परिभाषा 6. एक बिंदु को किसी फ़ंक्शन के हटाने योग्य असंततता का बिंदु कहा जाता है यदि इस बिंदु पर परिमित सीमाएं हैं और वे एक दूसरे के बराबर हैं: लेकिन फ़ंक्शन स्वयं बिंदु पर परिभाषित नहीं है, या परिभाषित नहीं है, लेकिन।

परिभाषा 7. एक बिंदु को दूसरे प्रकार के फ़ंक्शन का एक असंततता बिंदु कहा जाता है यदि इस बिंदु पर कम से कम एक तरफा सीमा (या) मौजूद नहीं है या अनंत के बराबर है।

उदाहरण 3. निम्नलिखित फलनों के विराम बिंदु ज्ञात कीजिए और उनके प्रकार ज्ञात कीजिए: a) b)

फेसला। ए) फ़ंक्शन परिभाषित और अंतराल पर निरंतर है, क्योंकि इनमें से प्रत्येक अंतराल पर यह निरंतर प्राथमिक कार्यों द्वारा दिया जाता है। नतीजतन, केवल वे बिंदु जिन पर फ़ंक्शन अपने विश्लेषणात्मक असाइनमेंट को बदलता है, किसी दिए गए फ़ंक्शन के असंततता बिंदु हो सकते हैं, अर्थात। अंक मैं। आइए बिंदु पर फ़ंक्शन की एक तरफा सीमाएँ खोजें:

चूंकि एकतरफा सीमाएं मौजूद हैं और परिमित हैं, लेकिन एक-दूसरे के बराबर नहीं हैं, बिंदु पहली तरह का एक असंततता बिंदु है। समारोह कूद:

एक बिंदु के लिए हम पाते हैं।

एक अंतराल पर एक समारोह की निरंतरता

मापदण्ड नाम	अर्थ
लेख विषय:	एक अंतराल पर एक समारोह की निरंतरता
रूब्रिक (विषयगत श्रेणी)	गणित

परिभाषा।एक फ़ंक्शन को अंतराल पर निरंतर कहा जाता है यदि यह इस अंतराल के प्रत्येक बिंदु पर निरंतर है।

यदि फ़ंक्शन के लिए परिभाषित किया गया है एक्स=एऔर जिसमें एफ(एक्स) = एफ(ए),

तब वे कहते हैं कि एफ(एक्स) बिंदु पर और दाईं ओर निरंतर. इसी प्रकार, यदि एफ(एक्स) = एफ(बी), तो हम कहते हैं कि बिंदु पर बीयह समारोह निरंतर छोड़ दिया.

परिभाषा।फ़ंक्शन को आमतौर पर खंड पर निरंतर कहा जाता है [ ए, बी], यदि यह अपने प्रत्येक बिंदु पर (बिंदु . पर) निरंतर है एदाईं ओर निरंतर, एक बिंदु पर बीबाईं ओर निरंतर है)।

उच्चतम मूल्यकार्यों पर = एफ(एक्स) खंड पर [ ए, बी एफ(एक्स 1) कि एफ(एक्स) £ एफ(एक्स 1) सबके लिए एक्स Î [ ए, बी].

न्यूनतम मूल्यकार्यों पर = एफ(एक्स) खंड पर [ ए, बी] इस तरह के इसके मूल्य को कॉल करने के लिए प्रथागत है एफ(एक्स 2) कि एफ(एक्स) ³ एफ(एक्स 2) सबके लिए एक्स Î [ ए, बी].

एक अंतराल पर निरंतर होने वाले कार्यों में कई महत्वपूर्ण गुण होते हैं, जिन्हें निम्नलिखित प्रमेयों द्वारा व्यक्त किया जाता है।

प्रमेय 3.3.1।खंड पर निरंतर एक फ़ंक्शन [ ए, बी], उस पर अपने न्यूनतम मान तक पहुँच जाता है एमऔर सबसे बड़ा मूल्य एम, यानी ऐसे बिंदु हैं एक्स 1 और एक्सइस खंड के 2, जो एफ(एक्स 1) = एम, एफ(एक्स 2) = एम.

प्रमेय का एक सरल ज्यामितीय अर्थ है (चित्र 2 देखें)।

प्रमेय 3.3.2।समारोह के मामले में पर = एफ(एक्स) अंतराल पर निरंतर है [ ए, बी] और अपने सिरों पर असमान मान लेता है एफ(ए) = ए, एफ(बी) = बी, ए बी, तो ए और बी के बीच जो भी संख्या सी है, वहां एक बिंदु है साथ Î [ ए, बी] ऐसा है कि एफ(साथ) = सी.

प्रमेय का ज्यामितीय अर्थ चित्र 3 में दिखाया गया है। कोई सीधी रेखा पर= सी, जहां ए< C < B (или A >C > B), फलन के ग्राफ को प्रतिच्छेद करता है पर = एफ(एक्स).

परिणाम।यदि फ़ंक्शन एक खंड पर निरंतर है और इसके सिरों पर विभिन्न संकेतों के मान लेता है, तो इस खंड पर कम से कम एक बिंदु होता है जिस पर फ़ंक्शन गायब हो जाता है।

परिणाम का ज्यामितीय अर्थ चित्र 4 में दिखाया गया है।

आत्म-नियंत्रण के लिए प्रश्न

1. एक बिंदु पर किस फलन को सतत कहते हैं?

2. फ़ंक्शन और तर्कों की वृद्धि के माध्यम से एक और समान परिभाषा दें।

3. दो सतत फलनों के योग, अंतर, गुणनफल और भागफल के बारे में क्या कहा जा सकता है?

4. तर्क के किन मूल्यों के लिए संपूर्ण तर्कसंगत और भिन्नात्मक-तर्कसंगत कार्य निरंतर हैं?

5. एक जटिल फलन एक बिंदु पर कब निरंतर होता है?

6. आमतौर पर कार्यों का ब्रेकिंग पॉइंट क्या कहा जाता है?

7. पहले प्रकार के कौन से बिंदु असंततता बिंदु कहलाते हैं?

8. आमतौर पर फंक्शन जंप किस मान को कहा जाता है?

9. "हटाने योग्य विराम बिंदु" की अवधारणाओं की व्याख्या करें। उदाहरण दो।

10. दूसरे प्रकार के किन बिंदुओं को असंततता बिंदु कहा जाता है? उदाहरण दो।

11. अवधारणाओं की व्याख्या करें: ""अंतराल पर निरंतरता"", ""दाईं ओर निरंतरता"", ""बाईं ओर निरंतरता"", ""खंड पर निरंतरता""।

12. कार्यों के सबसे बड़े और सबसे छोटे मूल्यों को परिभाषित करें।

13. फलन के सबसे बड़े और सबसे छोटे मान वाले खंड पर निरंतरता के संबंध पर एक प्रमेय तैयार करें। इसे चित्र द्वारा स्पष्ट कीजिए।

14. एक खंड पर कार्यों की निरंतरता और फ़ंक्शन मानों के खंड के बीच संबंध पर एक प्रमेय तैयार करें। आकृति में इसका ज्यामितीय अर्थ स्पष्ट कीजिए।

15. उपरोक्त प्रमेय का परिणाम और उसकी ज्यामितीय व्याख्या कीजिए।

व्याख्यान 4

व्याख्यान विषय: फ़ंक्शन व्युत्पन्न

व्याख्यान योजना:व्युत्पन्न की अवधारणा, इसका ज्यामितीय और भौतिक अर्थ। भेदभाव के बुनियादी नियम। एक जटिल कार्य का व्युत्पन्न। व्युत्पन्न के कुछ अनुप्रयोग।

4.1. व्युत्पन्न की अवधारणा, इसका ज्यामितीय और भौतिक अर्थ

समारोह पर विचार करें पर = एफ(एक्स) अंतराल में निर्दिष्ट] ए, बी[. रहने दो एक्सÎ ] ए, बी[ और एक्स Î ] ए, बी[, फिर बिंदु पर फ़ंक्शन वृद्धि एक्स 0 सूत्र D . द्वारा व्यक्त किया जाता है पर = एफ(एक्स 0+डी एक्स) – एफ(एक्स 0).

परिभाषा। फ़ंक्शन का व्युत्पन्न y = एफ(एक्स) बिंदु पर एक्स 0 को आमतौर पर इस फ़ंक्शन की वृद्धि के अनुपात की सीमा कहा जाता है जब तर्क की वृद्धि शून्य हो जाती है:

एफ'(एक्स 0) = या वाई"(एक्स 0) =.

व्युत्पन्न का ज्यामितीय अर्थ: एक बिंदु पर इस फलन का अवकलज, ऑक्स अक्ष के बीच के कोण की स्पर्शरेखा और संबंधित बिंदु पर इस फलन के ग्राफ की स्पर्शरेखा के बराबर होता है (चित्र 1 देखें):

एफ"(एक्स 0) = तन ए।

परिभाषा. यदि समारोह एफ(एक्स) अंतराल पर परिभाषित किया गया है [ ए, बी], अंतराल के प्रत्येक बिंदु पर निरंतर है ( ए, बी), बिंदु पर एदाईं ओर निरंतर, एक बिंदु पर बीबाईं ओर निरंतर है, तो हम कहते हैं कि फलन एफ(एक्स) खंड पर निरंतर [ए, बी].

दूसरे शब्दों में, फ़ंक्शन एफ(एक्स) अंतराल पर निरंतर है [ ए, बी] अगर तीन शर्तें पूरी होती हैं:

1) "एक्स 0 Î( ए, बी): एफ(एक्स) = एफ(एक्स 0);

2) एफ(एक्स) = एफ(ए);

3) एफ(एक्स) = एफ(बी).

एक अंतराल पर सतत फलन के लिए, हम कुछ गुणों पर विचार करते हैं, जिन्हें हम बिना प्रमाण के निम्नलिखित प्रमेयों के रूप में बनाते हैं।

प्रमेय 1. यदि समारोह एफ(एक्स) अंतराल पर निरंतर है [ ए, बी], तब यह इस सेगमेंट में अपने सबसे छोटे और सबसे बड़े मान तक पहुंच जाता है।

यह प्रमेय बताता है (चित्र 1.15) कि खंड पर [ ए, बी] ऐसा एक बिंदु है एक्स 1 कि एफ(एक्स 1) £ एफ(एक्स) किसी के लिए एक्ससे [ ए, बी] और यह कि एक बिंदु है एक्स 2 (एक्स 2 [ ए, बी]) ऐसा है कि " एक्सÎ[ ए, बी] (एफ(एक्स 2) एफ(एक्स)).

अर्थ एफ(एक्स 1) दिए गए फ़ंक्शन के लिए सबसे बड़ा है [ ए, बी], ए एफ(एक्स 2) - सबसे छोटा। निरूपित करें: एफ(एक्स 1) = एम, एफ(एक्स 2) =एम. तब से एफ(एक्स) निम्नलिखित असमानता रखती है: " एक्सÎ[ ए, बी] एम£ एफ(एक्स) £ एम, तब हम प्रमेय 1 से निम्नलिखित उपफल प्राप्त करते हैं।

परिणाम. यदि समारोह एफ(एक्स) एक खंड पर निरंतर है, तो यह इस खंड पर घिरा है।

प्रमेय 2. यदि समारोह एफ(एक्स) अंतराल पर निरंतर है [ ए, बी] और खंड के सिरों पर विभिन्न संकेतों के मूल्यों को ग्रहण करता है, तो ऐसा आंतरिक बिंदु होता है एक्स 0 खंड [ ए, बी], जिसमें फ़ंक्शन 0 हो जाता है, अर्थात। $ एक्स 0 Î ( ए, बी) (एफ(एक्स 0) = 0).

यह प्रमेय बताता है कि एक फ़ंक्शन का ग्राफ वाई = एफ(एक्स), अंतराल पर निरंतर [ ए, बी], अक्ष को पार करता है बैलकम से कम एक बार यदि मान एफ(ए) और एफ(बी) विपरीत संकेत हैं। अतः, (चित्र 1.16) एफ(ए) > 0, एफ(बी) < 0 и функция एफ(एक्स) बिंदुओं पर गायब हो जाता है एक्स 1 , एक्स 2 , एक्स 3 .

प्रमेय 3. चलो समारोह एफ(एक्स) अंतराल पर निरंतर है [ ए, बी], एफ(ए) = ए, एफ(बी) = बीऔर ए¹ बी. (चित्र 1.17)। फिर किसी भी संख्या के लिए सी, संख्याओं के बीच निष्कर्ष निकाला गया एऔर बी, ऐसा एक आंतरिक बिंदु है एक्स 0 खंड [ ए, बी], क्या एफ(एक्स 0) = सी.

परिणाम. यदि समारोह एफ(एक्स) अंतराल पर निरंतर है [ ए, बी], एम- सबसे छोटा मान एफ(एक्स), एम- समारोह का सबसे बड़ा मूल्य एफ(एक्स) खंड पर [ ए, बी], तब फ़ंक्शन (कम से कम एक बार) कोई मान लेता है एमके बीच एमऔर एम, और इसलिए खंड [ एम, एम] फ़ंक्शन के सभी मानों का समुच्चय है एफ(एक्स) खंड पर [ ए, बी].

ध्यान दें कि यदि फलन अंतराल पर सतत है ( ए, बी) या खंड पर है [ ए, बी] असंततता बिंदु पर, तब प्रमेय 1, 2, 3 ऐसे फलन के लिए सत्य नहीं रह जाते हैं।

निष्कर्ष में, व्युत्क्रम फलन के अस्तित्व पर प्रमेय पर विचार करें।

याद रखें कि एक अंतराल एक खंड, एक अंतराल या एक परिमित या अनंत आधा-अंतराल है।

प्रमेय 4. रहने दो एफ(एक्स) अंतराल पर निरंतर है एक्स, बढ़ जाता है (या घटता है) एक्सऔर मूल्यों की एक श्रृंखला है यू. फिर समारोह के लिए वाई = एफ(एक्स) एक उलटा कार्य है एक्स= जे(आप) अंतराल पर परिभाषित यू, निरंतर और बढ़ती (या घटती) पर यूकई अर्थों के साथ एक्स.

टिप्पणी. चलो समारोह एक्स= जे(आप) फ़ंक्शन के लिए उलटा है एफ(एक्स) चूंकि तर्क आमतौर पर द्वारा निरूपित किया जाता है एक्स, और समारोह के माध्यम से आप, तब हम प्रतिलोम फलन को इस प्रकार लिखते हैं वाई =जे(एक्स).

उदाहरण 1. समारोह वाई = एक्स 2 (चित्र। 1.8, ए) सेट पर एक्स= यदि यह इस खंड के सभी आंतरिक बिंदुओं पर और इसके सिरों पर निरंतर है, अर्थात। बिंदुओं पर एऔर बी, क्रमशः दाएं और बाएं ओर निरंतर है।

प्रमेय 1.खंड पर निरंतर एक फ़ंक्शन [ ए, बी], इस खंड का कम से कम एक बिंदु सबसे बड़ा मान लेता है और कम से कम एक बिंदु पर - सबसे छोटा।

प्रमेय कहता है कि यदि फलन वाई = एफ (एक्स)खंड पर निरंतर [ ए, बी], तो कम से कम एक बिंदु है एक्स 1 Î [ ए, बी] जैसे कि फ़ंक्शन का मान एफ (एक्स)इस बिंदु पर इस खंड पर अपने सभी मूल्यों में सबसे बड़ा होगा: एफ (एक्स 1) ≥ एफ (एक्स). इसी तरह, एक ऐसा बिंदु है x2, जिसमें फ़ंक्शन का मान सेगमेंट के सभी मानों में सबसे छोटा होगा: एफ (एक्स 1) ≤ एफ (एक्स).

यह स्पष्ट है कि ऐसे कई बिंदु हो सकते हैं, उदाहरण के लिए, चित्र दिखाता है कि फ़ंक्शन एफ (एक्स)दो बिंदुओं पर सबसे छोटा मान लेता है x2और एक्स 2 ".

टिप्पणी. यदि हम अंतराल पर फलन के मान पर विचार करें तो प्रमेय का कथन असत्य हो सकता है ( ए, बी) दरअसल, अगर हम समारोह पर विचार करें वाई = एक्सपर (0, 2), तो यह इस अंतराल पर निरंतर है, लेकिन इसमें अपने अधिकतम या न्यूनतम मूल्यों तक नहीं पहुंचता है: यह अंतराल के अंत में इन मूल्यों तक पहुंचता है, लेकिन अंत हमारे नहीं होते हैं क्षेत्र।

साथ ही, असंतत कार्यों के लिए प्रमेय सत्य नहीं रह जाता है। एक उदाहरण दें।

परिणाम।यदि समारोह एफ (एक्स)निरंतर [ ए, बी], तो यह इस अंतराल पर आबद्ध है।

प्रमेय 2।चलो समारोह वाई = एफ (एक्स)खंड पर निरंतर [ ए, बी] और इस खंड के सिरों पर विभिन्न चिह्नों के मान लेता है, तो खंड के अंदर कम से कम एक बिंदु होता है एक्स = सी, जहां समारोह गायब हो जाता है: च (सी)= 0, जहां ए< C< b

इस प्रमेय का एक सरल ज्यामितीय अर्थ है: यदि एक सतत कार्य के ग्राफ के बिंदु वाई = एफ (एक्स), खंड के सिरों के अनुरूप [ ए, बी] अक्ष के विपरीत पक्षों पर झूठ बोलो बैल, तो यह ग्राफ खंड के कम से कम एक बिंदु पर अक्ष को काटता है बैल. असंतत कार्यों में यह गुण नहीं हो सकता है।

यह प्रमेय निम्नलिखित सामान्यीकरण को स्वीकार करता है।

प्रमेय 3 (मध्यवर्ती मूल्यों पर प्रमेय)।चलो समारोह वाई = एफ (एक्स)खंड पर निरंतर [ ए, बी] और एफ (ए) = ए, एफ (बी) = बी. फिर किसी भी संख्या के लिए सीके बीच एऔर बी, इस खंड के अंदर एक ऐसा बिंदु है सीÎ [ ए, बी], क्या एफ (सी) = सी.

यह प्रमेय ज्यामितीय रूप से स्पष्ट है। फ़ंक्शन के ग्राफ़ पर विचार करें वाई = एफ (एक्स). रहने दो एफ (ए) = ए, एफ (बी) = बी. फिर कोई लाइन वाई = सी, कहाँ पे सी- के बीच कोई भी संख्या एऔर बी, फ़ंक्शन के ग्राफ़ को कम से कम एक बिंदु पर प्रतिच्छेद करता है। प्रतिच्छेदन बिंदु का भुज वह मान होगा एक्स = सी, जिस पर एफ (सी) = सी.

इस प्रकार, एक निरंतर कार्य, अपने मूल्यों में से एक से दूसरे में जाना, आवश्यक रूप से सभी मध्यवर्ती मूल्यों से होकर गुजरता है। विशेष रूप से:

परिणाम।यदि समारोह वाई = एफ (एक्स)कुछ अंतराल पर निरंतर है और सबसे बड़ा और सबसे छोटा मान लेता है, तो इस अंतराल पर, कम से कम एक बार, इसके सबसे छोटे और सबसे बड़े मूल्यों के बीच कोई भी मान लेता है।

व्युत्पन्न और उसके अनुप्रयोग। व्युत्पन्न परिभाषा

चलो कुछ कार्य करते हैं वाई = एफ (एक्स),कुछ अंतराल पर परिभाषित। प्रत्येक तर्क मान के लिए एक्सइस अंतराल से फलन वाई = एफ (एक्स)एक निश्चित अर्थ है।

दो तर्क मानों पर विचार करें: प्रारंभिक एक्स 0 और नया एक्स.

अंतर एक्स-एक्स 0 कहा जाता है तर्क की वृद्धि xबिंदु पर एक्स 0 और निरूपित x. इस प्रकार, एक्स = एक्स - एक्स 0 (तर्क वृद्धि या तो सकारात्मक या नकारात्मक हो सकती है)। इस समानता से यह इस प्रकार है कि एक्स = एक्स 0 +Δx, अर्थात। चर के प्रारंभिक मूल्य में कुछ वृद्धि हुई है। फिर, यदि बिंदु पर एक्स 0 फ़ंक्शन मान था च (एक्स 0 ), फिर नए बिंदु पर एक्सफ़ंक्शन मान लेगा एफ(एक्स) = एफ(एक्स 0 +∆x).

अंतर Y y 0 = f(x) - f(x 0 ) बुलाया समारोह वृद्धि वाई = एफ (एक्स)बिंदु पर एक्स 0 और प्रतीक . द्वारा निरूपित किया जाता है y. इस प्रकार,

y = f(x) – f(x 0 ) = एफ (एक्स 0 +Δx) - f(x .) 0 ) .

(1)

आमतौर पर तर्क का प्रारंभिक मूल्य एक्स 0 को निश्चित माना जाता है और नया मान एक्स- चर। फिर आप 0 = एफ (एक्स 0 ) स्थिर हो जाता है और वाई = एफ (एक्स)- चर। वेतन वृद्धि yऔर xचर भी होंगे और सूत्र (1) दर्शाता है कि डीवाईचर का एक कार्य है x.

तर्क की वृद्धि के लिए फ़ंक्शन की वृद्धि का अनुपात लिखें

आइए इस संबंध की सीमा ज्ञात करें x→0। यदि यह सीमा मौजूद है, तो इसे इस फ़ंक्शन का व्युत्पन्न कहा जाता है। एफ (एक्स)बिंदु पर एक्स 0 और निरूपित करें एफ "(एक्स 0)। इसलिए,

यौगिकयह समारोह वाई = एफ (एक्स)बिंदु पर एक्स 0 को फलन के वृद्धि अनुपात की सीमा कहा जाता है आपतर्क की वृद्धि के लिए एक्सजब उत्तरार्द्ध मनमाने ढंग से शून्य हो जाता है।

ध्यान दें कि एक ही कार्य के लिए विभिन्न बिंदुओं पर अवकलज एक्सविभिन्न मूल्यों पर ले सकते हैं, अर्थात्। व्युत्पन्न को तर्क के कार्य के रूप में माना जा सकता है एक्स. यह फ़ंक्शन निरूपित है एफ "(एक्स)

व्युत्पन्न प्रतीकों द्वारा निरूपित किया जाता है एफ "(एक्स), वाई", . व्युत्पन्न का विशिष्ट मान at एक्स = एलक्षित एफ "(ए) या आप "| एक्स = ए.

किसी फ़ंक्शन के व्युत्पन्न को खोजने का संचालन एफ (एक्स)इस फ़ंक्शन का विभेदन कहा जाता है।

परिभाषा के अनुसार व्युत्पन्न को सीधे खोजने के लिए, आप निम्नलिखित लागू कर सकते हैं अंगूठे का नियम:

उदाहरण।

व्युत्पन्न का यांत्रिक अर्थ

भौतिकी से ज्ञात होता है कि एकसमान गति के नियम का रूप होता है एस = वी टी, कहाँ पे एस- पथ समय में बिंदु तक यात्रा करता है टी, वीएकसमान गति की गति है।

हालांकि, चूंकि प्रकृति में होने वाली अधिकांश हलचलें असमान होती हैं, फिर सामान्य स्थिति में, गति, और, परिणामस्वरूप, दूरी एससमय पर निर्भर करेगा टी, अर्थात। समय का कार्य होगा।

तो, नियम के अनुसार भौतिक बिंदु को एक सीधी रेखा में एक दिशा में चलने दें एस = एस (टी)।

समय में एक पल नोट करें टी 0. इस बिंदु तक, बिंदु पथ से गुजर चुका है एस = एस (टी 0 ). आइए गति निर्धारित करें वीसमय पर सामग्री बिंदु टी 0 .

ऐसा करने के लिए, समय के किसी अन्य क्षण पर विचार करें टी 0 + Δ टी. यह तय की गई दूरी s . से मेल खाती है =एस(टी 0 + Δ टी) फिर समय अंतराल के लिए टीबिंदु ने पथ s . की यात्रा की है =एस(टी 0 + Δ टी)–अनुसूचित जनजाति)।

आइए रिश्ते पर विचार करें। इसे समय अंतराल में औसत चाल कहते हैं टी. औसत गति इस समय किसी बिंदु की गति की गति को सटीक रूप से नहीं बता सकती है टी 0 (क्योंकि गति असमान है)। औसत गति का उपयोग करके इस वास्तविक गति को अधिक सटीक रूप से व्यक्त करने के लिए, आपको एक छोटा समय अंतराल लेने की आवश्यकता है टी.

तो, एक निश्चित समय पर गति की गति टी 0 (तात्कालिक गति) से अंतराल में औसत गति की सीमा है टी 0 से टी 0 +Δ टीजब टी→0:

,

वे। असमान गति की गतिसमय के संबंध में तय की गई दूरी का व्युत्पन्न है।

व्युत्पन्न का ज्यामितीय अर्थ

आइए पहले हम किसी दिए गए बिंदु पर वक्र के स्पर्शरेखा की परिभाषा का परिचय दें।

मान लीजिए कि हमारे पास एक वक्र और उस पर एक निश्चित बिंदु है एम 0(आंकड़ा देखें) एक और बिंदु पर विचार करें एमयह वक्र और एक छेदक ड्रा एम 0 एम. अगर बिंदु एमवक्र के साथ चलना शुरू होता है, और बिंदु एम 0स्थिर रहता है, सेकेंट अपनी स्थिति बदलता है। यदि, बिंदु के असीमित सन्निकटन के साथ एमवक्र से बिंदु एम 0किसी भी तरफ, छेदक एक निश्चित सीधी रेखा की स्थिति लेता है एम 0 टी, फिर सीधी रेखा एम 0 टीदिए गए बिंदु पर वक्र की स्पर्श रेखा कहलाती है एम 0.

उस।, स्पर्शरेखाकिसी दिए गए बिंदु पर वक्र के लिए एम 0 secant की सीमा स्थिति कहा जाता है एम 0 एमजब बिंदु एमवक्र के साथ एक बिंदु पर जाता है एम 0.

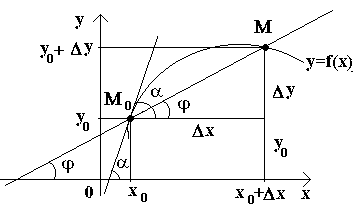
अब निरंतर कार्य पर विचार करें वाई = एफ (एक्स)और इस फ़ंक्शन के अनुरूप वक्र। कुछ मूल्य के लिए एक्स 0 फ़ंक्शन एक मान लेता है y0=f(x0).ये मान एक्स 0 और आप 0 वक्र पर एक बिंदु से मेल खाती है एम 0 (एक्स 0; वाई 0)।आइए एक तर्क दें X 0वेतन वृद्धि एक्स. तर्क का नया मान फ़ंक्शन के बढ़े हुए मान से मेल खाता है आप 0 +Δ वाई = एफ (एक्स 0 –Δ एक्स). हमें एक बिंदु मिलता है एम (एक्स 0+Δ एक्स; वाई 0+Δ वाई)।आइए एक सेकेंट ड्रा करें एम 0 एमऔर अक्ष की धनात्मक दिशा के साथ छेदक द्वारा बनाए गए कोण से निरूपित करें बैल. चलो एक रिश्ता बनाते हैं और उस पर ध्यान देते हैं।

अगर अब एक्स→0, तब, फलन की निरंतरता के कारण पर→0, और इसलिए बिंदु एम, वक्र के साथ आगे बढ़ते हुए, अनिश्चित काल तक बिंदु पर पहुंचता है एम 0. फिर secant एम 0 एमबिंदु पर स्पर्शरेखा की स्थिति को वक्र पर ले जाने की प्रवृत्ति होगी एम 0, और कोण φ→α Δ . पर एक्स→0, जहाँ α स्पर्शरेखा और अक्ष की धनात्मक दिशा के बीच के कोण को दर्शाता है बैल. चूँकि फलन tg लगातार पर /2 पर निर्भर करता है, फिर φ→α tg φ → tg α पर और, इसलिए, स्पर्शरेखा का ढलान होगा:

वे। च"(एक्स)= tgα.

इस प्रकार, ज्यामितीय रूप से वाई "(एक्स 0)बिंदु पर इस फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के ढलान का प्रतिनिधित्व करता है X 0, अर्थात। तर्क के दिए गए मान के लिए एक्स, अवकलज फलन के ग्राफ़ की स्पर्शरेखा द्वारा बनाए गए कोण की स्पर्श रेखा के बराबर होता है एफ (एक्स)संबंधित बिंदु पर एम 0 (एक्स; वाई)सकारात्मक अक्ष दिशा के साथ बैल।

उदाहरण।वक्र के स्पर्शरेखा की ढलान खोजें वाई = एक्स 2 बिंदु पर एम(-1; 1).

हम पहले ही देख चुके हैं कि ( एक्स 2)" = 2एक्स. लेकिन वक्र के स्पर्शरेखा का ढलान है tg α = आप"| x=-1 = - 2.

कार्यों की भिन्नता। एक अलग समारोह की निरंतरता

समारोह वाई = एफ (एक्स)बुलाया विभेदककिन्हीं बिंदुओं पर एक्स 0 यदि इस बिंदु पर इसका एक निश्चित व्युत्पन्न है, अर्थात। यदि संबंध की सीमा मौजूद है और परिमित है।

यदि कोई फलन किसी खंड के प्रत्येक बिंदु पर अवकलनीय है [ ए; बी] या अंतराल ( ए; बी), तो वे कहते हैं कि यह विभेदकखंड पर [ ए; बी] या, क्रमशः, अंतराल में ( ए; बी).

निम्नलिखित प्रमेय मान्य है, जो अवकलनीय और सतत फलनों के बीच संबंध स्थापित करता है।

प्रमेय।यदि समारोह वाई = एफ (एक्स)किसी बिंदु पर अलग-अलग X 0, तो यह इस बिंदु पर निरंतर है।

इस प्रकार, किसी फ़ंक्शन की भिन्नता का तात्पर्य उसकी निरंतरता से है।

प्रमाण. यदि एक , तब

,

जहाँ α एक अतिसूक्ष्म मान है, अर्थात्। . पर शून्य की ओर प्रवृत्त मात्रा एक्स→0। परन्तु फिर

Δ आप=एफ "(X 0) Δ एक्स+αΔ एक्स=> Δ आप→0 पर एक्स→0, यानी एफ (एक्स) - एफ (एक्स 0)→0 पर एक्स→एक्स 0 , जिसका अर्थ है कि फ़ंक्शन एफ (एक्स)बिंदु पर निरंतर एक्स 0. क्यू.ई.डी.

इस प्रकार, असंततता बिंदुओं पर, फ़ंक्शन का व्युत्पन्न नहीं हो सकता है। विपरीत कथन सत्य नहीं है: ऐसे निरंतर कार्य हैं जो कुछ बिंदुओं पर भिन्न नहीं होते हैं (अर्थात, इन बिंदुओं पर उनका कोई व्युत्पन्न नहीं होता है)।

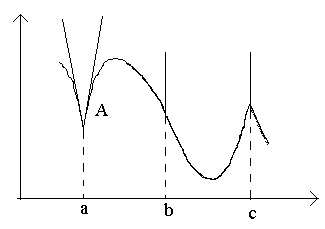
आकृति में बिंदुओं पर विचार करें ए, बी, सी।

बिंदु पर ए. पर एक्स→0 संबंध की कोई सीमा नहीं है (क्योंकि . के लिए एकतरफा सीमा भिन्न होती है) एक्स→0–0 और एक्स→0+0)। बिंदु पर एग्राफ में कोई परिभाषित स्पर्शरेखा नहीं है, लेकिन ढलान के साथ दो अलग-अलग एकतरफा स्पर्शरेखा हैं को 1 और को 2. इस प्रकार के बिंदु को कोने बिंदु कहा जाता है।

बिंदु पर बी. पर एक्स→0 अनुपात अचर चिन्ह का होता है जो अपरिमित रूप से बड़ा होता है। फ़ंक्शन में एक अनंत व्युत्पन्न है। इस बिंदु पर, ग्राफ में एक लंबवत स्पर्शरेखा होती है। बिंदु प्रकार - एक ऊर्ध्वाधर स्पर्शरेखा के साथ "विभक्ति बिंदु"।

बिंदु पर सीएकतरफा व्युत्पन्न विभिन्न संकेतों की असीम रूप से बड़ी मात्रा में हैं। इस बिंदु पर, ग्राफ़ में दो मर्ज किए गए लंबवत स्पर्शरेखा हैं। प्रकार - "पुच्छ" एक ऊर्ध्वाधर स्पर्शरेखा के साथ - एक कोने बिंदु का एक विशेष मामला।