एक स्वतंत्र समाधान के लिए कार्य भी होंगे, जिनके उत्तर आप देख सकते हैं।

वेक्टर अवधारणा

इससे पहले कि आप वैक्टर और उन पर संचालन के बारे में जानें, एक साधारण समस्या को हल करने के लिए ट्यून करें। आपके उद्यम का एक वेक्टर है और आपकी नवीन क्षमताओं का एक वेक्टर है। उद्यमिता का वेक्टर आपको लक्ष्य 1 तक ले जाता है, और नवीन क्षमताओं के वेक्टर - लक्ष्य 2 तक। खेल के नियम ऐसे हैं कि आप एक ही बार में इन दो वैक्टरों की दिशा में आगे नहीं बढ़ सकते हैं और एक ही बार में दो लक्ष्य प्राप्त कर सकते हैं। वेक्टर इंटरैक्ट करते हैं, या, गणितीय रूप से बोलते हुए, वैक्टर पर कुछ ऑपरेशन किया जाता है। इस ऑपरेशन का परिणाम "परिणाम" वेक्टर है, जो आपको लक्ष्य 3 तक ले जाता है।

अब मुझे बताओ: वैक्टर "एंटरप्राइज" और "इनोवेटिव क्षमताओं" पर किस ऑपरेशन का परिणाम वेक्टर "परिणाम" है? यदि आप तुरंत नहीं कह सकते हैं, तो निराश न हों। जब आप इस पाठ का अध्ययन करेंगे तो आप इस प्रश्न का उत्तर देने में सक्षम होंगे।

जैसा कि हमने ऊपर देखा, सदिश अनिवार्य रूप से किसी बिंदु से आता है एकिसी बिंदु पर एक सीधी रेखा में बी. नतीजतन, प्रत्येक वेक्टर का न केवल एक संख्यात्मक मान - लंबाई है, बल्कि एक भौतिक और ज्यामितीय - दिशा भी है। इससे सदिश की पहली, सरलतम परिभाषा प्राप्त होती है। तो, एक सदिश एक बिंदु से जाने वाला एक निर्देशित खंड है एमुद्दे पर बी. इसे इस तरह चिह्नित किया गया है:

और अलग शुरू करने के लिए वेक्टर संचालन , हमें वेक्टर की एक और परिभाषा से परिचित होने की आवश्यकता है।

एक वेक्टर एक बिंदु का एक प्रकार का प्रतिनिधित्व है जिस पर किसी प्रारंभिक बिंदु से पहुंचा जा सकता है। उदाहरण के लिए, एक त्रि-आयामी वेक्टर को आमतौर पर इस प्रकार लिखा जाता है (एक्स, वाई, जेड) . सीधे शब्दों में कहें, तो ये संख्याएं दर्शाती हैं कि बिंदु तक पहुंचने के लिए आपको तीन अलग-अलग दिशाओं में कितनी दूर जाना है।

एक वेक्टर दिया जाए। जिसमें एक्स = 3 (दाहिना हाथ दाईं ओर इशारा करता है) आप = 1 (बाएं हाथ आगे की ओर इशारा करता है) जेड = 5 (बिंदु के नीचे एक सीढ़ी ऊपर की ओर जाती है)। इस डेटा से, आप दाहिने हाथ से इंगित दिशा में 3 मीटर चलकर बिंदु पाएंगे, फिर बाएं हाथ द्वारा इंगित दिशा में 1 मीटर, और फिर एक सीढ़ी आपका इंतजार कर रही है और 5 मीटर चढ़ते हुए, आप अंत में पाएंगे अपने आप को अंतिम बिंदु पर।

अन्य सभी शर्तें ऊपर प्रस्तुत स्पष्टीकरण के परिशोधन हैं, जो वैक्टर पर विभिन्न कार्यों के लिए आवश्यक हैं, अर्थात व्यावहारिक समस्याओं को हल करने के लिए। आइए इन अधिक कठोर परिभाषाओं को देखें, जो विशिष्ट वेक्टर समस्याओं पर आधारित हैं।

भौतिक उदाहरणसदिश राशियां अंतरिक्ष में गतिमान किसी भौतिक बिंदु का विस्थापन, इस बिंदु की गति और त्वरण, साथ ही उस पर कार्य करने वाला बल भी हो सकती हैं।

ज्यामितीय वेक्टरद्वि-आयामी और त्रि-आयामी अंतरिक्ष में रूप में दर्शाया गया है निर्देशित खंड. यह एक ऐसा खंड है जिसकी शुरुआत और अंत है।

यदि एक एवेक्टर की शुरुआत है, और बीइसका अंत है, तो वेक्टर को प्रतीक या एकल लोअरकेस अक्षर द्वारा दर्शाया जाता है। आकृति में, सदिश का अंत एक तीर द्वारा दर्शाया गया है (चित्र 1)

लंबाई(या मापांक) एक ज्यामितीय वेक्टर की लंबाई उस खंड की लंबाई है जो इसे उत्पन्न करता है

दो वैक्टर को कहा जाता है बराबर , यदि उन्हें समानांतर अनुवाद द्वारा जोड़ा जा सकता है (जब दिशाएं मिलती हैं), यानी। यदि वे समानांतर हैं, तो एक ही दिशा में इंगित करें और उनकी लंबाई समान है।

भौतिकी में, इसे अक्सर माना जाता है पिन किए गए वैक्टर, आवेदन बिंदु, लंबाई और दिशा द्वारा दिया गया। यदि सदिश के अनुप्रयोग का बिंदु कोई मायने नहीं रखता है, तो इसे अंतरिक्ष में किसी भी बिंदु पर लंबाई और दिशा रखते हुए स्थानांतरित किया जा सकता है। इस मामले में, वेक्टर कहा जाता है नि: शुल्क. हम केवल विचार करने के लिए सहमत हैं मुक्त वैक्टर.

ज्यामितीय वैक्टर पर रैखिक संचालन

एक वेक्टर को एक संख्या से गुणा करें

वेक्टर उत्पाद प्रति संख्याएक सदिश को एक सदिश कहा जाता है जो सदिश को खींचकर (एट) या सिकोड़कर (एट) बार प्राप्त करता है, और सदिश की दिशा को संरक्षित किया जाता है यदि , और यदि उलट दिया जाता है। (रेखा चित्र नम्बर 2)

इस परिभाषा से यह पता चलता है कि सदिश और = हमेशा एक या समानांतर रेखाओं पर स्थित होते हैं। ऐसे वैक्टर कहलाते हैं समरेख. (आप यह भी कह सकते हैं कि ये वैक्टर समानांतर हैं, लेकिन वेक्टर बीजगणित में इसे "कोलीनियर" कहने की प्रथा है।) विलोम भी सत्य है: यदि वैक्टर और संरेख हैं, तो वे संबंध से संबंधित हैं

इसलिए, समानता (1) दो सदिशों की संरेखता की स्थिति को व्यक्त करती है।

वेक्टर जोड़ और घटाव

वैक्टर जोड़ते समय, आपको यह जानना होगा कि जोड़वैक्टर और एक वेक्टर कहा जाता है जिसकी शुरुआत वेक्टर की शुरुआत के साथ मेल खाती है, और अंत वेक्टर के अंत के साथ मेल खाता है, बशर्ते कि वेक्टर की शुरुआत वेक्टर के अंत से जुड़ी हो। (चित्र 3)

यह परिभाषा किसी भी सीमित संख्या में वैक्टर पर वितरित की जा सकती है। लेट इन स्पेस दी गई एनमुक्त वैक्टर। कई वैक्टर जोड़ते समय, उनका योग समापन वेक्टर के रूप में लिया जाता है, जिसकी शुरुआत पहले वेक्टर की शुरुआत के साथ होती है, और अंत अंतिम वेक्टर के अंत के साथ होता है। यही है, यदि वेक्टर की शुरुआत वेक्टर के अंत से जुड़ी हुई है, और वेक्टर की शुरुआत वेक्टर के अंत तक है, आदि। और, अंत में, वेक्टर के अंत तक - वेक्टर की शुरुआत, फिर इन वैक्टरों का योग समापन वेक्टर है , जिसकी शुरुआत पहले वेक्टर की शुरुआत के साथ मेल खाती है, और जिसका अंत अंतिम वेक्टर के अंत के साथ मेल खाता है। (चित्र 4)

शब्दों को सदिश के घटक कहा जाता है, और सूत्रबद्ध नियम है बहुभुज नियम. यह बहुभुज समतल नहीं हो सकता है।

जब एक सदिश को संख्या -1 से गुणा किया जाता है, तो विपरीत सदिश प्राप्त होता है। वैक्टर और समान लंबाई और विपरीत दिशाएं हैं। उनका योग देता है शून्य वेक्टर, जिसकी लंबाई शून्य है। शून्य वेक्टर की दिशा परिभाषित नहीं है।

सदिश बीजगणित में, घटाव के संचालन पर अलग से विचार करने की आवश्यकता नहीं है: एक सदिश से एक सदिश को घटाने का अर्थ है सदिश में विपरीत सदिश जोड़ना, अर्थात्।

उदाहरण 1अभिव्यक्ति को सरल बनाएं:

.

,

अर्थात्, सदिशों को उसी तरह संख्याओं से जोड़ा और गुणा किया जा सकता है जैसे बहुपद (विशेषकर, व्यंजकों को सरल बनाने में भी समस्याएँ)। आमतौर पर, वैक्टर के उत्पादों की गणना करने से पहले वैक्टर के साथ रैखिक रूप से समान अभिव्यक्तियों को सरल बनाने की आवश्यकता होती है।

उदाहरण 2सदिश और समांतर चतुर्भुज ABCD के विकर्णों के रूप में कार्य करते हैं (चित्र 4a)। के पदों में व्यक्त करें तथा सदिश , , तथा , जो इस समांतर चतुर्भुज की भुजाएँ हैं।

फेसला। एक समांतर चतुर्भुज के विकर्णों का प्रतिच्छेदन बिंदु प्रत्येक विकर्ण को समद्विभाजित करता है। समस्या की स्थिति में आवश्यक वैक्टर की लंबाई या तो वैक्टर के आधे योग के रूप में पाई जाती है जो वांछित लोगों के साथ एक त्रिकोण बनाते हैं, या आधे अंतर के रूप में (एक विकर्ण के रूप में सेवारत वेक्टर की दिशा के आधार पर), या, जैसा कि बाद के मामले में है, आधी राशि ऋण चिह्न के साथ ली गई है। परिणाम समस्या की स्थिति में आवश्यक वैक्टर हैं:

यह मानने का हर कारण है कि अब आपने इस पाठ की शुरुआत में "एंटरप्राइज़" और "इनोवेटिव एबिलिटीज़" वैक्टर के बारे में प्रश्न का सही उत्तर दिया है। सही उत्तर: ये वैक्टर एक अतिरिक्त ऑपरेशन के अधीन हैं।

वैक्टर पर समस्याओं को स्वयं हल करें, और फिर समाधान देखें

वैक्टर के योग की लंबाई कैसे ज्ञात करें?

यह समस्या वैक्टर के साथ संचालन में एक विशेष स्थान रखती है, क्योंकि इसमें त्रिकोणमितीय गुणों का उपयोग शामिल है। मान लें कि आपके पास निम्न जैसा कार्य है:

वैक्टर की लंबाई को देखते हुए और इन वैक्टरों के योग की लंबाई। इन सदिशों के अंतर की लंबाई ज्ञात कीजिए।

इस और इसी तरह की अन्य समस्याओं के समाधान और उन्हें हल करने के तरीके के बारे में स्पष्टीकरण - पाठ में " वेक्टर जोड़: वैक्टर और कोसाइन प्रमेय के योग की लंबाई ".

और आप इस तरह की समस्याओं के समाधान की जांच कर सकते हैं ऑनलाइन कैलकुलेटर "एक त्रिभुज की अज्ञात भुजा (सदिश जोड़ और कोज्या प्रमेय)" .

वैक्टर के उत्पाद कहां हैं?

एक वेक्टर द्वारा एक वेक्टर के उत्पाद रैखिक संचालन नहीं होते हैं और उन्हें अलग से माना जाता है। और हमारे पास "वेक्टर के डॉट उत्पाद" और "वेक्टर के वेक्टर और मिश्रित उत्पाद" पाठ हैं।

एक अक्ष पर एक वेक्टर का प्रक्षेपण

एक अक्ष पर एक वेक्टर का प्रक्षेपण प्रक्षेपित वेक्टर की लंबाई और वेक्टर और अक्ष के बीच के कोण के कोसाइन के उत्पाद के बराबर होता है:

जैसा कि ज्ञात है, एक बिंदु का प्रक्षेपण एरेखा (तल) पर इस बिंदु से रेखा (तल) पर गिराए गए लंब का आधार है।

चलो - एक मनमाना वेक्टर (चित्र 5), और - इसकी शुरुआत के अनुमान (अंक ए) और अंत (डॉट्स .) बी) प्रति धुरा मैं. (एक बिंदु के प्रक्षेपण का निर्माण करने के लिए ए) बिंदु के माध्यम से सीधे ड्रा करें एरेखा के लंबवत समतल। एक रेखा और एक समतल का प्रतिच्छेदन आवश्यक प्रक्षेपण का निर्धारण करेगा।

वेक्टर का घटक एल अक्ष परइस अक्ष पर पड़ा हुआ ऐसा वेक्टर कहा जाता है, जिसकी शुरुआत शुरुआत के प्रक्षेपण के साथ मेल खाती है, और अंत - वेक्टर के अंत के प्रक्षेपण के साथ।

अक्ष पर वेक्टर का प्रक्षेपण मैंएक नंबर कहा जाता है

,

इस अक्ष पर घटक वेक्टर की लंबाई के बराबर, एक प्लस चिह्न के साथ लिया जाता है यदि घटक की दिशा अक्ष की दिशा के साथ मेल खाती है मैं, और एक ऋण चिह्न के साथ यदि ये दिशाएं विपरीत हैं।

अक्ष पर वेक्टर अनुमानों के मुख्य गुण:

1. समान अक्ष पर समान सदिशों के प्रक्षेपण एक दूसरे के बराबर होते हैं।

2. जब किसी सदिश को किसी संख्या से गुणा किया जाता है, तो उसके प्रक्षेपण को उसी संख्या से गुणा किया जाता है।

3. किसी भी अक्ष पर सदिशों के योग का प्रक्षेपण, सदिशों के पदों के समान अक्ष पर प्रक्षेपों के योग के बराबर होता है।

4. एक अक्ष पर एक वेक्टर का प्रक्षेपण प्रक्षेपित वेक्टर की लंबाई और वेक्टर और अक्ष के बीच के कोण के कोसाइन के उत्पाद के बराबर है:

.

फेसला। आइए वैक्टर को अक्ष पर प्रोजेक्ट करें मैंजैसा कि ऊपर सैद्धांतिक संदर्भ में परिभाषित किया गया है। Fig.5a से यह स्पष्ट है कि वैक्टर के योग का प्रक्षेपण वैक्टर के अनुमानों के योग के बराबर है। हम इन अनुमानों की गणना करते हैं:

हम वैक्टर के योग का अंतिम प्रक्षेपण पाते हैं:

अंतरिक्ष में एक आयताकार कार्टेशियन समन्वय प्रणाली के साथ एक वेक्टर का संबंध

साथ परिचित अंतरिक्ष में आयताकार कार्टेशियन समन्वय प्रणाली इसी पाठ में हुई, अधिमानतः इसे एक नई विंडो में खोलें।

निर्देशांक अक्षों की एक क्रमबद्ध प्रणाली में 0xyzएक्सिस बैलबुलाया X- अक्ष, एक्सिस 0y – शाफ़्ट, और अक्ष 0z – अनुप्रयुक्त अक्ष.

मनमाना बिंदु के साथ एमअंतरिक्ष टाई वेक्टर

बुलाया त्रिज्या वेक्टरअंक एमऔर इसे प्रत्येक समन्वय अक्ष पर प्रोजेक्ट करें। आइए हम संबंधित अनुमानों के मूल्यों को निरूपित करें:

नंबर एक्स, वाई, जेडबुलाया बिंदु M . के निर्देशांक, क्रमश सूच्याकार आकृति का भुज, तालमेलऔर पिपली, और संख्याओं के एक क्रमबद्ध बिंदु के रूप में लिखे गए हैं: एम (एक्स; वाई; जेड)(चित्र 6)।

इकाई लंबाई का एक सदिश जिसकी दिशा अक्ष की दिशा से मेल खाती है, कहलाती है इकाई वेक्टर(या ओर्टोम) कुल्हाड़ियों। द्वारा निरूपित करें

तदनुसार, निर्देशांक अक्षों के इकाई सदिश बैल, ओए, आउंस

प्रमेय।किसी भी सदिश को निर्देशांक अक्षों के इकाई सदिशों में विघटित किया जा सकता है:

(2)

समता (2) को निर्देशांक अक्षों के अनुदिश सदिश का प्रसार कहते हैं। इस विस्तार के गुणांक निर्देशांक अक्षों पर वेक्टर के प्रक्षेपण हैं। इस प्रकार, निर्देशांक अक्षों के साथ वेक्टर के विस्तार गुणांक (2) वेक्टर के निर्देशांक हैं।

अंतरिक्ष में एक निश्चित समन्वय प्रणाली को चुनने के बाद, वेक्टर और उसके निर्देशांक के ट्रिपल एक दूसरे को विशिष्ट रूप से निर्धारित करते हैं, इसलिए वेक्टर को फॉर्म में लिखा जा सकता है

(2) और (3) के रूप में सदिश निरूपण समान हैं।

निर्देशांक में संरेखीय सदिशों की स्थिति

जैसा कि हम पहले ही नोट कर चुके हैं, सदिशों को संरेख कहा जाता है यदि वे संबंध से संबंधित हों

चलो वैक्टर . ये सदिश संरेख हैं यदि सदिशों के निर्देशांक संबंध द्वारा संबंधित हैं

,

अर्थात् सदिशों के निर्देशांक समानुपाती होते हैं।

उदाहरण 6दिए गए वैक्टर . क्या ये सदिश संरेख हैं?

फेसला। आइए इन सदिशों के निर्देशांकों का अनुपात ज्ञात करें:

.

सदिशों के निर्देशांक समानुपाती होते हैं, इसलिए सदिश संरेखी होते हैं, या, जो समान है, समांतर है।

सदिश लंबाई और दिशा कोज्या

निर्देशांक अक्षों की परस्पर लंबवतता के कारण, सदिश की लंबाई

सदिशों पर बने एक आयताकार समानांतर चतुर्भुज के विकर्ण की लंबाई के बराबर है

और समानता द्वारा व्यक्त किया जाता है

(4)

एक वेक्टर पूरी तरह से दो बिंदुओं (शुरुआत और अंत) को निर्दिष्ट करके परिभाषित किया गया है, इसलिए वेक्टर के निर्देशांक इन बिंदुओं के निर्देशांक के रूप में व्यक्त किए जा सकते हैं।

मान लीजिए कि दिए गए निर्देशांक प्रणाली में वेक्टर की शुरुआत बिंदु पर है

और अंत बिंदु पर है

समानता से

अनुसरण करता है कि

या समन्वय रूप में

इसलिये, वेक्टर के निर्देशांक अंत और वेक्टर की शुरुआत के समान नाम के निर्देशांक के अंतर के बराबर हैं . सूत्र (4) इस मामले में रूप लेता है

वेक्टर की दिशा निर्धारित की जाती है दिशा कोज्या . ये उन कोणों की कोज्या हैं जो वेक्टर कुल्हाड़ियों के साथ बनाता है बैल, ओएऔर आउंस. आइए इन कोणों को क्रमशः नामित करें α , β और γ . तब इन कोणों की कोज्या सूत्रों द्वारा ज्ञात की जा सकती है

एक वेक्टर की दिशा कोसाइन भी वेक्टर के वेक्टर के निर्देशांक होते हैं और इस प्रकार वेक्टर के वेक्टर

.

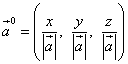
यह देखते हुए कि वेक्टर वेक्टर की लंबाई एक इकाई के बराबर है, अर्थात,

,

हमें दिशा कोज्या के लिए निम्नलिखित समानता मिलती है:

उदाहरण 7वेक्टर की लंबाई पाएं एक्स = (3; 0; 4).

फेसला। वेक्टर की लंबाई है

उदाहरण 8दिए गए अंक:

ज्ञात कीजिए कि क्या इन बिन्दुओं पर बना त्रिभुज समद्विबाहु है।

फेसला। सदिश लंबाई सूत्र (6) का उपयोग करते हुए, हम भुजाओं की लंबाई ज्ञात करते हैं और पता लगाते हैं कि क्या उनमें से दो बराबर हैं:

दो समान भुजाएँ मिली हैं, इसलिए तीसरी भुजा की लंबाई देखने की कोई आवश्यकता नहीं है, और दिया गया त्रिभुज समद्विबाहु है।

उदाहरण 9एक सदिश की लंबाई और उसकी दिशा कोज्या ज्ञात कीजिए यदि .

फेसला। वेक्टर निर्देशांक दिए गए हैं:

.

वेक्टर की लंबाई वेक्टर के निर्देशांक के वर्गों के योग के वर्गमूल के बराबर होती है:

.

दिशा कोसाइन ढूँढना:

वैक्टर पर समस्या को स्वयं हल करें, और फिर समाधान देखें

निर्देशांक रूप में दिए गए वैक्टर पर संचालन

मान लीजिए कि दो सदिश और उनके अनुमानों द्वारा दिए गए हैं:

आइए हम इन वैक्टरों पर कार्रवाई का संकेत दें।

2 का पृष्ठ 1

प्रश्न 1।एक वेक्टर क्या है? वैक्टर को कैसे परिभाषित किया जाता है?
जवाब।हम एक निर्देशित खंड को एक वेक्टर कहेंगे (चित्र 211)। एक वेक्टर की दिशा इसकी शुरुआत और अंत को निर्दिष्ट करके निर्धारित की जाती है। ड्राइंग में, वेक्टर की दिशा को एक तीर से चिह्नित किया गया है। वैक्टर को नामित करने के लिए, हम लोअरकेस लैटिन अक्षरों ए, बी, सी, ... का उपयोग करेंगे। आप इसकी शुरुआत और अंत निर्दिष्ट करके एक वेक्टर भी नामित कर सकते हैं। इस मामले में, वेक्टर की शुरुआत को पहले स्थान पर रखा गया है। "वेक्टर" शब्द के बजाय, एक तीर या डैश को कभी-कभी वेक्टर के अक्षर पदनाम के ऊपर रखा जाता है। आकृति 211 में सदिश को निम्नानुसार दर्शाया जा सकता है:

\(\overline(a)\), \(\overrightarrow(a)\) या \(\overline(AB)\), \(\overrightarrow(AB)\)।

प्रश्न 2।किन वैक्टरों को समान रूप से निर्देशित (विपरीत रूप से निर्देशित) कहा जाता है?
जवाब।सदिश \(\overline(AB)\) और \(\overline(CD)\) को समान रूप से निर्देशित कहा जाता है यदि अर्ध-रेखा AB और CD समान रूप से निर्देशित हों।
सदिश \(\overline(AB)\) और \(\overline(CD)\) को विपरीत दिशा में कहा जाता है यदि अर्ध-रेखा AB और CD विपरीत दिशा में हों।
चित्र 212 में, सदिश \(\overline(a)\) और \(\overline(b)\) की दिशा समान है, जबकि सदिश \(\overline(a)\) और \(\overline(c) \) विपरीत दिशाएं हैं।

प्रश्न 3।वेक्टर का निरपेक्ष मान क्या होता है?
जवाब।वेक्टर का निरपेक्ष मान (या मापांक) वेक्टर का प्रतिनिधित्व करने वाले खंड की लंबाई है। सदिश \(\overline(a)\) का निरपेक्ष मान |\(\overline(a)\)| द्वारा निरूपित किया जाता है।

प्रश्न 4.एक शून्य वेक्टर क्या है?
जवाब।एक वेक्टर की शुरुआत इसके अंत के साथ मेल खा सकती है। ऐसे वेक्टर को शून्य वेक्टर कहा जाएगा। शून्य वेक्टर को शून्य से डैश (\(\overline(0)\)) से दर्शाया जाता है। शून्य वेक्टर की दिशा के बारे में कोई बात नहीं करता है। शून्य सदिश का निरपेक्ष मान शून्य के बराबर माना जाता है।

प्रश्न 5.क्या वैक्टर को समान कहा जाता है?
जवाब।दो वैक्टर को समान कहा जाता है यदि उन्हें समानांतर अनुवाद द्वारा जोड़ा जाता है। इसका मतलब है कि एक समानांतर अनुवाद है जो एक वेक्टर की शुरुआत और अंत को क्रमशः दूसरे वेक्टर की शुरुआत और अंत तक ले जाता है।

प्रश्न 6.सिद्ध कीजिए कि समान सदिशों की दिशा समान होती है और निरपेक्ष मान समान होते हैं। और इसके विपरीत: समान रूप से निर्देशित वैक्टर जो निरपेक्ष मूल्य में बराबर होते हैं, समान होते हैं।
जवाब।समानांतर अनुवाद के साथ, वेक्टर अपनी दिशा, साथ ही साथ इसका निरपेक्ष मान बनाए रखता है। इसका अर्थ है कि समान सदिशों की दिशा समान होती है और निरपेक्ष मान में समान होते हैं।
मान लीजिए \(\overline(AB)\) और \(\overline(CD)\) समान रूप से निरपेक्ष मान के बराबर निर्देशित सदिश हैं (चित्र 213)। एक समानांतर अनुवाद जो बिंदु C को बिंदु A पर ले जाता है, आधी-पंक्ति CD को आधी-पंक्ति AB के साथ जोड़ता है, क्योंकि वे समान रूप से निर्देशित होते हैं। और चूंकि खंड AB और CD बराबर हैं, तो बिंदु D, बिंदु B के साथ संपाती है, अर्थात। समानांतर अनुवाद सदिश \(\overline(CD)\) को सदिश \(\overline(AB)\) में बदल देता है। इसलिए, सदिश \(\overline(AB)\) और \(\overline(CD)\) समान हैं, आवश्यकतानुसार।

प्रश्न 7.सिद्ध कीजिए कि किसी भी बिंदु से दिए गए सदिश के बराबर सदिश खींच सकते हैं, और केवल एक।
जवाब।माना CD एक रेखा है और सदिश \(\overline(CD)\) रेखा CD का एक भाग है। मान लीजिए AB वह रेखा है जिसमें रेखा CD समानांतर अनुवाद के दौरान जाती है, \(\overline(AB)\) वह सदिश हो जिसमें सदिश \(\overline(CD)\) समानांतर अनुवाद के दौरान प्रवेश करता है, और इसलिए सदिश \(\ overline(AB)\) और \(\overline(CD)\) बराबर हैं, और रेखाएं AB और CD समानांतर हैं (चित्र 213 देखें)। जैसा कि हम जानते हैं, एक बिंदु के माध्यम से जो दी गई रेखा पर स्थित नहीं है, विमान पर दी गई रेखा (समांतर रेखाओं का अभिगृहीत) के समानांतर अधिकतम एक रेखा खींचना संभव है। अत: बिंदु A से होकर कोई व्यक्ति रेखा CD के समांतर एक रेखा खींच सकता है। चूंकि वेक्टर \(\overline(AB)\) रेखा AB का हिस्सा है, इसलिए बिंदु A से होकर एक सदिश \(\overline(AB)\) खींचना संभव है, जो सदिश \(\overline) के बराबर है (सीडी)\).

प्रश्न 8.वेक्टर निर्देशांक क्या हैं? निर्देशांक a 1 , a 2 वाले सदिश का निरपेक्ष मान क्या है ?
जवाब।मान लीजिए सदिश \(\overline(a)\) बिंदु A 1 (x 1 ; y 1) से शुरू होता है और बिंदु A 2 (x 2 ; y 2) पर समाप्त होता है। सदिश \(\overline(a)\) के निर्देशांक a 1 = x 2 - x 1 , a 2 = y 2 - y 1 संख्याएं होंगी। हम वेक्टर निर्देशांक को वेक्टर के अक्षर पदनाम के बगल में रखेंगे, इस मामले में \(\overline(a)\) (a 1 ; a 2) या बस \((\overline(a 1 ; a 2 ))\ ) शून्य वेक्टर निर्देशांक शून्य के बराबर हैं।
दो बिंदुओं के बीच की दूरी को उनके निर्देशांक के रूप में व्यक्त करने वाले सूत्र से, यह इस प्रकार है कि निर्देशांक a 1 , a 2 वाले वेक्टर का निरपेक्ष मान \(\sqrt(a^2 1 + a^2 2 )\) है।

प्रश्न 9.सिद्ध कीजिए कि समान सदिशों के क्रमशः समान निर्देशांक होते हैं, और क्रमशः समान निर्देशांक वाले सदिश समान होते हैं।
जवाब।मान लीजिए A 1 (x 1 ; y 1) और A 2 (x 2 ; y 2) सदिश \(\overline(a)\) का आरंभ और अंत है। चूँकि सदिश \(\overline(a")\) इसके बराबर सदिश \(\overline(a)\) से समानांतर अनुवाद द्वारा प्राप्त किया जाता है, तो इसकी शुरुआत और अंत क्रमशः A" 1 (x 1 + c) होगा ; y 1 + d ), A" 2 (x 2 + c; y 2 ​​+ d)। इससे पता चलता है कि दोनों वैक्टर \(\overline(a)\) और \(\overline(a")\) में हैं वही निर्देशांक: x 2 - x 1 , y 2 - y 1 ।
आइए अब विलोम कथन को सिद्ध करें। मान लीजिए कि सदिशों के संगत निर्देशांक \(\overline(A 1 A 2 )\) और \(\overline(A" 1 A" 2 )\) बराबर हैं। हम सिद्ध करते हैं कि सदिश समान हैं।
मान लीजिए x" 1 और y" 1 बिंदु A" 1 के निर्देशांक हैं, और x" 2, y" 2 बिंदु A" 2 के निर्देशांक हैं। प्रमेय की स्थिति से x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. अत: x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. सूत्रों द्वारा दिया गया समानांतर अनुवाद

x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,

बिंदु A 1 को बिंदु A" 1 पर स्थानांतरित करता है, और बिंदु A 2 को बिंदु A" 2 पर स्थानांतरित करता है, अर्थात। सदिश \(\overline(A 1 A 2 )\) और \(\overline(A" 1 A" 2 )\) समान हैं, आवश्यकतानुसार।

प्रश्न 10.वैक्टर के योग को परिभाषित करें।
जवाब।सदिशों का योग \(\overline(a)\) और \(\overline(b)\) निर्देशांक a 1 , a 2 और b 1 , b 2 के साथ सदिश \(\overline(c)\) है निर्देशांक a 1 + b 1 , a 2 + b a 2 , अर्थात।

\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\)।

निर्माण तिथि: 2009-04-11 15:25:51
अंतिम संपादित: 2012-02-08 09:19:45

लंबे समय से मैं यह लेख नहीं लिखना चाहता था - मैंने सोचा कि सामग्री को कैसे प्रस्तुत किया जाए। आपको चित्र बनाने की भी आवश्यकता है। लेकिन, जाहिरा तौर पर, आज सितारे सफलतापूर्वक बन गए हैं और वैक्टर के बारे में एक लेख होगा। हालांकि यह सिर्फ एक मसौदा है। भविष्य में, मैं इस लेख को कई अलग-अलग हिस्सों में तोड़ दूंगा - पर्याप्त सामग्री है। साथ ही, लेख में धीरे-धीरे सुधार होगा: मैं इसमें बदलाव करूंगा - क्योंकि। एक बैठक में सभी पहलुओं का खुलासा करना संभव नहीं होगा।

उन्नीसवीं सदी में गणित में सदिशों का परिचय उन मात्राओं का वर्णन करने के लिए किया गया था जिनका वर्णन अदिश मानों का उपयोग करके करना मुश्किल था।

कंप्यूटर गेम के विकास में वेक्टर का अत्यधिक उपयोग किया जाता है। उनका उपयोग न केवल पारंपरिक रूप से किया जाता है - ऐसी मात्राओं को बल या गति के रूप में वर्णित करने के लिए, बल्कि उन क्षेत्रों में भी जिनका वैक्टर से कोई लेना-देना नहीं है: रंग भंडारण, छाया निर्माण।

अदिश और सदिश

सबसे पहले, मैं आपको याद दिला दूं कि एक अदिश क्या है और यह एक सदिश से कैसे भिन्न है।

स्केलर मान कुछ मान संग्रहीत करते हैं: द्रव्यमान, आयतन। अर्थात्, यह एक इकाई है जिसकी विशेषता केवल एक संख्या है (उदाहरण के लिए, किसी चीज़ की मात्रा)।

एक अदिश के विपरीत एक सदिश को दो मानों का उपयोग करके वर्णित किया जाता है: परिमाण और दिशा।

वैक्टर और निर्देशांक के बीच एक महत्वपूर्ण अंतर: वैक्टर एक विशिष्ट स्थान से बंधे नहीं होते हैं! एक बार फिर, वेक्टर में मुख्य चीज लंबाई और दिशा है।

एक वेक्टर को लैटिन वर्णमाला के एक मोटे अक्षर से दर्शाया जाता है। उदाहरण के लिए: ए, बी, वी.

पहली आकृति में, आप देख सकते हैं कि सदिश को समतल पर कैसे निरूपित किया जाता है।

अंतरिक्ष में वेक्टर

अंतरिक्ष में, वैक्टर को निर्देशांक का उपयोग करके व्यक्त किया जा सकता है। लेकिन पहले हमें एक अवधारणा पेश करनी होगी:

बिंदु त्रिज्या वेक्टर

आइए अंतरिक्ष में कोई बिंदु M(2,1) लें। एक बिंदु का त्रिज्या वेक्टर एक वेक्टर है जो मूल बिंदु से शुरू होता है और बिंदु पर समाप्त होता है।

हमारे यहां जो कुछ है वह एक वेक्टर से ज्यादा कुछ नहीं है ओएम. वेक्टर प्रारंभ निर्देशांक (0,0), अंत निर्देशांक (2,1)। आइए इस वेक्टर को इस रूप में निरूपित करें ए.

इस मामले में, वेक्टर को निम्नानुसार लिखा जा सकता है ए = <2, 1>. यह वेक्टर का निर्देशांक रूप है ए.

एक सदिश के निर्देशांक अक्षों के सापेक्ष उसके घटक कहलाते हैं। उदाहरण के लिए, 2 एक वेक्टर घटक है एएक्स-अक्ष के बारे में।

आइए एक बार फिर ध्यान दें कि किसी बिंदु के निर्देशांक क्या होते हैं। एक बिंदु का निर्देशांक (उदाहरण के लिए, x) अक्ष पर बिंदु का प्रक्षेपण है, अर्थात। एक बिंदु से एक अक्ष पर गिराए गए लंबवत का आधार। हमारे उदाहरण में 2.

लेकिन वापस पहली तस्वीर पर। यहाँ हमारे पास दो बिंदु A और B हैं। मान लीजिए कि बिंदुओं के निर्देशांक (1,1) और (3,3) हैं। वेक्टर वीइस मामले में इसे परिभाषित किया जा सकता है वी = <3-1, 3-1>. त्रि-आयामी अंतरिक्ष में दो बिंदुओं पर स्थित एक वेक्टर इस तरह दिखेगा:

वी =

मुझे नहीं लगता कि यहां कोई समस्या है।

एक सदिश को एक अदिश से गुणा करें

एक सदिश को अदिश मानों से गुणा किया जा सकता है:

क वी = =

इस मामले में, स्केलर मान वेक्टर के प्रत्येक घटक के साथ गुणा किया जाता है।

यदि k > 1 है, तो सदिश बढ़ जाएगा, यदि k एक से कम है लेकिन शून्य से अधिक है, तो सदिश लंबाई में घट जाएगा। यदि k शून्य से कम है, तो सदिश दिशा बदल देगा।

यूनिट वैक्टर

इकाई सदिश वे सदिश होते हैं जिनकी लंबाई एक के बराबर होती है। ध्यान दें कि निर्देशांक के साथ वेक्टर<1,1,1>एक के बराबर नहीं होगा! एक सदिश की लंबाई ज्ञात करना नीचे वर्णित है।

तथाकथित ऑर्ट्स हैं - ये यूनिट वैक्टर हैं जो समन्वय अक्ष के साथ दिशा में मेल खाते हैं। मैं- एक्स अक्ष की इकाई वेक्टर, जे- y अक्ष का इकाई सदिश, क- z अक्ष का इकाई सदिश।

जिसमें मैं = <1,0,0>, जे = <0,1,0>, क = <0,0,1>.

अब हम जानते हैं कि एक अदिश से सदिश का गुणन क्या होता है और इकाई सदिश क्या होते हैं। अब हम लिख सकते हैं वीवेक्टर रूप में।

वी= वी एक्स मैं+वी जे+vz क, जहाँ v x , v y , v z सदिश के संगत घटक हैं

वेक्टर जोड़

पिछले फॉर्मूले को पूरी तरह से समझने के लिए, आपको यह समझने की जरूरत है कि वेक्टर जोड़ कैसे काम करता है।

यहाँ सब कुछ सरल है। दो सदिश लें v1 = और v2 =

v1 + v2 =

हम सिर्फ दो वैक्टर के संबंधित घटकों को जोड़ते हैं।

अंतर की गणना उसी तरह की जाती है।

यह गणितीय रूप के बारे में है। पूर्णता के लिए, यह विचार करने योग्य है कि वेक्टर जोड़ना और घटाना ग्राफिक रूप से कैसा दिखेगा।

दो वैक्टर जोड़ने के लिए ए+बी. हमें वेक्टर की शुरुआत से मेल खाना चाहिए बीऔर वेक्टर का अंत ए. फिर, वेक्टर की शुरुआत के बीच एऔर वेक्टर का अंत बीएक नया वेक्टर ड्रा करें। स्पष्टता के लिए, दूसरा आंकड़ा देखें (अक्षर "ए")।

वैक्टर को घटाने के लिए, आपको दो वैक्टर की शुरुआत को जोड़ना होगा और दूसरे वेक्टर के अंत से पहले के अंत तक एक नया वेक्टर बनाना होगा। दूसरी तस्वीर (अक्षर "बी") दिखाती है कि यह कैसा दिखता है।

वेक्टर लंबाई और दिशा

आइए पहले लंबाई को देखें।

लंबाई दिशा की परवाह किए बिना वेक्टर का संख्यात्मक मान है।

लंबाई सूत्र द्वारा निर्धारित की जाती है (तीन-आयामी वेक्टर के लिए):

वेक्टर घटकों के वर्गों के योग का वर्गमूल।

परिचित सूत्र, है ना? सामान्य तौर पर, यह एक खंड की लंबाई के लिए सूत्र है

सदिश की दिशा सदिश और निर्देशांक अक्षों के बीच बने कोणों की दिक्-कोज्या द्वारा निर्धारित होती है। दिशा कोसाइन खोजने के लिए, उपयुक्त घटकों और लंबाई का उपयोग किया जाता है (चित्र बाद में होगा)।

कार्यक्रमों में वैक्टर का प्रतिनिधित्व

कार्यक्रमों में वेक्टरों का विभिन्न तरीकों से प्रतिनिधित्व किया जा सकता है। दोनों साधारण चर की मदद से, जो अक्षम है, और सरणियों, वर्गों और संरचनाओं की मदद से।

फ्लोट वेक्टर3 = (1,2,3); // वेक्टर स्ट्रक्चर वेक्टर 3 को स्टोर करने के लिए ऐरे // वैक्टर को स्टोर करने के लिए स्ट्रक्चर (फ्लोट एक्स, वाई, जेड;);

वैक्टर को स्टोर करने की सबसे बड़ी संभावनाएं कक्षाओं द्वारा प्रदान की जाती हैं। कक्षाओं में, हम न केवल स्वयं वेक्टर (चर) का वर्णन कर सकते हैं, बल्कि वेक्टर संचालन (कार्य) भी कर सकते हैं।

वैक्टर का डॉट उत्पाद

सदिश गुणन दो प्रकार के होते हैं: सदिश और अदिश।

अदिश उत्पाद की एक विशिष्ट विशेषता यह है कि परिणाम हमेशा एक अदिश मान होगा, अर्थात। संख्या।

यहां इस क्षण पर ध्यान देने योग्य है। यदि इस ऑपरेशन का परिणाम शून्य है, तो दो वैक्टर लंबवत हैं - उनके बीच का कोण 90 डिग्री है। यदि परिणाम शून्य से अधिक है, तो कोण 90 डिग्री से कम है। यदि परिणाम शून्य से कम है, तो कोण 90 डिग्री से अधिक है।

इस ऑपरेशन को निम्न सूत्र द्वारा दर्शाया गया है:

ए · बी= ए एक्स * बी एक्स + ए वाई * बी वाई + ए जेड * बी जेड

अदिश उत्पाद दो सदिशों के संगत घटकों के गुणनफलों का योग होता है। वे। हम दो सदिशों के x "s लेते हैं, उन्हें गुणा करते हैं, फिर उन्हें y" s के गुणनफल में जोड़ते हैं और इसी तरह आगे भी।

वैक्टर का क्रॉस उत्पाद

दो वैक्टरों के क्रॉस उत्पाद का परिणाम इन वैक्टरों के लंबवत वेक्टर होगा।

एएक्स बी =

हम अभी इस सूत्र पर विस्तार से चर्चा नहीं करेंगे। इसके अलावा, यह याद रखना काफी कठिन है। हम निर्धारकों से परिचित होने के बाद इस बिंदु पर लौटेंगे।

खैर, सामान्य विकास के लिए यह जानना उपयोगी है कि परिणामी वेक्टर की लंबाई वैक्टर पर बने समांतर चतुर्भुज के क्षेत्रफल के बराबर होती है एऔर बी.

वेक्टर सामान्यीकरण

एक सामान्यीकृत वेक्टर एक वेक्टर होता है जिसकी लंबाई एक होती है।

सामान्यीकृत वेक्टर खोजने का सूत्र इस प्रकार है - वेक्टर के सभी घटकों को इसकी लंबाई से विभाजित किया जाना चाहिए:

वीएन = वी/|वी| =

अंतभाषण

जैसा कि आपने शायद देखा है, वैक्टर को समझना मुश्किल नहीं है। हमने सदिशों पर अनेक संक्रियाओं पर विचार किया है।

"गणित" खंड के निम्नलिखित लेखों में, हम मैट्रिक्स, निर्धारक, रैखिक समीकरणों के सिस्टम पर चर्चा करेंगे। यह सब सिद्धांत है।

उसके बाद, हम मैट्रिक्स रूपांतरणों को देखेंगे। तभी आप समझ पाएंगे कि कंप्यूटर गेम बनाने में गणित कितना महत्वपूर्ण है। यह विषय पिछले सभी विषयों के लिए सिर्फ एक अभ्यास बन जाएगा।

वैक्टर. कार्रवाईऊपरवैक्टर। अदिश,

वेक्टर, वैक्टर का मिश्रित उत्पाद।

1. वैक्टर, वैक्टर पर कार्रवाई।

बुनियादी परिभाषाएँ।

परिभाषा 1.एक मात्रा जिसे इकाइयों की चुनी हुई प्रणाली में उसके संख्यात्मक मान द्वारा पूरी तरह से चित्रित किया जाता है, कहलाती है अदिशया अदिश .

(शरीर का वजन, आयतन, समय, आदि)

परिभाषा 2.एक संख्यात्मक मान और दिशा की विशेषता वाली मात्रा कहलाती है वेक्टर या वेक्टर .

(विस्थापन, बल, गति, आदि)

पदनाम: , या , .

एक ज्यामितीय वेक्टर एक निर्देशित खंड है।

वेक्टर के लिए - बिंदु लेकिन- प्रारंभ बिंदु परवेक्टर का अंत है।

परिभाषा 3.मापांक वेक्टर खंड AB की लंबाई है।

परिभाषा 4.एक सदिश जिसका मापांक शून्य होता है, कहलाता है शून्य , संकेत दिए है।

परिभाषा 5.समांतर रेखाओं या एक ही रेखा पर स्थित सदिश कहलाते हैं समरेख . यदि दो संरेखी सदिशों की दिशा समान हो, तो वे कहलाते हैं सह-दिशात्मक .

परिभाषा 6.दो वैक्टर माने जाते हैं बराबर , यदि वे सह-निर्देशन किया और मापांक में बराबर हैं।

वैक्टर पर कार्रवाई।

1) वैक्टर का जोड़।

डीईएफ़। 6.जोड़ दो वैक्टर और इन वैक्टरों पर बने समांतर चतुर्भुज का विकर्ण है, जो उनके आवेदन के एक सामान्य बिंदु से आता है (समांतर चतुर्भुज नियम).

चित्र .1।

डीईएफ़। 7.तीन सदिशों का योग , , इन सदिशों पर निर्मित समांतर चतुर्भुज का विकर्ण है (समानांतर नियम)।

डीईएफ़। आठ।यदि एक लेकिन, पर, साथ में मनमाना बिंदु हैं, तो + = (त्रिकोण नियम).

रेखा चित्र नम्बर 2

अतिरिक्त गुण।

1 के विषय में . + = + (विस्थापन कानून)।

2 के विषय में . + (+) = (+) + = (+) + (सहयोगी कानून)।

3 के विषय में . + (– ) + .

2) वैक्टर का घटाव।

डीईएफ़। नौ।नीचे अंतर वैक्टर और वेक्टर को समझें = - ऐसा कि + = .

एक समांतर चतुर्भुज में, यह एक और है विकर्णएसडी (अंजीर देखें। 1)।

3) किसी संख्या से सदिश का गुणन।

डीईएफ़। दस। काम अदिश करने के लिए वेक्टर क वेक्टर कहा जाता है

= क = क ,

लंबा का , और दिशा, जो:

1. वेक्टर की दिशा के साथ मेल खाता है यदि क > 0;

2. सदिश की दिशा के विपरीत यदि क < 0;

3. मनमाने ढंग से यदि क = 0.

किसी संख्या से सदिश के गुणन के गुण।

1 के विषय में . (क + मैं ) = क + मैं .

क ( + ) = क + क .

2 हे . क (मैं ) = (केएलई ) .

3 हे . 1  = , (–1)  = – , 0  = .

वेक्टर गुण।

डीईएफ़। ग्यारह।दो सदिश और कहलाते हैं समरेख अगर वे पर स्थित हैं समानांतर रेखाएंया कि एक सीधी रेखा।

शून्य सदिश किसी भी सदिश के संरेख होता है।

प्रमेय 1.दो शून्येतर सदिश और समरेख, जब वे आनुपातिक होते हैं अर्थात।

= क , क - अदिश।

डीईएफ़। 12.तीन सदिश , , कहलाते हैं समतलीय यदि वे किसी समतल के समानांतर हों या उसमें पड़े हों।

प्रमेय 2।तीन शून्येतर सदिश , , समतलीय, जब उनमें से एक अन्य दो का एक रैखिक संयोजन है, अर्थात।

= क + मैं , क , मैं - अदिश।

एक अक्ष पर एक वेक्टर का प्रक्षेपण।

प्रमेय 3.एक अक्ष पर एक वेक्टर का प्रक्षेपण (निर्देशित रेखा) मैंसदिश की लंबाई और सदिश की दिशा और अक्ष की दिशा के बीच के कोण की कोज्या के गुणनफल के बराबर है, अर्थात। = ए  सीओएस  ,  = ( , मैं).

2. वेक्टर निर्देशांक

डीईएफ़। तेरह।निर्देशांक अक्षों पर वेक्टर अनुमान ओह, कहां, आउंसबुलाया वेक्टर निर्देशांक। पदनाम: ए एक्स , ए आप , ए जेड .

वेक्टर लंबाई:

उदाहरण:वेक्टर की लंबाई की गणना करें।

फेसला:

बिंदुओं के बीच की दूरी और सूत्र द्वारा गणना: .

उदाहरण:बिंदु M (2,3,-1) और K (4,5,2) के बीच की दूरी ज्ञात कीजिए।

निर्देशांक रूप में सदिशों पर क्रियाएँ।

दिए गए सदिश = ए एक्स , ए आप , ए जेडऔर = बी एक्स , बी आप , बी जेड .

1. (  )= ए एक्स  बी एक्स , ए आप  बी आप , ए जेड  बी जेड .

2.  =   ए एक्स ,  ए आप ,  ए जेड, कहाँ  - अदिश।

वैक्टर के स्केलर उत्पाद।

परिभाषा:दो सदिशों के अदिश गुणनफल के अंतर्गत तथा

इन सदिशों की लंबाई और उनके बीच के कोण की कोज्या के गुणनफल के बराबर एक संख्या के रूप में समझा जाता है, अर्थात। = , - वैक्टर और के बीच का कोण।

डॉट उत्पाद गुण:

1.  =

2. ( + ) =

3.

4.

5. , अदिश कहाँ हैं।

6. दो सदिश लंब (लंबकोणीय) हैं यदि .

7. यदि और केवल यदि .

निर्देशांक रूप में अदिश उत्पाद का रूप है: , और कहां .

उदाहरण:वैक्टर के अदिश उत्पाद का पता लगाएं और

फेसला:

वेक्टर होल्डिंग वैक्टर।

परिभाषा: दो वैक्टर का वेक्टर उत्पाद और एक वेक्टर के रूप में समझा जाता है जिसके लिए:

मॉड्यूल इन वैक्टरों पर बने समांतर चतुर्भुज के क्षेत्रफल के बराबर है, अर्थात। , सदिशों और . के बीच का कोण कहाँ है

यह सदिश गुणित सदिशों के लम्बवत है, अर्थात्।

यदि सदिश असंरेखीय हैं, तो वे सदिशों का दायां त्रिक बनाते हैं।

क्रॉस उत्पाद गुण:

1. जब कारकों का क्रम बदल जाता है, तो वेक्टर उत्पाद मॉड्यूल को संरक्षित करते हुए, इसके संकेत को विपरीत में बदल देता है, अर्थात।

2 .वेक्टर वर्ग शून्य-वेक्टर के बराबर है, अर्थात।

3 अदिश गुणनखंड को सदिश गुणनफल के चिह्न से निकाला जा सकता है, अर्थात्।

4 । किन्हीं तीन सदिशों के लिए, समानता

5 .दो सदिशों की संरेखता के लिए आवश्यक और पर्याप्त शर्त और :

निर्देशांक रूप में वेक्टर उत्पाद।

यदि सदिशों के निर्देशांक तथा , तो उनका वेक्टर उत्पाद सूत्र द्वारा पाया जाता है:

.

फिर क्रॉस उत्पाद की परिभाषा से यह निम्नानुसार है कि वैक्टर पर बने समांतर चतुर्भुज का क्षेत्रफल और सूत्र द्वारा गणना की जाती है:

उदाहरण:कोने (1;-1;2), (5;-6;2), (1;3;-1) वाले त्रिभुज के क्षेत्रफल की गणना करें।

फेसला: .

तब त्रिभुज ABC के क्षेत्रफल की गणना इस प्रकार की जाएगी:

,

वैक्टर का मिश्रित उत्पाद।

परिभाषा:वैक्टर का मिश्रित (वेक्टर-स्केलर) उत्पाद सूत्र द्वारा निर्धारित एक संख्या है: .

मिश्रित उत्पाद गुण:

1. मिश्रित उत्पाद अपने कारकों के चक्रीय क्रमपरिवर्तन के साथ नहीं बदलता है, अर्थात। .

2. जब दो पड़ोसी कारकों को आपस में बदल दिया जाता है, तो मिश्रित उत्पाद अपना चिन्ह विपरीत में बदल देता है, अर्थात। .

3 .तीन सदिशों के समतलीय होने के लिए आवश्यक और पर्याप्त शर्त : =0.

4 .तीन वैक्टर का मिश्रित उत्पाद इन वैक्टरों पर बने समानांतर चतुर्भुज के आयतन के बराबर होता है, यदि ये वेक्टर एक राइट ट्रिपल बनाते हैं, और एक माइनस साइन के साथ एक प्लस साइन के साथ लिया जाता है, अगर वे एक लेफ्ट ट्रिपल बनाते हैं, यानी। .

यदि परिचित हो COORDINATESवैक्टर , तब मिश्रित उत्पाद सूत्र द्वारा ज्ञात किया जाता है:

उदाहरण:वैक्टर के मिश्रित उत्पाद की गणना करें।

फेसला:

3. वैक्टर की प्रणाली का आधार।

परिभाषा।वैक्टर की एक प्रणाली को एक ही स्थान से संबंधित कई वैक्टर के रूप में समझा जाता है आर.

टिप्पणी।यदि सिस्टम में वैक्टर की एक सीमित संख्या होती है, तो उन्हें अलग-अलग सूचकांकों के साथ एक ही अक्षर से दर्शाया जाता है।

उदाहरण।

परिभाषा। रूप का कोई सदिश = सदिशों का रैखिक संयोजन कहलाता है। संख्याएं रैखिक संयोजन के गुणांक हैं।

उदाहरण। .

परिभाषा. यदि वेक्टर वैक्टर का एक रैखिक संयोजन है , तब हम कहते हैं कि सदिश को सदिशों के पदों में रैखिक रूप से व्यक्त किया जाता है .

परिभाषा।वैक्टर की प्रणाली को कहा जाता है रैखिक रूप से स्वतंत्र, यदि निकाय का कोई भी सदिश शेष सदिशों के रैखिक संयोजन के रूप में नहीं हो सकता है। अन्यथा, सिस्टम को रैखिक रूप से निर्भर कहा जाता है।

उदाहरण. वेक्टर सिस्टम रैखिक रूप से निर्भर, वेक्टर के बाद से .

आधार परिभाषा।वैक्टर की एक प्रणाली एक आधार बनाती है यदि:

1) यह रैखिक रूप से स्वतंत्र है,

2) इसके माध्यम से अंतरिक्ष के किसी भी वेक्टर को रैखिक रूप से व्यक्त किया जाता है।

उदाहरण 1अंतरिक्ष आधार:।

2. वैक्टर की प्रणाली में सदिश आधार हैं: , क्योंकि वैक्टर के संदर्भ में रैखिक रूप से व्यक्त किया गया।

टिप्पणी।वैक्टर की दी गई प्रणाली का आधार खोजने के लिए, आपको यह करना होगा:

1) मैट्रिक्स में वैक्टर के निर्देशांक लिखें,

2) प्रारंभिक परिवर्तनों का उपयोग करके, मैट्रिक्स को त्रिकोणीय रूप में लाएं,

3) मैट्रिक्स की गैर-शून्य पंक्तियाँ सिस्टम का आधार होंगी,

4) आधार में वैक्टर की संख्या मैट्रिक्स के रैंक के बराबर है।

परिभाषा

वेक्टर(अक्षांश से।" वेक्टर"-" असर") - अंतरिक्ष में या एक विमान पर एक सीधी रेखा का एक निर्देशित खंड।

ग्राफिक रूप से, एक वेक्टर को एक निश्चित लंबाई के निर्देशित सीधी रेखा खंड के रूप में दर्शाया जाता है। जिस सदिश का आरंभ बिंदु पर और अंत बिंदु पर होता है, उसे (चित्र 1) के रूप में दर्शाया जाता है। इसके अलावा, एक वेक्टर को एक छोटे अक्षर से दर्शाया जा सकता है, उदाहरण के लिए, .

यदि अंतरिक्ष में एक समन्वय प्रणाली दी गई है, तो वेक्टर को इसके निर्देशांक के एक सेट द्वारा विशिष्ट रूप से निर्दिष्ट किया जा सकता है। यानी एक वेक्टर को एक ऐसी वस्तु के रूप में समझा जाता है जिसमें एक मान (लंबाई), दिशा और अनुप्रयोग बिंदु (वेक्टर की शुरुआत) होती है।

वेक्टर कैलकुलस की शुरुआत 1831 में जर्मन गणितज्ञ, मैकेनिक, भौतिक विज्ञानी, खगोलशास्त्री और सर्वेक्षक जोहान कार्ल फ्रेडरिक गॉस (1777-1855) के कार्यों में दिखाई दी। वैक्टर के साथ संचालन पर काम आयरिश गणितज्ञ, यांत्रिकी और सैद्धांतिक भौतिक विज्ञानी, सर विलियम रोवन हैमिल्टन (1805-1865) द्वारा उनके क्वाटरनियन कैलकुलस के हिस्से के रूप में प्रकाशित किया गया था। वैज्ञानिक ने "वेक्टर" शब्द का प्रस्ताव रखा और वैक्टर पर कुछ संचालन का वर्णन किया। ब्रिटिश भौतिक विज्ञानी, गणितज्ञ और मैकेनिक जेम्स क्लर्क मैक्सवेल (1831-1879) के विद्युत चुंबकत्व पर काम के लिए वेक्टर कैलकुलस को और विकसित किया गया था। 1880 के दशक में, अमेरिकी भौतिक विज्ञानी, भौतिक रसायनज्ञ, गणितज्ञ और मैकेनिक जोशिया विलार्ड गिब्स (1839-1903) की पुस्तक "एलिमेंट्स ऑफ वेक्टर एनालिसिस" प्रकाशित हुई थी। आधुनिक वेक्टर विश्लेषण का वर्णन 1903 में अंग्रेजी स्व-सिखाया वैज्ञानिक, इंजीनियर, गणितज्ञ और भौतिक विज्ञानी ओलिवर हीविसाइड (1850-1925) द्वारा किया गया था।

परिभाषा

लंबाईया वेक्टर मॉड्यूलनिर्देशित खंड की लंबाई है जो वेक्टर को परिभाषित करती है। के रूप में नामित ।

मूल प्रकार के वैक्टर

शून्य वेक्टरएक सदिश कहलाती है जिसका प्रारंभ बिंदु और अंत बिंदु समान होता है। शून्य वेक्टर की लंबाई शून्य है।

एक ही रेखा के समानांतर या एक ही रेखा पर स्थित सदिश कहलाते हैं समरेख(रेखा चित्र नम्बर 2)।

सह-दिशात्मकयदि उनकी दिशा समान है।

चित्र 2 में, ये सदिश और . सदिशों की सह-दिशा को इस प्रकार निरूपित किया जाता है: .

दो संरेख सदिश कहलाते हैं विपरीत दिशाओं मेयदि उनकी दिशा विपरीत है।

चित्र 3 में, ये सदिश हैं और . पद: ।