Nilai yang diharapkan. harapan matematis variabel acak diskrit X, yang mengambil sejumlah nilai yang terbatas Xsaya dengan probabilitas Rsaya, disebut jumlah:
harapan matematis variabel acak kontinu X disebut integral dari produk dari nilai-nilainya X pada densitas distribusi probabilitas f(x):
 (6b)
(6b)
Integral tak wajar (6 b) diasumsikan benar-benar konvergen (jika tidak, kita katakan bahwa ekspektasi M(X) tidak ada). Ekspektasi matematis mencirikan berarti variabel acak X. Dimensinya bertepatan dengan dimensi variabel acak.
Sifat-sifat ekspektasi matematis:
Penyebaran. penyebaran variabel acak X nomor disebut:
dispersi adalah karakteristik hamburan nilai variabel acak X relatif terhadap nilai rata-ratanya M(X). Dimensi varians sama dengan dimensi kuadrat variabel acak. Berdasarkan definisi varians (8) dan ekspektasi matematis (5) untuk variabel acak diskrit dan (6) untuk variabel acak kontinu, kita memperoleh ekspresi serupa untuk varians:
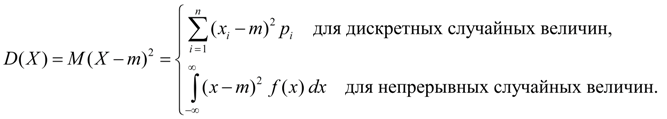 (9)
(9)
Di Sini m = M(X).
Sifat dispersi:
Standar deviasi:
![]() (11)
(11)
Karena dimensi simpangan baku sama dengan variabel acak, maka lebih sering daripada varians yang digunakan sebagai ukuran dispersi.
momen distribusi. Konsep ekspektasi matematis dan varians adalah kasus khusus dari konsep yang lebih umum untuk karakteristik numerik variabel acak - momen distribusi. Momen distribusi dari variabel acak diperkenalkan sebagai ekspektasi matematis dari beberapa fungsi sederhana dari variabel acak. Jadi, momen pemesanan k relatif terhadap titik X 0 disebut harapan M(X–X 0 )k. Momen relatif terhadap asal X= 0 disebut momen awal dan ditandai:
![]() (12)
(12)
Momen awal orde pertama adalah pusat distribusi dari variabel acak yang dipertimbangkan:
![]() (13)
(13)
Momen relatif terhadap pusat distribusi X= m ditelepon momen sentral dan ditandai:
![]() (14)
(14)
Dari (7) berikut bahwa momen pusat orde pertama selalu sama dengan nol:
Momen pusat tidak bergantung pada asal mula nilai variabel acak, karena dengan pergeseran nilai konstan Dengan pusat distribusinya digeser oleh nilai yang sama Dengan, dan deviasi dari pusat tidak berubah: X – m = (X – Dengan) – (m – Dengan).
Sekarang jelas bahwa penyebaran- Ini momen sentral orde dua:
Asimetri. Momen sentral orde ketiga:
![]() (17)
(17)
berfungsi untuk menilai kecondongan distribusi. Jika distribusinya simetris terhadap titik X= m, maka momen pusat orde ketiga akan sama dengan nol (begitu juga semua momen sentral orde ganjil). Oleh karena itu, jika momen pusat orde ketiga berbeda dengan nol, maka distribusinya tidak dapat simetris. Besarnya asimetri diperkirakan menggunakan tak berdimensi koefisien asimetri:
 (18)
(18)
Tanda koefisien asimetri (18) menunjukkan asimetri sisi kanan atau kiri (Gbr. 2).

Beras. 2. Jenis asimetri distribusi.
Kelebihan. Momen sentral orde keempat:
![]() (19)
(19)
berfungsi untuk mengevaluasi apa yang disebut kurtosis, yang menentukan derajat kecuraman (pointiness) dari kurva distribusi dekat pusat distribusi terhadap kurva distribusi normal. Karena untuk distribusi normal, besaran yang dianggap sebagai kurtosis adalah:
 (20)
(20)
pada gambar. 3 menunjukkan contoh kurva distribusi dengan nilai kurtosis yang berbeda. Untuk distribusi normal E= 0. Kurva yang lebih berpuncak dari biasanya memiliki kurtosis positif, dan kurva dengan puncak yang lebih datar memiliki kurtosis negatif.

Beras. 3. Kurva distribusi dengan derajat kecuraman yang berbeda (kurtosis).
Momen orde tinggi dalam aplikasi rekayasa statistik matematika biasanya tidak digunakan.
Mode
diskrit variabel acak adalah nilai yang paling mungkin. Mode kontinu variabel acak adalah nilainya di mana kepadatan probabilitas maksimum (Gbr. 2). Jika kurva distribusi memiliki satu maksimum, maka distribusi tersebut disebut unimodal. Jika kurva distribusi memiliki lebih dari satu maksimum, maka distribusi tersebut disebut polimodal. Terkadang ada distribusi yang kurvanya tidak maksimum, tetapi minimum. Distribusi seperti ini disebut antimodal. Dalam kasus umum, modus dan harapan matematis dari variabel acak tidak bertepatan. Dalam kasus tertentu, untuk modal, yaitu memiliki modus, distribusi simetris, dan asalkan ada harapan matematis, yang terakhir bertepatan dengan modus dan pusat simetri distribusi.
median variabel acak X apakah artinya? Saya, yang persamaannya berlaku: yaitu. kemungkinan yang sama bahwa variabel acak X akan kurang atau lebih Saya. Secara geometris median adalah absis dari titik di mana area di bawah kurva distribusi dibagi dua (Gbr. 2). Dalam kasus distribusi modal simetris, median, modus, dan mean adalah sama.
Modus adalah nilai yang paling mungkin dari variabel acak. Dengan distribusi simetris terhadap mean, modus bertepatan dengan harapan matematis. Jika nilai variabel acak tidak berulang, tidak ada mode.
Titik pada sumbu x yang bersesuaian dengan kurva densitas distribusi maksimum disebut modus, yaitu modus adalah nilai yang paling mungkin dari variabel acak. Namun, mode tidak ada untuk semua distribusi. Contohnya adalah distribusi seragam. Dalam hal ini, definisi pusat distribusi sebagai mode tidak mungkin. Fashion biasanya disebut sebagai Mo.
Ada konsep modus dan median dari variabel acak.
Jelas bahwa dalam kasus median simetris bertepatan dengan modus dan harapan matematis.
Berdasarkan fakta bahwa mode tidak didasarkan pada pengukuran tunggal, tetapi pada volume pengamatan yang besar, itu tidak dapat dianggap sebagai variabel acak. Besarnya mode tidak terpengaruh oleh berbagai macam keterlambatan dalam pekerjaan dan hilangnya tingkat normalnya.
Kadang-kadang, dalam analisis distribusi empiris, konsep modus dan median distribusi digunakan, "... Modus adalah nilai yang paling mungkin dari variabel acak,
Interpretasi probabilistik yang diperluas dari fenomena lotere adalah konsep distribusi probabilistik dari variabel acak. Ini digunakan untuk menentukan probabilitas bahwa variabel acak akan mengambil satu atau lain dari nilai yang mungkin. Dilambangkan dengan y variabel acak , dan dengan y kemungkinan nilainya. Kemudian untuk variabel acak diskrit , yang dapat mengambil kemungkinan nilai Y, y2, US,. .., yn bentuk yang mudah dari distribusi probabilitas harus dipertimbangkan ketergantungan P(y = y), yang biasanya disebut deret probabilitas, deret distribusi n. Dalam praktiknya, untuk penilaian umum operasional dari distribusi probabilitas nilai risiko, apa yang disebut numerik dan karakteristik lain dari distribusi hasil acak sering digunakan: ekspektasi matematis, varians, standar deviasi, koefisien variasi, mode, median, dll. (lihat, misalnya, dan lain-lain .). Dengan kata lain, untuk persepsi yang cepat dan holistik, wirausahawan mencari (atau hanya Anda
Berdasarkan data Komite Statistik Negara Uni Soviet tentang distribusi populasi dengan total pendapatan per kapita, kami akan mencoba membandingkan indikator pendapatan rata-rata, median dan modal (Tabel 1). Tabel tersebut menunjukkan bahwa pendapatan rata-rata secara absolut melebihi pendapatan median dan modal, dan pertumbuhannya terjadi terutama karena peningkatan proporsi orang dengan pendapatan tinggi, yaitu, penggunaan indikator pendapatan rata-rata menyebabkan perkiraan yang terlalu tinggi secara signifikan. tingkat pendapatan sebagian besar penduduk dan sebagian besar menyembunyikan proses diferensiasi mereka. Nilai pendapatan modal condong ke kelompok distribusi yang lebih rendah dan menyimpang dari pendapatan rata-rata ke bawah. Namun, hit mode dalam satu atau lain interval sering acak di alam, perubahan yang agak kecil dalam distribusi - dan mode sudah akan berada di interval tetangga. Misalnya, pada tahun 1989, tingkat pendapatan yang paling umum adalah dari 100 hingga 125 rubel (16,1% dari populasi menerima pendapatan seperti itu), tetapi karena perubahan kecil dalam pendapatan yang terjadi pada tahun 1989-1990, interval yang paling umum adalah interval berikut (125-150 rubel): , dan nilai mode itu sendiri meningkat 15,6 rubel. Selain itu, bagian populasi dalam interval pendapatan modal mungkin sedikit melebihi bagian lainnya.
Untuk mengkarakterisasi pusat distribusi dari variabel acak normal logaritmik a, kita dapat menggunakan, bersama dengan ekspektasi matematis Ma yang sudah dihitung, mode
Mode - mode. Nilai yang paling mungkin dari variabel acak.
FASHION - konsep
Selain ekspektasi matematis dan dispersi, sejumlah karakteristik numerik digunakan dalam teori probabilitas, yang mencerminkan fitur distribusi tertentu.
Definisi. Modus Mo(X) dari variabel acak X adalah nilai yang paling mungkin(untuk itu probabilitas r atau kepadatan probabilitas
Jika probabilitas atau kerapatan probabilitas mencapai maksimum tidak pada satu, tetapi pada beberapa titik, distribusi disebut polimodal(Gbr. 3.13).

Mode Lumut), di mana probabilitas R ( atau densitas probabilitas (p(x) mencapai maksimum global, disebut nilai yang paling mungkin variabel acak (pada Gambar 3.13 ini Mo(X) 2).
Definisi. Median Me(X) dari variabel acak kontinu X adalah nilainya, untuk itu
itu. peluang munculnya peubah acak X mengambil nilai lebih kecil dari median Bulu) atau lebih besar dari itu, sama dan sama dengan 1/2. Garis vertikal geometris X = Bulu) melalui suatu titik yang absisnya sama dengan Bulu), membagi luas gambar kurva distribusi menjadi dua bagian yang sama (Gbr. 3.14). Jelas, pada intinya X = Bulu) fungsi distribusi sama dengan 1/2, yaitu P(Saya(X))= 1/2 (Gbr. 3.15).


Perhatikan properti penting dari median variabel acak: ekspektasi matematis dari nilai absolut deviasi variabel acak X dari nilai konstanta C adalah minimal, ketika konstanta C ini sama dengan median Me(X) = m, yaitu 
(properti ini mirip dengan properti (3,10") dari minimalitas kuadrat rata-rata deviasi variabel acak dari ekspektasi matematisnya).
o Contoh 3.15. Tentukan modus, median, dan mean dari variabel acak X s kepadatan probabilitas (x) = 3x 2 untuk xx.
Keputusan. Kurva distribusi ditunjukkan pada gambar. 3.16. Jelas, kepadatan probabilitas (x) maksimum di X= Mo(X) = 1.
median Bulu) = b kita temukan dari kondisi (3.28):

di mana 
Ekspektasi matematis dihitung dengan rumus (3,25):
Susunan titik bersama M(X) > Saya(X) dan Lumut) dalam urutan absis menaik ditunjukkan pada gambar. 3.16. ?
Seiring dengan karakteristik numerik yang disebutkan di atas, konsep kuantil dan poin persentase digunakan untuk menggambarkan variabel acak.
Definisi. kuantil tingkat y-kuantil )
disebut nilai x q dari variabel acak , di mana fungsi distribusinya mengambil nilai yang sama dengan d, yaitu
Beberapa kuantil telah menerima nama khusus. Jelas, di atas median variabel acak adalah kuantil tingkat 0,5, yaitu Saya (X) \u003d x 05. Kuantil dg 0 2 5 dan x 075 diberi nama masing-masing lebih rendah dan kuartil atasK
Terkait erat dengan konsep kuantil adalah konsep poin persentase. Di bawah YuOuHo-noi dot
kuantil tersirat xx (( ,
itu. nilai variabel acak seperti itu x,
di bawah mana ![]()
0 Contoh 3.16. Menurut contoh 3.15 temukan kuantil x 03 dan 30% titik variabel acak x.
Keputusan. Menurut rumus (3.23), fungsi distribusi
Kami menemukan kuantil r 0 z dari persamaan (3.29), yaitu. x$ 3 \u003d 0,3, dari mana L "oz -0,67. Temukan titik 30% dari variabel acak x, atau kuantil x 0 7, dari persamaan x$7 = 0,7, dari mana x 0 7 "0,89. ?
Di antara karakteristik numerik dari variabel acak, momen - awal dan pusat - sangat penting.
Definisi. Momen awalurutan ke-k dari variabel acak X adalah ekspektasi matematis dari pangkat ke-k dari variabel ini :
Definisi. Titik tengahorde ke-k dari variabel acak X adalah ekspektasi matematis dari derajat deviasi ke-k variabel acak X dari ekspektasi matematisnya:
Rumus untuk menghitung momen untuk variabel acak diskrit (mengambil nilai x 1 dengan probabilitas p,) dan kontinu (dengan kepadatan probabilitas cp(x)) diberikan pada Tabel. 3.1.
Tabel 3.1
Sangat mudah untuk melihat bahwa ketika k = 1 momen awal pertama variabel acak X adalah harapan matematisnya, yaitu h x \u003d M [X) \u003d a, pada ke= 2 momen sentral kedua adalah dispersi, mis. hal 2 = T)(X).
Momen pusat p A dapat dinyatakan dalam momen awal menggunakan rumus:
dll. 
Misalnya, c3 \u003d M (X-a) * \u003d M (X * -ZaX 2 + Za 2 X-a-\u003e) \u003d M (X *) ~ -ZaM (X 2) + Za 2 M (X) ~ a3 \u003d y 3 -Zy ^ + Zy (y, -y ^ \u003d y 3 - Zy ^ + 2y ^ (saat menurunkan, kami memperhitungkan bahwa sebuah = M(X)= V, - nilai non-acak). ?
Seperti disebutkan di atas, ekspektasi matematis M(X), atau momen awal pertama, mencirikan nilai atau posisi rata-rata, pusat distribusi variabel acak X pada garis bilangan; penyebaran OH), atau momen pusat kedua p 2 , - s t s - hamburan distribusi X relatif M(X). Momen orde tinggi berfungsi untuk deskripsi distribusi yang lebih rinci.
Momen sentral ketiga p 3 berfungsi untuk mencirikan asimetri distribusi (kemiringan). Ini memiliki dimensi kubus dari variabel acak. Untuk mendapatkan nilai tak berdimensi, dibagi dengan sekitar 3, di mana a adalah simpangan baku dari variabel acak x. Nilai yang diterima TETAPI ditelepon koefisien asimetri variabel acak.
Jika distribusi simetris terhadap ekspektasi matematis, maka koefisien skewness adalah A = 0.
pada gambar. 3.17 menunjukkan dua kurva distribusi: I dan II. Kurva I memiliki asimetri positif (sisi kanan) (L > 0), dan kurva II memiliki asimetri negatif (sisi kiri) (L 

Momen sentral keempat p 4 berfungsi untuk mencirikan kecuraman (puncak atas atau puncak datar - tiang) dari sebaran.
Mode- nilai dalam himpunan pengamatan yang paling sering terjadi
Mo \u003d X Mo + h Mo * (f Mo - f Mo-1) : ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),
di sini X Mo adalah batas kiri dari interval modal, h Mo adalah panjang dari interval modal, f Mo-1 adalah frekuensi dari interval modal, f Mo adalah frekuensi dari interval modal, f Mo+1 adalah frekuensi interval postmodal.
Modus distribusi kontinu mutlak adalah setiap titik maksimum lokal dari densitas distribusi. Untuk distribusi diskrit, mode adalah nilai a i yang probabilitas p i lebih besar dari probabilitas nilai tetangga
median variabel acak kontinu X nilainya Me disebut seperti itu, yang kemungkinannya sama apakah variabel acak akan menjadi lebih kecil atau lebih besar Saya, yaitu
M e \u003d (n + 1) / 2 P(X < Saya) = P(X > Saya)
Terdistribusi merata BARU
Distribusi merata. Variabel acak kontinu disebut terdistribusi seragam pada segmen () jika fungsi densitas distribusinya (Gbr. 1.6, sebuah) seperti:
Peruntukan : - SW berdistribusi merata pada .
Dengan demikian, fungsi distribusi pada segmen (Gbr. 1.6, b):
![]()
Beras. 1.6. Fungsi dari variabel acak terdistribusi seragam pada [ sebuah,b]: sebuah– kepadatan probabilitas f(x); b– distribusi F(x)
Ekspektasi matematis dan varians dari RV ini ditentukan oleh ekspresi:
Karena simetri fungsi kerapatan, itu bertepatan dengan median. Fashion tidak memiliki distribusi yang seragam
Contoh 4 Waktu tunggu untuk jawaban panggilan telepon adalah variabel acak yang mematuhi hukum distribusi seragam dalam kisaran 0 hingga 2 menit. Temukan fungsi distribusi integral dan diferensial dari variabel acak ini.
27. Hukum normal distribusi probabilitas
Sebuah variabel acak kontinu x berdistribusi normal dengan parameter: m,s > 0, jika rapat distribusi peluang berbentuk:
dimana: m adalah ekspektasi matematis, s adalah standar deviasi.
Distribusi normal juga disebut Gaussian setelah ahli matematika Jerman Gauss. Fakta bahwa variabel acak memiliki distribusi normal dengan parameter: m, , dinotasikan sebagai berikut: N (m, s), di mana: m=a=M[X];
Cukup sering, dalam rumus, ekspektasi matematis dilambangkan dengan sebuah . Jika suatu peubah acak terdistribusi menurut hukum N(0,1), maka disebut nilai normal ternormalisasi atau terstandarisasi. Fungsi distribusi untuk itu memiliki bentuk:
Grafik densitas distribusi normal, yang disebut kurva normal atau kurva Gaussian, ditunjukkan pada Gambar 5.4.
Beras. 5.4. Kepadatan distribusi normal
properti variabel acak dengan hukum distribusi normal.
1. Jika , maka untuk menemukan probabilitas bahwa nilai ini jatuh ke dalam interval tertentu ( x 1; x 2) rumus yang digunakan:
2. Probabilitas penyimpangan variabel acak dari ekspektasi matematisnya tidak akan melebihi nilai (dalam nilai absolut) adalah sama dengan:
3. "Aturan Tiga Sigma". Jika variabel acak , maka dapat dipastikan bahwa nilainya terkandung dalam interval (). (Probabilitas melampaui batas-batas ini adalah 0,0027.) Aturannya memungkinkan, mengetahui parameter ( dan ), untuk secara kira-kira menentukan interval nilai praktis dari variabel acak.
distribusi eksponensial
Sebuah variabel acak X memiliki distribusi eksponensial dengan parameter jika kerapatannya berbentuk
Mengintegrasikan densitas, kita memperoleh fungsi distribusi eksponensial:
![]()
karakteristik utama dari distribusi eksponensial:
Plot densitas dan fungsi dari distribusi eksponensial yang dihasilkan
![]()
