შესავალი
ზოგადსაგანმანათლებლო სკოლაში მიღებული მათემატიკური განათლება ზოგადი განათლებისა და თანამედროვე ადამიანის ზოგადი კულტურის აუცილებელი კომპონენტია. თითქმის ყველაფერი, რაც გარშემორტყმულია თანამედროვე ადამიანს, ამა თუ იმ გზით უკავშირდება მათემატიკას. და ფიზიკის, ინჟინერიისა და საინფორმაციო ტექნოლოგიების უახლესი მიღწევები ეჭვს არ ტოვებს, რომ მომავალში ვითარება იგივე დარჩება. აქედან გამომდინარე, მრავალი პრაქტიკული პრობლემის გადაწყვეტა მცირდება სხვადასხვა ტიპის განტოლებების ამოხსნით, რომელთა ამოხსნა უნდა ვისწავლოთ.
ელემენტარულ მათემატიკაში განასხვავებენ განტოლების ორ ტიპს: ალგებრულ და ტრანსცენდენტურ.ალგებრულ განტოლებებს მიეკუთვნება:
ხაზოვანი;
მოედანი; კუბური; ბიკვადი; ზოგადი ფორმის მეოთხე ხარისხის განტოლება; n ხარისხის ორწლიან ალგებრულ განტოლებას; სიმძლავრე ალგებრული; - დაბრუნება (ალგებრული); – ზოგადი ფორმის მე-ე ხარისხის ალგებრული განტოლება; 10. წილადი ალგებრული განტოლებები, ე.ი. მრავალწევრებისა და ალგებრული წილადების შემცველი განტოლებები (ფორმის წილადები
, სადაც და არის მრავალწევრები);11. ირაციონალური განტოლებები, ე.ი. რადიკალების შემცველი განტოლებები, რომლებშიც განლაგებულია პოლინომები და ალგებრული წილადები;
12. მოდულის შემცველი განტოლებები, რომლის მოდულის ქვეშ მოთავსებულია მრავალწევრები და ალგებრული წილადები.
ტრანსცენდენტული ფუნქციების შემცველ განტოლებებს, როგორიცაა ლოგარითმული, ექსპონენციალური ან ტრიგონომეტრიული ფუნქციები, ეწოდება ტრანსცენდენტური. ჩვენს ნაშრომში უფრო დეტალურად განვიხილავთ ალგებრულ განტოლებებს.
საგანმანათლებლო და მეთოდურ ლიტერატურაში ტრადიციულად განიხილება განტოლებების ამოხსნის სპეციალური მეთოდები. იმავდროულად, თითოეული მონაკვეთის განტოლებების ამოხსნის სპეციფიკა მეორეხარისხოვანი საკითხია. ძირითადად, არსებობს ოთხი ძირითადი მეთოდი:
h (f(x))=h (g(x)) განტოლების შეცვლა f(x)=g(x) განტოლებით;
ცვლადი ჩანაცვლების მეთოდი;
ფაქტორინგის მეთოდი;
ფუნქციონალურ-გრაფიკული მეთოდი და მათი სხვადასხვა მოდიფიკაცია.
მათგან ყველაზე გავრცელებულია ცვლადი ჩანაცვლების მეთოდი.
ამის საფუძველზე ვაყალიბებთ ჩვენი სამუშაოს მიზანს: შევისწავლოთ ალგებრული განტოლებების ამოხსნის უცნობის ჩანაცვლების მეთოდის შესაძლებლობები და ვაჩვენოთ მათი გამოყენება სტანდარტულ და არასტანდარტულ სიტუაციებში. ამ მიზნის მისაღწევად აუცილებელია შემდეგი ამოცანების გადაჭრა:
1. განავრცე განტოლებების ამოხსნის თეორიასთან დაკავშირებული ძირითადი ცნებებისა და დებულებების შინაარსი: განტოლების ამოხსნა, ეკვივალენტობა და შედეგი, განტოლებების ამოხსნის ზოგადი მეთოდები.
2. სტანდარტულ და არასტანდარტულ სიტუაციებში ალგებრული განტოლებების ამოხსნისას უცნობის ჩანაცვლების მეთოდის გამოყენების შესაძლებლობების იდენტიფიცირება.
3. განახორციელოს ალგებრული განტოლებების ამოხსნისას ახალი უცნობების შემოტანის მეთოდების ტიპიზაცია და მათი გამოყენებადობის კრიტერიუმების დადგენა.
4. შეადგინეთ ტიპიური ამოცანების ნაკრები, რომელიც ემყარება განტოლებების ამოხსნის ჩანაცვლების მეთოდის გამოყენებას და აჩვენეთ მათი ამოხსნა.
1. განტოლებების ამოხსნის თეორიასთან დაკავშირებული ძირითადი ცნებები და დებულებები
ჩვენი ნაშრომის პირველ თავში გამოვავლენთ განტოლებების ამოხსნის თეორიასთან დაკავშირებული ძირითადი ცნებებისა და დებულებების შინაარსს.
„განტოლების“ ცნებას მათემატიკის გაკვეთილებზე უკვე დაწყებით სკოლაში ვეცნობით და „განტოლების ამოხსნის“ ამოცანა ალბათ ყველაზე გავრცელებული ამოცანაა. მიუხედავად ამისა, ჩვენ არ შეგვიძლია მივცეთ „განტოლების“ ცნების ზუსტი განმარტება, ზუსტად განვსაზღვროთ რას ნიშნავს „განტოლების ამოხსნა“, ელემენტარული მათემატიკის კურსის ჩარჩოებიდან შორს გასვლის გარეშე. ამისათვის საჭიროა ძალიან სერიოზული ლოგიკური და თუნდაც ფილოსოფიური კატეგორიების ჩართვა. ჩვენთვის სრულიად საკმარისია ამ ცნებების „საღი აზრის“ დონეზე გაცნობა.
განვიხილოთ ორი განტოლება A და B ერთნაირი უცნობით. ჩვენ ვიტყვით, რომ განტოლება B არის შედეგიგანტოლება A, თუ A განტოლების რომელიმე ფესვი არის B განტოლების ფესვი.
განტოლებები ე.წ ექვივალენტითუ რომელიმე მათგანის რომელიმე ფესვი მეორის ფესვია და პირიქით. ამრიგად, განტოლებები ექვივალენტურია, თუ თითოეული მათგანი მეორის შედეგია.
ამ განმარტებებიდან გამომდინარეობს, რომ, მაგალითად, ორი განტოლება, რომლებსაც ამონახსნები არ აქვთ, ეკვივალენტურია. თუ A არ აქვს ამონახსნები, მაშინ B არის შედეგი A, როგორიც არ უნდა იყოს B განტოლება.
განვსაზღვროთ „განტოლების ამოხსნის“ ცნება. განტოლების ამოხსნა- ნიშნავს მასში შემავალი უცნობის ყველა ისეთი მნიშვნელობის პოვნას, რომელიც განტოლებას იდენტურად აქცევს. ამ მნიშვნელობებს უწოდებენ განტოლების ფესვებს.
განტოლებების ამოხსნის პროცესი ძირითადად შედგება მოცემული განტოლების სხვა მისი ეკვივალენტით ჩანაცვლებაში.
როგორც უკვე აღვნიშნეთ, არსებობს ოთხი ყველაზე გავრცელებული მეთოდი, რომლებიც გამოიყენება ნებისმიერი სახის განტოლების ამოხსნისას. მოდით უფრო დეტალურად განვიხილოთ თითოეული მეთოდი.
h (f(x))=h (g(x)) განტოლების f(x)=g(x) განტოლებით ჩანაცვლების მეთოდი შეიძლება გამოყენებულ იქნას მხოლოდ მაშინ, როდესაც
არის მონოტონური ფუნქცია, რომელიც იღებს მის თითოეულ მნიშვნელობას ერთხელ. თუ ეს ფუნქცია არამონოტონურია, მაშინ ამ მეთოდის გამოყენება შეუძლებელია, რადგან ფესვების დაკარგვა შესაძლებელია.ფაქტორილიზაციის მეთოდის არსი შემდეგია: განტოლება
შეიძლება შეიცვალოს: ამ სიმრავლის განტოლებების ამოხსნის შემდეგ, თქვენ უნდა აიღოთ ის ფესვები, რომლებიც მიეკუთვნება ორიგინალური განტოლების განსაზღვრის სფეროს, ხოლო დანარჩენი გადააგდოთ როგორც გარე. განტოლების ამოხსნის გრაფიკული მეთოდის იდეა.
არის შემდეგი: თქვენ უნდა ააწყოთ ფუნქციების გრაფიკები და იპოვოთ მათი გადაკვეთის წერტილები. განტოლების ფესვები არის ამ წერტილების აბსციები. ეს მეთოდი საშუალებას გაძლევთ განსაზღვროთ განტოლების ფესვების რაოდენობა, გამოიცნოთ ფესვის მნიშვნელობა, იპოვოთ ფესვების სავარაუდო და ზოგჯერ ზუსტი მნიშვნელობები. ზოგ შემთხვევაში ფუნქციათა გრაფიკების აგება შეიძლება შეიცვალოს ფუნქციების ზოგიერთი თვისების მითითებით (ამიტომაც საუბარია არა გრაფიკულ, არამედ განტოლებების ამოხსნის ფუნქციურ-გრაფიკულ მეთოდზე). თუ, მაგალითად, ერთ-ერთი ფუნქცია
იზრდება და მეორე მცირდება, მაშინ განტოლებას ან არ აქვს ფესვები ან აქვს ერთი ფესვი.აღვნიშნოთ ფუნქციონალურ-გრაფიკული მეთოდის კიდევ ერთი საკმაოდ ლამაზი სახეობა: თუ ინტერვალზე ერთ-ერთი ფუნქციის უდიდესი მნიშვნელობა უდრის და სხვა ფუნქციის უმცირესი მნიშვნელობა ასევე ტოლია, მაშინ განტოლება ტოლია განტოლებათა სისტემის ინტერვალზე. გამოვავლინოთ ცვლადის ცვლილების მეთოდის არსი: თუ განტოლება
განტოლებების ამოხსნა ცვლადების ცვლილებით
ცხოვრებისეული ამოცანების უმეტესობა
წყდება ალგებრული განტოლებების სახით:
მათი დაყვანა უმარტივეს ფორმამდე.
L.N. ტოლსტოი.
გაკვეთილის მიზანი: მოსწავლეთა საგანმანათლებლო საქმიანობის ორგანიზება ცვლადის შეცვლის მეთოდით უმაღლესი ხარისხის განტოლებების ამოხსნის მეთოდების დაუფლებაში; გააცნოს მოსწავლეებს საპასუხო და სიმეტრიული განტოლებების ამოხსნის ცნებები, მეთოდები.
Დავალებები:საგანმანათლებლო:განაგრძეთ ჩანაცვლების მეთოდის გამოყენების უნარის განვითარება
ცვლადი განტოლებების ამოხსნისას; განტოლებების ამოხსნის ერთი და იგივე მეთოდის დანახვის უნარის ფორმირება სხვადასხვა სიტუაციაში; ჩამოაყალიბეთ იდეა არასტანდარტული ამოცანებისა და ალგებრული განტოლებების გადაჭრის მეთოდებისა და გზების შესახებ სახელმწიფო საგანმანათლებლო სტანდარტების დონეს აღემატება;
განვითარებადი:მოსწავლეთა აზროვნების განვითარება; მეხსიერების განვითარება; განვითარება
ლოგიკური აზროვნება, აზრების მკაფიოდ გამოხატვის უნარი; მოსწავლეთა წარმოსახვის განვითარება; ზეპირი მეტყველების განვითარება.
საგანმანათლებლო:დაკვირვების განათლება; სიზუსტის განათლება
დაფაზე და რვეულში ჩანაწერების გაკეთებისას; დამოუკიდებლობის განათლება პრაქტიკული სამუშაოს შესრულებისას.
გაკვეთილების დროს
ორგანიზების დრო.
ცოდნის აქტუალიზაცია და სისტემატიზაცია.
დავალება ნომერი 1. ამოხსენით კროსვორდი. დაწერეთ თქვენი პასუხები მხოლოდ ნომინალურ შემთხვევაში.
ჰორიზონტალურად:4. რა არის გამოხატულება კვადრატული განტოლებისთვის? (დისკრიმინაციული)
6. ცვლადის მნიშვნელობა, რომლის დროსაც განტოლება იქცევა ნამდვილ ტოლობაში. (ფესვი)
8. ფორმის განტოლება 
, სად 
. (ორ კვადრატი)
9. ფრანგი მათემატიკოსი დაკავშირებული კვადრატულ განტოლებებთან. (ვიეტი)
10. განტოლება, რომელშიც მარცხენა და მარჯვენა ნაწილები მთელი რიცხვებია. (მთელი)
11. განტოლებები ერთი ცვლადის მქონე ფესვების ერთნაირი სიმრავლით. (ექვივალენტი)
ვერტიკალურად:
1. განტოლების ფესვთა სიმრავლე. (გადაწყვეტილება)
2. განტოლების ამოხსნა 
. (ნული)
3.ტოლობა, რომელიც შეიცავს ცვლადს. (განტოლება)
5. კვადრატული განტოლება, რომელშიც b ან c კოეფიციენტებიდან ერთ-ერთი უდრის 0-ს. (არასრული)
7. კვადრატული განტოლება, რომელშიც პირველი კოეფიციენტი უდრის ერთს. (შემცირებული)
რას მივუძღვნით დღევანდელ გაკვეთილს? (განტოლებების ამოხსნა )
დავალება ნომერი 2. როგორ ამოხსნით თითოეული ჯგუფის განტოლებებს?
პასუხები: 1 ჯგუფის მაგალითები საუკეთესოდ გადაიჭრება ფაქტორინგით ფრჩხილებიდან საერთო კოეფიციენტის ამოღებით ან შემოკლებული გამრავლების ფორმულების გამოყენებით.
ჯგუფი 2) მაგალითები უკეთ წყდება დაჯგუფებითა და ფაქტორინგით.
მე-3 ჯგუფის მაგალითები უკეთ ამოიხსნება ახალი ცვლადის შემოტანით და კვადრატულ განტოლებაზე გადასვლით.
1 რა მულტიპლიკატორს ამოიღებთ ფრჩხილებიდან 1 ჯგუფის მაგალითებში?
პასუხები:
როგორ დააჯგუფებდით ტერმინებს მე-2 ჯგუფის მაგალითებში?
პასუხები:
რას აღვნიშნავთ ახალი ცვლადით მე-3 ჯგუფის მაგალითებში?
პასუხები:
როგორ შეიძლება მრავალწევრის ფაქტორიზირება 
?
პასუხები: .
დღეს გაკვეთილზე გაჩვენებთ თქვენს ცოდნას თემაზე "განტოლების ამოხსნა ცვლადის შეცვლით"
ჩაწერეთ გაკვეთილის თემა რვეულებში.
დღეს გაკვეთილზე განვიხილავთ უმაღლესი ხარისხის განტოლებების ამოხსნის ერთ-ერთ ხერხს - ცვლადის შეცვლის მეთოდს; გავეცნობით ორმხრივი და სიმეტრიული განტოლებების ამოხსნის ცნებებს, მეთოდებს.
ცვლადების ჩანაცვლების ხელოვნება არის იმის დანახვა, თუ რომელი ჩანაცვლებაა უფრო რაციონალური და იწვევს უფრო სწრაფ წარმატებას.
დავალება ნომერი 3.
ამოხსენით განტოლება.(დავალს დაფაზე ერთდროულად ხსნის 2 მოსწავლე.)
ა) (პირველი მოსწავლე წყვეტს დაფაზე განმარტებით.)
ბ) (მეორე მოსწავლე ჩუმად ხსნის განტოლებას, შემდეგ ხსნის ამოხსნას, კლასი უსმენს და სვამს კითხვებს, თუ რამე გაუგებარია.)
1 სტუდენტიჩანაცვლება: 
.
2 სტუდენტიჩანაცვლება: 
.
(დამატებითი მათთვის, ვინც ადრე გაუმკლავდა წინა განტოლებებს).
. .
3 სტუდენტი
(სტუდენტები კომენტარს აკეთებენ გადაწყვეტილების მიმდინარეობაზე.)
გამოსავალი: ამოიღეთ საერთო ფაქტორი:
სადაც 
ან 
, ე.ი.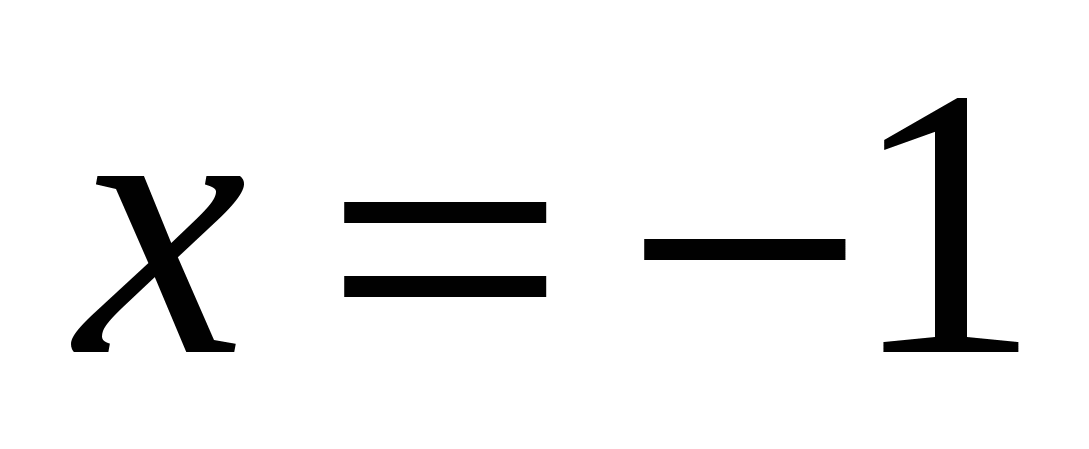 
პასუხი: 
ცოდნის გაღრმავება და გაფართოება
ჩვენ ვაგრძელებთ მუშაობას. თქვენ ხედავთ განტოლებას სლაიდზე: x 4 -5x 3 +6x 2 -5x + 1 = 0.
როგორ შესთავაზებთ მის მოგვარებას? როგორ ვიყოთ?
შესაძლებელია თუ არა მისი გადაჭრა მათემატიკაში სასკოლო პროგრამების ფარგლებში? შეგიძლიათ უპასუხოთ არა. ყოველივე ამის შემდეგ, სკოლაში განტოლებების ამოხსნის სტანდარტული მეთოდები ითვალისწინებს განტოლებების ამოხსნას არაუმეტეს მეორე ხარისხის. მაგრამ შეგვიძლია გავიხსენოთ, რომ უმაღლესი ხარისხის ინდივიდუალური განტოლებები ჯერ კიდევ სკოლაში იყო ამოხსნილი. მართალია, მათი ამოხსნის მეთოდებია ცნობილი მეთოდების კრეატიული გამოყენება, მათი შემცირება ერთი ან რამდენიმე ხარისხის განტოლების ამოხსნამდე, რომელიც არ აღემატება მეორეს.
დააკვირდით ამ განტოლებას? რა შეამჩნიე ?(ამ განტოლებაში ბოლოებიდან თანაბარი დაშორებული კოეფიციენტები ტოლია)
ბიჭებო, ასეთი განტოლება, როდესაც ბოლოებიდან თანაბარი დაშორებული კოეფიციენტები ერთნაირია, ე.წ. დასაბრუნებელი. ეს განტოლება მცირდება კვადრატულ განტოლებამდე ჩანაცვლების გამოყენებით.
მე გთავაზობთ მათ გადაჭრის შემდეგ ალგორითმს:
ორმხრივი განტოლებების ამოხსნის ალგორითმი.
1. გაყავით განტოლების ორივე მხარე x 2-ზე.
2. დააჯგუფე ტერმინები (პირველი ბოლოთი, მეორე მეოთხეთი).
მიიტანეთ განტოლება ფორმაში ა
+ c = 0
3.შემოიღეთ ახალი ცვლადი t = , შემდეგ ტ 2 =, ე.ი. \u003d t 2 - 2.
4. შეასრულეთ ჩანაცვლება და ამოხსენით კვადრატული განტოლება.
5. დაუბრუნდით ჩანაცვლებას და ამოხსენით მიღებული განტოლებები.
6. ჩაწერეთ პასუხი.
ბიჭები სწავლობენ ალგორითმს.
მოსწავლე დაფაზე ალგორითმის მიხედვით და მასწავლებლის დახმარებით ხსნის განტოლებას, დანარჩენები წერენ რვეულებში.
6x 4 - 5x 3 - 38x 2 - 5x + 6 = 0.
გადაწყვეტილება.
6x 2 - 5x - 38 - 5 / x + 6 / x 2 \u003d 0.
6 (x 2 + 1 / x 2) - 5 (x + 1 / x) - 38 \u003d 0.
შეიყვანეთ t: ჩანაცვლება (x + 1/x) = t. ჩანაცვლება: (x 2 + 1 / x 2) \u003d t 2 - 2, გვაქვს:
6t 2 – 5t – 50 = 0.
t = -5/2 ან t = 10/3.
დავუბრუნდეთ x-ს. საპირისპირო ჩანაცვლების შემდეგ ჩვენ ვხსნით მიღებულ ორ განტოლებას:
1) x + 1/x = -5/2;
x 2 + 5/2 x +1 = 0;
x = -2 ან x = -1/2.
2) x + 1/x = 10/3;
x 2 - 10/3 x + 1 = 0;
x = 3 ან x = 1/3.
პასუხი: -2; -1/2; 1/3; 3.
მე-3 და მე-4 ხარისხის განტოლებების პრობლემაში დიდი წვლილი შეიტანეს მე-16 საუკუნის იტალიელმა მათემატიკოსებმა ნ.ტარტალიამ, ა.ფიორემ, დ.კარდანომ და სხვებმა.1535 წელს ა.ფიორესა და ნ.ს შორის გაიმართა სამეცნიერო დუელი. ტარტალია, რომელზეც ამ უკანასკნელმა გაიმარჯვა. 2 საათში მან მოაგვარა ფიორეს მიერ შემოთავაზებული 30 პრობლემა და თავად ფიორემ ვერ გადაჭრა ტარტაგლიას მიერ მისთვის მიცემული ერთიც.
ბიჭებო, დღეს კიდევ ერთი განტოლება მინდა შემოგთავაზოთ, ის ავიღე OGE-სთვის მომზადებისთვის დავალებების კრებულიდან.
. ((x + 1) (x + 4)) ((x + 2) (x + 3)) = 24,
(x 2 + 5x + 4) (x 2 + 5x + 6) = 24.
x 2 + 5x + 4 = t ცვლილების შესრულებით, გვაქვს განტოლება
t(t + 2) = 24, ეს არის კვადრატი:
t 2 + 2t - 24 = 0.
t = -6 ან t = 4.
საპირისპირო ჩანაცვლების შესრულების შემდეგ, ჩვენ ადვილად ვიპოვით საწყისი განტოლების ფესვებს.
პასუხი: -5; 0.
ცოდნისა და უნარების კრეატიული გადაცემა ახალ პირობებში.
გაკვეთილის დასაწყისში ვისაუბრეთ იმაზე, რომ თუ განტოლებაში განმეორებითი ელემენტებია, მაშინ შესაძლებელია ცვლადის ჩანაცვლების მეთოდის გამოყენება. ჩვენ ჯერ კიდევ არ ვიცით როგორ ამოხსნათ ტრიგონომეტრიული და ირაციონალური განტოლებები. ვნახოთ, შეგვიძლია თუ არა გამოვიყენოთ ეს მეთოდი მათთვის, თუ ვიცით როგორ ამოხსნათ უმარტივესი ტრიგონომეტრიული და ირაციონალური განტოლებები.
სავარჯიშო 1:დაასახელეთ ცვლადის ცვლილება შემდეგ განტოლებებში.
დავალება 2:დაწერეთ რამდენიმე განტოლება ცვლადის მეთოდის ცვლილების საფუძველზე.
შეჯამება.
ასე რომ, ბიჭებო, ჩვენი გაკვეთილი დასრულდა. მოდით შევაჯამოთ ჩვენი გაკვეთილი.
რა მიზნები დავისახეთ გაკვეთილის დასაწყისში?
მიღწეულია თუ არა ჩვენი მიზნები?
რა ახალი ვისწავლეთ გაკვეთილზე?
Საშინაო დავალება.
4x 4 - 8x 3 + 3x 2 - 8x + 4 = 0
(x+1)(x+2)(x+4)(x+5) = 40
. (იტალიელი მათემატიკოსების განტოლება)
და მინდა დავასრულო გაკვეთილი დიდი მეცნიერის აინშტაინ ა.-ს სიტყვებით:
„ჩემი დრო პოლიტიკასა და განტოლებებს შორის უნდა გავყო. თუმცა, განტოლება, ჩემი აზრით, ბევრად უფრო მნიშვნელოვანია, რადგან პოლიტიკა მხოლოდ ამ მომენტისთვის არსებობს და განტოლება იარსებებს სამუდამოდ.
გმადლობთ გაკვეთილისთვის! ნახვამდის!
ცვლადის ცვლილება განუსაზღვრელ ინტეგრალში. დიფერენციალების გარდაქმნის ფორმულა. ინტეგრაციის მაგალითები. ხაზოვანი ჩანაცვლების მაგალითები.
ცვლადი ჩანაცვლების მეთოდი
ცვლადის ცვლილების დახმარებით შეგიძლიათ გამოთვალოთ მარტივი ინტეგრალები და, ზოგიერთ შემთხვევაში, გაამარტივოთ უფრო რთულის გამოთვლა.
ცვლადის ჩანაცვლების მეთოდი არის ის, რომ ჩვენ გადავდივართ ორიგინალური ინტეგრაციის ცვლადიდან, მოდით ეს იყოს x, სხვა ცვლადზე, რომელსაც აღვნიშნავთ როგორც t. ამავდროულად, ჩვენ ვვარაუდობთ, რომ x და t ცვლადები დაკავშირებულია x = x-ით (ტ), ან t = t (x). მაგალითად x = ჟურნალი ტ, x = ცოდვა თ, t = 2 x + 1და ა.შ. ჩვენი ამოცანაა ავირჩიოთ ისეთი კავშირი x-სა და t-ს შორის ისე, რომ თავდაპირველი ინტეგრალი ან შემცირდეს ცხრილამდე ან გამარტივდეს.
ძირითადი ცვლადის ცვლილების ფორმულა
განვიხილოთ გამოხატულება, რომელიც არის ინტეგრალური ნიშნის ქვეშ. იგი შედგება ინტეგრანის ნამრავლისაგან, რომელსაც აღვნიშნავთ როგორც f (x)და დიფერენციალური dx : . მოდით გადავიდეთ ახალ t ცვლადზე x = x მიმართების არჩევით (ტ). მაშინ უნდა გამოვხატოთ ფუნქცია f (x)და დიფერენციალური dx t ცვლადის მიხედვით.
ინტეგრანდ ვ (x) t ცვლადის მეშვეობით, თქვენ უბრალოდ უნდა ჩაანაცვლოთ არჩეული თანაფარდობა x = x ცვლადის x-ის ნაცვლად (ტ).
დიფერენციალური ტრანსფორმაცია ხდება შემდეგნაირად:
.
ანუ დიფერენციალური dx ტოლია x-ის წარმოებულის ნამრავლის t და დიფერენციალური dt-ის მიმართ.
მერე
.
პრაქტიკაში, ყველაზე გავრცელებული შემთხვევაა, როდესაც ჩანაცვლებას ვასრულებთ ახალი ცვლადის არჩევით, როგორც ძველის ფუნქცია: t = t. (x). თუ გამოვიცნობდით, რომ ინტეგრანტი შეიძლება წარმოდგენილი იყოს როგორც
,
სად ტ (x)არის t-ის წარმოებული x-ის მიმართ, მაშინ
.
ამრიგად, ცვლადის ცვლილების ძირითადი ფორმულა შეიძლება წარმოდგენილი იყოს ორი ფორმით.
(1)
,
სადაც x არის t-ის ფუნქცია.
(2)
,
სადაც t არის x-ის ფუნქცია.
Მნიშვნელოვანი ჩანაწერი
ინტეგრალების ცხრილებში ინტეგრაციის ცვლადი ყველაზე ხშირად აღინიშნება როგორც x. თუმცა, გასათვალისწინებელია, რომ ინტეგრაციის ცვლადი შეიძლება აღინიშნოს ნებისმიერი ასოთი. უფრო მეტიც, ნებისმიერი გამოხატულება შეიძლება გამოყენებულ იქნას როგორც ინტეგრაციის ცვლადი.
მაგალითად, განიხილეთ ცხრილი ინტეგრალური
.
აქ x შეიძლება შეიცვალოს ნებისმიერი სხვა ცვლადით ან ცვლადის ფუნქციით. აქ მოცემულია შესაძლო ვარიანტების მაგალითები:
;
;
.
ბოლო მაგალითში უნდა გაითვალისწინოთ, რომ ინტეგრაციის x ცვლადზე გადასვლისას დიფერენციალი შემდეგნაირად გარდაიქმნება:
.
მერე
.
ეს მაგალითი არის ჩანაცვლებითი ინტეგრაციის არსი. ანუ ეს უნდა გამოვიცნოთ
.
ამის შემდეგ, ინტეგრალი მცირდება ცხრილის სახით.
.
თქვენ შეგიძლიათ გამოთვალოთ ეს ინტეგრალი ცვლადის ცვლილების გამოყენებით, ფორმულის გამოყენებით (2)
. მოდით t = x 2+x. მერე
;
;
.
ცვლადის ცვლილებით ინტეგრაციის მაგალითები
1)
ჩვენ ვიანგარიშებთ ინტეგრალს
.
ჩვენ ამას ვამჩნევთ (sin x)′ = cos x. მერე
.
აქ გამოვიყენეთ ჩანაცვლება t = ცოდვა x.
2)
ჩვენ ვიანგარიშებთ ინტეგრალს
.
ჩვენ ამას ვამჩნევთ. მერე
.
აქ ჩვენ შევასრულეთ ინტეგრაცია t = ცვლადის შეცვლით arctg x.
3)
მოდით ინტეგრირება
.
ჩვენ ამას ვამჩნევთ. მერე
. აქ, ინტეგრაციის დროს, იცვლება t = x ცვლადი 2 + 1
.
ხაზოვანი ჩანაცვლებები
ალბათ ყველაზე გავრცელებული არის ხაზოვანი ჩანაცვლება. ეს არის ფორმის ცვლადის ჩანაცვლება
t = ცული + ბ
სადაც a და b მუდმივებია. ასეთი ცვლილებისას, დიფერენციაციები დაკავშირებულია მიმართებით
.
ხაზოვანი ჩანაცვლებით ინტეგრაციის მაგალითები
ა)გამოთვალეთ ინტეგრალი
.
გადაწყვეტილება.
.
ბ)იპოვნეთ ინტეგრალი
.
გადაწყვეტილება.
გამოვიყენოთ ექსპონენციალური ფუნქციის თვისებები.
.
2-ში- მუდმივია. ჩვენ ვიანგარიშებთ ინტეგრალს.
.
გ)გამოთვალეთ ინტეგრალი
.
გადაწყვეტილება.
წილადის მნიშვნელში კვადრატულ მრავალწევრს მივყავართ კვადრატების ჯამამდე.
.
ჩვენ ვიანგარიშებთ ინტეგრალს.
.
დ)იპოვნეთ ინტეგრალი
.
გადაწყვეტილება.
ჩვენ გარდაქმნით მრავალწევრს ფესვის ქვეშ.
.
ჩვენ ვაერთიანებთ ცვლადის მეთოდის ცვლილების გამოყენებით. 
.
ჩვენ ადრე მივიღეთ ფორმულა
.
აქედან
.
ამ გამოთქმის ჩანაცვლებით მივიღებთ საბოლოო პასუხს.
მათემატიკა არის ჭაბურღილი, რომლის მეშვეობითაც ლოგიკურ გონებას შეუძლია იდეალური სამყაროს თვალთვალი.
კროტოვი ვიქტორ
სკოლაში ალგებრის კურსში წამყვანი ადგილი რაციონალურ განტოლებებს უჭირავს. უფრო მეტი დრო ეთმობა მათ შესწავლას, ვიდრე სხვა თემებს. ეს უპირველეს ყოვლისა განპირობებულია იმით, რომ განტოლებებს არა მხოლოდ დიდი თეორიული მნიშვნელობა აქვს, არამედ ბევრ პრაქტიკულ მიზანსაც ემსახურება. რეალურ სამყაროში პრობლემების დიდი რაოდენობა მოდის სხვადასხვა განტოლების ამოხსნაზე და მხოლოდ მას შემდეგ რაც დაეუფლებით მათ გადაჭრის მეთოდებს, იპოვით პასუხებს მეცნიერებისა და ტექნოლოგიების სხვადასხვა კითხვებზე.
რაციონალური განტოლებების ამოხსნის უნარის ფორმირებისათვის დიდი მნიშვნელობა აქვს მოსწავლის დამოუკიდებელ მუშაობას. თუმცა, სანამ დამოუკიდებელ სამუშაოზე გადავიდოდეთ, აუცილებელია მკაფიოდ იცოდეთ და შეძლოთ პრაქტიკაში რაციონალური განტოლებების ამოხსნის ყველა შესაძლო მეთოდის გამოყენება.
მოდით განვიხილოთ მაგალითები დეტალურად ცვლადი ცვლილების მეთოდირაციონალური განტოლებების ამოხსნისთვის.
მაგალითი 1
ამოხსენით განტოლება (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.
გადაწყვეტილება.
განტოლებას ვწერთ ფორმაში
(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. მოდით შევცვალოთ ცვლილება. მოდით 2x 2 - 3x \u003d t, მაშინ განტოლება მიიღებს ფორმას:
(t + 1) 2 = 11t + 1.
ახლა ვხსნით ფრჩხილებს და ვაძლევთ მსგავსებს, ვიღებთ:
t2 + 2t + 1 = 11t + 1;
მიღებულ არასრულ კვადრატულ განტოლებაში ფრჩხილებიდან ვიღებთ საერთო ფაქტორს, გვექნება:
t = 0 ან t = 9.
ახლა თქვენ უნდა გააკეთოთ შებრუნებული ჩანაცვლება და ამოხსნათ თითოეული მიღებული განტოლება:
2x 2 - 3x = 0 ან 2x 2 - 3x = 9
x(2x - 3) = 0 2x 2 - 3x - 9 = 0
x = 0 ან x = 3/2 x = 3 ან x = -3/2
პასუხი: -1,5; 0; 1.5; 3.
მაგალითი 2
ამოხსენით განტოლება (x 2 - 6x) 2 - 2 (x - 3) 2 = 81.
გადაწყვეტილება.
გამოვიყენოთ სხვაობის კვადრატული ფორმულა (a - b) 2 = a 2 - 2ab + b 2 . ჩვენ ვწერთ ორიგინალურ განტოლებას ფორმაში
(x 2 - 6x) 2 - 2 (x 2 - 6x + 9) = 81. ახლა თქვენ შეგიძლიათ გააკეთოთ ჩანაცვლება.
მოდით x 2 - 6x \u003d t, მაშინ განტოლება ასე გამოიყურება:
t 2 - 2 (t + 9) \u003d 81.
t 2 - 2t - 18 - 81 = 0;
t 2 - 2t - 99 = 0.
ვიეტას თეორემის მიხედვით, მიღებული განტოლების ფესვები იქნება რიცხვები -9 და 11.
მოდით გავაკეთოთ საპირისპირო ჩანაცვლება:
x 2 - 6x = -9 ან x 2 - 6x = 11
x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0
(x - 3) 2 = 0 D = 80
x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.
პასუხი: 3 - 2√5; 3; 3 + 2√5.
მაგალითი 3
ამოხსენით განტოლება (x - 1)(x - 3)(x + 5)(x + 7) = 297 და იპოვეთ მისი ფესვების ნამრავლი.
გადაწყვეტილება.
მოდი ვიპოვოთ „მომგებიანი“ გზა ფაქტორების დასაჯგუფებლად და ფრჩხილების წყვილების გასახსნელად:
((x - 1)(x + 5))((x - 3)(x + 7)) = 297;
(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;
(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.
მოდით გავაკეთოთ ცვლილება x 2 + 4x = t, მაშინ განტოლება ასე გამოიყურება:
(t - 5) (t - 21) = 297.
გავხსნათ ფრჩხილები, მივცეთ მსგავსი ტერმინები:
t 2 - 21t - 5t + 105 = 297;
t 2 - 26t - 192 = 0.
ვიეტას თეორემის მიხედვით, ჩვენ განვსაზღვრავთ, რომ მიღებული განტოლების ფესვები იქნება რიცხვები -6 და 32.
საპირისპირო ჩანაცვლების შემდეგ გვექნება:
x 2 + 4x = -6 ან x 2 + 4x = 32
x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0
D = 16 - 24< 0 D = 16 + 128 > 0
ფესვების გარეშე x 1 = -8; x 2 = 4
ვიპოვოთ ფესვების ნამრავლი: -8 4 = -32.
პასუხი: -32.
მაგალითი 4
იპოვეთ განტოლების ფესვების ჯამი (x 2 - 2x + 2) 2 + 3x (x 2 - 2x + 2) = 10x 2.
გადაწყვეტილება.
მოდით x 2 - 2x + 2 \u003d t, მაშინ განტოლება მიიღებს ფორმას:
t 2 + 3xt - 10x 2 \u003d 0.
მივიღოთ მიღებული განტოლება, როგორც კვადრატული განტოლება t-ის მიმართ.
D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤
t 1 = (-3x - 7x) / 2 და t 2 = (-3x + 7x) / 2;
t 1 = -5x და t 2 = 2x.
ვინაიდან t \u003d x 2 - 2x + 2, მაშინ
x 2 - 2x + 2 = -5x ან x 2 - 2x + 2 = 2x. ამოვხსნათ თითოეული მიღებული განტოლება.
x 2 + 3x + 2 = 0 ან x 2 - 4x + 2 = 0.
ორივე განტოლებას აქვს ფესვები, რადგან D > 0.
ვიეტას თეორემის გამოყენებით შეგვიძლია დავასკვნათ, რომ პირველი განტოლების ფესვების ჯამი არის -3, ხოლო მეორე განტოლება არის 4. მივიღებთ, რომ საწყისი განტოლების ფესვების ჯამი არის -3 + 4 = 1.
პასუხი: 1.
მაგალითი 5
იპოვეთ განტოლების ფესვი (x + 1) 4 + (x + 5) 4 = 32, რომელიც ეკუთვნის [-5; ათი].
გადაწყვეტილება.
მოდით x = t - 3, შემდეგ x + 1 = t - 2; x + 5 = t + 2 და თავდაპირველი განტოლება ხდება:
(t - 2) 4 + (t + 2) 4 \u003d 32. გამონათქვამების მეოთხე ხარისხზე ასამაღლებლად შეგიძლიათ გამოიყენოთ პასკალის სამკუთხედი (ნახ. 1); 
(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;
(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .
მსგავსი პირობების შემცირების შემდეგ მივიღებთ:
2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;
t 4 + 6t 2 2 2 + 2 4 = 16;
t 4 + 24t 2 + 16 = 16;
t4 + 24t2 = 0;
t 2 (t 2 + 24) = 0;
t \u003d 0 ან t 2 \u003d -24.
მეორე განტოლებას არ აქვს ფესვები, რაც ნიშნავს, რომ t = 0 და საპირისპირო ჩანაცვლების შემდეგ
x \u003d t - 3 \u003d 0 - 3 \u003d -3. -3 განტოლების ფესვი ეკუთვნის [-5; ათი].
პასუხი: -3.
როგორც ხედავთ, რაციონალური განტოლებების ამოხსნისას თქვენ უნდა იცოდეთ ზემოაღნიშნული ფორმულები და შეძლოთ სწორად დათვლა. შეცდომები ყველაზე ხშირად ხდება შემცვლელის არჩევისას და უკან ჩანაცვლებისას. ამის თავიდან ასაცილებლად, თქვენ უნდა აღწეროთ დეტალურად თითოეული მოქმედება, მაშინ არ იქნება შეცდომები თქვენს გადაწყვეტილებებში.
საიტი, მასალის სრული ან ნაწილობრივი კოპირებით, საჭიროა წყაროს ბმული.
მათემატიკა არის ჭაბურღილი, რომლის მეშვეობითაც ლოგიკურ გონებას შეუძლია იდეალური სამყაროს თვალთვალი.
კროტოვი ვიქტორ
სკოლაში ალგებრის კურსში წამყვანი ადგილი რაციონალურ განტოლებებს უჭირავს. უფრო მეტი დრო ეთმობა მათ შესწავლას, ვიდრე სხვა თემებს. ეს უპირველეს ყოვლისა განპირობებულია იმით, რომ განტოლებებს არა მხოლოდ დიდი თეორიული მნიშვნელობა აქვს, არამედ ბევრ პრაქტიკულ მიზანსაც ემსახურება. რეალურ სამყაროში პრობლემების დიდი რაოდენობა მოდის სხვადასხვა განტოლების ამოხსნაზე და მხოლოდ მას შემდეგ რაც დაეუფლებით მათ გადაჭრის მეთოდებს, იპოვით პასუხებს მეცნიერებისა და ტექნოლოგიების სხვადასხვა კითხვებზე.
რაციონალური განტოლებების ამოხსნის უნარის ფორმირებისათვის დიდი მნიშვნელობა აქვს მოსწავლის დამოუკიდებელ მუშაობას. თუმცა, სანამ დამოუკიდებელ სამუშაოზე გადავიდოდეთ, აუცილებელია მკაფიოდ იცოდეთ და შეძლოთ პრაქტიკაში რაციონალური განტოლებების ამოხსნის ყველა შესაძლო მეთოდის გამოყენება.
მოდით განვიხილოთ მაგალითები დეტალურად ცვლადი ცვლილების მეთოდირაციონალური განტოლებების ამოხსნისთვის.
მაგალითი 1
ამოხსენით განტოლება (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.
გადაწყვეტილება.
განტოლებას ვწერთ ფორმაში
(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. მოდით შევცვალოთ ცვლილება. მოდით 2x 2 - 3x \u003d t, მაშინ განტოლება მიიღებს ფორმას:
(t + 1) 2 = 11t + 1.
ახლა ვხსნით ფრჩხილებს და ვაძლევთ მსგავსებს, ვიღებთ:
t2 + 2t + 1 = 11t + 1;
მიღებულ არასრულ კვადრატულ განტოლებაში ფრჩხილებიდან ვიღებთ საერთო ფაქტორს, გვექნება:
t = 0 ან t = 9.
ახლა თქვენ უნდა გააკეთოთ შებრუნებული ჩანაცვლება და ამოხსნათ თითოეული მიღებული განტოლება:
2x 2 - 3x = 0 ან 2x 2 - 3x = 9
x(2x - 3) = 0 2x 2 - 3x - 9 = 0
x = 0 ან x = 3/2 x = 3 ან x = -3/2
პასუხი: -1,5; 0; 1.5; 3.
მაგალითი 2
ამოხსენით განტოლება (x 2 - 6x) 2 - 2 (x - 3) 2 = 81.
გადაწყვეტილება.
გამოვიყენოთ სხვაობის კვადრატული ფორმულა (a - b) 2 = a 2 - 2ab + b 2 . ჩვენ ვწერთ ორიგინალურ განტოლებას ფორმაში
(x 2 - 6x) 2 - 2 (x 2 - 6x + 9) = 81. ახლა თქვენ შეგიძლიათ გააკეთოთ ჩანაცვლება.
მოდით x 2 - 6x \u003d t, მაშინ განტოლება ასე გამოიყურება:
t 2 - 2 (t + 9) \u003d 81.
t 2 - 2t - 18 - 81 = 0;
t 2 - 2t - 99 = 0.
ვიეტას თეორემის მიხედვით, მიღებული განტოლების ფესვები იქნება რიცხვები -9 და 11.
მოდით გავაკეთოთ საპირისპირო ჩანაცვლება:
x 2 - 6x = -9 ან x 2 - 6x = 11
x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0
(x - 3) 2 = 0 D = 80
x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.
პასუხი: 3 - 2√5; 3; 3 + 2√5.
მაგალითი 3
ამოხსენით განტოლება (x - 1)(x - 3)(x + 5)(x + 7) = 297 და იპოვეთ მისი ფესვების ნამრავლი.
გადაწყვეტილება.
მოდი ვიპოვოთ „მომგებიანი“ გზა ფაქტორების დასაჯგუფებლად და ფრჩხილების წყვილების გასახსნელად:
((x - 1)(x + 5))((x - 3)(x + 7)) = 297;
(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;
(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.
მოდით გავაკეთოთ ცვლილება x 2 + 4x = t, მაშინ განტოლება ასე გამოიყურება:
(t - 5) (t - 21) = 297.
გავხსნათ ფრჩხილები, მივცეთ მსგავსი ტერმინები:
t 2 - 21t - 5t + 105 = 297;
t 2 - 26t - 192 = 0.
ვიეტას თეორემის მიხედვით, ჩვენ განვსაზღვრავთ, რომ მიღებული განტოლების ფესვები იქნება რიცხვები -6 და 32.
საპირისპირო ჩანაცვლების შემდეგ გვექნება:
x 2 + 4x = -6 ან x 2 + 4x = 32
x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0
D = 16 - 24< 0 D = 16 + 128 > 0
ფესვების გარეშე x 1 = -8; x 2 = 4
ვიპოვოთ ფესვების ნამრავლი: -8 4 = -32.
პასუხი: -32.
მაგალითი 4
იპოვეთ განტოლების ფესვების ჯამი (x 2 - 2x + 2) 2 + 3x (x 2 - 2x + 2) = 10x 2.
გადაწყვეტილება.
მოდით x 2 - 2x + 2 \u003d t, მაშინ განტოლება მიიღებს ფორმას:
t 2 + 3xt - 10x 2 \u003d 0.
მივიღოთ მიღებული განტოლება, როგორც კვადრატული განტოლება t-ის მიმართ.
D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤
t 1 = (-3x - 7x) / 2 და t 2 = (-3x + 7x) / 2;
t 1 = -5x და t 2 = 2x.
ვინაიდან t \u003d x 2 - 2x + 2, მაშინ
x 2 - 2x + 2 = -5x ან x 2 - 2x + 2 = 2x. ამოვხსნათ თითოეული მიღებული განტოლება.
x 2 + 3x + 2 = 0 ან x 2 - 4x + 2 = 0.
ორივე განტოლებას აქვს ფესვები, რადგან D > 0.
ვიეტას თეორემის გამოყენებით შეგვიძლია დავასკვნათ, რომ პირველი განტოლების ფესვების ჯამი არის -3, ხოლო მეორე განტოლება არის 4. მივიღებთ, რომ საწყისი განტოლების ფესვების ჯამი არის -3 + 4 = 1.
პასუხი: 1.
მაგალითი 5
იპოვეთ განტოლების ფესვი (x + 1) 4 + (x + 5) 4 = 32, რომელიც ეკუთვნის [-5; ათი].
გადაწყვეტილება.
მოდით x = t - 3, შემდეგ x + 1 = t - 2; x + 5 = t + 2 და თავდაპირველი განტოლება ხდება:
(t - 2) 4 + (t + 2) 4 \u003d 32. გამონათქვამების მეოთხე ხარისხზე ასამაღლებლად შეგიძლიათ გამოიყენოთ პასკალის სამკუთხედი (ნახ. 1);
(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;
(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .
მსგავსი პირობების შემცირების შემდეგ მივიღებთ:
2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;
t 4 + 6t 2 2 2 + 2 4 = 16;
t 4 + 24t 2 + 16 = 16;
t4 + 24t2 = 0;
t 2 (t 2 + 24) = 0;
t \u003d 0 ან t 2 \u003d -24.
მეორე განტოლებას არ აქვს ფესვები, რაც ნიშნავს, რომ t = 0 და საპირისპირო ჩანაცვლების შემდეგ
x \u003d t - 3 \u003d 0 - 3 \u003d -3. -3 განტოლების ფესვი ეკუთვნის [-5; ათი].
პასუხი: -3.
როგორც ხედავთ, რაციონალური განტოლებების ამოხსნისას თქვენ უნდა იცოდეთ ზემოაღნიშნული ფორმულები და შეძლოთ სწორად დათვლა. შეცდომები ყველაზე ხშირად ხდება შემცვლელის არჩევისას და უკან ჩანაცვლებისას. ამის თავიდან ასაცილებლად, თქვენ უნდა აღწეროთ დეტალურად თითოეული მოქმედება, მაშინ არ იქნება შეცდომები თქვენს გადაწყვეტილებებში.
blog.site, მასალის სრული ან ნაწილობრივი კოპირებით, საჭიროა წყაროს ბმული.
