ჩვენს წელთაღრიცხვამდე მეხუთე საუკუნეში ძველმა ბერძენმა ფილოსოფოსმა ზენომ ელეამ ჩამოაყალიბა თავისი ცნობილი აპორიები, რომელთაგან ყველაზე ცნობილია აპორია „აქილევსი და კუს“. აი, როგორ ჟღერს:

ვთქვათ აქილევსი კუზე ათჯერ უფრო სწრაფად დარბის და ათასი ნაბიჯით ჩამორჩება. იმ დროის განმავლობაში, როცა აქილევსი ამ მანძილს გარბის, კუ ასი ნაბიჯით ცოცავს იმავე მიმართულებით. როცა აქილევსი ას ნაბიჯს გარბის, კუს კიდევ ათი ნაბიჯი დაცოცავს და ა.შ. პროცესი უსასრულოდ გაგრძელდება, აქილევსი კუს ვერასოდეს მიაღწევს.

ეს მსჯელობა ლოგიკური შოკი გახდა ყველა შემდგომი თაობისთვის. არისტოტელე, დიოგენე, კანტი, ჰეგელი, გილბერტი... ყველა მათგანი ასე თუ ისე ზენონის აპორიებს თვლიდა. შოკი იმდენად ძლიერი იყო, რომ " ... მსჯელობა ამჟამად გრძელდება, სამეცნიერო საზოგადოებას ჯერ არ მიუღწევია პარადოქსების არსის შესახებ საერთო მოსაზრებამდე... საკითხის შესწავლაში ჩართული იყო მათემატიკური ანალიზი, სიმრავლეების თეორია, ახალი ფიზიკური და ფილოსოფიური მიდგომები. ; არცერთი მათგანი არ გახდა პრობლემის საყოველთაოდ მიღებული გადაწყვეტა ..."[ვიკიპედია," ზენონის აპორია "]. ყველას ესმის, რომ ატყუებენ, მაგრამ არავის ესმის, რა არის მოტყუება.

მათემატიკის თვალსაზრისით, ზენონმა თავის აპორიაში ნათლად აჩვენა გადასვლა მნიშვნელობიდან. ეს გადასვლა გულისხმობს გამოყენებას მუდმივების ნაცვლად. რამდენადაც მე მესმის, საზომი ცვლადი ერთეულების გამოყენების მათემატიკური აპარატი ან ჯერ არ არის შემუშავებული, ან არ არის გამოყენებული ზენონის აპორიაზე. ჩვენი ჩვეული ლოგიკის გამოყენება მახეში მიგვიყვანს. ჩვენ, აზროვნების ინერციით, ვიყენებთ დროის მუდმივ ერთეულებს ურთიერთსაწინააღმდეგოზე. ფიზიკური თვალსაზრისით, ეს ჰგავს დროის შენელებას, სანამ ის მთლიანად არ შეჩერდება იმ მომენტში, როდესაც აქილევსი დაეწევა კუს. თუ დრო გაჩერდება, აქილევსი ვეღარ გაუსწრებს კუს.

თუ შევეჩვიეთ ლოგიკას, ყველაფერი თავის ადგილზე დგება. აქილევსი მუდმივი სიჩქარით დარბის. მისი გზის ყოველი მომდევნო სეგმენტი წინაზე ათჯერ მოკლეა. შესაბამისად, მის დაძლევაზე დახარჯული დრო წინაზე ათჯერ ნაკლებია. თუ ამ სიტუაციაში „უსასრულობის“ ცნებას გამოვიყენებთ, მაშინ სწორი იქნება ვთქვათ „აქილევსი უსაზღვროდ სწრაფად გაუსწრებს კუს“.

როგორ ავიცილოთ თავიდან ეს ლოგიკური ხაფანგი? დარჩით დროის მუდმივ ერთეულებში და არ გადახვიდეთ საპასუხო მნიშვნელობებზე. ზენონის ენაზე ასე გამოიყურება:

იმ დროს, რაც აქილევსს სჭირდება ათასი ნაბიჯის გასაშვებად, კუ ასი ნაბიჯით მიიწევს იმავე მიმართულებით. შემდეგი დროის ინტერვალის განმავლობაში, პირველის ტოლფასი, აქილევსი კიდევ ათას ნაბიჯს გაივლის, კუს კი ასი ნაბიჯით გაივლის. ახლა აქილევსი რვაასი ნაბიჯით უსწრებს კუს.

ეს მიდგომა ადეკვატურად აღწერს რეალობას ყოველგვარი ლოგიკური პარადოქსების გარეშე. მაგრამ ეს არ არის პრობლემის სრული გადაწყვეტა. აინშტაინის განცხადება სინათლის სიჩქარის დაუძლეველობის შესახებ ძალიან ჰგავს ზენონის აპორიას „აქილევსი და კუს“. ჩვენ ჯერ კიდევ უნდა შევისწავლოთ, გადავხედოთ და გადავჭრათ ეს პრობლემა. და გამოსავალი უნდა ვეძიოთ არა უსასრულოდ დიდი რაოდენობით, არამედ გაზომვის ერთეულებში.

ზენონის კიდევ ერთი საინტერესო აპორია მოგვითხრობს მფრინავი ისრის შესახებ:

მფრინავი ისარი უმოძრაოა, რადგან დროის ყოველ მომენტში ის ისვენებს, და რადგან ის ისვენებს დროის ყოველ მომენტში, ის ყოველთვის ისვენებს.

ამ აპორიაში ლოგიკური პარადოქსი დაძლეულია ძალიან მარტივად - საკმარისია იმის გარკვევა, რომ დროის ყოველ მომენტში მფრინავი ისარი ისვენებს სივრცის სხვადასხვა წერტილში, რაც, ფაქტობრივად, მოძრაობაა. აქ უნდა აღინიშნოს კიდევ ერთი წერტილი. გზაზე მანქანის ერთი ფოტოსურათიდან შეუძლებელია მისი გადაადგილების ფაქტის და მასამდე მანძილის დადგენა. მანქანის მოძრაობის ფაქტის დასადგენად საჭიროა ერთი და იმავე წერტილიდან დროის სხვადასხვა მომენტში გადაღებული ორი ფოტო, მაგრამ მათი გამოყენება მანძილის დასადგენად არ შეიძლება. მანქანამდე მანძილის დასადგენად, საჭიროა ერთდროულად ორი ფოტო გადაღებული სივრცეში სხვადასხვა წერტილიდან, მაგრამ მათგან გადაადგილების ფაქტს ვერ განსაზღვრავთ (რა თქმა უნდა, გამოთვლებისთვის დამატებითი მონაცემები მაინც გჭირდებათ, ტრიგონომეტრია დაგეხმარებათ) . კონკრეტულად მინდა აღვნიშნო, რომ ორი წერტილი დროისა და ორი წერტილი სივრცეში არის ორი განსხვავებული რამ, რაც არ უნდა აგვერიოს, რადგან ისინი აძლევენ სხვადასხვა შესაძლებლობებს კვლევისთვის.

ოთხშაბათი, 4 ივლისი, 2018 წ

ძალიან კარგად არის განსხვავებები კომპლექტსა და მრავალნაკრებს შორის აღწერილი ვიკიპედიაში. ჩვენ ვუყურებთ.

როგორც ხედავთ, „კომპლექტს არ შეიძლება ჰქონდეს ორი იდენტური ელემენტი“, მაგრამ თუ ნაკრებში იდენტური ელემენტებია, ასეთ კომპლექტს „მულტისეტი“ ეწოდება. გონივრული არსებები ვერასოდეს გაიგებენ აბსურდის ასეთ ლოგიკას. ეს არის მოლაპარაკე თუთიყუშების და გაწვრთნილი მაიმუნების დონე, რომელშიც გონება აკლია სიტყვას „მთლიანად“. მათემატიკოსები მოქმედებენ როგორც რიგითი ტრენერები და ქადაგებენ თავიანთ აბსურდულ იდეებს.

ოდესღაც ინჟინრები, რომლებმაც ხიდი ააშენეს, ხიდის გამოცდების დროს ნავით იმყოფებოდნენ ხიდის ქვეშ. თუ ხიდი ჩამოინგრა, უღიმღამო ინჟინერი მისი შემოქმედების ნანგრევების ქვეშ გარდაიცვალა. თუ ხიდი დატვირთვას გაუძლებდა, ნიჭიერმა ინჟინერმა სხვა ხიდები ააგო.

რაც არ უნდა იმალებოდნენ მათემატიკოსები ფრაზის მიღმა, „იგონე, მე სახლში ვარ“, უფრო სწორად, „მათემატიკა სწავლობს აბსტრაქტულ ცნებებს“, არის ერთი ჭიპლარი, რომელიც განუყოფლად აკავშირებს მათ რეალობასთან. ეს ჭიპლარი ფულია. მოდით გამოვიყენოთ მათემატიკური სიმრავლეების თეორია თავად მათემატიკოსებზე.

მათემატიკა ძალიან კარგად ვისწავლეთ და ახლა სალაროსთან ვსხედვართ და ხელფასს ვიხდით. აქ მათემატიკოსი მოდის ჩვენთან თავისი ფულისთვის. ჩვენ მას მთელ თანხას ვითვლით და ჩვენს მაგიდაზე ვდებთ სხვადასხვა გროვად, რომელშიც ერთი და იმავე ნომინალის კუპიურებს ვდებთ. შემდეგ ყოველი წყობიდან ვიღებთ თითო კუპიურას და ვაძლევთ მათემატიკოსს მის „მათემატიკურ სახელფასო კომპლექტს“. მათემატიკას ავხსნით, რომ ის მიიღებს დანარჩენ ქვითრებს მხოლოდ მაშინ, როცა დაამტკიცებს, რომ იდენტური ელემენტების გარეშე ნაკრები არ უდრის იდენტური ელემენტების სიმრავლეს. სწორედ აქ იწყება გართობა.

უპირველეს ყოვლისა, იმუშავებს დეპუტატების ლოგიკა: „შეგიძლიათ სხვებს მიმართოთ, ჩემზე კი არა! გარდა ამისა, დაიწყება გარანტიები, რომ ერთი და იმავე ნომინალის ბანკნოტებზე არის სხვადასხვა ბანკნოტების ნომრები, რაც ნიშნავს, რომ ისინი არ შეიძლება ჩაითვალოს იდენტურ ელემენტებად. აბა, ხელფასს მონეტებში ვითვლით - მონეტებზე ნომრები არ არის. აქ მათემატიკოსი სასტიკად გაიხსენებს ფიზიკას: სხვადასხვა მონეტებს აქვთ სხვადასხვა რაოდენობის ჭუჭყიანი, კრისტალური სტრუქტურა და ატომების განლაგება თითოეული მონეტისთვის უნიკალურია ...

და ახლა მე მაქვს ყველაზე საინტერესო კითხვა: სად არის საზღვარი, რომლის მიღმაც მულტისიმრავლის ელემენტები გადაიქცევა სიმრავლის ელემენტებად და პირიქით? ასეთი ხაზი არ არსებობს - ყველაფერს შამანები წყვეტენ, მეცნიერება აქაც არ არის ახლოს.

ნახე აქ. ჩვენ ვირჩევთ საფეხბურთო სტადიონებს იმავე მოედანზე. ველების ფართობი იგივეა, რაც ნიშნავს, რომ ჩვენ გვაქვს მულტიკომპლექტი. მაგრამ ერთი და იგივე სტადიონების სახელებს თუ გავითვალისწინებთ, ბევრს მივიღებთ, რადგან სახელები განსხვავებულია. როგორც ხედავთ, ელემენტების ერთიდაიგივე კომპლექტი ერთდროულად არის კომპლექტიც და მულტიკომპლექტიც. რამდენად სწორად? აქ კი მათემატიკოსი-შამან-შულერი ამოიღებს ყდიდან კოზირის ტუზს და იწყებს ჩვენთვის მოყოლას ან კომპლექტზე ან მულტისეტზე. ყოველ შემთხვევაში, ის დაგვარწმუნებს, რომ მართალია.

იმის გასაგებად, თუ როგორ მოქმედებენ თანამედროვე შამანები სიმრავლეების თეორიასთან, აკავშირებენ მას რეალობასთან, საკმარისია ვუპასუხოთ ერთ კითხვას: რით განსხვავდება ერთი ნაკრების ელემენტები სხვა ნაკრების ელემენტებისაგან? მე გაჩვენებთ, ყოველგვარი „წარმოდგენელი, როგორც არა ერთი მთლიანი“ ან „არა წარმოდგენა, როგორც ერთი მთლიანობა“.

კვირა, 18 მარტი, 2018 წ

რიცხვის ციფრების ჯამი არის შამანების ცეკვა ტამბურთან, რომელსაც არაფერი აქვს საერთო მათემატიკასთან. დიახ, მათემატიკის გაკვეთილებზე გვასწავლიან რიცხვის ციფრების ჯამის პოვნას და მის გამოყენებას, მაგრამ ისინი ამისთვის შამანები არიან, რათა შთამომავლებს ასწავლონ თავიანთი უნარები და სიბრძნე, წინააღმდეგ შემთხვევაში შამანები უბრალოდ დაიღუპებიან.

გჭირდებათ მტკიცებულება? გახსენით ვიკიპედია და სცადეთ იპოვოთ გვერდი "რიცხვის ციფრთა ჯამი". ის არ არსებობს. მათემატიკაში არ არსებობს ფორმულა, რომლითაც შეგიძლიათ იპოვოთ ნებისმიერი რიცხვის ციფრების ჯამი. რიცხვები ხომ გრაფიკული სიმბოლოებია, რომლებითაც ციფრებს ვწერთ და მათემატიკის ენაზე დავალება ასე ჟღერს: „იპოვე ნებისმიერი რიცხვის გამოსახული გრაფიკული სიმბოლოების ჯამი“. მათემატიკოსებს არ შეუძლიათ ამ პრობლემის გადაჭრა, მაგრამ შამანებს ეს ელემენტარულად შეუძლიათ.

მოდით გავარკვიოთ რას და როგორ ვაკეთებთ იმისათვის, რომ ვიპოვოთ მოცემული რიცხვის ციფრების ჯამი. ასე რომ, ვთქვათ გვაქვს რიცხვი 12345. რა უნდა გაკეთდეს იმისათვის, რომ ვიპოვოთ ამ რიცხვის ციფრების ჯამი? განვიხილოთ ყველა ნაბიჯი თანმიმდევრობით.

1. ჩაწერეთ რიცხვი ფურცელზე. რა გავაკეთეთ? რიცხვი გადავაქციეთ რიცხვის გრაფიკულ სიმბოლოდ. ეს არ არის მათემატიკური ოპერაცია.

2. ერთი მიღებული სურათი დავჭრათ რამდენიმე ნახატად, რომლებიც შეიცავს ცალკეულ ნომრებს. სურათის ამოჭრა არ არის მათემატიკური ოპერაცია.

3. ინდივიდუალური გრაფიკული სიმბოლოების რიცხვებად გადაქცევა. ეს არ არის მათემატიკური ოპერაცია.

4. შეკრიბეთ მიღებული რიცხვები. ახლა ეს მათემატიკაა.

12345 რიცხვის ციფრების ჯამი არის 15. ეს არის შამანების მიერ გამოყენებული მათემატიკოსების მიერ გამოყენებული "ჭრის და კერვის კურსები". მაგრამ ეს ყველაფერი არ არის.

მათემატიკის თვალსაზრისით არ აქვს მნიშვნელობა რომელ რიცხვთა სისტემაში დავწერთ რიცხვს. ასე რომ, სხვადასხვა რიცხვების სისტემაში, ერთი და იგივე რიცხვის ციფრების ჯამი განსხვავებული იქნება. მათემატიკაში რიცხვითი სისტემა მითითებულია როგორც ქვემოწერა ნომრის მარჯვნივ. დიდი რაოდენობით 12345, არ მინდა მოვიტყუო ჩემი თავი, განიხილეთ ნომერი 26 სტატიიდან. ჩავწეროთ ეს რიცხვი ორობით, რვადიან, ათობითი და თექვსმეტობით რიცხვთა სისტემებში. ჩვენ არ განვიხილავთ თითოეულ ნაბიჯს მიკროსკოპის ქვეშ, ეს უკვე გავაკეთეთ. მოდით შევხედოთ შედეგს.

როგორც ხედავთ, სხვადასხვა რიცხვთა სისტემაში ერთი და იგივე რიცხვის ციფრების ჯამი განსხვავებულია. ამ შედეგს საერთო არაფერი აქვს მათემატიკასთან. ეს იგივეა, თუ მართკუთხედის ფართობის პოვნა მეტრებში და სანტიმეტრებში მოგცემთ სრულიად განსხვავებულ შედეგებს.

ნული ყველა რიცხვთა სისტემაში ერთნაირად გამოიყურება და არ აქვს ციფრების ჯამი. ეს არის კიდევ ერთი არგუმენტი იმისა, რომ . კითხვა მათემატიკოსებს: როგორ აღინიშნება მათემატიკაში ის, რაც არ არის რიცხვი? რა, მათემატიკოსებისთვის, რიცხვების გარდა არაფერი არსებობს? შამანებისთვის მე შემიძლია ამის დაშვება, მაგრამ მეცნიერებისთვის არა. რეალობა არ არის მხოლოდ რიცხვები.

მიღებული შედეგი უნდა ჩაითვალოს მტკიცებულებად იმისა, რომ რიცხვითი სისტემები არის რიცხვების საზომი ერთეული. ჩვენ ხომ ვერ შევადარებთ რიცხვებს სხვადასხვა საზომ ერთეულებს. თუ ერთი და იგივე მოქმედებები ერთი და იგივე რაოდენობის საზომი სხვადასხვა ერთეულებით იწვევს განსხვავებულ შედეგებს მათი შედარების შემდეგ, მაშინ ამას არაფერი აქვს საერთო მათემატიკასთან.

რა არის ნამდვილი მათემატიკა? ეს არის მაშინ, როდესაც მათემატიკური მოქმედების შედეგი არ არის დამოკიდებული რიცხვის მნიშვნელობაზე, გამოყენებული ზომის ერთეულზე და იმაზე, თუ ვინ ასრულებს ამ მოქმედებას.

მოაწერე კარზე კარს აღებს და ამბობს:

ოჰ! ეს ქალის საპირფარეშო არ არის?
- Ახალგაზრდა ქალი! ეს არის ზეცაში ამაღლებისას სულების განუსაზღვრელი სიწმინდის შესწავლის ლაბორატორია! ნიმბუსი თავზე და ისარი ზევით. სხვა რა ტუალეტი?

ქალი... ზევით ჰალო და ქვემოთ ისარი მამრობითია.

თუ თქვენ გაქვთ ასეთი დიზაინის ნამუშევარი თქვენს თვალწინ დღეში რამდენჯერმე ციმციმებს,

მაშინ გასაკვირი არ არის, რომ მოულოდნელად თქვენს მანქანაში აღმოაჩენთ უცნაურ ხატს:

პირადად მე საკუთარ თავზე ვცდილობ დავინახო მინუს ოთხი გრადუსი მოღუშულ ადამიანში (ერთი სურათი) (რამდენიმე სურათის შემადგენლობა: მინუს ნიშანი, ნომერი ოთხი, გრადუსის აღნიშვნა). და მე არ ვთვლი ამ გოგოს სულელად, რომელმაც ფიზიკა არ იცის. მას უბრალოდ აქვს გრაფიკული სურათების აღქმის რკალის სტერეოტიპი. და მათემატიკოსები ამას ყოველთვის გვასწავლიან. აი მაგალითი.

1A არ არის "მინუს ოთხი გრადუსი" ან "ერთი ა". ეს არის "გაფუჭებული კაცი" ან რიცხვი "ოცდაექვსი" თექვსმეტობით რიცხვთა სისტემაში. ის ადამიანები, რომლებიც მუდმივად მუშაობენ ამ რიცხვების სისტემაში, ავტომატურად აღიქვამენ რიცხვს და ასოს, როგორც ერთ გრაფიკულ სიმბოლოს.

ტრიგონომეტრიული ფუნქციების მნიშვნელობების ცხრილი

შენიშვნა. ტრიგონომეტრიული ფუნქციების მნიშვნელობების ეს ცხრილი იყენებს √ ნიშანს კვადრატული ფესვის აღსანიშნავად. წილადის აღსანიშნავად - სიმბოლო "/".

იხილეთ ასევესასარგებლო მასალები:

ამისთვის ტრიგონომეტრიული ფუნქციის მნიშვნელობის განსაზღვრაიპოვეთ ის ტრიგონომეტრიული ფუნქციის მითითებით წრფის გადაკვეთაზე. მაგალითად, 30 გრადუსიანი სინუსი - ჩვენ ვეძებთ სვეტს სათაურით sin (sine) და ვპოულობთ ცხრილის ამ სვეტის გადაკვეთას ხაზთან "30 გრადუსი", მათ გადაკვეთაზე ვკითხულობთ შედეგს - ერთი. მეორე. ანალოგიურად, ჩვენ ვპოულობთ კოსინუსი 60გრადუსი, სინუსი 60გრადუსი (კიდევ ერთხელ, სინუს (სინუს) სვეტისა და 60 გრადუსიანი მწკრივის გადაკვეთაზე, ვპოულობთ მნიშვნელობას sin 60 = √3/2) და ა.შ. ანალოგიურად, გვხვდება სხვა "პოპულარული" კუთხეების სინუსების, კოსინუსების და ტანგენტების მნიშვნელობები.

პი-ს სინუსი, პი-ს კოსინუსი, პი-ს ტანგენსი და სხვა კუთხეები რადიანებში

ქვემოთ მოყვანილი კოსინუსების, სინუსების და ტანგენტების ცხრილი ასევე შესაფერისია ტრიგონომეტრიული ფუნქციების მნიშვნელობის საპოვნელად, რომელთა არგუმენტიც არის მოცემულია რადიანებში. ამისათვის გამოიყენეთ კუთხის მნიშვნელობების მეორე სვეტი. ამის წყალობით, თქვენ შეგიძლიათ გადაიყვანოთ პოპულარული კუთხეების მნიშვნელობა გრადუსიდან რადიანებში. მაგალითად, ვიპოვოთ 60 გრადუსიანი კუთხე პირველ სტრიქონში და წავიკითხოთ მისი მნიშვნელობა რადიანებში მის ქვეშ. 60 გრადუსი უდრის π/3 რადიანს.

რიცხვი pi ცალსახად გამოხატავს წრის გარშემოწერილობის დამოკიდებულებას კუთხის ხარისხის ზომაზე. ასე რომ, პი რადიანები უდრის 180 გრადუსს.

ნებისმიერი რიცხვი, რომელიც გამოხატულია pi-ში (რადიანი) შეიძლება ადვილად გარდაიქმნას ხარისხებად პი (π) რიცხვის 180-ით ჩანაცვლებით..

მაგალითები:
1. sine pi.
sin π = sin 180 = 0
ამრიგად, pi-ს სინუსი იგივეა, რაც 180 გრადუსის სინუსი და უდრის ნულს.

2. კოსინუსი პი.
cos π = cos 180 = -1
ამგვარად, pi-ს კოსინუსი იგივეა, რაც 180 გრადუსის კოსინუსი და უდრის მინუს ერთს.

3. ტანგენტი პი
tg π = tg 180 = 0
ამრიგად, pi-ს ტანგენსი იგივეა, რაც 180 გრადუსიანი ტანგენსი და უდრის ნულს.

სინუსის, კოსინუსის, ტანგენტის მნიშვნელობების ცხრილი 0 - 360 გრადუსი კუთხეებისთვის (ხშირი მნიშვნელობები)

კუთხე α (გრადუსები)	კუთხე α რადიანებში (pi-ს მეშვეობით)	ცოდვა (სინუსი)	cos (კოსინუსი)	ტგ (ტანგენტი)	ctg (კოტანგენსი)	წმ (სეკანტი)	მიზეზი (თანამედროვე)
0	0	0	1	0	-	1	-
15	π/12			2 - √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
75	5π/12			2 + √3	2 - √3
90	π/2	1	0	-	0	-	1
105	7π/12		-	- 2 - √3	√3 - 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	-	-1	-
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	-	0	-	-1
360	2π	0	1	0	-	1	-

თუ ტრიგონომეტრიული ფუნქციების მნიშვნელობების ცხრილში, ფუნქციის მნიშვნელობის ნაცვლად, მითითებულია ტირე (ტანგენსი (tg) 90 გრადუსი, კოტანგენსი (ctg) 180 გრადუსი), მაშინ ხარისხის საზომი მოცემული მნიშვნელობისთვის. კუთხეს, ფუნქციას არ აქვს გარკვეული მნიშვნელობა. თუ ტირე არ არის, უჯრედი ცარიელია, ამიტომ ჯერ არ შეგვიყვანია სასურველი მნიშვნელობა. ჩვენ გვაინტერესებს რა მოთხოვნით მოდიან მომხმარებლები ჩვენთან და ავსებენ ცხრილს ახალი მნიშვნელობებით, მიუხედავად იმისა, რომ ყველაზე გავრცელებული კუთხის მნიშვნელობების კოსინუსების, სინუსების და ტანგენტების მნიშვნელობების შესახებ არსებული მონაცემები საკმარისია უმეტესობის გადასაჭრელად. პრობლემები.

ტრიგონომეტრიული ფუნქციების მნიშვნელობების ცხრილი sin, cos, tg ყველაზე პოპულარული კუთხისთვის
0, 15, 30, 45, 60, 90 ... 360 გრადუსი
(რიცხობრივი მნიშვნელობები "ბრედისის ცხრილების მიხედვით")

კუთხის მნიშვნელობა α (გრადუსები)	α კუთხის მნიშვნელობა რადიანებში	ცოდვა (სინუსი)	cos (კოსინუსი)	tg (ტანგენსი)	ctg (კოტანგენსი)
0	0
15		0,2588	0,9659	0,2679
30		0,5000		0,5774
45		0,7071
		0,7660
60		0,8660	0,5000	1,7321
	7π/18

სტატიაში ჩვენ სრულად გავიგებთ როგორ გამოიყურება ტრიგონომეტრიული სიდიდეების ცხრილი, სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი. განვიხილოთ ტრიგონომეტრიული ფუნქციების ძირითადი მნიშვნელობა 0,30,45,60,90,...,360 გრადუსიანი კუთხიდან. და ვნახოთ, როგორ გამოვიყენოთ ეს ცხრილები ტრიგონომეტრიული ფუნქციების მნიშვნელობის გამოსათვლელად.
ჯერ განიხილეთ კოსინუსების, სინუსების, ტანგენტებისა და კოტანგენტების ცხრილი 0, 30, 45, 60, 90,... გრადუსიანი კუთხიდან. ამ რაოდენობების განსაზღვრა შესაძლებელს ხდის 0 და 90 გრადუსიანი კუთხეების ფუნქციების მნიშვნელობის განსაზღვრას:

sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, 00-ის კოტანგენსი განუსაზღვრელი იქნება
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0-ის ტანგენსი განუსაზღვრელი იქნება

თუ ავიღებთ მართკუთხა სამკუთხედებს, რომელთა კუთხეებია 30-დან 90 გრადუსამდე. ჩვენ ვიღებთ:

sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3

ჩვენ წარმოვადგენთ ყველა მიღებულ მნიშვნელობას ფორმაში ტრიგონომეტრიული ცხრილი:

სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების ცხრილი!

თუ ჩამოსხმის ფორმულას გამოვიყენებთ, ჩვენი ცხრილი გაიზრდება, დაემატება მნიშვნელობები 360 გრადუსამდე კუთხეებისთვის. ეს ასე გამოიყურება:

ასევე, პერიოდულობის თვისებებიდან გამომდინარე, ცხრილი შეიძლება გაიზარდოს, თუ კუთხეებს შევცვლით 0 0 +360 0 *z .... 330 0 +360 0 *z, რომელშიც z არის მთელი რიცხვი. ამ ცხრილში შესაძლებელია გამოვთვალოთ ყველა კუთხის მნიშვნელობა, რომელიც შეესაბამება ერთ წრის წერტილებს.

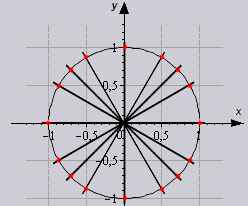
მოდით ნათლად ვნახოთ, როგორ გამოვიყენოთ ცხრილი ხსნარში.
ყველაფერი ძალიან მარტივია. ვინაიდან ჩვენ გვჭირდება მნიშვნელობა დევს უჯრედების გადაკვეთის წერტილში, რომელიც გვჭირდება. მაგალითად, ავიღოთ 60 გრადუსიანი კუთხის cos, ცხრილში ის ასე გამოიყურება:

ტრიგონომეტრიული ფუნქციების ძირითადი მნიშვნელობების საბოლოო ცხრილში ჩვენ ვმოქმედებთ იმავე გზით. მაგრამ ამ ცხრილში შესაძლებელია იმის გარკვევა, თუ რამდენი იქნება ტანგენსი 1020 გრადუსიანი კუთხიდან, ის = -√3 შევამოწმოთ 1020 0 = 300 0 +360 0 *2. მოდი ვიპოვოთ მაგიდა.

ბრედის მაგიდა. სინუსისთვის, კოსინუსისთვის, ტანგენსისთვის და კოტანგენსისთვის.

ბრედისის ცხრილები დაყოფილია რამდენიმე ნაწილად, ისინი შედგება კოსინუსის და სინუსის, ტანგენტისა და კოტანგენტის ცხრილებისგან - რომელიც იყოფა ორ ნაწილად (90 გრადუსამდე კუთხის tg და მცირე კუთხეების ctg).

სინუსი და კოსინუსი

კუთხე tg 00-დან 760-მდე, კუთხე ctg 140-დან 900-მდე.

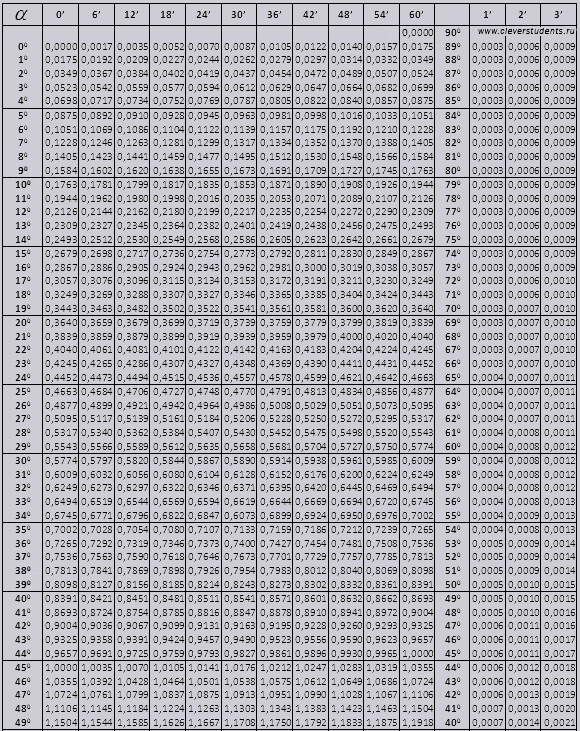
tg 900-მდე და ctg მცირე კუთხეები.

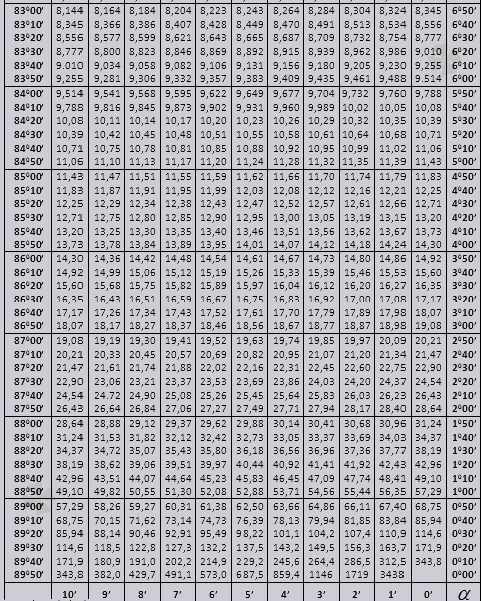
მოდით გაერკვნენ, თუ როგორ გამოვიყენოთ ბრედის ცხრილები პრობლემების გადაჭრაში.

ვიპოვოთ აღნიშვნა sin (აღნიშვნა სვეტში მარცხენა კიდიდან) 42 წუთი (აღნიშვნა არის ზედა ხაზზე). გადაკვეთით ჩვენ ვეძებთ აღნიშვნას, ეს არის = 0.3040.

წუთების მნიშვნელობები მითითებულია ექვსი წუთის ინტერვალით, რა მოხდება, თუ ჩვენთვის საჭირო მნიშვნელობა ამ ინტერვალში მოხვდება. ავიღოთ 44 წუთი და ცხრილში მხოლოდ 42. საფუძვლად ავიღებთ 42-ს და ვიყენებთ დამატებით სვეტებს მარჯვენა მხარეს, ვაკეთებთ მე-2 შესწორებას და ვუმატებთ 0,3040 + 0,0006-ს მივიღებთ 0,3046.

ცოდვით 47 წთ ვიღებთ საფუძვლად 48 წუთს და ვაკლებთ 1 შესწორებას, ანუ 0,3057 - 0,0003 = 0,3054

cos-ის გამოთვლისას ჩვენ ვმუშაობთ ცოდვის მსგავსად, მხოლოდ ცხრილის ქვედა სტრიქონს ვიღებთ საფუძვლად. მაგალითად cos 20 0 = 0.9397

90 0-მდე კუთხის tg და მცირე კუთხის საწოლის მნიშვნელობები სწორია და მათში შესწორებები არ არის. მაგალითად, იპოვეთ tg 78 0 37min = 4.967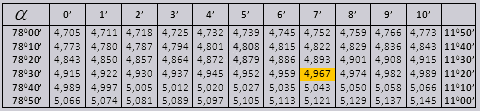


და ctg 20 0 13 წთ = 25.83

აქ ჩვენ განვიხილეთ მთავარი ტრიგონომეტრიული ცხრილები. ვიმედოვნებთ, რომ ეს ინფორმაცია ძალიან სასარგებლო იყო თქვენთვის. თქვენი კითხვები მაგიდებზე, ასეთის არსებობის შემთხვევაში, აუცილებლად დაწერეთ კომენტარებში!

შენიშვნა: კედლის ფარები - ფარიკაობის დაფა კედლების დასაცავად. მიჰყევით ბმულს უკედლო ჩარჩოს ფარაკები (http://www.spi-polymer.ru/otboyniki/) და გაიგეთ მეტი.

ეს სტატია შეგროვდა სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების ცხრილები. პირველ რიგში, ჩვენ ვაძლევთ ტრიგონომეტრიული ფუნქციების ძირითადი მნიშვნელობების ცხრილს, ანუ 0, 30, 45, 60, 90, ..., 360 გრადუსიანი კუთხეების სინუსების, კოსინუსების, ტანგენტებისა და კოტანგენტების ცხრილს. 0, π/6, π/4, π/3, π/2, …, 2πრადიანი). ამის შემდეგ ჩვენ მივცემთ სინუსებისა და კოსინუსების ცხრილს, ასევე V.M. Bradis-ის ტანგენტებისა და კოტანგენტების ცხრილს და ვაჩვენებთ, თუ როგორ გამოვიყენოთ ეს ცხრილები ტრიგონომეტრიული ფუნქციების მნიშვნელობების პოვნისას.

გვერდის ნავიგაცია.

სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების ცხრილი 0, 30, 45, 60, 90, ... გრადუსი კუთხეებისთვის

ბიბლიოგრაფია.

• Ალგებრა:პროკ. 9 უჯრედისთვის. საშ. სკოლა / იუ. ნ.მაკარიჩევი, ნ.გ.მინდიუკი, კ.ი.ნეშკოვი, ს.ბ.სუვოროვა; რედ. S. A. Telyakovsky.- M.: განმანათლებლობა, 1990.- 272 გვ.: Ill.- ISBN 5-09-002727-7
• ბაშმაკოვი მ.ი.ალგებრა და ანალიზის დასაწყისი: პროკ. 10-11 უჯრედისთვის. საშ. სკოლა - მე-3 გამოცემა. - მ.: განმანათლებლობა, 1993. - 351გვ.: ილ. - ISBN 5-09-004617-4.
• Ალგებრადა ანალიზის დასაწყისი: პროკ. 10-11 უჯრედისთვის. ზოგადი განათლება ინსტიტუტები / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn და სხვები; რედ. A. N. Kolmogorova.- 14th ed.- M.: განმანათლებლობა, 2004.- 384 გვ.: ill.- ISBN 5-09-013651-3.
• გუსევი V.A., Mordkovich A.G.მათემატიკა (სახელმძღვანელო ტექნიკური სასწავლებლების მსურველთათვის): პროკ. შემწეობა.- მ. უმაღლესი სკოლა, 1984.-351გვ., ილ.
• ბრედის V.M.ოთხნიშნა მათემატიკური ცხრილები: ზოგადი განათლებისთვის. სახელმძღვანელო დაწესებულებები. - მე-2 გამოცემა. - M.: Bustard, 1999.- 96გვ.: ავად. ISBN 5-7107-2667-2

1. ტრიგონომეტრიული ფუნქციებიარის ელემენტარული ფუნქციები, რომელთა არგუმენტი არის კუთხე. ტრიგონომეტრიული ფუნქციები აღწერს ურთიერთობას გვერდებსა და მახვილ კუთხეებს შორის მართკუთხა სამკუთხედში. ტრიგონომეტრიული ფუნქციების გამოყენების სფეროები უკიდურესად მრავალფეროვანია. მაგალითად, ნებისმიერი პერიოდული პროცესი შეიძლება წარმოდგენილი იყოს ტრიგონომეტრიული ფუნქციების ჯამის სახით (ფურიეს სერია). ეს ფუნქციები ხშირად ჩნდება დიფერენციალური და ფუნქციური განტოლებების ამოხსნისას.

2. ტრიგონომეტრიული ფუნქციები მოიცავს შემდეგ 6 ფუნქციას: სინუსი, კოსინუსი, ტანგენსი,კოტანგენსი, სეკანტიდა კოსეკანტი. თითოეული ამ ფუნქციისთვის არის შებრუნებული ტრიგონომეტრიული ფუნქცია.

3. მოსახერხებელია ტრიგონომეტრიული ფუნქციების გეომეტრიული განსაზღვრების დანერგვა გამოყენებით ერთეული წრე. ქვემოთ მოყვანილ სურათზე ნაჩვენებია წრე r=1 რადიუსით. წრეზე მონიშნულია წერტილი M(x,y). კუთხე OM რადიუსის ვექტორსა და Ox ღერძის დადებით მიმართულებას შორის არის α.

4. სინუსიკუთხე α არის M(x,y) წერტილის y ორდინატის შეფარდება r რადიუსთან:
sinα=y/r.
ვინაიდან r=1, მაშინ სინუსი უდრის M(x,y) წერტილის ორდინატს.

5. კოსინუსიკუთხე α არის M(x,y) წერტილის x აბსცისის შეფარდება r რადიუსთან:
cosα=x/r

6. ტანგენსიკუთხე α არის M(x,y) წერტილის y ორდინატის შეფარდება მის აბსციზასთან x:
tanα=y/x,x≠0

7. კოტანგენსიკუთხე α არის M(x,y) წერტილის x აბსცისის შეფარდება მის ორდინატთან y:
cotα=x/y,y≠0

8. სეკანტიკუთხე α არის r რადიუსის შეფარდება M(x,y) წერტილის x აბსცისასთან:
secα=r/x=1/x,x≠0

9. კოზეკანტიკუთხე α არის r რადიუსის შეფარდება M(x,y) წერტილის y ორდინატთან:
cscα=r/y=1/y,y≠0

10. x, y პროექციის ერთეულ წრეში M(x, y) წერტილები და r რადიუსი ქმნიან მართკუთხა სამკუთხედს, რომელშიც x, y არის ფეხები, r კი ჰიპოტენუზა. ამრიგად, ტრიგონომეტრიული ფუნქციების ზემოაღნიშნული განმარტებები, რომლებიც გამოიყენება მართკუთხა სამკუთხედზე, ჩამოყალიბებულია შემდეგნაირად:
სინუსიკუთხე α არის მოპირდაპირე ფეხის შეფარდება ჰიპოტენუზასთან.
კოსინუსიკუთხე α არის მიმდებარე ფეხის თანაფარდობა ჰიპოტენუზასთან.
ტანგენსიკუთხე α-ს ეწოდება მეზობელთან საპირისპირო ფეხი.
კოტანგენსიკუთხე α ეწოდება მოპირდაპირე მხარეს მიმდებარე ფეხს.
სეკანტიკუთხე α არის ჰიპოტენუზის თანაფარდობა მიმდებარე ფეხთან.
კოზეკანტიკუთხე α არის ჰიპოტენუზის შეფარდება მოპირდაპირე ფეხთან.

11. სინუსური ფუნქციის გრაფიკი
y=sinx, დომენი: x∈R, დომენი: −1≤sinx≤1

12. კოსინუსის ფუნქციის გრაფიკი
y=cosx, დომენი: x∈R, დიაპაზონი: −1≤cosx≤1

13. ტანგენტის ფუნქციის გრაფიკი
y=tanx, დომენი: x∈R,x≠(2k+1)π/2, დომენი: −∞

14. კოტანგენტის ფუნქციის გრაფიკი
y=cotx, დომენი: x∈R,x≠kπ, დომენი: −∞

15. სექციური ფუნქციის გრაფიკი
y=secx, დომენი: x∈R,x≠(2k+1)π/2, დომენი: secx∈(−∞,−1]∪∪)