დახაზეთ მრავალკუთხედი ქაღალდზე. მაგალითად, როგორც ნაჩვენებია სურათზე 1.

ახლა ვცადოთ მისი ფართობის გამოთვლა. Როგორ გავაკეთო ეს? ალბათ უმარტივესი გზაა მისი დაყოფა მართკუთხა სამკუთხედებად და მართკუთხედებად, რომელთა ფართობები ისედაც ადვილი გამოსათვლელი და შედეგების შეკრებაა. მეთოდი, რომელიც მე გამოვიყენე არის მარტივი, მაგრამ ძალიან შრომატევადი და გარდა ამისა, ის არ არის შესაფერისი ყველა პოლიგონისთვის.

განვიხილოთ არადეგენერაციული მარტივი მთელი მრავალკუთხედი (ანუ ის დაკავშირებულია - მისი ნებისმიერი ორი წერტილი შეიძლება იყოს დაკავშირებული უწყვეტი მრუდით, რომელიც მთლიანად შეიცავს მასში, და მის ყველა წვეროს აქვს მთელი რიცხვი კოორდინატები, მისი საზღვარი არის დაკავშირებული მრავალწრეტის გარეშე. თვითგადაკვეთები და მას აქვს არანულოვანი კვადრატი). ასეთი მრავალკუთხედის ფართობის გამოსათვლელად შეგიძლიათ გამოიყენოთ შემდეგი თეორემა:

პიკის თეორემა.მოდით იყოს მრავალკუთხედის შიგნით მთელი რიცხვი, იყოს მთელი რიცხვი მის საზღვარზე და იყოს მისი ფართობი. მაშინ პიკის ფორმულა:

მაგალითი. 1-ში მოცემული მრავალკუთხედისთვის (ყვითელი წერტილები), (ლურჯი წერტილები, ნუ დაგავიწყდებათ წვეროები!), ასე რომ, კვადრატული ერთეულები.

პიკის თეორემის დადასტურება.პირველი, გაითვალისწინეთ, რომ პიკის ფორმულა ჭეშმარიტია ერთეულის კვადრატისთვის. მართლაც, ამ შემთხვევაში გვაქვს

განვიხილოთ მართკუთხედი, რომლის გვერდები დევს გისოსების ხაზებზე. მისი გვერდების სიგრძე იყოს ტოლი და. ჩვენ გვაქვს ამ შემთხვევაში და Pick ფორმულის მიხედვით,

ახლა განვიხილოთ მართკუთხა სამკუთხედი, რომლის ფეხები კოორდინატთა ღერძებზე დევს. ასეთი სამკუთხედი მიიღება გვერდებით მართკუთხედიდან და, წინა შემთხვევაში, მისი დიაგონალზე ჭრით. დაე, მთელი რიცხვი იყოს დიაგონალზე. მაშინ ამ შემთხვევისთვის მივიღებთ იმას

ახლა განიხილეთ თვითნებური სამკუთხედი. მისი მიღება შესაძლებელია რამდენიმე მართკუთხა სამკუთხედის და, შესაძლოა, მართკუთხედის ამოჭრით (იხ. ნახატები 2 და 3). ვინაიდან პიკის ფორმულა მართალია როგორც მართკუთხედისთვის, ასევე მართკუთხა სამკუთხედისთვის, მივიღებთ, რომ ის ასევე იქნება მართალი თვითნებური სამკუთხედისთვის.

რჩება ბოლო ნაბიჯის გადადგმა: სამკუთხედებიდან მრავალკუთხედებზე გადასვლა. ნებისმიერი მრავალკუთხედი შეიძლება დაიყოს სამკუთხედებად (მაგალითად, დიაგონალებით). ამიტომ, ჩვენ უბრალოდ უნდა დავამტკიცოთ, რომ რაიმე სამკუთხედის დამატებისას თვითნებურ მრავალკუთხედს, პიკის ფორმულა რჩება ჭეშმარიტი.

მრავალკუთხედს და სამკუთხედს ჰქონდეთ საერთო გვერდი. დავუშვათ, რომ Pick-ის ფორმულა მოქმედებს და ჩვენ დავამტკიცებთ, რომ ის ასევე მართებულია მიმატებიდან მიღებული მრავალკუთხედისთვის. ვინაიდან და აქვს საერთო გვერდი, ამ მხარეს მდებარე ყველა მთელი წერტილი, გარდა ორი წვერისა, ხდება ახალი მრავალკუთხედის შიდა წერტილები. წვეროები იქნება სასაზღვრო წერტილები. ავღნიშნოთ საერთო წერტილების რაოდენობა და მივიღოთ

ახალი მრავალკუთხედის შიდა მთელი რიცხვების რაოდენობა,

ახალი მრავალკუთხედის სასაზღვრო წერტილების რაოდენობა.

ამ თანასწორობიდან ვიღებთ

ვინაიდან ჩვენ ვივარაუდეთ, რომ თეორემა ჭეშმარიტია ცალკე და ცალკე, მაშინ

ამრიგად, Pick ფორმულა დადასტურებულია.

ეს ფორმულა აღმოაჩინა ავსტრიელმა მათემატიკოსმა პიკ გეორგ ალექსანდროვმა (1859 - 1943) 1899 წელს. ამ ფორმულის გარდა, გეორგ პიკმა აღმოაჩინა პიკი, პიკი - ჯულია, პიკი - ნევალინას თეორემები, დაამტკიცა შვარცი - პიკის უტოლობა. AT დანართი 1თქვენ შეგიძლიათ იხილოთ არასტანდარტული ამოცანები, რომლებიც განვიხილე Pick ფორმულის გამოსაყენებლად.

პიკის ფორმულა

1. შესავალი

2. პიკის ფორმულა. მტკიცებულება I.

მტკიცებულება II.

მტკიცებულება შ.

3. ამოცანები.

4. მრავალკუთხედის ფართობის ფორმულა წვეროების კოორდინატების მიხედვით.

5. ამოცანები.

6. ლიტერატურა

პიკის ფორმულა.

1. შესავალი.

სიბრძნეს ვიღებთ ისტორიიდან,

პოეზიაში - ჭკუა,

მათემატიკაში – გამჭრიახობა.

ფ.ბეკონი

ნაკვეთი გაიშლება ჩვეულებრივი ქაღალდის ფურცელზე.

უჯრედების გვერდებზე მიმავალი ხაზები ქმნიან ბადეს, ხოლო უჯრედების წვეროები არის ამ ბადის კვანძები. ფურცელზე დავხატოთ მრავალკუთხედი კვანძებში წვეროებით და ვიპოვოთ მისი ფართობი.

თქვენ შეგიძლიათ მოძებნოთ იგი სხვადასხვა გზით. მაგალითად, შეგიძლიათ დაჭრათ მრავალკუთხედი საკმაოდ მარტივ ფორმებად, იპოვოთ მათი არეები და დაამატოთ ისინი.

მაგრამ აქ ჩვენ ბევრი უბედურება გვაქვს. ფიგურა ადვილად იყოფა მართკუთხედებად, ტრაპეციებად და სამკუთხედებად და მისი ფართობი გამოითვლება ძალისხმევის გარეშე.

მიუხედავად იმისა, რომ მრავალკუთხედი საკმარისად მარტივი გამოიყურება, მისი ფართობის გამოთვლას დიდი შრომა დასჭირდება. რა მოხდება, თუ მრავალკუთხედი უფრო მიმზიდველად გამოიყურებოდა? გამოდის, რომ მრავალკუთხედების არეები, რომელთა წვეროები განლაგებულია ქსელის კვანძებში, შეიძლება გამოითვალოს ბევრად უფრო მარტივად: არსებობს ფორმულა, რომელიც აკავშირებს მათ ფართობს მრავალკუთხედის შიგნით და საზღვარზე მდებარე კვანძების რაოდენობასთან. ამ შესანიშნავ და მარტივ ფორმულას პიკის ფორმულა ჰქვია.

2. პიკის ფორმულა.

მრავალკუთხედის წვეროები (აუცილებლად ამოზნექილი არ არის) განლაგებულია მთელი რიცხვითი გისოსის კვანძებში. მის შიგნით დევს გისოსის B კვანძები და G კვანძების საზღვარზე. დავამტკიცოთ, რომ მისი ფართობი არის B + – 1 (პიკის ფორმულა).

მტკიცებულება I.

განვიხილოთ მრავალკუთხედი, რომლის წვეროები არის მთელი რიცხვის ბადის კვანძებში, ანუ მათ აქვთ მთელი კოორდინატები.

მრავალკუთხედს ვყოფთ სამკუთხედებად, წვეროებით გისოსების კვანძებში, რომლებიც არ შეიცავს კვანძებს არც შიგნით და არც გვერდებზე.

აღნიშნე:

ნარის მრავალკუთხედის გვერდების რაოდენობა,

მარის სამკუთხედების რიცხვი წვეროებით გისოსების კვანძებში, რომლებიც არ შეიცავს კვანძებს არც შიგნით და არც გვერდებზე,

B არის კვანძების რაოდენობა მრავალკუთხედის შიგნით,

Г არის კვანძების რაოდენობა გვერდებზე, წვეროების ჩათვლით.

ყველა ამ სამკუთხედის ფართობი ერთნაირი და ტოლია.

ამრიგად, მრავალკუთხედის ფართობი არის
.

180 0 მ .

ახლა სხვაგვარად ვიპოვოთ ეს თანხა.

ნებისმიერ შიდა კვანძზე წვეროს მქონე კუთხეების ჯამი არის 360 0.

მაშინ ყველა შიდა კვანძზე წვეროების მქონე კუთხეების ჯამი არის 360 0 ვ.

კუთხეების ჯამი გვერდებზე კვანძებში, მაგრამ არა წვეროებზე, არის 180 0 (G - ნ).

მრავალკუთხედის წვეროებზე კუთხეების ჯამი არის 180 0 ( ნ – 2) .

ყველა სამკუთხედის კუთხის ჯამი არის 360 0 V + 180 0 (G - ნ) + 180 0 (ნ – 2).

ანუ 1800 მ\u003d 360 0 V + 180 0 (G - ნ) + 180 0 (ნ – 2),

180 0 მ\u003d 360 0 V + 180 0 G - 180 0 ნ + 180 0 ნ– 180 0 2,

180 0 მ\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

საიდანაც ვიღებთ გამოსახულებას მრავალკუთხედის S ფართობისთვის:

ს= B + – 1 ,

ცნობილია როგორც პიკის ფორმულა.

ფიგურაში: V = 24, D = 9, შესაბამისად,ს = 24 + – 1 = 27,5.

იპოვეთ პირველი მრავალკუთხედის ფართობი Peak ფორმულის გამოყენებით:

B = 28 (მწვანე წერტილები);

D = 20 (ლურჯი წერტილები).

ვიღებთ, S =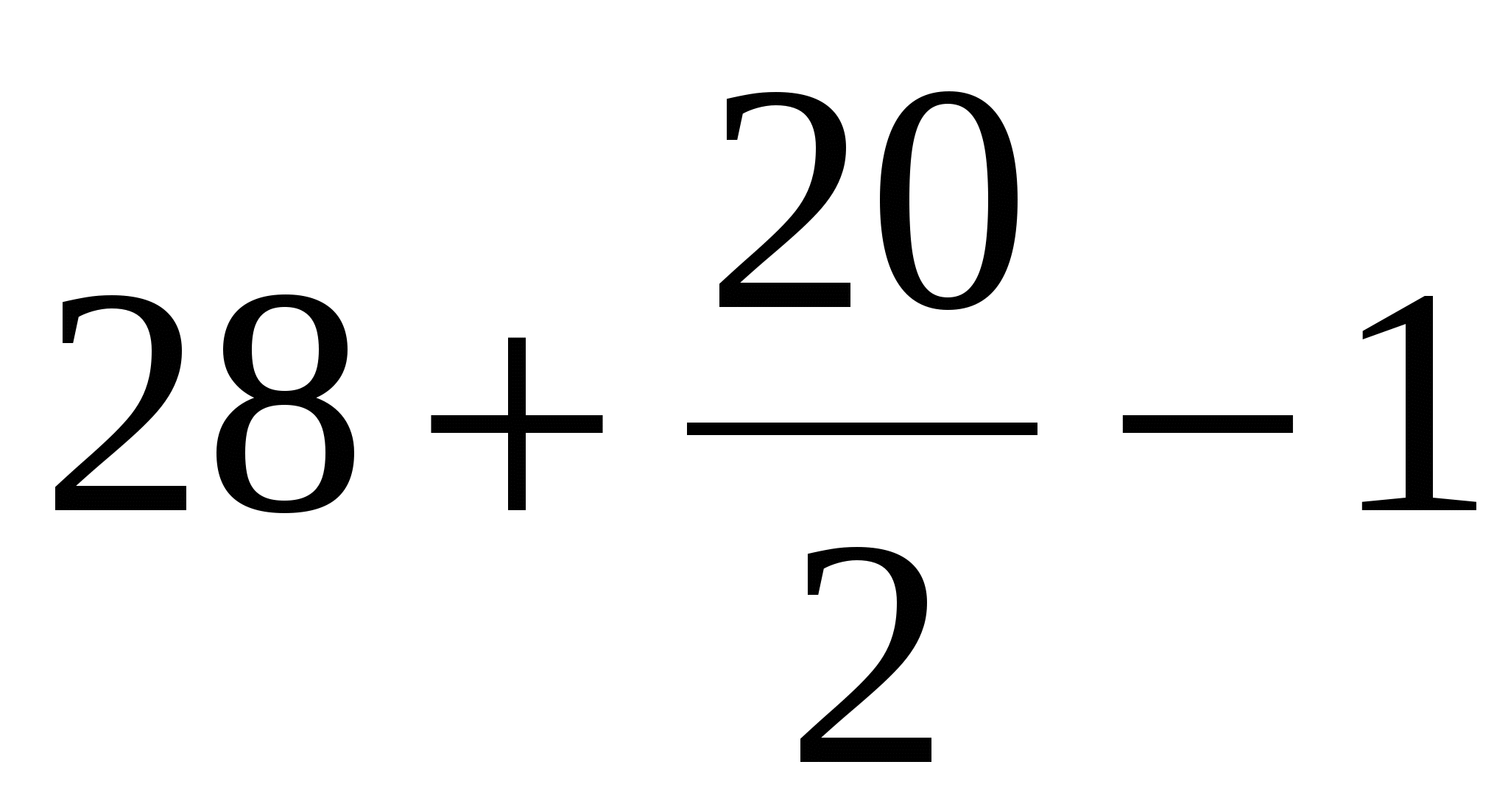
= 37 კვადრატული ერთეული

მტკიცებულება II.

თითოეულ მრავალკუთხედს M-ს, რომელსაც აქვს წვეროები მთელი რიცხვის ბადის კვანძებში, ჩვენ ვანიჭებთ რიცხვს f (M) =
, სადაც ჯამი არის M-ის კუთვნილი ყველა გისოსის კვანძზე და კუთხეზე განისაზღვრება შემდეგნაირად: =
მრავალკუთხედის შიდა წერტილისთვის, =
წვეროს გარდა სხვა სასაზღვრო წერტილისთვის და – კუთხე წვეროზე, თუ მოცემული კვანძი არის წვერო. ადვილი მისახვედრია, რომ f (M) =
+
= B + – 1. რჩება იმის შემოწმება, რომ რიცხვი f (M) უდრის მრავალკუთხედის M ფართობს.

მრავალკუთხედი M დაიჭრას მრავალკუთხედებად M 1 და M 2 წვეროებით გისოსის კვანძებში. შემდეგ f(M) = f(M 1) + f(M 2), რადგან თითოეული კვანძისთვის კუთხეები იკრიბება. მაშასადამე, თუ პიკის ფორმულა ჭეშმარიტია M, M 1 და M 2 მრავალკუთხედის ორზე, მაშინ ის ასევე მართალია მესამესთვის.

თუ M არის გვერდებით მართკუთხედი გვდა ქ, მიმართულია გისოსების ხაზების გასწვრივ, შემდეგ

f (M) = (p – 1) (q – 1) +
= pq.

ამ შემთხვევაში პიკის ფორმულა მოქმედებს. M მართკუთხედის დიაგონალურად M 1 და M 2 სამკუთხედებად დაჭრით და იმ ფაქტის გამოყენებით, რომ f (M) = f (M 1) + f (M 2) და f (M 1) = f (M 2), ადვილია. დაამტკიცოს პიკის ფორმულის მართებულობა ნებისმიერი მართკუთხა სამკუთხედისთვის, რომლის ფეხები მიმართულია გისოსების ხაზების გასწვრივ. მართკუთხედიდან რამდენიმე ასეთი სამკუთხედის მოწყვეტით, ნებისმიერი სამკუთხედის მიღება შეიძლება.

პიკის ფორმულის დასადასტურებლად, უნდა აღინიშნოს, რომ ნებისმიერი მრავალკუთხედი შეიძლება დაიჭრას სამკუთხედებად, რომლებიც არ იკვეთებიან დიაგონალებით.

მტკიცებულება შ.

კავშირი ფიგურის ფართობსა და ამ ფიგურაში მოხვედრილი კვანძების რაოდენობას შორის განსაკუთრებით ნათელია მართკუთხედის შემთხვევაში.

დაე იყოს Ა Ბ Გ Დ- მართკუთხედი წვეროებით კვანძებსა და გვერდებზე, რომლებიც მიდიან ბადის ხაზების გასწვრივ.

აღნიშნეთ მიერ ATკვანძების რაოდენობა, რომლებიც დევს მართკუთხედის შიგნით და მეშვეობით გარის კვანძების რაოდენობა მის საზღვარზე. გადაიტანეთ ბადე ნახევარი უჯრედით მარჯვნივ და ნახევარი უჯრედით ქვემოთ.

შემდეგ მართკუთხედის ტერიტორია შეიძლება "განაწილდეს" კვანძებს შორის შემდეგნაირად: თითოეული ATკვანძები „აკონტროლებენ“ გადანაცვლებული ბადის მთელ უჯრედს, თითოეულ მათგანს გ- 4 სასაზღვრო არაკუთხის კვანძი - უჯრედის ნახევარი და თითოეული კუთხის წერტილი - უჯრედის მეოთხედი. ამრიგად, S მართკუთხედის ფართობი არის

ასე რომ, მართკუთხედებისთვის, რომელთა წვეროები კვანძებში და გვერდებზე მიდის ბადის ხაზების გასწვრივ, ჩვენ დავადგინეთ ფორმულა

მოდით დავამტკიცოთ, რომ ეს ფორმულა მართალია არა მხოლოდ მართკუთხედებისთვის, არამედ თვითნებური მრავალკუთხედებისთვისაც, რომელთა წვეროებია ქსელის კვანძებში.

აღნიშნეთ მიერ ს მ პოლიგონის ფართობიმ კვანძებით წვეროებით და მეშვეობითპ მ - ღირებულება
, სადAT მ არის შიგნით არსებული კვანძების რაოდენობამ,ა გ მ არის კვანძების რაოდენობა საზღვარზე. მაშინ Pick ფორმულა შეიძლება დაიწეროს როგორც
.

ჩვენ ვყოფთ ფორმულის მტკიცებულებას რამდენიმე ეტაპად.

Ნაბიჯი 1.

თუ მრავალკუთხედიმ 2 პოლიგონად მოჭრილი ქსელის კვანძების წვეროებითმ 1 და მ 2 , ასევე აქვს წვეროები მხოლოდ ქსელის კვანძებში, მაშინ
. დაუშვით მრავალკუთხედიმ მოჭრილი მრავალკუთხედებადმ 1 და მ 2 კვანძებში წვეროებით სეგმენტის მიხედვით AB. ყველა კვანძი, გარდა იმ კვანძებისა, რომლებიც ხვდება სეგმენტზეAB, იგივე წვლილი შეიტანეთ ფორმულის მარცხენა და მარჯვენა მხარეს. განვიხილოთ AB სეგმენტზე მდებარე კვანძები.

თუ ასეთი კვანძი მდებარეობს A-სა და B-ს შორის (მაგალითად, C), მაშინ მრავალკუთხედისთვისმ ეს არის შიდა და მრავალკუთხედებისთვისმ 1 და მ 2 - საზღვარი. ამიტომ, მისი წვლილიპ მ უდრის 1-ს და თითოეულ გამონათქვამში
და
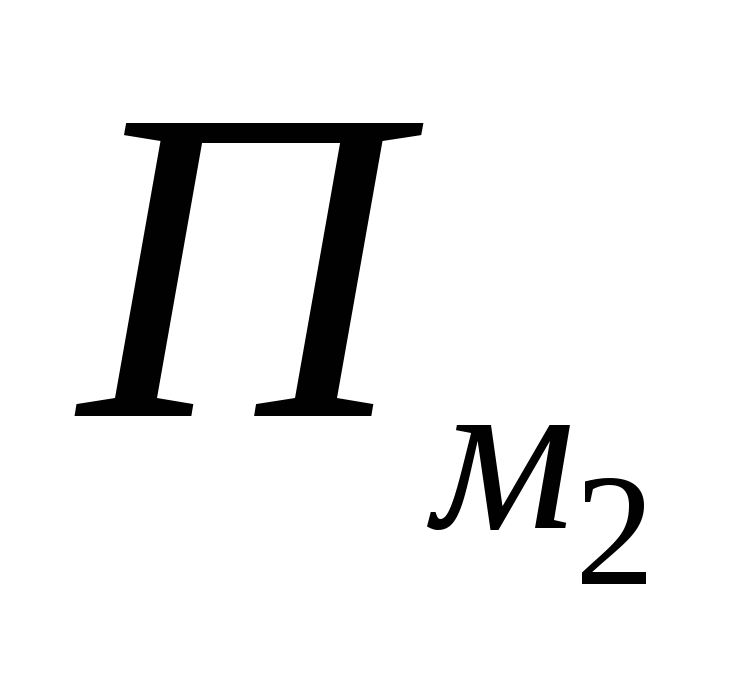– თითოეული 0,5, ანუ ასეთი კვანძის წვლილიპ მ და
თანაბარი არიან.

განვიხილოთ კვანძები A და B. ისინი ორივეს საზღვარია მდა ამისთვის მ 1 , მ 2 .

აქედან გამომდინარე, თითოეული ამ კვანძის წვლილიპ მ არის 0,5 ა
- ერთეული. ეს ნიშნავს, რომ A და B კვანძების მთლიანი წვლილიპ მ უდრის 1-ს, რაც 1-ით ნაკლებია მათ წვლილზე
. მაგრამ
, ა .

ყველა კვანძის მთლიანი „წვლილიდან“. პ მ 1 გამოკლებულია
2 გამოკლებულია და ეს ანაზღაურებს A და B კვანძების წვლილის სხვაობას.

Ისე,
.

ნაბიჯი 2

თუ მრავალკუთხედი მორ მრავალკუთხედად მოჭრილი ქსელის კვანძების წვერით მ 1 და მ 2 (ასევე კვანძებით წვეროებით) და ფორმულა მართალია ზოგიერთი პოლიგონისთვის მმ 1 , მ 2 , მაშინ ეს ასევე მართალია მესამე მრავალკუთხედისთვის.

მოდით, მაგალითად, ეს მართალიამ 1 და მ 2 , ე.ი
. შემდეგ (პირველ საფეხურზე), მაგრამ ზე პირველი ნაბიჯი), ბოლო გამონათქვამი უდრისპ მ , და თანასწორობა
და არსებობს Pick ფორმულა.

ნაბიჯი 3

მოდით დავამტკიცოთ Pick-ის ფორმულა მართკუთხა სამკუთხედისთვის, წვეროებით ქსელის კვანძებთან და ბადის ხაზებზე განლაგებული ფეხებით.

სამკუთხედი ABCმართკუთხედად აშენება Ა Ბ Გ Დ .

მართკუთხედებისთვის პიკის ფორმულა სწორია: ს Ა Ბ Გ Დ = პ Ა Ბ Გ Დ . პირველი ნაბიჯის მიხედვით პ Ა Ბ Გ Დ = პ ABC + პ ACD , პ ABC = პ ACD , ისე პ Ა Ბ Გ Დ = 2P ABC . მაგრამ ს Ა Ბ Გ Დ = 2 ს ABC . Ისე ს ABC = პ ABC .

ნაბიჯი 4

პიკის ფორმულა სწორია თვითნებური სამკუთხედისთვის, რომელსაც აქვს წვეროები ქსელის კვანძებში.

ფიგურის შესწავლის შემდეგ, ადვილი გასაგებია: ნებისმიერი ასეთი სამკუთხედის მიღება შესაძლებელია რომელიმე მართკუთხედის „მოწყვეტით“, გვერდებით, რომლებიც გადის ბადის ხაზების გასწვრივ, რამდენიმე მართკუთხედი და მართკუთხა სამკუთხედი, რომელსაც აქვს ფეხები ქსელის ხაზებზე. და რადგან პიკის ფორმულა მართებულია მართკუთხედებისთვის და მართკუთხა სამკუთხედებისთვის, მაშინ (გაიხსენეთ ნაბიჯი 2) ის ასევე მართალია თავდაპირველი სამკუთხედისთვის.

ჩვენ დავამტკიცეთ, რომ თუ მრავალკუთხედი შეიძლება დაიჭრას სამკუთხედებად, წვეროებით ქსელის კვანძებში, მაშინ პიკის ფორმულა მისთვის ჭეშმარიტია.

3. ამოცანები.

იპოვეთ ფიგურების ფართობი:

1
.

B=9

G = 4

B=9

G = 5

ფიგურის ფართობის გამოთვლა.

არჩევის მეთოდი

ირკუტსკის 5B MBOU №23 საშუალო სკოლის მოსწავლის ნამუშევარი

ბალსუკოვა ალექსანდრა

ხელმძღვანელი: ხოდირევა თ.გ.

2014 წელი

ფიგურის ფართობის გამოთვლა. არჩევის მეთოდი

კვლევის ობიექტი : ამოცანები ქაღალდზე

შესწავლის საგანი : მრავალკუთხედის ფართობის გამოთვლის პრობლემები ქაღალდზე, მათი გადაჭრის მეთოდები და ტექნიკა.

Კვლევის მეთოდები საკვანძო სიტყვები: შედარება, განზოგადება, ანალოგია, ლიტერატურისა და ინტერნეტ რესურსების შესწავლა, ინფორმაციის ანალიზი.

კვლევის მიზანი:

აირჩიეთ მთავარი, საინტერესო, გასაგები ინფორმაცია

მიღებული ინფორმაციის გაანალიზება და ორგანიზება

იპოვნეთ ქაღალდზე ამოცანების გადაჭრის სხვადასხვა მეთოდი და ტექნიკა

შეამოწმეთ ფორმულები გეომეტრიული ფიგურების ფართობის გამოსათვლელად Peak ფორმულის გამოყენებით

შეგროვებული მასალის წარმოსაჩენად ნაწარმოების ელექტრონული პრეზენტაციის შექმნა

გეომეტრია არის ყველაზე ძლიერი ინსტრუმენტი ჩვენი გონებრივი შესაძლებლობების დახვეწისთვის და საშუალებას გვაძლევს ვიფიქროთ და ვიმსჯელოთ სწორად.

(გ. გალილეო)

თემის აქტუალობა

მათემატიკისადმი გატაცება ხშირად იწყება პრობლემის შესახებ ფიქრით. ასე რომ, თემის „მრავალკუთხედების ფართობების“ შესწავლისას ჩნდება კითხვა, არის თუ არა დავალებები, რომლებიც განსხვავდება სახელმძღვანელოში განხილული ამოცანებისგან. ასეთი ამოცანები მოიცავს დავალებებს ქაღალდზე. რა არის ასეთი პრობლემების თავისებურება, არსებობს თუ არა ჭურჭლის ფურცელზე ამოცანების გადაჭრის სპეციალური მეთოდები და ტექნიკა. მათემატიკის გაკვეთილზე მასწავლებელმა გაგვაცნო მრავალკუთხედების გამოთვლის საინტერესო მეთოდი. დავიწყე ამ თემაზე ლიტერატურის, ინტერნეტ რესურსების შესწავლა. როგორც ჩანს, მომხიბლავი ნივთები შეგიძლიათ ნახოთ უჯრიან თვითმფრინავზე, ანუ გაუთავებელ ქაღალდზე, რომელიც გაფორმებულია იდენტურ კვადრატებად. ირკვევა, რომ ქაღალდთან დაკავშირებული ამოცანები საკმაოდ მრავალფეროვანია. ვისწავლე, როგორ გამოვთვალო ფურცელზე დახატული მრავალკუთხედების ფართობები. გალიაში ქაღალდზე მრავალი ამოცანისთვის არ არსებობს ამოხსნის ზოგადი წესი, კონკრეტული მეთოდები და ტექნიკა. ეს არის მათი თვისება, რომელიც განსაზღვრავს მათ ღირებულებას არა კონკრეტული საგანმანათლებლო უნარის ან უნარის განვითარებისთვის, არამედ ზოგადად აზროვნების, ასახვის, ანალიზის, ანალოგიების ძიების უნარს, ანუ ეს ამოცანები ავითარებს აზროვნების უნარს მათი ფართო გაგებით.

და ასევე გავიგე, რომ ასეთი ამოცანები განიხილება GIA-ს საკონტროლო-გაზომვის მასალებში და ერთიანი სახელმწიფო გამოცდაში. ამიტომ ამ მასალის შესწავლა სასარგებლოდ მიმაჩნია მისი გამოყენებისთვის არა მხოლოდ შემდგომ სასწავლო პროცესში, არამედ არასტანდარტული ოლიმპიადის პრობლემების გადასაჭრელად.

2.ფართობის ცნება

მოედანი- ორგანზომილებიანი გეომეტრიული ფიგურის რიცხვითი მახასიათებელი, რომელიც აჩვენებს ამ ფიგურის ზომას. ისტორიულად ფართობის გამოთვლას ეძახდნენ . ფიგურას, რომელსაც აქვს ფართობი, ეწოდება კვადრატი .

ბრტყელი ფიგურის ფართობი გეომეტრიის თვალსაზრისით

1. მოედანი- ბრტყელი ფიგურის ზომა სტანდარტულ ფიგურასთან მიმართებაში, რომელიც არის კვადრატი, რომლის გვერდი ტოლია ერთი სიგრძისა.

2. მოედანი- რიცხვითი მახასიათებელი, რომელიც მიეკუთვნება გარკვეული კლასის ბრტყელ ფიგურებს (მაგალითად, მრავალკუთხედებს). კვადრატის ფართობი, რომლის გვერდი უდრის სიგრძის ერთეულს, აღებულია ფართობის ერთეულის ტოლი

3. მოედანი- დადებითი მნიშვნელობა, რომლის რიცხვითი მნიშვნელობა აქვს შემდეგი თვისებები:

 თანაბარ ფიგურებს აქვთ თანაბარი ფართობები;

 თუ ფიგურა იყოფა ნაწილებად, რომლებიც არის მარტივი ფიგურები (ანუ ისინი, რომლებიც შეიძლება დაიყოს ბრტყელ სამკუთხედების სასრულ რაოდენობად), მაშინ ამ ფიგურის ფართობი უდრის მისი ფართობების ჯამს. ნაწილები;

 კვადრატის ფართობი, რომლის გვერდიც ტოლია საზომი ერთეულის ტოლი.

ამრიგად, შეგვიძლია დავასკვნათ, რომ ფართობი არ არის კონკრეტული მნიშვნელობა, მაგრამ მხოლოდ იძლევა ბრტყელი ფიგურის გარკვეულ პირობით მახასიათებელს. თვითნებური ფიგურის ფართობის საპოვნელად საჭიროა განვსაზღვროთ რამდენ კვადრატს შეიცავს ის სიგრძის ერთეულის ტოლი გვერდით. მაგალითად, ავიღოთ მართკუთხედი, რომელშიც კვადრატული სანტიმეტრი ჯდება ზუსტად 6-ჯერ. ეს ნიშნავს, რომ მართკუთხედის ფართობია 6 სმ2.

კვადრატის ფართობის არჩევა, რომლის გვერდიც ტოლია გაზომვის ერთეულისთვის, როგორც მინიმალური საზომი ერთეული ყველა ფართობისთვის, შემთხვევითი არ არის. ეს არის ხალხის შეთანხმების შედეგი, რომელიც წარმოიშვა „ბუნებრივი“ მრავალსაუკუნოვანი შერჩევის დროს. გარდა ამისა, იყო სხვა წინადადებები საზომი ერთეულის შესახებ. ასე, მაგალითად, შემოთავაზებული იყო ტოლგვერდა სამკუთხედის ფართობის აღება, როგორც ასეთი ერთეული (ანუ ნებისმიერი ბრტყელი ფიგურა შეიძლება იყოს წარმოდგენილი ტოლგვერდა სამკუთხედების გარკვეული რაოდენობის „ჯამად“), რაც გამოიწვევს არეების რიცხვითი წარმოდგენის ცვლილება.

ამრიგად, მათემატიკაში გაჩნდა ფართობების გამოთვლის ფორმულები და ადამიანმა მაშინვე არ გააცნობიერა - ეს მრავალი მეცნიერი, რომელიც ცხოვრობს სხვადასხვა ეპოქაში და სხვადასხვა ქვეყანაში. (მცდარი ფორმულები მეცნიერებაში ვერ იპოვეს ადგილი და დავიწყებას მიეცა). ჭეშმარიტი ფორმულები ავსებდნენ, ასწორებდნენ და ასაბუთებდნენ ათასობით წლის განმავლობაში, სანამ ჩვენამდე მოაღწიეს თანამედროვე სახით.

Რა თქმა უნდა ფართობის გაზომვამოიცავს მოცემული ფიგურის ფართობის შედარებას საზომ ერთეულად აღებული ფიგურის ფართობთან. შედარების შედეგად მიიღება გარკვეული რიცხვი - მოცემული ფიგურის ფართობის რიცხვითი მნიშვნელობა. ეს რიცხვი გვიჩვენებს, რამდენჯერ მეტია (ან ნაკლები) მოცემული ფიგურის ფართობი ფიგურის ფართობზე, ფართობის ერთეულად აღებული.

თ ამრიგად, შეგვიძლია დავასკვნათ, რომ ფართობი არის ხელოვნური რაოდენობა, რომელიც ისტორიულად შემოიღო ადამიანმა ბრტყელი ფიგურის ზოგიერთი თვისების გასაზომად. ასეთი მნიშვნელობის შეყვანის აუცილებლობა განპირობებული იყო მზარდი მოთხოვნილებებით იმის ცოდნა, თუ რამდენად დიდია ესა თუ ის ტერიტორია, რამდენი მარცვალია საჭირო მინდვრის დასათესად ან იატაკის ზედაპირის ფართობის გამოსათვლელად დეკორატიული ფილების გასაფორმებლად.

პიკის ფორმულა

ქაღალდზე მრავალკუთხედის ფართობის შესაფასებლად საკმარისია გამოვთვალოთ რამდენ უჯრედს ფარავს ეს პოლიგონი (უჯრედის ფართობს ვიღებთ ერთეულად). უფრო ზუსტად, თუს არის მრავალკუთხედის ფართობი, B არის უჯრედების რაოდენობა, რომლებიც მთლიანად დევს მრავალკუთხედის შიგნით, და G არის უჯრედების რაოდენობა, რომლებსაც აქვთ ინტერიერი. ჩვენ განვიხილავთ მხოლოდ ისეთ მრავალკუთხედებს, რომელთა ყველა წვერო დევს ღერძიანი ქაღალდის კვანძებში - მათში, სადაც მრავალკუთხედის ბადის ხაზები კვეთს მინიმუმ ერთ საერთო წერტილს.

მოხაზულ ქაღალდზე დახატული ნებისმიერი სამკუთხედის ფართობი მარტივად შეიძლება გამოითვალოს მართკუთხა სამკუთხედების და მართკუთხედების ფართობების ჯამის ან სხვაობის წარმოდგენით, რომელთა გვერდები მიჰყვება ბადის ხაზებს, რომლებიც გადის დახატული სამკუთხედის წვეროებზე.

ასეთი მრავალკუთხედის ფართობის გამოსათვლელად შეგიძლიათ გამოიყენოთ შემდეგი თეორემა:

თეორემა . დაე იყოს - მრავალკუთხედის შიგნით მთელი რიცხვების რაოდენობა, - მის საზღვარზე მთელი პუნქტების რაოდენობა, - მისი ტერიტორია. მაშინპიკის ფორმულა:

მაგალითი. ნახატზე მრავალკუთხედისთვისლ = 7 (წითელი წერტილები), 9 (მწვანე წერტილები), ასე რომს = 7+ 9/2 -1 = 10,5 კვადრატული ერთეული.

პიკის თეორემა- კლასიკური შედეგი და .

სამკუთხედის ფართობი კვანძებში წვეროებით და არ შეიცავს კვანძებს არც შიგნით, არც გვერდებზე (გარდა წვეროებისა) უდრის 1/2-ს. Ეს ფაქტი.

3. ისტორია

პიკის ფორმულა აღმოაჩინა ავსტრიელმა მათემატიკოსმა გეორგ ალექსანდრემ (1859-1942 წწ.). . 16 წლის ასაკში გიორგიმ სკოლა დაამთავრა და შევიდა. 20 წლისამ მიიღო ფიზიკისა და მათემატიკის სწავლების უფლება. 1884 წელს პიკი წავიდარომ . იქ ის შეხვდა კლეინის სხვა სტუდენტს,. მოგვიანებით, 1885 წელს, იგი დაბრუნდასადაც მან გაატარა სამეცნიერო მოღვაწეობის დარჩენილი ნაწილი.

გეორგ პიკი აინშტაინს მეგობრობდა. პიკი და აინშტაინი არა მხოლოდ იზიარებდნენ სამეცნიერო ინტერესებს, არამედ გატაცებულნი იყვნენ მუსიკით. პიკმა, რომელიც უკრავდა კვარტეტში, რომელიც შედგებოდა უნივერსიტეტის პროფესორებისგან, გააცნო აინშტაინი პრაღის სამეცნიერო და მუსიკალურ საზოგადოებებში.

პიკის მათემატიკური ინტერესების წრე უკიდურესად ფართო იყო. კერძოდ, მას აქვს 50-ზე მეტი სამეცნიერო ნაშრომი. პიკის თეორემა, რომელიც მან აღმოაჩინა 1899 წელს, ფართოდ იყო ცნობილი მრავალკუთხედის ფართობის გამოთვლით. გერმანიაში ეს თეორემა შედის სასკოლო სახელმძღვანელოებში.

4.პიკის ფორმულის გამოყენება

Pick ფორმულა გამოიყენება არა მხოლოდ მრავალკუთხედების ფართობის გამოსათვლელად, არამედ ოლიმპიადის დონის მრავალი პრობლემის გადასაჭრელად.

Pick-ის ფორმულის გამოყენების რამდენიმე მაგალითი ამოცანების გადაჭრისას:

1) ჭადრაკის მეფემ შემოიარა 8 × 8 უჯრედის დაფა და თითოეულს ესტუმრა

მთავარი ველი ზუსტად ერთხელ და ბოლო სვლით თავდაპირველს დაუბრუნდება

ველი. გატეხილი ხაზი, რომელიც სერიულად აკავშირებს ველების ცენტრებს

მეფე გავიდა, არ აქვს თვითგადაკვეთა. რა ტერიტორია შეიძლება

შეზღუდოს ეს გატეხილი ხაზი? (უჯრედის მხარე არის 1.)

Pick-ის ფორმულიდან დაუყოვნებლივ გამომდინარეობს, რომ ფართობი, რომელიც შემოსაზღვრულია ლო-

მანა არის 64/2 − 1 = 31; აქ გისოსების კვანძები არის ცენტრები 64

ველები და, ვარაუდით, ისინი ყველა დევს მრავალკუთხედის საზღვარზე. Ისე

ამრიგად, მართალია, მეფის ასეთი „ტრაექტორია“ საკმაოდ ბევრია, მაგრამ ყველა მათგანი

ტოლი ფართობის მრავალკუთხედების შეზღუდვა.

ამოცანები გსსა და ერთიანი სახელმწიფო გამოცდის საკონტროლო-საზომი მასალებიდან

დავალება B3

იპოვეთ ფიგურის ფართობი, რომელიც გამოსახულია 1 სმ 1 სმ უჯრედის ზომით (იხ. ნახ.). მიეცით პასუხი კვადრატულ სანტიმეტრებში.

4. დასკვნა

კვლევის პროცესში ვსწავლობდი საცნობარო, პოპულარულ სამეცნიერო ლიტერატურას. გავიგე, რომ 1899 წელს ავსტრიელ მათემატიკოს პიკს შთააგონებდა მშვენიერი პიკის ფორმულის დასამტკიცებლად მრავალკუთხედის ფართობის პოვნის პრობლემამ, რომელსაც აქვს წვეროები ქსელის კვანძებში.

ჩემი მუშაობის შედეგად გავაფართოვე ცოდნა ჩექმულ ფურცელზე ამოცანების ამოხსნის შესახებ, თავად განვსაზღვრე შესასწავლი ამოცანების კლასიფიკაცია და დავრწმუნდი მათ მრავალფეროვნებაში.

ვისწავლე უჯრაზე დახატული მრავალკუთხედების ფართობების გამოთვლა.განხილულ ამოცანებს სირთულის განსხვავებული დონე აქვს - მარტივიდან ოლიმპიადამდე. ყველას შეუძლია მათ შორის აღმოაჩინოს სირთულის შესასრულებელი დონის ამოცანები, საიდანაც შესაძლებელი იქნება უფრო რთული ამოცანების გადაჭრაზე გადასვლა.

მივედი დასკვნამდე, რომ თემა, რომელიც მაინტერესებდა, საკმაოდ მრავალმხრივია, ამოცანები ქაღალდზე მრავალფეროვანია, მათი ამოხსნის მეთოდები და ტექნიკაც მრავალფეროვანია. ამიტომ ჩვენი გადავწყვიტე ამ მიმართულებით მუშაობა გამეგრძელებინა.

5. გამოყენებული ლიტერატურა:

1. ნ.ბ. ვასილევი, „პიკის ფორმულის გარშემო“, კვანტი. - 1974. - No12

2. Kokse Prasolov VV ამოცანები პლანიმეტრიაში. - M.: MTsNMO, 2006.t e r G.S.M. შესავალი გეომეტრიაში. - მ.: ნაუკა, 1966 წ

3. როსლოვა ლ.ო., შარიგინი ი.ფ. გაზომვები. - მ.: ედ. "ღია სამყარო", 2005 წ.

ინტერნეტ რესურსები:

:

კავშირი სამუშაოზე

„სიბრტყე ფიგურების ფართობების გამოთვლა. არჩევის მეთოდი"

ამ თემის განხილვა გაზრდის მოსწავლის შემეცნებით აქტივობას, რომელიც მოგვიანებით გეომეტრიის გაკვეთილებზე დაიწყებს ნახატის ჰარმონიის დანახვას და შეწყვეტს გეომეტრიის (და ზოგადად მათემატიკის) მოსაწყენ მეცნიერებად აღქმას.

განხილულია მათემატიკის მასწავლებლის მიერ

ხოდირევა ტატიანა გეორგიევნა

არსებობს შესანიშნავი ფორმულა, რომელიც საშუალებას გაძლევთ დათვალოთ პოლიგონის ფართობიკოორდინატთა ბადეზე თითქმის შეცდომების გარეშე. ეს ფორმულა კი არა, რეალურია თეორემა. ერთი შეხედვით, ეს შეიძლება რთულად მოგეჩვენოთ. მაგრამ საკმარისია რამდენიმე ამოცანის გადაჭრა - და მიხვდებით, რამდენად მაგარია ეს ფუნქცია. ასე რომ, წინ წადით!

დავიწყოთ ახალი განმარტებით:

კოორდინატთა სტეკის კვანძი არის ნებისმიერი წერტილი, რომელიც მდებარეობს ამ ბადის ვერტიკალური და ჰორიზონტალური ხაზების გადაკვეთაზე.

Დანიშნულება:

პირველ სურათზე კვანძები საერთოდ არ არის მონიშნული. მეორეს აქვს 4 კვანძი. ბოლოს მესამე სურათზე 16-ვე კვანძია მონიშნული.

რა კავშირშია ეს პრობლემა B5-თან? ფაქტია, რომ მრავალკუთხედის წვეროები ასეთ ამოცანებში ყოველთვისდაწექი ქსელის კვანძებში. შედეგად, მათთვის მუშაობს შემდეგი თეორემა:

თეორემა. განვიხილოთ მრავალკუთხედი კოორდინატთა ბადეზე, რომლის წვეროები დევს ამ ბადის კვანძებში. მაშინ მრავალკუთხედის ფართობია:

სადაც n არის მოცემული მრავალკუთხედის შიგნით არსებული კვანძების რაოდენობა, k არის კვანძების რაოდენობა, რომლებიც მდებარეობს მის საზღვარზე (სასაზღვრო კვანძები).

მაგალითად, განვიხილოთ ჩვეულებრივი სამკუთხედი კოორდინატთა ბადეზე და შეეცადეთ მონიშნოთ შიდა და სასაზღვრო კვანძები.

პირველ სურათზე ნაჩვენებია ჩვეულებრივი სამკუთხედი. მეორე სურათზე მონიშნულია მისი შიდა კვანძები, რომელთა რიცხვი არის n = 10. მესამე სურათზე შემოხაზულია საზღვარზე დაწოლილი კვანძები, სულ k = 6.

შესაძლოა, ბევრ მკითხველს არ ესმის, როგორ დათვალოს n და k რიცხვები. დაიწყეთ შიდა კვანძებით. აქ ყველაფერი აშკარაა: ჩვენ ვხატავთ სამკუთხედს ფანქრით და ვხედავთ, რამდენი კვანძია დაჩრდილული.

სასაზღვრო კვანძებით, ეს ცოტა უფრო რთულია. პოლიგონის საზღვარი - დახურული გატეხილი ხაზი, რომელიც კვეთს კოორდინატთა ბადეს ბევრ წერტილში. უმარტივესი გზაა რაიმე „საწყისი“ წერტილის მონიშვნა, შემდეგ კი დანარჩენის შემოვლა.

სასაზღვრო კვანძები იქნება მხოლოდ ის წერტილები პოლიხაზზე, რომლებზეც ისინი ერთდროულად იკვეთებიან სამი ხაზი:

1. ფაქტობრივად, გატეხილი ხაზი;
2. ჰორიზონტალური ბადის ხაზი;
3. ვერტიკალური ხაზი.

ვნახოთ, როგორ მუშაობს ეს ყველაფერი რეალურ პრობლემებში.

დავალება. იპოვეთ სამკუთხედის ფართობი, თუ უჯრედის ზომაა 1 x 1 სმ:

პირველ რიგში, მოდი აღვნიშნოთ კვანძები, რომლებიც დევს სამკუთხედის შიგნით, ისევე როგორც მის საზღვარზე:

გამოდის, რომ არსებობს მხოლოდ ერთი შიდა კვანძი: n = 1. არის ექვსი სასაზღვრო კვანძი: სამი ემთხვევა სამკუთხედის წვეროებით, და კიდევ სამი წევს გვერდებზე. სულ k = 6.

ახლა ჩვენ ვიანგარიშებთ ფართობს ფორმულის გამოყენებით:

Სულ ეს არის! პრობლემა მოგვარებულია.

დავალება. იპოვეთ ოთხკუთხედის ფართობი, რომელიც გამოსახულია უჯრის ზომით 1 სმ 1 სმ-ზე. პასუხი მიეცით კვადრატულ სანტიმეტრებში.

კვლავ აღვნიშნავთ შიდა და სასაზღვრო კვანძებს. არის n = 2 შიდა კვანძი სასაზღვრო კვანძები: k = 7, აქედან 4 არის ოთხკუთხედის წვეროები, და კიდევ 3 წევს გვერდებზე.

რჩება n და k რიცხვების ჩანაცვლება ფართობის ფორმულაში:

ყურადღება მიაქციეთ ბოლო მაგალითს. ეს პრობლემა რეალურად იქნა შემოთავაზებული 2012 წელს სადიაგნოსტიკო სამუშაოზე. თუ სტანდარტული სქემით მუშაობთ, ბევრი დამატებითი კონსტრუქციის გაკეთება მოგიწევთ. კვანძების მეთოდით კი ყველაფერი თითქმის ზეპირად წყდება.

მნიშვნელოვანი შენიშვნა ტერიტორიებზე

მაგრამ ფორმულა არ არის ყველაფერი. მოდით გადავიწეროთ ფორმულა ცოტათი და მივიყვანოთ ტერმინები მარჯვენა მხარეს საერთო მნიშვნელისკენ. ჩვენ ვიღებთ:

რიცხვები n და k არის კვანძების რაოდენობა, ისინი ყოველთვის მთელი რიცხვებია. ასე რომ, მთელი მრიცხველიც მთელი რიცხვია. ჩვენ მას ვყოფთ 2-ზე, რაც გულისხმობს მნიშვნელოვან ფაქტს:

ტერიტორია ყოველთვის გამოხატულია მთელი რიცხვი ან წილადი. უფრო მეტიც, წილადის ბოლოს ყოველთვის არის „ხუთი მეათედი“: 10,5; 17.5 და ა.შ.

ამრიგად, B5 ამოცანის ფართობი ყოველთვის გამოიხატება როგორც ***.5 ფორმის მთელი რიცხვი ან წილადი. თუ პასუხი განსხვავებულია, ეს ნიშნავს, რომ სადღაც შეცდომაა დაშვებული. გაითვალისწინეთ ეს, როდესაც მათემატიკაში ჩააბარებთ რეალურ გამოცდას!

პრეზენტაციების წინასწარი გადახედვის გამოსაყენებლად შექმენით Google ანგარიში (ანგარიში) და შედით: https://accounts.google.com

სლაიდების წარწერები:

დაასრულა მე-7 საშუალო სკოლის მოსწავლემ 8 "ა" კლასი იუნოშევა ქსენია ინსტრუქტორი: ბაბინა ნატალია ალექსეევნა სალსკი 2011 წ. "პიკის ფორმულა"

სამუშაოს მიზნები: სასკოლო სასწავლო გეგმისგან განსხვავებული სხვას არსებობის გარკვევა, ფორმულა გისოსების მრავალკუთხედის ფართობის საპოვნელად. სასურველი ფორმულის გამოყენების სფეროები.

შესავალი. ზოგადსაგანმანათლებლო სკოლებში მიღებული მათემატიკური განათლება ზოგადი განათლებისა და თანამედროვე ადამიანის ზოგადი კულტურის აუცილებელი კომპონენტია. ამ ეტაპზე სასკოლო სისტემა გათვლილია თერთმეტწლიან განათლებაზე. მეთერთმეტე კლასის ბოლოს ყველა მოსწავლეს მოუწევს ერთიანი სახელმწიფო გამოცდის ჩაბარება, რომელიც აჩვენებს სკოლაში სწავლისას მიღებული ცოდნის დონეს. მაგრამ სასკოლო სასწავლო გეგმა ყოველთვის არ იძლევა რაიმე პრობლემის გადაჭრის ყველაზე რაციონალურ გზებს. მაგალითად, 2010 წლის USE-ის შედეგების დათვალიერებისას ჩანს, რომ ბევრი სტუდენტი კარგავს ქულებს B6 დავალების გამო. დავიწყე იმის გარკვევა, თუ როგორ დავზოგო დრო და როგორ მოვაგვარო ეს პრობლემა სწორად.

დავალება B6. ფიგურები გამოსახულია კარკასულ ქაღალდზე 1 სმ-ზე 1 სმ ზომის უჯრედებით (იხ. სურათი). იპოვეთ მათი ფართობი კვადრატულ სანტიმეტრებში.

ასე რომ, ამ ამოცანის გადასაჭრელად, მე უნდა გამოვიყენო ფორმულები ფართობის საპოვნელად, რომელსაც ვსწავლობთ მე-8 კლასში. მაგრამ ამას დიდი დრო დასჭირდება და მე უნდა ვუპასუხო კითხვას რაც შეიძლება სწრაფად, რადგან გამოცდის დრო მკაცრად შეზღუდულია. ამიტომ, კვლევის ჩატარების შემდეგ აღმოვაჩინე, რომ არსებობს პიკის თეორემა, რომელიც არ არის შესწავლილი სასკოლო სასწავლო გეგმაში, მაგრამ დამეხმარება დავალების უფრო სწრაფად შესრულებაში.

ისტორიის მინიშნება. გეორგ ალექსანდრ პიკი (დ. 10 აგვისტო , 1859 — გ. 26 ივლისი , 1942 ) — ავსტრიელი მათემატიკოსი. გარდაიცვალა ტერეზინის საკონცენტრაციო ბანაკში. ის დღეს ცნობილია პიკის ფორმულის გამო მრავალკუთხედების გისოსების ფართობის დასადგენად. მან გამოაქვეყნა თავისი ფორმულა ნაშრომში 1899 წელს, იგი პოპულარული გახდა, როდესაც ჰუგო სტეინჰაუსმა შეიტანა იგი მათემატიკური სურათების 1969 წლის გამოცემაში. პიკი სწავლობდა ვენის უნივერსიტეტში და დაამთავრა დოქტორი 1880 წელს. დოქტორის მიღების შემდეგ დაინიშნა ერნესტ მახის ასისტენტად პრაღის შერლ-ფერდინანდის უნივერსიტეტში. 1881 წელს იქ მასწავლებელი გახდა. 1884 წელს შვებულება მიიღო უნივერსიტეტიდან და დაიწყო მუშაობა ფელიქს კლაინთან ლაიფციგის უნივერსიტეტში. ის პრაღაში დარჩა 1927 წელს პენსიაზე გასვლამდე, როდესაც დაბრუნდა ვენაში. პიკი თავმჯდომარეობდა პრაღის (მაშინდელი) გერმანული უნივერსიტეტის კომიტეტს, რომელმაც ალბერტ აინშტაინი დანიშნა მათემატიკური ფიზიკის პროფესორად 1911 წელს. პიკი აირჩიეს ჩეხეთის მეცნიერებათა და ხელოვნების აკადემიის წევრად, მაგრამ გააძევეს ნაცისტების მიერ პრაღის ხელში ჩაგდების შემდეგ. 1927 წელს პენსიაზე გასვლის შემდეგ პიკი დაბრუნდა ვენაში, ქალაქში, სადაც დაიბადა. ანშლუსის შემდეგ, როდესაც ნაცისტები ავსტრიაში შევიდნენ 1938 წლის 12 მარტს, პიკი დაბრუნდა პრაღაში. 1939 წლის მარტში ნაცისტები შეიჭრნენ ჩეხოსლოვაკიაში. გეორგი 1942 წლის 13 ივლისს გაგზავნეს ტერეზინის საკონცენტრაციო ბანაკში. ორი კვირის შემდეგ გარდაიცვალა.

პიკის თეორემა. პიკის თეორემა არის კომბინატორიული გეომეტრიისა და რიცხვების გეომეტრიის კლასიკური შედეგი. მრავალკუთხედის ფართობი მთელი რიცხვის წვეროებით უდრის ჯამს B + D/2 - 1, სადაც B არის მრავალკუთხედის შიგნით არსებული მთელი რიცხვი, ხოლო D არის მრავალკუთხედის საზღვარზე მთელი რიცხვი.

პიკის თეორემის მაამებელი დადასტურება. ნებისმიერი ასეთი მრავალკუთხედი ადვილად შეიძლება დაიყოს სამკუთხედებად, წვეროებით გისოსების კვანძებში, არ შეიცავს კვანძებს არც შიგნით და არც გვერდებზე. შეიძლება აჩვენოს, რომ ყველა ამ სამკუთხედის ფართობი ერთნაირია და ტოლია 1/2-ის და, შესაბამისად, მრავალკუთხედის ფართობი უდრის მათი რიცხვის T ნახევარს. ამ რიცხვის საპოვნელად აღვნიშნავთ n-ით. მრავალკუთხედის გვერდების რაოდენობა, i-ით - მის შიგნით არსებული კვანძების რაოდენობა და b-ით - გვერდების კვანძების რაოდენობა, წვეროების ჩათვლით. ყველა სამკუთხედის კუთხის ჯამი არის πТ. ახლა სხვაგვარად ვიპოვოთ ეს თანხა. ნებისმიერ შიდა კვანძზე წვეროს მქონე კუთხეების ჯამი არის 2 π, ანუ ასეთი კუთხეების ჯამი არის 2 π i; გვერდებზე მდებარე კვანძების კუთხეების ჯამი, მაგრამ არა წვეროებზე, არის (b - n) π, ხოლო მრავალკუთხედის წვეროებზე კუთხეების ჯამი არის (n - 2) π. ამრიგად, π T \u003d 2i π + (b - n) π + (n - 2) π, საიდანაც ვიღებთ გამოხატულებას მრავალკუთხედის S ფართობისთვის, რომელიც ცნობილია როგორც პიკის ფორმულა. მაგალითად, ფიგურაში b = 9, i = 24 და, შესაბამისად, მრავალკუთხედის ფართობი არის 27.5.

განაცხადი. ასე რომ, დავუბრუნდეთ დავალებას B6. ახლა, ახალი ფორმულის ცოდნით, ჩვენ მარტივად შეგვიძლია ვიპოვოთ ამ ოთხკუთხედის ფართობი. ვინაიდან B არის 5; D - 14, შემდეგ 5 + 14: 2-1 \u003d 11 (სმ კვადრატში) ამ ოთხკუთხედის ფართობი არის 11 სმ კვადრატში.

იგივე ფორმულით შეგვიძლია ვიპოვოთ სამკუთხედის ფართობი. ვინაიდან B-14, G-10, შემდეგ 14+10:2-1=18 (კვადრატული სმ) ამ სამკუთხედის ფართობი არის 18 სმ კვადრატში.

თუ B-9, D-12, მაშინ: 9+12:2-1=14 (სმ კვადრატში) ამ ოთხკუთხედის ფართობი არის 14 სმ კვადრატში.

ფორმულის ფარგლები. გარდა იმისა, რომ ფორმულა გამოიყენება სხვადასხვა სახის გამოცდებში, დავალებებსა და ა.შ, ის თან ახლავს მთელ სამყაროს ჩვენს ირგვლივ.

პიკის ფორმულის მიხედვით S = B + ½ G-1 1) სხეული B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) კუდი B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

პიკის ფორმულის მიხედვით S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5

დასკვნა. შედეგად, მივედი დასკვნამდე, რომ არსებობს მრავალი განსხვავებული გზა არეალის ამოცანების გადასაჭრელად, რომლებიც არ არის შესწავლილი სასკოლო სასწავლო გეგმაში და ვაჩვენე ისინი მაგალითად Pick ფორმულის გამოყენებით.

დირექტორია. მრავალკუთხედს თვითგადაკვეთების გარეშე ეწოდება მედის პოლიგონი, თუ მისი ყველა წვერო არის მთელი რიცხვის კოორდინატების წერტილებში (დეკარტის კოორდინატთა სისტემაში). კოორდინატთა სიბრტყეში წერტილს ეწოდება მთელი რიცხვი, თუ მისი ორივე კოორდინატი მთელი რიცხვია.