განვიხილოთ სამი სხივი a, b, c, რომლებიც გამოდიან ერთი და იმავე წერტილიდან და არ დევს ერთ სიბრტყეში. სამკუთხედი (abc) არის ფიგურა, რომელიც შედგება "სამი ბრტყელი კუთხისგან (ab), (bc) და (ac) (ნახ. 2). ამ კუთხეებს ეწოდება სამკუთხედის სახეები, ხოლო მათი გვერდები კიდეებია. ბრტყელი კუთხის საერთო წვერო ეწოდება.

ანალოგიურად არის განსაზღვრული მრავალწახნაგოვანი კუთხის კონცეფცია (ნახ. 3).

პოლიჰედრონი

სტერეომეტრიაში სწავლობენ სივრცეში არსებულ ფიგურებს, რომლებსაც სხეულებს უწოდებენ. ვიზუალურად, (გეომეტრიული) სხეული უნდა წარმოვიდგინოთ, როგორც ფიზიკური სხეულის მიერ დაკავებული და ზედაპირით შემოსაზღვრული სივრცის ნაწილი.

მრავალედრონი არის სხეული, რომლის ზედაპირი შედგება ბრტყელი მრავალკუთხედების სასრული რაოდენობისგან (ნახ. 4). მრავალკუთხედს ეწოდება ამოზნექილი, თუ ის მდებარეობს მის ზედაპირზე არსებული ყველა ბრტყელი მრავალკუთხედის სიბრტყის ერთ მხარეს. ასეთი სიბრტყის საერთო ნაწილს და ამოზნექილი პოლიედრონის ზედაპირს სახე ეწოდება. ამოზნექილი მრავალკუთხედის სახეები ბრტყელი ამოზნექილი მრავალკუთხედებია. სახეების გვერდებს მრავალწახნაგების კიდეები ეწოდება, წვეროებს კი მრავალწახნაგა.

ავხსნათ რა ითქვა ნაცნობი კუბის მაგალითზე (სურ. 5). კუბი არის ამოზნექილი პოლიედონი. მისი ზედაპირი შედგება ექვსი კვადრატისაგან: ABCD, BEFC, .... ისინი მისი სახეებია. კუბის კიდეები არის ამ კვადრატების გვერდები: AB, BC, BE,.... კუბის წვეროები არის კვადრატების წვეროები: A, B, C, D, E, .... კუბს აქვს ექვსი სახე, თორმეტი კიდე და რვა წვერო.

უმარტივესი პოლიედრები - პრიზმები და პირამიდები, რომლებიც ჩვენი შესწავლის მთავარი ობიექტი იქნება - მივცემთ განმარტებებს, რომლებიც, არსებითად, არ იყენებენ სხეულის ცნებას. ისინი განისაზღვრება როგორც გეომეტრიული ფიგურები მათ კუთვნილი სივრცის ყველა წერტილის მითითებით. გეომეტრიული სხეულის და მისი ზედაპირის კონცეფცია ზოგად შემთხვევაში მოგვიანებით იქნება მოცემული.

მრავალმხრივი კუთხეები

მრავალკუთხედი არის მრავალკუთხედის სივრცითი ანალოგი. შეგახსენებთ, რომ პოლიგონი სიბრტყეზე არის ფიგურა, რომელიც წარმოიქმნება მარტივი დახურული გატეხილი ხაზით და მისით შემოსაზღვრული შიდა რეგიონით. სივრცეში სხივს განვიხილავთ, როგორც სიბრტყის წერტილის ანალოგს, ხოლო სიბრტყეზე ბრტყელ კუთხეს, როგორც სიბრტყის სეგმენტის ანალოგს. მაშინ სიბრტყეში მარტივი დახურული გატეხილი ხაზის ანალოგი არის ზედაპირი, რომელიც წარმოიქმნება სიბრტყის კუთხეების სასრული სიმრავლით.ა 1 SA 2 , ა 2 SA 3 , …, ნ -1 SA n, A n SA 1 საერთო ზედას (ნახ. 1), რომელშიც მიმდებარე კუთხეებს არ აქვთ საერთო წერტილები, გარდა საერთო სხივის წერტილებისა, ხოლო არამეზობელ კუთხეებს არ აქვთ საერთო წერტილები, გარდა საერთო წვერისა. მითითებული ზედაპირით და მის მიერ შემოსაზღვრული სივრცის ორი ნაწილიდან ერთ-ერთ ფიგურას ეძახიან მრავალწახნაგოვანი კუთხე. საერთო ზედასდაურეკა სამიტიმრავალმხრივი კუთხე. სხივებიSA 1 , …, SA nდაურეკა ნეკნებიმრავალწახნაგოვანი კუთხე და თავად ბრტყელი კუთხეებია 1 SA 2 , ა 2 SA 3 , …, ნ -1 SA n, A n SA 1 – სახეებიმრავალმხრივი კუთხე. მრავალწახნაგოვანი კუთხე აღინიშნება ასოებითSA 1 … ნ, მიუთითებს წვეროზე და მის კიდეებზე მდებარე წერტილებზე. სახეების რაოდენობის მიხედვით მრავალწახნაგა კუთხეებს უწოდებენ სამკუთხედს, ოთხკუთხედს, ხუთკუთხედს (სურ. 2) და ა.შ.

მრავალწახნაგოვანი კუთხე ეწოდება ამოზნექილი, თუ ის ამოზნექილი ფიგურაა, ე.ი. შეიცავს მის ნებისმიერ ორ წერტილთან ერთად დამაკავშირებელ პუნქტსხაზის სეგმენტი. სურათზე 2, სამკუთხედი და ოთხკუთხა კუთხეები ამოზნექილია, მაგრამ ხუთკუთხედი არა.
განვიხილოთ სამკუთხედების ზოგიერთი თვისება და სამკუთხედის მსგავსი თვისებები.
საკუთრება 1(სამკუთხედის უტოლობა). სამკუთხედის თითოეული გვერდი ნაკლებია დანარჩენი ორი გვერდის ჯამს.
მსგავსი თვისება სამკუთხედის კუთხეებისთვის არის შემდეგი თვისება.
საკუთრება 1სამკუთხედის ყოველი ბრტყელი კუთხე ნაკლებია მისი დანარჩენი ორი ბრტყელი კუთხის ჯამზე.
მტკიცებულება. განვიხილოთ სამკუთხა კუთხე SABC . მისი ბრტყელი კუთხიდან ყველაზე დიდი იყოს კუთხე ASC. შემდეგ უტოლობები

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

ამრიგად, რჩება უთანასწორობის დამტკიცება ASC< ASB+ BSC.
ზღვარზე დავაყენოთ ASCინექცია ASD, ტოლია ASB , და წერტილი ბაირჩიე ისე SB=SD(ნახ. 3). შემდეგ სამკუთხედები ASBდა ASDტოლია (ორ მხარეს და მათ შორის კუთხეს) და, შესაბამისად, AB=AD. გამოვიყენოთ სამკუთხედის უტოლობა AC< AB + BC . ორივე ნაწილის გამოკლება AD=AB, ვიღებთ უთანასწორობას DC< BC. სამკუთხედებში DSCდა BSCერთი მხარე საერთო სკ), SD=SBდა DC< BC. ამ შემთხვევაში, უფრო დიდი კუთხე დევს დიდი მხარის საპირისპიროდ და, შესაბამისად, DSC< BSC . ამ უტოლობის ორივე მხარეს კუთხის დამატება ASD , თანაბარი ASBვიღებთ საჭირო უტოლობას ASC< ASB+ BSC.

შედეგი 1.სამკუთხედის სიბრტყის კუთხეების ჯამი 360-ზე ნაკლებია° .
მტკიცებულება. დაე იყოს SABCარის მოცემული სამკუთხედი. განვიხილოთ სამკუთხედი წვერით ასახეებით ჩამოყალიბებული ABS, ACSდა კუთხე BAC. დადასტურებული თვისების ძალით გვაქვს უთანასწორობა BAC< BAS+ CAS. ანალოგიურად, სამკუთხა კუთხეებისთვის წვეროებით ბდა თანარის უთანასწორობები: ABS< ABS+ CBS, ACB< ACS+ BCS. ამ უტოლობების დამატება და იმის გათვალისწინებით, რომ სამკუთხედის კუთხეების ჯამი ABCუდრის 180-ს° , ვიღებთ 180 ° < BAS+CAS+ ABS + CBS + BCS+ ACS= 180 ° - ASB+ 180°- BSC+180° - ASC. აქედან გამომდინარე, ASB + BSC + ASC< 360 ° .
შედეგი 2.ამოზნექილი მრავალწახნაგოვანი კუთხის სიბრტყის კუთხეების ჯამი 360-ზე ნაკლებია.
მტკიცებულება წინას მსგავსია.
შედეგი 3.სამკუთხედის ორმხრივი კუთხეების ჯამი 180-ზე მეტია° .
მტკიცებულება. დაე იყოს SABC- სამკუთხა კუთხე. მოდი ავირჩიოთ წერტილი პმის შიგნით და ჩამოაგდეს მისგან პერპენდიკულარები PA 1 , PB 1 , კომპიუტერი 1 კიდეზე (ნახ. 4).

ბრტყელი კუთხეები ბ 1 კომპიუტერი 1 , ა 1 კომპიუტერი 1 , ა 1 PB 1 შეავსეთ შესაბამისი დიჰედრული კუთხეები ნეკნებით SA, SB, SC 180-მდე° . ამრიგად, ამ ორმხრივი კუთხეების ჯამი არის 540° - ( ბ 1 კომპიუტერი 1 +A 1 კომპიუტერი 1 + ა 1 PB 1 ). იმის გათვალისწინებით, რომ სამკუთხედის სიბრტყე კუთხეების ჯამი წვეროსთან პკუთხე 360-ზე ნაკლები° , მივიღებთ, რომ თავდაპირველი სამკუთხედის ორმხრივი კუთხეების ჯამი 180-ზე მეტია° .
საკუთრება 2.სამკუთხედის ბისექტრები ერთ წერტილში იკვეთება.
საკუთრება 2".სამკუთხა კუთხის ორწახნაგოვანი კუთხეების ორმხრივი სიბრტყეები იკვეთება ერთი სწორი ხაზის გასწვრივ.
მტკიცებულება თვითმფრინავის შემთხვევის მსგავსია. კერძოდ, ნება SABC- სამკუთხა კუთხე. ორწახნაგოვანი კუთხის ბისექტორული სიბრტყე SAარის კუთხის GMT, რომელიც თანაბარი მანძილით არის დაშორებული მისი სახეებიდან ASCდა ASB. ანალოგიურად, დიედრული კუთხის ბისექტრული სიბრტყე სბარის კუთხის GMT, რომელიც თანაბარი მანძილით არის დაშორებული მისი სახეებიდან BSAდა BSC . მათი გადაკვეთის ხაზი ᲘᲡᲔიქნება თანაბარი მანძილი სამკუთხედის კუთხის ყველა გვერდიდან და, შესაბამისად, მასში გაივლის დიედრული კუთხის ბისექტორული სიბრტყე სკ .
საკუთრება 3.სამკუთხედის გვერდების პერპენდიკულარული ბისექტრები ერთ წერტილში იკვეთება.
საკუთრება 3".სიბრტყეები, რომლებიც გადიან სამკუთხა კუთხის და ამ სახეების პერპენდიკულარულ სახეების ბისექტორებზე, იკვეთება ერთი სწორი ხაზის გასწვრივ.
მტკიცებულება წინა ქონების მტკიცებულების მსგავსია.
საკუთრება 4.სამკუთხედის შუალედები იკვეთება ერთ წერტილში.
ქონება 4"სამკუთხა კუთხის კიდეებზე გამავალი სიბრტყეები და მოპირდაპირე სახეების ბისექტრები იკვეთება ერთი სწორი ხაზის გასწვრივ.
მტკიცებულება. განვიხილოთ სამკუთხა კუთხე SABC, SA = SB = SC(ნახ. 5). შემდეგ ბისექტრები SA 1 , სბ 1 , სკ 1 კუთხეები BSC, ASC, ASB არის შესაბამისი სამკუთხედების მედიანა. Ისე აა 1 , BB 1 , CC 1 - სამკუთხედის შუალედები ABC. დაე იყოს ოარის მათი გადაკვეთის წერტილი. პირდაპირ ᲘᲡᲔშეიცავს სამივე განხილულ სიბრტყეში და, შესაბამისად, არის მათი გადაკვეთის ხაზი.

საკუთრება 5.სამკუთხედის სიმაღლეები ერთ წერტილში იკვეთება.
საკუთრება 5„სამკუთხა კუთხის კიდეებზე გამავალი და მოპირდაპირე სახეების პერპენდიკულარული სიბრტყეები იკვეთება ერთი სწორი ხაზის გასწვრივ.
მტკიცებულება. განვიხილოთ სამკუთხედი წვერით სდა ნეკნები ა, ბ, გ.აღნიშნეთ ა 1 , ბ 1 , გ 1 – სახეების გადაკვეთის ხაზები სიბრტყეებთან, რომლებიც გადიან შესაბამის კიდეებზე და ამ სახეებზე პერპენდიკულარულია (სურ. 6). დააფიქსირეთ წერტილი Cზღვარზე გდა ჩამოაგდეთ მისგან პერპენდიკულარები CA 1 და CB 1 პირდაპირ ა 1 და ბ 1 . აღნიშნეთ ადა ბხაზის კვეთები CA 1 და CB 1 სწორით ადა ბ. მაშინ SA 1 არის პროექცია აა 1 ზღვარზე BSC. როგორც ძვ.წპერპენდიკულარული SA 1 , მაშინ ის პერპენდიკულარულია და აა 1 . ანალოგიურად, ACპერპენდიკულარული BB 1 . ამრიგად, აა 1 და BB 1 არის სამკუთხედის სიმაღლეები ABC. დაე იყოს ოარის მათი გადაკვეთის წერტილი. თვითმფრინავები, რომლებიც გადიან სწორ ხაზებზე ადა ა 1 , ბდა ბ 1 სიბრტყეზე პერპენდიკულარული ABCდა აქედან გამომდინარე, მათი გადაკვეთის ხაზი ᲘᲡᲔპერპენდიკულარული ABC. ნიშნავს, ᲘᲡᲔპერპენდიკულარული AB. Მეორეს მხრივ, COპერპენდიკულარული AB. აქედან გამომდინარე, თვითმფრინავი გადის ზღვარზე გდა ᲘᲡᲔმოპირდაპირე მხარის პერპენდიკულარული იქნება.
თვისება 6 (სინუს თეორემა). სამკუთხედში ABCმხარეებთან ერთად ა, ბ, გშესაბამისად, გვაქვს თანასწორობა ა : ცოდო A=b: ცოდო B=c: ცოდო C.
ქონება 6"მოდით a , b , g - სამკუთხა კუთხის ბრტყელი კუთხეები, ა, ბ, გარის მათი საპირისპირო დიედრული კუთხეები. მაშინცოდვა ა: ცოდვა ა= ცოდვა ბ: ცოდვა ბ= ცოდვა გ: ცოდვა გ.
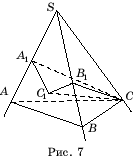
მტკიცებულება.დაე იყოს SABC- სამკუთხა კუთხე. ჩამოაგდეს წერტილიდან Cპერპენდიკულარული CC 1 თვითმფრინავამდე ASBდა პერპენდიკულარული CA 1 ზღვარზე SA(ნახ. 7). შემდეგ კუთხე CA 1 C 1 იქნება დიედრული კუთხის წრფივი კუთხე ა. Ისე CC 1 = CA 1 ცოდვა ა = სკცოდვა ბ ცოდვა ა. ანალოგიურად, ნაჩვენებია, რომ CC 1 = CB 1 ცოდვა b=SCცოდვა როგორც ბ. ამიტომ, თანასწორობის ცოდვაბ ცოდვა a =ცოდვა ა ცოდვა ბდა, შესაბამისად, თანასწორობის ცოდვაროგორც ა= სინბ : ცოდო ბ. ანალოგიურად, ჩვენ ვამტკიცებთ, რომ თანასწორობა ცოდავსბ: ცოდვა ბ= ცოდვა გ: ცოდვა გ.

საკუთრება 7.თუ წრე შეიძლება ჩაიწეროს ამოზნექილ ოთხკუთხედში, მაშინ მოპირდაპირე გვერდების ჯამები ტოლია.
ქონება 7"თუ სფერო შეიძლება ჩაიწეროს ამოზნექილ ოთხკუთხედში, მაშინ საპირისპირო სიბრტყის კუთხეების ჯამები ტოლია.

ლიტერატურა
1. Hadamard J. ელემენტარული გეომეტრია. ნაწილი II. სტერეომეტრია. – მ.: უჭპედგიზი, 1938 წ.
2. პერეპელკინი დ.ი. ელემენტარული გეომეტრიის კურსი. ნაწილი II. გეომეტრია სივრცეში. - მ.-ლ.: გოსტეხიზდატი, 1949 წ.
3. ელემენტარული მათემატიკის ენციკლოპედია. წიგნი IV. გეომეტრია. - მ. 1963 წ.
4. სმირნოვა ი.მ. პოლიედრონების სამყაროში. – მ.: განმანათლებლობა, 1995 წ.

დიჰედრული კუთხე არის ფიგურა, რომელიც წარმოიქმნება ორი ნახევრად სიბრტყით, მათ შორის საერთო სწორი ხაზით. ნახევრად სიბრტყეებს სახეები ეწოდება, ხოლო მათ შემოსაზღვრულ სწორ ხაზს დიედრული კუთხის კიდე ეწოდება.

ნახაზი 142 გვიჩვენებს დიედრალურ კუთხეს a კიდით და მიმართულია a და (3.

ორმხრივი კუთხის კიდეზე პერპენდიკულარული სიბრტყე კვეთს მის სახეებს ორი ნახევარწრფის გასწვრივ. ამ ნახევარხაზებით წარმოქმნილ კუთხეს დიედრული კუთხის წრფივი კუთხე ეწოდება. დიედრული კუთხის ზომა აღებულია შესაბამისი წრფივი კუთხის საზომად. თუ ორწახნაგოვანი კუთხის a კიდის A წერტილის გავლით დავხატავთ სიბრტყეს y ამ კიდეს პერპენდიკულარულად, მაშინ ის გადაკვეთს a და (3) სიბრტყეებს ნახევარხაზების გასწვრივ (სურ. 142); მოცემული ორკუთხედის წრფივი კუთხე. კუთხე.ამ წრფივი კუთხის გრადუსული საზომი არის დიედრული კუთხის გრადუსული საზომი დიედრული კუთხის გაზომვა არ არის დამოკიდებული წრფივი კუთხის არჩევაზე.

სამკუთხედი არის ფიგურა, რომელიც შედგება სამი ბრტყელი კუთხით (სურ. 143). ამ კუთხეებს ეწოდება სამკუთხედის კუთხის სახეები, ხოლო მათ გვერდებს კიდეები. ბრტყელი კუთხეების საერთო წვეროს ეწოდება სამკუთხედის წვერო. ორთავიან კუთხეებს, რომლებიც წარმოიქმნება სახეებით და მათი გაფართოებით, ეწოდება სამკუთხედის ორკუთხედის კუთხეებს.

ანალოგიურად, მრავალწახნაგოვანი კუთხის კონცეფცია განისაზღვრება, როგორც ბრტყელი კუთხით შედგენილი ფიგურა (ნახ. 144). მრავალწახნაგოვანი კუთხისთვის, სახეების, კიდეების და ორთავიანი კუთხეების ცნებები განისაზღვრება ისევე, როგორც სამკუთხედის კუთხისთვის.

მრავალედრონი არის სხეული, რომლის ზედაპირი შედგება ბრტყელი მრავალკუთხედების სასრული რაოდენობისგან (სურ. 145).

მრავალკუთხედს ეწოდება ამოზნექილი, თუ იგი მდებარეობს თითოეული მრავალკუთხედის სიბრტყის ერთ მხარეს მის ზედაპირზე (სურ. 145, ა, ბ). ასეთი სიბრტყის საერთო ნაწილს და ამოზნექილი პოლიედრონის ზედაპირს სახე ეწოდება. ამოზნექილი მრავალკუთხედის სახეები ამოზნექილი მრავალკუთხედებია. სახეების გვერდებს მრავალწახნაგების კიდეები ეწოდება, წვეროებს კი მრავალწახნაგა.

განმარტებები. ავიღოთ რამდენიმე კუთხე (სურ. 37): ASB, BSC, CSD, რომლებიც ერთმანეთზე რიგად მიმდებარედ, განლაგებულია ერთ სიბრტყეში S საერთო წვერის გარშემო.

მოდით მოვატრიალოთ ASB კუთხის სიბრტყე საერთო SB გვერდის გარშემო ისე, რომ ამ სიბრტყემ შექმნას რაღაც ორმხრივი კუთხე BSC სიბრტყესთან. შემდეგ, მიღებული დიედრული კუთხის შეცვლის გარეშე, ჩვენ ვატრიალებთ მას SC სწორი ხაზის გარშემო ისე, რომ BSC სიბრტყემ შექმნას გარკვეული დიედრული კუთხე CSD სიბრტყით. გავაგრძელოთ ეს თანმიმდევრული ბრუნვა თითოეული საერთო მხარის გარშემო. თუ ამ შემთხვევაში SF-ის ბოლო მხარე შერწყმულია SA-ს პირველ მხარეს, მაშინ იქმნება ფიგურა (სურ. 38), რომელიც ე.წ. მრავალწახნაგოვანი კუთხე. კუთხეებს ASB, BSC,... ეწოდება ბრტყელი კუთხეებიან სახეები, მათ მხარეებს SA, SB, ... ეძახიან ნეკნებიდა საერთო წვერო S- სამიტიმრავალმხრივი კუთხე.

თითოეული კიდე ასევე არის რაღაც დიედრული კუთხის კიდე; მაშასადამე, მრავალწახნაგა კუთხეში იმდენივე ორთავიანი კუთხეა და იმდენი ბრტყელი კუთხე, რამდენი კიდეა მასში. მრავალწახნაგოვანი კუთხით სახეების ყველაზე მცირე რაოდენობა არის სამი; ამ კუთხეს უწოდებენ სამკუთხა. შეიძლება იყოს ოთხმხრივი, ხუთგვერდიანი და ა.შ.

მრავალწახნაგოვანი კუთხე აღინიშნება წვეროზე მოთავსებული ერთი ასო S-ით, ან SABCDE ასოების სერიით, რომელთაგან პირველი აღნიშნავს წვეროს, ხოლო დანარჩენები კიდეებია მათი მდებარეობის მიხედვით.

მრავალწახნაგოვანი კუთხე ეწოდება ამოზნექილს, თუ ის განლაგებულია მისი თითოეული სახის სიბრტყის ერთ მხარეს, რომელიც განუსაზღვრელი ვადით არის გაშლილი. ასეთია, მაგალითად, 38-ე ნახატზე ნაჩვენები კუთხე. პირიქით, 39-ე ნახაზის კუთხეს არ შეიძლება ეწოდოს ამოზნექილი, ვინაიდან იგი მდებარეობს ASB სახის ან BSC სახის ორივე მხარეს.

თუ მრავალწახნაგოვანი კუთხის ყველა სახე იკვეთება სიბრტყით, მაშინ განყოფილებაში წარმოიქმნება მრავალკუთხედი ( ა ბ ც დ ე ). ამოზნექილ მრავალკუთხედში ეს მრავალკუთხედი ასევე ამოზნექილია.

განვიხილავთ მხოლოდ ამოზნექილ მრავალწახნაგა კუთხეებს.

თეორემა. სამკუთხედში თითოეული ბრტყელი კუთხე ნაკლებია დანარჩენი ორი ბრტყელი კუთხის ჯამზე.

სამკუთხედში SABC (ნახ. 40) ბრტყელ კუთხეებს შორის ყველაზე დიდი იყოს ASC კუთხე.

მოდით დავხატოთ ASD კუთხე ამ კუთხეზე, რომელიც უდრის ASB კუთხს და დავხატოთ სწორი ხაზი AC, რომელიც კვეთს SD-ს რაღაც D წერტილში. დააყენეთ SB = SD. B-ს A-სთან და C-თან შეერთებით ვიღებთ \(\Delta\)ABC, რომელშიც

AD+DC< АВ + ВС.

სამკუთხედები ASD და ASB თანმიმდევრულია, რადგან თითოეული მათგანი შეიცავს თანაბარ კუთხეს თანაბარ გვერდებს შორის: აქედან გამომდინარე, AD = AB. მაშასადამე, თუ გამოვიყვანთ AD და AB თანაბარ წევრებს გამოყვანილ უტოლობაში, მივიღებთ რომ DC< ВС.

ახლა ჩვენ შევნიშნავთ, რომ SCD და SCB სამკუთხედებს აქვთ ერთის ორი გვერდი, რომელიც ტოლია მეორის ორ მხარეს, ხოლო მესამე გვერდები არ არის ტოლი; ამ შემთხვევაში, უფრო დიდი კუთხე დევს ამ მხარის დიდის საპირისპიროდ; ნიშნავს,

∠CSD< ∠ CSВ.

ამ უტოლობის მარცხენა მხარეს ASD კუთხის დამატება და მარჯვენა მხარეს მის ტოლ კუთხის ASB, მივიღებთ უტოლობას, რომელიც საჭირო იყო დასამტკიცებლად:

∠ASC< ∠ CSB + ∠ ASB.

ჩვენ დავამტკიცეთ, რომ ყველაზე დიდი ბრტყელი კუთხეც კი ნაკლებია დანარჩენი ორი კუთხის ჯამზე. ასე რომ, თეორემა დამტკიცებულია.

შედეგი. გამოვაკლოთ ბოლო უტოლობის ორივე ნაწილს ASB კუთხეში ან CSB კუთხეში; ჩვენ ვიღებთ:

∠ASC - ∠ASB< ∠ CSB;

∠ASC - ∠CSB< ∠ ASB.

ამ უტოლობების გათვალისწინებით მარჯვნიდან მარცხნივ და იმის გათვალისწინებით, რომ ASC კუთხე, როგორც სამი კუთხიდან ყველაზე დიდი, მეტია, ვიდრე დანარჩენი ორი კუთხის სხვაობა, დავასკვნით, რომ სამკუთხედში, თითოეული სიბრტყის კუთხე უფრო დიდია, ვიდრე სხვა ორი კუთხის სხვაობა.

თეორემა. ამოზნექილი მრავალწახნაგოვანი კუთხით, ყველა პლანშეტური კუთხის ჯამი ნაკლებია 4d-ზე (360°) .

გადავკვეთოთ SABCDE ამოზნექილი კუთხის სახეები (სურ. 41) რომელიმე სიბრტყეს; აქედან განყოფილებაში ვიღებთ ამოზნექილს ნ-გონ ABCDE.

ადრე დადასტურებული თეორემის გამოყენება თითოეულ სამკუთხედზე, რომლის წვეროები არის A, B, C, D და E წერტილებზე, paholim:

∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

მოდით დავამატოთ ყველა ეს უტოლობა ტერმინით. შემდეგ მარცხენა მხარეს ვიღებთ ABCDE მრავალკუთხედის ყველა კუთხის ჯამს, რომელიც უდრის 2-ს. დნ - 4დ , ხოლო მარჯვნივ - სამკუთხედების ABS, SBC და ა.შ. X დამატების შემდეგ ვიღებთ:

2დნ - 4დ < 2dn - x .

ვინაიდან განსხვავებები 2 დნ - 4დ და 2 dn - x მინუენდები იგივეა, მაშინ იმისთვის, რომ პირველი სხვაობა მეორეზე ნაკლები იყოს, აუცილებელია, რომ სუბტრაჰენდი 4 დ გამოკლებული იყო X ; ნიშნავს 4 დ > X , ე.ი. X < 4დ .

სამკუთხედის ტოლობის უმარტივესი შემთხვევები

თეორემები. სამკუთხედი კუთხეები ტოლია, თუ მათ აქვთ:

1) თანაბარი დიედრული კუთხით, რომელიც ჩაკეტილია ორ, შესაბამისად, თანაბარ და თანაბრად დაშორებულ სიბრტყე კუთხეს შორის, ან

2) თანაბარი სიბრტყის კუთხის გასწვრივ, რომელიც ჩასმულია ორ, შესაბამისად, თანაბარ და თანაბრად დაშორებულ დიედრალურ კუთხეს შორის.

1) მოდით S და S 1 იყოს ორი სამკუთხედი (ნახ. 42), რომლებშიც ∠ASB = ∠A 1 S 1 B 1 , ∠ASC = ∠A 1 S 1 C 1 (და ეს თანაბარი კუთხეები თანაბრად მდებარეობს) და დიედრული კუთხე AS უდრის A 1 S 1 ორწახნაგოვანი კუთხის.

მოდით ჩავსვათ კუთხე S 1 კუთხეში S ისე, რომ წერტილები S 1 და S, წრფეები S 1 A 1 და SA და სიბრტყეები A 1 S 1 B 1 და ASB ემთხვევა ერთმანეთს. შემდეგ კიდე S 1 B 1 წავა SB-ის გასწვრივ (კუთხების A 1 S 1 B 1 და ASB ტოლობის გამო), სიბრტყე A 1 S 1 C 1 წავა ASC-ის გასწვრივ (დიედრული კუთხეების ტოლობის გამო), ხოლო კიდე S 1 C 1 წავა SC კიდის გასწვრივ (A 1 S 1 C 1 და ASC კუთხეების თანასწორობის გამო). ამრიგად, სამკუთხედი კუთხეები გაერთიანდება ყველა მათი კიდეებით, ე.ი. ისინი თანაბარი იქნებიან.

2) მეორე კრიტერიუმი, ისევე როგორც პირველი, დასტურდება ჩანერგვით.

სიმეტრიული მრავალწახნაგოვანი კუთხეები

მოგეხსენებათ, ვერტიკალური კუთხეები თანაბარია, როდესაც საქმე ეხება სწორი ხაზებით ან სიბრტყეებით წარმოქმნილ კუთხეებს. ვნახოთ, მართალია თუ არა ეს განცხადება მრავალწახნაგოვანი კუთხეებისთვის.

ვაგრძელებთ (სურ. 43) SABCDE კუთხის ყველა კიდეს S წვეროს მიღმა, შემდეგ წარმოიქმნება კიდევ ერთი მრავალწახნაგოვანი კუთხე SA 1 B 1 C 1 D 1 E 1, რომელიც შეიძლება ე.წ. ვერტიკალურიპირველ კუთხესთან მიმართებაში. ადვილი მისახვედრია, რომ ორივე კუთხეს აქვს თანაბარი სიბრტყე და დიედრული კუთხეები, შესაბამისად, მაგრამ ორივე საპირისპირო თანმიმდევრობითაა. მართლაც, თუ წარმოვიდგენთ დამკვირვებელს, რომელიც უყურებს მრავალწახნაგოვანი კუთხის გარედან მის წვეროზე, მაშინ SA, SB, SC, SD, SE კიდეები მას მოეჩვენება, რომ მდებარეობს საათის ისრის საწინააღმდეგო მიმართულებით, ხოლო კუთხეს უყურებს. SA 1 B 1 C 1 D 1 E 1 , ის ხედავს კიდეებს SA 1 , SВ 1 , ... მდებარეობს საათის ისრის მიმართულებით.

მრავალწახნაგოვანი კუთხეები, შესაბამისად თანაბარი სიბრტყით და ორმხრივი კუთხეებით, მაგრამ განლაგებულია საპირისპირო თანმიმდევრობით, საერთოდ არ შეიძლება გაერთიანდეს ჩადგმისას; ეს ნიშნავს, რომ ისინი არ არიან თანაბარი. ასეთ კუთხეებს ე.წ სიმეტრიული(ზედა S-თან შედარებით). მეტი სივრცეში ფიგურების სიმეტრიის შესახებ ქვემოთ იქნება განხილული.

სხვა მასალები

№1 თარიღი 05.09.14

საგანი გეომეტრია

Კლასი 11

გაკვეთილის თემა: მრავალწახნაგოვანი კუთხის კონცეფცია. სამკუთხა კუთხე.

გაკვეთილის მიზნები:

გააცანით ცნებები: „სამკუთხედი კუთხეები“, „მრავალედრული კუთხეები“, „მრავალედრები“;

გააცნოს მოსწავლეებს სამკუთხედის და მრავალწახნაგოვანი კუთხეების ელემენტები, მრავალწახნაგები, აგრეთვე ამოზნექილი მრავალწახნაგოვანი კუთხის განმარტებები და მრავალწახნაგოვანი კუთხის ბრტყელი კუთხეების თვისებები;

გააგრძელონ მუშაობა სივრცითი წარმოდგენებისა და სივრცითი წარმოსახვის განვითარებაზე, ასევე მოსწავლეთა ლოგიკურ აზროვნებაზე.

გაკვეთილის ტიპი: ახალი მასალის შესწავლა

გაკვეთილების დროს

1. საორგანიზაციო მომენტი.

მოსწავლეების მისალმება, გაკვეთილისთვის კლასის მზადყოფნის შემოწმება, მოსწავლეთა ყურადღების ორგანიზება, გაკვეთილის ზოგადი მიზნების და მისი გეგმის გამჟღავნება.

2. ახალი ცნებებისა და მოქმედების მეთოდების ჩამოყალიბება.

ამოცანები: უზრუნველყოს მოსწავლეთა მიერ შესწავლილი მასალის აღქმა, გააზრება და დამახსოვრება. სტუდენტების მიერ შესწავლილი მასალის რეპროდუცირების მეთოდოლოგიის ათვისების უზრუნველყოფა, ასიმილირებული ცნებების, კანონების, წესების, ფორმულების ფილოსოფიური გაგების ხელშეწყობა. მოსწავლეთა მიერ შესწავლილი მასალის სისწორის და ცნობადობის დადგენა, პირველადი გააზრების ხარვეზების გამოვლენა, შესწორების განხორციელება. იმის უზრუნველსაყოფად, რომ მოსწავლეებმა დააკავშირონ თავიანთი სუბიექტური გამოცდილება სამეცნიერო ცოდნის ნიშნებთან.

მიეცით სამი სხივია, ბ დას ს საერთო საწყისი წერტილიო (ნახ. 1.1). ეს სამი სხივი სულაც არ დევს ერთ სიბრტყეში. სურათზე 1.2, სხივებიბ დათან თვითმფრინავში დაწოლაR, სხივია არ წევს ამ თვითმფრინავში.

სხივებია, ბ დათან წყვილი განსაზღვრავს სამ ბრტყელ კუთხეს, რომლებიც გამოირჩევიან რკალებით (ნახ. 1.3).

განვიხილოთ ფიგურა, რომელიც შედგება ზემოთ მითითებული სამი კუთხისგან და სივრცის ნაწილისგან, რომელიც შემოიფარგლება ამ ბრტყელი კუთხით. ეს სივრცითი ფიგურა ე.წსამკუთხა კუთხე (ნახ. 2).

სხივებია, ბ და თან დაურეკასამკუთხა კუთხის კიდეები, და კუთხეები: = AOC, = AOB,

= BOC , სამკუთხა კუთხის შეზღუდვა, - მისისახეები. ეს კუთხეები ყალიბდებასამკუთხა ზედაპირი. Წერტილიო დაურეკასამკუთხა კუთხის წვერო. სამკუთხედი შეიძლება აღვნიშნოთ შემდეგნაირად: OABC

3-ზე ნაჩვენები ყველა მრავალწახნაგოვანი კუთხის გულდასმით შესწავლის შემდეგ, შეგვიძლია დავასკვნათ, რომ თითოეულ მრავალკუთხედს აქვს იგივე რაოდენობის კიდეები და სახეები:

4 სახე და ერთი წვერო;

ხუთმხრივ კუთხეს აქვს 5 კიდე, 5 სახე და ერთი წვერო;

• 
  ექვსკუთხა კუთხეს აქვს 6 კიდე, 6 სახე და ერთი წვერო და ა.შ.

მრავალწახნაგოვანი კუთხეებია ამოზნექილი და არაამოზნექილი.

წარმოიდგინეთ, რომ ჩვენ ავიღეთ ოთხი სხივი საერთო წარმოშობით, როგორც სურათზე 4. ამ შემთხვევაში მივიღეთარაამოზნექილი მრავალწახნაგოვანი კუთხე.

განმარტება 1. მრავალწახნაგა კუთხეს ეწოდება ამოზნექილი კუთხე,თუ ისდევს მისი თითოეული სახის სიბრტყის ერთ მხარეს.

სხვა სიტყვებით რომ ვთქვათ, ამოზნექილი მრავალწახნაგოვანი კუთხე ყოველთვის შეიძლება განთავსდეს მის რომელიმე სახეზე რომელიმე სიბრტყეზე. თქვენ ხედავთ, რომ მე-4 სურათზე ნაჩვენები შემთხვევაში ეს ყოველთვის არ არის შესაძლებელი. 4-ზე ნაჩვენები ოთხკუთხედის კუთხე არის არაამოზნექილი.

გაითვალისწინეთ, რომ ჩვენს სახელმძღვანელოში, თუ ვამბობთ "მრავალედრიანი კუთხე", ვგულისხმობთ, რომ ის ამოზნექილია. თუ განხილული მრავალწახნაგოვანი კუთხე არაამოზნექილია, ეს ცალკე იქნება განხილული.

მრავალწახნაგოვანი კუთხის სიბრტყე კუთხეების თვისებები

თეორემა 1.სამკუთხედის თითოეული ბრტყელი კუთხე ნაკლებია დანარჩენი ორი ბრტყელი კუთხის ჯამზე.

თეორემა 2.ამოზნექილი მრავალწახნაგოვანი კუთხის ყველა სიბრტყის კუთხის მნიშვნელობების ჯამი 360°-ზე ნაკლებია.

3. განაცხადი. უნარებისა და შესაძლებლობების ფორმირება.

მიზნები: უზრუნველყოს, რომ მოსწავლეებმა გამოიყენონ ის ცოდნა და მოქმედების მეთოდები, რაც მათ სჭირდებათ SW-სთვის, შექმნან პირობები სტუდენტებისთვის, რათა გამოავლინონ ნასწავლის გამოყენების ინდივიდუალური გზები.

6. სასცენო ინფორმაცია საშინაო დავალების შესახებ.

მიზნები: უზრუნველყოს, რომ მოსწავლეებმა გაიგონ საშინაო დავალების შესრულების მიზანი, შინაარსი და მეთოდები.

§1 (1.1, 1.2) გვ. 4, No. 9.

7. გაკვეთილის შეჯამება.

მიზანი: კლასის და ცალკეული მოსწავლეების მუშაობის ხარისხობრივი შეფასება.

8. რეფლექსიის ეტაპი.

ამოცანები: წამოიწყონ მოსწავლეთა რეფლექსია მათი საქმიანობის თვითშეფასებაზე. უზრუნველყოს, რომ მოსწავლეებმა ისწავლონ თვითრეგულირებისა და თანამშრომლობის პრინციპები.

საუბარი თემაზე:

რა მოგეჩვენათ საინტერესო გაკვეთილზე?

რა გაუგებარია?

რას უნდა მიაქციოს მასწავლებელმა ყურადღება მომდევნო გაკვეთილზე?

როგორ შეაფასებდით თქვენს სამუშაოს კლასში?