A მატრიცით, თუ არის რიცხვი l ისეთი, რომ AX = lX.

ამ შემთხვევაში იწოდება რიცხვი l საკუთარი ღირებულება X ვექტორის შესაბამისი ოპერატორი (მატრიცა A).

სხვა სიტყვებით რომ ვთქვათ, საკუთრივ ვექტორი არის ვექტორი, რომელიც წრფივი ოპერატორის მოქმედებით გარდაიქმნება კოლინურ ვექტორად, ე.ი. უბრალოდ გაამრავლე რაღაც რიცხვზე. ამის საპირისპიროდ, არასწორი ვექტორების გარდაქმნა უფრო რთულია.

ჩვენ ვწერთ საკუთრივ ვექტორის განმარტებას, როგორც განტოლებათა სისტემას:

მოდით გადავიტანოთ ყველა ტერმინი მარცხენა მხარეს:

ბოლო სისტემა შეიძლება დაიწეროს მატრიცის სახით შემდეგნაირად:

(A - lE)X \u003d O

მიღებულ სისტემას ყოველთვის აქვს ნულოვანი ამონახსნი X = O. ისეთ სისტემებს, რომლებშიც ყველა თავისუფალი წევრი ნულის ტოლია, ე.წ. ერთგვაროვანი. თუ ასეთი სისტემის მატრიცა არის კვადრატი, ხოლო მისი განმსაზღვრელი არ არის ნულის ტოლი, მაშინ კრამერის ფორმულების მიხედვით, ყოველთვის მივიღებთ უნიკალურ ამონახსნებს - ნულს. შეიძლება დადასტურდეს, რომ სისტემას აქვს არანულოვანი ამონახსნები, თუ და მხოლოდ იმ შემთხვევაში, თუ ამ მატრიცის განმსაზღვრელი ნულის ტოლია, ე.ი.

|A - lE| = = 0

ეს განტოლება უცნობი l-ით ე.წ დამახასიათებელი განტოლება (დამახასიათებელი მრავალწევრი) მატრიცა A (წრფივი ოპერატორი).

შეიძლება დადასტურდეს, რომ ხაზოვანი ოპერატორის დამახასიათებელი პოლინომი არ არის დამოკიდებული საფუძვლის არჩევანზე.

მაგალითად, ვიპოვოთ ხაზოვანი ოპერატორის საკუთრივ მნიშვნელობები და საკუთრივვექტორები, რომლებიც მოცემულია A = მატრიცით.

ამისთვის ვადგენთ დამახასიათებელ განტოლებას |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; საკუთარი მნიშვნელობები l 1 = (2 - 12) / 2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

საკუთარი ვექტორების საპოვნელად, ჩვენ ვხსნით განტოლებების ორ სისტემას

(A + 5E) X = O

(A - 7E) X = O

პირველი მათგანისთვის გაფართოებული მატრიცა მიიღებს ფორმას

,

საიდანაც x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, ე.ი. X (1) \u003d (- (2/3) s; s).

მეორე მათგანისთვის გაფართოებული მატრიცა მიიღებს ფორმას

,

საიდანაც x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, ე.ი. X (2) \u003d ((2/3) s 1; s 1).

ამრიგად, ამ წრფივი ოპერატორის საკუთრივ ვექტორები არის (-(2/3)c; c) ფორმის ვექტორები (-5) და ((2/3)c 1; c 1) ფორმის ყველა ვექტორი. საკუთარი მნიშვნელობა 7.

შეიძლება დადასტურდეს, რომ A ოპერატორის მატრიცა, რომელიც შედგება მისი საკუთრივვექტორებისგან, დიაგონალურია და აქვს ფორმა:

,

სადაც l i არის ამ მატრიცის საკუთარი მნიშვნელობები.

პირიქითაც მართალია: თუ მატრიცა A ზოგიერთ საფუძველში დიაგონალურია, მაშინ ამ საფუძვლის ყველა ვექტორი იქნება ამ მატრიცის საკუთრივ ვექტორები.

ასევე შეიძლება დადასტურდეს, რომ თუ წრფივ ოპერატორს აქვს n წყვილი განსხვავებული საკუთარი მნიშვნელობები, მაშინ შესაბამისი საკუთრივექტორები წრფივად დამოუკიდებელია და ამ ოპერატორის მატრიცას შესაბამის ბაზაზე აქვს დიაგონალური ფორმა.

ეს ავხსნათ წინა მაგალითით. ავიღოთ თვითნებური არანულოვანი მნიშვნელობები c და c 1 , მაგრამ ისეთი, რომ ვექტორები X (1) და X (2) წრფივად დამოუკიდებელი იყოს, ე.ი. საფუძველს შექმნიდა. მაგალითად, მოდით c \u003d c 1 \u003d 3, შემდეგ X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

მოდით გადავამოწმოთ ამ ვექტორების წრფივი დამოუკიდებლობა:

12 ≠ 0. ამ ახალ საფუძველზე, A მატრიცა მიიღებს A * = ფორმას.

ამის დასადასტურებლად ვიყენებთ ფორმულას A * = C -1 AC. ჯერ ვიპოვოთ C -1.

C -1 = ;

კვადრატული ფორმები

კვადრატული ფორმა f (x 1, x 2, x n) n ცვლადიდან ეწოდება ჯამი, რომლის თითოეული წევრი არის ან ერთ-ერთი ცვლადის კვადრატი, ან ორი განსხვავებული ცვლადის ნამრავლი, აღებული გარკვეული კოეფიციენტით: f (x 1 , x 2, x n) = (a ij = a ji).

მატრიცა A, რომელიც შედგება ამ კოეფიციენტებისგან, ე.წ მატრიცაკვადრატული ფორმა. ყოველთვის არის სიმეტრიულიმატრიცა (ანუ მატრიცა სიმეტრიულია მთავარი დიაგონალის მიმართ, a ij = a ji).

მატრიცული აღნიშვნისას კვადრატულ ფორმას აქვს ფორმა f(X) = X T AX, სადაც

Ნამდვილად

მაგალითად, დავწეროთ კვადრატული ფორმა მატრიცის სახით.

ამისათვის ჩვენ ვპოულობთ კვადრატული ფორმის მატრიცას. მისი დიაგონალური ელემენტები უდრის კოეფიციენტებს ცვლადების კვადრატებზე, ხოლო დარჩენილი ელემენტები უდრის კვადრატული ფორმის შესაბამისი კოეფიციენტების ნახევარს. Ისე

მოდით, X ცვლადების მატრიცა-სვეტი მივიღოთ მატრიცა-სვეტის Y არადეგენერაციული წრფივი გარდაქმნით, ე.ი. X = CY, სადაც C არის n რიგის არადეგენერირებული მატრიცა. მაშინ კვადრატული ფორმა f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

ამრიგად, C არადეგენერაციული წრფივი ტრანსფორმაციის დროს კვადრატული ფორმის მატრიცა იღებს ფორმას: A * = C T AC.

მაგალითად, ვიპოვოთ კვადრატული ფორმა f(y 1, y 2) მიღებული კვადრატული ფორმიდან f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 წრფივი გარდაქმნით.

კვადრატული ფორმა ეწოდება კანონიკური(Მას აქვს კანონიკური შეხედულება) თუ მისი ყველა კოეფიციენტი a ij = 0 i ≠ j-სთვის, ე.ი.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

მისი მატრიცა დიაგონალურია.

თეორემა(მტკიცებულება აქ არ არის მოცემული). ნებისმიერი კვადრატული ფორმა შეიძლება შემცირდეს კანონიკურ ფორმამდე არადეგენერაციული ხაზოვანი ტრანსფორმაციის გამოყენებით.

მაგალითად, კანონიკურ ფორმამდე მივიყვანოთ კვადრატული ფორმა
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

ამისათვის ჯერ აირჩიეთ x 1 ცვლადის სრული კვადრატი:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

ახლა ჩვენ ვირჩევთ სრულ კვადრატს x 2 ცვლადისთვის:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

შემდეგ არადეგენერაციული წრფივი ტრანსფორმაცია y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 და y 3 \u003d x 3 მოაქვს ამ კვადრატულ ფორმას კანონიკურ ფორმამდე f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

გაითვალისწინეთ, რომ კვადრატული ფორმის კანონიკური ფორმა ორაზროვნად არის განსაზღვრული (იგივე კვადრატული ფორმა კანონიკურ ფორმამდე სხვადასხვა გზით შეიძლება შემცირდეს). თუმცა, სხვადასხვა მეთოდით მიღებულ კანონიკურ ფორმებს არაერთი საერთო თვისება აქვთ. კერძოდ, კვადრატული ფორმის დადებითი (უარყოფითი) კოეფიციენტების მქონე ტერმინების რაოდენობა არ არის დამოკიდებული იმაზე, თუ როგორ მცირდება ფორმა ამ ფორმამდე (მაგალითად, განხილულ მაგალითში ყოველთვის იქნება ორი უარყოფითი და ერთი დადებითი კოეფიციენტი). ამ თვისებას კვადრატული ფორმების ინერციის კანონი ეწოდება.

მოდით გადავამოწმოთ ეს იგივე კვადრატული ფორმის კანონიკურ ფორმაზე სხვაგვარად შემცირებით. დავიწყოთ ტრანსფორმაცია x 2 ცვლადით:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, სადაც y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 და y 3 = x 1. აქ უარყოფითი კოეფიციენტი -3 y 1-ზე და ორი დადებითი კოეფიციენტი 3 და 2 y 2 და y 3-ზე (და სხვა მეთოდის გამოყენებით მივიღეთ უარყოფითი კოეფიციენტი (-5) y 2-ზე და ორი დადებითი კოეფიციენტი: 2 y 1-ზე. და 1/20 y 3-ისთვის).

აქვე უნდა აღინიშნოს, რომ კვადრატული ფორმის მატრიცის რანგი, ე.წ კვადრატული ფორმის წოდება, უდრის კანონიკური ფორმის არანულოვანი კოეფიციენტების რაოდენობას და არ იცვლება წრფივი გარდაქმნებისას.

კვადრატული ფორმა f(X) ეწოდება დადებითად (უარყოფითი) გარკვეულითუ ცვლადის ყველა მნიშვნელობისთვის, რომლებიც ერთდროულად არ არის ნულის ტოლი, ეს დადებითია, ე.ი. f(X) > 0 (უარყოფითი, ე.ი.
f(X)< 0).

მაგალითად, კვადრატული ფორმა f 1 (X) \u003d x 1 2 + x 2 2 არის დადებითი განსაზღვრული, რადგან არის კვადრატების ჯამი და კვადრატული ფორმა f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 არის უარყოფითი განსაზღვრული, რადგან წარმოადგენს ის შეიძლება წარმოდგენილი იყოს როგორც f 2 (X) \u003d - (x 1 - x 2) 2.

უმეტეს პრაქტიკულ სიტუაციებში, გარკვეულწილად უფრო რთულია კვადრატული ფორმის ნიშან-განსაზღვრულის დადგენა, ამიტომ ამისთვის გამოიყენება შემდეგი თეორემებიდან ერთ-ერთი (ჩვენ ვაყალიბებთ მათ მტკიცებულებების გარეშე).

თეორემა. კვადრატული ფორმა არის დადებითი (უარყოფითი) განსაზღვრული, თუ და მხოლოდ იმ შემთხვევაში, თუ მისი მატრიცის ყველა საკუთარი მნიშვნელობა დადებითია (უარყოფითი).

თეორემა(სილვესტერის კრიტერიუმი). კვადრატული ფორმა დადებითია განსაზღვრული, თუ და მხოლოდ იმ შემთხვევაში, თუ ამ ფორმის მატრიცის ყველა ძირითადი მინორი დადებითია.

მაიორი (კუთხა) მინორი n-ე რიგის A მატრიცის k-ე წესრიგს ეწოდება მატრიცის განმსაზღვრელი, რომელიც შედგება A (A) მატრიცის პირველი k რიგებისა და სვეტებისგან.

გაითვალისწინეთ, რომ უარყოფით-განსაზღვრული კვადრატული ფორმებისთვის, ძირითადი მცირეწლოვანთა ნიშნები ერთმანეთს ენაცვლება, ხოლო პირველი რიგის მინორი უარყოფითი უნდა იყოს.

მაგალითად, ჩვენ განვიხილავთ კვადრატულ ფორმას f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 ნიშნის განსაზღვრულობისთვის.

= (2 - ლ)*
*(3 - ლ) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. ამიტომ, კვადრატული ფორმა დადებითი განსაზღვრულია.

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 = 2 > 0. მეორე რიგის მთავარი მინორი D 2 = = 6 - 4 = 2 > 0. ამიტომ, სილვესტერის კრიტერიუმის მიხედვით, კვადრატული ფორმა დადებითი განსაზღვრულია.

ჩვენ განვიხილავთ ნიშნის განსაზღვრულობის სხვა კვადრატულ ფორმას, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

მეთოდი 1. ავაშენოთ А = კვადრატული ფორმის მატრიცა. დამახასიათებელ განტოლებას ექნება ფორმა = (-2 - ლ)*
*(-3 - ლ) - 4 = (6 + 2ლ + 3ლ + ლ 2) - 4 = ლ 2 + 5ლ + 2 = 0; D = 25 - 8 = 17;
. ამიტომ, კვადრატული ფორმა უარყოფითი განსაზღვრულია.

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. მაშასადამე, სილვესტერის კრიტერიუმის მიხედვით, კვადრატული ფორმა უარყოფითი განსაზღვრულია (ძირითადი არასრულწლოვანთა ნიშნები ერთმანეთს ენაცვლება, დაწყებული მინუსიდან).

და როგორც სხვა მაგალითი, ჩვენ განვიხილავთ კვადრატულ ფორმას f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 ნიშნის განსაზღვრულობისთვის.

მეთოდი 1. ავაშენოთ А = კვადრატული ფორმის მატრიცა. დამახასიათებელ განტოლებას ექნება ფორმა = (2 - ლ)*
*(-3 - ლ) - 4 = (-6 - 2ლ + 3ლ + ლ 2) - 4 = ლ 2 + ლ - 10 = 0; D = 1 + 40 = 41;
.

ამ რიცხვებიდან ერთი უარყოფითია, მეორე კი დადებითი. საკუთრივ მნიშვნელობების ნიშნები განსხვავებულია. მაშასადამე, კვადრატული ფორმა არ შეიძლება იყოს არც უარყოფითი და არც დადებითი განსაზღვრული, ე.ი. ეს კვადრატული ფორმა არ არის ნიშან-განსაზღვრული (მას შეუძლია მიიღოს ნებისმიერი ნიშნის მნიშვნელობები).

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 = 2 > 0. მეორე რიგის მთავარი მინორი D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

პირველი ნაწილი ასახავს დებულებებს, რომლებიც მინიმალურად აუცილებელია ქიმიომეტრიის გასაგებად, ხოლო მეორე ნაწილი შეიცავს ფაქტებს, რომლებიც უნდა იცოდეთ მულტივარიანტული ანალიზის მეთოდების უფრო ღრმად გასაგებად. პრეზენტაცია ილუსტრირებულია Excel-ის სამუშაო წიგნში გაკეთებული მაგალითებით. მატრიცა.xlsრომელიც ახლავს ამ დოკუმენტს.

მაგალითების ბმულები მოთავსებულია ტექსტში Excel-ის ობიექტების სახით. ეს მაგალითები აბსტრაქტული ხასიათისაა და არანაირად არ არის დაკავშირებული ანალიტიკური ქიმიის პრობლემებთან. ქიმიომეტრიაში მატრიცული ალგებრის გამოყენების რეალური მაგალითები განხილულია სხვა ტექსტებში, რომლებიც ეძღვნება სხვადასხვა ქიმიომეტრიულ გამოყენებას.

ანალიზურ ქიმიაში ჩატარებული გაზომვების უმეტესობა არ არის პირდაპირი, მაგრამ არაპირდაპირი. ეს ნიშნავს, რომ ექსპერიმენტში სასურველი ანალიზის C მნიშვნელობის ნაცვლად (კონცენტრაცია) მიიღება სხვა მნიშვნელობა. x(სიგნალი) დაკავშირებული, მაგრამ არა ტოლი C-სთან, ე.ი. x(C) ≠ C. როგორც წესი, დამოკიდებულების ტიპი x(C) უცნობია, მაგრამ საბედნიეროდ ანალიტიკურ ქიმიაში გაზომვების უმეტესობა პროპორციულია. ეს ნიშნავს, რომ როგორც C-ის კონცენტრაცია აჯერ, სიგნალი X გაიზრდება იმავე რაოდენობით., ე.ი. x(აგ) = ნაჯახი(C). გარდა ამისა, სიგნალები ასევე არის დანამატი, ასე რომ, სიგნალი ნიმუშიდან, რომელიც შეიცავს ორ ნივთიერებას C 1 და C 2 კონცენტრაციით, ტოლი იქნება თითოეული კომპონენტის სიგნალების ჯამის, ე.ი. x(C1 + C2) = x(C1)+ x(C2). პროპორციულობა და მიმატება ერთად იძლევა წრფივობა. მრავალი მაგალითის მოყვანა შეიძლება წრფივობის პრინციპის საილუსტრაციოდ, მაგრამ საკმარისია მოვიხსენიოთ ორი ყველაზე თვალსაჩინო მაგალითი - ქრომატოგრაფია და სპექტროსკოპია. მეორე თვისება, რომელიც თან ახლავს ექსპერიმენტს ანალიზურ ქიმიაში არის მრავალარხიანი. თანამედროვე ანალიტიკური აღჭურვილობა ერთდროულად ზომავს სიგნალებს მრავალი არხისთვის. მაგალითად, სინათლის გადაცემის ინტენსივობა იზომება ერთდროულად რამდენიმე ტალღის სიგრძეზე, ე.ი. დიაპაზონი. ამიტომ, ექსპერიმენტში საქმე გვაქვს მრავალფეროვან სიგნალებთან x 1 , x 2 ,...., x n შესწავლილ სისტემაში არსებული ნივთიერებების C 1 , C 2 , ..., C m კონცენტრაციების ერთობლიობის დამახასიათებელი.

ბრინჯი. 1 სპექტრი

ასე რომ, ანალიტიკურ ექსპერიმენტს ახასიათებს წრფივი და მრავალგანზომილებიანი. ამიტომ, მოსახერხებელია ექსპერიმენტული მონაცემების ვექტორებად და მატრიცებად განხილვა და მათი მანიპულირება მატრიცული ალგებრის აპარატის გამოყენებით. ამ მიდგომის ნაყოფიერება ილუსტრირებულია მაგალითით, რომელიც გვიჩვენებს სამ სპექტრს, აღებული 200 ტალღის სიგრძეზე 4000-დან 4796 სმ–1-მდე. Პირველი ( x 1) და მეორე ( x 2) სპექტრები მიიღეს სტანდარტული ნიმუშებისთვის, რომლებშიც ცნობილია ორი ნივთიერების კონცენტრაცია A და B: პირველ ნიმუშში [A] = 0,5, [B] = 0,1 და მეორე ნიმუშში [A] = 0,2, [ B] = 0.6. რა შეიძლება ითქვას ახალ, უცნობ ნიმუშზე, რომლის სპექტრი მითითებულია x 3 ?

განვიხილოთ სამი ექსპერიმენტული სპექტრი x 1 , x 2 და x 3, როგორც 200 განზომილების სამი ვექტორი. წრფივი ალგებრის გამოყენებით, შეგვიძლია ამის ჩვენება მარტივად x 3 = 0.1 x 1 +0.3 x 2, ასე რომ, მესამე ნიმუში აშკარად შეიცავს მხოლოდ A და B ნივთიერებებს კონცენტრაციებში [A] = 0,5×0,1 + 0,2×0,3 = 0,11 და [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. ძირითადი ინფორმაცია

1.1 მატრიცები

მატრიცამაგალითად, რიცხვების მართკუთხა ცხრილს უწოდებენ

ბრინჯი. 2 მატრიცა

მატრიცები აღინიშნება დიდი დიდი ასოებით ( ა), ხოლო მათი ელემენტები - შესაბამისი მცირე ასოებით ინდექსებით, ე.ი. ა ij . პირველი ინდექსი ნომრავს რიგებს, მეორე კი სვეტებს. ქიმიომეტრიაში ჩვეულებრივია ინდექსის მაქსიმალური მნიშვნელობის დანიშვნა იმავე ასოებით, როგორც თავად ინდექსი, მაგრამ დიდი ასოებით. ამიტომ, მატრიცა აასევე შეიძლება დაიწეროს როგორც ( ა იჯ , მე = 1,..., მე; ჯ = 1,..., ჯ). მაგალითის მატრიცისთვის მე = 4, ჯ= 3 და ა 23 = −7.5.

რიცხვების წყვილი მედა ჯეწოდება მატრიცის განზომილება და აღინიშნება როგორც მე× ჯ. მატრიცის მაგალითი ქიმიომეტრიაში არის სპექტრების ნაკრები, რომელიც მიღებულია მენიმუშები ჯტალღის სიგრძე.

1.2. უმარტივესი ოპერაციები მატრიცებით

მატრიცებს შეუძლიათ რიცხვებით გამრავლება. ამ შემთხვევაში, თითოეული ელემენტი მრავლდება ამ რიცხვზე. Მაგალითად -

ბრინჯი. 3 მატრიცის გამრავლება რიცხვზე

ერთი და იგივე განზომილების ორი მატრიცა შეიძლება იყოს ელემენტის მიხედვით ჩამოყაროსდა გამოკლება. Მაგალითად,

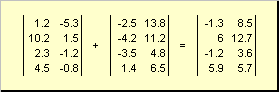
ბრინჯი. 4 მატრიცის დამატება

რიცხვზე გამრავლებისა და შეკრების შედეგად მიიღება ერთი და იგივე განზომილების მატრიცა.

ნულოვანი მატრიცა არის მატრიცა, რომელიც შედგება ნულებისაგან. დანიშნულია ო. აშკარაა რომ ა+ო = ა, ა−ა = ოდა 0 ა = ო.

მატრიცას შეუძლია გადატანა. ამ ოპერაციის დროს მატრიცა ტრიალდება, ე.ი. რიგები და სვეტები იცვლება. ტრანსპოზიცია მითითებულია ტირეთი, ა" ან ინდექსი ატ . ამრიგად, თუ ა = {ა იჯ , მე = 1,..., მე; ჯ = 1,...,ჯ), შემდეგ ა t = ( ა ჯი , ჯ = 1,...,ჯ; i = 1,..., მე). მაგალითად

ბრინჯი. 5 მატრიცის ტრანსპოზიცია

აშკარაა, რომ ( აუ) t = ა, (ა+ბ) ტ = ა t+ ბტ .

1.3. მატრიცული გამრავლება

მატრიცებს შეუძლიათ გამრავლება, მაგრამ მხოლოდ იმ შემთხვევაში, თუ მათ აქვთ შესაბამისი ზომები. რატომ არის ეს ასე, გასაგები იქნება განმარტებიდან. მატრიცული პროდუქტი ა, განზომილება მე× კდა მატრიცები ბ, განზომილება კ× ჯ, ეწოდება მატრიცა C, განზომილება მე× ჯ, რომლის ელემენტებია რიცხვები

ამრიგად, პროდუქტისთვის ABაუცილებელია მარცხენა მატრიცაში სვეტების რაოდენობა ატოლი იყო მარჯვენა მატრიცის მწკრივების რაოდენობას ბ. მატრიცული პროდუქტის მაგალითი -

ნახ.6 მატრიცების პროდუქტი

მატრიცის გამრავლების წესი შეიძლება ჩამოყალიბდეს შემდეგნაირად. მატრიცის ელემენტის პოვნა Cგზაჯვარედინზე დგას მე-მე ხაზი და ჯ- ე სვეტი ( გ იჯ) უნდა გამრავლდეს ელემენტად ელემენტზე მე- პირველი მატრიცის რიგი აზე ჯ-მეორე მატრიცის მე-ე სვეტი ბდა დაამატეთ ყველა შედეგი. ასე რომ, ნაჩვენები მაგალითში, ელემენტი მესამე მწკრივიდან და მეორე სვეტიდან მიიღება, როგორც მესამე რიგის ელემენტების პროდუქტთა ჯამი. ადა მეორე სვეტი ბ

ნახ.7 მატრიცების ნამრავლის ელემენტი

მატრიცების ნამრავლი დამოკიდებულია თანმიმდევრობაზე, ე.ი. AB ≠ BA, ყოველ შემთხვევაში განზომილებიანი მიზეზების გამო. ნათქვამია, რომ ის არაკომუტაციურია. თუმცა, მატრიცების ნამრავლი ასოციაციურია. Ეს ნიშნავს, რომ ABC = (AB)C = ა(ძვ.წ). უფრო მეტიც, ის ასევე გამანაწილებელია, ე.ი. ა(ბ+C) = AB+AC. აშკარაა რომ AO = ო.

1.4. კვადრატული მატრიცები

თუ მატრიცის სვეტების რაოდენობა უდრის მისი რიგების რაოდენობას ( მე = J=N), მაშინ ასეთ მატრიცას კვადრატი ეწოდება. ამ განყოფილებაში განვიხილავთ მხოლოდ ასეთ მატრიცებს. ამ მატრიცებს შორის შეიძლება გამოვყოთ სპეციალური თვისებების მქონე მატრიცები.

Მარტოხელამატრიცა (აღნიშნული მედა ზოგჯერ ე) არის მატრიცა, რომელშიც ყველა ელემენტი ნულის ტოლია, გარდა დიაგონალურისა, რომელიც უდრის 1-ს, ე.ი.

ცხადია AI = ი.ა = ა.

მატრიცა ე.წ დიაგონალითუ მისი ყველა ელემენტი, გარდა დიაგონალისა ( ა ii) ნულის ტოლია. მაგალითად

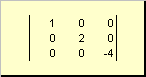
ბრინჯი. 8 დიაგონალური მატრიცა

მატრიცა ამოუწოდა ზედა სამკუთხა, თუ მისი ყველა ელემენტი, რომელიც მდებარეობს დიაგონალის ქვემოთ, ნულის ტოლია, ე.ი. ა იჯ= 0, at მე>ჯ. მაგალითად

ბრინჯი. 9 ზედა სამკუთხა მატრიცა

ქვედა სამკუთხა მატრიცა განისაზღვრება ანალოგიურად.

მატრიცა ადაურეკა სიმეტრიული, თუ ა t = ა. Სხვა სიტყვებით ა იჯ = ა ჯი. მაგალითად

ბრინჯი. 10 სიმეტრიული მატრიცა

მატრიცა ადაურეკა ორთოგონალური, თუ

ატ ა = აა t = მე.

მატრიცა ე.წ ნორმალურითუ

1.5. კვალი და განმსაზღვრელი

მიჰყვებაკვადრატული მატრიცა ა(აღნიშნულია Tr( ა) ან Sp( ა)) არის მისი დიაგონალური ელემენტების ჯამი,

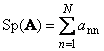
Მაგალითად,

ბრინჯი. 11 მატრიცული კვალი

აშკარაა რომ

Sp(α ა) = α Sp( ა) და

Sp( ა+ბ) = Sp( ა)+ Sp( ბ).

ამის ჩვენება შეიძლება

Sp( ა) = Sp( ა t), Sp( მე) = ნ,

და ასევე ის

Sp( AB) = Sp( BA).

კვადრატული მატრიცის კიდევ ერთი მნიშვნელოვანი მახასიათებელია მისი განმსაზღვრელი(აღნიშნულია det ( ა)). დეტერმინანტის განმარტება ზოგად შემთხვევაში საკმაოდ რთულია, ამიტომ დავიწყებთ უმარტივესი ვარიანტით - მატრიცით აგანზომილება (2×2). მერე

(3×3) მატრიცისთვის დეტერმინანტი ტოლი იქნება

მატრიცის შემთხვევაში ( ნ× ნ) განმსაზღვრელი გამოითვლება ჯამის სახით 1 2 3 ... ნ= ნ! ტერმინები, რომელთაგან თითოეული ტოლია

ინდექსები კ 1 , კ 2 ,..., კ ნგანისაზღვრება, როგორც ყველა შესაძლო მოწესრიგებული პერმუტაცია რრიცხვები კომპლექტში (1, 2, ... , ნ). მატრიცის დეტერმინანტის გამოთვლა რთული პროცედურაა, რომელიც პრაქტიკაში ხორციელდება სპეციალური პროგრამების გამოყენებით. Მაგალითად,

ბრინჯი. 12 მატრიცის განმსაზღვრელი

ჩვენ აღვნიშნავთ მხოლოდ აშკარა თვისებებს:

დეტ( მე) = 1, დეტ( ა) = დეტ( აუ),

დეტ( AB) = დეტ( ა)დეტ( ბ).

1.6. ვექტორები

თუ მატრიცას აქვს მხოლოდ ერთი სვეტი ( ჯ= 1), მაშინ ასეთი ობიექტი ეწოდება ვექტორი. უფრო ზუსტად, სვეტის ვექტორი. მაგალითად

ასევე შეიძლება ჩაითვალოს ერთი მწკრივისაგან შემდგარი მატრიცები, მაგალითად

ეს ობიექტიც არის ვექტორი, მაგრამ მწკრივის ვექტორი. მონაცემების გაანალიზებისას მნიშვნელოვანია გვესმოდეს, რომელ ვექტორებთან გვაქვს საქმე – სვეტებთან თუ მწკრივებთან. ასე რომ, ერთი ნიმუშისთვის აღებული სპექტრი შეიძლება ჩაითვალოს მწკრივის ვექტორად. შემდეგ სპექტრალური ინტენსივობის ნაკრები ყველა ნიმუშისთვის ტალღის სიგრძის გარკვეულ ნაწილზე უნდა განიხილებოდეს, როგორც სვეტის ვექტორი.

ვექტორის განზომილება არის მისი ელემენტების რაოდენობა.

ნათელია, რომ ნებისმიერი სვეტის ვექტორი შეიძლება გარდაიქმნას მწკრივის ვექტორად ტრანსპოზიციით, ე.ი.

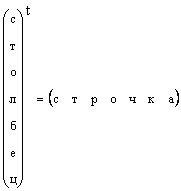
იმ შემთხვევებში, როდესაც ვექტორის ფორმა კონკრეტულად არ არის მითითებული, მაგრამ უბრალოდ ვექტორია ნათქვამი, მაშინ ისინი გულისხმობენ სვეტის ვექტორს. ჩვენც დავიცავთ ამ წესს. ვექტორი აღინიშნება მცირე ასოებით. ნულოვანი ვექტორი არის ვექტორი, რომლის ყველა ელემენტი ნულის ტოლია. იგი აღინიშნება 0 .

1.7. უმარტივესი ოპერაციები ვექტორებით

ვექტორები შეიძლება დაემატოს და გამრავლდეს რიცხვებით ისევე, როგორც მატრიცები. Მაგალითად,

ბრინჯი. 13 მოქმედებები ვექტორებით

ორი ვექტორი xდა წდაურეკა კოლინარული, თუ არსებობს α რიცხვი ისეთი, რომ

1.8. ვექტორების პროდუქტები

ერთი და იგივე განზომილების ორი ვექტორი ნშეიძლება გამრავლდეს. იყოს ორი ვექტორი x = (x 1 , x 2 ,...,xნ) ტ და წ = (წ 1 , წ 2 ,...,წნ) ტ. გამრავლების წესით „სტრიქონი სვეტად“ ხელმძღვანელობით, შეგვიძლია მათგან ორი პროდუქტის გაკეთება: xტ წდა xyტ . პირველი ნამუშევარი

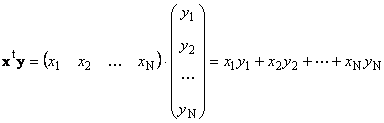
დაურეკა სკალარულიან შიდა. მისი შედეგი არის რიცხვი. ის ასევე იყენებს აღნიშვნას ( x,წ)= xტ წ. Მაგალითად,

ბრინჯი. 14 შიდა (სკალარული) პროდუქტი

მეორე ნამუშევარი

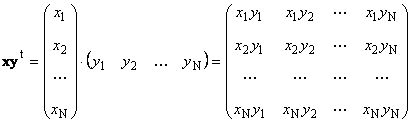
დაურეკა გარე. მისი შედეგი არის განზომილების მატრიცა ( ნ× ნ). Მაგალითად,

ბრინჯი. 15 გარე პროდუქტი

ვექტორებს, რომელთა სკალარული ნამრავლი ნულის ტოლია, ეწოდება ორთოგონალური.

1.9. ვექტორული ნორმა

ვექტორის სკალარული ნამრავლს თავისთან ერთად ეწოდება სკალარული კვადრატი. ეს ღირებულება

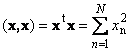
განსაზღვრავს კვადრატს სიგრძევექტორი x. სიგრძის აღსანიშნავად (ასევე ე.წ ნორმავექტორი) გამოიყენება აღნიშვნა

Მაგალითად,

ბრინჯი. 16 ვექტორული ნორმა

ერთეულის სიგრძის ვექტორი (|| x|| = 1) ეწოდება ნორმალიზებულს. არანულოვანი ვექტორი ( x ≠ 0 ) შეიძლება ნორმალიზდეს სიგრძეზე გაყოფით, ე.ი. x = ||x|| (x/||x||) = ||x|| ე. Აქ ე = x/||x|| არის ნორმალიზებული ვექტორი.

ვექტორებს უწოდებენ ორთონორმალურს, თუ ისინი ყველა ნორმალიზებულია და წყვილში ორთოგონალურია.

1.10. კუთხე ვექტორებს შორის

სკალარული პროდუქტი განსაზღვრავს და ინექციაφ ორ ვექტორს შორის xდა წ

თუ ვექტორები ორთოგონალურია, მაშინ cosφ = 0 და φ = π/2, ხოლო თუ ისინი ხაზოვანია, მაშინ cosφ = 1 და φ = 0.

1.11. მატრიცის ვექტორული წარმოდგენა

თითოეული მატრიცა აზომა მე× ჯშეიძლება წარმოდგენილი იყოს ვექტორების სიმრავლის სახით

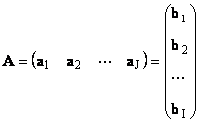
აქ თითოეული ვექტორი ა ჯარის ჯ- სვეტისა და მწკრივის ვექტორი ბ მეარის მე- მატრიცის რიგი ა

1.12. ხაზობრივად დამოკიდებული ვექტორები

იგივე განზომილების ვექტორები ( ნ) შეიძლება დაემატოს და გამრავლდეს რიცხვზე, ისევე როგორც მატრიცები. შედეგი არის იგივე განზომილების ვექტორი. მოდით არსებობდეს ერთი და იგივე განზომილების რამდენიმე ვექტორი x 1 , x 2 ,...,x K და რიცხვების იგივე რაოდენობა α α 1 , α 2 ,...,α კ. ვექტორი

წ= α 1 x 1 + α 2 x 2 +...+α კ x კ

დაურეკა ხაზოვანი კომბინაციავექტორები x კ .

თუ არსებობს ასეთი არანულოვანი რიცხვები α კ ≠ 0, კ = 1,..., კ, რა წ = 0 , მაშინ ვექტორების ასეთი ნაკრები x კდაურეკა წრფივად დამოკიდებული. წინააღმდეგ შემთხვევაში, ვექტორებს უწოდებენ წრფივად დამოუკიდებელ. მაგალითად, ვექტორები x 1 = (2, 2) ტ და x 2 = (−1, −1) t არის წრფივი დამოკიდებული, ვინაიდან x 1 +2x 2 = 0

1.13. მატრიცის რანგი

განვიხილოთ კომპლექტი კვექტორები x 1 , x 2 ,...,x კზომები ნ. ვექტორთა ამ სისტემის რანგი არის ხაზობრივად დამოუკიდებელი ვექტორების მაქსიმალური რაოდენობა. მაგალითად კომპლექტში

არსებობს მხოლოდ ორი წრფივად დამოუკიდებელი ვექტორი, მაგალითად x 1 და x 2, ამიტომ მისი წოდებაა 2.

ცხადია, თუ ნაკრებში მეტი ვექტორია, ვიდრე მათი განზომილება ( კ>ნ), მაშინ ისინი აუცილებლად წრფივად არიან დამოკიდებული.

მატრიცის რანგი(მინიშნება წოდებით ( ა)) არის ვექტორთა სისტემის რანგი, საიდანაც იგი შედგება. მიუხედავად იმისა, რომ ნებისმიერი მატრიცა შეიძლება წარმოდგენილი იყოს ორი გზით (სვეტის ვექტორები ან მწკრივის ვექტორები), ეს გავლენას არ ახდენს რანგის მნიშვნელობაზე, რადგან

1.14. ინვერსიული მატრიცა

კვადრატული მატრიცა აეწოდება არადეგენერატი, თუ მას აქვს უნიკალური საპირისპირომატრიცა ა-1, განისაზღვრება პირობებით

აა −1 = ა −1 ა = მე.

ინვერსიული მატრიცა არ არსებობს ყველა მატრიცისთვის. არადეგენერატობის აუცილებელი და საკმარისი პირობაა

დეტ( ა) ≠ 0 ან წოდება( ა) = ნ.

მატრიცის ინვერსია რთული პროცედურაა, რომლისთვისაც არსებობს სპეციალური პროგრამები. Მაგალითად,

ბრინჯი. 17 მატრიცის ინვერსია

ჩვენ ვაძლევთ ფორმულებს უმარტივესი შემთხვევისთვის - მატრიცები 2 × 2

თუ მატრიცები ადა ბარიან არადეგენერატები, მაშინ

(AB) −1 = ბ −1 ა −1 .

1.15. ფსევდო-ინვერსიული მატრიცა

თუ მატრიცა აარის გადაგვარებული და ინვერსიული მატრიცა არ არსებობს, მაშინ ზოგიერთ შემთხვევაში შეიძლება გამოიყენო ფსევდოინვერსიამატრიცა, რომელიც განისაზღვრება, როგორც ასეთი მატრიცა ა+ ეს

აა + ა = ა.

ფსევდო-ინვერსიული მატრიცა არ არის ერთადერთი და მისი ფორმა დამოკიდებულია მშენებლობის მეთოდზე. მაგალითად, მართკუთხა მატრიცისთვის შეგიძლიათ გამოიყენოთ მურ-პენროსის მეთოდი.

თუ სვეტების რაოდენობა მწკრივების რაოდენობაზე ნაკლებია, მაშინ

ა + =(ატ ა) −1 ატ

Მაგალითად,

ბრინჯი. 17a ფსევდო მატრიცის ინვერსია

თუ სვეტების რაოდენობა სტრიქონების რაოდენობაზე მეტია, მაშინ

ა + =ა t ( ააუ) −1

1.16. ვექტორის გამრავლება მატრიცით

ვექტორი xშეიძლება გამრავლდეს მატრიცით აშესაფერისი განზომილება. ამ შემთხვევაში სვეტის ვექტორი მრავლდება მარჯვნივ Ნაჯახი, და ვექტორული სტრიქონი არის მარცხნივ xტ ა. თუ ვექტორის განზომილება ჯდა მატრიცის განზომილება მე× ჯმაშინ შედეგი არის განზომილების ვექტორი მე. Მაგალითად,

ბრინჯი. 18 ვექტორ-მატრიცული გამრავლება

თუ მატრიცა ა- კვადრატი ( მე× მე), შემდეგ ვექტორი წ = Ნაჯახიაქვს იგივე ზომები, რაც x. აშკარაა რომ

ა(α 1 x 1 + α 2 x 2) = α 1 Ნაჯახი 1 + α 2 Ნაჯახი 2 .

ამიტომ მატრიცები შეიძლება ჩაითვალოს ვექტორების წრფივ გარდაქმნად. Კერძოდ x = x, ოქსი = 0 .

2. დამატებითი ინფორმაცია

2.1. წრფივი განტოლებათა სისტემები

დაე იყოს ა- მატრიცის ზომა მე× ჯ, ა ბ- განზომილების ვექტორი ჯ. განვიხილოთ განტოლება

Ნაჯახი = ბ

ვექტორთან მიმართებაში x, ზომები მე. არსებითად, ეს არის სისტემა მეწრფივი განტოლებები ჯუცნობი x 1 ,...,x ჯ. გამოსავალი არსებობს თუ და მხოლოდ მაშინ

წოდება ( ა) = წოდება ( ბ) = რ,

სადაც ბარის გაფართოებული განზომილების მატრიცა მე×( J+1) რომელიც შედგება მატრიცისგან ა, შეფუთული სვეტით ბ, ბ = (ა ბ). წინააღმდეგ შემთხვევაში, განტოლებები არათანმიმდევრულია.

Თუ რ = მე = ჯ, მაშინ გამოსავალი უნიკალურია

x = ა −1 ბ.

Თუ რ < მე, მაშინ არსებობს მრავალი განსხვავებული ამონახსნი, რომელიც შეიძლება გამოიხატოს წრფივი კომბინაციის სახით ჯ−რვექტორები. ერთგვაროვანი განტოლებათა სისტემა Ნაჯახი = 0 კვადრატული მატრიცით ა (ნ× ნაქვს არატრივიალური გადაწყვეტა ( x ≠ 0 ) თუ და მხოლოდ იმ შემთხვევაში ( ა) = 0. თუ რ= წოდება ( ა)<ნ, მაშინ არის ნ−რხაზოვანი დამოუკიდებელი გადაწყვეტილებები.

2.2. ორხაზოვანი და კვადრატული ფორმები

Თუ აარის კვადრატული მატრიცა და xდა წ- შესაბამისი განზომილების ვექტორები, შემდეგ ფორმის სკალარული ნამრავლი xტ აიდაურეკა ორმხრივიმატრიცით განსაზღვრული ფორმა ა. ზე x = წგამოხატულება xტ Ნაჯახიდაურეკა კვადრატულიფორმა.

2.3. დადებითი განსაზღვრული მატრიცები

კვადრატული მატრიცა ადაურეკა დადებითი გარკვეული, თუ რომელიმე არანულოვანი ვექტორისთვის x ≠ 0 ,

xტ Ნაჯახი > 0.

The უარყოფითი (xტ Ნაჯახი < 0), არაუარყოფითი (xტ Ნაჯახი≥ 0) და არაპოზიტიური (xტ Ნაჯახი≤ 0) გარკვეული მატრიცები.

2.4. ქოლესკის დაშლა

თუ სიმეტრიული მატრიცა აარის დადებითი განსაზღვრული, მაშინ არის უნიკალური სამკუთხა მატრიცა Uდადებითი ელემენტებით, რისთვისაც

ა = Uტ U.

Მაგალითად,

ბრინჯი. 19 ქოლესკის დაშლა

2.5. პოლარული დაშლა

დაე იყოს აარის განზომილების არადეგენერაციული კვადრატული მატრიცა ნ× ნ. შემდეგ არის უნიკალური პოლარულიშესრულება

ა = SR,

სადაც სარის არაუარყოფითი სიმეტრიული მატრიცა და რარის ორთოგონალური მატრიცა. მატრიცები სდა რშეიძლება ცალსახად განისაზღვროს:

ს 2 = აატ ან ს = (ააუ) ½ და რ = ს −1 ა = (ააუ) −½ ა.

Მაგალითად,

ბრინჯი. 20 პოლარული დაშლა

თუ მატრიცა აარის გადაგვარებული, მაშინ დაშლა არ არის უნიკალური - კერძოდ: სისევ მარტო, მაგრამ რშეიძლება ბევრი იყოს. პოლარული დაშლა წარმოადგენს მატრიცას აროგორც შეკუმშვის/გაჭიმვის კომბინაცია სდა მოქცევა რ.

2.6. საკუთრივ ვექტორები და საკუთრივ მნიშვნელობები

დაე იყოს აარის კვადრატული მატრიცა. ვექტორი ვდაურეკა საკუთარი ვექტორიმატრიცები ა, თუ

ავ = λ ვ,

სადაც იწოდება რიცხვი λ საკუთარი ღირებულებამატრიცები ა. ამრიგად, ტრანსფორმაცია, რომელსაც მატრიცა ასრულებს ავექტორზე მეტი ვ, მცირდება მარტივ გაჭიმვამდე ან შეკუმშვამდე λ ფაქტორით. საკუთარი ვექტორი გამრავლებამდე განისაზღვრება α ≠ 0 მუდმივზე, ე.ი. თუ ვარის საკუთრივვექტორი, შემდეგ α ვასევე არის საკუთარი ვექტორი.

2.7. საკუთრივ მნიშვნელობები

მატრიცაზე ა, განზომილება ( ნ× ნ) არ შეიძლება იყოს მეტი ნსაკუთარი მნიშვნელობები. ისინი აკმაყოფილებენ დამახასიათებელი განტოლება

დეტ( ა − λ მე) = 0,

რომელიც არის ალგებრული განტოლება ნ- ბრძანება. კერძოდ, 2×2 მატრიცისთვის დამახასიათებელ განტოლებას აქვს ფორმა

Მაგალითად,

ბრინჯი. 21 საკუთრივ მნიშვნელობები

საკუთრივ მნიშვნელობების ნაკრები λ 1 ,..., λ ნმატრიცები ადაურეკა სპექტრი ა.

სპექტრს აქვს სხვადასხვა თვისებები. Კერძოდ

დეტ( ა) = λ 1×...×λ ნ, სპ ( ა) = λ 1 +...+λ ნ.

თვითნებური მატრიცის საკუთრივ მნიშვნელობები შეიძლება იყოს რთული რიცხვები, მაგრამ თუ მატრიცა არის სიმეტრიული ( ა t = ა), მაშინ მისი საკუთრივ მნიშვნელობები რეალურია.

2.8. საკუთრივ ვექტორები

მატრიცაზე ა, განზომილება ( ნ× ნ) არ შეიძლება იყოს მეტი ნსაკუთრივ ვექტორები, რომელთაგან თითოეული შეესაბამება საკუთარ მნიშვნელობას. საკუთარი ვექტორის დასადგენად ვ ნთქვენ უნდა ამოხსნათ ერთგვაროვანი განტოლებების სისტემა

(ა − λ ნ მე)ვ ნ = 0 .

მას აქვს არატრივიალური გადაწყვეტა, რადგან det( A-λ ნ მე) = 0.

Მაგალითად,

ბრინჯი. 22 საკუთრივ ვექტორები

სიმეტრიული მატრიცის საკუთრივვექტორები ორთოგონალურია.

კვადრატული მატრიცის საკუთრივვექტორი არის ის, რომელიც მოცემულ მატრიცზე გამრავლებისას მიიღება კოლინარული ვექტორი. მარტივი სიტყვებით, როდესაც მატრიცა მრავლდება საკუთრივ ვექტორზე, ეს უკანასკნელი იგივე რჩება, მაგრამ მრავლდება რაღაც რიცხვზე.

განმარტება

საკუთარი ვექტორი არის არანულოვანი ვექტორი V, რომელიც კვადრატულ მატრიცზე M-ზე გამრავლებისას იქცევა თავისთავად, გაზრდილი რაღაც λ რიცხვით. ალგებრული აღნიშვნით, ეს ასე გამოიყურება:

M × V = λ × V,

სადაც λ არის M მატრიცის საკუთრივ მნიშვნელობა.

განვიხილოთ რიცხვითი მაგალითი. ჩაწერის მოხერხებულობისთვის მატრიცაში რიცხვები გამოყოფილი იქნება მძიმით. ვთქვათ, გვაქვს მატრიცა:

• M = 0; 4;
• 6; 10.

მოდით გავამრავლოთ იგი სვეტის ვექტორზე:

• V = -2;

მატრიცის სვეტის ვექტორზე გამრავლებისას ასევე ვიღებთ სვეტის ვექტორს. მკაცრი მათემატიკური ენით, 2 × 2 მატრიცის სვეტის ვექტორზე გამრავლების ფორმულა ასე გამოიყურება:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 ნიშნავს M მატრიცის ელემენტს, რომელიც დგას პირველ რიგში და პირველ სვეტში, ხოლო M22 არის ელემენტი, რომელიც მდებარეობს მეორე რიგში და მეორე სვეტში. ჩვენი მატრიცისთვის ეს ელემენტებია M11 = 0, M12 = 4, M21 = 6, M22 10. სვეტის ვექტორისთვის ეს მნიშვნელობებია V11 = –2, V21 = 1. ამ ფორმულის მიხედვით ვიღებთ შემდეგს. კვადრატული მატრიცის ნამრავლის შედეგი ვექტორით:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

მოხერხებულობისთვის ჩვენ ვწერთ სვეტის ვექტორს მწკრივად. ამგვარად, ჩვენ გავამრავლეთ კვადრატული მატრიცა ვექტორზე (-2; 1), შედეგად ვიღებთ ვექტორს (4; -2). ცხადია, ეს არის იგივე ვექტორი, გამრავლებული λ = -2-ზე. ლამბდა ამ შემთხვევაში აღნიშნავს მატრიცის საკუთრივ მნიშვნელობას.

მატრიცის საკუთრივვექტორი არის კოლინარული ვექტორი, ანუ ობიექტი, რომელიც არ იცვლის თავის პოზიციას სივრცეში მატრიცით გამრავლებისას. კოლინარობის ცნება ვექტორულ ალგებრაში გეომეტრიაში პარალელურობის ტერმინის მსგავსია. გეომეტრიულ ინტერპრეტაციაში, კოლინარული ვექტორები არის სხვადასხვა სიგრძის პარალელურად მიმართული სეგმენტები. ევკლიდეს დროიდან ჩვენ ვიცით, რომ ერთ წრფეს აქვს უსასრულო რაოდენობის წრფეები მის პარალელურად, ამიტომ ლოგიკურია ვივარაუდოთ, რომ თითოეულ მატრიცას აქვს უსასრულო რაოდენობის საკუთარი ვექტორები.

წინა მაგალითიდან ჩანს, რომ ორივე (-8; 4), და (16; -8), და (32, -16) შეიძლება იყოს საკუთრივ ვექტორები. ყველა ეს არის კოლინარული ვექტორები, რომლებიც შეესაბამება λ = -2 საკუთრივ მნიშვნელობას. ამ ვექტორებზე თავდაპირველი მატრიცის გამრავლებისას მაინც მივიღებთ ვექტორს, რომელიც ორიგინალისგან 2-ჯერ განსხვავდება. სწორედ ამიტომ, საკუთარი ვექტორის პოვნის ამოცანების გადაჭრისას საჭიროა მხოლოდ წრფივად დამოუკიდებელი ვექტორული ობიექტების პოვნა. ყველაზე ხშირად, n × n მატრიცისთვის არის n-ე ნომერი საკუთრივვექტორები. ჩვენი კალკულატორი შექმნილია მეორე რიგის კვადრატული მატრიცების ანალიზისთვის, ასე რომ, თითქმის ყოველთვის ორი საკუთრივვექტორი იქნება ნაპოვნი, გარდა იმ შემთხვევისა, როდესაც ისინი ერთმანეთს ემთხვევა.

ზემოთ მოყვანილ მაგალითში წინასწარ ვიცოდით ორიგინალური მატრიცის საკუთრივვექტორი და ვიზუალურად განვსაზღვრეთ ლამბდა რიცხვი. თუმცა, პრაქტიკაში, ყველაფერი პირიქით ხდება: დასაწყისში არის საკუთარი მნიშვნელობები და მხოლოდ ამის შემდეგ საკუთრივ ვექტორები.

ამოხსნის ალგორითმი

მოდით კიდევ ერთხელ გადავხედოთ ორიგინალურ მატრიცას M და შევეცადოთ ვიპოვოთ მისი ორივე საკუთრივექტორი. ასე რომ, მატრიცა ასე გამოიყურება:

• M = 0; 4;
• 6; 10.

დასაწყისისთვის, ჩვენ უნდა განვსაზღვროთ λ საკუთრივ მნიშვნელობა, რისთვისაც უნდა გამოვთვალოთ შემდეგი მატრიცის განმსაზღვრელი:

• (0 − λ); 4;
• 6; (10 − λ).

ეს მატრიცა მიიღება უცნობი λ-ის გამოკლებით მთავარ დიაგონალზე არსებულ ელემენტებს. განმსაზღვრელი განისაზღვრება სტანდარტული ფორმულით:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

ვინაიდან ჩვენი ვექტორი არ უნდა იყოს ნული, მივიღებთ მიღებულ განტოლებას, როგორც წრფივად დამოკიდებულს და ვატოლებთ ჩვენს განმსაზღვრელს detA ნულს.

(0 − λ) × (10 − λ) − 24 = 0

გავხსნათ ფრჩხილები და მივიღოთ მატრიცის დამახასიათებელი განტოლება:

λ 2 − 10λ − 24 = 0

ეს არის სტანდარტული კვადრატული განტოლება, რომელიც უნდა გადაწყდეს დისკრიმინანტის თვალსაზრისით.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

დისკრიმინანტის ფესვი არის sqrt(D) = 14, ამიტომ λ1 = -2, λ2 = 12. ახლა თითოეული ლამბდას მნიშვნელობისთვის, ჩვენ უნდა ვიპოვოთ საკუთრივვექტორი. გამოვხატოთ სისტემის კოეფიციენტები λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

ამ ფორმულაში E არის პირადობის მატრიცა. მიღებული მატრიცის საფუძველზე ვადგენთ წრფივი განტოლებების სისტემას:

2x + 4y = 6x + 12y

სადაც x და y არის საკუთრივვექტორის ელემენტები.

მოდით შევაგროვოთ ყველა X მარცხნივ და ყველა Y მარჯვნივ. ცხადია - 4x = 8y. გაყავით გამოხატულება -4-ზე და მიიღეთ x = -2y. ახლა ჩვენ შეგვიძლია განვსაზღვროთ მატრიცის პირველი საკუთარი ვექტორი უცნობის ნებისმიერი მნიშვნელობის აღებით (გაიხსენეთ წრფივად დამოკიდებული საკუთრივექტორების უსასრულობა). ავიღოთ y = 1, შემდეგ x = -2. მაშასადამე, პირველი საკუთარი ვექტორი ჰგავს V1 = (–2; 1). დაუბრუნდით სტატიის დასაწყისში. სწორედ ამ ვექტორულ ობიექტზე გავამრავლეთ მატრიცა საკუთარი ვექტორის ცნების საჩვენებლად.

ახლა ვიპოვოთ საკუთარი ვექტორი λ = 12-ისთვის.

• M - λ × E = -12; 4
• 6; -2.

შევადგინოთ წრფივი განტოლებათა იგივე სისტემა;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

ახლა ავიღოთ x = 1, მაშასადამე, y = 3. ამრიგად, მეორე საკუთრივექტორი გამოიყურება V2 = (1; 3). ორიგინალური მატრიცის ამ ვექტორზე გამრავლებისას შედეგი ყოველთვის იქნება იგივე ვექტორი გამრავლებული 12-ზე. ეს ასრულებს ამოხსნის ალგორითმს. ახლა თქვენ იცით, როგორ განვსაზღვროთ მატრიცის საკუთარი ვექტორი ხელით.

• განმსაზღვრელი;
• კვალი, ანუ ელემენტების ჯამი მთავარ დიაგონალზე;
• რანგი, ანუ წრფივად დამოუკიდებელი მწკრივების/სვეტების მაქსიმალური რაოდენობა.

პროგრამა მუშაობს ზემოაღნიშნული ალგორითმის მიხედვით, რაც ამცირებს გადაწყვეტის პროცესს. მნიშვნელოვანია აღინიშნოს, რომ პროგრამაში ლამბდა აღინიშნება ასო „c“-ით. მოდით შევხედოთ ციფრულ მაგალითს.

პროგრამის მაგალითი

შევეცადოთ განვსაზღვროთ საკუთრივ ვექტორები შემდეგი მატრიცისთვის:

• M=5; ცამეტი;
• 4; 14.

მოდით შევიტანოთ ეს მნიშვნელობები კალკულატორის უჯრედებში და მივიღოთ პასუხი შემდეგი ფორმით:

• მატრიცის წოდება: 2;
• მატრიცის განმსაზღვრელი: 18;
• მატრიცული კვალი: 19;
• საკუთრივვექტორის გამოთვლა: c 2 − 19.00c + 18.00 (მახასიათებელი განტოლება);
• Eigenvector გაანგარიშება: 18 (პირველი ლამბდა მნიშვნელობა);
• საკუთრივვექტორის გაანგარიშება: 1 (მეორე ლამბდა მნიშვნელობა);
• ვექტორი 1-ის განტოლებათა სისტემა: -13x1 + 13y1 = 4x1 − 4y1;
• ვექტორი 2 განტოლების სისტემა: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• საკუთრივ ვექტორი 2: (-3.25; 1).

ამრიგად, ჩვენ მივიღეთ ორი წრფივად დამოუკიდებელი საკუთარი ვექტორი.

დასკვნა

ხაზოვანი ალგებრა და ანალიტიკური გეომეტრია სტანდარტული საგნებია ინჟინერიის ნებისმიერი პირველკურსელისთვის. ვექტორებისა და მატრიცების დიდი რაოდენობა საშინელებაა და ადვილია შეცდომის დაშვება ასეთ რთულ გამოთვლებში. ჩვენი პროგრამა სტუდენტებს საშუალებას მისცემს შეამოწმონ თავიანთი გამოთვლები ან ავტომატურად გადაჭრას საკუთრივვექტორის პოვნის პრობლემა. ჩვენს კატალოგში არის სხვა ხაზოვანი ალგებრის კალკულატორები, გამოიყენეთ ისინი თქვენს სწავლაში ან სამუშაოში.

www.siteსაშუალებას გაძლევთ იპოვოთ. საიტი აკეთებს გაანგარიშებას. რამდენიმე წამში სერვერი მოგცემთ სწორ გადაწყვეტილებას. მატრიცის დამახასიათებელი განტოლებაიქნება დეტერმინანტის გამოთვლის წესით ნაპოვნი ალგებრული გამოხატულება მატრიცები მატრიცები, ხოლო მთავარ დიაგონალზე იქნება განსხვავებები დიაგონალური ელემენტებისა და ცვლადის მნიშვნელობებში. გაანგარიშებისას დამახასიათებელი განტოლება მატრიცისთვის ონლაინ, თითოეული ელემენტი მატრიცებიგამრავლდება სხვა შესაბამის ელემენტებთან მატრიცები. მოძებნეთ რეჟიმში ონლაინშესაძლებელია მხოლოდ მოედანზე მატრიცები. იპოვნეთ ოპერაცია დამახასიათებელი განტოლება მატრიცისთვის ონლაინამცირებს ელემენტების ნამრავლის ალგებრული ჯამის გამოთვლას მატრიცებიდეტერმინანტის პოვნის შედეგად მატრიცები, მხოლოდ დადგენის მიზნით დამახასიათებელი განტოლება მატრიცისთვის ონლაინ. ამ ოპერაციას თეორიაში განსაკუთრებული ადგილი უჭირავს მატრიცებისაშუალებას გაძლევთ იპოვოთ საკუთარი მნიშვნელობები და ვექტორები ფესვების გამოყენებით. ამოცანის პოვნა დამახასიათებელი განტოლება მატრიცისთვის ონლაინარის ელემენტების გამრავლება მატრიცებიამ პროდუქტების შემდგომი შეჯამებით გარკვეული წესის მიხედვით. www.siteაღმოაჩენს მატრიცის დამახასიათებელი განტოლებამოცემული განზომილება რეჟიმში ონლაინ. გაანგარიშება დამახასიათებელი განტოლება მატრიცისთვის ონლაინმოცემული განზომილებისთვის ეს არის მრავალწევრის პოვნა რიცხვითი ან სიმბოლური კოეფიციენტებით, რომლებიც ნაპოვნია დეტერმინანტის გამოთვლის წესით. მატრიცები- როგორც შესაბამისი ელემენტების ნამრავლების ჯამი მატრიცები, მხოლოდ დადგენის მიზნით დამახასიათებელი განტოლება მატრიცისთვის ონლაინ. მრავალწევრის პოვნა კვადრატისთვის ცვლადის მიმართ მატრიცები, როგორც განმარტება მატრიცის დამახასიათებელი განტოლება, თეორიულად გავრცელებული მატრიცები. მრავალწევრის ფესვების მნიშვნელობა დამახასიათებელი განტოლება მატრიცისთვის ონლაინგამოიყენება საკუთარი ვექტორებისა და საკუთრივ მნიშვნელობების დასადგენად მატრიცები. თუმცა თუ განმსაზღვრელი მატრიცებინული იქნება მაშინ მატრიცის დამახასიათებელი განტოლებამაინც იარსებებს, პირიქით მატრიცები. იმისათვის რომ გამოვთვალოთ მატრიცის დამახასიათებელი განტოლებაან მოძებნეთ რამდენიმე ერთდროულად მატრიცების დამახასიათებელი განტოლებები, თქვენ უნდა დახარჯოთ ბევრი დრო და ძალისხმევა, სანამ ჩვენი სერვერი იპოვის დამახასიათებელი განტოლება ონლაინ მატრიცისთვის. ამ შემთხვევაში პასუხი მოძიებით დამახასიათებელი განტოლება მატრიცისთვის ონლაინიქნება სწორი და საკმარისი სიზუსტით, თუნდაც ნომრები მოძიებისას დამახასიათებელი განტოლება მატრიცისთვის ონლაინირაციონალური იქნება. ონლაინ www.siteსიმბოლოების ჩანაწერები დაშვებულია ელემენტებში მატრიცები, ე.ი დამახასიათებელი განტოლება ონლაინ მატრიცისთვისგაანგარიშებისას შეიძლება წარმოდგენილი იყოს ზოგადი სიმბოლური ფორმით დამახასიათებელი განტოლების მატრიცა ონლაინ რეჟიმში. სასარგებლოა მოძიების პრობლემის გადაჭრისას მიღებული პასუხის შემოწმება დამახასიათებელი განტოლება მატრიცისთვის ონლაინსაიტის გამოყენებით www.site. მრავალწევრის გამოთვლის ოპერაციის შესრულებისას - მატრიცის დამახასიათებელი განტოლება, აუცილებელია იყოთ ყურადღებიანი და უკიდურესად კონცენტრირებული ამ პრობლემის გადაჭრაში. თავის მხრივ, ჩვენი საიტი დაგეხმარებათ შეამოწმოთ თქვენი გადაწყვეტილება თემაზე დამახასიათებელი განტოლების მატრიცა ონლაინ რეჟიმში. თუ არ გაქვთ დრო მოგვარებული პრობლემების ხანგრძლივი შემოწმებისთვის, მაშინ www.siteრა თქმა უნდა, მოსახერხებელი ინსტრუმენტი იქნება პოვნისა და გაანგარიშებისას შესამოწმებლად დამახასიათებელი განტოლება მატრიცისთვის ონლაინ.

განმარტება 9.3.ვექტორი X დაურეკა საკუთარი ვექტორიმატრიცები მაგრამთუ არის ასეთი რიცხვი λ, რომ თანასწორობა მოქმედებს: მაგრამ X= λ X, ანუ მიმართვის შედეგი X მატრიცით მოცემული წრფივი ტრანსფორმაცია მაგრამ, არის ამ ვექტორის გამრავლება რიცხვზე λ . თავად ნომერი λ დაურეკა საკუთარი ნომერიმატრიცები მაგრამ.

ჩანაცვლება ფორმულებში (9.3) x` j = λx j,ვიღებთ განტოლებათა სისტემას საკუთარი ვექტორის კოორდინატების დასადგენად:

. (9.5)

ამ წრფივ ერთგვაროვან სისტემას ექნება არატრივიალური ამოხსნა მხოლოდ იმ შემთხვევაში, თუ მისი მთავარი განმსაზღვრელი არის 0 (კრამერის წესი). ამ პირობის ჩაწერით ფორმაში:

ვიღებთ განტოლებას საკუთრივ მნიშვნელობების დასადგენად λ დაურეკა დამახასიათებელი განტოლება. მოკლედ, ის შეიძლება წარმოდგენილი იყოს შემდეგნაირად:

| A-λE | = 0, (9.6)

რადგან მისი მარცხენა მხარე არის მატრიცის განმსაზღვრელი A-λE. პოლინომიის მიმართ λ | A-λE| დაურეკა დამახასიათებელი მრავალწევრიმატრიცები ა.

დამახასიათებელი მრავალწევრის თვისებები:

1) წრფივი გარდაქმნის დამახასიათებელი პოლინომი არ არის დამოკიდებული საფუძვლის არჩევანზე. მტკიცებულება. (იხ. (9.4)), მაგრამ აქედან გამომდინარე, . ამრიგად, ეს არ არის დამოკიდებული საფუძვლის არჩევანზე. აქედან გამომდინარე, და | A-λE| არ იცვლება ახალ ბაზაზე გადასვლისას.

2) თუ მატრიცა მაგრამწრფივი ტრანსფორმაცია არის სიმეტრიული(ისინი. ა ი = ა ჯი), მაშინ დამახასიათებელი განტოლების (9.6) ყველა ფესვი რეალური რიცხვია.

საკუთარი მნიშვნელობების და საკუთრივ ვექტორების თვისებები:

1) თუ ჩვენ ვირჩევთ საფუძველს საკუთრივ ვექტორებიდან x 1, x 2, x 3 საკუთარი მნიშვნელობების შესაბამისი λ 1, λ 2, λ 3მატრიცები მაგრამ, მაშინ ამ საფუძველზე A წრფივ ტრანსფორმაციას აქვს დიაგონალური მატრიცა:

(9.7) ამ თვისების დადასტურება გამომდინარეობს საკუთრივ ვექტორების განმარტებიდან.

2) თუ ტრანსფორმაციის საკუთრივ მნიშვნელობები მაგრამგანსხვავებულია, მაშინ მათ შესაბამისი საკუთრივვექტორები წრფივად დამოუკიდებელია.

3) თუ მატრიცის დამახასიათებელი მრავალწევრი მაგრამაქვს სამი განსხვავებული ფესვი, შემდეგ გარკვეულწილად მატრიცა მაგრამაქვს დიაგონალური ფორმა.

ვიპოვოთ მატრიცის საკუთრივ მნიშვნელობები და საკუთრივვექტორები, გავაკეთოთ დამახასიათებელი განტოლება: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

იპოვეთ თითოეული ნაპოვნი მნიშვნელობის შესაბამისი საკუთარი ვექტორების კოორდინატები λ. (9.5)-დან გამომდინარეობს, რომ თუ X (1) ={x 1, x 2, x 3) არის შესაბამისი საკუთრივვექტორი λ 1 = -2, მაშინ

არის თანამშრომლობითი, მაგრამ განუსაზღვრელი სისტემა. მისი ამოხსნა შეიძლება დაიწეროს როგორც X (1) ={ა,0,-ა), სადაც a არის ნებისმიერი რიცხვი. კერძოდ, თუ თქვენ მოითხოვთ, რომ | x (1) |=1, X (1) =

ჩანაცვლება სისტემაში (9.5) λ 2 =3, ვიღებთ სისტემას მეორე საკუთარი ვექტორის კოორდინატების დასადგენად - x (2) ={y1, y2, y3}:

, სად X (2) ={ბ,-ბ,ბ) ან, გათვალისწინებული | x (2) |=1, x (2) =

ამისთვის λ 3 = 6 იპოვნეთ საკუთარი ვექტორი x (3) ={z1, z2, z3}:

, x (3) ={გ,2c,c) ან ნორმალიზებულ ვერსიაში

x (3) = ჩანს რომ X (1) X (2) = აბ-აბ= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = ძვ.წ- 2ძვ.წ+ძვ.წ= 0. ამრიგად, ამ მატრიცის საკუთრივ ვექტორები წყვილი ორთოგონალურია.

ლექცია 10

კვადრატული ფორმები და მათი კავშირი სიმეტრიულ მატრიცებთან. სიმეტრიული მატრიცის საკუთრივ ვექტორების და საკუთრივ მნიშვნელობების თვისებები. კვადრატული ფორმის შემცირება კანონიკურ ფორმამდე.

განმარტება 10.1.კვადრატული ფორმარეალური ცვლადები x 1, x 2,…, x nამ ცვლადებთან მიმართებაში მეორე ხარისხის პოლინომი ეწოდება, რომელიც არ შეიცავს პირველი ხარისხის თავისუფალ წევრს და ტერმინებს.

კვადრატული ფორმების მაგალითები:

(ნ = 2),

(ნ = 3). (10.1)

გაიხსენეთ სიმეტრიული მატრიცის განმარტება, რომელიც მოცემულია ბოლო ლექციაში:

განმარტება 10.2.კვადრატული მატრიცა ეწოდება სიმეტრიული, თუ , ანუ თუ მატრიცის ელემენტები სიმეტრიული მთავარი დიაგონალის მიმართ ტოლია.

სიმეტრიული მატრიცის საკუთრივ მნიშვნელობებისა და საკუთრივვექტორების თვისებები:

1) სიმეტრიული მატრიცის ყველა საკუთრივ მნიშვნელობა რეალურია.

მტკიცებულება (ამისთვის ნ = 2).

მოდით მატრიცა მაგრამროგორც ჩანს: . მოდით გავაკეთოთ დამახასიათებელი განტოლება:

(10.2) იპოვეთ დისკრიმინანტი:

მაშასადამე, განტოლებას მხოლოდ რეალური ფესვები აქვს.

2) სიმეტრიული მატრიცის საკუთრივვექტორები ორთოგონალურია.

მტკიცებულება (ამისთვის ნ= 2).

საკუთრივ ვექტორების კოორდინატები და უნდა აკმაყოფილებდეს განტოლებებს.