របៀបបញ្ចូលរូបមន្តគណិតវិទ្យានៅលើគេហទំព័រ?

ប្រសិនបើអ្នកត្រូវបន្ថែមរូបមន្តគណិតវិទ្យាមួយ ឬពីរទៅគេហទំព័រ នោះវិធីងាយស្រួលបំផុតដើម្បីធ្វើដូចបានរៀបរាប់ក្នុងអត្ថបទ៖ រូបមន្តគណិតវិទ្យាត្រូវបានបញ្ចូលយ៉ាងងាយស្រួលទៅក្នុងគេហទំព័រក្នុងទម្រង់ជារូបភាពដែល Wolfram Alpha បង្កើតដោយស្វ័យប្រវត្តិ។ បន្ថែមពីលើភាពសាមញ្ញ វិធីសាស្ត្រជាសកលនេះនឹងជួយកែលម្អភាពមើលឃើញនៃគេហទំព័រនៅក្នុងម៉ាស៊ីនស្វែងរក។ វាបានដំណើរការជាយូរមកហើយ (ហើយខ្ញុំគិតថាវានឹងដំណើរការជារៀងរហូត) ប៉ុន្តែវាហួសសម័យហើយ។

ប្រសិនបើអ្នកកំពុងប្រើរូបមន្តគណិតវិទ្យាជាប្រចាំនៅលើគេហទំព័ររបស់អ្នក នោះខ្ញុំណែនាំអ្នកឱ្យប្រើ MathJax ដែលជាបណ្ណាល័យ JavaScript ពិសេសដែលបង្ហាញសញ្ញាណគណិតវិទ្យានៅក្នុងកម្មវិធីរុករកតាមអ៊ីនធឺណិតដោយប្រើ MathML, LaTeX ឬ ASCIIMathML markup ។

មានវិធីពីរយ៉ាងក្នុងការចាប់ផ្តើមប្រើប្រាស់ MathJax៖ (1) ដោយប្រើកូដសាមញ្ញ អ្នកអាចភ្ជាប់ស្គ្រីប MathJax ទៅកាន់គេហទំព័ររបស់អ្នកបានយ៉ាងឆាប់រហ័ស ដែលនឹងត្រូវបានផ្ទុកដោយស្វ័យប្រវត្តិពីម៉ាស៊ីនមេពីចម្ងាយនៅពេលត្រឹមត្រូវ (បញ្ជីម៉ាស៊ីនមេ); (2) ផ្ទុកឡើងស្គ្រីប MathJax ពីម៉ាស៊ីនមេពីចម្ងាយទៅកាន់ម៉ាស៊ីនមេរបស់អ្នក ហើយភ្ជាប់វាទៅគ្រប់ទំព័រនៃគេហទំព័ររបស់អ្នក។ វិធីសាស្ត្រទីពីរគឺកាន់តែស្មុគស្មាញ និងចំណាយពេលច្រើន ហើយនឹងអនុញ្ញាតឱ្យអ្នកបង្កើនល្បឿននៃការផ្ទុកទំព័រនៃគេហទំព័ររបស់អ្នក ហើយប្រសិនបើម៉ាស៊ីនមេ MathJax មេមិនអាចប្រើបានជាបណ្ដោះអាសន្នដោយសារហេតុផលមួយចំនួន វានឹងមិនប៉ះពាល់ដល់គេហទំព័រផ្ទាល់ខ្លួនរបស់អ្នកតាមមធ្យោបាយណាមួយឡើយ។ ទោះបីជាមានគុណសម្បត្តិទាំងនេះក៏ដោយ ខ្ញុំបានជ្រើសរើសវិធីសាស្ត្រដំបូង ព្រោះថាវាសាមញ្ញជាង លឿនជាងមុន ហើយមិនត្រូវការជំនាញបច្ចេកទេសទេ។ ធ្វើតាមគំរូរបស់ខ្ញុំ ហើយក្នុងរយៈពេល 5 នាទី អ្នកនឹងអាចប្រើមុខងារទាំងអស់របស់ MathJax នៅលើគេហទំព័ររបស់អ្នក។

អ្នកអាចភ្ជាប់ស្គ្រីបបណ្ណាល័យ MathJax ពីម៉ាស៊ីនមេពីចម្ងាយ ដោយប្រើជម្រើសកូដពីរដែលយកចេញពីគេហទំព័រ MathJax មេ ឬពីទំព័រឯកសារ៖

ជម្រើស​កូដ​មួយ​ក្នុង​ចំណោម​ជម្រើស​កូដ​ទាំង​នេះ​ត្រូវ​ការ​ចម្លង និង​បិទ​ភ្ជាប់​ទៅ​ក្នុង​កូដ​នៃ​ទំព័រ​បណ្ដាញ​របស់​អ្នក ជា​ជម្រើស​រវាង​ស្លាក និងឬភ្លាមៗបន្ទាប់ពីស្លាក . យោងតាមជម្រើសដំបូង MathJax ផ្ទុកលឿនជាងមុន និងបន្ថយទំព័រតិចជាងមុន។ ប៉ុន្តែជម្រើសទីពីរតាមដាន និងផ្ទុកកំណែចុងក្រោយបំផុតរបស់ MathJax ដោយស្វ័យប្រវត្តិ។ ប្រសិនបើអ្នកបញ្ចូលលេខកូដដំបូង នោះវានឹងចាំបាច់ត្រូវធ្វើបច្ចុប្បន្នភាពជាប្រចាំ។ ប្រសិនបើអ្នកបិទភ្ជាប់កូដទីពីរ នោះទំព័រនឹងផ្ទុកយឺតជាងមុន ប៉ុន្តែអ្នកនឹងមិនចាំបាច់តាមដានការអាប់ដេត MathJax ជានិច្ចនោះទេ។

មធ្យោបាយងាយស្រួលបំផុតដើម្បីភ្ជាប់ MathJax គឺនៅក្នុង Blogger ឬ WordPress៖ នៅក្នុងផ្ទាំងគ្រប់គ្រងគេហទំព័រ បន្ថែមធាតុក្រាហ្វិកដែលត្រូវបានរចនាឡើងដើម្បីបញ្ចូលកូដ JavaScript ភាគីទីបី ចម្លងកំណែទីមួយ ឬទីពីរនៃកូដផ្ទុកខាងលើទៅក្នុងវា ហើយដាក់ធាតុក្រាហ្វិកឱ្យជិត។ ការចាប់ផ្តើមនៃគំរូ (ដោយវិធីនេះ វាមិនចាំបាច់ទាល់តែសោះ ចាប់តាំងពីស្គ្រីប MathJax ត្រូវបានផ្ទុកដោយអសមកាល)។ អស់ហើយ។ ឥឡូវនេះរៀនវាក្យសម្ព័ន្ធសម្គាល់ MathML, LaTeX និង ASCIIMathML ហើយអ្នកត្រៀមខ្លួនរួចរាល់ហើយក្នុងការបង្កប់រូបមន្តគណិតវិទ្យាទៅក្នុងគេហទំព័ររបស់អ្នក។

ប្រភាគណាមួយត្រូវបានបង្កើតឡើងដោយយោងទៅតាមច្បាប់ជាក់លាក់មួយ ដែលត្រូវបានអនុវត្តជាបន្តបន្ទាប់ចំនួនដងគ្មានដែនកំណត់។ រាល់ពេលបែបនេះត្រូវបានគេហៅថាការធ្វើម្តងទៀត។

ក្បួនដោះស្រាយដដែលៗសម្រាប់ការសាងសង់អេប៉ុង Menger គឺសាមញ្ញណាស់៖ គូបដើមដែលមានជ្រុង 1 ត្រូវបានបែងចែកដោយយន្តហោះស្របទៅនឹងមុខរបស់វាទៅជា 27 គូបស្មើគ្នា។ គូបកណ្តាលមួយនិង 6 គូបដែលនៅជាប់នឹងវានៅតាមបណ្តោយមុខត្រូវបានយកចេញពីវា។ វាប្រែចេញនូវសំណុំមួយដែលមាន 20 គូបតូចៗដែលនៅសល់។ ធ្វើដូចគ្នាជាមួយនឹងគូបនីមួយៗនេះ យើងទទួលបានសំណុំមួយដែលមាន 400 គូបតូចជាង។ ការបន្តដំណើរការនេះដោយគ្មានកំណត់ យើងទទួលបានអេប៉ុង Menger ។

ក្នុង​ករណី​ជា​ច្រើន ការ​គូស​ប្លង់​អនុគមន៍​គឺ​ងាយ​ស្រួល​ជាង​ប្រសិន​បើ​អ្នក​គូស​ប្លង់ asymtotes នៃ​ខ្សែ​កោង​ដំបូង។

និយមន័យ 1. Asymptotes ត្រូវបានគេហៅថាបន្ទាត់បែបនេះ ដែលក្រាហ្វនៃអនុគមន៍ចូលទៅជិតដូចការចង់បាន នៅពេលដែលអថេរមានទំនោរទៅបូកនឹងភាពគ្មានកំណត់ ឬដកគ្មានដែនកំណត់។

និយមន័យ 2. បន្ទាត់ត្រង់ត្រូវបានគេហៅថា asymptote នៃក្រាហ្វនៃអនុគមន៍ ប្រសិនបើចម្ងាយពីចំណុចអថេរ មក្រាហ្វនៃអនុគមន៍រហូតដល់បន្ទាត់នេះមានទំនោរទៅសូន្យ នៅពេលដែលចំណុចផ្លាស់ទីទៅឆ្ងាយដោយគ្មានកំណត់ មពីប្រភពដើមនៃកូអរដោណេតាមសាខាណាមួយនៃក្រាហ្វនៃអនុគមន៍។

មាន asymptotes បីប្រភេទគឺ បញ្ឈរ ផ្ដេក និង oblique ។

រោគសញ្ញាបញ្ឈរ

និយមន័យ. ត្រង់ x = កគឺ asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារ ប្រសិនបើចំណុច x = កគឺ ចំណុចបំបែកនៃប្រភេទទីពីរសម្រាប់លក្ខណៈពិសេសនេះ។

វាធ្វើតាមនិយមន័យថាបន្ទាត់ x = កគឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍ f(x) ប្រសិនបើយ៉ាងហោចណាស់លក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោមត្រូវបានបំពេញ៖

ទន្ទឹមនឹងនេះមុខងារ f(x) ប្រហែលជាមិនត្រូវបានកំណត់ទាល់តែសោះ រៀងគ្នាសម្រាប់ x ≥ កនិង x ≤ ក .

មតិយោបល់៖

ឧទាហរណ៍ ១ក្រាហ្វមុខងារ y=ln xមាន asymptote បញ្ឈរ x= 0 (ឧ. ស្របគ្នានឹងអ័ក្ស អូ) នៅលើព្រំដែននៃដែននិយមន័យ ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍ជា x ទំនោរទៅសូន្យនៅខាងស្តាំគឺស្មើនឹងដកគ្មានដែនកំណត់៖

(រូបភាពខាងលើ) ។

ដោយខ្លួនឯង ហើយបន្ទាប់មកមើលដំណោះស្រាយ

ឧទាហរណ៍ ២ស្វែងរក asymtotes នៃក្រាហ្វនៃអនុគមន៍។

ឧទាហរណ៍ ៣ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

asymtotes ផ្ដេក

ប្រសិនបើ (ដែនកំណត់នៃអនុគមន៍នៅពេលដែលអាគុយម៉ង់មានទំនោរទៅបូកឬដកអគ្មានកំណត់គឺស្មើនឹងតម្លៃមួយចំនួន ខ), នោះ។ y = ខ – asymptote ផ្ដេក កោង y = f(x ។

ឧទាហរណ៍ 5ក្រាហ្វមុខងារ

នៅ ក> 1 មាន asymptote ផ្ដេកខាងឆ្វេង y= 0 (ឧ. ស្របគ្នានឹងអ័ក្ស គោ), ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍នៅពេលដែល "x" ទំនោរទៅដកគ្មានដែនកំណត់គឺស្មើនឹងសូន្យ:

ខ្សែកោងមិនមាន asymptote ផ្ដេកត្រឹមត្រូវទេ ព្រោះដែនកំណត់នៃអនុគមន៍ដែល x ទំនោរទៅបូកនឹងភាពគ្មានកំណត់គឺស្មើនឹងគ្មានកំណត់៖

រោគសញ្ញា Oblique

asymptotes បញ្ឈរ និងផ្ដេកដែលយើងបានពិចារណាខាងលើគឺស្របទៅនឹងអ័ក្សកូអរដោណេ ដូច្នេះដើម្បីសាងសង់ពួកវា យើងត្រូវការតែចំនួនជាក់លាក់មួយប៉ុណ្ណោះ - ចំណុចនៅលើអ័ក្ស abscissa ឬ ordinate ដែល asymptote ឆ្លងកាត់។ ច្រើនទៀតគឺត្រូវការសម្រាប់ asymptote oblique - ជម្រាល kដែលបង្ហាញពីមុំទំនោរនៃបន្ទាត់ត្រង់ និងស្ទាក់ចាប់ ខដែលបង្ហាញពីចំនួនបន្ទាត់ខាងលើ ឬខាងក្រោមប្រភពដើម។ អ្នកទាំងឡាយណាដែលមិនមានពេលវេលាដើម្បីបំភ្លេចធរណីមាត្រវិភាគ ហើយពីវា - សមីការនៃបន្ទាត់ត្រង់នឹងសម្គាល់ថាសម្រាប់ asymptote oblique ពួកគេរកឃើញ សមីការជម្រាល. អត្ថិភាពនៃ asymptote oblique ត្រូវបានកំណត់ដោយទ្រឹស្តីបទខាងក្រោម ដោយឈរលើមូលដ្ឋាននៃមេគុណដែលទើបតែដាក់ឈ្មោះត្រូវបានរកឃើញ។

ទ្រឹស្តីបទ។ដើម្បីធ្វើខ្សែកោង y = f(x) មាន asymptote y = kx + ខ វាចាំបាច់ និងគ្រប់គ្រាន់ដែលមានដែនកំណត់កំណត់ kនិង ខនៃអនុគមន៍ដែលកំពុងពិចារណាដូចដែលអថេរមានទំនោរទៅ xបូក​នឹង​ភាព​គ្មាន​កំណត់ និង​ដក​គ្មាន​កំណត់៖

(1)

(2)

លេខ​នេះ​បាន​រក​ឃើញ kនិង ខនិងជាមេគុណនៃ asymptote oblique ។

ក្នុងករណីទី 1 (នៅពេល x ទំនោរទៅបូកនឹងភាពគ្មានទីបញ្ចប់) សញ្ញា asymptote oblique ខាងស្តាំត្រូវបានទទួល ហើយនៅក្នុងទីពីរ (នៅពេលដែល x ទំនោរទៅដកគ្មានដែនកំណត់) វានៅសល់។ asymptote oblique ត្រឹមត្រូវត្រូវបានបង្ហាញនៅក្នុងរូបភព។ ពី​ខាងក្រោម។

នៅពេលស្វែងរកសមីការនៃ oblique asymptote វាចាំបាច់ត្រូវគិតគូរពីទំនោរនៃ x ទៅទាំងបូក infinity និង minus infinity ។ សម្រាប់អនុគមន៍មួយចំនួន ឧទាហរណ៍ សម្រាប់ប្រភាគប្រភាគ ដែនកំណត់ទាំងនេះស្របគ្នា ប៉ុន្តែសម្រាប់មុខងារជាច្រើន ដែនកំណត់ទាំងនេះគឺខុសគ្នា ហើយមានតែមួយក្នុងចំណោមពួកវាប៉ុណ្ណោះដែលអាចមាន។

នៅពេលដែលដែនកំណត់ស្របគ្នាជាមួយនឹង x ទំនោរទៅបូកនឹងភាពគ្មានទីបញ្ចប់ និងដកអគ្មានកំណត់ បន្ទាត់ត្រង់ y = kx + ខ គឺជា asymptote ពីរជ្រុងនៃខ្សែកោង។

ប្រសិនបើយ៉ាងហោចណាស់មួយនៃដែនកំណត់កំណត់ asymptote y = kx + ខ មិនមានទេ បន្ទាប់មកក្រាហ្វនៃមុខងារមិនមាន asymptote oblique (ប៉ុន្តែអាចមានបញ្ឈរមួយ)។

វាងាយស្រួលមើលថា asymptote ផ្ដេក y = ខគឺជាករណីពិសេសនៃ oblique y = kx + ខនៅ k = 0 .

ដូច្នេះ ប្រសិនបើខ្សែកោងមាន asymptote ផ្ដេកក្នុងទិសដៅណាមួយ នោះមិនមាន asymptote oblique នៅក្នុងទិសដៅនោះទេ ហើយច្រាសមកវិញ។

ឧទាហរណ៍ ៦ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារត្រូវបានកំណត់នៅលើបន្ទាត់លេខទាំងមូល លើកលែងតែ x= 0, i.e.

ដូច្នេះនៅចំណុចបំបែក x= 0 ខ្សែកោងអាចមាន asymptote បញ្ឈរ។ ជាការពិត ដែនកំណត់នៃអនុគមន៍ដែល x មានទំនោរទៅសូន្យពីខាងឆ្វេងគឺបូកនឹងភាពគ្មានទីបញ្ចប់៖

អាស្រ័យហេតុនេះ x= 0 គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារនេះ។

ក្រាហ្វនៃអនុគមន៍នេះមិនមាន asymptote ផ្តេកទេ ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍ នៅពេលដែល x ទំនោរទៅបូកគ្មានដែនកំណត់ គឺស្មើនឹងបូកគ្មានដែនកំណត់៖

ចូរយើងស្វែងយល់ពីវត្តមានរបស់ asymptote oblique៖

មានដែនកំណត់កំណត់ k= 2 និង ខ= 0 ។ ត្រង់ y = 2xគឺ​ជា​គំនូស​តាង​ពីរ​ជ្រុង​នៃ​ក្រាហ្វ​នៃ​អនុគមន៍​នេះ (រូប​ក្នុង​ឧទាហរណ៍)។

ឧទាហរណ៍ ៧ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារមានចំណុចបំបែកមួយ។ x= −1 ។ អនុញ្ញាតឱ្យយើងគណនាដែនកំណត់ម្ខាង និងកំណត់ប្រភេទនៃភាពមិនដំណើរការ៖

សេចក្តីសន្និដ្ឋាន៖ x= −1 គឺជាចំណុចដាច់នៃប្រភេទទីពីរ ដូច្នេះបន្ទាត់ x= −1 គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍នេះ។

កំពុងរកមើល asymtotes oblique ។ ដោយសារមុខងារនេះគឺប្រភាគប្រភាគ ដែនកំណត់សម្រាប់ និងសម្រាប់នឹងស្របគ្នា។ ដូច្នេះ យើងរកឃើញមេគុណសម្រាប់ជំនួសបន្ទាត់ត្រង់ - asymptote oblique ទៅក្នុងសមីការ៖

ការជំនួសមេគុណដែលបានរកឃើញទៅក្នុងសមីការនៃបន្ទាត់ត្រង់ជាមួយជម្រាលមួយ យើងទទួលបានសមីការនៃ asymptote oblique៖

y = −3x + 5 .

នៅក្នុងរូបភាព ក្រាហ្វនៃមុខងារត្រូវបានសម្គាល់ជាពណ៌ប៊ឺហ្គូឌី ហើយ asymtotes មានពណ៌ខ្មៅ។

ឧទាហរណ៍ ៨ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ ដោយសារមុខងារនេះបន្ត ក្រាហ្វរបស់វាមិនមានសញ្ញាបញ្ឈរទេ។ យើងកំពុងស្វែងរករោគសញ្ញា oblique៖

.

ដូច្នេះក្រាហ្វនៃមុខងារនេះមាន asymptote y= 0 នៅ និងមិនមាន asymptote នៅ .

ឧទាហរណ៍ ៩ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ ដំបូងយើងរកមើល asymtotes បញ្ឈរ។ ដើម្បីធ្វើដូចនេះយើងរកឃើញដែននៃមុខងារ។ មុខងារត្រូវបានកំណត់នៅពេលដែលវិសមភាពរក្សា និង . សញ្ញាអថេរ xផ្គូផ្គងសញ្ញា។ ដូច្នេះ សូម​ពិចារណា​អំពី​វិសមភាព​សមមូល។ ពីនេះយើងទទួលបានវិសាលភាពនៃមុខងារ៖ . asymptote បញ្ឈរអាចស្ថិតនៅលើព្រំដែននៃដែននៃអនុគមន៍ប៉ុណ្ណោះ។ ប៉ុន្តែ x= 0 មិនអាចជា asymptote បញ្ឈរបានទេ ព្រោះមុខងារត្រូវបានកំណត់សម្រាប់ x = 0 .

ពិចារណាដែនកំណត់ខាងស្តាំនៅ (ដែនកំណត់ដៃឆ្វេងមិនមានទេ)៖

.

ចំណុច x= 2 គឺជាចំនុចដាច់នៃប្រភេទទីពីរ ដូច្នេះបន្ទាត់ x= 2 - asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារនេះ។

យើងកំពុងស្វែងរករោគសញ្ញា oblique៖

ដូច្នេះ y = x+ 1 - asymptote oblique នៃក្រាហ្វនៃមុខងារនេះនៅ . យើងកំពុងស្វែងរក asymptote oblique សម្រាប់៖

ដូច្នេះ y = −x − 1 - oblique asymptote នៅ។

ឧទាហរណ៍ 10ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារមានវិសាលភាព . ចាប់តាំងពី asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍នេះអាចស្ថិតនៅលើព្រំដែននៃដែននៃនិយមន័យ នោះយើងនឹងរកឃើញដែនកំណត់ម្ខាងនៃអនុគមន៍នៅ .

Asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ខ្មោច asymptote បានវង្វេងជុំវិញគេហទំព័រអស់រយៈពេលជាយូរដើម្បីក្លាយជាការពិតនៅក្នុងអត្ថបទតែមួយ និងនាំមកនូវសេចក្តីរីករាយពិសេសដល់អ្នកអានដែលឆ្ងល់។ ការសិក្សាមុខងារពេញលេញ. ការស្វែងរក asymtotes នៃក្រាហ្វគឺជាផ្នែកមួយក្នុងចំណោមផ្នែកមួយចំនួននៃកិច្ចការដែលបានបញ្ជាក់ ដែលត្រូវបានគ្របដណ្តប់នៅក្នុងវគ្គសិក្សារបស់សាលាតែក្នុងលំដាប់ទិដ្ឋភាពទូទៅប៉ុណ្ណោះ ចាប់តាំងពីព្រឹត្តិការណ៍វិលជុំវិញការគណនា ដែនកំណត់មុខងារប៉ុន្តែពួកគេនៅតែជាកម្មសិទ្ធិរបស់គណិតវិទ្យាខ្ពស់ជាង។ អ្នកទស្សនាដែលមិនសូវពូកែក្នុងការវិភាគគណិតវិទ្យា ខ្ញុំគិតថាគន្លឹះគឺអាចយល់បាន ;-) ... ឈប់-ឈប់ តើអ្នកនឹងទៅណា? ដែនកំណត់- វា​ងាយស្រួល!

ឧទាហរណ៍នៃ asymtotes បានជួបភ្លាមៗនៅក្នុងមេរៀនដំបូងអំពី ក្រាហ្វនៃមុខងារបឋមហើយឥឡូវនេះប្រធានបទកំពុងទទួលបានការពិចារណាលម្អិត។

ដូច្នេះតើអ្វីទៅជា asymptote?

ស្រមៃ ចំណុចអថេរដែល "ធ្វើដំណើរ" តាមក្រាហ្វនៃមុខងារ។ asymptote គឺ ត្រង់, ទៅ whcih បិទគ្មានដែនកំណត់ក្រាហ្វនៃអនុគមន៍ជិតដល់ពេលដែលចំណុចអថេររបស់វាទៅដល់គ្មានកំណត់។

ចំណាំ ៖ និយមន័យមានអត្ថន័យ ប្រសិនបើអ្នកត្រូវការរូបមន្តក្នុងសញ្ញាណនៃការវិភាគគណិតវិទ្យា សូមយោងទៅសៀវភៅសិក្សា។

នៅលើយន្តហោះ, asymtotes ត្រូវបានចាត់ថ្នាក់តាមការរៀបចំធម្មជាតិរបស់ពួកគេ៖

1) រោគសញ្ញាបញ្ឈរដែលត្រូវបានផ្តល់ឱ្យដោយសមីការនៃទម្រង់ដែល "អាល់ហ្វា" គឺជាចំនួនពិត។ អ្នកតំណាងដ៏ពេញនិយមកំណត់អ័ក្ស y ខ្លួនវា
ជាមួយនឹងការវាយប្រហារនៃការចង្អោរកម្រិតស្រាល យើងរំលឹកឡើងវិញនូវ hyperbole ។

2) រោគសញ្ញា Obliqueសរសេរជាប្រពៃណី សមីការបន្ទាត់ត្រង់ជាមួយនឹងកត្តាជម្រាល។ ពេលខ្លះករណីពិសេសមួយត្រូវបានជ្រើសរើសជាក្រុមដាច់ដោយឡែក - asymtotes ផ្ដេក. ឧទាហរណ៍ អ៊ីពែបូឡាដូចគ្នាជាមួយ asymptote ។

យើង​ចេញ​ទៅ​វិញ​យ៉ាង​ឆាប់​រហ័ស សូម​ចូល​ទៅ​លើ​ប្រធានបទ​ដោយ​ស្វ័យ​ប្រវត្តិ​ខ្លីៗ៖

តើក្រាហ្វនៃអនុគមន៍មួយអាចមាន asymtotes ប៉ុន្មាន?

គ្មាន, មួយ, ពីរ, បី... ឬចំនួនគ្មានកំណត់។ យើងនឹងមិនទៅឆ្ងាយសម្រាប់ឧទាហរណ៍ទេយើងនឹងចងចាំ មុខងារបឋម. ប៉ារ៉ាបូឡា, ប៉ារ៉ាបូឡាគូប, sinusoid មិនមានរោគសញ្ញាអ្វីទាំងអស់។ ក្រាហ្វនៃអនុគមន៍លោការីតអិចស្ប៉ូណង់ស្យែលមាន asymptote តែមួយ។ arctangent, arccotangent មាន​ពីរ​ក្នុង​ចំណោម​ពួក​គេ ហើយ​តង់ហ្សង់, កូតង់សង់​មាន​ចំនួន​គ្មាន​កំណត់។ វាមិនមែនជារឿងចម្លែកទេសម្រាប់ក្រាហ្វដែលមាន asymtotes ផ្ដេក និងបញ្ឈរ។ Hyperbole នឹងស្រឡាញ់អ្នកជានិច្ច។

មានន័យថាម៉េច?

asymtotes បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍មួយ។

asymptote បញ្ឈរនៃក្រាហ្វគឺជាធម្មតា នៅចំណុចនៃភាពគ្មានទីបញ្ចប់មុខងារ។ វាសាមញ្ញ៖ ប្រសិនបើនៅចំណុចមួយ មុខងារទទួលរងការបំបែកគ្មានកំណត់ នោះបន្ទាត់ត្រង់ដែលផ្តល់ដោយសមីការគឺជា asymptote បញ្ឈរនៃក្រាហ្វ។

ចំណាំ ៖ ចំណាំថាសញ្ញាណត្រូវបានប្រើដើម្បីសំដៅទៅលើគោលគំនិតខុសគ្នាទាំងស្រុង។ ចំនុចគឺបង្កប់ន័យឬសមីការនៃបន្ទាត់ត្រង់ - អាស្រ័យលើបរិបទ។

ដូច្នេះ ដើម្បីបង្កើតវត្តមាននៃ asymptote បញ្ឈរនៅចំណុចមួយ វាគ្រប់គ្រាន់ដើម្បីបង្ហាញថា យ៉ាងហោចណាស់​មួយពីដែនកំណត់ឯកតោភាគី គ្មានទីបញ្ចប់។ ភាគច្រើនជាញឹកញាប់ នេះគឺជាចំណុចដែលភាគបែងនៃអនុគមន៍ស្មើនឹងសូន្យ។ តាមការពិត យើងបានរកឃើញសញ្ញាបញ្ឈររួចហើយនៅក្នុងឧទាហរណ៍ចុងក្រោយនៃមេរៀន។ នៅលើការបន្តនៃមុខងារ. ប៉ុន្តែក្នុងករណីខ្លះមានដែនកំណត់ម្ខាងតែមួយប៉ុណ្ណោះ ហើយប្រសិនបើវាគ្មានដែនកំណត់ នោះម្តងទៀត - ស្រឡាញ់និងពេញចិត្ត asymptote បញ្ឈរ។ រូបភាពសាមញ្ញបំផុត៖ និងអ័ក្ស y (សូមមើល។ ក្រាហ្វនិងលក្ខណៈសម្បត្តិនៃអនុគមន៍បឋម).

ពីខាងលើ ការពិតជាក់ស្តែងក៏មានដូចខាងក្រោម៖ ប្រសិនបើមុខងារបន្តបន្ទាប់មកមិនមាន asymtotes បញ្ឈរទេ។. ដោយហេតុផលខ្លះ ប៉ារ៉ាបូឡាបានមកក្នុងគំនិត។ ពិតហើយ តើអ្នកអាច "បិទ" បន្ទាត់ត្រង់ត្រង់នេះនៅឯណា? ... បាទ ... ខ្ញុំយល់ ... អ្នកដើរតាមពូ Freud ញាប់ញ័រ =)

សេចក្តីថ្លែងការណ៍របស់ converse ជាទូទៅមិនពិតទេ៖ ឧទាហរណ៍ មុខងារមិនត្រូវបានកំណត់នៅលើបន្ទាត់ពិតទាំងមូលទេ ប៉ុន្តែវាត្រូវបានដកហូតទាំងស្រុងនូវ asymtotes ។

asymtotes Oblique នៃក្រាហ្វនៃអនុគមន៍មួយ។

Oblique (ជាករណីពិសេស - ផ្តេក) asymptotes អាចត្រូវបានគូរ ប្រសិនបើអាគុយម៉ង់មុខងារមាននិន្នាការទៅជា "បូកគ្មានដែនកំណត់" ឬ "ដកគ្មានដែនកំណត់" ។ នោះ​ហើយ​ជា​មូល​ហេតុ​ដែល ក្រាហ្វនៃអនុគមន៍មិនអាចមាន asymptotes oblique ច្រើនជាងពីរទេ។. ឧទាហរណ៍ ក្រាហ្វនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែលមាន asymptote ផ្តេកតែមួយនៅ ហើយក្រាហ្វនៃតង់ហ្សង់ធ្នូនៅមាន asymptotes បែបនេះពីរ និងមួយផ្សេងគ្នា។

នៅពេលដែលក្រាហ្វនៅទីនេះ និងទីនោះខិតជិត asymptote oblique តែមួយគត់ នោះវាជាទម្លាប់ក្នុងការបង្រួបបង្រួម "ភាពគ្មានទីបញ្ចប់" នៅក្រោមធាតុតែមួយ។ ឧទាហរណ៍ ... អ្នកទាយត្រូវ៖ .

ច្បាប់ទូទៅនៃមេដៃ:

ប្រសិនបើមានពីរ ចុងក្រោយដែនកំណត់ បន្ទាប់មកបន្ទាត់ត្រង់គឺជា asymptote oblique នៃក្រាហ្វនៃអនុគមន៍នៅ . ប្រសិនបើ យ៉ាងហោចណាស់​មួយនៃដែនកំណត់ខាងលើគឺគ្មានកំណត់ បន្ទាប់មកមិនមាន asymptote oblique ទេ។

ចំណាំ ៖ រូបមន្ត​នៅ​តែ​មាន​សុពលភាព ប្រសិនបើ "x" ទំនោរ​ទៅ​ជា "បូក​គ្មាន​កំណត់" ឬ​ត្រឹម "ដក​គ្មាន​កំណត់"។

ចូរយើងបង្ហាញថាប៉ារ៉ាបូឡាមិនមាន asymptotes oblique៖

ដែនកំណត់គឺគ្មានកំណត់ ដូច្នេះមិនមាន asymptote oblique ទេ។ ចំណាំថាក្នុងការស្វែងរកដែនកំណត់ លែងត្រូវការទៀតហើយ ព្រោះចម្លើយបានទទួលរួចហើយ។

ចំណាំ ៖ ប្រសិនបើអ្នកមាន (ឬនឹងមាន) ការលំបាកក្នុងការយល់ដឹងពីសញ្ញាបូក-ដក ដក-បូក សូមមើលជំនួយនៅដើមមេរៀន
អំពីមុខងារគ្មានកំណត់ដែលជាកន្លែងដែលខ្ញុំបានប្រាប់ពីរបៀបបកស្រាយសញ្ញាទាំងនេះឱ្យបានត្រឹមត្រូវ។

វាច្បាស់ណាស់ថា មុខងារបួនជ្រុង គូបពហុធានៃដឺក្រេទី 4 និងខ្ពស់ជាងនេះក៏មិនមាន asymptotes oblique ដែរ។

ហើយ​ឥឡូវ​នេះ​សូម​ធ្វើ​ឱ្យ​ប្រាកដ​ថា​នៅ​ក្រាហ្វិក​ក៏​មិន​មាន asymptote oblique ។ ដើម្បីបង្ហាញភាពមិនច្បាស់លាស់ យើងប្រើ ច្បាប់របស់ L'Hopital:
ដែលត្រូវផ្ទៀងផ្ទាត់។

ទោះយ៉ាងណាក៏ដោយ នៅពេលដែលមុខងាររីកចម្រើនដោយគ្មានកំណត់ វាមិនមានបន្ទាត់ត្រង់ដែលក្រាហ្វរបស់វានឹងចូលទៅជិតនោះទេ។ ជិតស្និទ្ធគ្មានកំណត់.

ចូរបន្តទៅផ្នែកជាក់ស្តែងនៃមេរៀន៖

តើធ្វើដូចម្តេចដើម្បីស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ?

នេះ​ជា​របៀប​ដែល​ភារកិច្ច​ធម្មតា​ត្រូវ​បាន​បង្កើត​ឡើង ហើយ​វា​ជាប់​ពាក់ព័ន្ធ​នឹង​ការ​ស្វែង​រក​គំនូស​តាង​ទាំង​អស់​នៃ​ក្រាហ្វ (បញ្ឈរ ទ្វេ / ផ្ដេក)។ ទោះបីជាដើម្បីឱ្យកាន់តែច្បាស់លាស់នៅក្នុងការបង្កើតសំណួរ យើងកំពុងនិយាយអំពីការសិក្សាអំពីវត្តមានរបស់ asymtotes (បន្ទាប់ពីទាំងអស់ ប្រហែលជាមិនមានអ្វីទាំងអស់)។ តោះចាប់ផ្តើមជាមួយអ្វីដែលសាមញ្ញ៖

ឧទាហរណ៍ ១

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយវាងាយស្រួលក្នុងការបំបែកវាជាពីរចំណុច៖

1) ដំបូងយើងពិនិត្យមើលថាតើមាន asymtotes បញ្ឈរដែរឬទេ។ ភាគបែងរលត់ទៅ ហើយវាច្បាស់ភ្លាមៗថា ត្រង់ចំណុចនេះ អនុគមន៍រងទុក្ខ គម្លាតគ្មានទីបញ្ចប់ហើយបន្ទាត់ត្រង់ដែលផ្តល់ដោយសមីការគឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍។ ប៉ុន្តែមុននឹងធ្វើការសន្និដ្ឋានបែបនេះ ចាំបាច់ត្រូវស្វែងរកដែនកំណត់មួយចំហៀង៖

ខ្ញុំរំលឹកអ្នកអំពីបច្ចេកទេសគណនា ដែលខ្ញុំធ្លាប់បានប្រើនៅក្នុងអត្ថបទ មុខងារបន្ត។ ចំណុចបំបែក. នៅក្នុងកន្សោមក្រោមសញ្ញាកំណត់ ជំនួសឱ្យ "x" យើងជំនួស . មិនមានអ្វីគួរឱ្យចាប់អារម្មណ៍នៅក្នុងភាគយកទេ៖
.

ប៉ុន្តែនៅក្នុងភាគបែងវាប្រែចេញ ចំនួនអវិជ្ជមានគ្មានកំណត់:
វាកំណត់ជោគវាសនានៃដែនកំណត់។

ដែនកំណត់ខាងឆ្វេងគឺគ្មានកំណត់ ហើយជាគោលការណ៍ វាអាចទៅរួចរួចហើយក្នុងការអនុម័តសាលក្រមលើវត្តមាននៃ asymptote បញ្ឈរមួយ។ ប៉ុន្តែដែនកំណត់ម្ខាងគឺចាំបាច់មិនត្រឹមតែសម្រាប់រឿងនេះប៉ុណ្ណោះទេ - ពួកគេជួយក្នុងការយល់, របៀបក្រាហ្វនៃមុខងារមានទីតាំងនៅ ហើយគ្រោងវា។ ត្រឹមត្រូវ។. ដូច្នេះ យើងក៏ត្រូវគណនាដែនកំណត់ខាងស្តាំ៖

សេចក្តីសន្និដ្ឋាន៖ ដែនកំណត់ម្ខាងគឺគ្មានកំណត់ ដែលមានន័យថាបន្ទាត់គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍នៅ .

ដែនកំណត់ដំបូង កំណត់ដែលមានន័យថា ចាំបាច់ត្រូវ "បន្តការសន្ទនា" និងស្វែងរកដែនកំណត់ទីពីរ៖

ដែនកំណត់ទីពីរផងដែរ។ កំណត់.

ដូច្នេះ asymptote របស់យើងគឺ:

សេចក្តីសន្និដ្ឋាន៖ បន្ទាត់ត្រង់ដែលផ្តល់ដោយសមីការគឺជា asymptote ផ្ដេកនៃក្រាហ្វនៃអនុគមន៍នៅ .

ដើម្បីស្វែងរក asymptote ផ្ដេក
អ្នកអាចប្រើរូបមន្តសាមញ្ញ:

ប្រសិនបើមាន កំណត់ដែនកំណត់ បន្ទាប់មកបន្ទាត់គឺជា asymptote ផ្ដេកនៃក្រាហ្វនៃអនុគមន៍នៅ .

វាងាយមើលឃើញថាភាគបែងនិងភាគបែងនៃអនុគមន៍ លំដាប់នៃកំណើនមួយ។ដែលមានន័យថាដែនកំណត់ដែលចង់បាននឹងមានកំណត់៖

ចម្លើយ:

យោងទៅតាមលក្ខខណ្ឌវាមិនចាំបាច់ក្នុងការបញ្ចប់គំនូរនោះទេប៉ុន្តែប្រសិនបើនៅក្នុងតំលៃពេញ ការស្រាវជ្រាវមុខងារបន្ទាប់មកនៅលើសេចក្តីព្រាងយើងធ្វើគំនូរព្រាងភ្លាមៗ៖

ដោយផ្អែកលើដែនកំណត់ចំនួនបីដែលបានរកឃើញ សូមព្យាយាមស្វែងយល់ដោយឯករាជ្យពីរបៀបដែលក្រាហ្វនៃមុខងារអាចស្ថិតនៅ។ ពិបាកណាស់? ស្វែងរកចំណុច 5-6-7-8 ហើយគូសវានៅលើគំនូរ។ ទោះជាយ៉ាងណាក៏ដោយក្រាហ្វនៃមុខងារនេះត្រូវបានសាងសង់ដោយប្រើ ការបំប្លែងក្រាហ្វមុខងារបឋមហើយអ្នកអានដែលបានពិនិត្យដោយប្រុងប្រយ័ត្នឧទាហរណ៍ទី 21 នៃអត្ថបទនេះនឹងអាចទាយបានយ៉ាងងាយស្រួលថាតើវាជាខ្សែកោងប្រភេទណា។

ឧទាហរណ៍ ២

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

នេះជាឧទាហរណ៍ធ្វើដោយខ្លួនអ្នក។ ខ្ញុំសូមរំលឹកអ្នកថា ដំណើរការនេះត្រូវបានបែងចែកយ៉ាងងាយស្រួលជាពីរចំណុច - asymptotes បញ្ឈរ និង asymptotes oblique ។ នៅក្នុងដំណោះស្រាយគំរូ, asymptote ផ្ដេកត្រូវបានរកឃើញដោយប្រើគ្រោងការណ៍សាមញ្ញមួយ។

នៅក្នុងការអនុវត្ត អនុគមន៍ប្រភាគ-សនិទានភាគត្រូវបានជួបប្រទះញឹកញាប់បំផុត ហើយបន្ទាប់ពីការបណ្តុះបណ្តាលលើអ៊ីពែបូឡា យើងនឹងធ្វើឱ្យកិច្ចការស្មុគស្មាញ៖

ឧទាហរណ៍ ៣

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ៖ មួយ ពីរ និងរួចរាល់៖

1) រោគសញ្ញាបញ្ឈរត្រូវបានរកឃើញ នៅចំណុចនៃការឈប់សម្រាកគ្មានកំណត់ដូច្នេះអ្នកត្រូវពិនិត្យមើលថាតើភាគបែងទៅសូន្យឬអត់។ យើងនឹងសម្រេចចិត្ត សមីការ​ការ៉េ:

ការរើសអើងគឺវិជ្ជមាន ដូច្នេះសមីការមានឫសពិតពីរ ហើយការងារត្រូវបានបន្ថែមយ៉ាងសំខាន់ =)

ដើម្បីស្វែងរកដែនកំណត់ម្ខាងទៀត វាជាការងាយស្រួលក្នុងការធ្វើកត្តាត្រីកោណការ៉េ:
(សម្រាប់កំណត់ចំណាំតូច "ដក" ត្រូវបានណែនាំនៅក្នុងតង្កៀបទីមួយ) ។ សម្រាប់សំណាញ់សុវត្ថិភាព យើងនឹងធ្វើការត្រួតពិនិត្យផ្លូវចិត្ត ឬនៅលើសេចក្តីព្រាង ដោយបើកតង្កៀប។

ចូរយើងសរសេរមុខងារឡើងវិញក្នុងទម្រង់

ស្វែងរកដែនកំណត់ម្ខាងនៅចំណុច៖

ហើយនៅចំណុច៖

ដូច្នេះបន្ទាត់ត្រង់គឺជា asymtotes បញ្ឈរនៃក្រាហ្វនៃមុខងារដែលកំពុងពិចារណា។

2) ប្រសិនបើអ្នកក្រឡេកមើលមុខងារ បន្ទាប់មក វាច្បាស់ណាស់ថាដែនកំណត់នឹងមានកំណត់ ហើយយើងមាន asymptote ផ្ដេក។ ចូរបង្ហាញវាដោយសង្ខេប៖

ដូច្នេះ បន្ទាត់ត្រង់ (abscissa) គឺជា asymptote ផ្ដេកនៃក្រាហ្វនៃមុខងារនេះ។

ចម្លើយ:

ដែនកំណត់ដែលបានរកឃើញ និង asymtotes ផ្តល់ព័ត៌មានជាច្រើនអំពីក្រាហ្វនៃមុខងារ។ ព្យាយាមស្រមៃមើលគំនូរដោយគិតគូរដោយពិចារណាលើការពិតដូចខាងក្រោមៈ

គូសវាសកំណែក្រាហ្វរបស់អ្នកនៅលើសេចក្តីព្រាង។

ជាការពិតណាស់ ដែនកំណត់ដែលបានរកឃើញមិនកំណត់ច្បាស់អំពីប្រភេទនៃក្រាហ្វនោះទេ ហើយអ្នកអាចមានកំហុស ប៉ុន្តែការធ្វើលំហាត់ប្រាណខ្លួនឯងនឹងមានប្រយោជន៍ដែលមិនអាចកាត់ថ្លៃបានក្នុងអំឡុងពេល ការសិក្សាមុខងារពេញលេញ. រូបភាពត្រឹមត្រូវគឺនៅចុងបញ្ចប់នៃមេរៀន។

ឧទាហរណ៍ 4

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ឧទាហរណ៍ 5

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ទាំងនេះគឺជាភារកិច្ចសម្រាប់ការសម្រេចចិត្តឯករាជ្យ។ ក្រាហ្វទាំងពីរម្តងទៀតមាន asymptotes ផ្ដេក ដែលត្រូវបានរកឃើញភ្លាមៗដោយលក្ខណៈពិសេសខាងក្រោម៖ ក្នុងឧទាហរណ៍ទី 4 លំដាប់នៃកំណើនភាគបែង ច្រើនទៀតជាងលំដាប់នៃកំណើននៃភាគយក ហើយក្នុងឧទាហរណ៍ទី 5 ភាគយក និងភាគបែង លំដាប់នៃកំណើនមួយ។. នៅក្នុងដំណោះស្រាយគំរូមុខងារទីមួយត្រូវបានស៊ើបអង្កេតសម្រាប់វត្តមាននៃ asymptotes oblique នៅក្នុងវិធីពេញលេញនិងទីពីរ - តាមរយៈដែនកំណត់។

asymptotes ផ្តេក នៅក្នុងចំណាប់អារម្មណ៏ ប្រធានបទរបស់ខ្ញុំ គឺគួរឱ្យកត់សម្គាល់ ច្រើនជាងធម្មតា ជាងអ្វីដែល "ផ្អៀង" ពិតប្រាកដ។ ករណីទូទៅដែលរង់ចាំជាយូរមកហើយ៖

ឧទាហរណ៍ ៦

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ: បុរាណ​នៃ​ប្រភេទ​:

1) ដោយសារភាគបែងគឺវិជ្ជមាន មុខងារ បន្តនៅលើបន្ទាត់លេខទាំងមូល ហើយមិនមាន asymtotes បញ្ឈរទេ។ …តើវាល្អទេ? មិនមែនជាពាក្យត្រឹមត្រូវទេ - អស្ចារ្យណាស់! ធាតុទី 1 ត្រូវបានបិទ។

2) ពិនិត្យមើលវត្តមានរបស់ oblique asymtotes:

ដែនកំណត់ដំបូង កំណត់ដូច្នេះសូមបន្តទៅមុខទៀត។ ក្នុងអំឡុងពេលនៃការគណនាដែនកំណត់ទីពីរដើម្បីលុបបំបាត់ ភាពមិនប្រាកដប្រជា "គ្មានដែនកំណត់ ដកគ្មានដែនកំណត់"យើងនាំយកកន្សោមទៅជាភាគបែងរួម៖

ដែនកំណត់ទីពីរផងដែរ។ កំណត់ដូច្នេះ ក្រាហ្វនៃមុខងារដែលកំពុងពិចារណាមាន asymptote oblique៖

សេចក្តីសន្និដ្ឋាន:

ដូច្នេះសម្រាប់ក្រាហ្វនៃមុខងារ ជិតស្និទ្ធគ្មានកំណត់ខិតទៅជិតបន្ទាត់ត្រង់៖

ចំណាំថាវាកាត់ asymptote oblique របស់វានៅប្រភពដើម ហើយចំនុចប្រសព្វបែបនេះគឺអាចទទួលយកបាន - វាជាការសំខាន់ណាស់ដែលថា "អ្វីគ្រប់យ៉ាងគឺធម្មតា" នៅគ្មានកំណត់ (តាមពិតទៅ យើងកំពុងនិយាយអំពី asymptotes នៅទីនោះ)។

ឧទាហរណ៍ ៧

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ៖ មិនមានអ្វីច្រើនក្នុងការធ្វើអត្ថាធិប្បាយទេ ដូច្នេះខ្ញុំនឹងគូរគំរូប្រហាក់ប្រហែលនៃដំណោះស្រាយចុងក្រោយ៖

1) រោគសញ្ញាបញ្ឈរ។ ចូរយើងស្វែងយល់ពីចំណុច។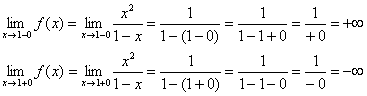

បន្ទាត់ត្រង់គឺជា asymptote បញ្ឈរសម្រាប់គ្រោងនៅ .

2) រោគសញ្ញា Oblique៖

បន្ទាត់ត្រង់គឺជា asymptote oblique សម្រាប់ក្រាហ្វនៅ .

ចម្លើយ:

ដែនកំណត់ និង asymtotes ម្ខាងដែលបានរកឃើញអនុញ្ញាតឱ្យយើងសន្មត់ដោយភាពប្រាកដប្រជាខ្ពស់ថាតើក្រាហ្វនៃមុខងារនេះមើលទៅដូចអ្វី។ គូរត្រឹមត្រូវនៅចុងបញ្ចប់នៃមេរៀន។

ឧទាហរណ៍ ៨

ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

នេះគឺជាឧទាហរណ៍មួយសម្រាប់ដំណោះស្រាយឯករាជ្យ ដើម្បីភាពងាយស្រួលនៃការគណនាដែនកំណត់មួយចំនួន អ្នកអាចបែងចែកភាគយកដោយភាគបែងដោយពាក្យ។ ហើយម្តងទៀត ការវិភាគលទ្ធផល សូមព្យាយាមគូរក្រាហ្វនៃមុខងារនេះ។

ជាក់ស្តែង ម្ចាស់នៃ asymptotes oblique "ពិត" គឺជាក្រាហ្វនៃអនុគមន៍ប្រភាគ-សនិទានកម្មទាំងនោះ ដែលកម្រិតខ្ពស់បំផុតនៃភាគយក មួយទៀតកំរិតខ្ពស់បំផុតនៃភាគបែង។ ប្រសិនបើច្រើនទៀត វានឹងមិនមាន asymptote oblique (ឧទាហរណ៍ ) ។

ប៉ុន្តែអព្ភូតហេតុផ្សេងទៀតកើតឡើងក្នុងជីវិត៖

ឧទាហរណ៍ ៩

ឧទាហរណ៍ 11

ពិនិត្យក្រាហ្វនៃមុខងារសម្រាប់ asymtotes

ដំណោះស្រាយ៖ វាច្បាស់ណាស់។ ដូច្នេះហើយ យើងពិចារណាតែពាក់កណ្តាលយន្តហោះត្រឹមត្រូវ ដែលមានក្រាហ្វនៃមុខងារ។

ដូច្នេះ បន្ទាត់ត្រង់ (អ័ក្ស y) គឺជា asymptote បញ្ឈរសម្រាប់ក្រាហ្វនៃអនុគមន៍នៅ .

2) ការសិក្សានៃ asymptote oblique អាចត្រូវបានអនុវត្តយោងទៅតាមគ្រោងការណ៍ពេញលេញប៉ុន្តែនៅក្នុងអត្ថបទ ច្បាប់របស់មន្ទីរពេទ្យ Lយើងបានរកឃើញថាអនុគមន៍លីនេអ៊ែរនៃលំដាប់នៃកំណើនខ្ពស់ជាងលោការីតមួយ ដូច្នេះ៖ (សូមមើលឧទាហរណ៍ទី 1 នៃមេរៀនដូចគ្នា) ។

សេចក្តីសន្និដ្ឋាន៖ អ័ក្ស abscissa គឺជា asymptote ផ្ដេកនៃក្រាហ្វនៃអនុគមន៍នៅ .

ចម្លើយ:
, ប្រសិនបើ ;
, ប្រសិនបើ .

គំនូរសម្រាប់ភាពច្បាស់លាស់៖

គួរឱ្យចាប់អារម្មណ៍មុខងារដែលហាក់ដូចជាស្រដៀងគ្នាមិនមាន asymtotes ទាល់តែសោះ (អ្នកដែលចង់បានអាចពិនិត្យមើលវាបាន) ។

ឧទាហរណ៍ពីរចុងក្រោយនៃការសិក្សាដោយខ្លួនឯង៖

ឧទាហរណ៍ 12

ពិនិត្យក្រាហ្វនៃមុខងារសម្រាប់ asymtotes

តើក្រាហ្វនៃអនុគមន៍មួយអាចមាន asymtotes ប៉ុន្មាន?

គ្មាន, មួយ, ពីរ, បី... ឬចំនួនគ្មានកំណត់។ យើងនឹងមិនទៅឆ្ងាយសម្រាប់ឧទាហរណ៍ទេយើងនឹងរំលឹកឡើងវិញនូវមុខងារបឋម។ ប៉ារ៉ាបូឡា, ប៉ារ៉ាបូឡាគូប, sinusoid មិនមានរោគសញ្ញាអ្វីទាំងអស់។ ក្រាហ្វនៃអនុគមន៍លោការីតអិចស្ប៉ូណង់ស្យែលមាន asymptote តែមួយ។ arctangent, arccotangent មាន​ពីរ​ក្នុង​ចំណោម​ពួក​គេ ហើយ​តង់ហ្សង់, កូតង់សង់​មាន​ចំនួន​គ្មាន​កំណត់។ វាមិនមែនជារឿងចម្លែកទេសម្រាប់ក្រាហ្វដែលមាន asymtotes ផ្ដេក និងបញ្ឈរ។ Hyperbole នឹងស្រឡាញ់អ្នកជានិច្ច។

តើវាមានន័យយ៉ាងណាក្នុងការស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ?

នេះមានន័យថាការស្វែងរកសមីការរបស់ពួកគេ ហើយគូរបន្ទាត់ត្រង់ប្រសិនបើលក្ខខណ្ឌនៃបញ្ហាទាមទារវា។ ដំណើរការពាក់ព័ន្ធនឹងការស្វែងរកដែនកំណត់នៃមុខងារ។

asymtotes បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍មួយ។

asymptote បញ្ឈរនៃក្រាហ្វជាក្បួនគឺនៅចំណុចនៃភាពមិនដំណើរការគ្មានកំណត់នៃមុខងារ។ វាសាមញ្ញ៖ ប្រសិនបើនៅចំណុចមួយ មុខងារទទួលរងការបំបែកគ្មានកំណត់ នោះបន្ទាត់ត្រង់ដែលផ្តល់ដោយសមីការគឺជា asymptote បញ្ឈរនៃក្រាហ្វ។

ចំណាំ៖ សូមចំណាំថាសញ្ញាណត្រូវបានប្រើដើម្បីសំដៅទៅលើគោលគំនិតពីរផ្សេងគ្នាទាំងស្រុង។ ចំនុចគឺបង្កប់ន័យឬសមីការនៃបន្ទាត់ត្រង់ - អាស្រ័យលើបរិបទ។

ដូច្នេះ ដើម្បីបង្កើតវត្តមាននៃ asymptote បញ្ឈរនៅចំណុចមួយ វាគ្រប់គ្រាន់ដើម្បីបង្ហាញថាយ៉ាងហោចណាស់មួយនៃដែនកំណត់ម្ខាងគឺគ្មានកំណត់។ ភាគច្រើនជាញឹកញាប់ នេះគឺជាចំណុចដែលភាគបែងនៃអនុគមន៍ស្មើនឹងសូន្យ។ តាមការពិត យើងបានរកឃើញសញ្ញាបញ្ឈររួចហើយនៅក្នុងឧទាហរណ៍ចុងក្រោយនៃមេរៀនស្តីពីការបន្តនៃមុខងារមួយ។ ប៉ុន្តែនៅក្នុងករណីមួយចំនួនមានដែនកំណត់ម្ខាងតែមួយប៉ុណ្ណោះ ហើយប្រសិនបើវាគ្មានដែនកំណត់ នោះម្តងទៀត - ស្រឡាញ់និងពេញចិត្ត asymptote បញ្ឈរ។ រូបភាពសាមញ្ញបំផុត៖ និងអ័ក្ស y ។

ការពិតជាក់ស្តែងក៏ធ្វើតាមពីខាងលើផងដែរ៖ ប្រសិនបើមុខងារបន្តដំណើរការ នោះមិនមានរោគសញ្ញាបញ្ឈរទេ។ ដោយហេតុផលខ្លះ ប៉ារ៉ាបូឡាបានមកក្នុងគំនិត។ ពិតហើយ តើអ្នកអាច "បិទ" បន្ទាត់ត្រង់ត្រង់នេះនៅឯណា? ... បាទ ... ខ្ញុំយល់ ... អ្នកដើរតាមពូ Freud ញាប់ញ័រ =)

សេចក្តីថ្លែងការណ៍របស់ converse ជាទូទៅមិនពិតទេ៖ ឧទាហរណ៍ មុខងារមិនត្រូវបានកំណត់នៅលើបន្ទាត់ពិតទាំងមូលទេ ប៉ុន្តែវាត្រូវបានដកហូតទាំងស្រុងនូវ asymtotes ។

asymtotes Oblique នៃក្រាហ្វនៃអនុគមន៍មួយ។

ភាពលំអៀង (ជាករណីពិសេស - ផ្តេក) អាចគូរបាន ប្រសិនបើអាគុយម៉ង់មុខងារមាននិន្នាការទៅជា "បូកគ្មានដែនកំណត់" ឬ "ដកគ្មានដែនកំណត់"។ ដូច្នេះ ក្រាហ្វនៃអនុគមន៍មួយមិនអាចមាន asymptotes oblique លើសពី 2 បានទេ។ ឧទាហរណ៍ ក្រាហ្វនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែលមាន asymptote ផ្តេកតែមួយនៅ ហើយក្រាហ្វនៃអាកតង់សង់នៅមាន asymptotes ពីរ និងមួយផ្សេងគ្នា។

Asymptote នៃក្រាហ្វនៃមុខងារមួយ។ y \u003d f (x) ត្រូវបានគេហៅថាបន្ទាត់ដែលមានលក្ខណៈសម្បត្តិថាចម្ងាយពីចំណុច (x, f (x)) ទៅបន្ទាត់នេះមានទំនោរទៅសូន្យជាមួយនឹងការដកយកចេញគ្មានដែនកំណត់នៃចំណុចក្រាហ្វពីប្រភពដើម។

រូបភាព 3.10 ។ ឧទាហរណ៍ក្រាហ្វិកត្រូវបានផ្តល់ឱ្យ បញ្ឈរ, ផ្ដេកនិង oblique asymptote ។

ការស្វែងរក asymtotes នៃក្រាហ្វគឺផ្អែកលើទ្រឹស្តីបទទាំងបីខាងក្រោម។

ទ្រឹស្តីបទ asymptote បញ្ឈរ។ អនុញ្ញាតឱ្យអនុគមន៍ y \u003d f (x) ត្រូវបានកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច x 0 (ប្រហែលជាមិនរាប់បញ្ចូលចំណុចនេះដោយខ្លួនវា) ហើយយ៉ាងហោចណាស់ដែនកំណត់ម្ខាងនៃអនុគមន៍គឺស្មើនឹងគ្មានកំណត់ ពោលគឺឧ។ បន្ទាប់មកបន្ទាត់ x \u003d x 0 គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារ y \u003d f (x) ។

ជាក់ស្តែង បន្ទាត់ x \u003d x 0 មិនអាចជា asymptote បញ្ឈរបានទេ ប្រសិនបើមុខងារបន្តនៅចំណុច x 0 ព្រោះក្នុងករណីនេះ . ដូច្នេះ asymptotes បញ្ឈរគួរតែត្រូវបានស្វែងរកនៅចំណុចដាច់នៃមុខងារមួយ ឬនៅចុងបញ្ចប់នៃដែនរបស់វា។

ទ្រឹស្តីបទនៅលើ asymptote ផ្ដេក។ អនុញ្ញាតឱ្យមុខងារ y \u003d f (x) ត្រូវបានកំណត់សម្រាប់ x ធំគ្រប់គ្រាន់ ហើយមានដែនកំណត់កំណត់នៃអនុគមន៍។ បន្ទាប់មកបន្ទាត់ y = b គឺជា asymptote ផ្ដេកនៃក្រាហ្វនៃអនុគមន៍។

មតិយោបល់។ ប្រសិនបើមានដែនកំណត់តែមួយគត់ នោះមុខងារមានរៀងៗខ្លួន។ ផ្នែកខាងឆ្វេងឬ ខាងស្តាំ asymptote ផ្ដេក។

នៅក្នុងព្រឹត្តិការណ៍នោះ មុខងារអាចមាន asymptote oblique ។

ទ្រឹស្ដី Oblique asymptote ។ អនុញ្ញាតឱ្យអនុគមន៍ y = f(x) ត្រូវបានកំណត់សម្រាប់ x ធំគ្រប់គ្រាន់ ហើយមានដែនកំណត់កំណត់ . បន្ទាប់មកបន្ទាត់ y = kx + b គឺជា asymptote oblique នៃក្រាហ្វនៃអនុគមន៍។

ដោយគ្មានភស្តុតាង។

asymptote oblique ក៏ដូចជាដៃផ្ដេក អាចជាដៃស្តាំ ឬដៃឆ្វេង ប្រសិនបើមូលដ្ឋាននៃដែនកំណត់ដែលត្រូវគ្នាគឺគ្មានដែនកំណត់នៃសញ្ញាជាក់លាក់មួយ។

ការសិក្សាអំពីមុខងារ និងការបង្កើតក្រាហ្វរបស់ពួកគេជាធម្មតារួមមានជំហានដូចខាងក្រោមៈ

1. ស្វែងរកដែននៃមុខងារ។

2. ស៊ើបអង្កេតមុខងារសម្រាប់គូ-សេស។

3. ស្វែងរក asymptotes បញ្ឈរដោយពិនិត្យមើលចំណុច discontinuity និងឥរិយាបទនៃអនុគមន៍នៅលើព្រំដែននៃដែននៃនិយមន័យប្រសិនបើពួកគេមានកំណត់។

4. ស្វែងរក asymptotes ផ្ដេក ឬ oblique ដោយពិនិត្យមើលឥរិយាបថនៃមុខងារនៅ infinity ។

5. ស្វែងរក extrema និងចន្លោះពេលនៃ monotonicity នៃមុខងារ។

6. ស្វែងរកចន្លោះប្រហោងនៃអនុគមន៍ និងចំនុច inflection ។

7. ស្វែងរកចំនុចប្រសព្វជាមួយអ័ក្សកូអរដោនេ ហើយប្រហែលជាចំនុចបន្ថែមមួយចំនួនដែលធ្វើអោយក្រាហ្វ។

មុខងារឌីផេរ៉ង់ស្យែល

វាអាចត្រូវបានបង្ហាញថាប្រសិនបើអនុគមន៍មួយមានដែនកំណត់ស្មើនឹងចំនួនកំណត់សម្រាប់មូលដ្ឋានជាក់លាក់មួយ នោះវាអាចត្រូវបានតំណាងថាជាផលបូកនៃចំនួននេះ និងតម្លៃគ្មានកំណត់សម្រាប់មូលដ្ឋានដូចគ្នា (និងច្រាសមកវិញ): ។

ចូរ​អនុវត្ត​ទ្រឹស្តីបទ​នេះ​ទៅ​មុខងារ​ដែល​អាច​បែងចែក​បាន៖ .

ដូច្នេះការបង្កើនអនុគមន៍ Dy មានពាក្យពីរ៖ 1) លីនេអ៊ែរទាក់ទងនឹង Dx, i.e. f`(x)Dx; 2) មិនមែនលីនេអ៊ែរទាក់ទងនឹង Dx, i.e. a(Dx)Dx ។ ក្នុងពេលជាមួយគ្នានេះចាប់តាំងពី ពាក្យទីពីរនេះគឺគ្មានដែនកំណត់នៃលំដាប់ខ្ពស់ជាង Dx (ដូចដែល Dx មានទំនោរទៅសូន្យ វាមានទំនោរទៅសូន្យកាន់តែលឿន)។

ឌីផេរ៉ង់ស្យែលមុខងារត្រូវបានគេហៅថាផ្នែកសំខាន់នៃមុខងារបង្កើន លីនេអ៊ែរទាក់ទងនឹង Dx ស្មើនឹងផលិតផលនៃដេរីវេ និងការកើនឡើងនៃអថេរឯករាជ្យ dy = f `(x)Dx ។

រកឌីផេរ៉ង់ស្យែលនៃអនុគមន៍ y = x ។

ចាប់តាំងពី dy = f `(x)Dx = x`Dx = Dx បន្ទាប់មក dx = Dx, i.e. ឌីផេរ៉ង់ស្យែលនៃអថេរឯករាជ្យគឺស្មើនឹងការកើនឡើងនៃអថេរនោះ។

ដូច្នេះរូបមន្តសម្រាប់ឌីផេរ៉ង់ស្យែលនៃអនុគមន៍អាចត្រូវបានសរសេរជា dy = f `(x)dх។ នោះហើយជាមូលហេតុដែលនិមិត្តសញ្ញាមួយសម្រាប់និស្សន្ទវត្ថុគឺប្រភាគ dy/dх។

អត្ថន័យធរណីមាត្រនៃឌីផេរ៉ង់ស្យែលត្រូវបានបង្ហាញ
រូបភាព 3.11 ។ យកចំណុចបំពាន M(x,y) នៅលើក្រាហ្វនៃអនុគមន៍ y = f(x)។ ចូរផ្តល់អាគុយម៉ង់ x បង្កើន Dx ។ បន្ទាប់មកអនុគមន៍ y = f(x) នឹងទទួលបានការកើនឡើង Dy = f(x + Dх) - f(x) ។ ចូរគូរតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុច M ដែលបង្កើតជាមុំ a ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស x ពោលគឺឧ។ f `(x) = tg a ។ ពីត្រីកោណកែង MKN
KN \u003d MN * tg a \u003d Dx * tg a \u003d f `(x) Dx \u003d dy ។

ដូច្នេះឌីផេរ៉ង់ស្យែលនៃអនុគមន៍គឺជាការបង្កើននៅក្នុងលំដាប់នៃតង់សង់ដែលទាញទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចដែលបានផ្តល់ឱ្យនៅពេល x ត្រូវបានបន្ថែមដោយ Dx ។

លក្ខណៈសម្បត្តិនៃឌីផេរ៉ង់ស្យែលគឺមានលក្ខណៈដូចគ្នាទៅនឹងឌីផេរ៉ង់ស្យែល៖

3. d(u ± v) = du ± dv ។

4. d(uv) = v du + u dv ។

5. d(u/v) = (v du - u dv)/v 2 .

ទោះយ៉ាងណាក៏ដោយមានទ្រព្យសម្បត្តិសំខាន់នៃឌីផេរ៉ង់ស្យែលនៃមុខងារដែលដេរីវេរបស់វាមិនមាន - នេះគឺ ភាពខុសគ្នានៃទម្រង់ឌីផេរ៉ង់ស្យែល.

ពីនិយមន័យនៃឌីផេរ៉ង់ស្យែលសម្រាប់អនុគមន៍ y = f(x) ឌីផេរ៉ង់ស្យែលគឺ dy = f`(x)dх។ ប្រសិនបើមុខងារនេះ y គឺស្មុគស្មាញ ឧ។ y = f(u) ដែល u = j(x) បន្ទាប់មក y = f និង f `(x) = f `(u)*u` ។ បន្ទាប់មក dy = f`(u)*u`dx ។ ប៉ុន្តែសម្រាប់មុខងារ
u = j(x) ឌីផេរ៉ង់ស្យែល du = u`dx ។ ដូច្នេះ dy = f `(u)*du ។

ការប្រៀបធៀបសមភាព dy = f `(x)dх និង dy = f `(u)*du យើងប្រាកដថារូបមន្តឌីផេរ៉ង់ស្យែលមិនផ្លាស់ប្តូរទេ ប្រសិនបើជំនួសឱ្យមុខងារនៃអថេរ x យើងពិចារណាមុខងារនៃ អថេរអាស្រ័យ u. ទ្រព្យសម្បត្តិនៃឌីផេរ៉ង់ស្យែលនេះត្រូវបានគេហៅថា invariance (ពោលគឺ invariance) នៃទម្រង់ (ឬរូបមន្ត) នៃឌីផេរ៉ង់ស្យែល។

ទោះយ៉ាងណាក៏ដោយ វានៅតែមានភាពខុសគ្នានៅក្នុងរូបមន្តទាំងពីរនេះ៖ នៅក្នុងទីមួយនៃពួកវា ឌីផេរ៉ង់ស្យែលនៃអថេរឯករាជ្យគឺស្មើនឹងការបង្កើននៃអថេរនេះ i.e. dx = Dx ហើយនៅក្នុងទីពីរ ឌីផេរ៉ង់ស្យែលនៃអនុគមន៍ du គឺគ្រាន់តែជាផ្នែកលីនេអ៊ែរនៃការបង្កើនមុខងារនេះ Du ហើយសម្រាប់តែ Dх du » Du តូចប៉ុណ្ណោះ។