ចូរនិយាយថា Achilles រត់លឿនជាងសត្វអណ្តើកដប់ដង ហើយមានល្បឿនមួយពាន់នៅពីក្រោយវា។ ក្នុងអំឡុងពេលដែល Achilles រត់ចម្ងាយនេះ អណ្តើកវារមួយរយជំហានក្នុងទិសដៅដូចគ្នា។ នៅពេលដែល Achilles រត់បានមួយរយជំហាន អណ្តើកនឹងវារដប់ជំហានទៀត។ ដំណើរការនឹងបន្តដោយគ្មានកំណត់ Achilles នឹងមិនតាមទាន់សត្វអណ្តើកទេ។
ហេតុផលនេះបានក្លាយជាការតក់ស្លុតឡូជីខលសម្រាប់មនុស្សជំនាន់ក្រោយៗទាំងអស់។ Aristotle, Diogenes, Kant, Hegel, Gilbert... ពួកគេទាំងអស់នៅក្នុងវិធីមួយឬមួយផ្សេងទៀតបានចាត់ទុកថា aporias របស់ Zeno ។ តក់ស្លុតខ្លាំងម្ល៉េះ»។ ... ការពិភាក្សាបន្តនៅពេលបច្ចុប្បន្ននេះ សហគមន៍វិទ្យាសាស្ត្រមិនទាន់អាចយល់ឃើញរួមអំពីខ្លឹមសារនៃពាក្យប្រៀបធៀប ... ការវិភាគគណិតវិទ្យា ទ្រឹស្ដីកំណត់ វិធីសាស្រ្តរូបវិទ្យា និងទស្សនវិជ្ជាថ្មីត្រូវបានចូលរួមនៅក្នុងការសិក្សាអំពីបញ្ហានេះ។ ; គ្មាននរណាម្នាក់ក្នុងចំណោមពួកគេក្លាយជាដំណោះស្រាយដែលទទួលយកជាសកលចំពោះបញ្ហា..."[Wikipedia, Zeno's Aporias"] មនុស្សគ្រប់គ្នាយល់ថាពួកគេកំពុងត្រូវបានបោកបញ្ឆោត ប៉ុន្តែគ្មាននរណាម្នាក់យល់ថាអ្វីជាការបោកប្រាស់នោះទេ។
តាមទស្សនៈនៃគណិតវិទ្យា Zeno នៅក្នុង aporia របស់គាត់បានបង្ហាញយ៉ាងច្បាស់ពីការផ្លាស់ប្តូរពីតម្លៃទៅ។ ការផ្លាស់ប្តូរនេះបង្កប់ន័យអនុវត្តជំនួសឱ្យថេរ។ តាមដែលខ្ញុំយល់ ឧបករណ៍គណិតវិទ្យាសម្រាប់អនុវត្តឯកតាអថេរនៃការវាស់វែងមិនទាន់ត្រូវបានបង្កើតឡើងនៅឡើយ ឬវាមិនត្រូវបានអនុវត្តចំពោះ aporia របស់ Zeno ទេ។ ការអនុវត្តតក្កវិជ្ជាធម្មតារបស់យើងនាំយើងចូលទៅក្នុងអន្ទាក់។ យើងដោយនិចលភាពនៃការគិត អនុវត្តឯកតាថេរនៃពេលវេលាទៅគ្នាទៅវិញទៅមក។ តាមទស្សនៈរូបវន្ត នេះមើលទៅដូចជាការយឺតយ៉ាវក្នុងពេលវេលា រហូតទាល់តែវាឈប់ទាំងស្រុងនៅពេល Achilles ចាប់សត្វអណ្តើក។ ប្រសិនបើពេលវេលាឈប់ Achilles មិនអាចយកឈ្នះអណ្តើកបានទៀតទេ។
បើយើងបង្វែរតក្កវិជ្ជាដែលយើងធ្លាប់ធ្វើ នោះអ្វីៗក៏នឹងទៅកន្លែងដែរ។ Achilles រត់ក្នុងល្បឿនថេរ។ ផ្នែកបន្តបន្ទាប់នីមួយៗនៃផ្លូវរបស់វាខ្លីជាងផ្នែកមុនដប់ដង។ ដូច្នោះហើយ ពេលវេលាដែលចំណាយលើការយកឈ្នះគឺតិចជាងការលើកមុនដប់ដង។ ប្រសិនបើយើងអនុវត្តគោលគំនិតនៃ "ភាពមិនចេះរីងស្ងួត" នៅក្នុងស្ថានភាពនេះ នោះវានឹងជាការត្រឹមត្រូវក្នុងការនិយាយថា "Achilles នឹងវ៉ាដាច់អណ្តើកយ៉ាងលឿនបំផុត"។
តើធ្វើដូចម្តេចដើម្បីជៀសវាងអន្ទាក់ឡូជីខលនេះ? រក្សានៅក្នុងឯកតានៃពេលវេលា ហើយកុំប្តូរទៅតម្លៃទៅវិញទៅមក។ នៅក្នុងភាសារបស់ Zeno វាមើលទៅដូចនេះ:
នៅពេលដែលវាត្រូវ Achilles រត់មួយពាន់ជំហាន អណ្តើកវារមួយរយជំហានក្នុងទិសដៅដូចគ្នា។ ក្នុងចន្លោះពេលបន្ទាប់ ស្មើនឹងលើកទីមួយ Achilles នឹងរត់មួយពាន់ជំហានទៀត ហើយអណ្តើកនឹងវារមួយរយជំហាន។ ឥឡូវនេះ Achilles គឺប្រាំបីរយជំហានមុនអណ្តើក។
វិធីសាស្រ្តនេះពិពណ៌នាឱ្យបានគ្រប់គ្រាន់នូវការពិតដោយគ្មានភាពផ្ទុយគ្នាឡូជីខល។ ប៉ុន្តែនេះមិនមែនជាដំណោះស្រាយពេញលេញចំពោះបញ្ហានោះទេ។ សេចក្តីថ្លែងការណ៍របស់ Einstein អំពីភាពមិនអាចគ្រប់គ្រងបាននៃល្បឿននៃពន្លឺគឺស្រដៀងទៅនឹង aporia របស់ Zeno "Achilles and the tortoise" ។ យើងមិនទាន់បានសិក្សា គិតឡើងវិញ និងដោះស្រាយបញ្ហានេះនៅឡើយទេ។ ហើយដំណោះស្រាយត្រូវតែស្វែងរកមិនមែនក្នុងចំនួនច្រើនគ្មានកំណត់ទេ ប៉ុន្តែជាឯកតារង្វាស់។
aporia គួរឱ្យចាប់អារម្មណ៍មួយទៀតនៃ Zeno ប្រាប់ពីព្រួញហោះ:
ព្រួញហោះគឺគ្មានចលនាទេ ព្រោះរាល់ពេលដែលវាសម្រាក ហើយចាប់តាំងពីពេលវាសម្រាកគ្រប់ពេល វាតែងតែសម្រាក។
នៅក្នុង aporia នេះ ភាពផ្ទុយគ្នានៃឡូជីខលត្រូវបានយកឈ្នះយ៉ាងសាមញ្ញ - វាគ្រប់គ្រាន់ដើម្បីបញ្ជាក់ថារាល់ពេលដែលព្រួញហោះហើរគឺសម្រាកនៅចំណុចផ្សេងៗគ្នាក្នុងលំហដែលតាមពិតគឺជាចលនា។ មានចំណុចមួយទៀតដែលត្រូវកត់សម្គាល់នៅទីនេះ។ ពីរូបថតមួយសន្លឹកនៃឡាននៅលើផ្លូវ វាមិនអាចកំណត់ពីការពិតនៃចលនារបស់វា ឬចម្ងាយទៅវាបានទេ។ ដើម្បីកំណត់ពីការពិតនៃចលនារបស់រថយន្ត រូបថតពីរសន្លឹកដែលថតពីចំណុចដូចគ្នា នៅចំណុចផ្សេងគ្នា ត្រូវការពេលវេលា ប៉ុន្តែពួកវាមិនអាចប្រើដើម្បីកំណត់ចម្ងាយបានទេ។ ដើម្បីកំណត់ចម្ងាយទៅរថយន្ត អ្នកត្រូវការរូបថតពីរសន្លឹកដែលថតពីចំណុចផ្សេងៗគ្នាក្នុងលំហក្នុងពេលតែមួយ ប៉ុន្តែអ្នកមិនអាចកំណត់ការពិតនៃចលនាពីពួកវាបានទេ (តាមធម្មជាតិ អ្នកនៅតែត្រូវការទិន្នន័យបន្ថែមសម្រាប់ការគណនា ត្រីកោណមាត្រនឹងជួយអ្នក)។ អ្វីដែលខ្ញុំចង់បញ្ជាក់ជាពិសេសនោះគឺថា ចំណុចពីរនៅក្នុងពេលវេលា និងពីរចំណុចនៅក្នុងលំហ គឺជារឿងពីរផ្សេងគ្នាដែលមិនគួរមានការភាន់ច្រឡំនោះទេ ព្រោះថាវាផ្តល់ឱកាសខុសៗគ្នាសម្រាប់ការរុករក។
ថ្ងៃពុធ ទី៤ ខែកក្កដា ឆ្នាំ២០១៨
ជាការប្រសើរណាស់ ភាពខុសគ្នារវាង set និង multiset ត្រូវបានពិពណ៌នានៅក្នុង Wikipedia ។ យើងមើលទៅ។
ដូចដែលអ្នកអាចឃើញ "សំណុំមិនអាចមានធាតុដូចគ្នាបេះបិទពីរ" ប៉ុន្តែប្រសិនបើមានធាតុដូចគ្នាបេះបិទនៅក្នុងសំណុំនោះ សំណុំបែបនេះត្រូវបានគេហៅថា "ពហុសិត" ។ សត្វដែលសមហេតុផលនឹងមិនយល់ពីតក្កវិជ្ជានៃភាពមិនសមហេតុផលបែបនេះឡើយ។ នេះជាកម្រិតនៃសត្វសេកដែលចេះនិយាយ និងស្វាដែលបានហ្វឹកហ្វឺនហើយ ដែលក្នុងចិត្តគឺអវត្តមានពីពាក្យ «ទាំងស្រុង»។ គណិតវិទូដើរតួជាអ្នកបង្ហាត់បង្រៀនធម្មតា ដោយអធិប្បាយគំនិតមិនសមហេតុសមផលរបស់ពួកគេមកកាន់យើង។
មានពេលមួយ វិស្វករដែលសាងសង់ស្ពានបានជិះទូកក្រោមស្ពាន កំឡុងពេលធ្វើតេស្តស្ពាន។ ប្រសិនបើស្ពានដួលរលំ វិស្វករមធ្យមបានស្លាប់នៅក្រោមគំនរបាក់បែកនៃការបង្កើតរបស់គាត់។ ប្រសិនបើស្ពានអាចទប់ទល់នឹងបន្ទុកបាន វិស្វករដែលមានទេពកោសល្យបានសាងសង់ស្ពានផ្សេងទៀត។
មិនថាគណិតវិទូលាក់ខ្លួននៅពីក្រោយឃ្លាថា "ចិត្តខ្ញុំ ខ្ញុំនៅក្នុងផ្ទះ" ឬ "គណិតវិទ្យាសិក្សាគំនិតអរូបី" មានទងផ្ចិតមួយដែលអាចភ្ជាប់ពួកវាជាមួយការពិត។ ទងផ្ចិតនេះគឺជាលុយ។ ចូរយើងអនុវត្តទ្រឹស្ដីសំណុំគណិតវិទ្យាចំពោះគណិតវិទូខ្លួនឯង។
យើងរៀនគណិតវិទ្យាបានយ៉ាងល្អ ហើយឥឡូវយើងកំពុងអង្គុយនៅតុបើកប្រាក់ខែ។ នៅទីនេះមានគណិតវិទូមករកយើងដើម្បីលុយរបស់គាត់។ យើងរាប់ចំនួនសរុបទៅគាត់ ហើយដាក់វានៅលើតុរបស់យើងជាគំនរផ្សេងៗគ្នា ដែលយើងដាក់វិក័យប័ត្រនៃនិកាយដូចគ្នា។ បន្ទាប់មកយើងយកវិក្កយបត្រមួយពីគំនរនីមួយៗ ហើយផ្តល់ឱ្យគណិតវិទូនូវ "ប្រាក់ខែគណិតវិទ្យា" របស់គាត់។ យើងពន្យល់គណិតវិទ្យាថា គាត់នឹងទទួលបានវិក្កយបត្រដែលនៅសល់ លុះត្រាតែគាត់បញ្ជាក់ថា សំណុំដែលគ្មានធាតុដូចគ្នាបេះបិទ មិនស្មើនឹងសំណុំដែលមានធាតុដូចគ្នាបេះបិទ។ នេះជាកន្លែងដែលការសប្បាយចាប់ផ្តើម។
ជាដំបូង តក្កវិជ្ជារបស់តំណាងរាស្ត្រនឹងដំណើរការ៖ "អ្នកអាចអនុវត្តវាចំពោះអ្នកដទៃ ប៉ុន្តែមិនមែនចំពោះខ្ញុំទេ!" លើសពីនេះ ការធានានឹងចាប់ផ្តើមថាមានលេខក្រដាសប្រាក់ផ្សេងៗគ្នានៅលើក្រដាសប្រាក់នៃនិកាយដូចគ្នា ដែលមានន័យថា ពួកវាមិនអាចចាត់ទុកជាធាតុដូចគ្នាបានទេ។ ជាការប្រសើរណាស់, យើងរាប់ប្រាក់ខែជាកាក់ - មិនមានលេខនៅលើកាក់ទេ។ នៅទីនេះ គណិតវិទូនឹងនឹកឃើញរូបវិទ្យាយ៉ាងក្លៀវក្លា៖ កាក់ផ្សេងៗគ្នាមានបរិមាណកខ្វក់ខុសៗគ្នា រចនាសម្ព័ន្ធគ្រីស្តាល់ និងការរៀបចំអាតូមសម្រាប់កាក់នីមួយៗគឺប្លែក...
ហើយឥឡូវនេះខ្ញុំមានសំណួរដែលគួរឱ្យចាប់អារម្មណ៍បំផុត: តើព្រំប្រទល់នៅឯណាដែលលើសពីធាតុនៃសំណុំច្រើនប្រែទៅជាធាតុនៃសំណុំមួយហើយច្រាសមកវិញ? បន្ទាត់បែបនេះមិនមានទេ - អ្វីគ្រប់យ៉ាងត្រូវបានសម្រេចដោយ shamans វិទ្យាសាស្ត្រនៅទីនេះមិនជិតទេ។
មើលនេះ។ យើងជ្រើសរើសកីឡដ្ឋានបាល់ទាត់ដែលមានផ្ទៃដីដូចគ្នា។ តំបន់នៃវាលគឺដូចគ្នាដែលមានន័យថាយើងមានសំណុំពហុ។ ប៉ុន្តែបើយើងពិចារណាឈ្មោះកីឡដ្ឋានដូចគ្នា យើងទទួលបានច្រើនព្រោះឈ្មោះខុសគ្នា។ ដូចដែលអ្នកអាចឃើញសំណុំនៃធាតុដូចគ្នាគឺទាំងសំណុំនិងសំណុំច្រើនក្នុងពេលតែមួយ។ ត្រឹមត្រូវទេ? ហើយនៅទីនេះ គណិតវិទូ-shaman-shuller យក trump ace ចេញពីដៃអាវរបស់គាត់ ហើយចាប់ផ្តើមប្រាប់យើងអំពីឈុត ឬ multiset ។ ក្នុងករណីណាក៏ដោយគាត់នឹងបញ្ចុះបញ្ចូលយើងថាគាត់និយាយត្រូវ។
ដើម្បីយល់ពីរបៀបដែល shamans សម័យទំនើបដំណើរការជាមួយទ្រឹស្តីសំណុំដោយភ្ជាប់វាទៅនឹងការពិតវាគ្រប់គ្រាន់ដើម្បីឆ្លើយសំណួរមួយ: តើធាតុនៃសំណុំមួយខុសគ្នាពីធាតុនៃសំណុំមួយផ្សេងទៀតយ៉ាងដូចម្តេច? ខ្ញុំនឹងបង្ហាញអ្នករាល់គ្នាដោយមិនមាន "អាចយល់បានថាមិនមែនជាមួយទាំងមូល" ឬ "មិនអាចយល់បានដូចជាទាំងមូល" ។
ថ្ងៃអាទិត្យ ទី១៨ ខែមីនា ឆ្នាំ២០១៨
ផលបូកនៃខ្ទង់នៃលេខគឺជាការរាំរបស់ shamans ជាមួយនឹង tambourine ដែលមិនទាក់ទងនឹងគណិតវិទ្យា។ មែនហើយ នៅក្នុងមេរៀនគណិតវិទ្យា យើងត្រូវបានបង្រៀនឱ្យស្វែងរកផលបូកនៃខ្ទង់នៃចំនួនមួយ ហើយប្រើវា ប៉ុន្តែពួកគេជា shamans សម្រាប់នោះ ដើម្បីបង្រៀនកូនចៅរបស់ពួកគេនូវជំនាញ និងប្រាជ្ញារបស់ពួកគេ បើមិនដូច្នេះទេ shamans នឹងស្លាប់។
តើអ្នកត្រូវការភស្តុតាងទេ? បើកវិគីភីឌា ហើយព្យាយាមស្វែងរកទំព័រ "ផលបូកនៃខ្ទង់នៃលេខមួយ"។ នាងមិនមានទេ។ មិនមានរូបមន្តនៅក្នុងគណិតវិទ្យាដែលអ្នកអាចរកផលបូកនៃខ្ទង់នៃចំនួនណាមួយនោះទេ។ យ៉ាងណាមិញ លេខគឺជានិមិត្តសញ្ញាក្រាហ្វិកដែលយើងសរសេរលេខ ហើយនៅក្នុងភាសាគណិតវិទ្យា កិច្ចការស្តាប់ទៅដូចនេះ៖ "រកផលបូកនៃនិមិត្តសញ្ញាក្រាហ្វិកដែលតំណាងឱ្យលេខណាមួយ"។ គណិតវិទូមិនអាចដោះស្រាយបញ្ហានេះបានទេ ប៉ុន្តែ shamans អាចធ្វើវាបានជាបឋម។
ចូរយើងស្វែងយល់ថាតើយើងធ្វើអ្វី និងរបៀបដើម្បីស្វែងរកផលបូកនៃខ្ទង់នៃលេខដែលបានផ្តល់ឱ្យ។ ដូច្នេះហើយ ឧបមាថាយើងមានលេខ 12345។ តើត្រូវធ្វើអ្វីដើម្បីស្វែងរកផលបូកនៃខ្ទង់នៃលេខនេះ? ចូរយើងពិចារណាជំហានទាំងអស់តាមលំដាប់លំដោយ។
1. សរសេរលេខនៅលើក្រដាសមួយ។ តើយើងបានធ្វើអ្វី? យើងបានបំប្លែងលេខទៅជានិមិត្តសញ្ញាក្រាហ្វិកលេខ។ នេះមិនមែនជាប្រតិបត្តិការគណិតវិទ្យាទេ។
2. យើងកាត់រូបភាពដែលទទួលបានមួយទៅជារូបភាពជាច្រើនដែលមានលេខដាច់ដោយឡែក។ ការកាត់រូបភាពមិនមែនជាប្រតិបត្តិការគណិតវិទ្យាទេ។
3. បំប្លែងតួអក្សរក្រាហ្វិកនីមួយៗទៅជាលេខ។ នេះមិនមែនជាប្រតិបត្តិការគណិតវិទ្យាទេ។
4. បន្ថែមលេខលទ្ធផល។ ឥឡូវនេះវាជាគណិតវិទ្យា។
ផលបូកនៃខ្ទង់នៃលេខ 12345 គឺ 15 ប៉ុន្តែនោះមិនមែនទាំងអស់នោះទេ។
តាមទស្សនៈគណិតវិទ្យា វាមិនមានបញ្ហាថាយើងសរសេរលេខប្រព័ន្ធណាទេ។ ដូច្នេះនៅក្នុងប្រព័ន្ធលេខផ្សេងគ្នា ផលបូកនៃខ្ទង់នៃលេខដូចគ្នានឹងខុសគ្នា។ នៅក្នុងគណិតវិទ្យា ប្រព័ន្ធលេខត្រូវបានចង្អុលបង្ហាញជាអក្សរតូចនៅខាងស្តាំនៃលេខ។ ជាមួយនឹងចំនួនដ៏ធំនៃ 12345 ខ្ញុំមិនចង់បញ្ឆោតក្បាលរបស់ខ្ញុំទេសូមពិចារណាលេខ 26 ពីអត្ថបទអំពី។ ចូរយើងសរសេរលេខនេះនៅក្នុងប្រព័ន្ធលេខគោលពីរ គោលប្រាំបី ទសភាគ និងគោលដប់ប្រាំមួយ។ យើងនឹងមិនពិចារណាជំហាននីមួយៗនៅក្រោមមីក្រូទស្សន៍ទេ យើងបានធ្វើរួចហើយ។ តោះមើលលទ្ធផល។
ដូចដែលអ្នកអាចឃើញនៅក្នុងប្រព័ន្ធលេខផ្សេងគ្នាផលបូកនៃខ្ទង់នៃលេខដូចគ្នាគឺខុសគ្នា។ លទ្ធផលនេះមិនទាក់ទងនឹងគណិតវិទ្យាទេ។ វាដូចជាការស្វែងរកតំបន់នៃចតុកោណជាម៉ែត្រ និងសង់ទីម៉ែត្រនឹងផ្តល់ឱ្យអ្នកនូវលទ្ធផលខុសគ្នាទាំងស្រុង។
លេខសូន្យនៅក្នុងប្រព័ន្ធលេខទាំងអស់មើលទៅដូចគ្នា និងមិនមានលេខសរុប។ នេះគឺជាអំណះអំណាងមួយផ្សេងទៀតក្នុងការពេញចិត្តចំពោះការពិតដែលថា . សំណួរសម្រាប់គណិតវិទូ៖ តើវាមានន័យដូចម្តេចក្នុងគណិតវិទ្យាដែលមិនមែនជាលេខ? ចុះសម្រាប់គណិតវិទូវិញ គ្មានអ្វីក្រៅពីលេខទេ? សម្រាប់ shamans, ខ្ញុំអាចអនុញ្ញាតនេះ, ប៉ុន្តែសម្រាប់អ្នកវិទ្យាសាស្រ្ត, ទេ។ ការពិតមិនមែនគ្រាន់តែជាលេខទេ។
លទ្ធផលដែលទទួលបានគួរតែត្រូវបានចាត់ទុកថាជាភស្តុតាងដែលថាប្រព័ន្ធលេខគឺជាឯកតានៃការវាស់វែងនៃលេខ។ យ៉ាងណាមិញ យើងមិនអាចប្រៀបធៀបលេខជាមួយនឹងឯកតារង្វាស់ផ្សេងគ្នាបានទេ។ ប្រសិនបើសកម្មភាពដូចគ្នាជាមួយនឹងឯកតារង្វាស់ផ្សេងគ្នានៃបរិមាណដូចគ្នានាំទៅរកលទ្ធផលផ្សេងគ្នាបន្ទាប់ពីការប្រៀបធៀបពួកវា នោះវាមិនមានអ្វីទាក់ទងនឹងគណិតវិទ្យាទេ។
តើគណិតវិទ្យាពិតគឺជាអ្វី? នេះគឺជាពេលដែលលទ្ធផលនៃសកម្មភាពគណិតវិទ្យាមិនអាស្រ័យលើតម្លៃនៃលេខ ឯកតារង្វាស់ដែលបានប្រើ និងលើអ្នកដែលធ្វើសកម្មភាពនេះ។
អុញ! តើនេះមិនមែនជាបន្ទប់ទឹករបស់ស្ត្រីទេឬ?
- នារីវ័យក្មេង! នេះជាបន្ទប់ពិសោធន៍សម្រាប់សិក្សាពីភាពបរិសុទ្ធគ្មានកំណត់នៃព្រលឹងពេលឡើងឋានសួគ៌! Nimbus នៅលើកំពូលហើយព្រួញឡើងលើ។ តើបង្គន់អ្វីទៀត?
ស្រី... សសរមួយនៅពីលើ ហើយព្រួញចុះក្រោមជាប្រុស។
បើអ្នកមានសិល្បៈរចនាបែបនេះភ្លឺភ្នែកច្រើនដងក្នុងមួយថ្ងៃ។
បន្ទាប់មកវាមិនគួរឱ្យភ្ញាក់ផ្អើលទេដែលអ្នកស្រាប់តែឃើញរូបតំណាងចម្លែកនៅក្នុងឡានរបស់អ្នក៖
ដោយផ្ទាល់ខ្ញុំខិតខំប្រឹងប្រែងដោយខ្លួនឯងដើម្បីមើលសញ្ញាដក 4 ដឺក្រេនៅក្នុងមនុស្សម្នាក់ដែលហៀរសំបោរ (រូបភាពមួយ) (សមាសភាពនៃរូបភាពជាច្រើន: សញ្ញាដកលេខ 4 ការរចនាដឺក្រេ) ។ ហើយខ្ញុំក៏មិនចាត់ទុកនារីម្នាក់នេះថាជាមនុស្សល្ងង់ដែលមិនចេះរូបវិទ្យាដែរ។ នាងគ្រាន់តែមានទម្រង់អ័ក្សនៃការយល់ឃើញនៃរូបភាពក្រាហ្វិក។ ហើយគណិតវិទូបង្រៀនយើងគ្រប់ពេល។ នេះគឺជាឧទាហរណ៍មួយ។
1A មិនមែនជា "ដកបួនដឺក្រេ" ឬ "មួយ a" ទេ។ នេះគឺជា "មនុស្សល្មោភកាម" ឬលេខ "ម្ភៃប្រាំមួយ" នៅក្នុងប្រព័ន្ធលេខគោលដប់ប្រាំមួយ។ មនុស្សទាំងនោះដែលធ្វើការឥតឈប់ឈរនៅក្នុងប្រព័ន្ធលេខនេះ យល់ដោយស្វ័យប្រវត្តិនូវលេខ និងអក្សរជានិមិត្តសញ្ញាក្រាហ្វិកតែមួយ។
តារាងតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រ
ចំណាំ. តារាងតម្លៃនេះសម្រាប់អនុគមន៍ត្រីកោណមាត្រប្រើសញ្ញា √ ដើម្បីសម្គាល់ឫសការេ។ ដើម្បីសម្គាល់ប្រភាគ - និមិត្តសញ្ញា "/" ។
សូមមើលផងដែរសម្ភារៈមានប្រយោជន៍:
សម្រាប់ កំណត់តម្លៃនៃអនុគមន៍ត្រីកោណមាត្ររកវានៅចំនុចប្រសព្វនៃបន្ទាត់ដែលបង្ហាញពីអនុគមន៍ត្រីកោណមាត្រ។ ឧទាហរណ៍ស៊ីនុស 30 ដឺក្រេ - យើងកំពុងស្វែងរកជួរឈរដែលមានចំណងជើង sin (sine) ហើយយើងរកឃើញចំនុចប្រសព្វនៃជួរឈរនៃតារាងនេះជាមួយនឹងបន្ទាត់ "30 ដឺក្រេ" នៅចំនុចប្រសព្វរបស់ពួកគេយើងអានលទ្ធផល - មួយ ទីពីរ ដូចគ្នានេះដែរយើងរកឃើញ កូស៊ីនុស ៦០ដឺក្រេ, ស៊ីនុស ៦០ដឺក្រេ (ម្តងទៀតនៅចំនុចប្រសព្វនៃជួរឈរ sin (sine) និងជួរ 60 ដឺក្រេយើងរកឃើញតម្លៃ sin 60 = √3/2) ។ល។ ដូចគ្នាដែរ តម្លៃនៃស៊ីនុស កូស៊ីនុស និងតង់សង់នៃមុំ "ពេញនិយម" ផ្សេងទៀតត្រូវបានរកឃើញ។
ស៊ីនុសនៃ pi, កូស៊ីនុសនៃ pi, តង់សង់នៃ pi និងមុំផ្សេងទៀតជារ៉ាដ្យង់
តារាងនៃកូស៊ីនុស ស៊ីនុស និងតង់សង់ខាងក្រោមក៏សមរម្យសម្រាប់ការស្វែងរកតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រដែលអាគុយម៉ង់គឺ ផ្តល់ជារ៉ាដ្យង់. ដើម្បីធ្វើដូចនេះសូមប្រើជួរទីពីរនៃតម្លៃមុំ។ សូមអរគុណចំពោះការនេះ អ្នកអាចបំប្លែងតម្លៃនៃមុំពេញនិយមពីដឺក្រេទៅជារ៉ាដ្យង់។ ជាឧទាហរណ៍ ចូរយើងស្វែងរកមុំ 60 ដឺក្រេក្នុងបន្ទាត់ទីមួយ ហើយអានតម្លៃរបស់វាជារ៉ាដ្យង់នៅក្រោមវា។ 60 ដឺក្រេស្មើនឹង π/3 រ៉ាដ្យង់។
លេខ pi បង្ហាញពីភាពអាស្រ័យនៃរង្វង់នៃរង្វង់លើរង្វាស់ដឺក្រេនៃមុំ។ ដូច្នេះ pi radians ស្មើនឹង 180 ដឺក្រេ។
លេខណាមួយដែលបង្ហាញក្នុងលក្ខខណ្ឌនៃ pi (រ៉ាដ្យង់) អាចត្រូវបានបម្លែងយ៉ាងងាយស្រួលទៅជាដឺក្រេដោយជំនួសលេខ pi (π) ជាមួយ 180 ។.
ឧទាហរណ៍:
1. ស៊ីនុ ភី.
sin π = sin 180 = 0
ដូច្នេះស៊ីនុសនៃ pi គឺដូចគ្នានឹងស៊ីនុសនៃ 180 ដឺក្រេ ហើយស្មើនឹងសូន្យ។
2. កូស៊ីនុស pi.
cos π = cos 180 = −1
ដូច្នេះ កូស៊ីនុសនៃ pi គឺដូចគ្នានឹងកូស៊ីនុស 180 ដឺក្រេ ហើយស្មើនឹងដកមួយ។
3. តង់សង់ pi
tg π = tg 180 = 0
ដូច្នេះតង់ហ្សង់នៃ pi គឺដូចគ្នានឹងតង់សង់នៃ 180 ដឺក្រេ ហើយស្មើនឹងសូន្យ។
តារាងស៊ីនុស កូស៊ីនុស តម្លៃតង់សង់សម្រាប់មុំ 0 - 360 ដឺក្រេ (តម្លៃញឹកញាប់)
|
មុំ α (ដឺក្រេ) |
មុំ α (តាមរយៈ pi) |
អំពើបាប (ប្រហោងឆ្អឹង) |
cos (កូស៊ីនុស) |
tg (តង់សង់) |
ctg (កូតង់សង់) |
វិ (វគ្គ) |
មូលហេតុ (កូសេខេន) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/១២ | 2 - √3 | 2 + √3 | ||||
| 30 | π/៦ | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/៣ | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | ៧π/១២ |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | ៣π/៤ | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | ៧π/៦ | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | ៤π/៣ | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2 ភី | 0 | 1 | 0 | - | 1 | - |
ប្រសិនបើនៅក្នុងតារាងតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រ ជំនួសឱ្យតម្លៃនៃអនុគមន៍ សញ្ញាសញ្ញាត្រូវបានចង្អុលបង្ហាញ (តង់សង់ (tg) 90 ដឺក្រេ កូតង់សង់ (ctg) 180 ដឺក្រេ) បន្ទាប់មកសម្រាប់តម្លៃដែលបានផ្តល់ឱ្យនៃរង្វាស់ដឺក្រេនៃ មុំ មុខងារមិនមានតម្លៃច្បាស់លាស់ទេ។ ប្រសិនបើគ្មានសញ្ញា ក្រឡាគឺទទេ ដូច្នេះយើងមិនទាន់បញ្ចូលតម្លៃដែលចង់បាន។ យើងចាប់អារម្មណ៍លើអ្វីដែលសំណើអ្នកប្រើប្រាស់មករកយើង ហើយបន្ថែមតារាងជាមួយនឹងតម្លៃថ្មី បើទោះបីជាទិន្នន័យបច្ចុប្បន្ននៅលើតម្លៃនៃកូស៊ីនុស ស៊ីនុស និងតង់ហ្សង់នៃតម្លៃមុំសាមញ្ញបំផុតគឺគ្រប់គ្រាន់ដើម្បីដោះស្រាយភាគច្រើន។ បញ្ហា។
តារាងតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រ sin, cos, tg សម្រាប់មុំពេញនិយមបំផុត
0, 15, 30, 45, 60, 90 ... 360 ដឺក្រេ
(តម្លៃលេខ "តាមតារាង Bradis")
| តម្លៃមុំ α (ដឺក្រេ) | តម្លៃនៃមុំαគិតជារ៉ាដ្យង់ | បាប (sine) | កូស (កូស៊ីនុស) | tg (តង់ហ្សង់) | ctg (កូតង់សង់) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
នៅក្នុងអត្ថបទយើងនឹងយល់យ៉ាងពេញលេញនូវអ្វីដែលវាមើលទៅ តារាងតម្លៃត្រីកោណមាត្រ ស៊ីនុស កូស៊ីនុស តង់សង់ និងកូតង់សង់. ពិចារណាតម្លៃមូលដ្ឋាននៃអនុគមន៍ត្រីកោណមាត្រពីមុំ 0,30,45,60,90,...,360 ដឺក្រេ។ ហើយសូមមើលពីរបៀបប្រើតារាងទាំងនេះក្នុងការគណនាតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រ។
ដំបូងពិចារណា តារាងនៃកូស៊ីនុស ស៊ីនុស តង់ហ្សង់ និងកូតង់សង់ពីមុំ 0, 30, 45, 60, 90, .. ដឺក្រេ។ និយមន័យនៃបរិមាណទាំងនេះធ្វើឱ្យវាអាចកំណត់តម្លៃនៃមុខងារនៃមុំ 0 និង 90 ដឺក្រេ៖
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, កូតង់សង់នៃ 00 នឹងមិនត្រូវបានកំណត់
sin 90 0 = 1, cos 90 0 = 0, ctg90 0 = 0, តង់សង់នៃ 90 0 នឹងមិនត្រូវបានកំណត់
បើយើងយកត្រីកោណកែងដែលមុំមានពី ៣០ ទៅ ៩០ ដឺក្រេ។ យើងទទួលបាន:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 = √3, ctg 60 0 = √3/3
យើងតំណាងឱ្យតម្លៃដែលទទួលបានទាំងអស់នៅក្នុងទម្រង់ តារាងត្រីកោណមាត្រ:
តារាងស៊ីនុស កូស៊ីនុស តង់ហ្សង់ និងកូតង់សង់!
ប្រសិនបើយើងប្រើរូបមន្តខាស តារាងរបស់យើងនឹងកើនឡើង តម្លៃសម្រាប់មុំរហូតដល់ 360 ដឺក្រេនឹងត្រូវបានបន្ថែម។ វានឹងមើលទៅដូចនេះ៖

ដូចគ្នានេះផងដែរដោយផ្អែកលើលក្ខណៈសម្បត្តិនៃវដ្តរដូវ តារាងអាចត្រូវបានបង្កើនប្រសិនបើយើងជំនួសមុំដោយ 0 0 +360 0 *z .... 330 0 +360 0 *z ដែលក្នុងនោះ z ជាចំនួនគត់។ ក្នុងតារាងនេះ គេអាចគណនាតម្លៃនៃមុំទាំងអស់ដែលត្រូវនឹងចំនុចក្នុងរង្វង់តែមួយ។
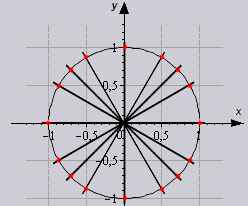
តោះមើលឱ្យច្បាស់ពីរបៀបប្រើតារាងក្នុងដំណោះស្រាយ។
អ្វីគ្រប់យ៉ាងគឺសាមញ្ញណាស់។ ដោយសារតម្លៃដែលយើងត្រូវការស្ថិតនៅចំណុចប្រសព្វនៃក្រឡាដែលយើងត្រូវការ។ ជាឧទាហរណ៍ ចូរយក cos នៃមុំ 60 ដឺក្រេ ក្នុងតារាងវានឹងមើលទៅដូចនេះ៖

នៅក្នុងតារាងចុងក្រោយនៃតម្លៃសំខាន់នៃអនុគមន៍ត្រីកោណមាត្រ យើងធ្វើសកម្មភាពតាមរបៀបដូចគ្នា។ ប៉ុន្តែនៅក្នុងតារាងនេះ គេអាចដឹងថាតើតង់សង់ពីមុំ 1020 ដឺក្រេនឹងមានប៉ុន្មាននោះ វា = -√3 តោះពិនិត្យមើល 1020 0 = 300 0 +360 0 *2 ។ ចូរយើងស្វែងរកតុ។

តារាង Bradis ។ សម្រាប់ស៊ីនុស កូស៊ីនុស តង់ហ្សង់ និងកូតង់សង់។
តារាងរបស់ Bradys ត្រូវបានបែងចែកជាផ្នែកជាច្រើន ពួកវាមានតារាងនៃកូស៊ីនុស និងស៊ីនុស តង់ហ្សង់ និងកូតង់សង់ ដែលបែងចែកជាពីរផ្នែក (tg នៃមុំរហូតដល់ 90 ដឺក្រេ និង ctg នៃមុំតូច) ។
ស៊ីនុស និងកូស៊ីនុស


មុំ tg ពី 00 ទៅ 760 មុំ ctg ពី 140 ទៅ 900 ។
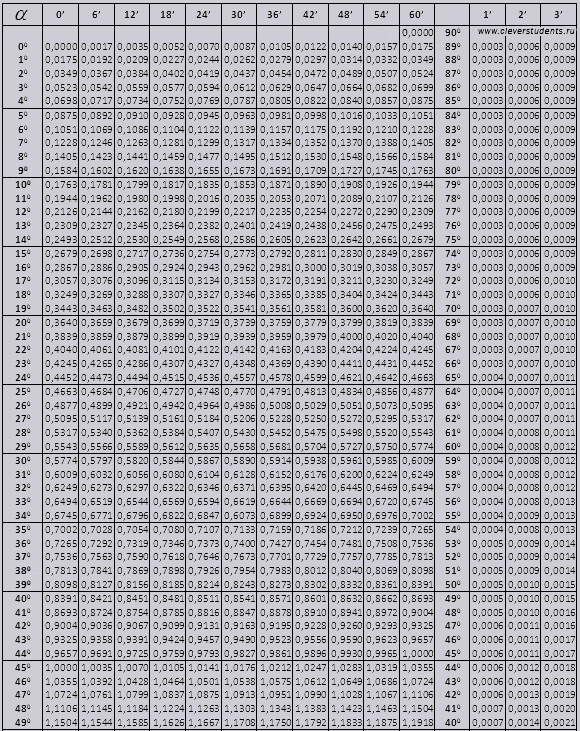

tg រហូតដល់ 900 និង ctg មុំតូច។

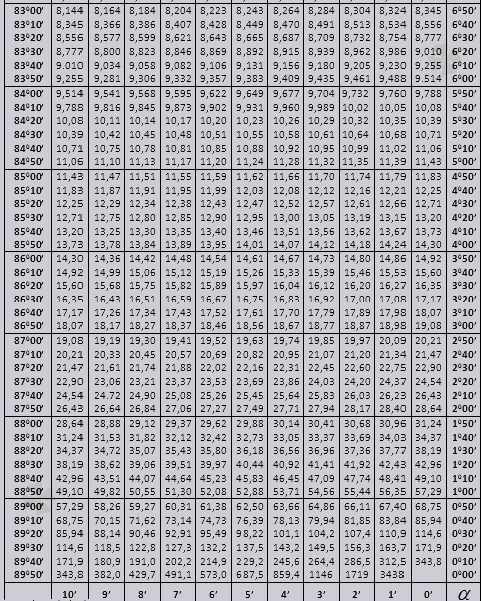
ចូរយើងស្វែងយល់ពីរបៀបប្រើតារាង Bradis ក្នុងការដោះស្រាយបញ្ហា។
ចូរយើងស្វែងរកការកំណត់បាប (ការកំណត់នៅក្នុងជួរឈរពីគែមខាងឆ្វេង) 42 នាទី (ការកំណត់គឺនៅលើបន្ទាត់កំពូល) ។ តាមរយៈការឆ្លងកាត់យើងកំពុងស្វែងរកការរចនាវាគឺ = 0.3040 ។
តម្លៃនៃនាទីត្រូវបានចង្អុលបង្ហាញជាមួយនឹងចន្លោះពេលប្រាំមួយនាទី តើមានអ្វីប្រសិនបើតម្លៃដែលយើងត្រូវការធ្លាក់ក្នុងចន្លោះពេលនេះ។ ចូរយើងចំណាយពេល 44 នាទី ហើយមានតែ 42 ក្នុងតារាង យើងយក 42 ជាមូលដ្ឋាន ហើយប្រើជួរឈរបន្ថែមនៅផ្នែកខាងស្តាំ យកការកែតម្រូវលើកទី 2 ហើយបន្ថែមទៅ 0.3040 + 0.0006 យើងទទួលបាន 0.3046 ។
ជាមួយនឹង sin 47 នាទី យើងយក 48 នាទីជាមូលដ្ឋាន ហើយដក 1 ការកែចេញពីវា ពោលគឺ 0.3057 - 0.0003 = 0.3054
នៅពេលគណនា cos យើងធ្វើការស្រដៀងនឹង sin ដែរ មានតែយើងយកជួរខាងក្រោមនៃតារាងជាមូលដ្ឋានប៉ុណ្ណោះ។ ឧទាហរណ៍ cos 20 0 = 0.9397
តម្លៃ tg នៃមុំមួយរហូតដល់ 90 0 និង cot នៃមុំតូចមួយគឺត្រឹមត្រូវ ហើយមិនមានការកែតម្រូវនៅក្នុងពួកវាទេ។ ឧទាហរណ៍ ស្វែងរក tg 78 0 37min = 4.967 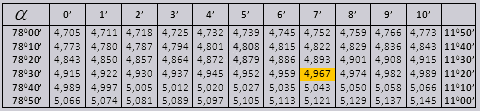
និង ctg 20 0 13 នាទី = 25.83 
ជាការប្រសើរណាស់, នៅទីនេះយើងបានពិចារណាតារាងត្រីកោណមាត្រសំខាន់។ យើងសង្ឃឹមថាព័ត៌មាននេះមានប្រយោជន៍ខ្លាំងណាស់សម្រាប់អ្នក។ សំណួររបស់អ្នកនៅលើតុ ប្រសិនបើមាន ត្រូវប្រាកដថាសរសេរនៅក្នុងមតិយោបល់!
ចំណាំ៖ របាំងការពារជញ្ជាំង - បន្ទះការពារសម្រាប់ការពារជញ្ជាំង។ អនុវត្តតាមតំណភ្ជាប់ របងគ្មានជញ្ជាំងគ្មានស៊ុម (http://www.spi-polymer.ru/otboyniki/) និងស្វែងយល់បន្ថែម។
អត្ថបទនេះត្រូវបានប្រមូល តារាងនៃស៊ីនុស កូស៊ីនុស តង់ហ្សង់ និងកូតង់សង់. ដំបូង យើងផ្តល់តារាងនៃតម្លៃចម្បងនៃអនុគមន៍ត្រីកោណមាត្រ នោះគឺតារាងស៊ីនុស កូស៊ីនុស តង់សង់ និងកូតង់សង់នៃមុំ 0, 30, 45, 60, 90, ..., 360 ដឺក្រេ ( 0, π/6, π/4, π/3, π/2, …, 2πរ៉ាដ្យង់) ។ បន្ទាប់ពីនោះ យើងនឹងផ្តល់តារាងនៃស៊ីនុស និងកូស៊ីនុស ព្រមទាំងតារាងតង់ហ្សង់ និងកូតង់សង់ដោយ V. M. Bradis ហើយបង្ហាញពីរបៀបប្រើប្រាស់តារាងទាំងនេះនៅពេលស្វែងរកតម្លៃនៃអនុគមន៍ត្រីកោណមាត្រ។
ការរុករកទំព័រ។
តារាងស៊ីនុស កូស៊ីនុស តង់សង់ និងកូតង់សង់សម្រាប់មុំ 0, 30, 45, 60, 90, ... ដឺក្រេ
គន្ថនិទ្ទេស។
- ពិជគណិត៖ប្រូក សម្រាប់ 9 កោសិកា។ មធ្យម សាលា / យូ។ N. Makarychev, N.G. Mindyuk, K. I. Neshkov, S. B. Suvorova; អេដ។ S. A. Telyakovsky.- M.: Enlightenment, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
- Bashmakov M.I.ពិជគណិត និងការចាប់ផ្តើមនៃការវិភាគ៖ Proc. សម្រាប់ 10-11 កោសិកា។ មធ្យម សាលា - ទី 3 ed ។ - M. : Enlightenment, 1993. - 351 p.: ill. - ISBN 5-09-004617-4 ។
- ពិជគណិតនិងការចាប់ផ្តើមនៃការវិភាគ៖ Proc ។ សម្រាប់ 10-11 កោសិកា។ ការអប់រំទូទៅ ស្ថាប័ន / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn និងអ្នកដទៃ; អេដ។ A. N. Kolmogorova.- 14th ed.- M.: Enlightenment, 2004.- 384 p.: ill.- ISBN 5-09-013651-3 ។
- Gusev V.A., Mordkovich A.G.គណិតវិទ្យា (សៀវភៅណែនាំសម្រាប់អ្នកដាក់ពាក្យទៅសាលាបច្ចេកទេស): Proc. ប្រាក់ឧបត្ថម្ភ។- M.; ខ្ពស់ជាង សាលា ១៩៨៤.-៣៥១ ទំ., ឈឺ។
- Bradis V.M.តារាងគណិតវិទ្យាបួនខ្ទង់៖ សម្រាប់ការអប់រំទូទៅ។ សៀវភៅសិក្សា គ្រឹះស្ថាន។ - លើកទី 2 ។ - M.: Bustard, 1999.- 96 p.: ill. ISBN 5-7107-2667-2
1. អនុគមន៍ត្រីកោណមាត្រគឺជាអនុគមន៍បឋមដែលអាគុយម៉ង់គឺ ការចាក់ថ្នាំ. អនុគមន៍ត្រីកោណមាត្រពណ៌នាអំពីទំនាក់ទំនងរវាងភាគី និងមុំស្រួចក្នុងត្រីកោណស្តាំ។ តំបន់នៃការអនុវត្តមុខងារត្រីកោណមាត្រគឺមានភាពចម្រុះណាស់។ ដូច្នេះ ជាឧទាហរណ៍ ដំណើរការតាមកាលកំណត់ណាមួយអាចត្រូវបានតំណាងថាជាផលបូកនៃអនុគមន៍ត្រីកោណមាត្រ (ស៊េរី Fourier)។ មុខងារទាំងនេះច្រើនតែលេចឡើងនៅពេលដោះស្រាយសមីការឌីផេរ៉ង់ស្យែល និងមុខងារ។
2. អនុគមន៍ត្រីកោណមាត្រមាន 6 មុខងារដូចខាងក្រោមៈ ប្រហោងឆ្អឹង, កូស៊ីនុស, តង់សង់,កូតង់សង់, វិនាទីនិង កូសេកង់. សម្រាប់មុខងារទាំងនេះនីមួយៗ មានអនុគមន៍ត្រីកោណមាត្របញ្ច្រាស។
3. វាងាយស្រួលក្នុងការណែនាំនិយមន័យធរណីមាត្រនៃអនុគមន៍ត្រីកោណមាត្រដោយប្រើ រង្វង់ឯកតា. រូបខាងក្រោមបង្ហាញពីរង្វង់ដែលមានកាំ r=1។ ចំណុច M (x, y) ត្រូវបានសម្គាល់នៅលើរង្វង់។ មុំរវាងកាំវ៉ិចទ័រ OM និងទិសដៅវិជ្ជមាននៃអ័ក្សអុកគឺα។
4. ប្រហោងឆ្អឹងមុំ α គឺជាសមាមាត្រនៃលំដាប់ y នៃចំណុច M (x, y) ទៅកាំ r:
sinα=y/r.
ចាប់តាំងពី r = 1 នោះស៊ីនុសស្មើនឹងការចាត់តាំងនៃចំណុច M (x, y) ។
5. កូស៊ីនុសមុំ α គឺជាសមាមាត្រនៃ abscissa x នៃចំណុច M (x, y) ទៅកាំ r:
cosα=x/r
6. តង់សង់មុំ α គឺជាសមាមាត្រនៃការចាត់តាំង y នៃចំណុច M (x, y) ទៅ abscissa x របស់វា៖
tanα=y/x,x≠0
7. កូតង់សង់មុំ α គឺជាសមាមាត្រនៃ abscissa x នៃចំណុច M (x, y) ទៅនឹងការចាត់តាំង y របស់វា៖
cotα=x/y,y≠0
8. សេកានមុំ α គឺជាសមាមាត្រនៃកាំ r ទៅ abscissa x នៃចំនុច M(x,y):
secα=r/x=1/x,x≠0
9. កូសេកានមុំ α គឺជាសមាមាត្រនៃកាំ r ទៅនឹងចំនុច y នៃចំនុច M(x,y):
cscα=r/y=1/y,y≠0
10. នៅក្នុងរង្វង់ឯកតានៃការព្យាករ x, y ចំនុច M(x,y) និងកាំ r បង្កើតជាត្រីកោណមុំខាងស្តាំ ដែលក្នុងនោះ x,y ជាជើង ហើយ r ជាអ៊ីប៉ូតេនុស។ ដូច្នេះនិយមន័យខាងលើនៃអនុគមន៍ត្រីកោណមាត្រដែលអនុវត្តចំពោះត្រីកោណកែងត្រូវបានបង្កើតដូចខាងក្រោមៈ
ប្រហោងឆ្អឹងមុំ α គឺជាសមាមាត្រនៃជើងទល់មុខទៅនឹងអ៊ីប៉ូតេនុស។
កូស៊ីនុសមុំ α គឺជាសមាមាត្រនៃជើងដែលនៅជាប់នឹងអ៊ីប៉ូតេនុស។
តង់សង់មុំ α ត្រូវបានគេហៅថាជើងផ្ទុយទៅនឹងជើងដែលនៅជាប់គ្នា។
កូតង់សង់មុំ α ត្រូវបានគេហៅថាជើងដែលនៅជាប់នឹងទល់មុខ។
សេកានមុំ α គឺជាសមាមាត្រនៃអ៊ីប៉ូតេនុសទៅនឹងជើងដែលនៅជាប់គ្នា។
កូសេកានមុំ α គឺជាសមាមាត្រនៃអ៊ីប៉ូតេនុសទៅនឹងជើងទល់មុខ។
11. ក្រាហ្វមុខងារស៊ីនុស
y=sinx, domain: x∈R, domain: −1≤sinx≤1
12. ក្រាហ្វនៃអនុគមន៍កូស៊ីនុស
y=cosx, ដែន៖ x∈R, ជួរ៖ −1≤cosx≤1
13. ក្រាហ្វមុខងារតង់សង់ 14. ក្រាហ្វនៃអនុគមន៍កូតង់សង់ 15. ក្រាហ្វនៃអនុគមន៍សេកុង
y=tanx, ដែន៖ x∈R,x≠(2k+1)π/2, ដែន៖ −∞ 
y=cotx, ដែន៖ x∈R,x≠kπ, ដែន៖ −∞ 
y=secx, domain: x∈R,x≠(2k+1)π/2, domain: secx∈(−∞,−1]∪∪)
