Funkciju y=f(x) sauc par diferencējamu kādā punktā x 0, ja tai šajā punktā ir noteikts atvasinājums, t.i. ja attiecību robeža pastāv un ir ierobežota.

Ja funkcija ir diferencējama katrā noteikta segmenta punktā [a; b] vai intervāls (a; b), tad sakām, ka tas ir diferencējams uz intervāla [a; b] vai attiecīgi intervālā (a; b).

Ir spēkā sekojošā teorēma, kas nosaka saikni starp diferencējamām un nepārtrauktām funkcijām.

Teorēma. Ja funkcija y=f(x) ir diferencējama kādā punktā x 0, tad tā šajā punktā ir nepārtraukta.

Tādējādi no funkcijas diferencējamības izriet tās nepārtrauktība.

Pierādījums. Ja tad

kur b ir bezgalīgi mazs lielums, t.i. daudzums, kas tiecas uz nulli, ja Dx>0. Bet tad

Dy=f "(x 0) Dx+bDx=> Dy>0 pie Dx>0, t.i., f(x) - f(x 0)>0 pie x>x 0,

un tas nozīmē, ka funkcija f(x) ir nepārtraukta punktā x 0 . Q.E.D.

Tādējādi funkcijai nevar būt atvasinājums pārtraukuma punktos. Pretēji tam nav taisnība: pastāv nepārtrauktas funkcijas, kuras dažos punktos nav diferencējamas (tas ir, šajos punktos nav atvasinājuma).

Apskatīsim punktus a, b, c attēlā.

Punktā a, ja Dx>0, attiecībai nav ierobežojumu (jo vienpusējās robežas atšķiras Dx>0-0 un Dx>0+0). Grafika punktā A nav noteiktas pieskares, bet ir divas dažādas vienvirziena pieskares ar slīpumu 1 un 2. Šāda veida punktu sauc par stūra punktu.

Punktā b, ja Dx>0, attiecība ir nemainīgas zīmes un bezgalīgi liela. Funkcijai ir bezgalīgs atvasinājums. Šajā brīdī grafikam ir vertikāla pieskare. Punkta tips - “locījuma punkts” ar vertikālu pieskari.

Punktā c vienpusējie atvasinājumi ir bezgalīgi liels dažādu zīmju daudzums. Šajā brīdī grafikā ir divas apvienotas vertikālās pieskares. Tips - "atgriešanās punkts" ar vertikālu pieskari - īpašs stūra punkta gadījums.

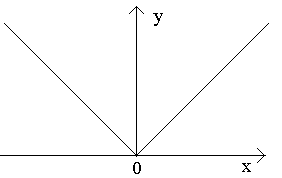
1. Aplūkosim funkciju y=|x|. Šī funkcija ir nepārtraukta punktā

Parādīsim, ka tai šobrīd nav atvasinājuma.

f(0+Dx) = f(Dx) = |Dx|. Tāpēc Дy = f(Дx) - f(0) = |Дx|

Bet tad Dx< 0 (т.е. при Дx стремящемся к 0 слева)

Un kad Dx > 0

Tādējādi attiecībai Dx> 0 labajā un kreisajā pusē ir dažādas robežas, kas nozīmē, ka attiecībai nav robežu, t.i. funkcijas y=|x| atvasinājums neeksistē punktā x= 0. Ģeometriski tas nozīmē, ka punktā x = 0 šai "līknei" nav noteiktas pieskares (šajā punktā ir divas).

2. Funkcija ir definēta un nepārtraukta visā skaitļu rindā. Noskaidrosim, vai šai funkcijai ir atvasinājums pie x= 0.

Līdz ar to aplūkojamā funkcija nav diferencējama punktā x= 0. Līknes pieskare šajā punktā veido leņķi p/2 ar abscisu asi, t.i. sakrīt ar Oy asi.

3 Funkcijas atvasinājuma definīcija punktā Ļaujiet funkcijai f(x) būt definētai kādā punkta x 0 apkārtnē. DEFINĪCIJA. Ja sakarībai ir (galīgs) ierobežojums, tad f(x) sauc par diferencējamo punktu x 0, bet pašu robežu sauc par funkcijas f(x) atvasinājumu punktā x 0 un apzīmē ar f. (x 0), tas ir, apzīmēsim, ka x = x – x 0 ir argumenta pieaugums, pārejot no punkta x 0 uz punktu x, un y = f(x 0 + x) – f(x 0) ir Pēc tam funkcijas f(x) atvasinājums punktā x 0 ir funkcijas pieauguma un argumenta pieauguma attiecības robeža, kas to izraisīja, ja argumenta pieaugumam ir tendence uz nulli.

4 1. piemērs. Sniegsim piemērus dažu vienkāršāko elementāru funkciju atvasinājumu aprēķināšanai, pamatojoties uz atvasinājuma definīciju. y = a x (0 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 0.Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad">

0.Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņemiet x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R." title=" 5 3. piemērs. Ņemsim x 0 > 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņem x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad ( sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Piemērs 3. Ņem x 0 > 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņemiet x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R. 0.Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņemiet x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R."> 0. Pieņemot, ka | x 0 – patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņem x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R."> 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņemiet x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R." title=" 5 3. piemērs. Ņemsim x 0 > 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņem x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad ( sinx) = cosx, x R."> title="5 Piemērs 3. Ņem x 0 > 0. Pieņemot, ka | x | 0 ir patvaļīgs punkts, tad 4. piemērs. y = sinx, x R. Ņemiet x 0 R un aprēķiniet funkcijas pieaugumu šajā punktā: Tātad (sinx) = cosx, x R."> !}

6. TEORĒMA. Ja funkcija f(x) ir diferencējama punktā x 0, tad tā šajā punktā ir nepārtraukta. Pierādījums. Ļaujiet pastāvēt Tad no šejienes mēs iegūstam, ka f (x) – f (x 0) = f "(x 0) (x - x 0) + (x - x 0) α(x) x x 0. Tas ir, f(x) ir nepārtraukts punktā x 0. Diferencējamās funkcijas nepārtrauktība (1)

7 PIEZĪME. Funkcijas nepārtrauktība punktā nav pietiekams nosacījums atvasinājuma pastāvēšanai šajā punktā. Piemērs 5. f(x) = x. Izpētīsim f (x) uzvedību x 0 = 0 tuvumā. Šeit f (x) f (0) = 0 pie x 0. Tas ir funkcija ir nepārtraukta punktā x 0 = 0. Apsveriet x y 0 Robeža nepastāv, jo Tātad funkcijai f (x) = x nav atvasinājuma punktā x = 0, lai gan tā ir nepārtraukta šajā punktā. punktu

8 Piemērs x y 0 pie x 0. pie x 0. Tas ir f(x) ir nepārtraukts punktā x = 0. Tas ir, f(x) nav atvasinājuma punktā x = 0, un tāpēc tas nav diferencējams šajā punktā. Izpētīsim f (x) uzvedību punkta x = 0 tuvumā.

9 Lai funkcija y = f(x) ir diferencējama punktā x 0. Tad saskaņā ar (1) tās pieaugumu punktā x 0 var uzrakstīt kā y = f(x 0 + x) – f(x) 0) = f ( x 0) x + o (x) pie x. Funkcijas diferenciālis f (x 0) x ir galvenā lineārā attiecība pret x funkcijas y = f(x) pieauguma daļu punktā x 0, ko sauc par funkcijas diferenciāli punktā x 0 ar palielinās x un tiek apzīmēts ar df(x 0 ; x) vai df(x 0 ) vai df vai dу. y = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) pie x. DEFINĪCIJA. Pieauguma galvenā daļa, lineāra attiecībā pret x. Bezgalīgi mazs skaitlis, kas ir augstāks par x. Tagad funkcijas pieaugumu var uzrakstīt šādi:

10 PIEZĪME. Pieaugums x bieži tiek apzīmēts ar simbolu dx un tiek saukts par neatkarīgā mainīgā diferenciāli. Tādējādi funkcijas diferenciāli punktā x 0 var uzrakstīt formā df(x 0) = f "(x 0) dx. Ja funkcija ir diferencējama katrā noteikta intervāla punktā, tad tās diferenciālis dy ir x un dx funkcija: dy = f "(x)dx. No šejienes jo īpaši iegūstam atvasinājuma izteiksmi, proti, atvasinājumu var uzskatīt par funkcijas diferenciāļa attiecību pret neatkarīgā mainīgā diferenciāli.

11 Atvasinātā un diferenciāļa ģeometriskā nozīme Funkcijas y = f(x) definēšana U(x 0) un diferencējama punktā x 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L – sekants L 0 – tangenss x y = f(x 0 + x) – f(x 0) pie x funkcijas nepārtrauktības dēļ. Funkcijas y = f(x) grafika pieskare punktā M 0 ir sekanta L ierobežojošais stāvoklis punktā x. y Ja funkcija ir diferencējama punktā x 0, tad sekantajā vienādojumā y/ x f (x 0) pie x un pieskares vienādojumam ir forma y = y 0 + f (x 0) (x – x 0).

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) pie x 0 L0L0 tg = f (x 0) Ja y/ x priekš x, tad taisne x = x 0, kas izriet no sekanta vienādojuma, tiek saukta par funkcijas grafika vertikālo tangensu punktā M 0. No pieskares vienādojuma iegūstam y – y 0 = f (x 0) (x – x 0) = df (x 0) – pieskares ordinātu pieaugumu, pārejot no punkta x 0 uz punktu x. Funkcijas grafika normāls punktā M 0 ir taisne, kas ir perpendikulāra pieskarei, kas iet caur punktu M 0. Tā vienādojuma forma ir y = y 0 – 1/f (x 0) (x – x 0). L 1 – normāli

13 Atvasinājuma un diferenciāļa fizikālie pielietojumi Ja S(t) ir ceļš, ko nobrauc materiāls punkts laikā t, tad S "(t) ir materiāla punkta momentānais ātrums, un dS = S "(t)dt ir attālums, ko materiālais punkts nobrauktu laika periodā no t līdz t + dt, ja tas kustētos ar ātrumu, kas vienāds ar momentāno ātrumu brīdī t. Ja Q(t) ir elektroenerģijas daudzums, kas plūst caur vadītāja šķērsgriezumu laikā t, tad Q "(t) = I ir strāvas stiprums. Ja N(t) ir vielas daudzums, kas veidojas laikā t laikā ķīmiska reakcija, tad N "(t) – ķīmiskās reakcijas ātrums.

Ja funkcija y = f(x) kādā brīdī ir atšķirīgs x = x 0, tad šajā punktā tas ir nepārtraukts.

Tādējādi funkcijai nevar būt atvasinājums pārtraukuma punktos. Pretējs secinājums ir nepareizs, t.i. no tā, ka kādā brīdī x = x 0 funkcija y = f(x) ir nepārtraukts, nenozīmē, ka tas šajā brīdī ir diferencējams. Piemēram, funkcija y = |x| nepārtraukts visiem x (–< X < ), но в точке x= 0 nav atvasinājuma. Šajā brīdī grafikam nav pieskares. Ir labā pieskare un kreisā tangensa, taču tās nesakrīt.

21 Noteikumu atrašana ražošanu summas

1. noteikums. Ja funkcijām y = f(x) un y = g(x) ir atvasinājums punktā x, tad to summai ir arī atvasinājums punktā x, un summas atvasinājums ir vienāds ar atvasinājumu summu:
(f(x) + 8(x))" =f (x)+ (x).
Praksē šis noteikums ir formulēts īsāk: summas atvasinājums ir vienāds ar tās atvasinājumu summu.
Piemēram,
2. noteikums. Ja funkcijai y = f(x) ir atvasinājums punktā x, tad funkcijai y = kf(x) ir arī atvasinājums punktā x, un:

Praksē šis noteikums ir formulēts īsāk: konstanto koeficientu var izņemt no atvasinājuma zīmes. Piemēram,

3. noteikums. Ja funkcijām y=f(x) un y =g(x) ir atvasinājums punktā x, tad arī to reizinājumam ir atvasinājums punktā x, un:

Praksē šis noteikums tiek formulēts šādi: divu funkciju reizinājuma atvasinājums ir vienāds ar abu vārdu summu. Pirmais termins ir pirmās funkcijas un otrās funkcijas atvasinājuma reizinājums, bet otrais termins ir pirmās funkcijas un otrās funkcijas atvasinājuma reizinājums.
Piemēram:
4. noteikums. Ja funkcijām y = f(x) un y=g(x) ir atvasinājums, tad koeficientam ir atvasinājums punktā x, un:

Sarežģītu atvasinājumu tabula

22 Dif. funkcionāls punktā

Funkcija y=f(x) tiek uzskatīts par diferencējamu punktā x 0, ja tā pieaugums ir Δ y(x 0,Δ x) var attēlot kā

Δ y(x 0,Δ x)=AΔ x+o(Δ x).

Galvenā lineārā daļa AΔ x soli Δ y sauc par šīs funkcijas diferenciāli punktā x 0, kas atbilst pieaugumam Δ x, un to apzīmē ar simbolu dy(x 0,Δ x).

Lai funkcija y=f(x) tajā brīdī bija atšķirīgs x 0, tas ir nepieciešams un pietiekams, lai atvasinājums pastāvētu f′( x 0), un vienlīdzība ir patiesa A=f′( x 0).

Diferenciāļa izteiksmei ir forma

dy(x 0,dx)=f′( x 0)dx,

Kur dx=Δ x.

23 Prod. Komplekss Funkcija

Sarežģītas funkcijas atvasinājums. Parametriski norādītas funkcijas atvasinājums

Ļaujiet y - sarežģīta funkcija x, t.i. y = f(u), u = g(x), vai

Ja g(x) Un f(u) – to argumentu diferencējamās funkcijas, attiecīgi, punktos x Un u = g(x), tad arī kompleksā funkcija ir diferencējama punktā x un tiek atrasts pēc formulas

Parametriski dotas funkcijas atvasinājums.

24 Prod. un diferenc. Augstākais pasūtījums

Tagad ļaujiet th kārtas atvasinājumu definēt noteiktā punkta apkārtnē un būt diferencējamam. Tad

Ja funkcijai ir daļējs atvasinājums attiecībā uz kādu no mainīgajiem kādā domēnā D, tad minētajam atvasinājumam, kas pats par sevi ir funkcija, var būt daļēji atvasinājumi attiecībā uz to pašu vai jebkuru citu mainīgo kādā brīdī. Sākotnējai funkcijai šie atvasinājumi būs otrās kārtas daļēji atvasinājumi (vai otrie daļējie atvasinājumi).

Otrās vai augstākas kārtas daļēju atvasinājumu, kas ņemts attiecībā uz dažādiem mainīgajiem, sauc par jauktu daļēju atvasinājumu. Piemēram,

Pasūtījuma diferenciālis n, Kur n > 1, funkcijas kādā brīdī sauc par diferenciāli šajā secības diferenciāļa punktā (n - 1), tas ir

Funkcijai, kas ir atkarīga no viena mainīgā, otrais un trešais diferenciālis izskatās šādi:

No šejienes mēs varam iegūt vispārīgu priekšstatu par diferenciāli n pasūtījums no funkcijas:

25 Fermata, Rolle, Langrange teorēmas

v Fermā teorēma:Ļaujiet funkcijai tikt definētai un sasniegt tās maksimālās un minimālās vērtības ( M Un m) dažās no . Ja ir atvasinājums, tad tas noteikti ir vienāds ar 0.

Pierādījums: pastāv. Ir divi iespējamie gadījumi:

1) , => , => .

2) , => , => .

No 1) un 2) izriet, ka

v Rolle teorēma (par atvasinājuma saknēm):Ļaujiet funkcijai būt nepārtrauktai ieslēgtai un diferencējamai, un segmenta galos ņemt tās pašas vērtības: . Tad ir vismaz viens punkts no , atvasinājums, kurā .

v Pierādījums: nepārtraukta stiepšanās ieslēgta M Un m. Tad ir iespējami divi gadījumi:

2) lielākā vērtība tiek sasniegta intervālā saskaņā ar Fermā teorēmu.

v Langdžera teorēma (par pēdējiem soļiem):Ļaujiet funkcijai būt nepārtrauktai ieslēgtai un diferencētai ieslēgtai . Tad ir vismaz viens no , kuram ir spēkā šāda vienādība: .

Pierādījums: Ieviesīsim funkciju . (nepārtraukta ieslēgta un diferencējama ).

Funkcija apmierina Rolle teorēmu, kurai: , , , .

· funkcija tiek izsaukta stingri pieaugot uz ja

· funkcija tiek izsaukta samazinās uz ja

· funkcija tiek izsaukta stingri samazinās uz ja

Definīcija: Funkcijas atvasinājums punktā ir robeža, līdz kurai tiecas tās pieauguma attiecība šajā punktā pret atbilstošo argumenta pieaugumu, kad pēdējam ir tendence uz nulli:

Tas ir, ja definēts, tad

1. teorēma:

Funkcijas grafikam ir nevertikāls tangenss tad un tikai tad, ja dotajā punktā ir šīs funkcijas atvasinājuma galīgā vērtība.

Pierādījums:

Tad lai ir vērtība f’()-galīgs

Lai ir nevertikāla tangensa => ir galīga.

Sekants tiecas uz tangensu.

Teorēma ir pierādīta.

2. biļete Funkcijas ar atvasinājumu nepārtrauktība.

Funkciju f (x), kas definēta kādā punkta a apkārtnē, šajā punktā sauc par nepārtrauktu if

Teorēma: (nepieciešams nosacījums atvasinājuma pastāvēšanai)

Ja funkcija punktā ir ierobežota, tā punktā nav nepārtraukta.

Pierādījums:

Tāpēc tas ir nepārtraukts punktā.

Teorēma ir pierādīta.

komentēt : apgrieztais apgalvojums nav patiess; ja funkcija ir nepārtraukta punktā, tad no tā neizriet, ka tai šajā punktā ir atvasinājums.

Paziņojums, apgalvojums : Ja funkcijai kādā punktā ir labās un kreisās puses atvasinājumi, tad tā ir nepārtraukta gan labajā, gan kreisajā pusē.

3. biļete

Summas, reizinājuma, koeficienta atvasinājums.

Apgrieztās funkcijas atvasinājums.

Diferencējamas funkcijas definīcija. Nepieciešams un pietiekams nosacījums diferencējamībai.

Lai funkcijai ir atvasinājums punktā (galīgs): .

Tad pietiekami maziem to varam uzrakstīt kā summu un kādu funkciju, ar kuru apzīmējam, kura mēdz uz nulli kopā ar:,

un pieaugumu punktā var uzrakstīt šādi:

vai (1) ,

galu galā izteiksme tiek saprasta kā tāda funkcija, ka tās attiecībai ir tendence uz nulli kopā ar.

Paskaidrojums:

Definīcija .

Tiek uzskatīts, ka funkcija ir diferencējama punktā, ja tās pieaugumu var attēlot kā: (2),

kur A nav atkarīgs no, bet kopumā ir atkarīgs no.

1. teorēma:

Lai funkcija kādā punktā būtu diferencējama, ir nepieciešams un pietiekami, ka tai šajā punktā ir ierobežots atvasinājums.

Pierādījums:

Nosacījuma pietiekamība tika pierādīts iepriekš: no galīga atvasinājuma esamības izrietēja iespēja attēlot formā (1), kur mēs varam ievietot.

Nepieciešamības nosacījums . Lai funkcija ir diferencējama punktā. Tad no (2), pieņemot, mēs iegūstam.

Labās puses robeža pie pastāv un ir vienāda ar A:.

Tas nozīmē, ka ir atvasinājums. Teorēma ir pierādīta.

6. biļete Funkcijas diferenciālis, tā ģeometriskā nozīme.

Ja funkcija f ir atvasinājums f΄(x o ) punktā x o, tad ir robeža, kur Δ f=f(x o + Δ x)-f(x o ) ,, vai, kur A=f΄(x o ) .

Definīcija:

Funkcija f punktā x o, ja tā pieaugumu var attēlot kā:

Kur AΔ x=df. (*)

Diferenciālis ir funkcijas pieauguma galvenā lineārā daļa.

Ja ir galīgs atvasinājums f΄(x o ) punktā x o, tad funkcija f(x)šajā brīdī ir atšķirīgs.

Ir arī otrādi: ja funkcija f punktā x o, t.i. tā pieaugumu var attēlot formā (*), tad tam ir atvasinājums punktā x o, vienāds ar A:

Diferenciāļa ģeometriskā nozīme:

A Un B– grafika punkti f(x), kas atbilst vērtībām x o Un (x o + Δ x) neatkarīgais mainīgais. Punktu ordinātas A Un B attiecīgi vienādi f(x o ) Un f(x o + Δ x). Funkcijas pieaugums Δ f=f(x o + Δ x)-f(x o ) punktā x o vienāds ar segmenta garumu BD un to var attēlot kā summu Δ f=BD=DC+CB, Kur DC=tgαΔ x=f΄(x o ) Δ x Un α ir leņķis starp pieskari punktā A uz grafiku un ass pozitīvo virzienu x. No tā ir skaidrs, ka DC ir diferenciāla funkcija f punktā x o :

DC=df=f΄(x o ) Δ x.

Tajā pašā laikā otrā dalībnieka daļa CB soli Δ fņemt vērā vērtību. Šī vērtība pie lielas Δ x, varbūt pat lielāks par galveno terminu, bet tas ir bezgalīgi mazs, kas ir augstāks par Δ x, kad Δ x→0.

INTERVIJAS NEPAREDZĒTO FUNKCIJU ĪPAŠĪBAS

Apskatīsim dažas intervālā nepārtrauktu funkciju īpašības. Mēs piedāvājam šīs īpašības bez pierādījumiem.

Funkcija y = f(x) sauca nepārtraukti segmentā [a, b], ja tas ir nepārtraukts visos šī posma iekšējos punktos, un tā galos, t.i. punktos a Un b, ir nepārtraukts attiecīgi labajā un kreisajā pusē.

1. teorēma. Funkcija, kas nepārtraukta intervālā [ a, b], vismaz vienā šī segmenta punktā ir vislielākā vērtība un vismaz vienā punktā ir mazākā vērtība.

Teorēma nosaka, ka, ja funkcija y = f(x) ir nepārtraukts intervālā [ a, b], tad ir vismaz viens punkts x 1 Î [ a, b] tā, lai funkcijas vērtība f(x)šajā brīdī būs lielākā no visām tā vērtībām šajā segmentā: f(x 1) ≥ f(x). Līdzīgi ir šāds punkts x2, kurā funkcijas vērtība būs mazākā no visām segmenta vērtībām: f(x 1) ≤ f(x).

Ir skaidrs, ka šādi punkti var būt vairāki, piemēram, attēlā redzams, ka funkcija f(x)ņem mazāko vērtību divos punktos x2 Un x 2 ".

komentēt. Teorēmas apgalvojums var kļūt nepareizs, ja ņemam vērā funkcijas vērtību intervālā ( a, b). Patiešām, ja ņemam vērā funkciju y = x uz (0, 2), tad tas ir nepārtraukts šajā intervālā, bet nesasniedz ne lielākās, ne mazākās vērtības tajā: ​​tas sasniedz šīs vērtības intervāla galos, bet gali nepieder uz mūsu domēnu.

Arī teorēma vairs nav patiesa attiecībā uz pārtrauktām funkcijām. Sniedziet piemēru.

Sekas. Ja funkcija f(x) ir nepārtraukts [ a, b], tad šajā segmentā tas ir ierobežots.

2. teorēma.Ļaujiet funkcijai y = f(x) ir nepārtraukts intervālā [ a, b] un šī segmenta beigās ņem dažādu zīmju vērtības, tad segmenta iekšpusē ir vismaz viens punkts x = C, kurā funkcija iet uz nulli: f(C)= 0, kur a< C< b

Šai teorēmai ir vienkārša ģeometriskā nozīme: ja nepārtrauktas funkcijas grafika punkti y = f(x), kas atbilst segmenta galiem [ a, b] atrodas pretējās ass pusēs Vērsis, tad šis grafiks krustojas ar asi vismaz vienā segmenta punktā Vērsis. Nepārtrauktām funkcijām šī īpašība var nebūt.

Šī teorēma pieļauj šādu vispārinājumu.

3. teorēma (starpvērtību teorēma).Ļaujiet funkcijai y = f(x) ir nepārtraukts intervālā [ a, b] Un f(a) = A, f(b) = B. Tad jebkuram skaitlim C, noslēgts starp A Un B, šajā segmentā ir šāds punkts CÎ [ a, b], Kas f(c) = C.

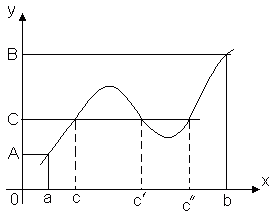
Šī teorēma ir ģeometriski acīmredzama. Apsveriet funkcijas grafiku y = f(x). Ļaujiet f(a) = A, f(b) = B. Tad jebkura taisna līnija y = C, Kur C– jebkurš skaitlis starp A Un B, vismaz vienā punktā krustos funkcijas grafiku. Šī vērtība būs krustpunkta abscisa x = C, kurā f(c) = C.

Tādējādi nepārtraukta funkcija, pārejot no vienas vērtības uz otru, obligāti iet cauri visām starpvērtībām. It īpaši:

Sekas. Ja funkcija y = f(x) ir nepārtraukts noteiktā intervālā un ņem lielāko un mazāko vērtību, tad šajā intervālā vismaz vienu reizi tiek ņemta jebkura vērtība, kas atrodas starp tās mazāko un lielāko vērtību.

ATVASINĀJUMS UN TĀ PIELIETOJUMS. ATvasinājuma DEFINĪCIJA

Ļaujiet mums veikt dažas funkcijas y=f(x), definēts kādā intervālā. Katrai argumenta vērtībai x no šī intervāla funkcija y=f(x) ir noteikta nozīme.

Apsveriet divas argumentu vērtības: sākotnējo x 0 un jauns x.

Atšķirība x–x 0 sauc palielinot argumentu x punktā x 0 un tiek apzīmēts Δx. Tādējādi Δx = x – x 0 (argumenta pieaugums var būt pozitīvs vai negatīvs). No šīs vienlīdzības izriet, ka x=x 0 +Δx, t.i. mainīgā sākotnējā vērtība ir saņēmusi zināmu pieaugumu. Tad, ja punktā x 0 funkcijas vērtība bija f(x 0 ), tad jaunā punktā x funkcija uzņems vērtību f(x) = f(x 0 +Δx).

Atšķirība y–y 0 = f(x) – f(x 0 ) sauca funkcijas pieaugums y = f(x) punktā x 0 un tiek apzīmēts ar simbolu Δy. Tādējādi

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Parasti argumenta sākotnējā vērtība x 0 tiek uzskatīts par fiksētu, un jaunā vērtība x- mainīgs. Tad y 0 = f(x 0 ) izrādās nemainīgs, un y = f(x)- mainīgs. Pieaugumi Δy Un Δx būs arī mainīgie un formula (1) to parāda Dy ir mainīgā funkcija Δx.

Izveidosim funkcijas pieauguma attiecību pret argumenta pieaugumu

Ļaujiet mums atrast šīs attiecības robežu pie Δx→0. Ja šī robeža pastāv, tad to sauc par šīs funkcijas atvasinājumu f(x) punktā x 0 un apzīmē f "(x 0). Tātad,

Atvasinājumsšī funkcija y = f(x) punktā x 0 sauc par funkcijas pieauguma koeficienta Δ robežu y līdz argumenta pieaugumam Δ x, kad pēdējais patvaļīgi tiecas uz nulli.

Ņemiet vērā, ka vienai un tai pašai funkcijai atvasinājums dažādos punktos x var pieņemt dažādas vērtības, t.i. atvasinājumu var uzskatīt par argumenta funkciju x. Šī funkcija ir norādīta f "(x)

Atvasinājumu apzīmē ar simboliem f "(x),y", . Atvasinājuma īpašā vērtība pie x = a apzīmē ar f "(a) vai y "| x=a.

Funkcijas atvasinājuma atrašanas operācija f(x) sauc par šīs funkcijas diferenciāciju.

Lai tieši atrastu atvasinājumu pēc definīcijas, varat izmantot šo: īkšķa noteikums:

Piemēri.

ATvasinājuma MEHĀNISKĀ SAJŪTA

No fizikas ir zināms, ka vienmērīgas kustības likumam ir forma s = v t, Kur s– ceļš, kas ceļojis uz laika brīdi t, v– vienmērīgas kustības ātrums.

Tomēr, jo Lielākā daļa dabā notiekošo kustību ir nevienmērīgas, tad kopumā ātrums un līdz ar to arī attālums s būs atkarīgs no laika t, t.i. būs laika funkcija.

Tātad, ļaujiet materiālam punktam pārvietoties taisnā līnijā vienā virzienā saskaņā ar likumu s=s(t).

Atzīmēsim noteiktu laiku t 0 . Šajā brīdī punkts ir šķērsojis ceļu s=s(t 0 ). Noteiksim ātrumu v materiālais punkts konkrētajā brīdī t 0 .

Lai to izdarītu, aplūkosim kādu citu laika momentu t 0 + Δ t. Tas atbilst nobrauktajam ceļam s =s(t 0 + Δ t). Pēc tam noteiktā laika periodā Δ t punkts ir nogājis ceļu Δs =s(t 0 + Δ t)–s(t).

Padomāsim par attieksmi. To sauc par vidējo ātrumu laika intervālā Δ t. Vidējais ātrums šobrīd nevar precīzi raksturot punkta kustības ātrumu t 0 (jo kustība ir nevienmērīga). Lai precīzāk izteiktu šo patieso ātrumu, izmantojot vidējo ātrumu, ir nepieciešams īsāks laika periods Δ t.

Tātad kustības ātrums noteiktā laika momentā t 0 (momentānais ātrums) ir vidējā ātruma robeža intervālā no t 0 līdz t 0 +Δ t, kad Δ t→0:

,

tie. nevienmērīgs ātrums tas ir nobrauktā attāluma atvasinājums attiecībā pret laiku.

ATvasinājuma ĢEOMETRISKĀ NOZĪME

Vispirms ieviesīsim līknes pieskares definīciju noteiktā punktā.

Ļaujiet mums izveidot līkni un fiksētu punktu uz tās M 0(skat. attēlu) Apsveriet citu punktu Mšo līkni un uzzīmējiet sekantu M 0 M. Ja punkts M sāk kustēties pa līkni, un punkts M 0 paliek nekustīgs, tad sekants maina savu pozīciju. Ja, ar neierobežotu punkta tuvinājumu M pa līkni līdz punktam M 0 jebkurā pusē sekants mēdz ieņemt noteiktas taisnes pozīciju M 0 T, tad taisni M 0 T sauc par līknes pieskari noteiktā punktā M 0.

Tas., pieskares uz līkni noteiktā punktā M 0 sauc par sekanta limita pozīciju M 0 M kad punkts M tiecas gar līkni uz punktu M 0.

Tagad apskatīsim nepārtraukto funkciju y=f(x) un šai funkcijai atbilstošo līkni. Par kādu vērtību X 0 funkcija iegūst vērtību y 0 = f(x 0).Šīs vērtības x 0 un y 0 uz līknes atbilst punktam M 0 (x 0 ; y 0). Sniegsim argumentu x 0 pieaugums Δ X. Argumenta jaunā vērtība atbilst palielinātajai funkcijas vērtībai y 0 +Δ y=f(x 0 –Δ x). Mēs saprotam būtību M(x 0+Δ x; g 0+Δ y). Uzzīmēsim sekantu M 0 M un apzīmē ar φ leņķi, ko veido sekants ar ass pozitīvo virzienu Vērsis. Izveidosim attiecības un atzīmēsim, ka .

Ja tagad Δ x→0, tad funkcijas Δ nepārtrauktības dēļ plkst→0, un tāpēc punkts M, virzoties pa līkumu, tuvojas punktam bez ierobežojumiem M 0. Pēc tam sekants M 0 M punktā ir tendence ieņemt līknes pieskares pozīciju M 0, un leņķis φ→α pie Δ x→0, kur α apzīmē leņķi starp pieskari un ass pozitīvo virzienu Vērsis. Tā kā funkcija tan φ nepārtraukti ir atkarīga no φ pie φ≠π/2, tad φ→α tan φ → tan α un līdz ar to pieskares slīpums būs:

tie. f "(x)= tg α .

Tādējādi ģeometriski y "(x 0) apzīmē šīs funkcijas grafika pieskares slīpumu punktā x 0, t.i. noteiktai argumenta vērtībai x, atvasinājums ir vienāds ar leņķa tangensu, ko veido pieskares funkcijas grafikam f(x) attiecīgajā punktā M 0 (x; y) ar pozitīvu ass virzienu Vērsis.

Piemērs. Atrodiet līknes pieskares slīpumu y = x 2 punktā M(-1; 1).

Mēs jau esam redzējuši, ka ( x 2)" = 2X. Bet līknes pieskares leņķiskais koeficients ir tan α = y"| x=-1 = – 2.

FUNKCIJU DIFERENCIĀCĪBA. ATŠĶIRĪMAS FUNKCIJAS NEPIRKŠANĀS

Funkcija y=f(x) sauca diferencējams kādā brīdī x 0, ja tam šajā punktā ir noteikts atvasinājums, t.i. ja attiecību robeža pastāv un ir ierobežota.

Ja funkcija ir diferencējama katrā noteikta segmenta punktā [ A; b] vai intervāls ( A; b), tad viņi saka, ka viņa diferencējams segmentā [ A; b] vai attiecīgi intervālā ( A; b).

Ir spēkā sekojošā teorēma, kas nosaka saikni starp diferencējamām un nepārtrauktām funkcijām.

Teorēma. Ja funkcija y=f(x) kādā brīdī atšķirties x 0, tad šajā brīdī tas ir nepārtraukts.

Tādējādi no funkcijas diferencējamības izriet tās nepārtrauktība.

Pierādījums. Ja , Tas

,

kur α ir bezgalīgi mazs lielums, t.i. lielums, kas tiecas uz nulli kā Δ x→0. Bet tad

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 pie Δ x→0, t.i. f(x) – f(x 0)→0 plkst x→x 0 , kas nozīmē, ka funkcija f(x) nepārtraukti kādā punktā x 0 . Q.E.D.

Tādējādi funkcijai nevar būt atvasinājums pārtraukuma punktos. Pretēji tam nav taisnība: pastāv nepārtrauktas funkcijas, kuras dažos punktos nav diferencējamas (tas ir, šajos punktos nav atvasinājuma).

Apsveriet punktus attēlā a, b, c.

Punktā a pie Δ x→0 attiecībai nav ierobežojumu (jo vienpusējās robežas ir atšķirīgas Δ x→0–0 un Δ x→0+0). Punktā A grafikā nav noteiktas pieskares, bet ir divas dažādas vienvirziena pieskares ar slīpumiem Uz 1 un Uz 2. Šāda veida punktu sauc par stūra punktu.

Punktā b pie Δ x Attiecība →0 ir nemainīga zīme bezgalīgi liels daudzums. Funkcijai ir bezgalīgs atvasinājums. Šajā brīdī grafikam ir vertikāla pieskare. Punkta tips – vertikālās pieskares “locījuma punkts”.

Punktā c vienpusēji atvasinājumi ir bezgala liels dažādu zīmju daudzums. Šajā brīdī grafikā ir divas apvienotas vertikālās pieskares. Tips - "atgriešanās punkts" ar vertikālu pieskari - īpašs stūra punkta gadījums.